Abstract
Flow-enhanced cell adhesion is a counterintuitive phenomenon that has been observed in several biological systems. Flow augments L-selectin-dependent adhesion by increasing the initial tethering of leukocytes to vascular surfaces and by strengthening their subsequent rolling interactions. Tethering or rolling might be influenced by physical factors that affect the formation or dissociation of selectin-ligand bonds. We recently demonstrated that flow enhanced rolling of L-selectin-bearing microspheres or neutrophils on P-selectin glycoprotein ligand-1 by force decreased bond dissociation. Here, we show that flow augmented tethering of these microspheres or cells to P-selectin glycoprotein ligand-1 by three transport mechanisms that increased bond formation: sliding of the sphere bottom on the surface, Brownian motion, and molecular diffusion. These results elucidate the mechanisms for flow-enhanced tethering through L-selectin.
INTRODUCTION
Interactions of selectins with cell-surface glycoconjugates mediate leukocyte tethering to and rolling on vascular surfaces during lymphocyte homing or leukocyte trafficking at sites of inflammation and injury (1–3). L-selectin is expressed on leukocytes, whereas P-selectin and E-selectin are expressed on activated platelets and/or endothelial cells. The leukocyte mucin P-selectin glycoprotein ligand-1 (PSGL-1) binds to all three selectins (2,3).
Cell tethering and rolling occur in a hydrodynamic environment. Paradoxically, flow can enhance selectin-mediated cell adhesion (4–6). As flow increases, more cells tether and the cells roll more slowly, which sharply increases the number of rollingly adherent cells despite higher dislodging forces, until an optimal flow level is achieved. The flow requirement for L-selectin to support adhesion is particularly striking and may prevent inappropriate leukocyte aggregation. Other cell adhesion systems also exhibit flow enhancement. Platelets require arterial flow rates to adhere to von Willebrand factor on damaged vascular surfaces (7,8). Many enteric bacteria require a minimum flow to adhere to intestinal epithelia, which likely prevents pathological attachments to bladder mucosa and other tissues during stasis (9). Flow-enhanced adhesion may therefore be a biologically important process for many cells.
Rolling requires a balance between the formation of new selectin-ligand bonds at the front edge of the cell and the dissociation of preexisting bonds at the rear edge. Force applied to the bonds influences the off-rates of their dissociation. Bonds that shorten their lifetimes in response to force are known as slip bonds. Bonds that prolong their lifetimes in response to force are known as catch bonds (10,11). The counterintuitive catch bonds cause the counterintuitive flow-enhanced rolling of L-selectin-bearing microspheres or neutrophils on PSGL-1 (12). Catch bonds enable increasing force to convert short-lived adhesive interactions into longer-lived interactions, which decrease rolling velocities and increase the regularity of rolling steps as shear rises from the threshold to an optimal value. Above the optimum, transitions to slip bonds shorten rolling-step lifetimes, which increase rolling velocities and decrease rolling regularity (12).
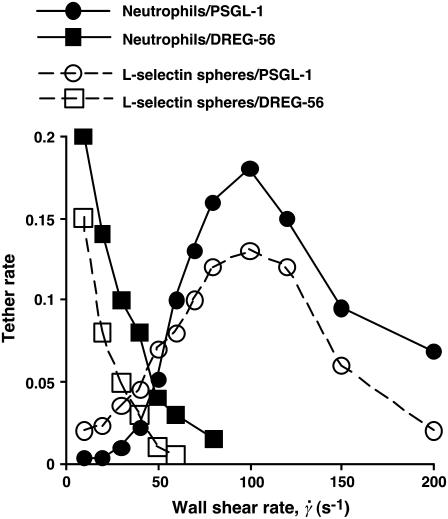
However, flow-enhanced adhesion also involves changes in the tethering of free-flowing cells. As the wall shear rate increases, the tether rate (TR) initially increases, reaches a maximum at an optimal shear, and then decreases, as shown in Fig. 1 and as described previously for leukocyte tethering to selectins or selectin ligands (4–6) and for platelet tethering to von Willebrand factor (8). The curves shown in Fig. 1 are determined primarily by the interacting molecules, as both L-selectin-bearing rigid microspheres and L-selectin-expressing cells exhibited similar tethering profiles on the same ligand. Flow increased L-selectin tethering to PSGL-1 but not to an anti-L-selectin monoclonal antibody (mAb), demonstrating its specificity (Fig. 1).
FIGURE 1.
Flow enhances tethering to an L-selectin ligand but not to an antibody. Neutrophils or L-selectin-bearing microspheres (3-μm radius) were perfused over immobilized PSGL-1 or anti-L-selectin mAb DREG-56 at various wall shear rates. The tethering rate was measured and normalized for cell or microsphere delivery.
If the tethering assay can detect the weakest and briefest bonds formed, flow-enhanced tethering cannot be explained solely by force-dependent decreases in bond dissociation. Flow may impose transport conditions that affect formation of bonds between receptors on the moving cells and ligands on the vessel wall. Mechanisms for flow-enhanced bond formation have been postulated (4,13–15), but they have not been thoroughly and rigorously tested.
Here, we measured the effects of multiple transport and force parameters on tethering of L-selectin-bearing microspheres or neutrophils to PSGL-1 below and above the flow optimum. Our results demonstrate that three distinct transport mechanisms enhance cell tethering through L-selectin at threshold shear.
MATERIALS AND METHODS
Proteins and cells
The following proteins have been described: L-selectin-Ig containing the lectin domain, epithelial growth factor domain, and both consensus repeats of human L-selectin fused to the Fc moiety of human IgG (11), soluble recombinant human PSGL-1 (16), and anti-human PSGL-1 mAb PL1 (16). Anti-human IgG Fc polyclonal antibody was from Chemicon International (Temecula, CA). Anti-human L-selectin mAb DREG-56 was purified from hybridoma cells from the American Type Culture Collection (Manassas, VA). Human neutrophils were isolated as described (17).
Coupling of L-selectin-Ig to microspheres and PSGL-1 to flow chambers
Polystyrene microspheres of 1-, 2.25-, or 3-μm radius (Polysciences, Warrington, PA) were adsorbed with anti-human IgG Fc antibody in 500 μl Hanks' balanced salt solution (HBSS), blocked with HBSS containing 1% human serum albumin (HSA), and incubated with L-selectin-Ig. Microspheres were stored at 4°C in phosphate-buffered saline containing 0.1% sodium azide for up to 5 days. The density of L-selectin remained constant during this period, which was maintained for all studies. An L-selectin site density of 250 sites/μm2 was calculated for neutrophils by dividing 57,000 ± 7000 molecules (N = 3, measured by binding of 125I-labeled DREG-56 (16)) by the area of a smooth sphere of 4.25-μm radius (which underrepresents the surface area of neutrophils with their many microvilli, and which has not taken into account the concentration of L-selectin on microvillus tips (18)). The L-selectin densities for microspheres, measured by flow cytometry with DREG-56, were 750 (3-μm radius), 980 (2.25-μm radius), and 2840 (1-μm radius), except for those indicated in the legend of Fig. 4. Biotinylated recombinant soluble PSGL-1 was captured on streptavidin (Pierce, Rockford, IL) adsorbed to flow-chamber floors. Site densities of PSGL-1 were determined by binding of 125I-labeled PL1 (16). DREG-56 was directly adsorbed to flow-chamber floors.
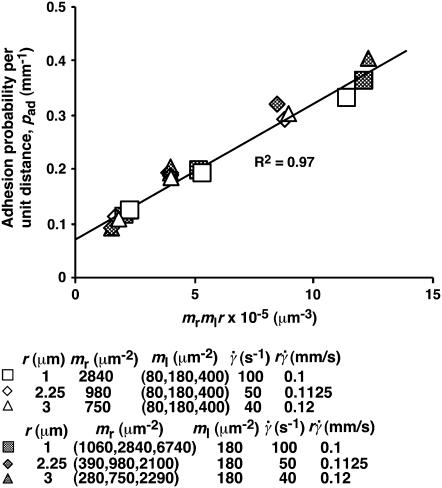
FIGURE 4.
Dependence of pad on receptors and ligands on the contact area. Rates of microspheres of indicated radii (r) bearing indicated L-selectin densities (mr) tethering to indicated PSGL-1 densities (ml) were measured at indicated shear rates (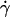 ) such that the
) such that the 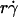 values were matched. The adhesion probability per distance, pad, was calculated from the TR data using Eq. 6 and plotted versus mlmrr. A straight line was fit to the data and the goodness of fit was indicated by the R2 value. Two sets of conditions were tested. In one set, ml was varied while the product mrr was kept constant, although different mr and r were used for different group of three ml levels (open symbols). In the other set, ml was kept constant whereas mr was varied for each of the three r levels (solid symbols).
values were matched. The adhesion probability per distance, pad, was calculated from the TR data using Eq. 6 and plotted versus mlmrr. A straight line was fit to the data and the goodness of fit was indicated by the R2 value. Two sets of conditions were tested. In one set, ml was varied while the product mrr was kept constant, although different mr and r were used for different group of three ml levels (open symbols). In the other set, ml was kept constant whereas mr was varied for each of the three r levels (solid symbols).
Flow assays
Microspheres or neutrophils (2 × 106/ml in HBSS containing 0.5% HSA) were perfused at various flow rates over PSGL-1 or DREG-56 in a parallel-plate flow chamber (16,17). To increase the viscosity in some experiments, 3%, 6%, or 10% (w/v) of Ficoll (400,000 molecular weight, Sigma Chemical, St. Louis, MO) were added to the media. The viscosities of the media were measured as 1.0, 1.8, 2.6, or 4.2 cP for 0, 3%, 6%, and 10% Ficoll, respectively, at room temperature in an Oswald dropping pipette viscometer (Fisher Scientific, Hampton, NH) (12).
Tether rates were measured by a previously described method (16,17), with some modifications. The flow chamber was placed on an inverted microscope such that the upstream end of the field of view was aligned with the demarcation line separating the HSA-coated surface (upstream to the field of view) and PSGL-1-coated surface (in the field of view) (cf. Fig. 2 B). Events of freely-flowing microspheres or neutrophils that tethered to PSGL-1 or DREG-56 for the first time were recorded at 250 or 500 frames/s (fps) by a FASTCAM-Super 10 K high-speed digital video camera (Photron, Narre Warren, Victoria, Australia) mounted on the microscope. Tethering events were identified by observing either the sudden stops directly from the videos played back in slow motion (30 fps) or the abrupt drops from the time courses of instantaneous velocity (cf. Fig. 3 A), which yielded comparable results. The instantaneous velocity was calculated from the frame-by-frame x and y coordinates of the mass center of each individual microsphere or neutrophil, determined using the tracking software Nanotrack (Isee program) (12). The tether rate was calculated by normalizing the number of observed tethering events in 1 min by the total number of cells flowing through the field of view in the same focal plane in the same period of time (19).
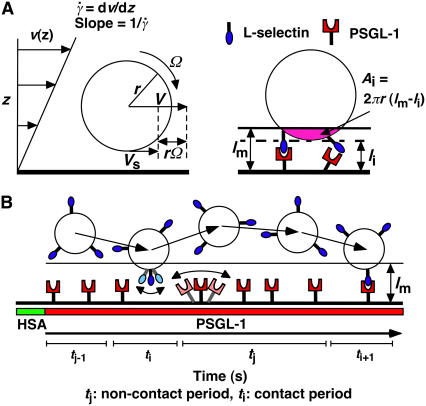
FIGURE 2.
Parameters of cell tethering under flow. (A) The fluid velocity v of a Couette flow field bordered with a solid surface (xy plane) is parallel to the surface and increases linearly with the distance from the surface (z direction). The shear rate 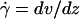 is reciprocal to the slope of the velocity profile. Fluid-mechanics theory predicts that the translational velocity V and angular velocity Ω of a sphere of radius r freely moving above a surface in an otherwise Couette flow are proportional to
is reciprocal to the slope of the velocity profile. Fluid-mechanics theory predicts that the translational velocity V and angular velocity Ω of a sphere of radius r freely moving above a surface in an otherwise Couette flow are proportional to 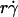 and
and 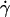 , respectively (29). The sphere bottom has a positive velocity Vs ≡ V – rΩ ∝
, respectively (29). The sphere bottom has a positive velocity Vs ≡ V – rΩ ∝ 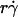 relative to the surface (13). The sphere and the surface are coated with receptors and ligands, respectively, whose combined length lm sets a contact threshold. When the gap distance li between the sphere bottom and the surface is <lm, the two are in contact with an area Ai = 2πr(lm − li). (B) Due to its small size, the sphere is susceptible to thermal excitations that cause Brownian motion. This produces fluctuations in velocity components parallel to the surface, which can be directly observed (cf. Fig. 3 A), as well as those perpendicular to the surface, which are depicted by the wavy trajectory of the sphere shown at five different times and positions. By randomly modulating the gap distance above and below the contact threshold z = lm (horizontal line), Brownian motion causes discontinuous contacts of different portions of the sphere with different portions of the surface, with alternating intervals of contact (ti) and noncontact (tj). A productive contact results in a tethering event, but many contacts are nonproductive. As schematically shown for one receptor and one ligand by the movements along the two-sided arrows (lighter colors), the binding sites of L-selectin and PSGL-1 can undergo rotational diffusion even though portions of the molecules are anchored to the respective sphere surface and chamber floor. To ensure that only first-time tethering events were observed, the chamber floor upstream to the microscope field of view was coated with HSA to allow measurement of the distance traveled by the sphere from the demarcation line to the location where tethering occurs. The cell, contact area, and molecular sizes are not drawn to scale.
relative to the surface (13). The sphere and the surface are coated with receptors and ligands, respectively, whose combined length lm sets a contact threshold. When the gap distance li between the sphere bottom and the surface is <lm, the two are in contact with an area Ai = 2πr(lm − li). (B) Due to its small size, the sphere is susceptible to thermal excitations that cause Brownian motion. This produces fluctuations in velocity components parallel to the surface, which can be directly observed (cf. Fig. 3 A), as well as those perpendicular to the surface, which are depicted by the wavy trajectory of the sphere shown at five different times and positions. By randomly modulating the gap distance above and below the contact threshold z = lm (horizontal line), Brownian motion causes discontinuous contacts of different portions of the sphere with different portions of the surface, with alternating intervals of contact (ti) and noncontact (tj). A productive contact results in a tethering event, but many contacts are nonproductive. As schematically shown for one receptor and one ligand by the movements along the two-sided arrows (lighter colors), the binding sites of L-selectin and PSGL-1 can undergo rotational diffusion even though portions of the molecules are anchored to the respective sphere surface and chamber floor. To ensure that only first-time tethering events were observed, the chamber floor upstream to the microscope field of view was coated with HSA to allow measurement of the distance traveled by the sphere from the demarcation line to the location where tethering occurs. The cell, contact area, and molecular sizes are not drawn to scale.
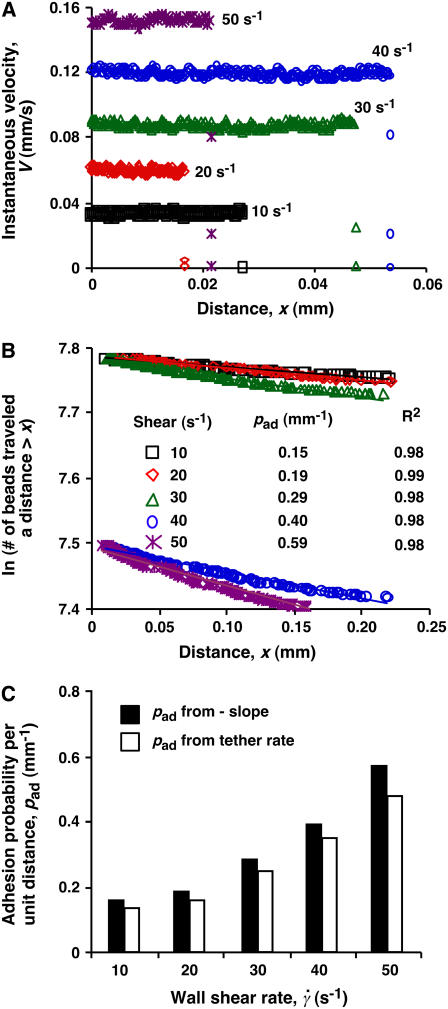
FIGURE 3.
Measurement of adhesion probability per unit distance. (A) Instantaneous velocities of 3-μm-radius microspheres bearing L-selectin flowing parallel to a surface coated with PSGL-1 were measured at 500 fps for five wall shear rates (indicated) as functions of distance. Shown are representative velocities with observed tethering events, which occurred randomly. Many more spheres did not tether in the field of view. (B) Data from a large number of such measurements were plotted as ln(number of microspheres traveling a distance ≥x) versus x curves. For each of the five wall shear rates (indicated) tested, the data were well fitted by a straight line (see the R2 values for the goodness of fit). The adhesion probability per unit distance (pad) was evaluated from the negative slope of the linear fit to the data. (C) Comparison of pad evaluated from the negative slopes (solid bars) and those calculated from the tether-rate data using Eq. 6 (open bars).
In some experiments, microspheres or neutrophils were perfused in media containing 20 μg/ml DREG-56 or PL1 or 10 mM EDTA. All tethering events were specific, because they were eliminated by inclusion of mAb or EDTA in the media.
MODEL DEVELOPMENT
We have previously developed a mathematical model for the adhesion probability Pa in terms of the contact time tc and area Ac, as well as the site densities of receptors mr and ligand ml (20):
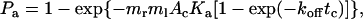 |
(1) |
where Ka is the binding affinity and koff is the off-rate. The on-rate can be calculated from kon = Ka × koff. This probabilistic model for kinetics of a low number of discrete bonds has been extensively used to analyze micropipette adhesion-frequency assays (20–25). In these experiments, the same portions of two interacting cell membranes are impinged against each other to form a large flat area of contact during the entire observation time t (i.e., tc). In flow-chamber experiments, by contrast, different membrane portions of the flowing cell transiently contact different portions of the chamber floor at different instances, as Brownian motion brings the cell away from the surface (Fig. 2 B). The observation time t is divided into a discontinuous series of n brief encounters of durations ti interlude with noncontact period tj (i, j = 1, 2, … , n). Each contact has a small and variable area Ai = 2πr(lm – li) for lm > li, where r is the radius of the cell, li is the variable gap distance between the cell bottom and the surface, and lm is the combined length of the interacting molecules (Fig. 2 A). Therefore, to apply to flow-chamber experiments, Eq. 1 should be modified as
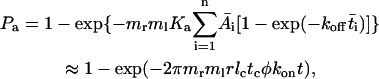 |
(2) |
where φ = n/t is the collision frequency, 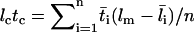 , and the overbar indicates the mean value over the contact period. The second equation is obtained by approximating 1 –
, and the overbar indicates the mean value over the contact period. The second equation is obtained by approximating 1 – 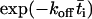 by
by 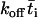 (≪ 1), which seems reasonable as the encounter duration ought to be much briefer than the mean bond half-life (∝ 1/koff). It can also be thought of as the solution of a first-order kinetic equation (13):
(≪ 1), which seems reasonable as the encounter duration ought to be much briefer than the mean bond half-life (∝ 1/koff). It can also be thought of as the solution of a first-order kinetic equation (13):
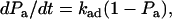 |
(3) |
where kad = 2πmrmlrlctcφkon is the cellular on-rate, which represents the probability for a cell to tether per unit time. Note that our result differs from a proposed equation (13) that lacks the expressions for the contact area and for the fractional contact time tcφ. Since the observation time t includes periods of both contact and noncontact (Fig. 2 B), tcφ < 1, so omitting this expression overestimates the cellular on-rate.
A related concept is the probability Pa for a cell to tether before it flows a distance x (26).
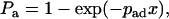 |
(4) |
where pad is the probability for a cell to tether per unit distance. It follows, from comparing Eq. 4 to Eq. 2 and converting time t to distance x by the flowing velocity V (= x/t), that
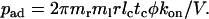 |
(5) |
RESULTS
Biophysical parameters that govern cell tethering
For a cell (or microsphere) that moves with flowing blood to tether, its receptors must contact ligands on the vascular surface (or flow-chamber floor). A contact requires a sufficiently small gap distance between the cell bottom and the surface for bond formation to occur. The contact area is proportional to the cell radius and the combined length of the interacting molecules in excess of the gap distance (Fig. 2 A). Such contact is dynamic, for flow causes the cell to glide along the surface as it translates and rotates downstream, transporting receptors to collide with ligands on the surface. The cell is subjected to Brownian motion that randomly modulates the gap distance above and below the contact threshold, breaking the observation time into alternating periods of brief contact and noncontact (Fig. 2 B). The receptors and ligands are also subjected to rotational diffusion, which orients their binding sites for molecular docking (Fig. 2 B). Sliding velocity, Brownian motion, and molecular diffusion constitute distinct transport mechanisms whose contributions to flow-enhanced bond formation will be explored.
Conceptually, bond formation can be divided into two steps: transport, which brings two molecules into close proximity, and reaction, during which the interacting molecules dock. Depending on the relative timescales of the two steps, tethering can be transport-limited or reaction-limited. Increasing transport should increase cell tethering in the transport-limited regime. However, transport takes receptors to, as well as away from, their ligands. A faster transport produces more frequent collisions but also shortens the contact durations, which decreases cell tethering in the reaction-limited regime. These concepts are summarized in Eq. 5, which serves to organize experiments that examine how the adhesion probability per distance, pad, depends on various transport mechanisms.
Measuring adhesion probability
To study these transport mechanisms, we measured tethering of L-selectin-bearing microspheres and neutrophils to PSGL-1 in a flow chamber. Unlike most previous studies (4,6,19,27), we used a high-speed camera to ensure that we recorded even the briefest and weakest adhesive tethers (see below). We analyzed only first-time tethers from free-flowing microspheres and cells that had never tethered before, to avoid complications from reattachment of microspheres and cells that tethered previously and detached. To exclude reattachments, only a portion of the flow chamber floor was coated with PSGL-1, and the rest was coated with the nonadhesive protein HSA. The demarcation between HSA and PSGL-1 was aligned with the upstream end of the microscope field of view (Fig. 2 B).
The instantaneous velocities of five representative microspheres were plotted against the distance from the demarcation along the flow direction (x axis) (Fig. 3 A). A sudden drop in velocity signified a tethering event, which was random due to stochasticity of low-number molecular interactions. However, the distribution of a large number of tethers should follow Eq. 4, because as the cell flowed sufficiently closely to the adhesive surface, it became exponentially increasingly harder not to tether (which has a probability of 1 − Pa) in all individual contacts that added up to the finite length x. We measured the number of L-selectin-bearing microspheres traveling a distance >x without tethering (∝ 1 − Pa) as a function of x; the measured value was converted to the natural log to linearize the exponential distribution (28). The data plots decreased linearly with x for all five wall shear rates tested (Fig. 3 B), supporting the prediction of Eq. 4. A larger pad favors tethering at shorter distances, manifested as steeper slopes of the distributions as seen for the higher wall shear-rate data in Fig. 3 B. The average distance that a cell travels before tethering can be expressed as 1/pad.
A common metric for cell tethering is tether rate, TR, defined as the ratio of the number of tethering events to the total number of cells flowing through the field of view in a given period (19,27), as exemplified in Fig. 1. For a large number of observations, the adhesion probability can be approximated by the tether rate observed in the field of view of length L (224 μm in our experiments), i.e., TR = [Pa]x = L = 1 – exp(−padL), or, equivalently,
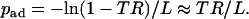 |
(6) |
The approximation on the far right-hand side is valid if TR ≪ 1, which was the case in our experiments (see Fig. 1). Comparison between pad evaluated from the negative slopes of the distribution plots (Fig. 3 B) and the corresponding values calculated from TR using Eq. 6 showed good agreement for all five wall shear rates tested (Fig. 3 C). Since tether rate was much simpler to measure, we used this method to collect the remaining data in this article.
Mass-action effect of receptors and ligands on the contact area
Equation 5 predicts that the adhesion probability per distance pad depends on the numbers of receptors and ligands on the contact area through a product mrmlr due to mass action. However, pad also depends on the sphere radius r through two transport mechanisms. One mechanism is sliding of the sphere bottom on the surface, which causes pad to be a function of 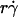 along the initial portion of the ascending phase of the tether rate versus wall shear rate (
along the initial portion of the ascending phase of the tether rate versus wall shear rate (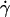 ) curve (Fig. 1, see Fig. 6 C). The other mechanism is Brownian motion, which influences the peak location and descending phase (to be shown later, see Fig. 6, C and D). Neither mechanism affects pad if we select the same
) curve (Fig. 1, see Fig. 6 C). The other mechanism is Brownian motion, which influences the peak location and descending phase (to be shown later, see Fig. 6, C and D). Neither mechanism affects pad if we select the same 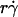 value along the initial portion of the ascending phase of the TR versus
value along the initial portion of the ascending phase of the TR versus 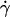 curve, thereby allowing us to isolate the mass-action effect. To test the prediction that pad is proportional to mrmlr, we perfused microspheres of different radii with different L-selectin densities over different PSGL-1 densities at various wall shear rates, which were selected to generate matched
curve, thereby allowing us to isolate the mass-action effect. To test the prediction that pad is proportional to mrmlr, we perfused microspheres of different radii with different L-selectin densities over different PSGL-1 densities at various wall shear rates, which were selected to generate matched 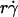 values at the beginning of the TR versus γ̇ curve. The measured TR was converted to pad using Eq. 6 and plotted against mrmlr. Fig. 4 shows that pad was a linearly increasing function of the product mrmlr, regardless of whether ml was varied while mrr was kept constant or mrr was varied while ml was kept constant, which supports Eq. 5. These results also allowed us to normalize pad values by dividing by mrmlr.
values at the beginning of the TR versus γ̇ curve. The measured TR was converted to pad using Eq. 6 and plotted against mrmlr. Fig. 4 shows that pad was a linearly increasing function of the product mrmlr, regardless of whether ml was varied while mrr was kept constant or mrr was varied while ml was kept constant, which supports Eq. 5. These results also allowed us to normalize pad values by dividing by mrmlr.
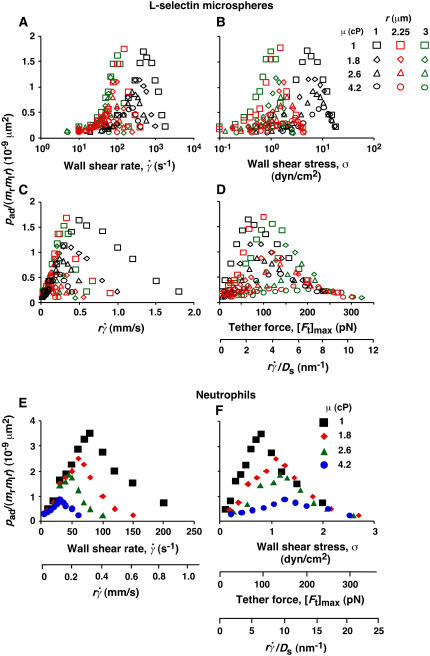
FIGURE 6.
Analysis of tether-rate curves. Adhesion probabilities per distance, pad, of L-selectin-bearing microspheres (A–D) and neutrophils (E and F) were calculated from the tether rate data, normalized by mrmlr, and plotted versus wall shear rate 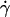 (A and E), wall shear stress σ =
(A and E), wall shear stress σ = 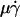 (B and F), product
(B and F), product 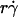 (C and E), and maximum tether force [Ft]max or
(C and E), and maximum tether force [Ft]max or 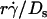 (D and F). Microspheres of three different radii and media of four different viscosities were used (indicated). The data were recorded at 250 fps.
(D and F). Microspheres of three different radii and media of four different viscosities were used (indicated). The data were recorded at 250 fps.
Identifying parameters that control transport
To identify parameters that control transport, we used high-speed video microscopy to record the continuous motions of individual microspheres of different radii in media of different viscosities, which were perfused by Couette flows of different shear rates. Time courses of instantaneous velocity were calculated from frame-by-frame displacements (measured at 500 fps), as exemplified in Fig. 3 A by those of five representative microspheres of 3-μm radius in media of 1-cP viscosity perfused at 10–50 s−1 wall shear rates. We analyzed hundreds of microspheres over a 1-s interval. All moved in nearly constant mean velocities (averaged over 10 frames or more) until tethering occurred (if it occurred), at which time the microsphere velocities abruptly dropped substantially (most often to zero) in just a few milliseconds. The mean velocity V increased with increasing wall shear rate 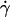 and microsphere radius r but was independent of the medium viscosity μ. When plotted against the product
and microsphere radius r but was independent of the medium viscosity μ. When plotted against the product 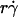 , all V values aligned in a straight line, regardless of the values of r,
, all V values aligned in a straight line, regardless of the values of r, 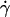 , and μ (Fig. 5 A), as predicted by fluid mechanics theory (29,30). Theory also predicts that the sphere rotates with an angular velocity Ω that is proportional to the shear rate (29,30). Thus, the sliding velocity Vs = V – rΩ of the sphere bottom relative to the surface is also proportional to
, and μ (Fig. 5 A), as predicted by fluid mechanics theory (29,30). Theory also predicts that the sphere rotates with an angular velocity Ω that is proportional to the shear rate (29,30). Thus, the sliding velocity Vs = V – rΩ of the sphere bottom relative to the surface is also proportional to 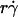 (see legend of Fig. 2 A). This identifies
(see legend of Fig. 2 A). This identifies 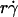 as a governing parameter for transport by the sliding velocity Vs.
as a governing parameter for transport by the sliding velocity Vs.
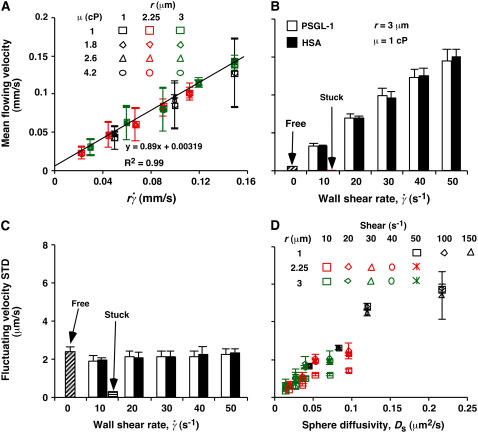
FIGURE 5.
Controlling parameters for sphere motions. Mean (A and B) and standard deviation (C and D) of velocities of L-selectin-bearing microspheres of different radii flowing in media of different viscosities at different wall shear rates over PSGL-1 or HSA. Instantaneous velocities were measured at 250 (A and D) or 500 (B and C) fps for 1 s for each microsphere, from which the mean and standard deviation of velocity were calculated for that microsphere. Data are presented as mean ± SD of 10 microspheres tested for each condition. (A) Linear relationship between mean flowing velocity and the product of the microsphere radius r and wall shear rate 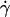 , which identifies
, which identifies 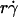 as a controlling parameter for convective transport by mean sliding of the sphere bottom on the surface. (B and C) Comparison between mean (B) or standard deviation (C) of velocities of 3-μm-radius microspheres bearing L-selectin flowing in 1-cP media at 10–50 s−1 wall shear rates over PSGL-1 or HSA. Measurements were also made for microspheres stuck at the surface at 10 s−1 wall shear rate and for free microspheres at zero flow on HSA. (D) Positive correlation between the standard deviation of fluctuating velocity and the sphere diffusivity Ds, which identifies Ds as a controlling parameter for transport by Brownian motion. Each sphere radius and shear rate combination includes four data points for different media viscosities (1, 1.8, 2.6, and 4.2 cP).
as a controlling parameter for convective transport by mean sliding of the sphere bottom on the surface. (B and C) Comparison between mean (B) or standard deviation (C) of velocities of 3-μm-radius microspheres bearing L-selectin flowing in 1-cP media at 10–50 s−1 wall shear rates over PSGL-1 or HSA. Measurements were also made for microspheres stuck at the surface at 10 s−1 wall shear rate and for free microspheres at zero flow on HSA. (D) Positive correlation between the standard deviation of fluctuating velocity and the sphere diffusivity Ds, which identifies Ds as a controlling parameter for transport by Brownian motion. Each sphere radius and shear rate combination includes four data points for different media viscosities (1, 1.8, 2.6, and 4.2 cP).
Instantaneous velocities of flowing microspheres and cells exhibited small fluctuations about the mean (Fig. 3 A). One proposal to explain these fluctuations is the formation of labile bonds between L-selectin on cells and surface-bound ligands, which may be stabilized by flow-driven cell rotation that increases bond number (15). The agreement of the measured mean flowing velocity with that predicted by fluid mechanics theory based on no interaction between the sphere and the surface and a gap distance well beyond the combined molecular length (Fig. 5 A) argues against the proposed labile bonds. To further rule out this possibility, we compared the mean (Fig. 5 B) and standard deviation (Fig. 5 C) of fluctuating velocities of untethered microspheres perfused in a range of wall shear rates over PSGL-1 with those over the nonadhesive protein HSA. For each shear rate tested, microspheres flowed with identical mean velocities (Fig. 5 B) and identical velocity standard deviations (Fig. 5 C) over PSGL-1 and over HSA. Importantly, the mean velocity (Fig. 5 B) and velocity standard deviation (Fig. 5 C) of microspheres stuck to the flow-chamber floor were zero, indicating that microscope drifting, particle tracking errors, and environmental noises were negligible. In the absence of flow, nonadherent (free) microspheres on HSA also had zero mean velocity (Fig. 5 B), but their nonzero velocity standard deviation was identical to those of flowing microspheres (Fig. 5 C). These data indicate that our experiments detected even the weakest and briefest L-selectin-PSGL-1 bonds. Such bonds did not form before the specific tethering events and hence could not cause the observed velocity fluctuations.
The marked difference in the velocity standard deviations of free and stuck microspheres suggests that the velocity fluctuations represent Brownian motion. To test this hypothesis, we plotted velocity standard deviation against the unconfined sphere diffusivity defined by the Stokes-Einstein relationship, Ds = kBT/(6πμr), where kB is the Boltzmann constant and T is the absolute temperature. kBT (4.1 pN-nm at room temperature) represents a thermal energy scale. The velocity standard deviation was insensitive to the wall shear rate (Fig. 5 C), but it clearly correlated with the sphere diffusivity, a variable that combined the effects of microsphere radius and medium viscosity (Fig. 5 D). Similar results were obtained for neutrophils perfused in media of different viscosities at different wall shear rates (data not shown). Since the standard deviation of fluctuating velocities equals the root mean-squared displacements between two consecutive video frames (after subtracting the mean convective motion), this correlation agrees with Brownian motion theory and supports the hypothesis that the observed velocity fluctuations originated from Brownian motion.
We could measure the velocity components parallel (i.e., xy plane), but not perpendicular (i.e., z direction), to the surface. However, the diffusivity in the z direction is related to those in the x and y directions by fluid mechanics theory (30,31). Brownian motion in the xy plane modulates the mean velocity. Brownian motion in the z direction enables the cell to collide with the surface, thereby modulating the collision frequency, the gap distance, and the encounter duration (Fig. 2 B). Therefore, cell tethering can be enhanced by Brownian motion. The Stokes-Einstein relationship calculates diffusivity of a sphere in an unbounded fluid; it must be multiplied by appropriate correction factors to calculate the respective diffusivities of a sphere near a planar surface diffusing parallel and perpendicular to the surface (29,30). Regardless of the correction factors, the strong correlation with standard deviation of fluctuating velocities identifies Ds calculated from the Stokes-Einstein relationship as a controlling parameter for Brownian motion (Fig. 5 D).
Enhancing tethering by mean sliding velocity
To evaluate the role of various transport mechanisms in cell tethering, we independently varied parameters that affect these mechanisms. We perfused cells or microspheres of different radii in media of different viscosities through a flow chamber at different wall shear rates. Shear stress (σ), the product of shear rate and viscosity, drives a free microsphere (or cell) to slide over the surface at a mean velocity proportional to 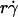 . The L-selectin-PSGL-1 interaction provides a tether force Ft that slows the sphere's velocity and reaches maximum, [Ft]max = 13.2r2σ, when the sphere stops (12,29). It also compresses the sphere bottom, which enlarges the contact area of a deformable cell but not of a rigid microsphere, and it may extrude membrane cylinders from a cell (32) but not from a microsphere. At the same shear rate, increasing the viscosity increases the shear stress and, in turn, the tether force on a sphere. It also decreases the sphere diffusivity and the molecular diffusivity. At the same shear stress, more force is applied to the adhesive tether of a larger sphere than a smaller sphere. Increasing the sphere size also increases the product
. The L-selectin-PSGL-1 interaction provides a tether force Ft that slows the sphere's velocity and reaches maximum, [Ft]max = 13.2r2σ, when the sphere stops (12,29). It also compresses the sphere bottom, which enlarges the contact area of a deformable cell but not of a rigid microsphere, and it may extrude membrane cylinders from a cell (32) but not from a microsphere. At the same shear rate, increasing the viscosity increases the shear stress and, in turn, the tether force on a sphere. It also decreases the sphere diffusivity and the molecular diffusivity. At the same shear stress, more force is applied to the adhesive tether of a larger sphere than a smaller sphere. Increasing the sphere size also increases the product 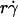 without changing the shear rate and decreases the sphere diffusivity without changing the molecular diffusivity. Tether-rate data were converted to the adhesion probability per distance pad using Eq. 6 and normalized by dividing by mrmlr to remove the mass action effect. pad/(mrmlr) was then plotted against different parameters to dissect which mechanism dominated which regime of the curve. Alignment of the entire curves or portions thereof when plotted against a parameter suggests the dominance of the mechanism controlled by this parameter in the regime where curves align. Lack of alignment suggests the presence of competing mechanisms. Lack of sensitivity to the change of a parameter indicates its irrelevance.
without changing the shear rate and decreases the sphere diffusivity without changing the molecular diffusivity. Tether-rate data were converted to the adhesion probability per distance pad using Eq. 6 and normalized by dividing by mrmlr to remove the mass action effect. pad/(mrmlr) was then plotted against different parameters to dissect which mechanism dominated which regime of the curve. Alignment of the entire curves or portions thereof when plotted against a parameter suggests the dominance of the mechanism controlled by this parameter in the regime where curves align. Lack of alignment suggests the presence of competing mechanisms. Lack of sensitivity to the change of a parameter indicates its irrelevance.
As flow increased, the L-selectin-PSGL-1-specific TR (Fig. 1) and pad/(mrmlr) (Fig. 6) increased initially, reached a maximum, and then decreased. When plotted against the wall shear rate 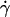 , initial portions of the ascending phase of curves for different medium viscosities aligned for microspheres of the same radius r (but shifted with r) (Fig. 6 A) and for neutrophils (Fig. 6 E), suggesting two competing mechanisms respectively governed by
, initial portions of the ascending phase of curves for different medium viscosities aligned for microspheres of the same radius r (but shifted with r) (Fig. 6 A) and for neutrophils (Fig. 6 E), suggesting two competing mechanisms respectively governed by 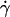 and r. When the abscissa was rescaled by multiplying
and r. When the abscissa was rescaled by multiplying 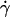 by r, the initial portions of the ascending phase of all microsphere curves collapsed (Fig. 6 C), indicating that the product
by r, the initial portions of the ascending phase of all microsphere curves collapsed (Fig. 6 C), indicating that the product 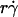 is the governing parameter in this regime. The sliding velocity of the sphere bottom relative to the chamber floor is proportional to
is the governing parameter in this regime. The sliding velocity of the sphere bottom relative to the chamber floor is proportional to 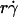 . Therefore, these results demonstrate that convective transport by sliding provides a dominant mechanism to enhance tethering when
. Therefore, these results demonstrate that convective transport by sliding provides a dominant mechanism to enhance tethering when 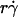 is small.
is small.
Enhancing tethering by Brownian motion
When pad/(mrmlr) was plotted against the wall shear stress σ, the final portions of the descending phase of different curves aligned for microspheres of the same radius r (but shifted with r) (Fig. 6 B) and for neutrophils (Fig. 6 F). When the abscissa was rescaled by multiplying σ by 13.2r2, the final portions of the descending phase of all microsphere curves aligned even for those of different radii (Fig. 6 D). At first, the correct scaling with [Ft]max = 13.2r2σ seems to suggest that tether force governs this regime of the curves. This might result from a force-dependent decrease in L-selectin-PSGL-1 on-rate, which has been hypothesized (33) but never demonstrated. Alternatively, it might result from a force-dependent increase in L-selectin-PSGL-1 off-rate that causes some tethers to dissociate too rapidly to be observed. However, the instantaneous velocities of free-flowing microspheres immediately before tethering to PSGL-1 were identical to those of microspheres freely flowing over HSA (Fig. 5, B and C), suggesting that we detected even the weakest and briefest bonds.
On the other hand, it follows from the expressions of [Ft]max (= 13.2r2μ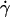 ) and Ds [= kBT/(6πμr)] that [Ft]max ≡ 13.2(kBT/6π)(
) and Ds [= kBT/(6πμr)] that [Ft]max ≡ 13.2(kBT/6π)(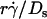 ). Since 13.2(kBT/6π) is a constant, the final portions of the descending phase of the curves also aligned when pad/(mrmlr) was plotted against
). Since 13.2(kBT/6π) is a constant, the final portions of the descending phase of the curves also aligned when pad/(mrmlr) was plotted against 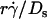 (Fig. 6, D and F). This suggests that
(Fig. 6, D and F). This suggests that 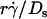 rather than [Ft]max is the governing parameter in this regime. Intuitively,
rather than [Ft]max is the governing parameter in this regime. Intuitively, 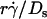 represents the combined effects of convective transport by sliding and Brownian motion. These observations suggest that Brownian motion is a transport mechanism that enhances tethering. Further support for this hypothesis is presented below.
represents the combined effects of convective transport by sliding and Brownian motion. These observations suggest that Brownian motion is a transport mechanism that enhances tethering. Further support for this hypothesis is presented below.
The increase of pad/(mrmlr) with increasing 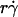 suggests that tethering is initially limited by insufficient sliding. As pad/(mrmlr) reached maximum, the continued increase in
suggests that tethering is initially limited by insufficient sliding. As pad/(mrmlr) reached maximum, the continued increase in 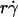 could no longer enhance tethering, suggesting that something other than sliding of the sphere on the surface becomes limiting. The
could no longer enhance tethering, suggesting that something other than sliding of the sphere on the surface becomes limiting. The 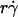 value where pad/(mrmlr) achieved maximum (referred to as optimal
value where pad/(mrmlr) achieved maximum (referred to as optimal 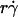 ) decreased with increasing sphere radius and/or medium viscosity for both microspheres (Fig. 6 C) and neutrophils (Fig. 6 E). Similarly, the reciprocal of the
) decreased with increasing sphere radius and/or medium viscosity for both microspheres (Fig. 6 C) and neutrophils (Fig. 6 E). Similarly, the reciprocal of the 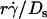 value where pad/(mrmlr) achieved maximum (referred to as optimal Ds/
value where pad/(mrmlr) achieved maximum (referred to as optimal Ds/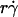 , or (Ds/
, or (Ds/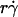 )opt) also decreased with increasing r and/or μ for both microspheres (Fig. 6 D) and neutrophils (Fig. 6 F). These observations suggest that the new limiting factors involve r and μ. We hypothesized that r and μ modulate tethering by influencing the Brownian motion of the microspheres and cells. To test this hypothesis, we examined the possible correlations of the optimal
)opt) also decreased with increasing r and/or μ for both microspheres (Fig. 6 D) and neutrophils (Fig. 6 F). These observations suggest that the new limiting factors involve r and μ. We hypothesized that r and μ modulate tethering by influencing the Brownian motion of the microspheres and cells. To test this hypothesis, we examined the possible correlations of the optimal 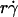 and optimal Ds/
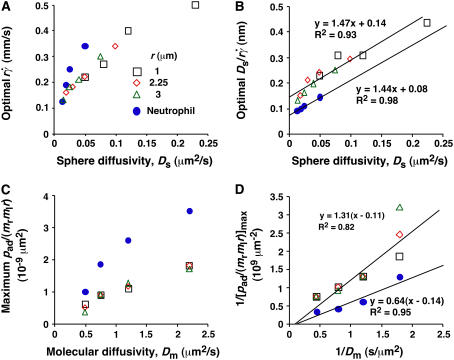
and optimal Ds/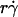 (inversely proportional to optimal [Ft]max) with Ds, a governing parameter for Brownian motion. When plotted against Ds, the optimal
(inversely proportional to optimal [Ft]max) with Ds, a governing parameter for Brownian motion. When plotted against Ds, the optimal 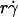 aligned into two nearly straight lines, one for microspheres and the other for neutrophils, regardless of the r and/or μ values (Fig. 7 A). Similarly, when plotted against Ds, the optimal Ds/
aligned into two nearly straight lines, one for microspheres and the other for neutrophils, regardless of the r and/or μ values (Fig. 7 A). Similarly, when plotted against Ds, the optimal Ds/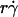 values also aligned into two nearly straight lines, one for microspheres and the other for neutrophils, regardless of the r and/or μ values (Fig. 7 B). These data support our hypothesis, which is intuitive. More vibrant Brownian motion should produce more frequent collisions with larger contact areas, expanding the capacity for sliding to enhance tethering.
values also aligned into two nearly straight lines, one for microspheres and the other for neutrophils, regardless of the r and/or μ values (Fig. 7 B). These data support our hypothesis, which is intuitive. More vibrant Brownian motion should produce more frequent collisions with larger contact areas, expanding the capacity for sliding to enhance tethering.
FIGURE 7.
Analysis of optimal values of tether-rate curves. (A) Peak locations of the pad/(mrmlr) versus 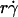 curves (optimal
curves (optimal 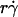 ) were plotted against the sphere diffusivity Ds. (B) Peak locations of the pad/(mrmlr) versus
) were plotted against the sphere diffusivity Ds. (B) Peak locations of the pad/(mrmlr) versus 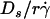 curves (optimal Ds/
curves (optimal Ds/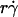 ) were plotted against the sphere diffusivity Ds. (C) Maximum pad/(mrmlr) values were plotted against the molecular diffusivity Dm. (D) Reciprocal of maximum pad/(mrmlr) values were plotted against reciprocal of the molecular diffusivity. Positive correlations were evident in all plots for both microspheres (open symbols) and neutrophils (solid circles). A straight line was fit to each set of the data for microspheres or neutrophils in B and D. The best-fit equations are indicated along with the R2 values.
) were plotted against the sphere diffusivity Ds. (C) Maximum pad/(mrmlr) values were plotted against the molecular diffusivity Dm. (D) Reciprocal of maximum pad/(mrmlr) values were plotted against reciprocal of the molecular diffusivity. Positive correlations were evident in all plots for both microspheres (open symbols) and neutrophils (solid circles). A straight line was fit to each set of the data for microspheres or neutrophils in B and D. The best-fit equations are indicated along with the R2 values.
We have seen that plotting pad/(mrmlr) versus 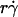 (Fig. 6, C and E) and versus
(Fig. 6, C and E) and versus 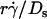 (Fig. 6, D and F) respectively aligned the initial portions of the ascending phase and final portions of the descending phase of different curves corresponding to different parameters. This observation suggests that combining
(Fig. 6, D and F) respectively aligned the initial portions of the ascending phase and final portions of the descending phase of different curves corresponding to different parameters. This observation suggests that combining 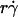 and
and 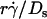 will provide an abscissa variable to align both phases provided that the ordinate is also rescaled. To construct such a combined variable, we fitted each data set in Fig. 7 B with a line, (Ds/
will provide an abscissa variable to align both phases provided that the ordinate is also rescaled. To construct such a combined variable, we fitted each data set in Fig. 7 B with a line, (Ds/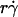 )opt = A(Ds + C1), where C1 = 0.09 μm2/s for microspheres and 0.05 μm2/s for neutrophils, and A ≈ 1.45 μm/s for both data sets. Multiplying the fitting equation by
)opt = A(Ds + C1), where C1 = 0.09 μm2/s for microspheres and 0.05 μm2/s for neutrophils, and A ≈ 1.45 μm/s for both data sets. Multiplying the fitting equation by 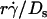 resulted in (
resulted in (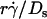 )(Ds/
)(Ds/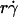 )opt = A
)opt = A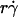 (1 + C1/Ds). The right-hand side is a linear combination of
(1 + C1/Ds). The right-hand side is a linear combination of 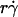 and
and 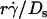 . On the left-hand side,
. On the left-hand side, 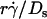 is scaled by its optimal value, which should align the locations where pad/(mrmlr) peaks when plotted against the combined variable. Since A is the same constant for both microspheres and neutrophils, plotting pad/(mrmlr) against
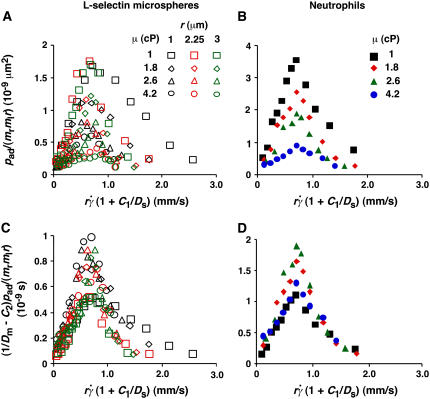
is scaled by its optimal value, which should align the locations where pad/(mrmlr) peaks when plotted against the combined variable. Since A is the same constant for both microspheres and neutrophils, plotting pad/(mrmlr) against 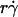 (1 + C1/Ds) should align the locations where pad/(mrmlr) peaks for both data. These predictions are confirmed by the data plots in Fig. 8, A and B, which emphasize that both mean sliding velocity and Brownian motion are important transport mechanisms for tethering.
(1 + C1/Ds) should align the locations where pad/(mrmlr) peaks for both data. These predictions are confirmed by the data plots in Fig. 8, A and B, which emphasize that both mean sliding velocity and Brownian motion are important transport mechanisms for tethering.
FIGURE 8.
Collapse of multiple data curves by proper scaling of the contributions by three transport mechanisms. When the normalized adhesion probabilities per distance for microspheres (A) and neutrophils (B), pad/(mrmlr), were plotted versus 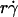 (1 + C1/Ds), a variable that combines sphere transport mechanisms for both relative sliding and Brownian motion, the ranges of all curves were aligned. When the pad/(mrmlr) values were further multiplied by (1/Dm − C2) to obtain a variable that combines molecular diffusion and molecular docking, all 12 microsphere curves collapsed into a single curve (C). Similarly, all four neutrophil curves collapsed into a single curve (D).
(1 + C1/Ds), a variable that combines sphere transport mechanisms for both relative sliding and Brownian motion, the ranges of all curves were aligned. When the pad/(mrmlr) values were further multiplied by (1/Dm − C2) to obtain a variable that combines molecular diffusion and molecular docking, all 12 microsphere curves collapsed into a single curve (C). Similarly, all four neutrophil curves collapsed into a single curve (D).
Enhancing tethering by molecular diffusion
As the medium viscosity decreased, both the 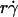 value where pad/(mrmlr) achieved maximum and the maximum pad/(mrmlr) value increased (Fig. 6, C and E). However, the maximum pad/(mrmlr) value was insensitive to the sphere radius (Fig. 6 B) and did not correlate with the sphere diffusivity. For example, a 1-μm microsphere in 4.2-cP medium had a Ds value larger than that of a 2.25-μm microsphere in 2.6-cP medium (0.05 vs. 0.04 μm2/s). However, the former had a maximum pad/(mrmlr) value smaller than the latter (0.54 vs. 0.85 × 10−9 μm2). Since the maximum pad/(mrmlr) value changed irrespective of the sphere diffusivity, some other factor must enhance tethering. This factor might be molecular diffusivity, represented by Dm = kBT/(6πμl) calculated from the Stokes-Einstein relationship, where l is a characteristic length in the molecular scale, e.g., l = 100 nm for an order-of-magnitude estimate. Dm represents a transport parameter that depends on medium viscosity but not on sphere radius, because the same molecules were coated on the microspheres of different radii. To test this hypothesis, we plotted the maximum pad/(mrmlr) value against Dm. These plots were nearly linear for both microspheres and neutrophils regardless of the sphere radius (Fig. 7 C), suggesting that molecular diffusion is the new limiting factor for tethering.
value where pad/(mrmlr) achieved maximum and the maximum pad/(mrmlr) value increased (Fig. 6, C and E). However, the maximum pad/(mrmlr) value was insensitive to the sphere radius (Fig. 6 B) and did not correlate with the sphere diffusivity. For example, a 1-μm microsphere in 4.2-cP medium had a Ds value larger than that of a 2.25-μm microsphere in 2.6-cP medium (0.05 vs. 0.04 μm2/s). However, the former had a maximum pad/(mrmlr) value smaller than the latter (0.54 vs. 0.85 × 10−9 μm2). Since the maximum pad/(mrmlr) value changed irrespective of the sphere diffusivity, some other factor must enhance tethering. This factor might be molecular diffusivity, represented by Dm = kBT/(6πμl) calculated from the Stokes-Einstein relationship, where l is a characteristic length in the molecular scale, e.g., l = 100 nm for an order-of-magnitude estimate. Dm represents a transport parameter that depends on medium viscosity but not on sphere radius, because the same molecules were coated on the microspheres of different radii. To test this hypothesis, we plotted the maximum pad/(mrmlr) value against Dm. These plots were nearly linear for both microspheres and neutrophils regardless of the sphere radius (Fig. 7 C), suggesting that molecular diffusion is the new limiting factor for tethering.
Similar to the preceding analysis, scaling pad/(mrmlr) by its maximum value should collapse the curves in Fig. 8, A and B. To relate the scaling factor to the molecular diffusivity, its reciprocal was plotted against 1/Dm in Fig. 7 D, which inverted the plots in Fig. 7 C. Each data set in Fig. 7 D was fitted by a straight line, 1/[ pad/(mrmlr)]max = B(1/Dm − C2), where the slope B differed for microspheres and neutrophils (1.31 vs. 0.64 μm4/s) but the x-intercept C2 was the same (∼0.1 s/μm2). Multiplying this fitting equation by pad/(mrmlr) resulted in (pad/(mrmlr))/(pad/(mrmlr))max = B(1/Dm − C2)pad/(mrmlr). Plotting (1/Dm − C2)pad/(mrmlr) vs. 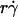 (1 + C1/Ds) collapsed all 12 microsphere curves to a single curve and all four neutrophil curves to a single curve (Fig. 8, C and D). Moreover, the curves in the two panels had the same shape and peak location; only the ordinate scales differed. A possible explanation is that neutrophils concentrate L-selectin on microvillus tips, which may offer a better presentation for tethering than the more uniformly distributed L-selectin on microspheres. If neutrophil L-selectin mediates tethering twice as effectively as microsphere L-selectin, the ordinate axis in Fig. 8 C should be expanded by a factor of 2, which would align the microsphere curves with the neutrophil curves in Fig. 8 D. Although deformation and membrane cylinder extrusion by the cells could potentially result in scaling with cell radius and medium viscosity, the agreement between the collapsed curves for microspheres that are rigid and those for neutrophils that are deformable suggests that these effects are irrelevant to tethering.
(1 + C1/Ds) collapsed all 12 microsphere curves to a single curve and all four neutrophil curves to a single curve (Fig. 8, C and D). Moreover, the curves in the two panels had the same shape and peak location; only the ordinate scales differed. A possible explanation is that neutrophils concentrate L-selectin on microvillus tips, which may offer a better presentation for tethering than the more uniformly distributed L-selectin on microspheres. If neutrophil L-selectin mediates tethering twice as effectively as microsphere L-selectin, the ordinate axis in Fig. 8 C should be expanded by a factor of 2, which would align the microsphere curves with the neutrophil curves in Fig. 8 D. Although deformation and membrane cylinder extrusion by the cells could potentially result in scaling with cell radius and medium viscosity, the agreement between the collapsed curves for microspheres that are rigid and those for neutrophils that are deformable suggests that these effects are irrelevant to tethering.
DISCUSSION
Flow enhances L-selectin-dependent adhesion by increasing the initial tethering of leukocytes to vascular surfaces and by strengthening their subsequent rolling interactions. Previously, we elucidated an off-rate mechanism—catch bonds that allow force to decelerate dissociation—for flow-enhanced rolling through L-selectin (12). Force regulation of off-rate is the dominant factor governing rolling velocity and rolling regularity, which suggests that on-rate is not a limiting factor for rolling. Here, we have demonstrated that on-rate was not limiting for L-selectin-mediated tethering at low flow rates. Therefore, on-rate should not be a limiting factor for rolling, because the briefer contact times during tethering than during rolling require faster on-rates to form bonds in tethering than in rolling. The fast on-rate of L-selectin-PSGL-1 interactions allows three distinct transport mechanisms to enhance tethering: mean sliding velocity, Brownian motion, and molecular diffusion. The sliding mechanism has been hypothesized (13) and was demonstrated experimentally for P-selectin-mediated tethering (27). A role for molecular diffusion in tethering has also been suggested (27). However, previous studies did not experimentally address the relative contributions of transport mechanisms to flow-enhanced tethering.
To identify transport mechanisms for tethering and to dissect their relative contributions under different conditions, media of different viscosities (12,27) and microspheres of different radii (12) were used to distinguish shear-rate-dependent mechanisms from shear-stress-dependent mechanisms. This further allowed us to separate the effects of Brownian motion and molecular diffusion by varying each of three governing parameters: 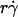 , Ds, and Dm. Important transport mechanisms were identified if 1), data were sensitive to changes in their governing parameters; and 2), multiple data curves (or portions thereof) measured under different conditions aligned and collapsed into a single curve (or a portion thereof). Irrelevant mechanisms were excluded if data were indifferent to changes in their controlling variables. Competing mechanisms were revealed if portions of data curves did not collapse. Further alignment was achieved by rescaling the axis using a combined variable to account for different competing mechanisms in different regimes.
, Ds, and Dm. Important transport mechanisms were identified if 1), data were sensitive to changes in their governing parameters; and 2), multiple data curves (or portions thereof) measured under different conditions aligned and collapsed into a single curve (or a portion thereof). Irrelevant mechanisms were excluded if data were indifferent to changes in their controlling variables. Competing mechanisms were revealed if portions of data curves did not collapse. Further alignment was achieved by rescaling the axis using a combined variable to account for different competing mechanisms in different regimes.
To construct combined variables, we recognized that four timescales are operative during tethering: three for the transport mechanisms, which are proportional to the reciprocal of their respective controlling parameters, and one for molecular docking, which is proportional to the reciprocal of on-rate kon. Like any multi-step kinetic process, tethering is limited by the slowest step, or the longest timescale. Shortening the limiting timescale should speed up the process and enhance tethering, which we expressed as the normalized adhesion probability pad/(mrmlr) to separate the transport effects from the mass-action effect. Convective transport by the mean sliding velocity is initially the slowest step, because increasing 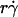 from low values enhanced tethering regardless of other controlling variables, as is evident by the alignment of the initial portions of curves corresponding to different values of these variables (Fig. 6, C and E). Achieving maximal tethering signified that the timescale governed by
from low values enhanced tethering regardless of other controlling variables, as is evident by the alignment of the initial portions of curves corresponding to different values of these variables (Fig. 6, C and E). Achieving maximal tethering signified that the timescale governed by 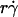 was shortened to the point where it became comparable to that of the second-slowest step. The alignment of optimal
was shortened to the point where it became comparable to that of the second-slowest step. The alignment of optimal 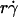 from different curves, when plotted against Ds, supports this argument and identifies this second-slowest step as Brownian motion (Fig. 7 A). The regime in which this mechanism governs was revealed by the observation that scaling
from different curves, when plotted against Ds, supports this argument and identifies this second-slowest step as Brownian motion (Fig. 7 A). The regime in which this mechanism governs was revealed by the observation that scaling 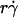 by Ds collapsed the final portions of pad/(mrmlr) curves (Fig. 6, D and F). It is therefore intuitive that a linear combination of
by Ds collapsed the final portions of pad/(mrmlr) curves (Fig. 6, D and F). It is therefore intuitive that a linear combination of 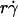 and
and 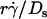 as the abscissa variable would align the entire x axis ranges of all data curves (Fig. 8). The constant C1 assigned the division of the two regimes where these two mechanisms dominated, since the proper choice of their values aligned the entire range of the respective curves for microspheres (Fig. 8 A) and neutrophils (Fig. 8 B).
as the abscissa variable would align the entire x axis ranges of all data curves (Fig. 8). The constant C1 assigned the division of the two regimes where these two mechanisms dominated, since the proper choice of their values aligned the entire range of the respective curves for microspheres (Fig. 8 A) and neutrophils (Fig. 8 B).
The alignment of the x axis range in Fig. 8, A and B, did not automatically collapse the pad/(mrmlr) curves, because the peak values still differed. This provided the opportunity to identify the next limiting timescale, which was based on the observation that peak tethering rate correlated with the medium viscosity but not the sphere diffusivity. Like the mean sliding velocity, Brownian motion uses convection as the transport mode, because it is the motions of the sphere that bring L-selectin to the vicinity of PSGL-1. By comparison, molecular diffusion should be more similar to molecular docking, which can also be described theoretically by a thermally excited diffusive process (34). Therefore, the maximum pad/(mrmlr) value should correlate with the molecular diffusivity (Fig. 7 C), just as the optimal 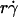 correlated with the sphere diffusivity (Fig. 7 A). Indeed, scaling pad/(mrmlr) by Dm collapsed the peak values of the curves, and a linear combination of pad/(mrmlr) and pad/(mrmlr)/Dm as the ordinate variable aligned the entire y axis ranges of all the data curves (Fig. 8, C and D). The constant C2 assigned the division between the two regimes where these two variables dominated, since the proper choice of its value aligned the entire range of the respective curves for microspheres (Fig. 8 C) and neutrophils (Fig. 8 D). In a recent study, we further demonstrated the tethering-enhancing role of molecular diffusion by using a mutated L-selectin with increased molecular diffusivity (35). We also showed that the three transport mechanisms demonstrated here were operative for a ligand that is molecularly distinct from PSGL-1 (35).
correlated with the sphere diffusivity (Fig. 7 A). Indeed, scaling pad/(mrmlr) by Dm collapsed the peak values of the curves, and a linear combination of pad/(mrmlr) and pad/(mrmlr)/Dm as the ordinate variable aligned the entire y axis ranges of all the data curves (Fig. 8, C and D). The constant C2 assigned the division between the two regimes where these two variables dominated, since the proper choice of its value aligned the entire range of the respective curves for microspheres (Fig. 8 C) and neutrophils (Fig. 8 D). In a recent study, we further demonstrated the tethering-enhancing role of molecular diffusion by using a mutated L-selectin with increased molecular diffusivity (35). We also showed that the three transport mechanisms demonstrated here were operative for a ligand that is molecularly distinct from PSGL-1 (35).
The observation that the tethering curve declined after reaching a maximum suggests that the contact time becomes shorter than the timescale for molecular docking and thus becomes limiting. It seems intuitive that the contact time should decrease with increasing 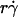 . Since a slower molecular docking rate requires a longer contact time, it should left-shift the tethering curve toward lower
. Since a slower molecular docking rate requires a longer contact time, it should left-shift the tethering curve toward lower 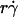 . This may explain why the two L-selectin-antibody curves were shifted leftward relative to the two L-selectin-PSGL-1 curves (Fig. 1), as on-rates are much slower for antibody-antigen interactions than for L-selectin-ligand interactions (36).
. This may explain why the two L-selectin-antibody curves were shifted leftward relative to the two L-selectin-PSGL-1 curves (Fig. 1), as on-rates are much slower for antibody-antigen interactions than for L-selectin-ligand interactions (36).
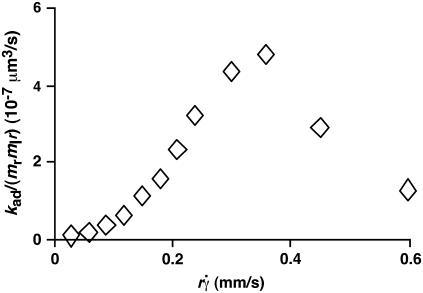
It has been predicted theoretically that the adhesion probability per unit time, kad, should increase initially with increasing flow when tethering is transport-limited, but should approach a plateau when tethering becomes reaction-limited (13). However, this prediction is not supported by our data, as illustrated in Fig. 9 for L-selectin-coated microspheres of 3-μm radius flowing in media of 1-cP viscosity tethering to PSGL-1. Other kad curves for different microsphere radii and different medium viscosities exhibit a similar biphasic shape. All scaling laws presented in Results for pad curves also apply to the kad curves. This is expected, because kad is related to pad through Eq. 5: kad = padV = 2πmrmlrlctcφkon. We should emphasize that the collision frequency, φ, and the correlation between the contact area and contact duration, 2πrlctc, are functions of the sliding velocity. Although it seems intuitive that φ should be an increasing function of 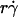 and 2πrlctc should be a decreasing function of
and 2πrlctc should be a decreasing function of 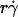 , our data indicate that their dependencies on
, our data indicate that their dependencies on 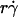 do not cancel each other to produce a constant kad in the reaction-limited regime.
do not cancel each other to produce a constant kad in the reaction-limited regime.
FIGURE 9.
Dependence of adhesion probability per unit time on sliding velocity. kad/(mrmlr) was calculated from pad/(mrmlr) using Eq. 5 and the linear data between the average microsphere flowing velocity V and 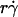 (Fig. 5 A). Data for 3-μm microspheres flowing in 1-cP medium are shown, but curves converted from other pad/(mrmlr) data in Fig. 6 have a similar biphasic shape.
(Fig. 5 A). Data for 3-μm microspheres flowing in 1-cP medium are shown, but curves converted from other pad/(mrmlr) data in Fig. 6 have a similar biphasic shape.
In summary, we have defined the contributions of three transport mechanisms to flow-enhanced leukocyte tethering through interactions of L-selectin with PSGL-1. Transport governs flow-enhanced tethering by augmenting bond formation. In contrast, force governs flow-enhanced rolling by decreasing bond dissociation (catch bonds) (12). Together, these results explain the shear-threshold requirement for leukocyte adhesion through L-selectin. Our studies also provide strategies to analyze flow-enhanced cell adhesion in other biological systems.
Acknowledgments
We thank Pierre Bongrand and David Schmidtke for carefully reading the manuscript.
This work was supported by National Institutes of Health grants AI 44902 (to C.Z.) and HL 65631 (to R.P.M.).
References
- 1.Vestweber, D., and J. E. Blanks. 1999. Mechanisms that regulate the function of the selectins and their ligands. Physiol. Rev. 79:181–213. [DOI] [PubMed] [Google Scholar]
- 2.McEver, R. P. 2001. Adhesive interactions of leukocytes, platelets, and the vessel wall during hemostasis and inflammation. Thromb. Haemost. 86:746–756. [PubMed] [Google Scholar]
- 3.McEver, R. P. 2002. Selectins: lectins that initiate cell adhesion under flow. Curr. Opin. Cell Biol. 14:581–586. [DOI] [PubMed] [Google Scholar]
- 4.Finger, E. B., K. D. Puri, R. Alon, M. B. Lawrence, U. H. von Andrian, and T. A. Springer. 1996. Adhesion through L-selectin requires a threshold hydrodynamic shear. Nature. 379:266–269. [DOI] [PubMed] [Google Scholar]
- 5.Lawrence, M. B., G. S. Kansas, E. J. Kunkel, and K. Ley. 1997. Threshold levels of fluid shear promote leukocyte adhesion through selectins (CD62L,P,E). J. Cell Biol. 136:717–727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Alon, R., S. Chen, K. D. Puri, E. B. Finger, and T. A. Springer. 1997. The kinetics of L-selectin tethers and the mechanics of selectin- mediated rolling. J. Cell Biol. 138:1169–1180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Savage, B., E. Saldivar, and Z. M. Ruggeri. 1996. Initiation of platelet adhesion by arrest onto fibrinogen or translocation on von Willebrand factor. Cell. 84:289–297. [DOI] [PubMed] [Google Scholar]
- 8.Doggett, T. A., G. Girdhar, A. Lawshe, J. L. Miller, I. J. Laurenzi, S. L. Diamond, and T. G. Diacovo. 2003. Alterations in the intrinsic properties of the GPIbα-VWF tether bond define the kinetics of the platelet-type von Willebrand disease mutation, Gly233Val. Blood. 102:152–160. [DOI] [PubMed] [Google Scholar]
- 9.Thomas, W. E., E. Trintchina, M. Forero, V. Vogel, and E. V. Sokurenko. 2002. Bacterial adhesion to target cells enhanced by shear force. Cell. 109:913–923. [DOI] [PubMed] [Google Scholar]
- 10.Marshall, B. T., M. Long, J. W. Piper, T. Yago, R. P. McEver, and C. Zhu. 2003. Direct observation of catch bonds involving cell-adhesion molecules. Nature. 423:190–193. [DOI] [PubMed] [Google Scholar]
- 11.Sarangapani, K. K., T. Yago, A. G. Klopocki, M. B. Lawrence, C. B. Fieger, S. D. Rosen, R. P. McEver, and C. Zhu. 2004. Low force decelerates L-selectin dissociation from P-selectin glycoprotein ligand-1 and endoglycan. J. Biol. Chem. 279:2291–2298. [DOI] [PubMed] [Google Scholar]
- 12.Yago, T., J. Wu, C. D. Wey, A. G. Klopocki, C. Zhu, and R. P. McEver. 2004. Catch bonds govern adhesion through L-selectin at threshold shear. J. Cell Biol. 166:913–923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Chang, K. C., and D. A. Hammer. 1999. The forward rate of binding of surface-tethered reactants: effect of relative motion between two surfaces. Biophys. J. 76:1280–1292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Chen, S., and T. A. Springer. 1999. An automatic braking system that stabilizes leukocyte rolling by an increase in selectin bond number with shear. J. Cell Biol. 144:185–200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Dwir, O., A. Solomon, S. Mangan, G. S. Kansas, U. S. Schwarz, and R. Alon. 2003. Avidity enhancement of L-selectin bonds by flow: shear-promoted rotation of leukocytes turn labile bonds into functional tethers. J. Cell Biol. 163:649–659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Yago, T., A. Leppanen, H. Qiu, W. D. Marcus, M. U. Nollert, C. Zhu, R. D. Cummings, and R. P. McEver. 2002. Distinct molecular and cellular contributions to stabilizing selectin-mediated rolling under flow. J. Cell Biol. 158:787–799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ramachandran, V., T. Yago, T. K. Epperson, M. M. Kobzdej, M. U. Nollert, R. D. Cummings, C. Zhu, and R. P. McEver. 2001. Dimerization of a selectin and its ligand stabilizes cell rolling and enhances tether strength in shear flow. Proc. Natl. Acad. Sci. USA. 98:10166–10171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bruehl, R. E., T. A. Springer, and D. F. Bainton. 1996. Quantitation of L-selectin distribution on human leukocyte microvilli by immunogold labeling and electron microscopy. J. Histochem. Cytochem. 44:835–844. [DOI] [PubMed] [Google Scholar]
- 19.Ramachandran, V., M. U. Nollert, H. Qiu, W. J. Liu, R. D. Cummings, C. Zhu, and R. P. McEver. 1999. Tyrosine replacement in P-selectin glycoprotein ligand-1 affects distinct kinetic and mechanical properties of bonds with P- and L-selectin. Proc. Natl. Acad. Sci. USA. 96:13771–13776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Chesla, S. E., P. Selvaraj, and C. Zhu. 1998. Measuring two-dimensional receptor-ligand binding kinetics with micropipette. Biophys. J. 75:1553–1572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Chesla, S. E., P. Li, S. Nagarajan, P. Selvaraj, and C. Zhu. 2000. The membrane anchor influences ligand binding 2D kinetics rates and 3D affinity of FcγRIII (CD16). J. Biol. Chem. 275:10235–10246. [DOI] [PubMed] [Google Scholar]
- 22.Long, M., H. Zhao, K. S. Huang, and C. Zhu. 2001. Kinetic measurements of cell surface E-selectin/carbohydrate ligand interactions. Ann. Biomed. Eng. 29:935–946. [DOI] [PubMed] [Google Scholar]
- 23.Williams, T. E., S. Nagarajan, P. Selvaraj, and C. Zhu. 2001. Quantifying the impact of membrane microtopology on effective two-dimensional affinity. J. Biol. Chem. 276:13283–13288. [DOI] [PubMed] [Google Scholar]
- 24.Huang, J., J. Chen, S. E. Chesla, T. Yago, P. Mehta, R. P. McEver, C. Zhu, and M. Long. 2004. Quantifying the effects of molecular orientation and length on two-dimensional receptor-ligand binding kinetics. J. Biol. Chem. 279:44915–44923. [DOI] [PubMed] [Google Scholar]
- 25.Zhang, F., W. D. Marcus, N. F. Goyal, S. Selvaraj, T. A. Springer, and C. Zhu. 2005. Two-dimensional kinetics regulation of αLβ2-ICAM-1 interaction by conformational changes of the αL inserted domain. J. Biol. Chem. 280:42207–42218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Mege, J. L., C. Capo, A. M. Benoliel, and P. Bongrand. 1986. Determination of binding strength and kinetics of binding initiation. A model study made on the adhesive properties of P388D1 macrophage-like cells. Cell Biophys. 8:141–160. [DOI] [PubMed] [Google Scholar]
- 27.Chen, S., and T. A. Springer. 2001. Selectin receptor-ligand bonds: formation limited by shear rate and dissociation governed by the Bell model. Proc. Natl. Acad. Sci. USA. 98:950–955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Swift, D. G., R. G. Posner, and D. A. Hammer. 1998. Kinetics of adhesion of IgE-sensitized rat basophilic leukemia cells to surface-immobilized antigen in Couette flow. Biophys. J. 75:2597–2611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Goldman, A. J., R. G. Cox, and H. Brenner. 1967. Slow viscous motion of a sphere parallel to a plane wall. II. Couette flow. Chem. Eng. Sci. 22:653–660. [Google Scholar]
- 30.Happel, J., and H. Brenner. 1991. Low Reynolds Number Hydrodynamics. Kluwer Academic Publishers, Dordrecht, The Netherlands.
- 31.Pierres, A., A. M. Benoliel, C. Zhu, and P. Bongrand. 2001. Diffusion of microspheres in shear flow near a wall: use to measure binding rates between attached molecules. Biophys. J. 81:25–42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Schmidtke, D. W., and S. L. Diamond. 2000. Direct observation of membrane tethers formed during neutrophil attachment to platelets or P-selectin under physiological flow. J. Cell Biol. 149:719–730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Dembo, M., D. C. Tourney, K. Saxman, and D. Hammer. 1988. The reaction-limited kinetics of membrane-to-surface adhesion and detachment. Proc. Royal Soc. London. 234:55–83. [DOI] [PubMed] [Google Scholar]
- 34.Evans, E. 2001. Probing the relation between force–lifetime–and chemistry in single molecular bonds. Annu. Rev. Biophys. Biomol. Struct. 30:105–128. [DOI] [PubMed] [Google Scholar]
- 35.Lou, J., Y. Yago, A. G. Klopocki, P. Mehta, W. Chen, V. I. Zarnitsyna, N. V. Bovin, C. Zhu, and R. P. McEver. 2006. Flow-enhanced adhesion regulated by a selectin interdomain hinge. J. Cell Biol. 174:1107–1117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Nicholson, M. W., A. N. Barclay, M. S. Singer, S. D. Rosen, and P. A. van der Merwe. 1998. Affinity and kinetic analysis of L-selectin (CD62L) binding to glycosylation-dependent cell-adhesion molecule-1. J. Biol. Chem. 273:763–770. [DOI] [PubMed] [Google Scholar]