pK_a Values for Side-Chain Carboxyl Groups of a PGB1 Variant Explain Salt and pH-Dependent Stability

Abstract

Determination of pK_a values of titrating residues in proteins provides a direct means of studying electrostatic coupling as well as pH-dependent stability. The B1 domain of protein G provides an excellent model system for such investigations. In this work, we analyze the observed pK_a values of all carboxyl groups in a variant of PGB1 (T2Q, N8D, N37D) at low and high ionic strength as determined using ¹H-¹³C heteronuclear NMR in a structural context. The pK_a values are used to calculate the pH-dependent stability in low and high salt and to investigate electrostatic coupling in the system. The observed pK_a values can explain the pH dependence of protein stability but require pK_a shifts relative to model values in the unfolded state, consistent with persistent residual structure in the denatured state. In particular, we find that most of the deviations from the expected random coil values can be explained by a significantly upshifted pK_a value. We show also that ¹³C backbone carbonyl data can be used to study electrostatic coupling in proteins and provide specific information on hydrogen bonding and electrostatic potential at nontitrating sites.

INTRODUCTION

The stability of proteins depends on a detailed balance of forces and interactions. Electrostatic interactions are known to affect protein stability and can be both stabilizing and destabilizing. Due to functional constraints, electrostatic interactions in proteins may not be optimized for maximal stability under native conditions. Thus studies of pH- and salt-dependent protein stability are not only useful in understanding of the detailed balance of forces and interactions in proteins but can also report on specific electrostatic interactions and functionally important charged groups (1).

The goal of the study presented here is to explain the pH-dependent stability of PGB1 at different salt concentrations based on its pK_a values, and to analyze its pH titration behavior in a structural context. PGB1 is a 56-residue protein that binds immunoglobulin G and is highly stable over a wide range of pH and temperatures (2). Wt PGB1 contains 11 titrating carboxyl groups, five Glu, five Asp, and the C-terminus. Here, a variant of PGB1, referred to as PGB1-QDD, was studied. In this triple mutant, the T2Q mutation is introduced to avoid N-terminal degradation (3), whereas N8D and N37D are inserted to avoid deamidation of the protein at high pH and temperature (4). pK_a values of wt PGB1 using proton NMR were previously reported (5). In a detailed analysis of nonideal proton-binding titration curves of acidic groups in PGB1-QDD at low and high (0.5 M NaCl) ionic strength, significant charge-charge interactions between negatively charged residues were observed (6). In another study, the pH-dependent stability of PGB1-QDD was determined at different ionic strengths (0, 0.15, and 2M NaCl) using thermal unfolding and urea denaturations (7). The pH-dependent protein stability of PGB1-QDD was found to be largely insensitive to high concentrations of salt. This surprising result called for measurements of pK_a values at both low and high salt to promote understanding of this behavior.

Differences in pK_a values of titrating groups between the folded and unfolded state give rise to pH-dependent protein stability, and the contribution of this difference to protein stability can be found through a thermodynamic cycle (8). A number of studies have therefore investigated the pH-dependent stability of proteins through the determination of pK_a values (9–14). To fully describe the pH dependence of protein stability, pK_a values of the unfolded state must be determined. This is often experimentally unfeasible since the unfolded state is not significantly populated under physiological conditions. Tollinger et al. presented the first, and so far to our knowledge, only site-specific determination of pK_a values in an unfolded protein where the intrinsically unstable drkN SH3 domain was studied (15). For the large majority of proteins, the unfolded state has to be modeled using theoretical methods. In particular, the Gaussian chain model that treats the unfolded state as a random coil has been shown to give excellent agreement between theory and experiment in a number of cases (16–21). By combining experimentally determined pK_a values of the folded protein together with pK_a values calculated for the unfolded state, the pH dependence of protein stability can be predicted and compared with experimental data. Using this approach, the properties of the unfolded state can be probed and nonelectrostatic effects on stability can be investigated.

In the study presented here, we analyze the pK_a values of side-chain carboxyl groups determined from ¹³C chemical shifts in a structural perspective and use the pK_a values to calculate the pH-dependent stability of PGB1-QDD at low and high ionic strength. Using this data, we can address the question of the insensitivity of the protein stability of PGB1-QDD to salt. Our calculations show that the pH dependence of the protein stability can be explained by the observed pK_a values in the native state but requires pK_a shifts relative to model values in the unfolded state that are not consistent with the presence of a random coil. Finally, we also measure the backbone carbonyl chemical shifts of PGB1-QDD as a function of pH and show that these can serve as useful probes on electrostatic coupling in the protein and report on hydrogen bonding. Backbone carbonyl shifts provide probes on electrostatic interactions in proteins that are independent of the titrating residues.

MATERIALS AND METHODS

NMR spectroscopy

All spectra were recorded on a 500 MHz Varian (Palo Alto, CA) UNITY PLUS spectrometer at 25°C. Processing of NMR data was performed using NMRPipe program suite (22), and Sparky (T. D. Goddard and D. G. Kneller, University of California, San Francisco) was used for assignment and peak analysis. All assignment experiments were recorded using an NMR sample with 1.5 mM ¹³C ¹⁵N-labeled PGB1-QDD at pH 5 in 93% H₂O, 7% D₂O, 0.1 mM NaN₃, and 0.1 mM DSS. ¹H shifts were referenced using DSS, and ¹³C and ¹⁵N were indirectly referenced from the ¹H shifts using the conversion factors specified by IUPAC (24).

The ¹⁵N-HSQC spectrum of PGB1-QDD was assigned with a 3D-HNCA experiment (25), where the amide nitrogen (N^H) (ω1) is correlated with the α-carbon (C^α) (ω2) and the amide proton (H^N) (ω3), using standard methods and with the assignment of wt PGB1 as reference (26). The spectrum was acquired with 16 transients using 32, 32, and 1024 points in ω1, ω2, and ω3, respectively. 2D ¹⁵N-¹H HSQC and 2D ¹³C-¹H HSQC spectra were collected with four transients using 1024 points in ω2 and 128 points in ω1.

The side-chain carboxyl groups and backbone carbonyl groups were assigned by correlating the side-chain carboxyl ¹³C chemical shifts with the backbone amide proton chemical shift of the following residue as previously described (15). The spectra were collected with 32 transients using 1024 and 256 points in ω1 and ω2, respectively. The backbone carbonyl chemical shifts were determined from an HNCO experiment (15). The HNCO spectrum was acquired with four transients using 40, 96, and 1024 points in ω1, ω2, and ω3 respectively.

The titration of acidic groups in PGB1-QDD was followed using an H(C)CO experiment where the side-chain carboxyl carbon is correlated with the H^β or H^γ protons of aspartic and glutamic acid, respectively (23). At each pH value, an H(C)CO spectrum was recorded using 16 transients with 1024 and 128 points in ω2 and ω1, respectively. The spectral widths were 6000 and 1500 Hz in ω2 and ω1. All spectra were processed with a sinebell typically shifted 90° in the indirect dimension. The data size was doubled by zero-filling and the HNCA and HNCO experiments were processed using linear prediction in the ¹⁵N dimension.

NMR sample preparation and pH titration

¹⁵N and ¹³C labeled PGB1-QDD was expressed and purified as previously described (6,7). The NMR samples were prepared by dissolving PGB1-QDD labeled with ¹⁵N and ¹³C in 90% H₂O/10% D₂O containing 0.1 mM NaN₃ and 0.1 mM DSS to a concentration of 1.5 mM, and the initial NaCl concentration was 0.0 M or 0.5 M. The initial pH was 5.1 of the sample without salt, and the pH of the sample containing 0.5 M NaCl was 4.7. In both cases, the sample was split in two to use the same sample for upward and downward titrations.

The pH was measured with a MP225 pH-meter equipped with a combination electrode; U402-M3-S7/200, calibrated with pH 4.01, 7.00, 9.21, 11.0 standard solutions (Mettler Toledo, Columbus, OH). pH was adjusted with 0.2 M HCl or NaOH, and the pH was measured before and after each titration point, and in all cases the variation before and after acquisition was no more than 0.05 pH units. In the adjustment of pH during downward and upward titrations, the total added salt concentration amounted to 0.03 M and 0.006 M, respectively. The pH was corrected by 0.04 units to account for the presence of 10% D₂O in the sample (27). Spectra were collected at ∼0.25 pH unit intervals from pH 1.5–10.

Data analysis

The observed ¹³C chemical shifts for the side-chain carboxyl and carbonyl chemical shifts were plotted and fitted with nonlinear least-square regression analysis using the software Kaleidagraph (Synergy Software, Essex Junction, VT). The Henderson-Hasselbalch equation using a Hill parameter (n_H) to account for nonideality (28) was fitted to data:

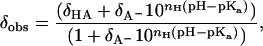(1)

where δ_obs, δ_HA, and δ_A− are the chemical shifts for the observed, protonated, and deprotonated species, respectively. The pH dependence of the carbonyl chemical shift for G14 and the side-chain carboxyl group chemical shift of E19 has two clearly distinguishable phases and were fitted with a two site model using

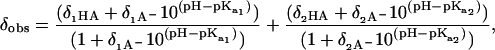(2)

Calculation of pK_a values in the unfolded state

A Gaussian chain model (16) of electrostatic interactions in the unfolded states of proteins was used to calculate the pK_a values in unfolded PGB1-QDD. In this model, the protein is described as an ideal chain where the distances between charge groups are distributed according to a Gaussian distribution p(r):

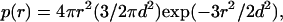(3)

where r is the distance between the charges in ångströms according to the amino acid sequence and d is the root mean-square (rms) distance (Å,) which is calculated as

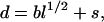(4)

where b is the effective bond length (7.5 Å) of each residue, l is the number of peptide bonds separating the two charged groups, and s (5 Å) is a shift that accounts for the average extension of side chains from the backbone (16,29). The electrostatic interaction between residue i and j is thought to follow the Debye-Hückel theory, i.e., a screened Coulombic interaction as

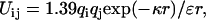(5)

where q is the charge, ɛ is the dielectric constant of the solvent, and κ the inverse of the Debye screening length. The mean electrostatic interaction energy (kJ/mol) between residue i and j is found as

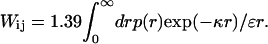(6)

The interaction energy is calculated using numerical integration. The average charge of a residue is found through Monte Carlo sampling using the following Boltzmann factor,

(7)

where W_tot is for the sum over all pairs of charges and is the model pK_a value (30). Values of 4.0, 4.4, and 3.8 were used for of Asp, Glu, and C-terminus, respectively.

Calculation of pH-dependent stability using generated pK_a values

The pH-dependent stability of a protein is predicted to be a direct function of the difference in charge between the native and unfolded state of a protein arising from differences in pK_a values (8). The free energy of unfolding 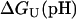for a protein depends on the charge of the residues in the folded and the unfolded state according to

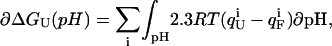(8)

where 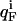and 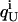represent the fractional charge of the residue i in the folded and unfolded state, respectively, calculated from the pK_a values according to

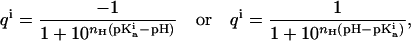(9a,b)

where Eq. 9a is used to calculate the charge of a negatively charged residue and 9b is used to calculate the charge of a positively charged residue.

The addition of salt was incorporated in the model as an increased Debye-Hückel screening. In a solution with 0.5 M NaCl, the Debye-Hückel length is decreased to 4.3 Å compared to >12 Å at the low salt concentration.

The calculated stability curve over the pH range only generates the pH-dependent electrostatic contributions, and therefore a baseline stability was added to qualitatively compare the curves to the previously achieved pH-dependent stability of PGB1-QDD (7). The reference shift was achieved by minimizing the rms deviation between the measured and calculated data.

RESULTS

Assignment

The ¹⁵N-HSQC spectrum of PGB1-QDD and the side-chain carboxyl chemical shifts were previously assigned (6). The backbone carbonyl chemical shifts were assigned using the HNCO experiment (15). Based on this assignment, the backbone carbonyl groups in the H(C)CO could be identified and followed as a function of pH. Due to overlap of ¹H chemical shifts with water, only 28 backbone carbonyl resonances could be identified and of those 21 showed significant pH-dependent chemical shift changes. The side-chain carbonyl resonances of Q2, Q32, and N35 were also recognized and showed slightly pH-dependent chemical shift changes.

pK_a values in PGB1-QDD

The electrostatic coupling between charges on Asp and Glu residues and the C-terminus in PGB1-QDD was previously studied in solutions without or with 0.5 M NaCl by monitoring the chemical shift of side-chain carboxyl carbons as a function of pH (6). The pK_a values resulting from an analysis of the titration curves are presented in Table 1. A number of residues have pK_a values significantly deviating from model values, which are 4.0, 4.4, and 3.8 for Asp, Glu, and C-terminus, respectively (30). For example, the pK_a values of D22, D47, and the C-terminus are significantly downshifted at low salt having pK_a values of 3.0, 3.1, and 3.1 respectively. The pK_a values of the mutated residues D8 (5.0) and D37 (6.6) are both upshifted compared to model compound values. The remaining pK_a values are found to be close to the values for model compounds. In 0.5 M NaCl, the pK_a values are closer to the model pK_a values for Glu and Asp but significant pK_a shifts remain in the presence of salt. The average change in pK_a value due to the addition of salt is 0.17 units. The pK_a value of the N-terminal amino group cannot be determined with the set of experiments used in this article. However, the titration curve of E19 clearly shows a second phase around pH 9 (Fig. 1). Due to the proximity of E19 to the N-terminus, we believe that the chemical shift changes of E19 at high pH correspond to the titration of the N-terminus. It is also the only residue likely to titrate at that pH. Using a two-site model, the pK_a of the N-terminal group could be determined to 8.9 and 9.0 in solutions containing no added and 0.5 M NaCl, respectively.

TABLE 1.

pK_a values for wt PGB1 (5), PGB1-QDD in low, 0.5 M NaCl and MC-simulated pK_a values of the unfolded state using a Gaussian chain model (16)

Residue No.	Wt	QDD low salt	Difference (QDD-wt)	QDD 0.5 M salt	nH low salt	nH 0.5 M salt	QDD unfolded
D8	–	5.0	–	4.7	0.6	0.8	3.5
E15	4.4	4.6	0.2	4.7	0.8	0.9	4.2
E19	3.7	3.9	0.2	4.0	1.0	1.0	4.4
D22	2.9	3.0	0.1	3.2	1.0	1.0	3.8
E27	4.5	4.8	0.3	4.9	0.8	0.9	4.0
D36	3.8	4.2	0.4	4.1	0.8	0.9	4.0
D37	–	6.6	–	6.2	1.1	1.1	4.1 (6.0)
D40	4.0	4.1	0.1	4.1	0.7	0.9	4.1
E42	4.4	4.9	0.5	4.6	0.7	0.9	4.7
D46	3.6	3.8	0.2	3.9	0.9	0.9	4.1
D47	3.4	3.1	−0.3	3.4	0.9	1.0	4.1
E56	4.0	3.8	−0.2	3.9	0.5	0.6	4.7
C-term		3.1		3.2	0.7	0.8	3.8

Hill parameters, n_H, derive from fitting Eq. 1 to data for PGB1-QDD in low and high ionic strength. The pK_a value in parenthesis for D37 in the unfolded state is the shifted value used in the calculations. The values are determined within ±<0.1 pH units.

FIGURE 1.

Titration curve of E19 analyzed with a two-state model, Eq. 2 (solid curve). The pK_a values for the shift change at high pH was determined as 8.9 in low salt (•) and to 9.0 in 0.5 M salt (○).

Shifts in PGB1-QDD compared to wt

Table 1 shows the pK_a differences between wt PGB1 (5) and PGB1-QDD, and Fig. 2 explicitly shows charged residues color-coded according to shifts relative to model values (30). Higher pK_a values of PGB1-QDD compared to wt are referred to as upshifted, and lower values are referred to as downshifted. Generally, the pK_a values are upshifted in the mutant compared to wt. This is expected from the larger net charge and the lower salt concentrations used in the study of the mutant. The total upshifts of carboxylates sum to 2.0 units (not including mutated residues), whereas the downshifts sum to 0.5 units. Both mutated residues, D8 and D37, have upshifted pK_a values compared to model values. Not surprisingly, D36, which is in close proximity to D37, has a markedly upshifted pK_a value compared to wt. E42 also has a highly upshifted pK_a value compared to wt, 0.5 pH units. There are two residues that are downshifted compared to wt; D47 and E56.

FIGURE 2.

Structure of PGB1-QDD with all charged side-chain groups explicitly shown prepared from the Protein Data Bank file 1PGB (42). Carboxyl groups are black and lysine residues are red. pK_a differences compared to model values are indicated in the backbone where red indicates upshifted and blue downshifted. The mutated residues were modeled into the structure using Swiss model (43) and the figure was prepared using MOLMOL software (44).

Protein net charge

The overall titration curve displays the net charge of the protein over the entire pH range and displays a flatter shape for PGB1-QDD compared to the ideal titration curve generated with model pK_a values (Fig. 3). PGB1-QDD in the presence of salt lies in between the low ionic strength and the ideal titration curve over the whole pH range, as expected. A flatter curve indicates electrostatic coupling in the system and a lower capacitance to bind protons for the protein as a whole (31). From the overall titration curve, the pI can be determined to 4.2 for the simulated curve using model pK_a values and to 4.3 using the experimental pK_a values both in high and low ionic strength (inset). The same calculations performed for wt PGB1 give a pI of 4.4 based on model pK_a values, whereas the previously reported pK_a values (5) give a pI of 4.2 (Fig. 3); hence the wt protein has a markedly downshifted pI compared to model values, which is not the case for PGB1-QDD.

FIGURE 3.

Protein net charge of folded PGB1-QDD according to model pK_a values (solid curve), pK_a values in low salt (solid curve with solid circles), and pK_a values in high salt (solid curve with open circles). Protein net charge of wt PGB1 according to model pK_a values (dashed curve) and pK_a values from (5) (solid curve with triangles). (Inset) pI for the different proteins and models.

Backbone carbonyl chemical shifts

For some residues, the backbone carbonyl carbon resonances could be located and assigned in the H(C)CO experiment and were found to display pH-dependent chemical shifts (Table 2). Since the carbonyl carbon is not involved in a proton binding process itself, this group must sense and display the titration processes of other groups. The carbonyl group of a residue with a side-chain Glu or Asp seems to report the same pK_a value as the carboxyl group. The carbonyl groups of D36 and D47 report pK_a values of 4.1 and 3.2, respectively, whereas the carboxyl groups give values of 4.2 and 3.1 (Table 1 and Fig. 4 a). The shift differences over the pH range are quite large, >1 ppm. pH-dependent ¹³C chemical shifts of the carbonyl group for other residues than Asp or Glu are also found. Shift differences in carbonyl carbon for G38 over the pH range report a pK_a value of 6.6, V21 a pK_a value of 3.0, A23 a value of 3.0, and A48 a pK_a value of 3.4. Hence, it seems that these residues report the pK_a value of the previous or following carboxyl group in the sequence D37, D22, and D47, respectively. K4 reports on a pK_a value of 4.7, but there is no nearby acidic group in the sequence. However, in a structural context, E15 is in the proximity and titrates with a pK_a value of 4.6. G14 reports on two distinct titration curves, one with decreasing chemical shift (pK_a = 4.4), which is probably due to E15, and one with increasing chemical shifts (pK_a = 6.8), probably from D37. Here, the shift differences over the pH range are much smaller (0.2–0.5 ppm) than the shift differences for carbonyl carbons reporting on a carboxyl group of the same residue. However, the carbonyl carbon of K10 also displays a quite large shift (1 ppm), and reports a pK_a value of 3.9 (Fig. 4 b), which agrees with the value obtained for the nearby E56 side chain.

TABLE 2.

pK_a values in low salt of some backbone carbonyl carbons that displayed pH-dependent chemical shift differences; the values are determined within ±<0.1 pH units

Residue	pKa value from carbonyl carbon	Δppm
Y3	4.9	−0.3
K4	4.7	−0.4
G9	4.5	0.9
K10	3.9	1.0
G14	4.4/6.8	−0.2/0.2
T17	4.6	0.2
E19	3.8	0.3
V21	3.0	−0.4
A23	3.0	0.5
K28	4.0	0.3
Q32	4.1	−0.7
D36	4.1	1.3
G38	6.6	0.2
G41	3.1	0.2
E42	5.1	0.2
D47	3.2	1.3
A48	3.4	0.5
T49	3.7	−0.3
T51	5.1	-0.3
T53	4.7	0.2

FIGURE 4.

(a) ¹³C backbone carbonyl chemical shifts A48 (○) and D47 (▴) with ¹³C side-chain carboxyl chemical shift of D47 (•). (b) The hydrogen bond between K10 and E56 (•) is displayed in pH-dependent ¹³C backbone carbonyl chemical shift of K10 (▴). In a and b, Eq. 1 was fit to data and is shown as a solid curve.

The backbone carbonyl carbon of M1 showed pH-dependent ¹³C chemical shifts where the shifts changed >0.9 ppm over the pH range. Due to spectral overlap, the shifts could not be monitored above pH 8 and a complete titration curve was not obtained. It is, however, evident that the shift differences report on a titration event starting above pH 7 in accordance with the proximity to the N-terminus.

For some residues (K4, V21, Q32, T49, T53, and G14 (titration with pK_a = 4.4)), a decrease in chemical shift with increasing pH is observed.

Model of pH-dependent stability using generated pK_a values

The electrostatic contribution to the pH dependence of protein stability can be readily obtained with the knowledge of pK_a values of the native and unfolded state of a protein. Alternatively, knowledge of the experimental pH dependence of protein stability can be used to determine the contribution of electrostatic interactions to the observed pH dependence and can also be used to probe the properties of the denatured state. Thus, simulations of the electrostatic contribution to the pH dependence of protein stability were performed using different descriptions of the unfolded state. Fig. 5 displays the stability curves generated from the experimental pK_a values of the native state and the calculated pK_a values for the unfolded state, using Eq. 8 and using model values (30). The calculations do not yield the absolute value of stability, so a reference stability was added to all calculated curves to simplify the comparison. This reference value was adjusted by minimizing the rms deviation between the calculated curve and experimental data. The smooth curves in Fig. 5 display the calculated stability curve from pK_a values in low and 0.5 M salt. The experimental stability determined from urea and thermal denaturations is displayed with circles and triangles, respectively (7), and was studied at low (a) and 2 M salt (b). The stability curves calculated by modeling the unfolded state as a random coil using the Gaussian chain model or with model pK_a values at low salt (dashed curves) disagree with the experimental stability both at pH values below and above the pI.

FIGURE 5.

Generated stability curves for PGB1-QDD based on experimental pK_a values for the native state and calculated pK_a values for the unfolded state (Table 1), which are compared to pH-dependent denaturation data (7). (a) Curves generated in low salt where the unfolded state is modeled as a Gaussian chain (dashed), model pK_a values (dashed-dotted) Gaussian chain but the pK_a value of D37 is shifted to 6.0 (solid), and a uniform pK_a shift of 0.2 units (dotted). All curves in a are generated using a pK_a value of 8.9 for the N-terminus in the folded state. (b) Curves generated in 0.5 M salt where the pK_a values of the unfolded state were modeled as a Gaussian chain but where the pK_a value of the N-terminus is 9.0 (solid) and 7.5 (dashed). Experimental stability data in low salt (•) and 2 M NaCl (▴). In a, the calculated curves were shifted to minimize the rms deviation between experimental and calculated data points. In b, the curve was shifted to fit experimental data at pH >5.

The electrostatic contribution to the pH dependence of the unfolded state is determined by the difference in charge between native and unfolded protein. With experimentally determined values of the pH dependence of protein stability and pK_a values of the native state, deviations between experiment and calculations can be attributed to an incorrect description of the unfolded state, and in particular its pK_a values. D37 is the only residue titrating in the pH range above the pI in the native state where a deviation is seen. A possible explanation is that the pK_a value of D37 is upshifted in the unfolded state. To test this hypothesis, a stability curve with an upshifted pK_a value of D37 to 6.0 in the unfolded state was generated. With this shift, most of the deviations between the experimental and simulated curve are removed (Fig. 5 a, solid curve). To investigate whether experimental data could be reproduced by evenly distributed shifts on all pK_a values in the unfolded state, a curve where all carboxyl-group pK_a values were upshifted 0.2 units was generated (Fig. 5 a, dotted curve). This shift was chosen to get the smallest rms deviation between calculations and experimental data, and showed a similar rms deviation when only one residue had a major shift. Nevertheless, the two shifted curves have different appearances where the curve with distributed shifts overestimates the stability maximum.

In the presence of 0.5 M NaCl, the pH dependence of the stability is reduced compared to low ionic strength as expected. Data can be compared to the experimental pH dependence at 2 M NaCl (triangles). The shape of the titration curve is well described by the calculation, but the pH optimum is overestimated. This is expected because the experimental data are collected in 2 M NaCl where electrostatic interactions should be further reduced. Therefore the curve is shifted to fit data at pH above 5. It is not necessary to introduce an upshifted pK_a value in the unfolded state to obtain a qualitative agreement between calculation and experiment. The calculated pK_a values in the unfolded state are almost identical with model values at 0.5 M NaCl due to screening (data not shown).

All the stability curves were calculated using an upshifted pK_a value of the N-terminus in the folded state, which is required to get a good agreement with experimental data at pH values above 7. As an example, the stability calculated without an upshifted pK_a value of the N-terminus is shown in Fig. 5 b (dashed line). The pK_a value of the N-terminus in the folded state could be estimated to 8.9 and 9.0 in low and high ionic strength, respectively, from the E19 titration curve (Fig. 1).

DISCUSSION

pK_a values of proteins provide valuable information about electrostatic interactions and their contribution to protein stability. Individual pK_a values report on the contribution of charged residues to protein stability without the need of mutations, which can have other stability effects. Proteins need not to be optimized for stability under physiological conditions and proteins can have charges that are destabilizing but essential for function and solubility. pK_a values are outstanding reporters of such possible interactions in a straightforward manner.

Shifted pK_a values in PGB1-QDD and comparison to wt PGB1

PGB1 serves as an excellent model protein to describe electrostatic interactions on the surface of proteins. The protein contains almost exclusively surface-exposed charged residues and shows distinct pH-dependent protein stability, which indicates significant electrostatic interactions. The pK_a values of wt PGB1 were previously determined with ¹H NMR (5). The variant used in our study, PGB1-QDD, contains two additional charges compared to wt PGB1. The pK_a values of the mutated residues, D8 and D37, are both upshifted. Strikingly, the pK_a value of D37 is significantly upshifted to 6.6, indicating that this residue is highly destabilizing in the charged state. Also the pK_a values of D36 and E42 are significantly upshifted compared to wt PGB1, showing that these are electrostatically affected by the mutations and sense repulsive forces. The opposite effect is found for D47 and E56, which have pK_a values that are downshifted compared to wt PGB1 and hence sense less repulsion or form interactions in the charged state that do not exist in wt PGB1. These residues with downshifts are located at opposite ends of the protein, and since they titrate at pH values below the pI, they report on the electrostatic potential in an overall positive protein. For the rest of the residues, the changes are relatively small but overall the pK_a values of the carboxyl-groups are significantly upshifted compared to wt PGB1, which results in the two variants having similar pI values (Fig. 3, inset) despite the two extra charges in PGB1-QDD. The adjustments of pK_a values due to the introduced mutations are not distributed evenly throughout the protein but rather with site-specific up- and downshifts as expected.

Origins of pK_a shifts

The structure of PGB1-QDD is not known but should resemble wt PGB1 based on the small chemical shift differences of this mutant compared to wt (7) and the similar pK_a values for a majority of the residues. However, subtle structural perturbations can give rise to significant changes in molecular properties due to, for example, changes in hydrogen bonding pattern.

The low pK_a value of D22 is also found in wt PGB1 and appears to be a consequence of hydrogen bond formation to T25 (5) and an attractive Coulombic interaction with the N-terminal amine group. This indicates that that the pK_a value of the N-terminus is upshifted in the native state.

The pK_a value of D37 is radically upshifted compared to its model value. Based on the overall negative charge of the protein, it is not surprising that the pK_a value of D37 gets upshifted so as to minimize repulsion with the rest of the protein. Similarly high pK_a values were observed in the highly negatively charged protein calbindin D_9k (32). The large pK_a shift of D37 can be partially explained by the repulsion of D36. However, calculations of Coulombic interactions for D37—with all other charges using experimentally determined pK_a values, and the assumption that all charges are fully solvent exposed—indicate that its pK_a value should not shift away from model values (data not shown). An alternative explanation to the large shift is that the protonated carboxyl group of D37 hydrogen bonds to a charged carboxyl group from another residue. This was suggested before by Chen et al. in another system (33) where the pK_a value of a glutamate was increased to 6.8 and believed to hydrogen-bond to another glutamate. Interestingly, the pK_a value of the hydrogen bond acceptor glutamate was only marginally shifted away from the model value for Glu. A hydrogen bond of this type would result in a favorable interaction that in our case keeps D37 protonated to high pH-values. Potentially the shift could be explained by D37 being deeply buried in an apolar environment thus preventing the deprotonation. However, the small core of PGB1 makes this explanation less plausible. Moreover, in the wt PGB1, N37 is on the surface, and the close chemical shift correspondence with wt makes substantial structural changes unlikely.

The C-terminus has a significantly downshifted pK_a value in PGB1-QDD, which is rather unexpected. At low pH, the C-terminus senses attractive forces from K10 and K13, but when the pH is increased there are also major repulsive forces from D40, E42, and E56. According to the structure, the carboxyl oxygens of E56 hydrogen bond to K10 and D40 backbone NH. These favorable interactions are probably responsible for the downshift of the pK_a value of E56 despite the proximity to the C-terminus. The hydrogen bond to K10 is supported by the fact that its carbonyl group reports on the pK_a value of E56 (3.8), has a very large chemical shift difference upon (de)protonation, and displays a similarly extended titration process (n_H = 0.6). Possibly, the C-terminus is also involved in hydrogen bonding to further generate favorable interactions. For example, the carbonyl carbon of G41 displays the same pK_a value as the C-terminus (3.1), indicating some interaction or proximity between these groups. The structure also suggests a hydrogen bond between the backbone amide of D36 and the backbone carbonyl of Q32; this is further supported by the pK_a value displayed by the carbonyl carbon of Q32 (4.1) that is similar to the pK_a value of D36 (4.2) carboxyl group.

Khare et al. (5) extensively discussed hydrogen bonding in wt PGB1, which affected its pK_a values. They suggested that the hydrogen bond between Y45 and D47 was strong, which also seems to be the case for PGB1-QDD, since the pK_a value of D47 is downshifted even further compared to wt.

Salt effects

With the addition of salt, the electrostatic interactions will be shielded and the pK_a values should on average approach model values. The salt dependence of pK_a values has previously been determined for His in staphylococcal nuclease, in horse and whale myoglobin, as well as for Glu in the N-terminal domain of rat CD2 (33–36). In myoglobin, the average change in pK_a value is 0.3 units from 0.02–1.5 M salt. In CD2, small changes toward model pK_a values were observed. As an example, the highly upshifted E41, pK_a of 6.8, only decreased to 6.7 with the addition of 300 mM salt.

In the study presented here, the pK_a values are also remarkably little affected (0.17 pH units on average) by the addition of salt, and all carboxyl groups tend to approach model values with added salt. In part, this small effect of salt may be due to the high protein concentration used (1.5 mM), which together with its counter ions offers significant screening of electrostatic interactions (37,38).

Shifts from model pK_a values do not only arise due to ionic interactions. Self-energies and specific dipole-dipole or charge-dipole interactions can perturb pK_a values away from model compound values. For example, it has been shown that hydrogen bonds in small molecules can drastically change pK_a values (39). At the same time, model pK_a values are dependent on the molecular context in which they are measured (40). The fact that the titration curves approach ideality with the addition of salt (as seen in the n_H values that approach unity) indicates that electrostatic coupling is reduced in the system, which contradicts the small salt-induced change in pK_a values (6). A possible explanation to this paradox would be to realize that non-Coulombic interactions can be the major determinant of the shift so that the measured pK_a values do not necessarily approach model compound values even after complete screening of charge-charge interactions by salt. Another support for pK_a shifts due to non-Coulombic effects is that the N-terminus has a shifted pK_a value at both high and low ionic strength (Fig. 1).

Interactions observed via ¹³C carbonyl chemical shifts

Electrostatic coupling in the system is also evident from the pH dependence of many carbonyl carbon chemical shifts. Here, the chemical shift differences of the carbonyl carbons over the pH range were much smaller than those observed for carboxyl groups. By analyzing the carbonyl chemical shifts of the titrating residues as well as the residues that precede and follow Glu and Asp residues, it is found that they report on the pK_a values of these acidic side chains. For carbonyl groups separated from a titration site by a small number of chemical bonds, a through-bond effect is expected. Indeed, for the two Asp carbonyl groups that could be identified, we observe shifts of 1.3 ppm, and the pK_a derived from these shifts agree with the values obtained from the side chain, as shown in Table 2. Of more interest are those carbonyls not adjacent to Asp or Glu in the sequence, for which the pH-dependent carbonyl chemical shift is necessarily due to pH-dependent structural changes, Coulombic interactions (charge-dipole interactions), or hydrogen bonding. Indeed, such interactions are probed: For example, the backbone carbonyl of K10 is hydrogen-bonded to the side-chain carboxyl group of E56. As a result, the carbonyl resonance is shifted with pH by 1.0 ppm and is found to accurately reflect the pK_a value of E56. As a second example, the carbonyl moiety of Q32 hydrogen-bonds to the backbone amide of D36, and displays the pK_a of the acceptor group. The backbone carbonyls of M1, Y3, K4, T49, T51, and T53 do not have any neighboring acidic residues and are not seen to be involved in any hydrogen bonds with titrating residues, so that the pH dependence most likely results from Coulombic effects. The apparent titration data are ill explained by a single protonation equilibrium for each of these residues, and presumably result from a combination of long-range effects. G14 exhibits two pK_a values: 4.4 due to the neighboring glutamate (E15) and 6.6, presumably as a result of the protonation of D37 (which is the only residue that titrates in that range). The structural coordinates of the D37 side chain are unknown, since this is an engineered residue, but is expected to be rather distant from the backbone carbonyl of G14 based on the modeled structure. Possibly the observed shift is transmitted due to a change in structure or hydrogen bonding network upon (de)protonation.

Side-chain ¹³C carboxyl chemical shifts are superior in determining the charge state of titrating residues because of their sensitivity and the fact that they only report on a single titration process (these are important advantages over ¹H chemical shifts). However, backbone ¹³C carbonyl chemical shifts provide unique reporters on the electrostatic potential at sites different from the proton binding site in the protein. They can also be used to probe hydrogen bonding of charged residues with backbone carbonyl oxygens as indicated by our result. Finally, by coupling the carbonyl that senses a protonation event to the group that undergoes the titration, a unique picture of the distance dependence of Coulombic interactions can be found (in most cases the titration will be a weighted sum of titration curves of multiple residues). Thus, the results presented here show that carbonyl chemical shifts can give additional information about electrostatic interactions in proteins. Although our understanding of the origin of carbonyl chemical shifts is limited, these shifts can provide useful information on electrostatic coupling, hydrogen bonding, and the dielectric properties of proteins. In particular, these shifts will be of great use if empirical rules can be established.

pH-dependent stability

The pH dependence of protein stability can be calculated indirectly from the pK_a values of the folded and unfolded state through a thermodynamic cycle (8). This method has been used to explain the pH-dependent stability of proteins (9–14) and to prove that it is of electrostatic origin. It has also been used as a means to study the properties of the unfolded state by allowing models of the unfolded state to be correlated against experiments (10,16,20,41) or by calculating the average pK_a shifts relative to model compound values (10). In this study, we present the pK_a values for the native state of PGB1-QDD. The pH-dependent stability is found as the difference in free energy between the unfolded state and folded state. Normally, it is difficult to measure pK_a values of the unfolded state under physiological conditions since their population is small. It is not possible to assure that the denatured state under nonphysiological conditions is the same state as the unfolded state under physiological conditions. The pK_a values of unfolded PGB1-QDD are unknown and a model had to be constructed to predict these values. In the simplest approach, the pK_a values of the unfolded state are assumed to approach model values. The model value assumption usually does not fit experimental data particularly well (10,16,41) (Fig. 5 a). A slightly more sophisticated model is to describe the unfolded state as an ideal chain with Gaussian-distributed distances between charged residues. This Gaussian chain model of electrostatic interactions in the unfolded state has been shown to give excellent agreement with experimental data for a number of proteins (16–21). In the case of PGB1-QDD, the generated model fails to describe data both below and above the pI (Fig. 5 a). This result indicates that either there is more to the pH dependence than electrostatic interactions or the unfolded state is not modeled in a correct way. The deviation above the pI must reflect one or more upshifted pK_a values in the unfolded state. In principle, this could be the pK_a value(s) of any residue(s), but since D37 is the only residue that in the native state titrates in the range where the discrepancy is found, it is plausible that the pK_a value of D37 is not correctly modeled in the unfolded state. By shifting the pK_a value of D37 in the unfolded state to 6.0, most of the deviation between the experimental and calculated pH dependence is removed and a good agreement is found. However, deviation between the experimental and calculated pH stability still exist at pH values below pI. Here it is not clear that a single shift can explain the data (although the pK_a value of D8 is suspiciously low for the denatured state) and simulations with perturbations of pK_a values below pI were not attempted since they could not be rationally performed. Raising the pK_a values of all Asp and Glu in the unfolded state by a small amount (0.2 pK_a units) also yields a stability curve that fits the data reasonably well (rms deviation is the same compared to the shifted Gaussian chain model) but clearly overestimates the maximum stability. However, the shifted Gaussian chain model represents a significantly better model for the general shape of the stability curve. Furthermore, there is no physical basis for modeling the unfolded state with a uniform pK_a shift. The pH dependence of stability above pH 7 clearly indicates that the pK_a value of the N-terminus is upshifted in both low and 0.5 M salt and the calculations confirm this result.

One explanation for the failure of the Gaussian chain model can be that it only accurately models the unfolded state when the shift differences are minor. In a highly charged system, it is not surprising that low resolution mean-field models fail to fully describe data, since it is not constructed to model specific interactions. In any case, we can conclude that the unfolded state of PGB1-QDD cannot be described by any of the theoretical models, neither with model pK_a values nor with a model treating the unfolded state as a random coil. Thus, the discrepancies between experimental and calculated pH stability below and above pI indicate that the unfolded state contains residual structure, perhaps around D37.

The pH dependence of the stability for PGB1-QDD is significantly different at high ionic strength. Using Eq. 8, we can only calculate the difference in stability from one pH value to another. This approach only accounts for screening of titrating groups and hence only affects repulsion among carboxylate-groups and attraction between carboxylate-groups and lysine residues. Screening of repulsion between lysine residues at lower pH does not affect the calculation, because these groups do not titrate in this pH interval and give a constant contribution. At high salt, the pH-dependent stability is well described by the calculation and the pK_a value of D37 in the unfolded state does not have to be adjusted. This is reasonable, because screening by salt should be significantly more effective in the unfolded state. This further supports the presence of the residual structure in the unfolded state at low ionic strength around D37. The fact that the pK_a value of the N-terminus in the native state in high ionic strength does not approach the model-value of 7.5 further supports that the shift is due to non-Coulombic interactions.