Contour Length and Refolding Rate of a Small Protein Controlled by Engineered Disulfide Bonds

Abstract

The introduction of disulfide bonds into proteins creates additional mechanical barriers and limits the unfolded contour length (i.e., the maximal extension) measured by single-molecule force spectroscopy. Here, we engineer single disulfide bonds into four different locations of the human cardiac titin module (I27) to control the contour length while keeping the distance to the transition state unchanged. This enables the study of several biologically important parameters. First, we are able to precisely determine the end-to-end length of the transition state before unfolding (53 Å), which is longer than the end-to-end length of the protein obtained from NMR spectroscopy (43 Å). Second, the measured contour length per amino acid from five different methods (4.0 ± 0.2 Å) is longer than the end-to-end length obtained from the crystal structure (3.6 Å). Our measurement of the contour length takes into account all the internal degrees of freedom of the polypeptide chain, whereas crystallography measures the end-to-end length within the “frozen” protein structure. Furthermore, the control of contour length and therefore the number of amino acids unraveled before reaching the disulfide bond (n) facilitates the test of the chain length dependence on the folding time (τ_F). We find that both a power law scaling τ_F ∝ n^λ with λ = 4.4, and an exponential scaling with n^0.6 fit the data range, in support of different protein-folding scenarios.

INTRODUCTION

Many important predictions of the physical models for protein folding and unfolding show a clear dependence on the number of amino acids, n, in a protein chain. These include the WLC theory of polymer elasticity (1) to measure the contour length of the molecule (2–7) and the scaling of protein-folding times with n (8–11). There is a wide discrepancy in the contour length contribution per amino acid for different proteins in the literature and, surprisingly, no apparent trend for the folding times as a function of the length of the chain. The diversity of the proteins used in previous studies and the variety of their respective transition state positions have precluded the investigation of the effect of n alone on contour length and folding rates.

With the aim of retaining the same transition state, yet unfolding varying numbers of amino acids, we engineer single disulfide bonds (S-S) into various locations of the human cardiac titin I27 module (12). We then study the folding and unfolding properties of the different constructs using the force-extension technique with an AFM (13). When a protein is placed under force, it first extends up to its mechanically stable transition state, where the protein's tertiary structure is still intact and able to store elastic energy. Stretching beyond this point disrupts the mechanical architecture and leads to the unraveling of the protein (14). These experiments are usually interpreted using the WLC theory of entropic elasticity (1), which predicts the total contour length, ΔL_u, of the protein, proportional to the number of unraveled amino acids in the chain. The contour length measured by force-extension experiments is therefore defined as the maximum distance between the mechanically stable transition state and the fully extended state of the linear protein chain with no degrees of freedom. All previous studies using force-extension experiments with an AFM have calculated the contour length as the distance between the native state and the extended state along the reaction coordinate, neglecting the important contribution of the distance up to the transition state (2–6,15,16). For this reason, the cited values for the contour length per amino acid, l, vary from protein to protein, spanning from 3.4 Å (2) to 3.6 Å (3,15,16), 3.8 Å (4–6), and further up to 4.0 Å (7).

The position of a disulfide bond was previously shown to uniquely determine the contour length associated with protein unfolding, ΔL_u, in a number of different proteins (17–20). In our study, varying ΔL_u within the same protein allows for the most accurate determination of the contour length per amino acid to date as well as the characterization of the end-to-end length of the transition state from the extrapolated value at zero contour length. We employ four independent measurements, including force-extension and force-clamp techniques as well as SMD simulations, to obtain the contour length of an amino acid.

The same disulfide-bonded constructs that allow for the controlled variation in the unfolded number of amino acids also provide a unique platform for studying the effects of chain length on protein folding. The architecture of the protein free energy landscape can be inferred from the scaling of the protein folding time, τ_F, with n. Several such theoretical predictions have been postulated in the literature, satisfying different folding scenarios (21–24). Furthermore, a variety of numerical simulations have predicted a strong dependence of folding times on n in model proteins (10,25,26) as well as its dependence on the interaction energies between the native contacts, the presence of side chains, and the topology of the native-state fold. However, previous ensemble refolding experiments have argued that the folding times are solely determined by the native state topology, as quantified by contact order (CO), exhibiting little or no correlation with the chain length (8–11,27). These experiments were performed on a variety of proteins, where the distinct amino acid sequences and the topologies of the native structures may have played a dominant role in the time scales of protein folding.

Because we precisely control the contour length with engineered disulfide bonds in our experiments, we can also measure the refolding time dependence on chain length within the same protein molecule and thus directly test the existing theoretical models for folding. The data indicate that an energy landscape with a power law scaling with n, as well as glassy models with a heterogeneous distribution of energy barriers successfully describe the experimentally observed trend.

MATERIALS AND METHODS

Protein engineering

We used I27_Cys-free protein, a cysteine-free version (Cys⁴⁷ to Ala, Cys⁶³ to Ala) of the 27th module of the I band of human cardiac titin (I27) as a platform to engineer the I27 mutants used in this study. Disulfide bonds at specific positions were engineered by introducing additional mutations according to methods described elsewhere (13): Gly³² to Cys, Ala⁷⁵ to Cys (I27_G32C-A75C); Pro²⁸ to Cys, Lys⁵⁴ to Cys (I27_P28C-K54C); Glu²⁴ to Cys, Lys⁵⁵ to Cys (I27_E24C-K55C); Asp⁴⁶ to Cys, His⁶¹ to Cys (I27_D46C-H61C). The residue pair for cysteine mutations was chosen such that their C_α atoms are separated by 3.5–5.5 Å in the NMR structure of titin I27 (Protein Data Bank file: 1TIT). This simple selection criterion proved to be very useful in comparison to the computationally intensive approach based on the disulfide bond prediction algorithm (28). In our experiments we used polyproteins made of eight identical repeats of a single type of mutant I27 protein. The (I27_P28C-K54C)₈ polyprotein was engineered with two C-terminal cysteines for attachment as described previously (13). However, because these cysteines proved unnecessary, they were not used in the other constructs. The synthetic polyproteins were cloned into pT7Blue vector-XL1Blue E. coli system and expressed in pQE80L vector-BLR(DE3) E. coli cells. The proteins were purified using Ni²⁺ affinity chromatography followed by size-exclusion chromatography.

Single-molecule force spectroscopy

The details of the AFM and its mode of operation have been described elsewhere (13,29). The spring constant of the cantilevers used in our experiment was measured using the equipartition theorem (30). We used silicon nitride cantilevers (Veeco, Santa Barbara, CA) with an average spring constant of ∼45 pN/nm in force-extension experiments and those with ∼15 pN/nm in force-clamp experiments. An aliquot of 5–10 μl of the polyprotein (0.1 mg/ml) solution was added to the PBS solution, pH 7.0, on a gold-coated cover slide and immobilized for 10 min. The presence of disulfide bond in the disulfide-engineered I27 modules was confirmed by recoding 2–10 sawtooth-patterned force-extension traces containing unsequestered unfolding events only. The disulfide reducing agent, DTT (5–100 mM), was then added to the solution from a stock solution of 1 M in PBS and thoroughly mixed. The pulling of the polyproteins was resumed to record the unsequestered unfolding and disulfide bond reduction events under a stretching force. However, in protein-refolding experiments and force-clamp experiments, the polyprotein is directly added to the PBS solution containing the specified amount of DTT. In all our force-extension experiments the pulling rate was 400 nm/s unless otherwise mentioned. All our experiments were performed at room temperature.

RESULTS AND DISCUSSION

The fingerprint of an engineered disulfide bond

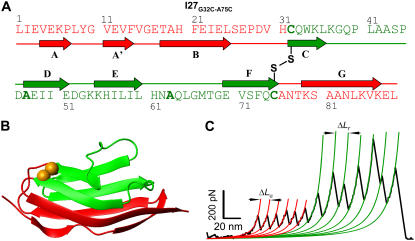
Fig. 1 demonstrates the engineering of a single disulfide bond into the I27_Cys-free protein. We engineered two Cys residues into positions 32 and 75 (G32C-A75C), which are distant in the sequence (Fig. 1 A) but are vicinal in the structure (Fig. 1 B). They are situated in the β-strands, which are flexible enough to allow for their spontaneous oxidation, forming a disulfide bond. In Fig. 1 B, we show the 46 amino acids that remain “unsequestered” by the disulfide bond (red) as well as the 43 amino acids that are “trapped” behind the mechanically strong disulfide bond (green). The reduction of the disulfide bond, which is a prerequisite for the unfolding of the trapped amino acids, is never observed in the absence of a reducing agent, such as DTT, independent of the position of the disulfide bond. This result is in agreement with the observation that covalent bonds are mechanically too strong for rupture below 1 nN of force (31). The kinetics of reduction of the disulfide bond under a stretching force has been established previously (32). The experiments are therefore performed in the presence of DTT, such that both the unfolding and reduction under a stretching force can be observed within the same force-extension trace. In all our experiments, we are concerned with measuring the contour length increase after the disulfide bond reduction but not the kinetics of reduction itself. Thus, we vary the concentration of DTT (5–100 mM) to maximize the observed disulfide reduction events in each experiment while minimizing the reduction of the disulfide bonds before mechanical unfolding.

FIGURE 1.

Design and reduction of individual disulfide bonds engineered into a titin immunoglobulin module (I27). Amino acid sequence (A) and cartoon representation (B) of the I27_G32C-A75C protein. The oxidized disulfide bond (B; golden-yellow spheres) “traps” 43 amino acids encompassing the C, D, E, and F β-strands (green), whereas the A, A', B, and G β-strands (red) remain “unsequestered”. (C) Force-extension curve obtained by pulling an (I27_G32C-A75C)₈ polyprotein in the presence of 100 mM DTT. The trace shows two distinct, equally spaced sawtooth patterns, which appear in sequence. Each peak in the first sawtooth pattern corresponds to the unsequestered unfolding of a single I27 module up to the disulfide bond. The second sawtooth observed at a higher force corresponds to the sequential reduction of individual disulfide bonds in each module. The WLC model fits are shown in thick lines, and the contour length per module for the unsequestered unfolding (ΔL_u) and disulfide bond reduction (ΔL_r) are 12.6 nm and 16.4 nm, respectively.

Force-extension curves obtained from stretching the (I27_G32C-A75C)₈ polyprotein in the presence of DTT (100 mM) reveal two consecutive sawtooth patterns, as shown in Fig. 1 C. The first series of equally spaced peaks corresponds to the unsequestered unfolding depicted in red, and the second sawtooth pattern at a much higher force corresponds to disulfide bond reduction events and the release of the trapped amino acids, completing the full unraveling of the I27 protein. We can therefore distinguish between unsequestered unfolding events and disulfide bond reduction events from the difference in the measured contour lengths, ΔL_u and ΔL_r, respectively. The unfolding force peaks are fitted with the WLC theory (1), yielding the persistence length and the contour length of each module (14). The unsequestered portion of the molecule unfolds at an unfolding force of F_u = 182 ± 33 pN with a contour length of ΔL_u = 12.7 ± 0.5 nm, whereas the disulfide bond reduction takes place at forces of F_r = 303 ± 135 pN with a contour length of ΔL_r = 16.5 ± 0.7 nm. The sum of the two contour lengths observed in the double sawtooth patterns, ΔL_u + ΔL_r = 29.2 nm, is comparable to the contour length observed from a fully unraveled I27 module (ΔL_u = 28.3 ± 1.1 nm).

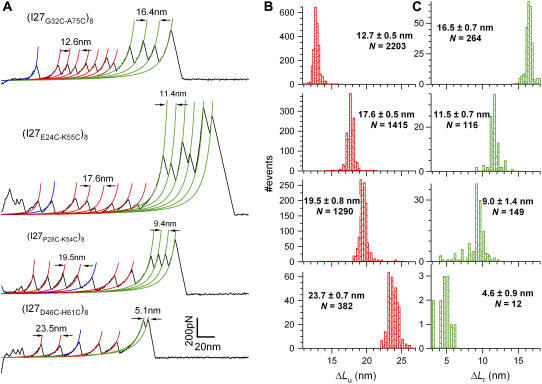
Contour lengths, ΔL_u and ΔL_r, depend on the position of the disulfide bond

Fig. 2 A shows force-extension traces for all four of our polyprotein constructs: (I27_G32C-A75C)₈, (I27_E24C-K55C)₈, (I27_P28C-K54C)₈, and (I27_D46C-H61C)₈. All of these experiments were performed in the presence of DTT. The contour lengths for the unfolding, ΔL_u, and the disulfide bond reduction, ΔL_r, are derived from the WLC theory, shown by the red and green curves. The characteristics of each construct in terms of the number of unsequestered amino acids, the number of trapped amino acids, their respective contour lengths, and force distributions are presented in Table 1. Fig. 2, B and C, shows histograms of the contour length increments measured from all four constructs (ΔL_u in Fig. 2 B and ΔL_r in Fig. 2 C). In all four cases, the sums of ΔL_u + ΔL_r (∼28.8 nm) are within the error of the contour length measured for the fully reduced proteins (∼28.4 nm), where the disulfide bond is reduced before mechanical stretching (Table 1). In addition, all the fully reduced proteins (shown in blue in Fig. 2 A) have the same contour length (ΔL_f) as the wild-type I27 (13) to within the error in the experiment. Because the contour length is measured from the transition state up to the fully extended molecule, the equivalence of these results suggests that the transition state remains the same between the different constructs. Next, we further confirm this assumption for one of the protein constructs.

FIGURE 2.

Contour length increments depend on the position of the engineered disulfide bond. (A) Force-extension curves in the presence of DTT were obtained from four different polyprotein constructs: (I27_G32C-A75C)₈, (I27_E24C-K55C)₈, (I27_P28C-K54C)₈, and (I27_D46C-H61C)₈. Each trace is fit by the WLC of polymer elasticity. The WLC fits measure the contour length increments of unfolding (red lines; ΔL_u) and of the bond reduction events (green lines; ΔL_r). Fits shown in blue indicate the unfolding of modules where the disulfide bond was reduced in solution before mechanical unfolding. The contour length increase of full-length I27 (ΔL_f) ≈ 28.4 nm is equivalent to the contour length observed on unfolding wild-type I27 (7). (B) Histograms of the measured values of ΔL_u for each construct. (C) Histograms of the measured values of ΔL_r for each construct. These values are summarized in Table 1. Note that for each construct ΔL_u + ΔL_r ≈ ΔL_f, demonstrating that the end-to-end length of the transition state remains the same for all the constructs.

TABLE 1.

Peak forces and contour length increments for the polyprotein constructs.

	Unfolding				Disulfide bond reduction				Unfolding fully reduced proteins
Protein	No. residues unsequestered	ΔLu(nm)	Fu(pN)	N	No. residues trapped	ΔLr (nm)	Fr(pN)	N	No. residues	ΔLf(nm)	Ff(pN)	N
(WT-I27)8	89	28.4 ± 0.3*	204 ± 26*	–	–	–	–	–	–	–	–	–
(I27G32C-A75C)8	46	12.7 ± 0.5	182 ± 33	2203	43	16.5 ± 0.7	303 ± 135	264	89	28.3 ± 1.1	170 ± 38	116
(I27E24C-K55C)8	58	17.6 ± 0.5	178 ± 31	1415	31	11.5 ± 0.7	363 ± 212	116	89	28.4 ± 0.9	180 ± 41	738
(I27P28C-K54C)8	63	19.5 ± 0.8	184 ± 39	1290	26	9.0 ± 1.4	427 ± 138	149	89	28.7 ± 0.8	183 ± 40	436
(I27D46C-H61C)8	74	23.7 ± 0.7	151 ± 31	382	15	4.6 ± 0.9	364 ± 117	12	89	28.1 ± 0.5	189 ± 31	142

^*Carrion-Vazquez et al. (13).

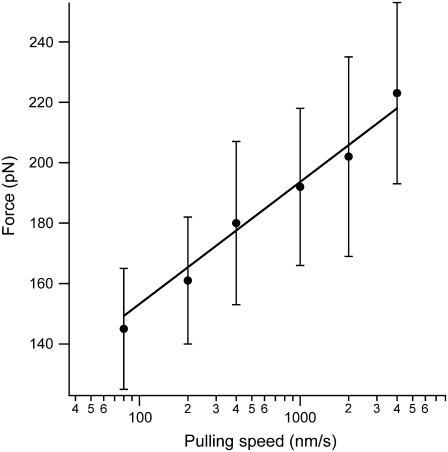
The distance to the transition state is unaltered by the disulfide bond

We vary the pulling speed from 80 nm/s to 4000 nm/s and measure the corresponding force distribution of the unsequestered unfolding (F_u) for the (I27_E24C-K55C)₈ polyprotein. The average unfolding force versus the pulling speed is shown in Fig. 3. Monte Carlo simulations using a two-state model for unfolding were performed to reproduce the experimental data, as described by Carrion-Vazquez et al. (13). The fit of the data in Fig. 3 has an unfolding distance of Δx_u = 0.25 nm and a spontaneous unfolding rate constant (i.e., at zero force) of 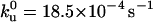as its only adjustable parameters. The unfolding distance (Δx_u) is identical to that of the wild-type protein, 0.25 nm (13), which indicates that the engineered disulfide bond has not altered the distance to the transition state. However, the spontaneous unfolding rate constant is increased 5.6 times, suggesting a reduced stability of the mutant protein.

FIGURE 3.

Distance to the transition state is unperturbed on disulfide bond insertion into I27. The unfolding forces of the (I27_E24C-K55C)₈ protein were obtained by varying the pulling speed from 40 nm/s to 4000 nm/s (solid circles). The solid line corresponds to the Monte Carlo simulation where the distance to the transition state is Δx_u = 0.25 nm, and the spontaneous unfolding rate constant is 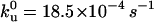. The value of Δx_u is identical to that of the wild-type I27 (0.25 nm), indicating that the position of the transition state remains the same. However, the spontaneous unfolding rate constant is increased by 5.6 times compared to that of the wild-type I27 (3.3 × 10^{−4 −1}).

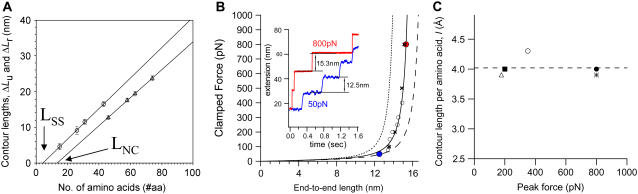
The contour length contribution of a single amino acid

Each polyprotein construct provides two contour length increments (ΔL_u and ΔL_r), and the number of amino acids contributing to each of them is determined by the position of the disulfide bond (Table 1). Fig. 4 A shows a plot of ΔL_u (triangles) and ΔL_r (circles) as a function of the number of contributing amino acids. Linear fits to the data, ΔL_u and ΔL_r, give the contour length contribution per amino acid, l_u and l_r, respectively (solid lines in Fig. 4 A). The measured slopes give l_u = 3.9 Å/aa and l_r = 4.3 Å/aa for the different regions of the protein. Because of the very broad mechanical stability of the disulfide bond (spanning from 100 pN to 1 nN), the typical sawtooth pattern is often jagged and leads to very narrow force ranges over which the WLC is fit to the data, as seen in Fig. 2 A. Fitting these force curves leads to a much higher uncertainty in the obtained values for the contour length, such that the value of 4.3 Å/aa is prone to error. Although it seems to signify a dependence of the measured contour length on the force range, force-clamp experiments and SMD simulations shown below confirm the absence of any force dependence.

FIGURE 4.

Determination of the contour length increment per amino acid (l). (A) Plot of the contour lengths ΔL_u (triangles) and ΔL_r (circles) versus the corresponding number of unsequestered and trapped amino acids (see Table 1) for all four polyprotein constructs. The slope of a linear fit to the data (solid lines) accurately measures the contour length per amino acid obtained by extending the unsequestered (l_u = 3.9 Å/aa) and trapped (l_r = 4.3 Å/aa) amino acids. The extrapolated intercepts with the abscissa (L_NC = 13.4 aa and L_SS = 4.3 aa) indicate the end-to-end length of the transition state of unfolding and the distance between the C_α atoms of the disulfide-bonded cysteines in the fully extended form. (B) Force-clamp experiments stretch the molecule under a constant force and measure the end-to-end length of 43 amino acids released by the forced reduction of the disulfide bond in the (I27_G32C-A75C)₈ polyprotein. Protein extensions measured at two clamping forces, 50 pN and 800 pN, are shown in the inset, giving rise to step sizes of 12.5 nm and 15.3 nm, respectively. A plot of the average step sizes (open circles and solid circles) as a function of force is fit with the WLC theory, using the contour length L_r = 16.4 nm (l_r = 4.0 Å/aa) and the persistence length of 0.3 nm. We superimpose four points (×) obtained by SMD simulations (rescaled by the protein length) to show further agreement with the obtained experimental values. WLC curves created using the contour lengths corresponding to the crystalline (3.6 Å/aa) and the linear (4.3 Å/aa) end-to-end lengths of an amino acid are shown as dotted and dashed lines, respectively, failing to fit the experimental data. (C) Contour length per amino acid (l) as a function of peak force measured in force-extension experiments of unsequestered unfolding (triangle), disulfide bond reduction (circle), unfolding of Gly⁵ inserted I27 (solid square), force-clamp experiments (solid circle), and SMD simulations (*). The dotted line represents the average (4.02 Å/aa) of l obtained using these five methods.

Both of these values are significantly longer than the end-to-end length between neighboring amino acids obtained from x-ray crystallography data on extended antiparallel β-sheets (3.6 Å/aa) (33). This is because the contour length takes into account the configurational entropy of the polypeptide chain arising from the internal degrees of freedom of the constituent bonds, discussed in detail below. They also deviate from the l values assumed by many groups employing AFM force spectroscopy (2–6,15,16). These experiments have relied on the folded length of the protein (obtained from NMR or x-ray crystallography) to determine l in the absence of an independent measurement of the end-to-end length of the transition state. However, our results are in good agreement with the only other experiment in which the transition state end-to-end length was accounted for by the measurement (7). In that experiment, five glycine amino acids were introduced into the I27 wild-type protein, such that the transition state remained unperturbed by the insertion. The difference in contour length between the wild-type and the modified I27 corresponded to l = 4.0 Å/aa (7).

In Fig. 4 A, both of the fitted straight lines to ΔL_u and ΔL_r have nonzero intercepts with the abscissa: 13.4 amino acids for the ΔL_u data and 4.3 amino acids for the ΔL_r data, respectively. The zero contour length measurement for ΔL_u corresponds to the end-to-end length of the protein (13.4 aa × l_u = 53 Å (L_NC)) at the transition state before unfolding, in agreement with previous studies (7). Earlier studies on wild-type I27 revealed the structure of the transition state (34,35) and its end-to-end length, which corresponds to 17 amino acids when a contour length per amino acid of ∼3.8 Å/aa is assumed (7). The measurement presented here is more accurate because it does not assume the contour length per amino acid. It should be noted that the transition state is longer than the end-to-end length of the native state of I27, measured to be 43 Å by NMR spectroscopy (12).

The assumption is that the intercept for the ΔL_r data in Fig. 4 A corresponds to the distance between the α-carbon atoms of the cysteines, L_SS, through the disulfide bond (C_α-C_β-S-S-C_β-C_α). However, the measured value of 4.3 aa × l_r = 18 Å is in excess of the range expected from the average crystallographic measurement of disulfide bonds (5.5 Å) in proteins (36), suggesting that further elements are present in the protein structure.

Independent confirmation of the contour length per amino acid

The preceding experiments measure the widely distributed force-versus-extension behavior as the protein is stretched under a constant velocity. To ensure a constant unfolding force to measure the corresponding end-to-end length as a function of time, we now stretch the protein using force-clamp spectroscopy (29). Such experiments on the (I27_G32C-A75C)₈ polyprotein have been done previously to investigate the kinetics of the disulfide bond reduction under a stretching force (32). The protein is first placed under a force of 130 pN for 1 s, during which the protein unfolds much faster than the disulfide bonds are reduced. After 1 s, the force is changed to a value between 50 pN and 800 pN for 5 s, during which the disulfide bond reduction takes place. The 43 amino acids trapped behind the disulfide bond are then unraveled under the stretching force in a two-state, stepwise manner for each protein module. This results in staircases, with each step corresponding to the reduction of a single disulfide bond (inset of Fig. 4 B). The constant stretching force is plotted against the average step length in Fig. 4 B. As the force is increased, the step size for the unraveling of the 43 amino acids increases according to the WLC theory of entropic elasticity. A Levenberg-Marquardt fit of the WLC results in a persistence length of 3 Å and a contour length of L_r = 16.4 nm. This contour length corresponds to the maximum distance between the transition state for disulfide bond reduction and the fully extended state of the 43 trapped amino acids. The transition-state length, which corresponds to the end-to-end length of the disulfide bond, is measured to be 0.55 nm by x-ray crystallography (36). Therefore, the total contour length obtained by extending the 43 residues is 17 nm (= 16.4 nm + 0.55 nm). The contour length per amino acid is then calculated to be l_r = 4.0 Å/aa.

All experimentally measured contour lengths per amino acid are much higher than the end-to-end length values of 3.6 Å/aa from x-ray crystallography (33). To examine the origin of this discrepancy, we next perform a series of SMD simulations to mimic our force-clamp experiments (34,37). We stretch the G strand of I27 protein (consisting of 12 amino acids) at four constant forces. In each simulation, the peptide segment is equilibrated under force for a period of 1 ns in explicit solvent with periodic boundary conditions. The equilibrium end-to-end distances of this peptide are then plotted in Fig. 4 B (cross symbols). They are in good agreement with the experimental data and are fitted well with the WLC theory, resulting in a contour length per amino acid of 3.9 Å/aa. This is an important result in that it shows that no enthalpic stretching elasticity component is necessary to explain the data in the range of 50–800 pN. Furthermore, studies on vibrational spectroscopy of bonds measure an elastic constant of >5 N/cm for C-C or C-N bonds (38), which translates to a stretching of <0.05 Å/aa at the highest force measured in our experiments (1 nN). Such a small elongation is not detectable from our data. As a result, the contour length is independent of the force.

Surprisingly, we find that within the polypeptide backbone, the dihedral angles and the bond angles allow the end-to-end length of the individual chemical bonds to fluctuate in the range of 0.1 Å, as compared to the 0.02 Å fluctuations usually observed in x-ray crystallography data. These fluctuations reveal the internal degrees of freedom of the chain that account for the difference between the measured contour length in our experiments and the end-to-end lengths of the individual bonds, as measured by the crystal structure. We thus demonstrate that AFM force spectroscopy can measure the degrees of freedom of chemical bonds that other structural characterization techniques overlook.

In summary, the disulfide bond variation first allows us to precisely measure the transition-state length under force, with no a priori assumptions. We then determine l by force-extension experiments (3.9 Å/aa and 4.3 Å/aa), force-clamp experiments (4.0 Å/aa), as well as SMD simulations (3.9 Å/aa), as shown in Fig. 4 C. Therefore, the average value for l from the five well-controlled measurements (dashed line), including the previous study using inserted glycines (4.0 Å/aa) (7), is found to be 4.02 ± 0.16 Å/aa. This value is a measure of the configurational entropy of the amino acids in a polypeptide chain arising from the internal degrees of freedom of the constituent bonds. If all the bonds could rotate freely, the sum of the lengths of the skeletal bonds of a single amino acid backbone, which is 4.3 Å/aa, would correspond to the accessible contour length in the experiment. However, the reduced degrees of freedom within the peptide backbone limit the measured contour length of an amino acid to l = 4.0 Å/aa, a value between the end-to-end length within the protein crystal of 3.6 Å/aa and the extended length of a purely linear molecule of 4.3 Å/aa. This is the first study that systematically varies the number of amino acids contributing to the contour length, takes the transition state for unfolding into account, and utilizes different experimental approaches to measure the contour length per amino acid.

Dependence of folding rates on protein length

We have demonstrated how the introduction of a disulfide bond precisely determines the unfolding contour length of the protein chain as the maximum distance between the transition state position and the rigid disulfide bond. This capability presents a unique opportunity to study the folding time (τ_F), defined as the time it takes to reform the transition state and therefore the protein's mechanical stability, solely as a function of the unfolded contour length, using the different disulfide bonded constructs. Previous attempts have been made to relate protein length with the experimental rate of folding between different proteins, showing a wide range of correlation (8–11,39). This is because other factors, such as the native state stability and topology, also play important roles in the folding mechanism, camouflaging the effect of protein length alone. Moreover, these ensemble refolding experiments lack a well-defined reaction coordinate such that the initial conditions, which influence the folding rate (40), vary for different proteins as well as within the ensemble of the same protein molecules. By contrast, limiting the unfolded length beyond the transition state within the same I27 molcule, with the same initial conditions, for the first time allows for a rigorous test of the theories of length dependence on folding time.

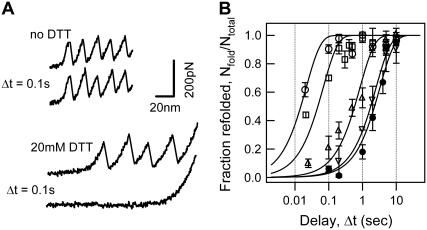
In force-extension mode, we first unfold the amino acids within each I27 module that are not arrested by the covalent disulfide bond (up to ΔL_u), as shown by the force peaks depicted in red in Fig. 1 C, such that the initial conditions are always kept the same. This is achieved by pulling the molecule a known distance away from the surface at a constant velocity of 400 nm/s. We then relax the molecule at very high velocity (4000 nm/s) and wait for the individual modules to refold during a waiting time Δt. The molecule is then extended for a second time to measure the fraction of protein modules (N_fold/N_total) in the single protein chain that refolded, that is, that regained mechanical stability. This experimental scheme is shown in Fig. 5 A for the disulfide-bonded construct (I27_E24C-K55C)₈, in which n = 58 amino acids refold in all the modules after a waiting time of 0.1 s, as seen by the two consecutive unfolding traces.

FIGURE 5.

Folding time dependence on the chain length (n, number of amino acids). (A) Force-extension curves of the (I27_E24C-K55C)₈ polyprotein unfolding and refolding cycles. The top two recordings were obtained with a relaxation delay of 0.1 s in the absence of DTT (top trace) and in 20 mM DTT (bottom trace). The same number of peaks in the consecutive unfolding trajectories provides evidence that the protein with an oxidized disulfide bond completely refolded in 0.1 s, whereas the absence of peaks in the second unfolding trace in DTT shows that the reduced protein is yet to begin folding at 0.1 s. (B) Graph of the fraction of refolded modules (N_fold/N_total) versus the delay time (Δt). Data obtained from (I27_G32C-A75C)₈ (squares), (I27_E24C-K55C)₈ (circles), (I27_P28C-K54C)₈ (triangles), and (I27_D46C-H61C)₈ (inverted triangles), as well as the reduced protein (I27_E24C-K55C)₈ obtained in 20 mM DTT (solid circles) are shown. The solid lines are fits of the data to the function P(t) = 1 − exp(−t/τ_F).

As a signature of the disulfide-bonded I27 polyprotein, in the same figure we show that on addition of the reducing agent DTT (20 mM), the disulfide bond in each module is reduced, leading to an increase in ΔL_f (28.4 nm) that is consistent with the complete unraveling of all the 89 amino acids in the protein. The refolding of the 89 amino acids drastically slows down the refolding process to a rate comparable to that of the wild-type. After the same waiting time of Δt = 0.1 s, none of the modules refold, as seen by the absence of peaks in the second unfolding trace.

By varying the waiting time Δt from 20 ms to 10 s and measuring the ratio of folded modules, N_fold/N_total, we deduce the rate constants of refolding for the polyprotein constructs with varying n. The plot in Fig. 5 B shows the time evolution of the fraction of refolded modules, in other words, the probability of refolding. The refolding rate constants (k_F) are deduced from the single exponential fits of a two-state model to the data. It is clear that the introduction of disulfide bonds that change the length of the folding protein chain drastically alters the rate of folding. The folding rate constants for the disulfide mutants are given in Table 2 and indicate a steep decrease in the folding rates with increasing length of the chain. This result is expected because of the increased conformational degrees of freedom for longer molecules. The effect of the disulfide bond restriction is observed between the rate of 46.7 s⁻¹ to fold 58 amino acids of the I27_E24C-K55C protein, as compared to the rate of 0.3 s⁻¹ for refolding the reduced form of the same molecule, corresponding to 89 amino acids, thus marking a >150-fold increase in the rate of folding.

TABLE 2.

Refolding rate constants of the polyprotein constructs

Protein	kF (s−1)	Number of amino acids to be folded (n)
(I27G32C-A75C)8	14.6	46
(I27E24C-K55C)8	46.7	58
(I27P28C-K54C)8	1.2	63
(I27D46C-H61C)8	0.4	74
(I27E24C-K55C)8 in 20 mM DTT	0.3	89
(WT-I27)8	1.2*	89

^*Carrion-Vazquez et al. (13).

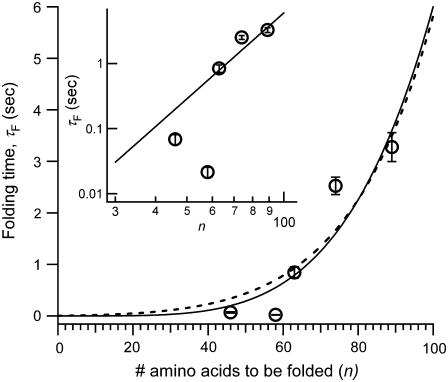
The dependence of the protein length n on folding times is shown in Fig. 6, where we plot the average refolding time (τ_F = 1/k_F determined in Fig. 5 B) against the number of amino acids in the chain. A strong trend is immediately apparent, in contrast to previous experimental studies on diverse proteins that show a wide range of correlation. Instead, this trend can be rationalized using the polymer physics models that have been applied to the study of proteins by means of numerical simulations. Simplified models of proteins have predicted a variety of scaling laws for folding times with size, ranging from a power law (23,25,26,41,42) to an exponential dependence (23,24), depending on the roughness of the underlying free energy landscape. Because of the limited size range of the protein molecules, between 46 and 89 amino acids, it is difficult to demonstrate a sharp contrast between the distinct theories. We show that the data points are fitted equally well with a power law scaling, τ_F ∼ n^λ (solid line), with the scaling exponent λ = 4.4, and with a barrier-activated process, giving τ_F ≈ exp(0.6n^0.6) (dotted line), in remarkable agreement with the different stages in protein folding in the model developed by Thirumalai (23). This does not preclude a fit with other rapidly rising functions, but we explain the data in terms of these existing models, which have been tested extensively using numerical simulations. The obtained power law exponent agrees well with the value predicted by Shakhanovich and co-workers (25) for a Go-model simulation of a designed peptide sequence but differs from other numerical simulation models (23,26,41). The scaling exponent is not universal because it depends on the energy landscape roughness of the models and therefore provides insight into the actual distribution of contact energies within the protein molecule (42).

FIGURE 6.

Plot of folding time (τ_F) versus the number of unsequestered amino acids (n). The solid lines show the power law fit, τ_F = B n^λ, where B = 10⁻⁸ s, λ = 4.4 (solid line), and the fit to a barrier-activated process, τ_F = A exp(Kn^γ), where A = 0.002 s, K = 0.6, and γ = 0.57 (dotted line). Inset shows the log-log plot of folding times as a function of the chain length, where the power law fit is a straight line.

We also investigated the influence of the proportion of native contacts, quantified by CO, on the folding rates (8). We found that CO calculated according to Baker et al. (8) from the I27 structure does not vary between the disulfide mutants (0.17–0.21). Yet, the folding times span almost three orders of magnitude (0.02–3.3 s). Therefore, we find that CO does not correlate with our observed folding times.

After the entropic collapse, the protein globule reptates, giving rise to the power law (21,22), followed by the search for a native state within a glassy energy landscape in a barrier-activated process (24). The obtained scaling with n^0.6 in the latter stage corresponds to the assumption of a Gaussian distribution of barrier heights. Most likely the two mechanisms are competing during folding, such that both play a role in the measured folding time scales. Further experiments are currently being performed to determine the rate-determining step in protein folding.

Most importantly, we have presented the first set of experiments to show that chain length plays a significant role in the rate at which proteins fold. We cannot, however, exclude the role of the polypeptide chain sequestered behind the disulfide bond during the folding process, but it clearly does not dominate over the observed length dependence. Moreover, the trend supports the view of protein folding in a complex energy landscape, in which the conformational degrees of freedom are affected by the size of the protein chain. These results emphasize the importance of single-molecule experiments in understanding the physical picture underlying the folding process.

Here we have shown how the introduction of disulfide bonds into the same protein molecule serves as the ideal control experiment to test several important biological questions: the length of the contour length per amino acid (l), the end-to-end length of the transition state of the protein, as well as the folding time (τ_F) dependence on the length of the protein chain (n). This technique allows for the characterization of the unfolding transition state in other proteins, as well as the study of their underlying protein folding dynamics.