Collagen Fibrils: Nanoscale Ropes

Abstract

The formation of collagen fibrils from staggered repeats of individual molecules has become “accepted” wisdom. However, for over thirty years now, such a model has failed to resolve several structural and functional questions. In a novel approach, it was found, using atomic force microscopy, that tendon collagen fibrils are composed of subcomponents in a spiral disposition—that is, their structure is similar to that of macroscale ropes. Consequently, this arrangement was modeled and confirmed using elastic rod theory. This work provides new insight into collagen fibril structure and will have wide application—from the design of scaffolds for tissue engineering and a better understanding of pathogenesis of diseases of bone and tendon, to the conservation of irreplaceable parchment-based museum exhibits.

INTRODUCTION

The process by which individual triple helical collagen molecules assemble into mesoscopic structures (1–5)—micron length fibrils with a regular axial periodic “D-banding” pattern that is independent of fibril diameter—remains an intriguing conundrum. The current, “accepted” model of tendon collagen (6) considers the characteristic “67 nm repeat” as being formed from a quarter staggered, side-by-side alignment of five triple helices(7,8), which was initially proposed by the early work of Hodges and Petruska (9). Essentially two-dimensional, this interpretation has several deficiencies that earlier theoretical work tried to address (10–12). One model suggested a layered, spiral arrangement of collagen molecules (13), though experimental data to support such a contention was lacking. The existing models for the supra-molecular structure of collagen fibrils presented in a review by Jäger and Fratzl (14), fail to explain how D-banding is preserved independent of fibril diameter; how collagen fibrils “grow” with pointed ends (15,16); why the surface of collagen fibrils is not flat but corrugated, with indentations at the D-band; and how fibrils (consisting of a few molecules and up to 10 nm in diameter) form into fibrils of greater diameter (from 50 to several hundred nm) (16,17) and thence into macroscale objects (e.g., tendons). Collagen structure thus follows a well-established principle in biology—that tissue form reflects functional requirements (18). Thus, Wolff's Law for bone expostulates that mechanical usage drives skeletal structure; likewise, variable ratios of fast and slow myofibrils are found in skeletal muscle undergoing differing amounts of work. Similarly, the spiral or twisted rope features observed by atomic force microscopy (AFM) are the nanoscale equivalent of microscopic crimps formed by relaxation of the subcomponents (plies) that make up collagen fibrils of tendon and contribute to some of their mechanical features (19). Although early transmission electron microscopy and freeze-fracture studies demonstrated the possible spiralization of the collagen structure, as presented in the pioneering work of Ruggeri (18,19), the interdependence between this behavior of the fibril and the consistent periodicity along its length remained unclear.

In this study, we provide AFM data that supports this twisted structure—in particular, we stress the attributes of the fibril morphology that make its structure intriguingly similar to a classical “rope”. We then take these observations at face value by applying a mechanical rope model, taking advantage of recent progress in the mechanical modeling of rope structure in such areas as textile yarns and DNA supercoiling (20–23). Although previous studies discussed the possible generation of a repeatable periodicity along a fibril, none considered the variation of the fibril diameter (20,21). We show that the rope hypothesis is consistent with experimental observations by taking reasonable values for the model parameters. In particular, the produced D-banding is found to be independent of the fibril diameter. In addition we observe that the model is not sensitive to the choice of parameters. The predicted rope angle is confirmed experimentally and provides an independent test of the model.

MATERIALS AND METHODS

Sample preparation

A suspension of native bovine digital tendon collagen fibrils was (Ethicon, Somerville, NJ) was dialyzed at 1 mg/ml against 10 mM acetic acid before use and stored at 4°C. This preparation has been used extensively in platelet function studies, for example (22). For topological assessment by atomic force microscopy, a sample was prepared by deposition of a 20 μl droplet of the stock solution (1 mg/ml) onto APTES-treated glass slides. A typical incubation time of < 5 s was used and followed by gentle drying under a weak flow of dry N₂. Collagen was also prepared from rat tail tendon (flexor digitalis tendon) by dissection into saline and stored at 4°C until use. Fibrils were deposited from saline onto plain glass slides and dried as above.

Atomic force microscopy

Commercial atomic force microscopes (Dimension 3000, Veeco, Santa Barbara, CA; JPK Nanowizard, Berlin, Germany) were used in contact mode (NPS tips, Veeco) to record both topologic (height) and error signal (deflection) images.

EXPERIMENTAL RESULTS

Topological diversity of collagen fibrils

We studied the topology of tendon collagen fibrils directly by AFM as shown in Fig. 1. Low-resolution images (Fig. 1, b and c) provide an overview at the micron scale of the nature and diversity of the fibrils obtained from digital tendon when compared with fibrils from tail tendon (Fig. 1 d). Fibrils from tail tendon, a relatively mechanically unloaded tissue, are more uniform in structure and generally straight over the length scale examined (23). In contrast, fibrils from the load-bearing digital tendon are heterogeneous and can be classified into two populations depending on whether or not a repeatable irregularity (spiral or twisted features) is observed along the length of the fibril (observed in 32% of the fibrils studied, n = 296). These are the nanoscale homologs of “crimps” that are characterized as wavy structures in light microscopic histology (24,25). The mechanics at low-strain range (<4% tendon extension) of tendons is governed by the stretching of these crimps, which disappear once sufficiently loaded (26). Diversity within the fibril population was not restricted to topological form—diameters are also inhomogeneous, implying that the original sample contained fibrils at different stages of their growth. It was found that the width of fibrils varied between 260 and 410 nm, whereas their height ranged from 35 to 60 nm (n = 296) on sample prepared from native bovine digital tendon. All collagen fibrils exhibited a common feature: D-banding periodicity (69.6 ± 2.9 nm, n = 239) regardless of fibril dimensions or overall topology. Thus, the following questions can be posed: How can fibrils of different topology have the same D-banding periodicity? And how do single molecules aggregate to form such a periodicity unrelated to fibril diameter?

FIGURE 1.

Atomic force microscopy of collagen fibrils. (a) Optical image showing the AFM tip above a sample of collagen fibrils on a glass slide (JPK Nanowizard). Scale bar, 10 μm. (b and c) Contact mode AFM images of digital tendon collagen fibrils. The AFM height (b; height range 0–242 nm) and error signal (deflection) (c) images show diversity in fibril morphology with several fibrils showing significant crimp (spiral morphology) along their length (arrowed in c), others retaining a straighter appearance; all display conserved axial D-banding. Scale bars = 5 μm (b) and 1 μm (c). (d) Contact mode AFM error signal image of rat tail collagen fibrils (scale bar, 1 μm). The fibrils are straighter (arrows) than those in (b and c) and display a similar D-banding size.

Unwinding of the collagen fibril

The AFM images of collagen fibrils in Fig. 2, a–d show features characteristic of a rope-like structure. There are evident substrands (Fig. 2, a and b). The observation of fibril substructure is further strengthened by Fig. 2, c and d, which show the phenomenon of “birdcaging” of a rope in which the strands making up the rope separate and open up into what looks like a bird's cage (27). Similar local unwindings and birdcaging of fibrils was also observed in freshly dissected flexor digitalis tendon extracts as depicted in Fig. 3, whereas the D-banding remained present over the altered section of the fibrils. Birdcaging is a well-known failure mode in industrial ropes such as mooring lines, induced either by compression or counterrotation of the rope. Further, the fibrils retained their overall appearance and D-banding even though they displayed signs of unwinding and, at a phenomenological level, this process also reveals the existence of multiple strands in the rope (at least three as shown in Fig. 2, c and d). In essence, this phenomenon of unwinding of the collagen fibril is not new in itself as it has been reported almost two decades ago (18); however, no D-banding periodicity was observed suggesting possible damage occurring to the fibril through sample preparation and/or techniques used (freeze-fracture and TEM).

FIGURE 2.

Local unwinding of collagen fibrils. Contact mode AFM error signal images of digital tendon collagen fibrils (scale bar, 500 nm). (a) A fibril is somewhat unwound (arrowed) but still displays axial D-banding. (b) The fibril is more unwound, has the appearance of a rope with linear substructures, and D-banding is less apparent. (c) The arrows indicate the presence of the “birdcaging” phenomenon along the length of the fibril, as seen in ropes or hawsers that are put under compressive forces or reverse twist. (d) Some of these regions (circled) display a multi-strand subfibrillar structure with at least three strands.

FIGURE 3.

Local unwinding of collagen fibrils extracted from freshly dissected digitalis flexor tendon (rat). The arrows point to local structural disruptions occurring similarly during failure mode in industrial ropes.

MODELING

Modeling a rope-like structure

If a collagen fibril is indeed a miniature rope, as suggested by our work as well as earlier studies (21,28), then it seems reasonable to apply mechanical modeling to further understand the behavior and structure of the fibril. The main problem that this presents is how to reconcile this rope structure with the characteristic D-banding. For this pattern to be generated on the overall rope it must be formed by the combined result of striped patterns on the individual strands and be independent of their diameter. Thus, for the resultant model to be considered successful, it must be able to reproduce this overall pattern or at least be compatible with it. There has been recent progress in modeling plied structures, such as supercoiled DNA and twisted textile yarns, using elastic rod theory which takes into account bending and twisting of the individual strands (29–32). To use the elastic rod theory, all collagen heterotrimers present in a given fibril are modeled as identical incompressible helical tubes (called here strands) in continuous contact with their neighbors and arranged symmetrically about the rope axis (i.e., all strand centerlines lie on a real cylinder). The strands form a self-balancing plied structure that requires no end forces or moments.

In Neukirch and van der Heijden (29), equations are derived for both the geometry and the mechanics of such plies composed of k helical strands. If no end forces or moments are applied the statical equilibrium equation is:

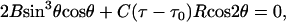(1)

where θ is the helical angle (the angle each strand makes with the axis of the cylinder), R the radius of the cylinder, B the bending stiffness, C the torsional stiffness, and τ the twist (axial torsional strain). In a slight extension of the model in Neukirch and van der Heijden (29), we have allowed for an initial twist τ₀ in each (tubular) strand. This initial twist may be thought of as describing the twist of a helical “groove” running along the surface of the unstressed strands and resulting from the substructure of the individual strands, which themselves must be composed of finer fibers.

Instead of specifying the twist τ, it is more intuitive to specify a quantity related to the creation of the ply. For instance, suppose that initially the (straight) strands lie side by side. If we now put an angle φ₀ into each of them, tape the ends together and then gradually release the ends, then the twist τ in each strand of the ply that forms is related to this angle φ₀ by:

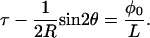(2)

φ₀ is called the pretwist; it is the twist locked in during creation. L is the length of each strand in the ply as seen in Fig. 4.

FIGURE 4.

Schematic of a two-ply model displaying L, the length of each strand; τ, the twist (angle per unit length) about the axis of each individual strand; and θ, the helical angle (the angle each strand makes with the axis of the cylinder).

The contact geometry of k helical strands is described by the equations (see Neukirch and van der Heijden (29))

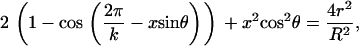(3)

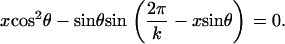(4)

Taken together, Eqs. 3 and 4 can be regarded as giving a relation between the helical angle θ and the helical radius R. r is the strand radius, and x is a dimensionless shift parameter, the difference in arc-length coordinate of contacting sections on two neighboring strands (see Neukirch and van der Heijden (29)). For given dimensionless (k, C/B, r/L, τ₀L, φ₀), Eqs. 1–4 yield four equations for the four unknowns (R/r, θ, x, τL).

To solve Eqs. 1–4, we proceed as follows. We fix k = 6, C/B = 1 and choose r/L = 0.01. This stiffness ratio C/B is that often taken for DNA molecules (no data for C appear to be available for collagen). With these values vertical fibril striping on the overall ply is obtained by assuming the right balance of intrinsic twist and overall fibril twist. We require (approximately) φ₀ = −30(2π), (τ − τ₀) L = 40. In fact, there appears to be a surprisingly large range of parameter values for which a vertical striped pattern is obtained. With these values the four equations can be solved and we find θ = 35°, R/r = 2.37.

Having managed to obtain a repetition pattern similar to that of the collagen fibril, it was necessary to cross-check the value of the periodicity or D-banding obtainable with this rope modeling approach. Given the parameter values above, we can compute the number of vertical stripes on a given piece of fibril that would result from a helical line (actually a groove) on each of the strands. A comparison of this number with the experimentally observed D-band spacing (∼70 nm) allows us to deduce the number of helical lines required for agreement, and hence the number of substrands in a strand. Taking into consideration the distribution of the fibril diameters, it was found that the width of fibrils varied between 260 and 410 nm. The thinner fibrils have a typical width of 260 nm. Thus, 2(R + r) = 260 nm. This gives r = 38.6 nm and hence L = 3860 nm. For one line drawn on each individual strand, this gives a spacing of 3860/30 = 129 nm. So, if we assume that the strands have a two-ply substructure (i.e., two lines on each strand) then we would expect a banding of 65 nm. Similarly, for the thicker fibrils, we have 2(R + r) = 410 nm, giving r = 60.8 nm and L = 6080 nm, for a spacing per strand line of 203 nm. This is consistent with a three-ply substructure of each strand and a banding of 68 nm. Note the distance L implies that the length of the strands is either 3.86 or 6.08μm, which is possible as collagen fibrils are often tens of microns longs.

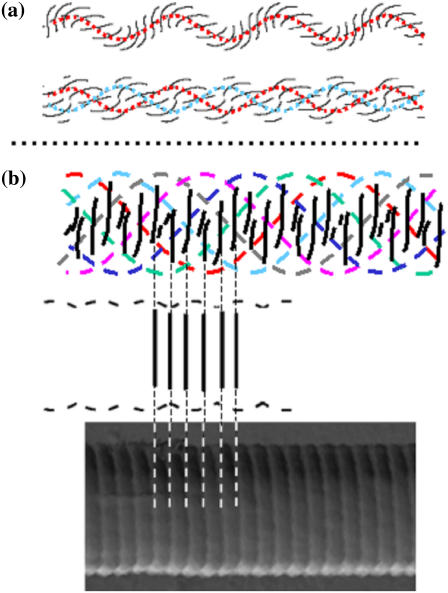
Fig. 5 shows the theoretical striped pattern obtained by displaying only the stripes on the strands nearest the reader's eye. In both cases the rope angle is computed as 35°, in good agreement with experimental observations in which the subfibril angle was found to be θ = (38.5 ± 8.0)°, n = 12 (see Fig. 6). We stress that this angle θ comes out of the model and the conditions for vertical striping. The comparison with the experimental value is thus an independent test of the model.

FIGURE 5.

Modeling the collagen fibril using elastic rod theory. (a) A single strand (top) and the corresponding full balanced two-ply (bottom) for φ₀ = −30(2π) and no intrinsic twist. The unstressed rod has four straight lines drawn equidistantly on its surface. Only lines in front view are shown (red, single strand model; red and blue, two-ply model). No vertical pattern is obtained. (b) Front view of the pattern predicted in the six-ply model with intrinsic twist (top; six individual strands are color coded to aid distinction) and correspond to AFM observations: twisted fibril pattern with vertical banding and corrugated surface. The banding predicted by the model is aligned with an AFM image showing axial D-banding (bottom).

FIGURE 6.

The inner structure of the collagen fibril. Contact mode AFM error signal image of digital tendon collagen fibrils (scale bar, 1 μm). The fibrils have “collapsed” onto the glass substrate and display their internal structure. This has a pleated or spiral conformation and closely resembles that of a rope, as shown in Fig. 4. The fibril presents a substructural pattern with an angle θ = (38.5 ± 8.0)°, n = 12 with respect to the long axis of the fibril (inset).

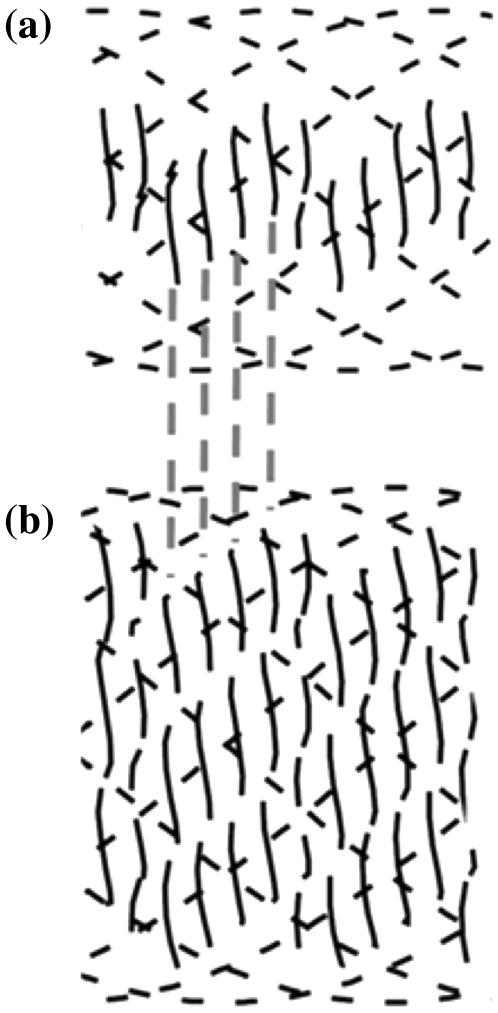
These results are not sensitively dependent on the assumed number of strands in the rope (here six). To illustrate this, in Fig. 7, we show rope solution with 9 and 12 strands, keeping all other model parameters fixed. The striping pattern is barely changed.

FIGURE 7.

Examples of a rope solution with 9 and 12 strands displaying in both cases strong vertical banding.

It is good to emphasize that our choice of r/L above is not an assumption of the model. Combined with an absolute length scale, such as R + r obtained from direct measurements, it merely selects the length of collagen fibril under consideration (e.g., for the 410 nm diameter fibrils used above we find L = 6.08 μm, which compares well with the length of the fibrils in the experimental samples). A different value for r/L would require a different pretwist φ₀ and the final spacing would not change. This has been confirmed numerically and we regard this behavior as an important consistency check on our model.

The vertical striping is also fairly robust against variations in the other model parameters (the various twist measures and the bending and torsional stiffnesses of the strands). Nevertheless, we feel that there is some tension between the presented model and the experimental observation that the pattern always appears to be vertical (i.e., 90-degrees to the fibril long axis).

Confirmation of the model proposed

There is further experimental evidence that the collagen fibrils may behave as ropes, as presented in Fig. 8. Here, two collagen fibrils combine to form a higher order structure that can be described as a two-ply rope. It is interesting to note that Holmes et al. suggested similar behavior at the level of the tropo-collagen molecule, implying that there may be an intrinsic rotational stress to their organization (5). Collagen molecules, with an inherent kink, thus could self-combine in the same manner as the collagen fibrils depicted in Fig. 8. This suggests that regardless of the order within the structural hierarchy of the fibril, the same assembly rules apply, giving collagen fibril assembly a self-similar or fractal nature. Based on our model, it appears that topological characteristics of the collagen fibril are not driven by the presence of the D-banding pattern itself, but more implicit in the inherent twist of the collagen molecule and thence to the repetition of the twist along the molecule as well as interactions between the strands.

FIGURE 8.

Micron-scale entanglement of two collagen fibrils. Contact mode AFM error signal image of digital tendon collagen fibrils (scale bar, 2.5 μm) (higher magnification, inset). Two fibrils are entangled, presenting a two-ply rope structure as predicted from the model. This finding suggests that the rope model could be applied to the entire hierarchy of the collagen structure and not only to the evolution of the microfibril to fibril.

SUMMARY

Our experimental and modeling data provides clear proof of collagen fibrils forming a rope-like structure. Existing high-resolution structural data sets, thus, need to be reevaluated in the light of these findings. This new model also makes predictions that can be tested experimentally. For example, if the spiral formation of collagen fibrils reflects their response to mechanical needs, then those exposed to varying degrees of tension should have a different propensity to twisting during their formation. For example, a tail tendon has different needs to an Achilles tendon and, as we show, spiral structures are seen in the mechanically stressed tendon. There are also several interesting clinical and other implications raised by these data. Thus, there may be differences in collagen structure between tendons that are liable to rupture during excessive mechanical strain (for example, the flexor digitalis tendon in thoroughbred racehorses) and those that are not. Collagen-based scaffolds are being developed for tissue engineering applications; our data indicate that twisted fibril materials should be used in scaffolds to be used at mechanically stressed locations, such as arteries. Similarly, a better understanding of the relationship of the structure and mechanical properties of collagen in situ may aid the conservation of the numerous and irreplaceable medieval parchments (made of animal skin collagen) that are slowly degrading in museums.