Protein Phase Diagrams II: Nonideal Behavior of Biochemical Reactions in the Presence of Osmolytes

Abstract

In the age of biochemical systems biology, proteomics, and high throughput methods, the thermodynamic quantification of cytoplasmatic reaction networks comes into reach of the current generation of scientists. What is needed to efficiently extract the relevant information from the raw data is a robust tool for evaluating the number and stoichiometry of all observed reactions while providing a good estimate of the thermodynamic parameters that determine the molecular behavior. The recently developed phase-diagram method, strictly speaking a graphical representation of linkage or Maxwell Relations, offers such capabilities. Here, we extend the phase diagram method to nonideal conditions. For the sake of simplicity, we choose as an example a reaction system involving the protein RNase A, its inhibitor CMP, the osmolyte urea, and water. We investigate this system as a function of the concentrations of inhibitor and osmolyte at different temperatures ranging from 280 K to 340 K. The most interesting finding is that the protein-inhibitor binding equilibrium depends strongly on the urea concentration—by orders-of-magnitude more than expected from urea-protein interaction alone. Moreover, the m-value of ligand binding is strongly concentration-dependent, which is highly unusual. It is concluded that the interaction between small molecules like urea and CMP can significantly contribute to cytoplasmic nonideality. Such a finding is highly significant because of its impact on renal tissue where high concentrations of cosolutes occur regularly.

INTRODUCTION

As a discipline, biochemistry is associated with explicit characterization of individual reactions and molecular events. Understanding these processes requires careful control of experimental variables, such as temperature, and the presence and concentrations of specifically, and nonspecifically interacting molecules. Clearly, there is a limit to the number of variables a researcher will undertake as part of a biochemical reaction study. It is important to recognize and acknowledge that the cell is not similarly constrained.

In living organisms, biomolecules participate in highly complex reaction networks. Even dilute isolated protein molecules are constantly changing between a vast number of different states. Such states can be very different, like native and denatured states, or less so as in differently protonated states. But they might also just differ with respect to some quantum-mechanical detail and behave biochemically as one state. To obtain quantitative biochemical information, a method is therefore needed that can resolve many different substates yet also average out biochemically irrelevant information. Also, such a method has to be robust to handle large reaction networks. The recently developed phase diagram method (1) is able to perform these tasks. It enables the fast and straightforward analysis of arrays of coupled equilibria.

There is, however, a second layer of complexity that makes cytoplasmic processes fundamentally different from typical dilute, aqueous in vitro experiments. The cytoplasm is highly crowded, and all molecules are exposed to an abundance of organic and inorganic molecular species of vastly variable size. This situation prohibits the use of concentrations as an approximation for the chemical activity. In fact, at near-physiological concentration the chemical activity of hemoglobin can deviate by several orders of magnitude from its concentration (2). Also, the nonspecific interaction of proteins with small organic molecules (osmolytes) can lead to both unfolding (3,4) and forced folding (5) of the protein molecules. In addition to these macromolecule-macromolecule and macromolecule-small molecule interactions, there is a mutual influence of the small molecules in solution that gives rise to solution nonideality. We recently provided a rigorous solution theory that accurately describes the nonideality of binary solutions of aqueous osmolytes (6–8).

Here, we show how to investigate reaction schemes under conditions of nonideality. We demonstrate how the phase diagram method (1) can be utilized to extract the desired information from a set of appropriate measurements. The method allows for a fast determination of stoichiometries and thermodynamic quantities that can be used as very good estimates for initial fit parameters in a global fit of the data. Knowledge of the reaction stoichiometries and initial fit parameters is especially valuable if large amounts of high throughput data have to be processed.

As an example of our current extension of the phase diagram method to nonideal conditions, we use a four-component system involving the protein RNase A, the specific inhibitor CMP, water, and the osmolyte urea. Protecting organic osmolytes are small molecules that are indispensable in essentially all taxa (9) to counteract extracellular as well as intracellular stress that regularly occurs during the lifetime of an organism. Protecting osmolytes are known to counteract the deleterious effects of the lone nonprotecting osmolyte, urea. Osmolytes can reach molar concentrations in vivo, an extreme example being 5.4 M urea in the kidney of water-stressed desert mice (10). On the other hand, low concentrations of osmolytes in the upper millimolar range are sufficient to protect kidney cells (11) or alleviate protein-folding issues that are due to mutations (12). The very broad range of physiologically relevant concentrations, their ubiquitous occurrence, and high relevance make osmolytes an important target for the investigation of nonideality on biochemical reactions.

Here, we find that urea has a remarkably large and nonlinear effect on the binding of CMP to RNase A. We conclude that solvation of free CMP has a larger impact on the RNase A-CMP affinity than does the urea-protein interaction. Such biochemically important interaction between small solute components could greatly influence renal function, because high and variable concentrations of cosolutes do occur during regular kidney function.

EXPERIMENTAL MATERIALS AND METHODS

Materials

Cytidine 2′-monophosphoric acid was purchased from Sigma-Aldrich (St. Louis, MO), Ribonuclease A from Worthington Biochemical (Lakewood, NJ), and ultrapure urea from USB. Millipore filtered water was used (Millipore, Billerica, MA).

The protein was extensively dialyzed against 10 mM sodium acetate buffer (adjusted to pH 5.0 at 25°C using HCl) before usage. The 2′CMP was dissolved in buffer to a stock solution concentration of ∼6 mM, the pH adjusted with NaOH and then further diluted with either buffer or urea-containing buffer. The urea stock was prepared by adding water to dry urea and dry sodium acetate to final concentrations of 10 mM acetate and 9.6 M urea. The pH was adjusted to 5.0 using HCl. Protein solutions of different urea concentrations were prepared by diluting the dialyzed protein stock with the urea stock solution and/or plain acetate buffer, and readjusting the pH as necessary.

The concentrations of protein and nucleotide were determined using an Aviv UV-spectrophotometer (Aviv Instruments, Lakewood, NJ). The extinction coefficients are ε₂₈₀ = 9487/M/cm for RNaseA (13) (average of six experimental values) and ε₂₆₀ = 7400/M/cm for 2′CMP (14).

Methods

A Microcal VP-ITC was used to measure the binding of 2′CMP to RNaseA (14). Thermal stability was measured using a Microcal VP-DSC (15) (Microcal, Northampton, MA) and a model 14DS Aviv UV-vis spectrophotometer. Urea-induced unfolding of RNaseA in the presence and absence of 2′CMP was measured by monitoring the signal change in second derivative spectroscopy.

Absorbance spectra were recorded using a Model 14DS Aviv UV-vis spectrophotometer equipped with a Peltier automated temperature control unit, with all measurements conducted at 25.0 ± 0.1°C, using a protein concentration of 0.75 mg/mL. Spectra were recorded from 333 to 250 nm every 0.1 nm with 1-nm bandwidth and 1 s averaging time, using a pair of matched tandem 1-cm path-length cuvettes. Savitzky-Golay filtering was performed twice on the spectral data using Aviv software to acquire second-derivative UV spectra (16). The first filtering involved using a 20-pt moving window size for third-degree polynomial approximations, with zero-order derivatives taken. The second filtering involved using a 25-pt moving window for third-degree polynomial approximations, and second-order derivatives were taken.

THEORY: THE PHASE DIAGRAM METHOD

This section provides a detailed description of the phase diagram method as used in this article. The reader may wish to read the Results and Discussion sections before this section.

Overview

Quantifying reaction schemes involves two major tasks: 1), determine the number of reactions and their stoichiometries; and 2), obtain good initial estimates of fitting parameters. The first task must be completed to know the general form of the reaction scheme, and the equation to be used for data fitting. Completing the second task is essential in preventing the fit from being trapped in a suboptimum. The phase diagram method offers straightforward solutions to both problems. In addition, the phase diagram method provides guidelines for the application of experimental methods that can give information on different molecular and conformational species in the solution, as explained below.

Phase diagrams for proteins give a quick overview as well as quantitative information on which protein states are populated under sets of different conditions, given by their position on a parameter-plane, e.g., temperature and pH. Regions of predominance of each protein state are separated by phase separation lines, on which population sizes are 50%. The phase separation lines can be measured in a series of experiments that allow us to determine these 50% lines as transition midpoints under variable conditions. Such midpoints could be pK values, or midpoint temperatures of thermal denaturation T_m, for instance.

Only a limited number of species in a reaction scheme can be usually distinguished experimentally. Therefore, in a typical experiment, one observes a group of protein states that is converted to another group of states by changing an intensive property, such as temperature or pH. Substates that are not directly detectable can be revealed using the phase diagram method (1). For instance, native and denatured protein states are readily distinguished via UV spectroscopy, but the various protonated species that populate these states are not generally distinguishable by this method. The phase diagram method, however, is adept at revealing protonation pK values and stoichiometries of these states (1). The procedure is discussed in below for several examples.

A phase diagram is based on at least one experimentally determined phase separation line, e.g., the dependence of the denaturation transition temperature T_m on pH. In the example of pH-dependent thermal denaturation, the phase separation line separates two groups of states: differently protonated native states on one side, and differently protonated denatured states on the other. For quantitation purposes, the relative population size of these two groups is expressed in terms of a ratio Q_R = Q_N/Q_D of their respective partition functions Q_N and Q_D. On the phase separation line, the populations are equal, so Q_N equals Q_D and Q_R is a constant value of unity.

Within this section, we systematically develop the phase diagram method for thermodynamically nonideal conditions, and use a specific reaction scheme as an example. The different planes in the temperature-ligand concentration-urea concentration space are sequentially covered.

Features of the reaction scheme

We consider a protein reaction scheme involving two steps that are matched to the experimental system we describe below. The first one is the binding of a ligand L to a native protein N,

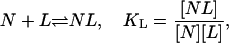(1)

with an affinity given by the binding constant K_L. The binding enthalpy is . The second part of the reaction system is the unfolding of the native state N resulting in the denatured state D,

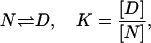(2)

where the protein stability is determined by the unfolding equilibrium constant K. The enthalpy of unfolding is ΔH⁰. Thermodynamically, this three-state reaction scheme is completely described in terms of the partition function Z = Z_N + Z_D + Z_NL or, more conveniently, the relative partition function Q = Z/Z_N (relative to the unliganded native state),

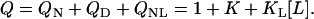(3)

As an example of such a reaction scheme, we will discuss the system RNase A—2′CMP at variable temperature and urea concentration.

Temperature-ligand phase diagram

This is the first of the three examples for a phase diagram plane in the considered three-dimensional space: temperature, ligand concentration, and osmolyte concentration.

Isothermal titration: liganded versus unliganded phase separation line

To measure the phase separation line between liganded and unliganded state, a method has to be employed that is able to distinguish between liganded and unliganded proteins, e.g., isothermal titration calorimetry. For a quantitative description of the phase separation line we have to consider the ratio Q_R of partition functions relating to liganded species Q_NL and unliganded native and denatured species Q_N + Q_D:

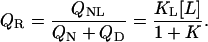(4)

Note that this definition of Q_R holds exactly for the definition of one phase separation line in the given phase diagram. To describe the other phase separation lines we will appropriately redefine Q_R. The resulting phase separation line corresponds to a pK_L of binding versus T plot. The population sizes of denatured f_D and native liganded state f_NL are given by

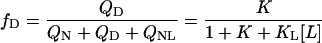and

Note that in Fig. 1 there is a switch between different slopes in the phase separation line between the native liganded protein and all unliganded species. The temperature at which this switch between the two slopes of the phase separation line takes place is defined by the unfolding temperature of the unliganded protein (perpendicular line in Fig. 1). This is a general property of protein phase diagrams: occurrence of additional states (in this example, the denatured state) causes sudden changes in the slope of phase separation lines (1). Based on this property, it is often possible to construct a whole phase diagram from one single phase-separation line (1).

FIGURE 1.

CMP-temperature phase diagram of RNase A, 10 mM sodium acetate pH 5.0. The regions in which native unliganded (N), native liganded (NL), and denatured (D) protein predominates are labeled accordingly. The phase separation lines between those regions indicate 50% population size of the neighboring species in the absence (solid lines) and presence (dotted lines) of 2 M urea. Points are experimental affinities obtained by ITC (solid squares and circles) or thermal stabilities obtained by DSC or UV (open squares). ITC data obtained with solutions containing 2 M urea are given by the solid circles. The phase separation lines were calculated using Eqs. 12–14. K was calculated from Eq. 20 and K_L analogously. The parameters for thermal denaturation are ΔH⁰ = 440 ± 30 kJ/mol, 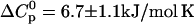, and 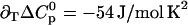, all at T_1/2 = 332 K. The parameters for ligand binding are pK = 6.55 ± 0.04, , , and 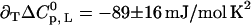, all at 25°C. For the dotted line, the following cross-correlation parameters were also used: ∂_cΔH⁰ = −17.8 ± 0.6 kJ/mol M, and 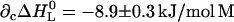. The point at the ordinate value of 7.5 was obtained in the absence of ligand.

T-scan: native versus denatured phase separation line

The previous definition (Eq. 4) of the ratio Q_R defined the 50% phase separation line between liganded native protein and other states, i.e., native unliganded plus denatured. Now an expression for Q_R is given that describes the phase separation line between denatured and native (liganded and unliganded) states:

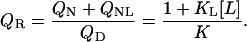(5)

Experimentally, such a distinction is easily made by way of a thermal scan using, e.g., spectroscopic techniques.

As in the previous example, at the pK_L of ligand binding, a sudden change of the slope takes place at the point where the third species occurs (see Fig. 1). Therefore, pK_L can be determined from the dependence of T_1/2 on ligand concentration.

Fitting of the phase separation lines

Having discussed the behavior of the phase separation lines, we now show which functions describe the lines. This makes possible a fit of experimental data as discussed below and shown in Fig. 1.

The relative partition function for the considered three-state system is Q = 1 + K + K_L[L]. If the population size of the liganded native protein is 50% (f_NL = 0.5), the relation Q_NL = Q_N + Q_D holds, or, in terms of the equilibrium constants, K_L[L]_1/2 = 1 + K. The phase separation line immediately follows from this equation. It is given by the temperature-dependent midpoint concentration [L]_1/2 of the binding equilibrium

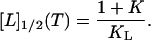(6)

Similarly, the phase separation line between denatured and nondenatured states (the line of f_D = 0.5) follows from the condition 1 + K_L[L]_1/2 = K to be

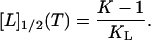(7)

On the phase separation line between native unliganded protein and other states (the line of f_N = 0.5) the condition K + K_L[L]_1/2 = 1 holds. The third phase separation line is therefore given by

(8)

Equations 6–8 were derived by separating all temperature-dependent terms (the equilibrium constants K and K_L, right-hand side of the equations) from the ligand concentration [L] (left-hand side of the equations). The temperature dependence of the equilibrium constants and their simultaneous dependence on cosolute concentration can be calculated as explained below.

Temperature-urea phase diagram

In the previous section, all dissolved components were assumed to be ideally dilute. As a consequence, all derivatives with respect to the chemical potential of the ligand could be replaced by derivatives with respect to the logarithm of the ligand concentration. In the case of the presence of highly concentrated cosolutes, this proportionality between the concentration and the activity of the cosolute is no longer a valid assumption. The nonideality of the solution can be taken into account in several different ways.

A formulation in terms of chemical activities would require not only knowledge about the activity coefficients at room temperature, but also about temperature-dependent enthalpies of dilution and partial heat capacities. It would also require an extensive equation network capable of describing these thermodynamic parameters (17,18). In contradistinction to such difficulties, a description of protein folding equilibria in terms of cosolute molarity is known to result often in a simple linear relationship behavior of the Gibbs free energy (linear extrapolation method (4,19–25)), although the origin of this simple linearity is not yet completely understood (26,27). For the purpose of the current work, a formulation in terms of cosolute molarities is preferable over a formulation in terms of activities, because of the much more straightforward handling and simplicity of the cosolute molarity approach.

Because in Results we use a phase separation line to derive the m-value of ligand binding, it is useful to shortly discuss the slope of this phase separation line. This generalized Clausius Claperyron equation (1) was not originally formulated to match this situation, but it can be readily accommodated, and it then reads

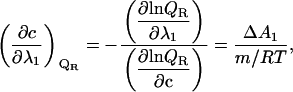(9)

where c is the cosolute molarity and the m value is defined as

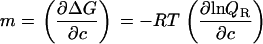(10)

In the current case of a cosolvent concentration versus temperature phase diagram, the intensive property λ₁ in Eq. 9 is the temperature (1/RT) and the extensive property ΔA₁ is the enthalpy ΔH. A combination of Eqs. 9 and 10 yields the slope of the phase separation lines

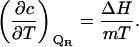(11)

Similar equations for the slope of the transition temperature with respect to osmolyte concentration have been reported previously (28–30). In those cases, the goal was to determine the change of the preferential interaction parameter upon unfolding. We will now discuss how this equation behaves in the example of a ligand binding and denaturing protein, and the information that can be extracted from the phase diagram.

T-scan: native versus denatured phase separation line

Thermal denaturation scans are a useful tool to determine the transition temperature, which gives experimental access to the line of 50% denaturation. This phase separation line between native (liganded and unliganded) and denatured protein is defined by

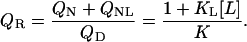(12)

Fitting of the phase separation lines

Here, we only consider the denaturational equilibrium between N and D in the absence of ligand L. The phase separation line is found at

(13)

and the stability equation can be expressed as a Taylor expansion. An extension to the classical stability equation (31) as a function of temperature is

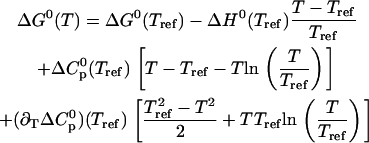(14)

This expression is based on a second-order Taylor Expansion of the Gibbs free energy using the Lagrange Remainder (32). The Gibbs free energy change at the reference temperature ΔG⁰(T_ref) = −RT ln [K(T_ref)] vanishes if the transition midpoint temperature T_m is chosen as reference temperature T_ref.

The protein stability can usually be expressed as a function of urea concentration using the linear extrapolation method (4,19),

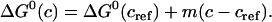(15)

A combination of the expressions for temperature and urea dependence of the Gibbs free energy in the form of a two-dimensional Taylor Expansion up to second-order requires one additional cross-term:

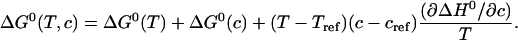(16)

As reference concentration we choose c_ref = 0 M. Since the condition Eq. 13 restricts us to the phase separation line, the concentrations c in the expansion have to be replaced by the midpoint concentrations c_u,1/2. Equation 13 then becomes

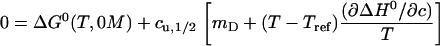(17)

Solving this expression for c_u,1/2 is straightforward:

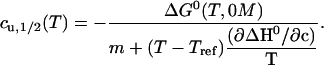(18)

As seen from this equation and the shape of its plot in Fig. 2, this curve is essentially a thermal stability curve (ΔG⁰) that is slightly modified by the nearly temperature-independent (33–35) m-value.

FIGURE 2.

Urea-temperature phase diagram of RNase A. The solid line represents the (50%) phase separation line between native and denatured protein (Eq. 24). Data-points (solid squares) were determined by urea-induced isothermal unfolding (upper point), or by thermally induced denaturation in the absence of urea (lower points) as observed by DSC and UV. The parameters used are the same given in Fig. 1 for the thermal stability, plus m = 6.6 ± 0.2 kJ/mol M, and c_{u, 1/2} = 5.15 M, both valid at 25°C.

Urea-ligand phase diagram

How the nonideality in the cytoplasm affects biochemical equilibria is an important question. The cosolvent-concentration versus ligand-concentration phase-diagram addresses this. While we restrict this article to simple examples, the phase diagram method can be readily extended to cases involving multiple components.

Isothermal titration, ligand binding: liganded versus unliganded phase separation line

The dependence of the affinity on cosolute concentration can be easily determined in a titration experiment, e.g., in an isothermal titration calorimeter. The phase separation line between liganded native protein and unliganded (native and denatured) protein is defined by

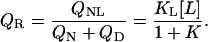(19)

Isothermal urea titration: native versus denatured phase separation line

Alternatively to a temperature scan, protein denaturation can be investigated isothermally at increasing denaturant concentration. If this is done in the absence of ligand, a point in the cosolute concentration versus temperature phase diagram is obtained. But it is also possible to define a ligand-concentration versus cosolute-concentration phase diagram if denaturation experiments are repeated at different ligand concentrations. Such experiments define a phase separation line between unfolded protein and native (liganded or unliganded) protein:

(20)

Fitting of the phase separation lines

The fitting procedure is the same as above. The basic equations are Eqs. 6–8. The stability of the protein ΔG⁰ = −RT ln K depends linearly on c_u for most osmolytes, as noted above. In the case of charged cosolutes, such as Guanidinium Hydrochloride, the Gibbs free energy might depend nonlinearly on cosolute concentration (20,23,36–38). Also, in the case of 2′CMP binding to RNaseA reported in this work, a nonlinear trend in 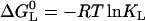is observed and a second-order term has to be added:

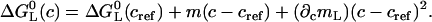(21)

RESULTS

We investigated the equilibrium behavior of RNase A as a function of three variables: temperature, urea concentration, and ligand (2′CMP) concentration. First, three planes were characterized: the urea-ligand plane (at room temperature), the temperature-ligand plane (in the absence of urea), and the urea-temperature plane (in the absence of ligand). The results obtained in these experiments were used to predict the phase separation lines (lines of 50% population size) in the three-dimensional space at variable temperature, urea, and ligand concentrations. The obtained phase diagrams reveal an unexpectedly large and nonlinear change of the RNase A:CMP affinity on urea concentration, which is attributed to the urea-dependent activity coefficient of the free CMP, as explained in Discussion. Note that protein transitions can be considered a special case of classical first-order phase transitions in the limit of small system size (39). They have characteristics of mesoscopic systems, such as cooperativities that are reduced in comparison to macroscopic systems. The same physical principles apply to both classical macroscopic phase diagrams and protein phase diagrams (1).

A proper choice of an optimal order in evaluating the phase diagram planes makes sure that, at most, two parameters have to be fitted in all curve fits. In this way, even very complex reaction schemes involving dozens of independent parameters can be quantified in a straightforward manner. An overview of the procedure is given in Fig. 3. Equations used and the theoretical background of the phase diagram method are given in Theory.

FIGURE 3.

Fitting strategy. The green boxed fitting steps are regular fittings using single experiments in which one of the concentration variables is zero. The other steps are performed to define cross-correlations between ligand-, urea-, and temperature-dependences of RNase A behavior. Derivatives with respect to temperature and urea concentration are abbreviated d_T and d_c, respectively. For details, see text.

Urea-ligand phase diagram

The urea-ligand phase diagram (Fig. 4) includes the liganded native state, the native unliganded, and the denatured state. Two sets of experiments quantify the urea-ligand phase diagram: 1), isothermal urea-induced unfolding in the presence or absence of ligand; and 2), isothermal titration of RNase A with the ligand 2′CMP in the presence of different urea concentrations. The resulting urea midpoint concentrations for denaturation and for ligand binding at 25°C are shown in Fig. 4.

FIGURE 4.

CMP-urea phase diagram of RNase A in 10 mM Sodium Acetate, pH 5.0. The phase separation lines are defined by ITC measurements (titration of RNase A with CMP in the presence and absence of urea, squares) and by UV measurements (titration of RNase A with urea in the presence and absence of CMP, circles). Note the curvature of the phase separation line between the native unliganded (N) and native liganded (NL) states, which corresponds to a nonconstant m-value. The phase separation lines were calculated using Eqs. 12–14. K and K_L were calculated from Eqs. 21 and 27, respectively. The used parameters are c_{u, 1/2} = 5.15 M, m = 6.6 ± 0.2 kJ/mol M, pK = 6.55 ± 0.04, m_L = −2.0 ± 0.1 kJ/mol M, and ∂_cm_L = 350 ± 40 J/mol M², all valid at 25°C. The point at the ordinate value of 7 was obtained in the absence of ligand.

The urea-induced unfolding of proteins is usually well described by the linear extrapolation method (4,19), which involves two parameters—the midpoint concentration of unfolding c_1/2 and the slope m of the Gibbs free energy of unfolding as a function of urea concentration. These two parameters c_1/2 and m are directly obtained from the isothermal titration of the protein with urea in the absence of ligand (Fig. 3, first step). From this fit, the uppermost point in Fig. 4 is obtained (plotted at an ordinate value of 7 instead of ∞ for display purposes). Since the relative concentrations of the native unliganded state N and the denatured state D do not depend on the presence of the ligand 2′CMP, the phase separation line between the native unliganded state N and the denatured state D (vertical line in Fig. 4) is already defined by c_1/2 and m. The parameters are shown in the first column of Table 1. The third parameter (∂_cm_D) is zero, since the linear extrapolation method is valid for the unfolding reaction.

TABLE 1.

Parameters up to second-order defining the ligand-urea phase diagram

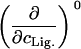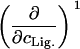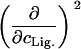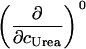	c1/2 or pKL	ΔN0	0
	m or mL	0
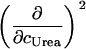	0 or ∂cmL

The columns are labeled according to the number of derivatives with respect to ligand concentration, the rows according to the urea-concentration derivatives.

Description of the ligand binding reaction in the urea-ligand phase diagram (Fig. 4) requires additional parameters, as shown in Table 1. Because the ligand is dilute, at least two of these six parameters are identical to zero: Neither the m-value nor the binding stoichiometry depend on the ligand concentration. From ITC measurements, 2′CMP affinities are obtained as pK values and stoichiometries ΔN⁰ in the absence of urea (Fig. 3, second step) and at different urea concentrations. The pK values do not follow a straight linear trend as a function of urea, in contrast to the linear extrapolation method (4,19). Hence, an additional parameter is needed, that is, the concentration-dependence of the m_L-value ∂_cm_L. The values of both m_L and ∂_cm_L are determined next by fitting the urea-ligand phase diagram (Fig. 3, third step). Combined with m_L and ∂_cm_L, the affinity in the absence of urea pK_L defines the N–NL phase separation line. The cooperativity of binding is already known, since it is the stoichiometry ΔN = 1 (14,40). This value was confirmed in the ITC experiments.

To summarize, there are six parameters defining the urea-ligand phase diagram. As shown in Fig. 3, two (c_1/2 and m_D) are determined by the unfolding in the absence of ligand, two (pK_L and ΔN) are determined by a titration of the protein with 2′CMP in the absence of urea, and the two residual parameters (m_L and ∂_cm_L) are determined from fitting the phase diagram. The resulting fit is shown in Fig. 2.

In addition to these six parameters defining the urea-ligand phase diagram, the ITC measurements yield the binding enthalpies of 2′CMP to RNaseA as a function of urea concentration (Fig. 3, fourth step). The data are linear as a function of urea concentration (data not shown). Therefore, two more parameters, ΔH_L and ∂_cΔH_L, are obtained.

Temperature-ligand phase diagram

We proceed with the temperature-ligand phase diagram at 0 M urea, which is given in Fig. 1. Two kinds of measurements were performed on the phase separation line between the native liganded and the denatured state: 1), the denatured protein was isothermally refolded in the ITC by addition of CMP; and 2), the protein was thermally denatured in the presence of different concentrations of CMP in the DSC and UV.

The description of protein unfolding over a larger range of temperatures requires at least four parameters given in Table 2: the transition midpoint temperature T_m, the transition enthalpy 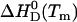, heat capacity 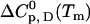, and its temperature-dependence 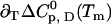. For the binding equilibrium, we also need the stoichiometry ΔN⁰, which is unity in our case. All other ligand-concentration-dependent terms vanish because the ligand is dilute. For convenience, the midpoint of the binding reaction is given by the affinity at room temperature pK_L(25°C) rather than by the transition midpoint temperature of binding. In total, nine parameters have to be determined (five for the ligand binding equilibrium and four for the folding equilibrium), and we follow again the strategy of doing this step by step.

TABLE 2.

Parameters up to third-order defining the ligand-temperature phase diagram

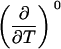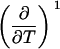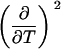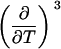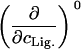	Tm or pK	ΔH0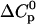
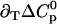	ΔN0	0	0
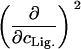	0	0
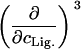	0

The columns are labeled according to the number of derivatives with respect to temperature, the rows according to the ligand-concentration derivatives. Since the stoichiometry of the reactions depends on neither temperature nor concentration, most of the derivatives are zero. See text for details.

First, we note that the number of parameters can be reduced to five. Three out of the nine parameters are already known: the affinity at room temperature, pK_L(25°C); the stoichiometry, ΔN⁰; and the ligand binding enthalpy at room temperature, ΔH_L(25°C). Another parameter of our choice can be eliminated as described below. We choose to eliminate the temperature-dependence of the heat capacity of denaturation, since it is difficult to determine.

We start with the first fitting step in the ligand-versus-temperature plane (Fig. 3, fifth step). The thermal unfolding experiments yield the midpoint of denaturation in the absence of ligand (the transition temperature T_m, see Fig. 2) and the width of the transition (the van' t Hoff enthalpy ΔH_{vH, D}). From the ITC measurements the binding enthalpy 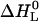as a function of temperature is obtained, and this yields 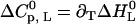(Fig. 3, sixth step). Finally, the entire temperature-ligand phase diagram is fitted (Fig. 1, solid lines) to determine the temperature-dependence of the heat capacity of ligand binding 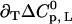and the heat capacity of unfolding 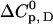(Fig. 3, seventh step). The temperature-dependence of the heat capacity of unfolding is directly obtained from all other parameters by the following procedure.

The Gibbs free energy of unfolding 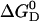can be given as a function of temperature in the absence of urea 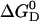(T, 0 M) (Eq. 14) and also as a function of urea concentration at room temperature 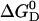(25°C, c_urea) (Eq. 15). Under the condition T = 25°C, c_urea = 0 M, these expressions can be equated. The resulting equation contains only fitting parameters and other constants, and thus it can be solved for one fitting parameter, which is thereby eliminated.

Temperature-urea phase diagram

The properties of RNase A as a function of temperature and urea concentration are best characterized using two methods: 1), thermal scans of the heat denaturation at constant urea concentration; and 2), isothermal urea-induced unfolding. The resulting midpoint concentration and transition temperatures are shown in Fig. 2.

It is known that in the presence of urea, the denaturation of RNase A becomes slow (41), so that in solvent-induced denaturation the samples have to be incubated over several hours. But even thermal denaturation may become kinetically distorted, depending on the heating rate (42). In addition, at elevated temperature the protein might not only misfold, it could also become chemically modified (carbamylated) by urea decomposition products (43), and this reaction can distort the DSC signal further. Because of these problems, and because the phase diagram is already sufficiently characterized by the other measurements, we refrained from doing temperature scans in the presence of urea.

Diagram cross correlations

Determining the parameters in the ligand-temperature plane and in the ligand-urea plane is sufficient to know the behavior in the urea-temperature plane (Fig. 2). In addition, we determined the cross correlations in the ligand-urea-temperature space ∂_cΔH⁰ and 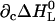using the slope of the calorimetric enthalpies with urea concentration. This allows us to plot the ligand-temperature phase diagram at 2 M urea (Fig. 1, dotted line). The predicted phase separation line between liganded and unliganded state agrees well with the experimental data-points (solid circles). This indicates that the first-order temperature dependence of m_L and m_D, as given in the square brackets of Eq. 17, is sufficient and no heat capacity terms (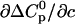) have to be taken into account.

As shown in Table 3, the cross-correlation parameters are of importance in the temperature-urea plane, in contrast to the other phase diagrams (Tables 1 and 2). Therefore, it is especially useful to systematically determine all parameters sequentially, when working in the temperature-cosolute plane. In general, medium-to-high affinity ligands are least problematic in terms of the number of needed derivatives (Table 1, first row), since the number of binding sites does not depend on their concentration. The m-value of ligand binding, as observed in this study, does depend on cosolute concentration, so higher-order derivatives are needed for the cosolute dimension (Table 1, first column). The most complex behavior occurs in the temperature dimension, where heat capacities and their dependence on temperature have to be considered (Table 2, first row). Therefore, calorimetry is of high value for such studies, because it directly measures enthalpies and heat capacities.

TABLE 3.

Parameters up to third-order defining the urea-temperature phase diagram

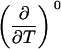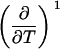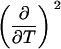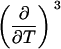	Tm or c1/2	ΔH0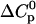
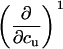	m	∂cΔH0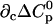
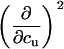	∂cm	(∂c, Tm)
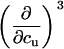	(∂c, cm)

The columns are labeled according to the number of derivatives of ΔG⁰ with respect to temperature, the rows according to the urea-concentration derivatives. The value ΔG⁰ can be conveniently expressed in terms of T_m or c_1/2. Parameters, which are insignificant and can therefore be set to zero, have been bracketed. See text for details.

DISCUSSION

As quantitative biochemistry progresses toward the investigation of systems that increasingly resemble the cytosol, major technical challenges arise. Huge numbers of experiments must be performed to elucidate reaction networks. Recent developments in high throughput spectroscopy allow for performing such numbers of experiments on protein stability and ligand binding (44). Data on reaction networks that go beyond very simple systems are, however, exceedingly difficult to analyze with classical methods. As shown in this article, the recently developed phase diagram method (1) can resolve this issue. Given that proper experimental data are available, interpretation and extraction of the pertinent information is straightforward, and independent of the number of molecular species.

The phase diagram previously relied on the solution conditions being thermodynamically ideal, an assumption very common in biochemistry. However, the biomolecules in vivo are far from approaching such ideal conditions. Rather, they are in a heavily crowded and nonideal environment. The current work bridges this gap and provides the extension to the phase diagram method that is needed to proceed toward the quantification of cytosolic reaction-networks that are near in vivo conditions.

In the current work, we emphasize an analytical approach, in which all equations for phase separation lines, free energies, etc., are explicitly solved. This approach is very useful, because it is straightforward to extract information from the equations independently of measurements. For much more complex systems than the one discussed in this article, a switch to numerical solutions of the equations might be required.

In demonstrating how the phase diagram method works for quantifying a reaction system under thermodynamically nonideal conditions, we found that the affinity of RNase A to CMP strongly and nonlinearly depends on urea concentration—a finding consistent with urea-dependent chemical activity of the free CMP. Before discussing this biochemical finding, we first turn to the phase diagram method.

The phase diagram method

We have shown in this work how to use the phase diagram method to define and quantify a reaction scheme under thermodynamically nonideal conditions. Our method reduces a 15-parameter fitting problem to several straightforward steps, each involving fits with not more than two parameters. Table 1 summarizes the procedure for the RNase A-CMP system. The principle of this procedure is to first fit each dimension in the phase diagram separately, such as temperature, ligand concentration, or urea concentration. This yields one midpoint-parameter (T_m, c_1/2, or pK_L) and one cooperativity parameter (ΔH⁰, m, or ΔN) each, as shown in the green shaded areas in Fig. 3.

Going into the second dimension of the phase diagrams is then straightforward. This is because only a few of the parameters necessary for the calculation of the phase-separation lines are left to be determined: four parameters (two per dimension) are already known. More cross-correlation parameters can be determined going into the third dimension. It is especially convenient, if some of the parameters can be determined independently of the phase diagram, because this reduces the number of parameters that have to be optimized per fit. For example, in our case we used ITC, which yields the enthalpies of binding in addition to the affinity and stoichiometry. The cross correlations between all three dimensions can then be used as an independent control, as shown in Fig. 1, where the derived urea-CMP-temperature cross correlations (represented by the dotted line) match the data-points well.

The ease and straightforward manner of this procedure is a prerequisite for automating the data evaluation process. Such automation will be necessary if a high-throughput method creates ten-thousands of data-points daily.

The RNase A equilibria

The RNase A-CMP-urea-water system provides interesting insights beyond its use as a model system for demonstrating the phase diagram method. Finding that the pK_L does not depend linearly on urea concentration (Fig. 4) is unexpected and intriguing. For protein conformational transitions such as the folding/unfolding transition, the Gibbs free energy is normally a linear function of urea concentration (4,20–23,45). The transfer model allows for predicting such m-values (46). In the case of RNase A ligand dissociation, the transfer model yields an m_L-value of –0.2 kJ/mol M using the PDB files 1ROB and 1FS3 for the calculation of the solvent-accessible protein surface areas of each chemical group in the presence and absence of bound ligand. This value is a factor of 10 smaller than the m_L-value of ligand dissociation at 0 M urea (–2.0 kJ/mol M). At elevated urea concentration, however, the experimental m_L value approaches zero, and thus comes close to the one predicted by the transfer model.

Moreover, not only protein transitions but also ligand binding pK values are normally found to linearly depend on osmolyte concentration or osmolality (47–53). In the case of urea, both molar concentration and activity are essentially equal over the range of solubility of urea (7), and the osmolality is approximately equal to the molar concentration up to 4 molar urea. At higher concentrations urea osmolality becomes gradually larger than its molarity, which corresponds to a greater curvature in the pK_L as a function of urea osmolality than seen in Fig. 4. The urea dependence of CMP binding to RNase A is therefore fundamentally different from what is expected both for protein transitions and protein-ligand binding, in that the m_L-value strongly depends on urea concentration.

Based on the two criteria of urea concentration-dependent m_L values and large m_L at low urea concentration, it is unlikely that the urea effect on protein molecules, with or without ligand bound, plays a major role in determining the magnitude and concentration-dependence of m_L. The pK_L of CMP binding to RNase A behaves both qualitatively and quantitatively different from a protein. It even behaves differently from normal protein-ligand interaction. It is therefore likely that the observed peculiar behavior of m_L and pK_L originates from the urea-dependent solvation of the free ligand CMP. The solvation behavior is important in this context, because it determines how the chemical activity of CMP depends on cosolute concentration (54). A urea-induced decrease in the chemical activity of CMP at constant CMP concentration would lead to a decreased protein-ligand affinity, as observed in our measurements.

The chemical activity of another nucleotide, ATP, has been previously determined as a function of urea concentration (55). Interestingly, those data match our pK_L observations in both the order-of-magnitude and functional dependence of the effect. Specifically, the chemical activity of ATP decreases by a factor of 5.2 between 0 M and 5.4 M urea, compared with the pK_L of CMP binding to RNase A decreasing by a factor of 10 within this range of urea concentration. Both ATP activity and RNase A-CMP affinity are strongly sloped at 0 M urea, but level-off at higher concentrations (note the initial slope and the curvature of the liganded-unliganded phase separation line on the left side of Fig. 4).

The observation that the enthalpy of binding is weakly and linearly dependent on urea concentration, but the pK_L is strongly and quadratically dependent on urea, might appear counterintuitive. However, this finding can be rationalized in the following way. The enthalpy that is linear in c_u represents a mixed derivative of the partition function with regard to temperature and concentration (see also Table 3). Reversing the order in which the derivatives are taken reveals that an enthalpy of binding that is linear in c_u corresponds to an m_L-value that is linear in temperature. As a result, the quadratic dependence of pK_L on c_u means that m_L also depends linearly on c_u. Thus, the conclusion is that m_L depends linearly on both temperature and urea concentration.

The interaction between urea and CMP can in principle be viewed as very weak binding as quantitatively discussed in the following. We have recently shown that this also holds for osmolyte-osmolyte interaction in approximately half of the investigated cases (6,7). Such interactions are sufficiently well represented by second-order terms of the partition function. Following these recent findings, the simplest second-order model for urea-CMP interaction in aqueous solution is

(22)

where Z is the semi-grand partition function, Y₀ is the canonical partition function for pure water, g₂ is a measure of apparent urea oligomerization, and g₁ is a measure of apparent urea-2′CMP interaction. The relative chemical activities of urea a_u and ligand a_L are obtained from the absolute activities by a base transform (6,7). Terms up to second-order (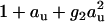) have been shown to be sufficient to capture the nonideality of urea over the solubility range (6,7). Since 2′CMP is dilute, only terms up to first-order (1 + a_L) are required. Possible correlations between urea and 2′CMP are taken into account through the cross-term g₁a_La_u.

The molarities of urea

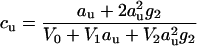(23)

and 2′CMP

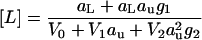(24)

are readily calculated. Because a_L is small compared to a_u (the ligand is dilute, but the urea concentrated), a_L-containing terms can be ignored in the expression for the urea molarity c_u and in the denominator of the expression for [L]. V₁ and V₂ are the apparent volumes occupied by one or two urea molecules, respectively, including hydration. V₀ is the volume occupied by the pure water. Division of Eq. 24 by Eq. 23 yields

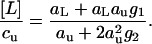(25)

This equation can be solved for a_L/[L] to obtain the activity coefficient of 2′CMP as a function of urea concentration

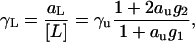(26)

where γ_u = a_u/c_u is the molar activity coefficient of urea. The pK_L or Gibbs free energy for the binding of 2′CMP to RNase A is then

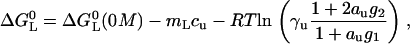(27)

where the logarithmic term replaces the term containing ∂_cm_L from the model-free analysis (Eq. 21). Using Eq. 27 for a curve-fit of the pK_L values results in a very reasonably sized m-value of m_L = −0.3 kJ/mol M. The urea-CMP interaction parameter is g₁ = 0.9/M. Our data are therefore well compatible with the idea of a direct binding between urea and CMP. Note, however, that the highly nonideal conditions as found in concentrated urea do not permit one to decide whether the observed effects are due to such direct binding, or to some more general solvation phenomena (8).

Independently of the cause for the strongly urea-dependent protein-ligand affinity, our finding has important implications for metabolism in urea-rich tissues, such as the human kidney. We report here that protein-nucleotide affinities can change by a factor of three over a range of urea concentration of zero to one or two molar, a urea concentration range that occurs in the inner kidney medulla upon antidiuresis (56,57). Such large changes in ligand affinity are capable of confounding the biochemistry of kidney inner medullary cells—especially because such changes in urea concentration can occur within hours, with such vitally important molecules as nucleotides strongly affected. The kidney cells must have a means to counteract these adverse effects, probably by their special mixture of protecting osmolytes (11). Much remains to be learned about such thermodynamically nonideal effects of mixtures of osmolytes. Exploration of multidimensional concentration spaces requires high-throughput techniques. The phase diagram method allows for straightforward evaluation of the massive amount of data generated.

CONCLUSION

We have demonstrated that the phase diagram method can successfully be used for deconvoluting reaction schemes, even in the case of thermodynamic nonideality. This approach is of high utility in several ways. We demonstrated previously for one example that the phase diagram method can reveal physiologically significant processes that are otherwise difficult to detect (58). Another application that will have increasing use is the evaluation of high-throughput thermodynamic data. Large quantities of thermal melt data collected on microtiter plates (44) can be efficiently compressed without losing the pertinent thermodynamic information, if the phase diagram method is used. Thousands of data points can be represented by a small set of midpoint-parameters and cooperativity-parameters (e.g., T_m and ΔH⁰). Dozens of these parameters can in turn be represented by a much smaller set of heterotropic cooperativity-parameters (mixed derivatives of the partition function). As high-throughput methods become more available, we are in dire need of such powerful thermodynamic data-compression tools.

On the biochemical side, our finding of strong osmolyte-dependent changes in ligand binding pK values, with the probable cause of osmolyte-nucleotide interaction, opens a new set of biochemical issues. Appropriate osmolyte-nucleotide interaction in the face of changing cosolute concentrations turns out to be a major challenge for human organs, such as kidney. The impact of detrimental osmolyte-metabolite and osmolyte-signaling molecule interactions must be investigated in detail to uncover the strategies of cells to cope with this problem.