Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2006 Oct 6;92(1):23–33. doi: 10.1529/biophysj.106.084715

Possible Pathway for Ubiquinone Shuttling in Rhodospirillum rubrum Revealed by Molecular Dynamics Simulation

A Aird *, J Wrachtrup *, K Schulten †, C Tietz *
PMCID: PMC1697858  PMID: 17028136

Abstract

In the last decade, the structures of many components of the photosynthetic apparatus of purple bacteria, as well as the mutual organization of these components within the purple membrane, were resolved. One key question that emerged concerned the assembly of the core complex consisting of the reaction center (RC) and the light-harvesting 1 (LH1) complex. In some species, like Rhodobacter sphaeroides, the ring-shaped LH1 complex was found to be open, whereas other species, like Rhodospirillum rubrum, have a closed ring surrounding the reaction center. This poses the question of how the ubiquinone molecule that transports electrons and protons from the RC to the cytochrome bc1 complex overcomes the apparent barrier of the LH1 ring. In this study, we investigated how, in the case of a closed LH1 ring, the ubiquinone molecule diffuses through the LH1 ring. For this purpose, the LH1 structure of R. rubrum was modeled and the potential of mean force along the diffusion pathway through the LH1 was determined by steered molecular-dynamics simulations. The potential was reconstructed using the fluctuation theorem in combination with the stiff spring approximation. An upper limit for the mean first-passage time for diffusion of ubiquinone through the LH1 ring, based on a worst-case scenario potential, was calculated as ∼8 × 10−3 s, which is still in agreement with known turnover rates of RC and RC-LH1 complexes in the range of ∼1000 Hz.

INTRODUCTION

The organization of the photosynthetic unit (PSU) of purple bacteria is structured more simply than that of cyanobacteria or higher plants. It consists of light-harvesting complexes (LH1 and LH2), the reaction center (RC), the cytochrome bc1 complex (Cyt bc1), and the ATP-synthase (ATPase). Some species of purple bacteria lack even the LH2 complex in the PSU.

After light absorption within the LH1 complex the excitation energy is transferred to the special pair of the RC, where charge separation takes place. Along a chain of several donator-acceptor molecules the electron is finally transferred to a mobile carrier molecule, ubiquinone. Uptake of another electron and of two protons from the cytoplasmic side of the purple membrane changes the ubiquinone into an ubiquinole. It leaves the RC and transports the electrons and protons to the Cyt bc1 complex, where the protons are released to the periplasmic side of the membrane and build up a proton gradient across the membrane, which finally drives the ATPase; the electrons are transported back to the RC by means of cytochrome c2.

Intensive investigations over the last decades have revealed an altogether good understanding of many structural and functional properties of the PSU of purple bacteria. The structure of several complexes was resolved at an atomic level (RC (1), LH2 (2,3), Cyt bc1 (4), and ATPase (5)) or at a level allowing the assignment of molecular entities like α-helices or pigments (core complex (6)). The energy transfer was unraveled for most of the intra- and intercomplex processes using transient absorption methods with femtosecond resolution (7). Single-molecule spectroscopy revealed structural interaction of the LH1 and LH2 complexes with the environment (8–10).

All light-harvesting complexes in purple bacteria display a rather analog architecture. The LH1 and LH2 complexes consist of certain numbers of identical pigment-protein subunits. Each subunit contains two separate membrane spanning helices (α- and β-polypeptide), each ∼50 amino acids in length, bacteriochlorophyll (BChl), and carotenoid (Car) molecules.

Even though the overall mechanism of photosynthesis in purple bacteria seems to be very similar, there are a number of differences between species. For example, the LH1 β-subunit from Rhodobacter sphaeroides consists of two helical transmembrane parts that are connected by a loop (11), whereas the NMR solution structure of the same subunit from Rhodospirillum rubrum revealed a single membrane-spanning helix (12), which in turn is very similar in structure to the LH2 β-subunit from crystallographically resolved structures of Rhodopseudomonas acidophila and Rhodospirillum molischianum (2,3). These observations were both made from solution NMR studies and it is not clear whether this difference is observable in the subunits of the complex structure. Such differences are more interesting when it comes to supramolecular organization. The LH2 structures, for example, show a different number of αβ-subunits needed for their assembly. In R. rubrum no LH2 complexes were even found. The most prominent complex of the photosynthetic apparatus to show such differences, however, is the core complex (LH1-RC). In this case, the differences can be directly connected to questions concerning functional aspects. A crystal structure with 4.8-Å resolution (6) as well as high-resolution electron microscopy (EM) studies (13–16) and AFM data (17–20), already give clear indications of the assembly in different species. Unfortunately, there is no atomic-resolution structure available for any core complex of purple bacteria so far. Nevertheless, judged from EM data (13), the Rb. sphaeroides core complex seems to have a dimeric structure with an additional protein referred to as PufX, connecting two LH1-complexes to form an S-shaped complex with two large openings in the LH1 rings. The crystal structure of the core complex from Rhodopseudomonas palustris (6) strongly indicates that the LH1 ring surrounding the RC consists of only 15 identical αβ-subunits with an additional α-helix (W-protein) that takes the place of the 16th subunit, creating an opening. Such openings are thought to be necessary for fast ubiquinone/ubiquinole diffusion from the RC to the Cyt bc1 complex. Such scenarios have also been discussed for R. rubrum (21), yet no PufX analogous gene has been identified so far.

EM projection maps with a resolution of 8.5 Å of 2D crystals on reconstituted LH1 rings from R. rubrum show a closed ring formed of 16 identical subunits (14). Electron cryomicroscopy on 2D crystals of core complexes (15) clearly indicate 16 LH1 αβ-subunits that are arranged in a closed ring around the RC. In addition, there seems to be a degree of flexibility within the LH1 ring, which can adopt a circular or an elliptical form. However, no evidence of any other small protein component in the LH1 ring was found in these projection maps. AFM studies on the LH1-RC complex (20) also suggest that the LH1 ring of R. rubrum completely encloses the RC. Accordingly ubiquinone diffusion in R. rubrum from the RC to the Cyt bc1 complex still remains an open matter in this framework. How is this molecule able to pass the pigment-protein barrier posed by the closed LH1 ring?

Ubiquinones are lipophilic, water-insoluble molecules that consist of a benzoquinone head and a tail consisting of a specific number of isoprenoid units. The ubiquinone molecule in this study consists of 10 isoprenoid units. Due to the hydrophobicity, these molecules are expected to be found in hydrophobic environments and indeed experiments show that they are located in the central part of the membrane (22,23). The diffusion constant of ubiquinone molecules in a membrane environment is in the range of 10−8 cm2/s to 10−7 cm2/s (23).

With this knowledge and the given structural data available at this time, a direct transport through the LH1 ring cannot be ruled out yet, and indeed has been discussed in the literature (15,16,20). Recently, ubiquinone turnover rates for Rb. sphaeroides have been determined experimentally for both an open, dimeric RC-LH1 structure and a closed, monomeric RC-LH1 mutant structure lacking PufX (24). The researchers conclude that the observed reduction in turnover by a factor of 2 in the mutant structure is not directly connected to blocking of ubiquinone transport through the closed LH1 ring, but could be a consequence of faulty LH1-RC interaction. Species without PufX or an additional helper polypeptide might have found different ways to compensate this by modification of the LH1-RC interface or the ubiquinone binding site to achieve efficient transport, even with an LH1 ring completely surrounding the RC.

In this article, we propose a simple diffusion process through the closed LH1 ring as a possible transport mechanism for ubiquinone shuttling. The aim of this study is to evaluate this proposed pathway by means of molecular-dynamics simulations. Such simulations allow to investigate the system at the atomic level. A model structure for the LH1 ring was used, as there is no structural data with atomic resolution available so far.

METHODS

Simulations

To get information on the transport pathway of the ubiquinone molecule through the LH1 ring, molecular-dynamics (MD) simulations on a model system were performed.

The LH1 complex consists of 16 identical pigment-protein subunits. Each subunit contains two individual membrane-spanning helices (α- and β-polypeptide, each ∼50 amino acids in length), two BChl molecules, and one Car molecule. The pigment molecules are sandwiched by the α- and β-polypetides. The subunits are arranged in a ringlike structure (16). Since there is no high-resolution structure available for the LH1 ring of R. rubrum, a model structure adapted from Hu and Schulten (25) was used. The resulting structure of the αβ-polypeptides of the model is in good agreement with the newly resolved NMR structure (12), and the overall structure fits well to the available EM projection maps (14).

MD setup

For computational efficiency, the system was designed to have the minimum number of atoms, yet incorporate all the necessary features to ensure the correctness of the simulations. Therefore, only a quarter of the LH1 ring (four protein subunits including all the corresponding pigments) was used in all of our simulations. The pigment-protein complex was then inserted in a 1-palmitoyl-2-oleoyl-phosphatidylcholine (POPC) lipid bilayer to account for the membrane environment, with the α-helices lying parallel to the membrane normal, and the system was fully hydrated using the TIP3P water model. The total number of atoms was 69,527, with 6940 protein atoms, 31,758 lipid atoms, 29,184 water atoms, and 1645 pigment atoms and counterions. To ensure the overall shape of the ringlike structure (16), the backbone of the outermost protein helices was harmonically constrained with a spring constant of 35 pN/Å. The pigments and the rest of the protein were free to move. This system was minimized and equilibrated for 4 ns. An integration time step of 1 fs was employed. Van der Waals interactions were calculated every step using a 10 Å cutoff and a smooth switching function. Electrostatic interactions were evaluated with a multiple time-stepping algorithm using the particle mesh Ewald method (26) with a 10 Å cutoff for the real-space sum and a grid spacing of 1 Å for the reciprocal sum.

The system was simulated using periodic boundary conditions and was kept at a temperature of 300 K and a pressure of 1 bar using the Langevin piston method (27), with an oscillation period of 200 fs and a damping time of 100 fs. After an equilibration time of ∼1.5 ns, the system was very stable, the structural deviation staying below 1.6 Å for the rest of the simulation for both the protein and the pigments. The height of the lipid bilayer (P-P distance) was ∼38 Å with an area/lipid of ∼67 Å2. All simulations were done with the program NAMD (28) using the CHARMM 27 parameter set (29). Force-field parameters for all nonstandard CHARMM molecules are the same as those used in Autenrieth and co-workers (30,31) and Damjanovich et al. (32).

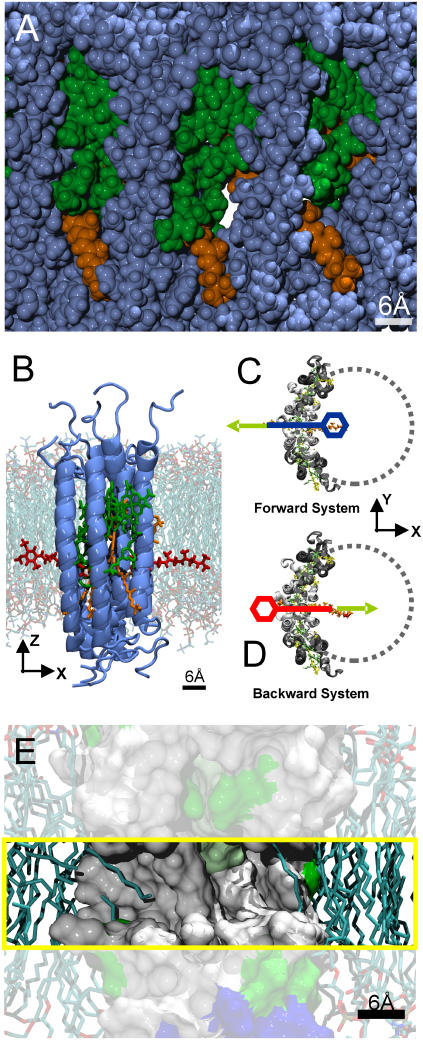
Fig. 1 A shows a snapshot of the system during equilibration. Here, a side view from the membrane plane onto the LH1 ring is shown in van der Waals representation, with the protein atoms in blue, the BChl atoms in green, and the Car atoms in orange. Lipid and water molecules are omitted for clarity.

FIGURE 1.

FIGURE 1

Open in a new tab

(A) Side view of part of the LH1 ring seen from the membrane plane in van der Waals representation. Protein atoms are shown in blue, BChl atoms in green, and Car atoms in orange. A channel through the LH1 ring is clearly visible. (B) Side view of one of the initial systems used to explore the ubiquinone diffusion through the LH1 ring. The protein subunits are shown in blue, ubiquinone atoms in red, BChl atoms in green, and Car atoms in orange. The ubiquinone headgroup is on the left side (outside) of the LH1 ring. The lipid environment is superimposed in the background. (C and D) Top view of the two initial systems used to find a suitable pathway for ubiquinone diffusion through the LH1 ring. Only protein (white and gray), ubiquinone (orange), and chlorophyll/carotenoid atoms (green/yellow) are shown for clarity. In the Forward system, the ubiquinone headgroup is on the inside of the LH1 ring (blue). In the Backward system, the headgroup is on the outside of the LH1 ring (red). The system's x axis lies parallel to the connecting line between the center of the LH1 ring and the channel opening. SMD simulations were performed on both initial systems, where the ubiquinone was pulled out of the LH1 ring. The focus in these simulations lies on the headgroup of the ubiquinone, which is more voluminous than the rest of the molecule and will therefore have the largest effect on the resulting PMF. The moving constraint was attached to the last carbon atom of the last isoprenoid unit of the ubiquinone tail. This was done to perturb the movement of the headgroup of the ubiquinone as little as possible to find an unbiased pathway. In the SMD simulations for reconstructing the potential of mean force along the pathway (see text), the moving constraint was attached to the center of gravity of the ubiquinone headgroup, which was chosen as the reaction coordinate. (E) Side view onto a cross section of the channel region of the LH1 ring shown in surface representation. The channel region is highlighted (yellow box). Hydrophobic regions are colored in white, polar regions in green, and charged amino acids in red and blue. The lipid environment is shown in licorice representation. The hydrophobic region of the channel is visible. Lipid tails partly occupy the entrance of the channel on both sides, as seen in equilibration runs of the LH1 ring.

The equilibrated structure was used in subsequent simulations to explore a possible pathway for ubiquinone diffusion through the LH1 ring, the first step being the identification of such a pathway. For this purpose, the ubiquinone molecule was prepared in a stretched conformation and was inserted already halfway through the protein barrier (Fig. 1 B). Two initial systems were prepared. In the first system (Forward system), the ubiquinone headgroup is lying on the inside, the tail on the outside. In the second system (Backward system), the headgroup is lying on the outside, the tail on the inside (Fig. 1, C and D). Both systems were equilibrated for 6 ns using an equilibration scheme as outlined above. To keep the ubiquinone molecule in the chosen configuration, a harmonic constraint was applied to the center of gravity of the headgroup and to the carbon atom of the last isoprenoid unit of the ubiquinone tail. A spring constant of 250 pN/Å was used for the two additional constraints. After equilibration, both systems were close to the initial starting structure. The root mean-square deviation (RMSD) value for all of the protein subunits and the overall protein structures stabilized after ∼2 ns below 1.5 Å, with the more flexible pigments showing slightly higher structural deviation.

To accelerate the diffusion of the ubiquinone (microseconds to milliseconds) to timescales that are accessible for MD simulations (nanoseconds), the method of steered molecular dynamics (SMD) is used (33). Here, a moving harmonic constraint is added to the potential energy function to apply an external force to the ubiquinone molecule. In our simulations, a constant-velocity scheme was used with a pulling speed of 10 Å/ns and a spring constant for the harmonic constraint of 500 pN/Å. This insures that the system closely follows the pulling potential and the stiff spring approximation (34,35) (see below) can be applied.

In the following SMD simulations, the ubiquinone molecule was completely pulled out of the LH1 ring into the lipid bilayer with the ubiquinone molecule on the outside of the LH1 ring in simulation 1 (Forward system) and on the inside in simulation 2 (Backward system).

The main focus was on the headgroup because it represents the most voluminous part of the ubiquinone molecule and will therefore have the largest effect on the simulation results. Pulling in both directions was done to gain information on the potential pathway from independent simulations. The atom used for attaching the moving constraint was the carbon atom of the last isoprenoid unit of the ubiquinone tail. By pulling the ubiquinone molecule only on the tail atom, the headgroup of the ubiquinone is almost free to move and can therefore find a suitable pathway through the LH1 ring. The system was prepared in an orientation such that the x axis was parallel to the direction connecting the center of the LH1 ring with the channel opening (see Fig. 1, C and D) and the z axis was parallel to the membrane normal. The SMD direction was parallel to the membrane plane along the positive (Forward system) and negative (Backward system) x-direction. The pulling distance was ∼40 Å, which resulted in a total simulation time of 4 ns per run.

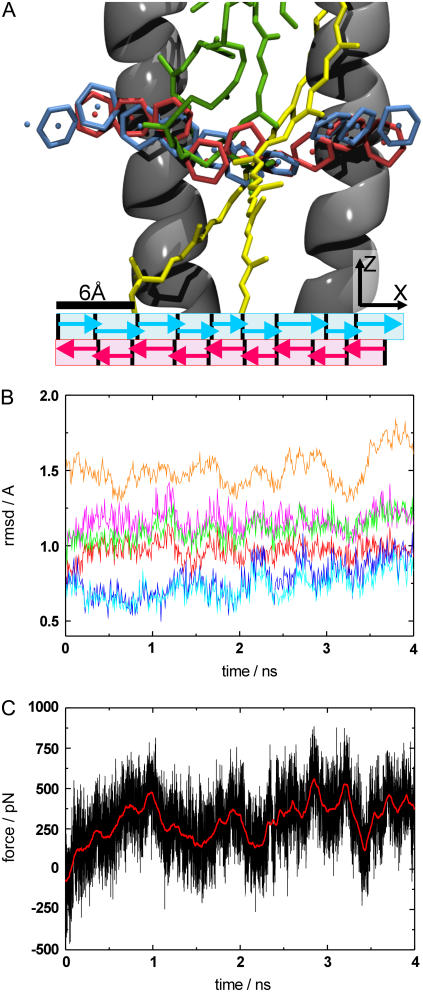
To reconstruct the potential of mean force (PMF) along the proposed pathway through the LH1 ring, the following SMD simulations were performed. This time the moving constraint was attached to the center of gravity of the ubiquinone headgroup, which was chosen as the reaction coordinate, because we expect this to be the dominating part for calculating the PMF (see section above). To keep the system close to equilibrium, the pathway was divided into nine sections and ubiquinone diffusion along the pathway was explored independently in these sections for both directions, as seen in Fig. 2 A. The sections are marked by arrows; the forward direction is shown in blue and the backward direction in red. The ubiquinone headgroup was placed at every section boundary, and all systems were equilibrated for up to 2 ns. To keep the ubiquinone head located at the initial position of each section during equilibration, a harmonic constraint with a spring constant of 500 pN/Å was applied to the ubiquinone headgroup in the pulling direction. Again the equilibration runs resulted in small structural deviations, with the RMSD value of the protein and the pigments staying below 1.3 Å. An ensemble of 10 starting structures for every section was extracted from the equilibration runs. With these starting structures, 10 SMD simulations per section were performed, where the head of the ubiquinone molecule was pulled along the specified pathway to the next section. The SMD velocity was 10 Å/ns and the spring constant used was 500 pN/Å. The length of the simulations was adapted to guarantee an overlap between adjacent pulling sections. This procedure was done for both the forward and the backward pulling direction.

FIGURE 2.

FIGURE 2

Open in a new tab

(A) Snapshots of the pathway of ubiquinone diffusion through the LH1 ring (side view). Parts of the protein/pigments are omitted for clarity. The protein is shown in cartoon representation in gray, with BChl molecules in green and Car molecules in yellow. The ubiquinone head (center of gravity of headgroup denoted by spheres) is shown in blue for the forward and red for the backward simulations. The different pulling sections are marked below by arrows. (B) RMSD plot of the SMD simulation for pulling the ubiquinone molecule through the LH1 ring. Different substructures are shown. The RMSD for the backbone atoms of the α-subunit is shown in red (helical part)/magenta (all atoms), the RMSD for the backbone atoms of the β-subunit is shown in blue (helical part)/cyan (all atoms), the RMSD of all the protein backbone atoms is shown in orange, and the RMSD for the transmembrane atoms is shown in green. (C) Force curve for the same simulation. The simulation data is shown in black, with a smoothed force curve shown in red to highlight the overall shape.

THEORY

The potential of mean force along a reaction pathway represents a very significant property for biological questions. This is, however, difficult to extract from standard MD simulations due to the inherent problem of insufficient sampling of phase space. One way to overcome this problem is the method of umbrella sampling (36), where the system is kept at specified positions along the reaction pathway using restraining potentials. Equilibrium MD simulations are performed and the PMF is extracted from the biased distributions using the weighted histogram analysis method (37).

For some practical applications (e.g., large systems, large number of restraining points along the reaction coordinate, long equilibration times), it can be computationally very demanding to collect enough data to sufficiently sample the whole reaction pathway. Another way to obtain free energy differences is to accelerate the reaction onto the accessible nanosecond timescale using SMD simulation and extract the equilibrium value ΔG from statistical analysis of nonequilibrium simulations using the fluctuation theorem.

In recent years, a number of different versions of the fluctuation theorem have been established to solve this problem (38,39). They have been checked for applicability in simulations and experiments in numerous studies (35,40–43).

In 1997, Jarzynski formulated an integral version of the fluctuation theorem, connecting the free energy difference to an exponential average of the external work. For a system that evolves according to a Markov process, the free-energy difference ΔG can be written as (39)

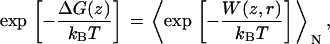graphic file with name M1.gif (1)

where W is the external work along a trajectory and angle brackets denote the ensemble average over N trajectories. For infinite sampling of work values, the free-energy estimate is exact; for finite sampling, it allows an estimate of this value. This is highly dependent on how well the distribution of work values can be described. In MD simulation of larger biomolecules, where in general only a small number of trajectories are affordable, this is practical only for a narrow work distribution, with a width σW ≈ kBT (34).

For a system driven further away from equilibrium, this is no longer possible for a limited number of trajectories and leads to an overestimation of the free energy change. The exponential average of the work in the Jarzynski equation is mainly determined by trajectories with small work values. These trajectories are rare events, which makes the exponential average very difficult to estimate accurately from a small number of trajectories and for systems driven far out of equilibrium due to insufficient sampling.

An approximation can be found by expanding the right side of Eq. 1 into a series of cumulants Cn(z):

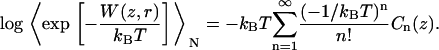graphic file with name M2.gif (2)

The cumulants Cn(z) in Eq. 2 describe the shape of the work distribution, e.g., 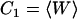Inline graphic is the mean work, 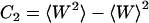Inline graphic the variance of the distribution. For the special case of a Gaussian-shaped work distribution, third- and higher order cumulants are identically zero. A Gaussian-shaped distribution would be expected for slow pulling speeds, i.e., if the system stays close to equilibrium, which is not necessarily the case for SMD simulations. Interestingly, using a sufficiently large spring constant for the moving harmonic constraint in the SMD simulations results in a Gaussian-shaped work distribution, independent of the pulling speed (34,35). For this case, the cumulant expansion up to second order is exact and the systematic error of truncating the expansion vanishes.

With only a limited number of trajectories available, the second-order cumulant expansion is also afflicted with a bias and a statistical error due to finite sampling. The bias is mainly caused by the calculation of the variance of the work distribution, leading to an underestimation of the variance and an overestimation of the resulting free-energy change. The accurate estimation of the free-energy difference becomes very difficult for systems far away from equilibrium (43). In this case, the work distribution will still be Gaussian but very broad. The calculation of the width of this distribution and therefore also the evaluation of free energy will result in both a large bias and statistical error. For a reasonable estimate of the free-energy difference using the second-order cumulant expansion with only a limited number of trajectories at hand, the system should be kept in the near-equilibrium regime (Wdiss in the range of some kBT(300K)), where the work distribution is narrow and the resulting bias should have little influence on the overall shape of the PMF and should lie within the statistical inaccuracy. In the case of SMD simulations, this can be achieved either by choosing a slow enough pulling velocity or, as done in this study, by dividing the reaction coordinate into individual sections. Each section is first equilibrated and afterward independently simulated. After reconstruction of the PMF in each section, the different PMF segments are joined together.

The harmonic constraint used in the SMD simulation also contributes to the free-energy difference calculated from the simulations. Since we are interested in free energy differences of the unbiased potential, the influence of the pulling potential has to be taken into account. Again the choice of the spring constant becomes important. The so called stiff spring approximation (34,35) states that a sufficiently large spring constant leads to the approximation 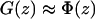Inline graphic, where G(z) denotes the free energy of the system including the SMD potential and Φ(z) is the unbiased PMF.

This kind of analysis was successfully applied to biological systems studied by SMD, namely, the conduction of glycerol through a protein channel, for the first time in 2002 (44).

For biological systems it is often very desirable to have information on the kinetics of the process under investigation. The kinetics of the diffusion of a molecule in a potential can be described by a Fokker-Planck-type equation, called a Smoluchowski equation. For a one-dimensional problem, like the PMF along a reaction coordinate, this equation can be written as

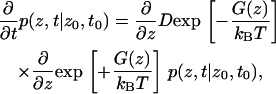graphic file with name M6.gif (3)

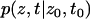where Inline graphic is the probability density of finding the system at position z at time t when it was at position z0 at time t0.

Using suitable boundary conditions (discussed later) and a constant diffusion coefficient for the ubiquinone molecule as a first approximation, an estimate of the mean first-passage time can be derived from the reconstructed PMF G(z) using the following equation: (45):

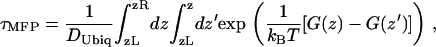graphic file with name M8.gif (4)

where τMFP is the mean first-passage time, DUbiq is the diffusion coefficient for the ubiquinone molecule along the PMF, and G(z) is the PMF. In our case, τMFP is the mean time for the ubiquinone molecule to diffuse from the outside of the LH1 ring to the inside, i.e., to overcome the diffusion barrier for the first time.

RESULTS AND DISCUSSION

Pathway through the LH1 ring

To answer the question of whether the ubiquinone is able to diffuse through the LH1 ring without additional help, e.g., from another protein, we first have to find out where possible pathways through the complex would be located. Indeed, a possible candidate for such a pathway is easily found by simple examination of the equilibrated structure of both the whole ring and the quarter-ring used for the final simulations (see MD setup). A space-filling representation of the structure reveals channels straight through the ring, as shown in Fig. 1 A. These channels have a diameter of ∼6 Å and the inside walls are built from the Car molecules, BChl tails, and amino acid residues like phenylalanine, leucine, and alanine of the αβ-subunit, i.e., built from rather hydrophobic components. Consequently, the inside of the channel should be hydrophobic, too. This can be seen in a cross section of the LH1 ring shown in Fig. 1 E in surface representation. The channel area is highlighted (yellow box), and the hydrophobic regions are colored in white, the polar regions in green, and the charged regions in red and blue. The lipid atoms are shown in licorice representation. Indeed, equilibration MD runs starting from an ordered lipid patch, where all lipid tails lie parallel to the membrane normal, show that the channels are occupied by lipid tails within nanoseconds of simulation time (see Fig. 1 E). Both the diameter of the channels as well as the occupation by lipid tails change between different subunits and within the same unit during the simulation time.

Analysis of SMD simulations pulling the ubiquinone molecule, which was halfway inserted in the LH1 ring, into the membrane area (see MD setup), revealed a possible pathway for ubiquinone diffusion. Fig. 2 A shows a side view onto a cross section of the LH1 ring channel and displays snapshots of the headgroup, which is larger than the average channel diameter in the middle of the protein barrier, every ∼300 ps for the forward pulling direction, from inside to outside of the ring, represented in blue, and the backward pulling direction, from outside to inside, in red (the sphere inside the nonaromatic carbon ring marks the center of gravity of the ubiquinone headgroup, with part of the protein omitted for clarity). The observed pathway is not along a straight line through the ring, but rather slightly curved to the cytoplasmic side of the membrane. There are three strong indications for the plausibility of this pathway:

  1. Forward and backward simulations result in almost identical pathways.

  2. There is very little structural deviation. Fig. 2 B shows the RMSD curves for all relevant components (substructures of the LH1 ring and the pigments) that could be disturbed by the ubiquinone headgroup. The maximum deviation of 1.6 Å for the protein backbone is comparably small and even, in the same region as the deviation during the equilibration runs.

  3. The forces along the pathway are rather low, <400 pN on average and <800 pN for the maximum forces appearing during the whole simulation (see Fig. 2 C), which is comparable to other SMD studies exploring ligand diffusion in protein channels (44,46).

Reconstructing the PMF along the proposed pathway

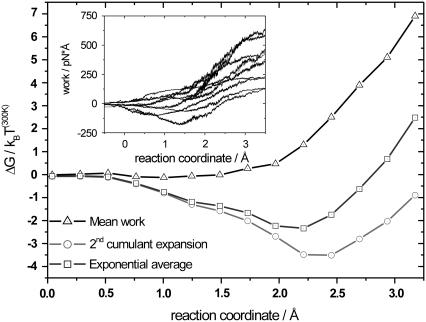
As described in MD setup, the pathway was divided into nine sections and independently explored in each section (see Fig. 2 A). Ten SMD runs per section for both the forward and backward directions were performed. From the simulation output, the forces applied on the ubiquinone molecule can be extracted. The forces fluctuate among different trajectories leading to different external work profiles. The resulting external work as a function of the reaction coordinate is shown in the inset of Fig. 3. Smoothed curves are shown for clarity. The spread of work values increases while moving along the reaction coordinate, meaning that as the molecule is pulled along the reaction coordinate, the dissipated work increases. To reconstruct the PMF, statistical analysis on the work profiles was performed. For this section, three different free energy estimators were used to calculate the changes in free energy along the reaction coordinate. In Fig. 3, we have plotted the mean work (triangles) together with the PMF resulting from the second-order cumulant expansion (circles) and the exponential average (squares). The mean work only gives the correct PMF for systems in equilibrium at all times, which is not the case here. Therefore, the mean work will always result in free energies Inline graphic, and is not applicable.

FIGURE 3.

FIGURE 3

Open in a new tab

Reconstructed potential of mean force for section 3 (backward pulling direction), calculated from the work profiles shown in the inset, using three different free-energy estimators. The mean work is represented by triangles, the second-order cumulant expansion by circles, and the exponential average by squares. Up to 2 Å, the exponential average and the second-order cumulant expansion show comparable results, with Wdiss <3 kBT(300K), meaning that the system is still sufficiently close to equilibrium. At the end of the section, the dissipative work is <8 kBT(300K). Here, both exponential average and second-order cumulant expansion show different results. The work profiles in the inset are smoothed for clarity.

As discussed in Theory, we can assume a Gaussian-shaped work distribution. The mean dissipated work can therefore be estimated from the calculated width of the work distribution. For systems close to equilibrium and with only a limited number of trajectories available, both the second-order cumulant expansion and the exponential average give comparable results (35). This is valid for Fig. 3 up to 2 Å, where the estimated mean dissipated work stays below ∼3 kBT(300K). At the end of the section, the exponential average is noticeably higher than the second-order cumulant expansion. Here, the mean dissipative work increases up to ∼8 kBT(300K). The exponential average suffers from lack of sufficient sampling of low-energy work values, which are exponentially rare, and will therefore strongly overestimate the resulting PMF. The second-order cumulant expansion is expected to work better in this regime. All of the sections, for both backward and forward pulling directions, showed estimated dissipated work values in the range of 0 kBT(300K) to 5 kBT(300K) for most of the pulling section and higher dissipated work values, sometimes up to 10 kBT(300K) toward the end of the section. From the three free-energy estimators mentioned before, the second-order cumulant expansion is the only practical method to reconstruct the PMF along the proposed pathway with acceptable errors, having only 10 trajectories at hand and dissipation in the near-equilibrium regime.

By assembling the different PMFs from the individual sections for both pulling directions, the free-energy difference profiles along the proposed pathway were obtained. This was done by matching the PMFs from adjacent sections at the section boundary. The starting point for the PMFs for the forward and backward pulling directions was set to zero.

A significant aspect of calculating the PMF for the ubiquinone shuttling through the LH1 ring concerns the conformational changes of the ubiquinone molecule itself during the SMD simulations. Due to the choice of unraveling an unbiased path through the ring, the starting structure of the ubiquinone molecule is in an almost stretched conformation for most of the pulling sections, which is rather unlikely for entropic reasons. A more realistic scenario would see the ubiquinone molecule stretched only within the channel through the LH1, i.e., for a distance of ∼20 Å, and rather coiled outside the channel. As the ubiquinone head is moved along the reaction coordinate in the different pulling sections, the molecule is stretched even further. For this reason, the force observed in the simulations mostly exceeds the force corresponding to the PMF by the entropic force necessary to additionally stretch the ubiquinone molecule during the SMD simulations.

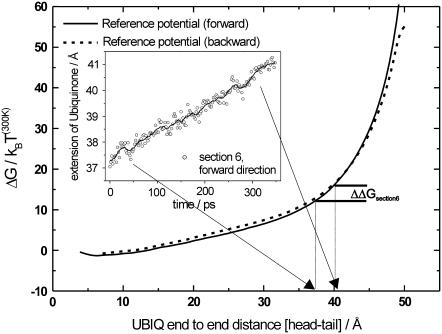
To determine this overestimation of the force, the free-energy difference between the coiled and stretched conformations of the ubiquinone molecule was obtained by additional SMD simulations in vacuum. In the first vacuum simulation, the ubiquinone molecule was pulled from a completely coiled conformation to a completely stretched conformation. In the second simulation, the starting point was a completely stretched conformation and the end point was a completely coiled conformation. The moving constraint was attached to the center of gravity of the ubiquinone headgroup while the tail atom was harmonically constrained in the pull direction. The spring constants were 500 pN/Å for the SMD potential and 500 pN/Å for the harmonic potential, whereas the SMD velocity was 0.1 Å/ns which resulted in a total simulation time of ∼500 ns per run. The external work is shown in Fig. 4 as a function of the end-to-end distance. Due to the slow pulling velocity, the system was in equilibrium at all times, resulting in identical work profiles for both directions and hence the free-energy difference for stretching the ubiquinone molecule, representing entropic changes of the ubiquinone molecule. For end-to-end distances up to 25 Å, the entropic force needed to stretch the ubiquinone molecule further is small and will therefore have only little effect on the overall PMF. For larger end-to-end distances, the slope of the free-energy profile becomes steeper, meaning a larger entropic contribution for further extension of the ubiquinone molecule. With this information, all SMD runs of all individual sections were analyzed with respect to additional ubiquinone extension. For each section, the mean additional extension of the ubiquinone molecule along the section was calculated and the corresponding entropic contribution was extracted from the reference potential for ubiquinone stretching (e.g., Fig. 4, inset) and then subtracted from the PMFs of each section. The entropic contribution was different for the individual sections, depending on the starting structures of the ubiquinone molecule in each section. Most of the sections showed an overestimation due to an additional extension of the ubiquinone molecule during the SMD simulations. However, we observed also sections where the molecule coiled up during the SMD runs, resulting in a negative entropic contribution. The resulting PMFs with and without entropic contribution are presented in Fig. 5, A and B.

FIGURE 4.

FIGURE 4

Open in a new tab

Free-energy profile for stretching the ubiquinone molecule. The solid line denotes the forward pulling direction and the dotted line the backward direction. Mean additional ubiquinone extension data is extracted from SMD simulations of the individual PMF sections. This is shown for pulling section 6 of the forward pulling direction in the inset. Here, for example, the ubiquinone molecule is additionally stretched by ∼3 Å during the simulation, corresponding to a maximum ΔΔG of ∼4 kBT(300K) at the end of the pulling section. Different pulling sections show different entropic contributions due to different starting structures of the ubiquinone molecule. The contribution along the pulling section is subtracted from the PMF. This is done for all sections for both pulling directions independently.

FIGURE 5.

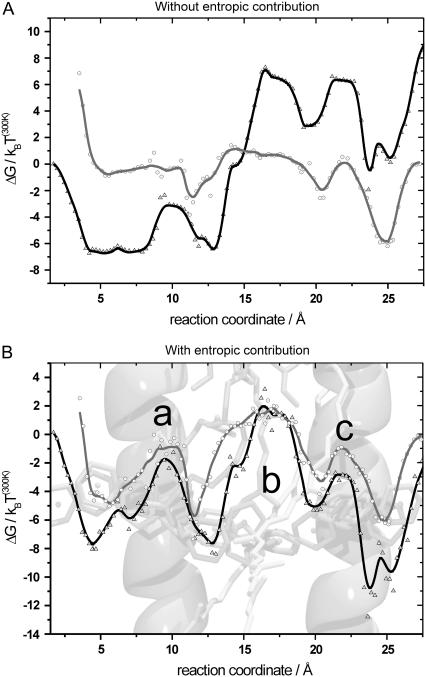
FIGURE 5

Open in a new tab

(A) Merged potential of mean force from the sectionwise calculated free-energy profiles without including the entropic effect. The forward direction is shown in black/triangles and the backward direction in gray/circles. (B) Merged potential of mean force including the entropic contributions. The forward direction is shown in black/triangles and the backward direction in gray/circles. The LH1 structure is superimposed in the background. The sections were merged to match at the section boundaries. Omitting the entropic contribution leads to a strong deviation between forward and backward pulling directions and between the left and right sides of the PMF. Including the entropic contribution results in very similar PMFs for both directions and comparable PMFs on the left and right sides. Both starting points of the potentials (left/right side) are set to zero. Main characteristic features of the potential (B) are denoted by a, b, and c (see text).

As mentioned previously, the headgroup is expected to have the largest effect on the resulting potential and therefore both directions should result in very similar PMFs. Still, minor deviations between both pulling directions are expected, since not only do the forward and backward simulations differ in the pull direction, but the ubiquinone molecule is flipped by 180°. The forward pulling direction is shown in black, and the backward pulling direction in gray. The entropic correction does not influence the maximum height of the PMF a lot, the differences being smaller than ΔΔG = ±4 kBT(300K), but mainly changes the overall shape of the potential.

Neglecting the entropic force of the ubiquinone molecule results in strong deviations in the shape of the PMF between the forward and backward pulling directions. In addition, there is a potential offset between start and endpoints for both directions, which is in the range of 10 kBT(300K). The potential modulation is in the range of 14 kBT(300K) (see Fig. 5 A).

Including the entropic contribution results in very similar PMFs for both pulling directions (see Fig. 5 B), forward and backward pulling directions show a smaller potential offset between start and endpoints in the range of ±2 kBT(300K). The overall potential modulation for both directions stays within 14 kBT(300). The calculated potentials display characteristics that can be closely connected to structural features along the pathway. There is a potential barrier of ∼7 kBT(300) at the position along the pathway between the two helices of the β-subunit (Fig. 5 B a). A slightly higher potential barrier can be seen at the appropriate position (Fig. 5 B c) at the α-subunit helices. An additional potential barrier is visible in the central region of the PMF (Fig. 5 B b), which can be attributed to the influence of the chlorophyll and carotenoid tails. The overall shape of the PMF for both directions leads to the conclusion that the inside of the protein barrier is in most cases more favorable than the outside, with both potentials smaller than zero for most of the simulation time. We believe that this can be partly attributed to the simulation setup. The starting point on the inside and outside of the PMF corresponds to the ubiquinone head being not in a pure lipid environment, but rather at the lipid-protein interface. By pulling the ubiquinone through the LH1 ring by its tail (see Pathway through the LH1 ring), lipid molecules occupying the channel entrance are removed. Due to this system preparation, the channel entrance on both sides is not occupied by lipid tails at the start of the appropriate SMD simulations and will therefore have an attractive effect on the ubiquinone head. Having the channel entrance occupied by lipid tails should lead to a potential profile with less prominent slopes at both sides of the PMF.

ACCURACY OF THE POTENTIAL

There are two criteria that can be chosen to prove the correctness of the calculated potential: 1), the total difference in free energy between the inside and outside has to be zero; and 2), the potentials derived from forward and backward pulling have to be identical.

Both criteria are achieved tolerably. Though there are obvious deviations between forward and backward potential, the overall shape and all characteristic properties like the attractive entrance of the channel, the barriers between the inner and outer pair of helices, and the steep rising (respectively falling) of the potential at the location of the pigments is in good agreement for both directions.

Let us now estimate the statistical error of the potential along the reaction coordinate that is the dominant source of error. The potential was calculated using the mean value and variance of the distribution of work values. Since we always maintain a stiff spring approximation, work values should be Gaussian-distributed. Hence, it is easily possible to calculate the statistical error of the potential, since both mean value and variance are subject to a statistical inaccuracy. This is done by calculating the variance of the free-energy changes with the second-order cumulant expansion, using a Gaussian work distribution with an estimated width, taken from the simulation results, and only 10 work values to describe the distribution. This was done for every point along the PMF and independently for all sections. As we pull along the section, more and more dissipated work is accumulated, which leads to a broadening of the work distribution and therefore to an increase in the statistical error of determining the free-energy change. The statistical error for most of the pulling sections is smaller than ∼3 kBT(300K). For some sections the error is larger at the end of the section, the worst case being ∼6 kBT(300K).

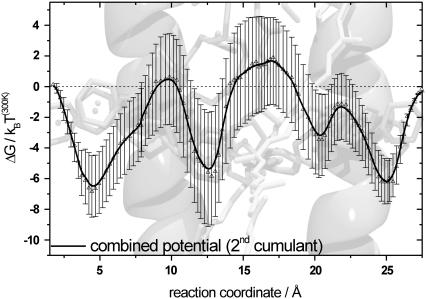
To get an estimate of the total statistical error for moving along the PMF, the errors of each section have to be combined using error propagation. This was done for both directions and results in large errors, in the same range as the potential modulation at the endpoints of both potential directions. This error can be reduced by using the following considerations. First, the endpoint of every pulling section (large errors) for the forward direction is at the same time the starting point for the backward direction (small errors). Second, the total difference in free energy between inside and outside has to be zero. This way, two points along the reaction coordinate are fixed. Calculating the statistical error for moving one step along the reconstructed potential for both directions allows to combine data from both pulling directions with the smallest statistical error. Using the additional information of a fixed start and endpoint of the PMF leads to a potential and resulting errors that are presented in Fig. 6. Part of the LH1 structure is superimposed in the background; the PMF is shown in black.

FIGURE 6.

FIGURE 6

Open in a new tab

Combined potential using sections from both forward and backward pulling directions. The combined PMF along the proposed pathway, including error bars, is shown in black. The error bars are calculated from the different sections, representing the statistical error for estimating the free-energy change from a work distribution with the second-order cumulant expansion using only 10 trajectories to describe the work distribution. Data from both pulling directions are combined to give the minimum statistical error along the PMF. Since start and endpoint of the potential are fixed (see text), the error decreases from its maximum in the midregion of the potential in both directions. Compared to the total modulation depth of the potential, the error is on average ∼25% and the maximum error is ∼50%.

All of the structural features are still visible, though the total potential modulation decreased to ∼8 kBT(300K). The error is on average ∼2 kBT(300K), and the maximum error is ∼4 kBT(300K), compared to the total modulation depth of the potential, ∼25% and ∼50%, respectively. This is an upper limit for the statistical error. We are using >10 work values for calculating the mean and the variance for each point of the potential because each point of the reaction coordinate is sampled several times by one trajectory due to fluctuations of the ubiquinone. Since start and endpoint of the potential are fixed, the error decreases from its maximum in the midregion of the potential toward both sides.

Mean first-passage time

To address the question of whether the proposed transport mechanism of diffusion along the PMF through the LH1 ring is realistic, the mean first-passage time was calculated and compared to the overall turnover rate of the RC in purple bacteria, with a maximum in the range of 1000 Hz (47,48). For estimating the mean first-passage time for the diffusion along the PMF from the outside (membrane area) to the inside of the LH1 ring (RC) we used the following boundary conditions. The diffusion on the outside of the LH1 ring is much faster than along the PMF, and we expect the rotational diffusion for ubiquinone (headgroup must have the correct orientation with respect to the channel opening) to be faster than the translational diffusion. Furthermore, there is a quinone pool on the outside of the LH1 ring, i.e., a ubiquinone headgroup should sufficiently often find the channel opening. Therefore, it is justified to use a reflective barrier on the outside of the LH1 ring (left side of the potential in Fig. 6) as a first approximation. An absorbing boundary condition was used on the inside, because we expect the ubiquinone to be efficiently directed to the binding site inside the RC, so every time the ubiquinone reaches the inside it will reach the RC. A constant diffusion coefficient for the ubiquinone molecule in a lipid environment in the range of 5 × 10−8 cm2/s, as determined by experiments, was used (23,49).

The statistical error from the potential strongly affects the result of the mean first-passage time. To get an order-of-magnitude estimation for the mean first-passage time, we scaled the potential modulation to include the error bars. Considering these assumptions, the mean first-passage time for diffusion along the proposed pathway is ∼8 × 10−3 s. This is slightly slower compared to the experimentally determined turnover rates for RCs in purple bacteria (24,47,48). However, the calculated mean first-passage time only serves as an upper limit. The underlying potential is a worst-case scenario and any deviation to smaller potential barriers will significantly reduce the mean first-passage time.

CONCLUSION

In this work, we used steered molecular-dynamics simulation to find a possible pathway for the ubiquinone molecule through the protein environment of the LH1 ring. Using the integral fluctuation theorem and the stiff spring approximation, it was possible to reconstruct the potential of mean force along that pathway for both inside-to-outside and outside-to-inside pulling. Both potentials are in agreement in regard to the main characteristic features, which can be directly attributed to structural features of the LH1 protein barrier and the corresponding pigments.

An upper limit for the mean first-passage time corresponding to a worst-case scenario potential, constructed using free-energy data from both pulling directions, was calculated as ∼8 × 10−3 s, i.e., we demonstrated that ubiquinone diffusion through the protein environment of the LH1 ring from R. rubrum is possible on that timescale or even faster. Compared with turnover rates of the RC in the range of 1000 Hz, this does not contradict the proposed model of a diffusion process for the ubiquinone through the closed LH1 ring. This can explain why cryoelectron microscopy and AFM studies of this species always find closed LH1 structures around the reaction center.

Acknowledgments

We thank Robin Ghosh for stimulating discussions.

This work was supported by grants from the National Institutes of Health (P41-RR05969) and the National Science Foundation (MCB02-34938). The authors gratefully acknowledge supercomputer time provided by the Pittsburgh Supercomputer Center and the National Center for Supercomputing Applications via a Large Resources Allocation Committee grant (MCA93S028). C.T. acknowledges financial support from the Volkswagenstiftung.

References

  • 1.Deisenhofer, J., O. Epp, K. Miki, R. Huber, and H. Michel. 1985. Structure of the protein subunits in the photosynthetic reaction center of Rhodopseudomonas viridis at 3Å resolution. Nature. 318:618–624. [DOI] [PubMed] [Google Scholar]
  • 2.McDermott, G., S. M. Prince, A. A. Freer, A. M. Hawthornthwaite-Lawless, M. Z. Papiz, R. J. Cogdell, and N. W. Isaacs. 1995. Crystal structure of an integral membrane light-harvesting complex from photosynthetic bacteria. Nature. 374:517–521. [Google Scholar]
  • 3.Koepke, J., X. C. Hu, C. Muenke, K. Schulten, and H. Michel. 1996. The crystal structure of the light-harvesting complex II (B800–850) from Rhodospirillum molischianum. Structure. 4:581–597. [DOI] [PubMed] [Google Scholar]
  • 4.Iwata, S., J. W. Lee, K. Okada, J. K. Lee, M. Iwata, B. Rasmussen, T. A. Link, S. Ramaswamy, and B. K. Jap. 1998. Complete structure of the 11-subunit bovine mitochondrial cytochrome bc(1) complex. Science. 281:64–71. [DOI] [PubMed] [Google Scholar]
  • 5.Abrahams, J. P., A. G. W. Leslie, R. Lutter, and J. E. Walker. 1994. Structure at 2.8-Å resolution of F1-Atpase from bovine heart mitochondria. Nature. 370:621–628. [DOI] [PubMed] [Google Scholar]
  • 6.Roszak, A. W., T. D. Howard, J. Southall, A. T. Gardiner, C. J. Law, N. W. Isaacs, and R. J. Cogdell. 2003. Crystal structure of the RC-LH1 core complex from Rhodopseudomonas palustris. Science. 302:1969–1972. [DOI] [PubMed] [Google Scholar]
  • 7.van Grondelle, R., and V. Novoderezhkin. 2001. Dynamics of excitation energy transfer in the LH1 and LH2 light-harvesting complexes of photosynthetic bacteria. Biochemistry. 40:15057–15068. [DOI] [PubMed] [Google Scholar]
  • 8.van Oijen, A. M., M. Ketelaars, J. Kohler, T. J. Aartsma, and J. Schmidt. 1999. Unraveling the electronic structure of individual photosynthetic pigment-protein complexes. Science. 285:400–402. [DOI] [PubMed] [Google Scholar]
  • 9.Gerken, U., F. Jelezko, B. Götze, M. Branschadel, C. Tietz, R. Ghosh, and J. Wrachtrup. 2003. Membrane environment reduces the accessible conformational space available to an integral membrane protein. J. Phys. Chem. B. 107:338–343. [Google Scholar]
  • 10.Gerken, U., D. Lupo, C. Tietz, J. Wrachtrup, and R. Ghosh. 2003. Circular symmetry of the light-harvesting 1 complex from Rhodospirillum rubrum is not perturbed by interaction with the reaction center. Biochemistry. 42:10354–10360. [DOI] [PubMed] [Google Scholar]
  • 11.Conroy, M. J., W. H. J. Westerhuis, P. S. Parkes-Loach, P. A. Loach, C. N. Hunter, and M. P. Williamson. 2000. The solution structure of Rhodobacter sphaeroides LH1 β reveals two helical domains separated by a more flexible region: structural consequences for the LH1 complex. J. Mol. Biol. 298:83–94. [DOI] [PubMed] [Google Scholar]
  • 12.Wang, Z. Y., K. Gokan, M. Kobayashi, and T. Nozawa. 2005. Solution structures of the core light-harvesting α and β polypeptides from Rhodospirillum rubrum: implications for the pigment-protein and protein-protein interactions. J. Mol. Biol. 347:465–477. [DOI] [PubMed] [Google Scholar]
  • 13.Jungas, C., J. L. Ranck, J. L. Rigaud, P. Joliot, and A. Vermeglio. 1999. Supramolecular organization of the photosynthetic apparatus of Rhodobacter sphaeroides. EMBO J. 18:534–542. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Karrasch, S., P. A. Bullough, and R. Ghosh. 1995. The 8.5-Å projection map of the light-harvesting complex-I from Rhodospirillum rubrum reveals a ring composed of 16 subunits. EMBO J. 14:631–638. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Jamieson, S. J., P. Y. Wang, P. Qian, J. Y. Kirkland, M. J. Conroy, C. N. Hunter, and P. A. Bullough. 2002. Projection structure of the photosynthetic reaction centre-antenna complex of Rhodospirillum rubrum at 8.5 Å resolution. EMBO J. 21:3927–3935. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Walz, T., and R. Ghosh. 1997. Two-dimensional crystallization of the light-harvesting I reaction centre photounit from Rhodospirillum rubrum. J. Mol. Biol. 265:107–111. [DOI] [PubMed] [Google Scholar]
  • 17.Bahatyrova, S., R. N. Frese, C. A. Siebert, J. D. Olsen, K. O. van der Werf, R. van Grondelle, R. A. Niederman, P. A. Bullough, C. Otto, and C. N. Hunter. 2004. The native architecture of a photosynthetic membrane. Nature. 430:1058–1062. [DOI] [PubMed] [Google Scholar]
  • 18.Scheuring, S., J. Busselez, and D. Levy. 2005. Structure of the dimeric PufX-containing core complex of Rhodobacter blasticus by in situ atomic force microscopy. J. Biol. Chem. 280:1426–1431. [DOI] [PubMed] [Google Scholar]
  • 19.Scheuring, S., J. N. Sturgis, V. Prima, A. Bernadac, D. Levy, and J. L. Rigaud. 2004. Watching the photosynthetic apparatus in native membranes. Proc. Natl. Acad. Sci. USA. 101:11293–11297. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Fotiadis, D., P. Qian, A. Philippsen, P. A. Bullough, A. Engel, and C. N. Hunter. 2004. Structural analysis of the reaction center light-harvesting complex I photosynthetic core complex of Rhodospirillum rubrum using atomic force microscopy. J. Biol. Chem. 279:2063–2068. [DOI] [PubMed] [Google Scholar]
  • 21.Stahlberg, H., J. Dubochet, H. Vogel, and R. Ghosh. 1998. The reaction centre of the photounit of Rhodospirillum rubrum is anchored to the light-harvesting complex with four-fold rotational disorder. Photosynth. Res. 55:363–368. [Google Scholar]
  • 22.Metz, G., K. P. Howard, W. B. S. Vanliemt, J. H. Prestegard, J. Lugtenburg, and S. O. Smith. 1995. NMR studies of ubiquinone location in oriented model membranes: evidence for a single motionally-averaged population. J. Am. Chem. Soc. 117:564–565. [Google Scholar]
  • 23.Di Bernardo, S., R. Fato, R. Casadio, P. Fariselli, and G. Lenaz. 1998. A high diffusion coefficient for coenzyme Q(10) might be related to a folded structure. FEBS Lett. 426:77–80. [DOI] [PubMed] [Google Scholar]
  • 24.Comayras, R., C. Jungas, and J. Lavergne. 2005. Functional consequences of the organization of the photosynthetic apparatus in Rhodobacter sphaeroides. II. A study of PufX(−) membranes. J. Biol. Chem. 280:11214–11223. [DOI] [PubMed] [Google Scholar]
  • 25.Hu, X., and K. Schulten. 1998. Model for the light-harvesting complex I (B875) of Rhodobacter sphaeroides. Biophys. J. 75:683–694. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Darden, T., D. York, and L. Pedersen. 1993. Particle mesh Ewald: an N.Log(N) method for Ewald sums in large systems. J. Chem. Phys. 98:10089–10092. [Google Scholar]
  • 27.Feller, S. E., Y. H. Zhang, R. W. Pastor, and B. R. Brooks. 1995. Constant-pressure molecular-dynamics simulation: the Langevin piston method. J. Chem. Phys. 103:4613–4621. [Google Scholar]
  • 28.Kale, L., R. Skeel, M. Bhandarkar, R. Brunner, A. Gursoy, N. Krawetz, J. Phillips, A. Shinozaki, K. Varadarajan, and K. Schulten. 1999. NAMD2: greater scalability for parallel molecular dynamics. J. Comput. Phys. 151:283–312. [Google Scholar]
  • 29.MacKerell, A. D., D. Bashford, M. Bellott, R. L. Dunbrack, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiorkiewicz-Kuczera, D. Yin, and M. Karplus. 1998. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B. 102:3586–3616. [DOI] [PubMed] [Google Scholar]
  • 30.Autenrieth, F., E. Tajkhorshid, J. Baudry, and Z. Luthey-Schulten. 2004. Classical force field parameters for the heme prosthetic group of cytochrome c. J. Comput. Chem. 25:1613–1622. [DOI] [PubMed] [Google Scholar]
  • 31.Autenrieth, F., E. Tajkhorshid, K. Schulten, and Z. Luthey-Schulten. 2004. Role of water in transient cytochrome c(2) docking. J. Phys. Chem. B. 108:20376–20387. [Google Scholar]
  • 32.Damjanovic, A., I. Kosztin, U. Kleinekathöfer, and K. Schulten. 2002. Excitons in a photosynthetic light-harvesting system: a combined molecular dynamics, quantum chemistry, and polaron model study. Phys. Rev. E. 65:031919. [DOI] [PubMed] [Google Scholar]
  • 33.Isralewitz, B., M. Gao, and K. Schulten. 2001. Steered molecular dynamics and mechanical functions of proteins. Curr. Opin. Struct. Biol. 11:224–230. [DOI] [PubMed] [Google Scholar]
  • 34.Park, S., and K. Schulten. 2004. Calculating potentials of mean force from steered molecular dynamics simulations. J. Chem. Phys. 120:5946–5961. [DOI] [PubMed] [Google Scholar]
  • 35.Park, S., F. Khalili-Araghi, E. Tajkhorshid, and K. Schulten. 2003. Free energy calculation from steered molecular dynamics simulations using Jarzynski's equality. J. Chem. Phys. 119:3559–3566. [Google Scholar]
  • 36.Torrie, G. M., and J. P. Valleau. 1974. Monte-Carlo free-energy estimates using non-Boltzmann sampling.: application to subcritical Lennard-Jones fluid. Chem. Phys. Lett. 28:578–581. [Google Scholar]
  • 37.Kumar, S., D. Bouzida, R. H. Swendsen, P. A. Kollman, and J. M. Rosenberg. 1992. The weighted histogram analysis method for free-energy calculations on biomolecules. 1. The method. J. Comput. Chem. 13:1011–1021. [Google Scholar]
  • 38.Crooks, G. E. 1999. Entropy production fluctuation theorem and the nonequilibrium work relation for free energy differences. Phys. Rev. E. 60:2721–2726. [DOI] [PubMed] [Google Scholar]
  • 39.Jarzynski, C. 1997. Nonequilibrium equality for free energy differences. Phys. Rev. Lett. 78:2690–2693. [Google Scholar]
  • 40.Hummer, G., and A. Szabo. 2001. Free energy reconstruction from nonequilibrium single-molecule pulling experiments. Proc. Natl. Acad. Sci. USA. 98:3658–3661. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 41.Collin, D., F. Ritort, C. Jarzynski, S. B. Smith, I. Tinoco, and C. Bustamante. 2005. Verification of the Crooks fluctuation theorem and recovery of RNA folding free energies. Nature. 437:231–234. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 42.Liphardt, J., S. Dumont, S. B. Smith, I. Tinoco, and C. Bustamante. 2002. Equilibrium information from nonequilibrium measurements in an experimental test of Jarzynski's equality. Science. 296:1832–1835. [DOI] [PubMed] [Google Scholar]
  • 43.Kosztin, I., B. Barz, and L. Janosi. 2006. Calculating potentials of mean force and diffusion coefficients from nonequilibrium processes without Jarzynski's equality. J. Chem. Phys. 124:64106. [DOI] [PubMed] [Google Scholar]
  • 44.Jensen, M. Ø., S. Park, E. Tajkhorshid, and K. Schulten. 2002. Energetics of glycerol conduction through aquaglyceroporin GlpF. Proc. Natl. Acad. Sci. USA. 99:6731–6736. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 45.Szabo, A., K. Schulten, and Z. Schulten. 1980. 1st Passage Time Approach to Diffusion Controlled Reactions. J. Chem. Phys. 72:4350–4357. [Google Scholar]
  • 46.Amaro, R., and Z. Luthey-Schulten. 2004. Molecular dynamics simulations of substrate channeling through an α-β barrel protein. Chem. Phys. 307:147–155. [Google Scholar]
  • 47.Osvath, S., and P. Maroti. 1997. Coupling of cytochrome and quinone turnovers in the photocycle of reaction centers from the photosynthetic bacterium Rhodobacter sphaeroides. Biophys. J. 73:972–982. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 48.Gerencsér, L., T. Jánosi, G. Laczkó, and P. Maróti. 2000. Kinetic limitations in turnover of photosynthetic bacterial reaction center protein. Acta Biol. Szeged. 44:45–52. [Google Scholar]
  • 49.Marchal, D., W. Boireau, J. M. Laval, J. Moiroux, and C. Bourdillon. 1998. Electrochemical measurement of lateral diffusion coefficients of ubiquinones and plastoquinones of various isoprenoid chain lengths incorporated in model bilayers. Biophys. J. 74:1937–1948. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES