A Mathematical Model of Glioblastoma Tumor Spheroid Invasion in a Three-Dimensional In Vitro Experiment

Abstract

Glioblastoma, the most malignant form of brain cancer, is responsible for 23% of primary brain tumors and has extremely poor outcome. Confounding the clinical management of glioblastomas is the extreme local invasiveness of these cancer cells. The mechanisms that govern invasion are poorly understood. To gain insight into glioblastoma invasion, we conducted experiments on the patterns of growth and dispersion of U87 glioblastoma tumor spheroids in a three-dimensional collagen gel. We studied two different cell lines, one with a mutation to the EGFR (U87ΔEGFR) that is associated with increased malignancy, and one with an endogenous (wild-type) receptor (U87WT). We developed a continuum mathematical model of the dispersion behaviors with the aim of identifying and characterizing discrete cellular mechanisms underlying invasive cell motility. The mathematical model quantitatively reproduces the experimental data, and indicates that the U87WT invasive cells have a stronger directional motility bias away from the spheroid center as well as a faster rate of cell shedding compared to the U87ΔEGFR cells. The model suggests that differences in tumor cell dispersion may be due to differences in the chemical factors produced by cells, differences in how the two cell lines remodel the gel, or different cell-cell adhesion characteristics.

INTRODUCTION

The outcome for patients with highly malignant brain tumors is extremely poor. Glioblastoma Multiforme (GBM), the most malignant form of brain cancer, is responsible for 23% of primary brain tumors and has a median survival time of <15 months (1). One factor that makes GBM so difficult to treat is its high invasiveness enabling tumor cells to disperse from the main tumor mass into the surrounding normal brain, so that dispersed glioma cells are out of reach of surgery, radiation, and chemotherapy. The invasive cells present a different phenotype than the cells of the main tumor mass. Factors responsible for conversion from a relatively stationary to a migratory/invasive phenotype are not completely understood. However, several mechanisms such as chemokinesis (undirected motility), chemotaxis (directed motility along chemical gradients), haptotaxis, cell-cell adhesion, and cell-cell signaling, upregulation of pro-survival pathways, and microenvironmental cues are involved in that process (1–4).

A genetic aberration that occurs in 40–60% of GBMs results in the amplification or overexpression of the Epidermal Growth Factor Receptor gene (EGFR), which has been related to poor prognosis in glioblastoma patients (5). The most common mutation (ΔEGFR) leads to an in-frame deletion resulting in a constitutively active receptor, deficient in the negative feedback mechanism normally triggered by binding of its ligand (6). It has been shown that cells with ΔEGFR proliferate slightly faster (7) and undergo less apoptosis both in serum-free in vitro conditions and in vivo than cells with the wild-type receptor, EGFRwt (8).

Lal et al. (9) showed that genes for matrix-degrading enzymes were upregulated in ΔEGFR cells both in vivo and in vitro. Chicoine and Silbergeld showed that increased malignancy in vivo is typically associated with increased motility in vitro (10). The extent to which each of these discreet functions is related to tumor cell invasiveness is unclear. The goal of this work is to better understand the mechanisms that govern invasive cell behavior. We specifically focus on the changes in the invasive phenotype caused by the ΔEGFR mutation. We present new results from experiments where tumor spheroids are grown in three-dimensional collagen gels. We then describe a continuum mathematical model that allows us to quantitatively interpret the data. Fitting the model to the experimental data indicates that, when compared to the U87ΔEGFR cell line, glioma cells with EGFRwt receptor invade in a more biased manner, away from the tumor spheroid and are shed from the spheroid at a greater rate, suggesting lower cell-cell adhesion.

EXPERIMENTAL BACKGROUND

Cell culture conditions

Human astrocytoma cell line U87 expressing EGFRwt (hereafter U87WT) (American Type Culture Collection, Manassas, VA) and a sub-line stably transfected with the truncated form of EGFR (U87ΔEGFR) (7,8,11) were maintained in minimum essential medium (Invitrogen, Carlsbad, CA) supplemented with 10% heat-inactivated fetal bovine serum (Hyclone Laboratories, Logan, UT) in a 37°C, 5% CO2 atmosphere at constant humidity.

Three-dimensional invasion assay

Spontaneously formed multicellular spheroids derived from U87WT and U87ΔEGFR glioma cell lines were implanted into self-assembling collagen-I gels (2.6 mg/ml; Vitrogen, Cohesion, Palo Alto, CA) supplemented with minimal essential media and 2% fetal bovine serum and cultured for seven days under standard cell culture conditions (12). Digital photomicrographs of the midplane of spheroids were taken daily (25× total magnification, Zeiss Axiovert 130, Carl Zeiss, Echingen, Germany). To find the radius of invasion in an image I, we calculated the magnitude of the gradient of the image, G = |∇I|, and averaged it over the azimuthal angle to find 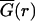. We then defined the radius of invasion to be the distance farthest from the center where 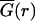was half its maximum. This calculation automatically circumscribes the dispersing glioma cells with high precision and accuracy, while also agreeing with manual assessment of the area occupied by dispersing cells. The radius of the compact cellular core of each spheroid was scored by first scaling a 120 μm × 120 μm gray-scale image centered on the tumor spheroid, such that the darkest pixel had value 0 and the lightest pixel had value 1. The core was identified as the set of pixels with an intensity of <0.12. This particular value was chosen because it is restricted to a region of the dispersing spheroid where cell (pixel) density is high, but falling rapidly; this measure also approached what an experimenter would identify by eye as the core boundary. Typical results are shown in Fig. 1.

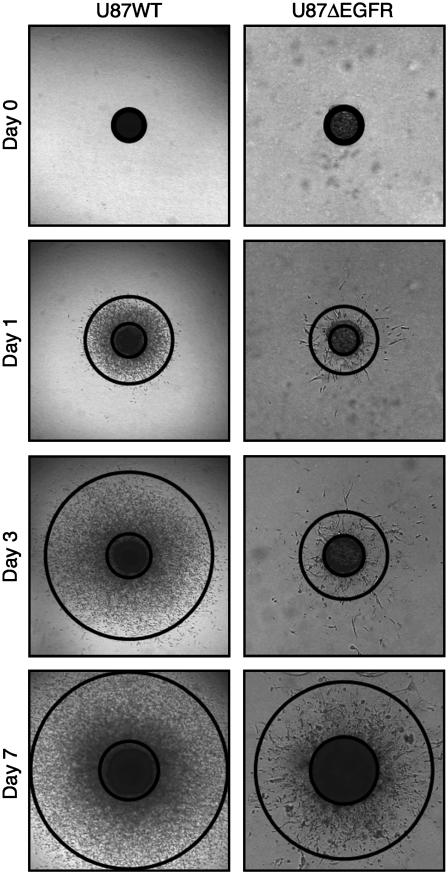
FIGURE 1.

The difference in invasion between U87WT and U87ΔEGFR. The tumor spheroid images (3 mm × 3 mm) were taken from the experiments. The inner and outer circles indicate the core boundary and invasive rim, respectively.

Histology

Collagen gels containing glioma spheroids were fixed in 10% neutral buffered formalin on days 3, 5, and 7. Fixed gels were paraffin-embedded using routine histological protocols then microtome-sectioned at 5-μm thickness. For each time point, slides were stained with hematoxylin and eosin for morphological evaluation. Immunohistochemistry of Ki67 antigen was performed on formalin-fixed-paraffin-embedded (FFPE) spheroid sections (13). Briefly, FFPE slides were baked at 65°C for 2 h, deparaffinized in xylenes, and then rehydrated in graded alcohol series followed by water. Antigen retrieval was performed in 10 mM sodium citrate buffer, pH 6.5 in a pressure cooker at 90°C for 1 min. Endogenous peroxidases were quenched in 3% hydrogen peroxide solution in Tris-buffered saline (TBS) for 10 min. The slides were blocked for 15 min in TBS containing 0.1% Triton X-100 with 3% normal horse serum provided in the Vectastain ABC Elite Mouse IgG kit (Vector Laboratories, Burlingame, CA). Primary anti-Ki67 antibody (#M7240, Dako, Santa Barbara, CA) was diluted 1:100 and incubated for 1 h at room temperature. Slides were rinsed for 5 min in TBS Tween (TBST) and horse anti-mouse IgG was added according to manufacturer instructions. Slides were rinsed for 5 min in TBST, then ABC reagent was added according to manufacturer instructions. Slides were rinsed again for 5 min in TBST and DAB peroxidase substrate (Sigma, St. Louis, MO) was added for 2 min. Lastly, slides were rinsed in water, counterstained with Mayer's hematoxylin, dehydrated in an alcohol series followed by xylene, and coverslipped. The number of cells exhibiting positive staining for Ki67 was expressed as percentage of total number of cells (Proliferative-index) in the core and rim areas. The slices from day 3 adequately captured cells in the invasive zone. The nuclei of the images were identified by a particle tracking method previously described by Crocker and Grier (14) and used to estimate the cell density as a function of radial distance from the spheroid center.

Experimental data

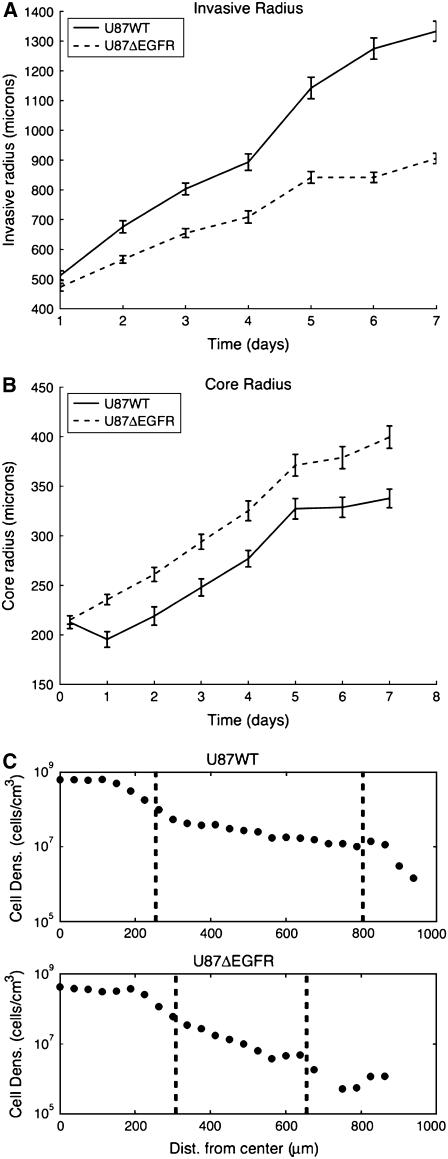
Images taken from the experiments are shown in Fig. 1. Averaged measurements of the core and invasive radii from 16 different experiments are shown in Fig. 2. There are two major features to note in the figure. First, the U87WT cells are more invasive than U87ΔEGFR. This was unexpected, since the mutant cell line was described to be more malignant in animal models (6); see Fig. 2 b. Second, the radius of the expanding U87WT spheroids decreases during the initial day in the gel, but subsequently increases at a rate ∼27 μm/day; see Fig. 2 b. The decrease in the radius of U87WT spheroids on day 1 occurred in all 16 experiments. The radius of spheroids from U87ΔEGFR cells did not show an initial decrease, but expanded at a steady rate of 27 μm/day. Enumeration of cells in the hematoxyln and eosin-stained FFPE sections of U87WT spheroids at days 3, 5, and 7 revealed 343, 709, and 811 cells in the core area per 20× objective field, while the core area of U87ΔEGFR spheroids contained only 132 cells on day 7. The differential cell density per field indicates lower cell compaction (possibly slower growth) of the U87ΔEGFR cells in spheroid conditions compared to U87WT. The Ki67 index of U87WT spheroids on day 5 was 22% in the core region compared to 6% in the invasive edge, suggesting that dispersing cells at the spheroid's edge have deferred proliferation. These data demonstrate pronounced differences between the cell lines relative to their interaction with a three-dimensional collagen matrix.

FIGURE 2.

Experimental results. Core radius is the radius of the central spheroid. Invasive radius denotes the outer rim of the invasive region. (a) U87WT spheroids are more invasive than U87ΔEGFR spheroids. (b) The cores of the U87WT and U87ΔEGFR spheroids grow at approximately the same speed after day 1, but the U87WT core decreases in size in the first day in the collagen gel. (c) A log plot of cell density on day 3 as a function of position. The dashed line on the left of each plot denotes the core boundary and the dashed line to the right denotes the boundary of invasion.

We could account for these features of glioma spheroid expansion in two different ways. The simplest explanation is that the EGFR-wild type cells are inherently more motile leading to a very high initial invasion rate on day 1 with considerable egress of cells out of the spheroid. This would result in a reduction of the compacted spheroid diameter. The burst of motility might be described by random motility or directed motility, or some combination of the two, which might differ for the two cell lines. Alternatively, the system could be dominated by cell-cell adhesion phenomenon in the spheroid. The U87WT and U87ΔEGFR cells might be equally motile in the absence of cell-cell connections, but if cell-cell adhesion is stronger in the mutant cells, the mutant cells would be less dispersive because they would be released at a slower rate from the surface of the spheroid.

In the mathematical model, we assume that the cell lines differ in their motility, shedding rates, and proliferation. Development of mathematical models of cell dispersion from solid tumor masses is needed to lay a foundation that will allow inclusion of more complex data such as gene-expression profiling, phosphoproteomics, cell-matrix interactions, signal transduction activation, cell traction forces in the matrix, etc.

MATHEMATICAL MODELING

In this section, we report attempts to assess the relative importance of the various biological processes underlying dispersion from multicellular spheroids using mathematical modeling of the patterns of invasion discerned from the images. As will be seen, the model affords quantitative comparisons between theory and experiment so that various hypotheses of the mechanisms governing invasive cell motility can be tested.

There are several mathematical models in the literature for cell invasion (15–17). For the specific case of GBM, see the literature (18–25). Frieboes et al. (26) model GBM growth for in vitro experiments. Their model is designed to explain the irregular shape of the tumor core (not seen in these experiments) while the model presented here is designed to describe the cells that leave the main tumor mass and invade the collagen gel. A design that is closest to our approach is reported by Swanson et al. (27). As will be discussed below, we think that Swanson et al. (27) must be generalized to account for differences between invasive and proliferative cells. Our work is based on new experimental data and describes the behavior of invasive cells in a way that can be quantitatively compared to the experimental measurements.

Single population model for core and invasive cell behavior

In the model of Swanson et al. (27), tumor growth is described by a reaction-diffusion equation:

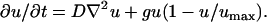(1)

This equation describes cells of concentration u(r, t) that move along undirected, random paths as a function of position and time. Cells throughout the tumor are assumed to proliferate at a constant rate g until they reach a limiting density, u_max. The value D is the diffusion (undirected motion); the larger D becomes, the more motile the cells. This model assumes spherical symmetry of the multicellular tumor spheroid. The reaction-diffusion model has been used with some success to describe how a tumor responds to chemotherapy and why surgical removal of GBM is usually not effective (27).

This model is only applicable for tumors that are >1 mm³ (27), whereas the tumor spheroids in the current experiments have an initial volume of 0.07 mm³. The reason the single-population reaction-diffusion model fails for small tumors is that for small spheroids the cell populations of core and rim manifest different proliferative and dispersive behaviors as a consequence of being in two distinct regions of the multicellular system: there is a central core and an invasive rim. The central core contains cells that proliferate rapidly but move slowly; the invasive rim contains cells that proliferate slowly but are highly motile (i.e., the go-or-grow hypothesis (2)).

The need to generalize Eq. 1 becomes evident when we attempt to model our experiments. We can either capture the behavior of the core or the invasive region, but not both. If we choose a D ≈ 10⁻⁴ cm²/day, we can fit the invasive radii plots in Fig. 2 b, but the cells in the core also rapidly diffuse throughout the environment and within a few days, the central core would almost disappear. If, on the other hand, we choose a smaller D, we can accurately model the core growth, but the invasive cells would move far too slowly. With a two-population model, we can simultaneously model both the core and the invasive region. This reflects the biology of the dispersive multicellular spheroid: the invasive cells are a different phenotype (2,3) from the core cells, and have different motility and proliferation rates.

Modeling the difference in behavior of the core and invasive cells

To account for the different behaviors of the tumor spheroid and the invasive cells, we model the tumor core as a sphere increasing in radius at a constant rate, v_c, and shedding invasive cells at a rate, s. To motivate such a model, we note that multicellular tumor spheroids, when grown in soft agar or methylcellulose, first grow exponentially, then linearly, and finally stop growing altogether (28). Linear growth typically occurs for spheroids that are between 0.1 mm and 0.5 mm in radius, as in our experiment (see Fig. 2 b). It has also been observed that spheroids cultured in spinner flasks (in liquid suspension) shed cells at a constant rate (29). Since the spheroids in these experiments are grown in a fluid, the cells that are shed are quickly whisked away from the neighborhood of the spheroid. In the collagen matrix, however, the cells that are shed are precisely the invasive cells in which we are interested.

The invasive cells, u_i(r, t), diffuse and proliferate as in Eq. 1. In addition, the invasive cells are biased to move away from the center of the tumor spheroid at an average speed, v_i. It has been observed that invasive cells may follow directed paths away from the tumor spheroid (30). The cause of this bias is not known. It may be due to attraction toward nutrients in the environment, repulsion from waste products produced by the spheroid, or a realignment of the collagen gel as the cells move. One purpose of this work is to determine whether such a velocity bias is present in these experiments.

The equation for the evolution of the invasive cell population, u_i(r, t) is given below.

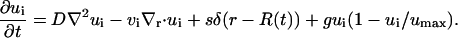(2)

The behavior of the invasive cells can be described by four parameters: {D, v_i, s, g}. Invasive cells are introduced into the population through shedding from the core surface, s, and proliferation, g. Cell motility is modeled as having an undirected component, D, and a radially biased component, v_i. Similar models have been used for describing the motility of macrophages and endothelial cells (31,32). In the above equation, δ is the Dirac delta function, r is the spatial coordinate for the radial distance from the tumor center, and R(t) is the radius of the core at time t. We take the core radius to be given by R(t) = R₀ + v_ct, where R₀ is the initial tumor radius, and v_c is the rate at which the core increases in radius. It should be noted that the model allows for invasive cells to be reabsorbed by the core, as observed in some experiments.

At time t = 0, there are no invasive cells present, and u_i(r, 0) = 0. The boundary condition at r = 0 is symmetric, and far from the tumor, u_i(r, t) = 0. Equation 2 was simulated using operator splitting. A Crank-Nicholson method was used for diffusion, upwind differencing was used for advection, and a first-order forward difference was used for proliferation and cell shedding.

Parameter estimation

The following parameters were fixed. The initial tumor radius, measured directly from the images, was R₀ = 250 μm. The core growth rate, obtained from a least-squares fit of Fig. 2 b, starting from day 1 gave v_c = 27 μm/h. To estimate u_max, we assume that the volume of a typical cell is 1200 μm³, as it is for EMT6/Ro tumor cells (33). Assuming that half the volume of the spheroid is made up of tumor cells, the maximum density is u_max = 4.2 × 10⁸ cells/cm³.

To quantitatively compare our model to Fig. 2 a, we need to choose a cutoff threshold for u(r, t), at which to define the invasive boundary of a continuous density function. We chose the threshold using the density plots shown in Fig. 2 c, and noting where the invasive boundary, indicated by the right-hand dashed line, intersects the density plot. The threshold was 1 × 10⁷ cells/cm³ for U87WT and 2.5 × 10⁶ cells/cm³ for U87ΔEGFR. We did not use the same threshold for both cell lines because this was not what was seen experimentally. A visual inspection of Fig. 1 supports this difference, where there appear to be more invasive cells at the boundary of the U87WT than at the boundary of the U87ΔEGFR spheroid.

The parameters for describing invasive cell behavior, {D, v_i, s, g}, are optimized to fit the data. While we do not know their exact values, we have identified reasonable ranges for these parameters. The results in Hegedus et al. (34) and the data of Demuth et al. (35) suggest a D between 1 × 10⁻⁵ and 2 × 10⁻⁴ cm²/day. It should be noted that these studies were for cells moving on a two-dimensional substrate. To our knowledge, there have been no direct estimates for D in three dimensions. It has been observed that invasive cells close to the tumor spheroid move at a velocity 0.05 cm/day away from the spheroid center (30). Thus, we assume v_i is between 0 and 0.1 cm/day. The shedding rate for EMT6/Ro spheroids grown in spinner flasks was 218 cells/(mm² min) or 5 × 10⁵ cells/(cm² day). The collagen matrix has the potential to enhance shedding, by providing the cells a substrate on which to move, but it also has the potential to inhibit shedding if the cells have difficulty moving through the collagen mesh. We assume that s is between 1 × 10⁴ and 1 × 10⁷ cells/(cm² day). The cell doubling time has been seen to be as fast as 20 h at the spheroid core (12), giving a g as large as 0.83/day. However, since GBM cells can be either highly proliferative or highly motile, but not both (2), g for the invasive cells is significantly lower. We assume that g is between 0 and 0.3/day. The bounds are summarized in Table 1.

TABLE 1.

Original and revised parameter bounds

	Original bounds		U87ΔEGFR (revised)		U87WT (revised)
Cell line	LB	UB	LB	UB	LB	UB
D × 10−4 (cm2/day)	0.1	2.0	0.1	2.0	0.1	2.0
vi (cm/day)	0	0.10	0	0.015	0.010	0.10
s × 106 cells/(cm2 day)	0.01	10	0.17	0.69	0.70	6.5
g (1/day)	0	0.30	0	0.30	.04	0.30

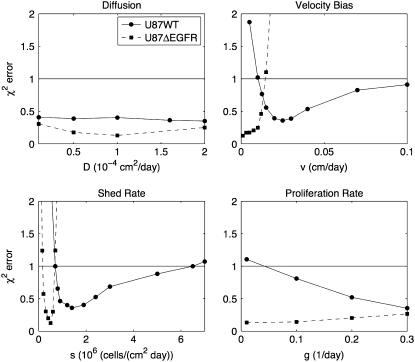
The model has led to tighter estimates (in bold) for v_i, s, and g than were previously known. LB indicates a lower bound and UB indicates an upper bound. The choice of the original bounds is explained in Parameter Estimation and Parameter Optimization. The revised bounds were based on Fig. 6. The bounds were chosen to be where the χ² error was <1.

Parameter optimization

We fit the model to the data by choosing {D, v_i, s, g} to minimize the χ² error function:

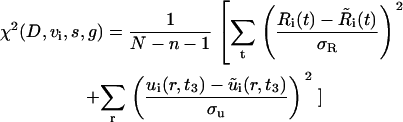(3)

Here, R_i(t) is the invasive radius, and u_i(r, t₃) is the cell density at day 3, both measured from experiment. The variables 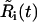and 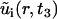, represent the corresponding quantities that were generated by the model for a particular choice of parameters {D, v_i, s, g}. The parameters, σ_R and σ_u, denote the standard deviation of the measurement of the invasive radius and cell density at day 3, respectively. The total number of data points, N, is 33, and the number of fitting parameters, n, is 4. We consider a χ² error <1 to be a good fit to the model. This corresponds to an average error of a mean ∼1 ± SD at each data point. The error function was minimized with a Sequential Quadratic Programming method, using the fmincon.m optimization function in MatLab (The MathWorks, Natick, MA).

RESULTS

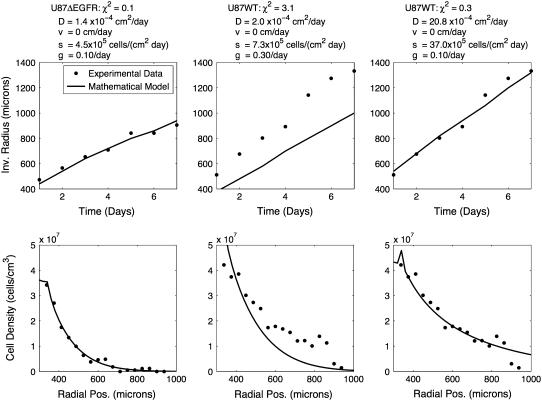
We first tested whether invasion was an undirected process (v_i = 0) for both cell lines, such that the difference between the two could be explained entirely by different D-values. The parameters were optimized to fit the data for both cell lines and the results are shown in Fig. 3, along with a list of parameters. The U87ΔEGFR cell line can adequately be described by undirected invasion, with a χ² error of 0.1. The best fit to the U87WT model, however, is quite poor, with an error of 3.1. The error could be reduced by a factor of 10 by loosening the restrictions on D and allowing D = 2 × 10⁻³ cm²/day, which is 10 times larger than what has been seen in other experiments. Thus the model indicates either that the primary mechanism of motility for the U87WT is not diffusion, or that the diffusion of the U87WT cells is an order-of-magnitude larger in this system than has been observed in any other system.

FIGURE 3.

U87ΔEGFR can be well described by unbiased motility alone, while U87WT cannot. The mathematical model (line) with only unbiased motion (v_i = 0) was optimized to fit the experimental data (dots) for the two cell lines. Each column uses a different set of parameters, given at the top of the column. The first column is fit to the U87ΔEGFR data and the second and third are fit to the U87WT data. Note that in column 2, D is at the maximum value it can take in the constrained optimization. Loosening the restrictions on D gave a better fit to the data, as shown in column 3, but here D is 10 times larger than is reasonable.

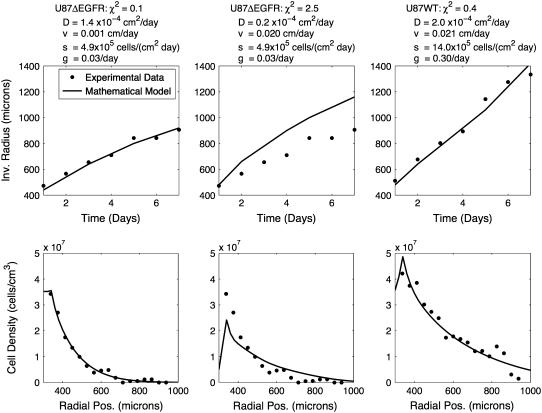
The next set of simulations, shown in Fig. 4, allowed v_i to be nonzero. The best fit for the U87WT, with an error of 0.4, was achieved when v_i = 0.021 cm/day, while for the U87ΔEGFR, v_i was essentially zero, with an error of 0.1. To test whether the U87ΔEGFR invasion could be as strongly biased as the U87WT, we fixed v_i to be 0.02 cm/day, and optimized the other three parameters, as shown in column 2 of Fig. 4. The fit was very poor, with an error of 2.5. This suggests that the U87WT invasive cells have a significantly higher radial velocity bias than the U87ΔEGFR invasive cells.

FIGURE 4.

A significant radial velocity bias is required to fit the U87WT with a reasonable set of parameters, as shown in column 3. The mathematical model (line) was optimized to fit the experimental data (dots) for the two cell lines. Each column uses a different set of parameters, given at the top of the column. Column 1 shows the best fit to the U87ΔEGFR data. Notice that in column 1, v_i = 0.001 cm/day, which is quite small. Column 2 shows the result when we fix v_i = 0.02 cm/day to be as large as it is for U87WT, and then optimize the other parameters to achieve the best fit. We see that the model cannot fit the data and that U87ΔEGFR cannot have an equally large velocity bias.

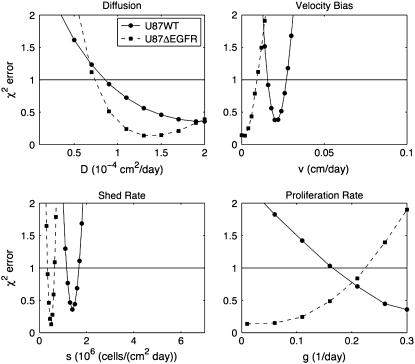
While Figs. 3 and 4 show best fits to the data, it is possible to perturb the parameters and still achieve fits of comparable χ² error. We explored the model sensitivity to changes in the parameters in two ways. The first was a traditional method, where one parameter was varied while the other three parameters were kept fixed at their optimal values found in Fig. 4. If one of the parameters was unimportant, we would expect a change in the parameter to have little effect on the error. The results of this sensitivity analysis, shown in Fig. 5, indicate that each parameter is important to the model.

FIGURE 5.

Sensitivity Analysis 1. In each plot, one parameter is varied while the other three remain fixed at their optimal values from Fig. 4. Notice that the model is sensitive to all four parameters. The horizontal line indicates where χ² = 1. Below this line, the fit to the data is considered good.

The above sensitivity does not explore what happens when combinations of parameters are varied together. For instance, although the error increases significantly when we vary v_i and keep {D, s, g} fixed, increasing v_i while decreasing D the proper amount may still give a good fit to the experiment. In a second sensitivity analysis, we explored this effect by varying one parameter and then optimizing the other three parameters to minimize the error. The results are shown in Fig. 6. From the figure, we see that if we set v_i = 0.02 cm/day for the ΔEGFR cell line, there is no possible choice for the other three parameters that give a good fit to the model. This analysis allows us to refine the parameter bounds from Parameter Estimation and Parameter Optimization, above, as shown in Table 1 using the range over which χ² < 1. This analysis indicates that both v_i and s are almost surely greater for U87WT than for U87ΔEGFR. Because χ² remains <1 for over almost the entire range of D and g, we have not gained any new information about these parameters.

FIGURE 6.

Sensitivity Analysis 2. In each plot, one parameter is fixed at different values while the other three are optimized to minimize error. This analysis is used to generate revised estimates of the original parameter bounds, shown in Table 1. Notice that the shed rate and velocity bias for the U87WT cell line were significantly higher than for the U87ΔEGFR. The horizontal line indicates where χ² = 1. Below this line, the fit to the data is considered good.

DISCUSSION AND CONCLUSIONS

We have presented new experimental data of the expansion and dispersion of Glioblastoma Multiforme tumor spheroids growing in three dimensions. We developed a continuum model that quantitatively fits the experimental data. The model differs from those used by Swanson et al. (27), because it focuses entirely on the invasive cells. This model is general and can be applied to any three-dimensional spheroid invasion assay.

The model describes invasion using four parameters: undirected motility, D; directed motility, v_i; shed rate, s; and proliferation rate, g. The biological meaning for these parameters is as follows. The unbiased motility, D is a measure for how “actively motile” these cells are. If glioblastoma cells are seeded on a two-dimensional substrate, they actively move around, but in no particular direction. The magnitude of D captures this phenomenon. The biased motility, v_i, is needed to account for the fact that for U87WT, the invasive cells detect where the spheroid is and actively migrate away from it. The biological mechanism for this is not known. It may be due to chemotaxis toward nutrients or away from spheroid waste products; or haptotaxis due to degradation of the gel by matrix metalloproteases; or a realignment of the gel by the cells as they move. The shed rate, s, is a measure of how quickly the cells leave the spheroid. It may also be viewed as the inverse of cell-cell adhesion. The stronger the cell-cell adhesion, the fewer invasive cells will be shed and the smaller s will be. The proliferation rate, g, is a measure of how fast the invasive cells increase in number once they are shed from the spheroid; this term is the net increase, so it includes loss of cells due to apoptosis. We chose these four parameters to describe invasion because this was the simplest model we could develop to quantitatively match the experimental data. This choice illustrates that the most impacting phenomena for describing invasion in this experiment are undirected motility, directed motility, shedding (or cell-cell adhesion), and proliferation.

Our models indicate that the difference in growth between the wild-type and the ΔEGFR cell lines is a result of a strong radially biased invasion of U87WT and a larger shedding rate (or smaller cell-cell adhesion) when compared to the U87ΔEGFR. This distinction in invasion between the two cell lines could result from alterations in the expression of cell surface receptors caused by the mutant EGF receptor in U87ΔEGFR.

This model can be extended in a variety of ways. To explore the cause of the directional bias we could add chemoattractants (36) or chemorepellants (37). The challenge, however, would be to verify the model by measuring various chemical concentrations in experiment. We could also attempt to describe why the U87WT core shrinks at day 1 while the U87ΔEGFR does not, by introducing a second partial differential equation for describing the cells in the core (see also (24)). This model assumes radial symmetry, and thus it does not capture the tenuous branches formed by the U87ΔEGFR cells (see Fig. 1). Such branching is addressed in Khain and Sander (25). While we indirectly model cell-cell adhesion at the core via the shed rate, we neglect any cell-cell adhesion in the invasive zone. Some models account for cell-cell adhesion in the tumor core through surface tension (38,39), but while this is appropriate where the cells are densely populated, it does not readily extend to the sparsely populated invasive zone. Thus to model cell-cell adhesion in the invasive zone, we believe a discrete model (16,17,23,40) would be most suitable.

That the U87WT spheroids were more invasive than those transfected with the mutant EGFR was unanticipated, since EGFR activity has long been implicated in increased malignancy of many cancers including glial cell tumors (41,42). When examined in two-dimensional radial migration assays, the opposite effects were observed: U87ΔEGFR exhibited a higher dispersion rate than U87WT (data not shown), a finding that points toward the influences of the extracellular matrix environment on cell phenotype and behavior (43). It has been shown that in most glioblastoma cell lines, EGFR amplification is lost when the cells are maintained in culture (44). We postulate that overexpression of ΔEGFR does not compensate for the loss of EGFR amplification, and therefore results in decreased invasion in the U87ΔEGFR spheroids in three dimensions. Despite this effect, we still see a dramatic difference in the phenotypes of the two cell lines: the U87WT invasive cells are shed faster and move in a more directed fashion. Both these effects may be the result of higher cell-cell adhesion in the U87ΔEGFR cells. Although the results of the in vitro experiments cannot directly be extrapolated to describe cell behavior in vivo, the experiments are valuable in that they allow us to test and develop novel hypotheses regarding a specific biological process: cell invasion in a three-dimensional matrix.

We hypothesize that the U87WT cells bind more strongly to the collagen-I than the U87ΔEGFR cells. If this were the case, then it would be easier for the WT cells to break cell-cell adhesion bonds and invade the matrix. Moreover, the WT cells would be better able to reshape the collagen matrix, forming directed highways in the matrix—and these highways could lead to increased directed motility.