Charge Delocalization in Proton Channels, II: The Synthetic LS2 Channel and Proton Selectivity

Abstract

In this study, the minimalist synthetic LS2 channel is used as a prototype to examine the selectivity of protons over other cations. The free-energy profiles along the transport pathway of LS2 are calculated for three cation species: a realistic delocalized proton (including Grotthuss shuttling)—H⁺, a classical (nonshuttling) hydronium—H₃O⁺, and a potassium cation—K⁺. The overall barrier for K⁺ is approximately twice as large as that for H⁺, explaining the >100 times larger maximal ion conductance for the latter, in qualitative agreement with the experimental result. The profile for the classical hydronium is quantitatively intermediate between those of H⁺ and K⁺ and qualitatively more similar to that of H⁺, for which the locations of the peaks are well correlated with the troughs of the pore radius profile. There is a strong correlation between the free-energy profiles and the very different characteristic hydration structures of the three cation species. This work suggests that the passage of various cations through ion channels cannot always be explained by simple electrostatic desolvation considerations.

INTRODUCTION

Proton transport (PT) plays a critical role in many biochemical functions. Classic examples are the biochemical “combustion” process (as catalyzed by the respiratory chain) and the cellular ATP synthesis, where protons are translocated across the membrane barrier by membrane proteins, e.g., cytochrome c oxidase (1,2) and F₀F₁ ATP synthase (3,4). These membrane proteins have a molecular construct known as a proton channel—a passive ion-conducting pathway with high selectivity for protons (5). Proton channels also exist in soluble (versus membrane) proteins providing a PT pathway between the solution and the reaction center. A few examples of such proteins are cytochrome c oxidase nitrogenases (6), Fe-only hydrogenases (7), and quinoprotein alcohol dehydrogenases (8). In all of these biochemical systems, a proton channel participates as a critical functional domain that controls the transition between conducting and blocking states, modulates the conductance magnitude, and rectificates the ion-flow direction.

An in-depth understanding of these biochemical functions requires detailed characterization and understanding of the properties of the corresponding proton channels, which is unfortunately still very limited (5). Probing the microscopic details of PT in channels is in general very difficult in experiments, in part due to the transient translocation signature of this lightest cation and in part to the complexity of protein systems themselves. This shortage of experimental results points to the importance of computational studies, which can provide important insight arising from the continuing advances in modeling, simulation algorithms, and computing resources that, in turn, allow increasingly accurate and realistic simulations to be performed. Although experimental information on the microscopic details of the channel proteins and the PT processes therein remains to be obtained, the above questions can now begin to be investigated using computational methods such as atomistic molecular dynamics (MD) simulations, especially for simpler, smaller, and yet realistic proton channel systems, for example, the gramicidin A (gA) channel (9) and the so-called LS2 channel as introduced below.

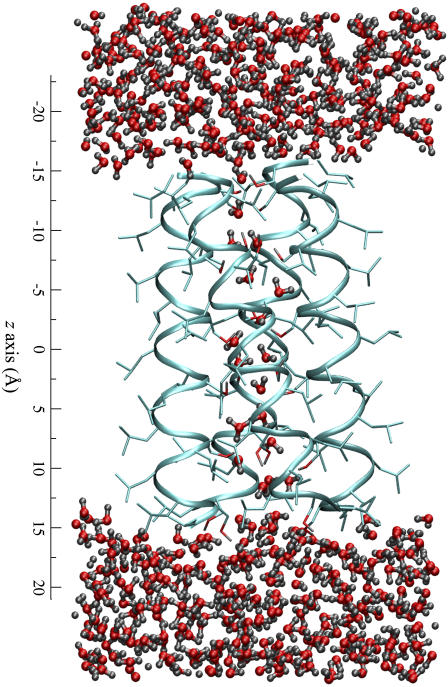
The LS2 channel, consisting of only Leu and Ser amino acid residues with a sequence of (LSLLLSL)₃NH₂, has been found to be proton selective with a proton conductance of 120 ps in 0.5 M HCl while being much less permeable to other cations (Li⁺, Na⁺, and K⁺) (10). It has a rather simple structure compared to most other natural channels (Fig. 1). A single LS2 peptide forms an α-helix structure in lipid bilayer, and four such helices can combine to form the LS2 channel by aggregating as a parallel bundle (10–13). Further structural details have been provided by atomistic MD simulation studies (14–17), revealing a tight and stable tetrameric α-helix bundle with all polar Ser side chains directed toward the channel lumen. Such an α-helix bundle structure, like barrel staves, forms a narrow hydrophilic transmembrane pore with a variable radius between ∼1.4 and 2.4 Å (15). The pore can be filled by ∼22 water molecules (15) that form a continuous water column through which protons can in principle shuttle across the membrane via the Grotthuss mechanism. The structural simplicity of LS2 is different from that of the well-studied gA channel (formed by unusual β-helices) in at least three aspects: i), the pore radius of LS2 is nonuniform along its axis and therefore the structure of its embedded water column deviates from the perfect single file as in gA; ii), the hydrophilicity of the pore of LS2 is provided mainly by the polar side chains of the Ser residues, whereas that of gA is provided by the helical carbonyl groups; and iii), the α-helices of LS2 form a macrodipole that does not exist in the head-to-head homodimer structure of gA. Although gA remains an important model for studies of proton conduction, LS2 shares secondary structural features that are much more commonly seen in proteins.

FIGURE 1.

MD snapshot illustrating the structure of the reduced LS2 channel system. The protein backbones and side chains are depicted as the ribbons and sticks, respectively. The water molecules are the angled sticks in red and gray. On the left is the scale of the channel along the z direction.

High proton selectivity is one of the most important properties of proton channels. Their proton conductivity is usually several orders of magnitude higher than for other cations (5). From a kinetic theory point of view, the selectivity is essentially governed by the overall free-energy barrier for translocation from one side of the bilayer to the other side through the transmembrane channel. Therefore, a quantitative description of the free-energy surface for ion transport through such a channel should be very informative for a clear understanding of the channel's selectivity, just as for the case of the aquaporin channels presented in the companion work (18) (in that case their proton blockage). A correlation of the free-energy barriers with the structural characteristics of both the protein and the translocation cations can provide further insight about the channel selectivity from a structural point of view.

Recently, free energies calculated from atomistic MD simulations have been used to shed light on many ion-channel-related problems, such as the mechanisms of ion transport (19,20) and selectivity (21) of the KcsA channel, the barriers of potassium (22) and proton (23) transport through the gA channel, the barriers to ion permeation in hydrophobic nanopores or channels (24), and the proton-blockage mechanism of aquaporin (see the companion work (18) and references within). However, there is only limited free-energy data directly concerning proton selectivity. The difficulties in this line of research has two origins: first, the free-energy barrier remains computationally expensive, especially the need to compute multiple free-energy profiles for both the conductible and nonconductible ion species; second, and perhaps more demanding, an excess proton is difficult to simulate due to its unique reactive (Grotthuss-shuttling) nature, which may in turn give rise to very different solvation structures and interactions that may have a significant influence on the free-energy barriers of PT.

In this work, the first difficulty stated above has been to some degree avoided by studying the simple yet representative synthetic LS2 proton channel as a prototype (see the Appendix for details). The second difficulty above has been largely resolved in our group through the development of the multi-state empirical valence bond (MS-EVB) model (25) for the simulations of an explicit excess proton in bulk water and biological systems, including proton delocalization and shuttling through the Grotthuss process. The LS2 permeation free-energy profile (or potential of mean force (PMF)—both terms are used in an exchangeable fashion in this article) has therefore been explicitly calculated via MD simulations for three cation species: a delocalized proton (H⁺) with explicit Grotthuss shuttling, a classical non-Grotthuss-shuttling hydronium cation (H₃O⁺), and a potassium cation (K⁺). These extensive MD studies provide a detailed account for the proton selectivity in terms of the permeation free energy. The selectivity mechanism is also studied by analyzing the desolvation patterns of the three cations and the dependence of the free energy profiles on the pore radius profile. Another important factor—the delocalized character of the excess proton for Grotthuss shuttling—is examined by comparing the free-energy profiles of H⁺ and H₃O⁺.

In the next section, the free-energy results for the three cation species will be presented, compared, and discussed, which is then followed by analyses of the dehydration and delocalization effects on the permeation free-energy profiles. Final conclusions drawn from these results will be given in the subsequent section. The results of this work are to be contrasted with those of the companion work (18) on the blockage of proton permeation by aquaporin channels.

RESULTS AND DISCUSSION

The free-energy profiles

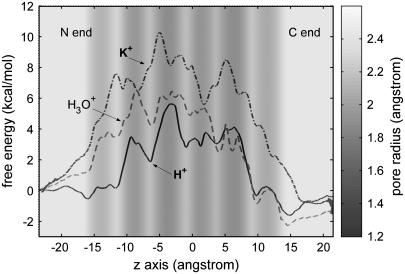
The LS2 permeation free-energy profiles for the three cation species: H⁺, H₃O⁺, and K⁺ are depicted in Fig. 2. Clearly, all PMFs exhibit multiple peaks and valleys along the transport pathways with the highest barrier located near the center of the channel at ∼−4.5 Å. The overall free-energy barrier of H⁺ is 5.6 kcal/mol, ∼5 kcal/mol lower than that of K⁺.

FIGURE 2.

Free-energy profiles for H⁺, K⁺, and H₃O⁺ as a function of the z axis through the LS2 channel, for which the pore radius is represented as the background gray scale (the exact pore radius profile can be found in Wu and Voth (15)). The error bars of the profiles range from ±0.2 to 0.5 kcal/mol and are omitted for the clarity of the curves.

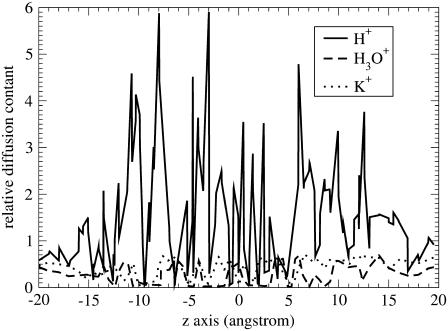
The profiles of position-dependent diffusion constants have been calculated for the three cations (Fig. 3), which allows us to estimate their maximal ion conductance using Eq. 1. The maximal conductance values for H⁺, H₃O⁺, and K⁺ are 2.8 pS, 0.0058 pS, and 0.0025 pS, respectively. These values are accurate at the level of an order of magnitude due to the uncertainties in both free energy and diffusion constant profiles (see the Appendix for the error analysis details). The conductance for H⁺ is ∼2 orders of magnitude lower than the experimental value (120 pS) (10). This underestimation can be attributed to the approximations from the reduced channel structure, the periodic boundary conditions, and the difference in the proton concentration between the systems in the simulation and in the experiment. Importantly, this result suggests that the H⁺ conductance is 1000 times larger than K⁺ conductance, which is in reasonable agreement with the experimental data (10) and thus further allows for a rationalization for the proton “selectivity” of the LS2 channel on the basis of the free-energy results.

FIGURE 3.

Relative diffusion constant profiles for H⁺, K⁺, and H₃O⁺ as a function of the z axis. The MS-EVB2 H⁺ diffusion constant for the bulk water phase (0.36 A²/ps) is taken as the reference.

Besides the overall barrier maxima, other important differences between the profiles are readily apparent. Near the channel mouths, the free-energy profile for H⁺ exhibits two dips of ∼−1.2 kcal/mol at the interface between the hydrophobic region and the bulk water. Interestingly enough, quantitatively similar free-energy dips have also been reported in a previous MS-EVB study of an excess proton at the membrane interface (ΔΔF = −1 kcal/mol) (26) and in a more recent MS-EVB study of proton leakage through a lipid bilayer (ΔΔF = −2 ± 0.5 kcal/mol) (27). Note that in contrast to these previous studies (26,27), the hydrophobic region is formed by the protein alone without lipid molecules. This study has been applied for a reduced LS2 system (see the Appendix)—with a simpler interface consisting only of Leu side chains—suggesting an attribution of free-energy dips at a bulk water/nonpolar region interface to the “amphiphilic” property of a hydrated excess proton as has been studied and reported recently (28). The fact that the interface free-energy dips are much less pronounced for H₃O⁺ while basically unnoticeable for K⁺ further supports this attribution to the amphiphilic proton hydration structure instead of to the details of the interface structure (e.g., the hydrogen-bonding network in a membrane/bulk water interface). It has long been hypothesized that membranes can play an “antenna” role that absorbs protons to the surface and subsequently funnels them toward a specific site via lateral diffusion. Absorbing protons to the surface is conventionally believed to be the electrostatic effect of negatively charged headgroups of the membrane (29). The results of this and previous explicit PT simulation studies, taken together, now suggest that the absorption of protons may be partly due to an inherent amphiphilic property of a hydrated proton.

The initial free-energy elevation for K⁺ starts at the channel mouths (z ≈ −22 Å or z ≈ 16 Å). The elevation for H⁺, on the other hand, starts much later—between the wide channel region (WCR) at z ≈ −11.5 Å (or z ≈ 9 Å) and the adjacent inner narrow channel region (NCR) at z ≈ −9 Å (or z ≈ 6.5 Å). The magnitudes of the corresponding barriers are 4–5 kcal/mol smaller than that of K⁺. As will be shown by the analyses below, these free-energy rises are well correlated with the dehydration that takes place during the entry process, and both the delay and the smaller magnitude of the initial free-energy elevation for H⁺ can be attributed to its much smaller extent of dehydration. A similar delay in free-energy rise can also be observed for classical H₃O⁺ but not as much as that for H⁺; in addition, the free-energy barriers for H₃O⁺ due to the elevations are 1–4 kcal/mol higher than those for H⁺. These differences between H⁺ and H₃O⁺, especially as compared to the free-energy profile for K⁺, clearly suggest that the delocalization property of the excess proton plays an important role in the PT process for this channel.

The free energy for K⁺ is elevated faster from the N end than from the C end. For example, the free energy at the first NCR from the N end (z ≈ −14 Å) is ∼0.8 kcal/mol larger than that from the C end (z ≈ 11 Å). This asymmetry in free-energy elevation is also very evident for H₃O⁺. The effect may be attributed to the α-helical structure of the protein that forms a macrodipole (30,31) with a magnitude normally at the order of 0.5e × L per helix (where L is the length of the helix; the N end is positive) (32,33) due to the consistent alignment of the backbone amide dipoles on an α-helix. This asymmetry is, however, not observed for H⁺ for which the free energy is elevated nearly at the same rate at both ends. It seems that the macrodipole is not felt by the proton, at least not as sensitively as by K⁺ and classical H₃O⁺. This observation is so far not completely understood, but one possible reason could be related to the anisotropic proton hydration structure and its delocalization behavior that can form counterdipoles to minimize the effect from the protein macrodipole.

It is interesting to observe the regular correspondence for H⁺ between the peaks/dips in the free-energy profile and the dips/peaks in the pore radius profile: most free-energy peaks are located at the NCRs, whereas most dips are at the WCRs; a similar but less regular correspondence can also be observed for H₃O⁺—however, not for K⁺. To understand these differences, the cations' solvation structures as well as the channel structure are analyzed below.

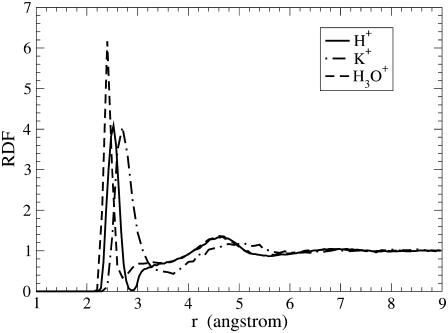
To characterize the solvation structures of the cations, the cation/water-oxygen radial distribution functions (RDF) of the cations in bulk water are plotted in Fig. 4. For the H₃O⁺ case, the central atom of the RDF is the oxygen atom of the hydronium; whereas for the H⁺ case, it is the oxygen atom of the pivot hydronium (which is the hydronium cation from the MS-EVB state with the highest instantaneous probability). Note that hydronium itself is already a hydrated species with the excess positive charge distributed among the four atoms; with this in mind, the term “solvating water molecules” hereinafter refers to those of the (pivot) hydronium unless specified otherwise. Clearly, the first RDF peak for H⁺ is much narrower than that for K⁺. The location of the first peak (referred to as the contact radius hereinafter) for K⁺ is 2.7 Å, ∼0.2 Å larger than that for H⁺. These data suggest that H⁺ forms a stronger inner hydration structure than K⁺, which is probably due to a stronger binding via the three hydrogen bonds in the former and because K⁺ has a larger coordination number (as will be confirmed in the third subsection). In the same way, the data also suggest that H₃O⁺ forms an even tighter hydration structure than H⁺, which is likely due to the localized charge of the non-Grotthuss-shuttling classical H₃O⁺ that enables the classical hydronium to have stronger electrostatic interactions with the solvating water molecules. In addition, one can see that the second solvation shell for H⁺ is essentially the same as that for H₃O⁺ but quite smaller than that for K⁺.

FIGURE 4.

Cation-water oxygen RDF for the cations in bulk water. For H⁺ and H₃O⁺, the central atom is the oxygen atom of the (pivot) hydronium.

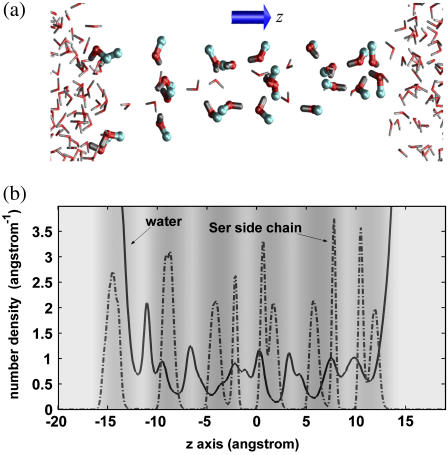
Fig. 5 a shows a simulation snapshot to intuitively illustrate the spatial distribution of the pore water and Ser side chains; Fig. 5 b shows the number-density profiles for the oxygen atoms of the water molecules and Ser side chains. These results reveal that the WCRs can on average accommodate one more water molecule than the NCRs and that the Ser side chains are mainly located at the NCRs.

FIGURE 5.

Distributions of the pore water and Ser side chains along the z axis. Panel a is an MD snapshot, illustrating the distribution of the water molecules and the Ser side chains. The hydrogen, oxygen, and carbon atoms are in gray, red, and blue, respectively. Panel b are the number-density profiles for the oxygen atoms of the pore water and the Ser side chains, respectively. The gray-scale background of panel b indicates the pore radius profile with their values given by the gray-scale bar as in Fig. 2.

Since K⁺ has a similar contact radius to that of a water molecule (2.73 Å) (34), one may expect that the peaks and the dips of the free energy profile for K⁺ would be located at the NCRs and WCRs, respectively, due both to the lower density of water molecules at the NCRs (Fig. 5 b) and to a steric-induced desolvation effect. However, this correspondence does not hold, suggesting that K⁺ adopts rather stable solvation structures at the NCRs. The K⁺ cation is largely solvated by the Ser side chains at the NCRs; since its presence requires a water molecule to be dispelled, the solvation at the WCRs is significantly reduced but not as much as at the NCRs. In contrast, an excess proton has a smaller van der Waals size, and its presence does not reduce the number of local water molecules, but rather slightly increases it due to the stronger hydrogen bonds that pack the molecules tighter in a protonated water cluster. For these reasons only the PMF for H⁺ exhibits correlation with the pore radius profile with dips at the WCRs where an extra water molecule can be accommodated. The hydration structure of classical H₃O⁺ is similar to that of H⁺, and therefore a similar PMF/pore radius correspondence to that for H⁺ is also observed for H₃O⁺. The above analysis provides a rationalization for the correspondence of the peaks and dips between the free energy and the pore radius profiles with a focus on the hydration structures. Note that the effect of the Ser side chains is probably of secondary importance for the problem since they are poorer solvent than the water molecules.

Effects of proton delocalization and dehydration on the free energy of PT

The delocalization effect results in two major hydration structures of an excess proton: one is the so-called Eigen cation 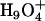, where the central hydronium is equally solvated by three water molecules; the other is called the Zundel cation 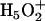, where the transferring proton is equally shared between two water molecules. Structures (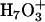) where the central hydronium is equally solvated by two water molecules were also observed in the channel. The 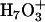structures are similar to the Eigen cation in the fact that the protonic charge is localized to the central water molecule where in the Zundel cation it is delocalized to two water molecules. The term “Eigen cation” hereafter will be used in a general sense referring to localized situations, and no particular distinction will be made between the 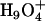and 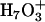structures. The relative stability of the two structures is affected by both the available cavity space and their intrinsic chemical stabilities. A relatively larger space is required by the Eigen cation to accommodate the three solvating water molecules, whereas the Zundel cation requires only two solvating water molecules and can hence fit into a smaller space. In the bulk water phase, the Zundel cation is probably less stable than the Eigen cation by <1 kcal/mol (25) and corresponds to the structure of an intermediate of the proton transfer reaction (25,35,36). In a narrow channel environment such as LS2, the Zundel cation may be more stable (15). By adjusting its hydration structure and delocalizing the excess charge, the proton can minimize the free-energy penalty during a transport process. This process can only be discriminated by an explicit multi-state implementation of the EVB model (25) as utilized in this work.

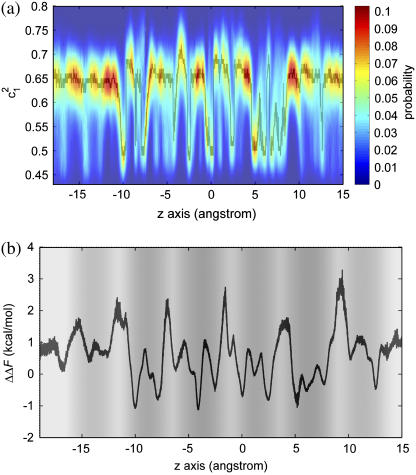
To demonstrate the alteration of the excess proton hydration structure, the probability distribution of the largest MS-EVB amplitude ( ) for each z point is calculated (shown as Fig. 6 a). The term 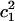is used here to quantify the proton hydration structure: values close to 0.5 correspond to the Zundel cation-like hydration structures, whereas those around 0.65 correspond to the Eigen cation-like hydration structures. The probability maxima are marked out as a function of the z axis by the black curve in Fig. 6 a, showing a periodic oscillation of the favorable hydration structure throughout the PT pathway, consistent with our previous results (15). The average length interval between two neighboring Zundel-cation-favored points is ∼2–3 Å—approximately the van der Waals size of a water molecule—suggesting that the contribution of hydronium translation to the charge propagation is relatively small and Grotthuss shuttling is the dominant PT mechanism for such a proton channel.

FIGURE 6.

Panel a is the population distribution along the largest MS-EVB amplitude ( 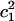) for each z point. The term 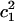is used here to quantify the proton hydration structure (see text for details). The black curve is probability maxima as a function of the z axis. Panel b shows the free-energy difference between the Eigen and Zundel cation hydration structures with the background gray scale indicating the pore radius profile (see the gray-scale bar in Fig. 2).

To see the effect of hydration structure transformation on the free energy, the free-energy difference between the two hydration structures has been calculated as a function of the z axis, shown as Fig. 6 b, which, in quantitative agreement with the previous results (15), shows that the Eigen cation is in general more stable by up to 3 kcal/mol than the Zundel cation in the WCRs. In the NCRs, the free-energy difference between the two structures is reduced and may even be inverted: the Zundel cation can be up to 1 kcal/mol more stable at certain points on the PT pathway. The sharp oscillation of the free-energy curves in Fig. 6 b suggests that the stability of the proton hydration structure is very sensitive to the local environment, confirming our previous conclusion (15).

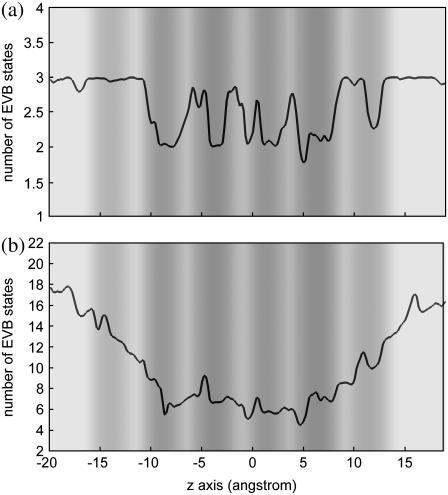
Fig. 7 examines the number of MS-EVB states as a function of the z axis with the panels a and b for the first solvation shell and for the first three solvation shells of the pivot hydronium, respectively. This quantity is a direct measure of the number of water molecules involved in stabilizing the excess proton; and for the first solvation shell it is equivalent to the coordination number of the pivot hydronium. From Fig. 7 a, one can see that in all WCRs, there are 2.8–3 first solvation shell water molecules, which is essentially the same as in the bulk water phase, whereas there are only 2–2.4 first solvation shell water molecules in most NCRs. The smaller coordination number at the NCRs suggests that dehydration from the first solvation shell of the pivot hydronium gives rise to the free-energy peaks, consistent with the analysis in the last subsection.

FIGURE 7.

Number of MS-EVB states as a function of the z axis for the first solvation shell (a) and for the first three solvation shells (b). The statistical uncertainties are ∼0.5 for (a) and 1 for (b). The background gray scale represents the pore radius profile (see the gray-scale bar in Fig. 2).

Fig. 7 b shows that H⁺ experiences a quite significant dehydration when it goes deep into the channel: ∼10 water molecules (amounting to ∼55%) are lost from the first three solvation shells when it reaches the second NCRs from the bulk water. The number of water molecules decreases gradually, in contrast to the quite sudden free-energy elevation for H⁺ that occurs within only 3–4 Å (at z ≈ −10 Å and z ≈ 7 Å), suggesting that loss of solvating water molecules from the distant solvation shells has a very small effect on the free energy of PT even though depletion of these water molecules is massive. The small effect of dehydration from distant solvation shells may be due to the hydrophilicity of the channel where the polar groups from the channel compensate for the loss of those solvating water molecules.

Effects of dehydration of K⁺ and H₃O⁺ on their permeation free energies

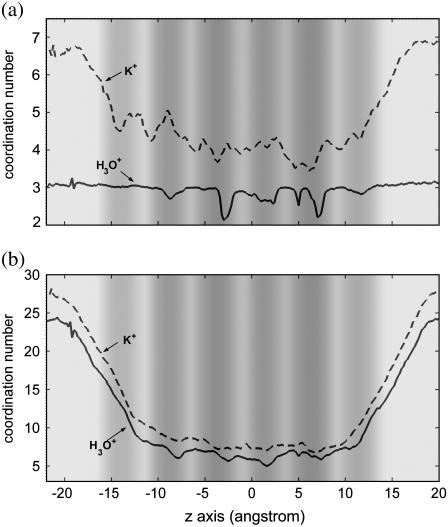
To account for the permeation free-energy barriers for K⁺ and classical H₃O⁺, the coordination number as a function of the z axis has been calculated for their first solvation shells (Fig. 8 a). The first solvation shell of H₃O⁺ and H⁺ has a maximal coordination number of 3 in the WCRs and in bulk water. In the NCRs, the coordination number decreases but not as much as in the H⁺ case. The smaller reduction of coordination number for H₃O⁺ in the NCRs is due to the fact that it has a tighter binding with its solvating water molecules, as seen in Fig. 4. The dips in this coordination number curve correspond well with the peaks of the PMF for H₃O⁺, confirming the suggestion that dehydration from the first solvation shell can definitely cause a free-energy penalty. However, note that this dehydration cannot account for all free-energy barriers. For example, H₃O⁺ experiences no loss of first solvation water molecules going from z = −15 Å to z = −10 Å, whereas the free energy increases by 3 kcal/mol.

FIGURE 8.

Coordination number as a function of the z axis for the first solvation shell (a) and for the first two solvation shells (b). The statistical uncertainties are ∼1 for (a) and 2 for (b). The background gray scale represents the pore radius profile (see the gray-scale bar in Fig. 2).

As mentioned above, K⁺ has a larger solvation shell. The coordination number from the first solvation shell is 6–7 in bulk water and gradually decreases when the cation enters the channel. The loss of solvating water molecules from the first solvation shell can be qualitatively correlated with the free-energy elevation of K⁺, which again indicates that dehydration from the first solvation shell is a clear source of free-energy penalty. Because of the larger solvation shell, the dehydration of K⁺ is much more extensive than that of H⁺ and H₃O⁺: when arriving at the first NCRs from the bulk water, K⁺ loses two solvating water molecules from its first solvation shell, whereas H₃O⁺ and H⁺ lose at most one water molecule.

Fig. 8 b shows similar functions for the first two solvation shells. The dehydration from the first two shells during the cation entry process is much larger than that from the first shell for both K⁺ and H₃O⁺. For both cases, though the free-energy increase has a qualitative correspondence to the decrease of the coordination number, the correlation is not very strong. For example, K⁺ loses ∼7 water molecules from the first two shells when going from z = 20 Å to z = 17 Å, whereas the free energy does not increase at all. This result suggests that loss of water molecules from the second solvation shell does not necessarily causes a free-energy penalty, whereas loss from more distant solvation shells will probably have only a negligible effect on the free energy. More of these effects argue for the importance of the near-range electrostatics over more continuum-like long-range electrostatic arguments.

CONCLUDING REMARKS

To study the proton selectivity of the LS2 channel, explicit free-energy profiles and maximum conductances have been calculated in this work for a fully Grotthuss-shuttling proton (H⁺), a classical nondissociable hydronium model (H₃O⁺), and a potassium cation (K⁺) along the transport pathway of the channel. As in the companion work (18), these profiles are calculated from explicit atomistic MD simulations. These results reveal that K⁺ has a considerably higher (by ∼5 kcal/mol) overall free-energy barrier than H⁺ (5.6 kcal/mol), explaining an at least 100 times larger ion conductance for the latter, in qualitative agreement with the experimental result (10). The large free-energy difference between H⁺ and K⁺ can be traced to their different dehydration patterns as revealed by the above analyses and further summarized here: the excess proton has a very tight hydration core that is formed by the hydronium and its first solvation shell water molecules. The hydration core provides a good solvation to the excess charge, and the water molecules therein cannot be easily depleted unless the pore is very narrow (i.e., pore radius ≤1.4 Å). This characteristic enables the proton to avoid a large dehydration free-energy penalty during PT. Due to the good solvation of the excess proton charge by the first solvation water molecules, dehydration from the second shell results only in a small free-energy penalty unless the dehydration is very large, which explains why the free-energy elevation is so delayed for H⁺ compared to that for K⁺ after entering the channel. In contrast, the first solvation shell of K⁺ is bulkier and much of it must be stripped earlier along the transport pathway: the dehydration from the first solvation shell water molecules starts at the mouths of the channel, explaining the earlier free-energy elevation for K⁺. In addition, further significant dehydration along the transport pathway results in a larger overall free-energy penalty.

The free-energy profile for classical H₃O⁺ is quantitatively intermediate between those for H⁺ and K⁺ and qualitatively more similar to that for H⁺ with a 1.6 kcal/mol higher overall free-energy barrier. The qualitative correspondence arises from the similarity of their dehydration patterns. The difference in the magnitude of the free-energy profiles between classical H₃O⁺ and H⁺ is perhaps more interesting, indicating a subtle and important issue concerning the charge delocalization effect. The delocalization results in a partition (or delocalization) of the excess protonic charge among a number of solvating water molecules (in the MS-EVB2 model, the number of involved water molecules amounts to 22 on average in bulk water): ∼40–60% of the excess charge is delocalized to the three nearest solvating water molecules of the pivot (instantaneous) hydronium. The more delocalized charge can therefore be solvated among several water molecules, resulting in a smaller free energy barrier of H⁺.

The charge delocalization effect on the free-energy profile of the excess proton is also rather subtle. The analysis of the delocalization effect on the favorable proton hydration structure demonstrates a clear transition between the Eigen and Zundel cation structures along the PT pathway of LS2. The more symmetrically delocalized Zundel structure may lead to a reduction of free-energy penalty by up to 1 kcal/mol, whereas the PMF results show that the magnitude of the free energy of H₃O⁺ can be up to 4 kcal/mol (e.g., at z = −8 Å) higher than that of H⁺. This apparent discrepancy is due to the fact that when considering the two hydration structures, the delocalization effect beyond the first solvation shell is not included. The smaller magnitude of the free-energy barrier to PT relative to that of H₃O⁺ makes sense physically for LS2 and for proton channels in general, highlighting the rather surprising (though relatively small) opposite correspondence for the GlpF aquaporin channels as reported in the companion work (18). The high barrier to PT in aquaporins arises from opposing shuttling pathways and the bipolar electrostatic field of the aquaporin matrix which serves to further block protons as discussed in the companion work (18).

In summary, the very different local dehydration pattern arising from the delocalization and tighter hydration of excess proton can discriminate this cation from the others (here K⁺ is used as a representative) during the ion transport process through a pore such as that found in the LS2 channel. This characteristic of the proton can presumably be utilized by biological proton channels to selectively conduct protons by forming a narrow pore with the suitable size and degree of hydrophilicity to maintain the desired low free-energy barrier for PT while excluding other cations via their large desolvation penalty.

APPENDIX

In this study, free-energy profiles have been calculated for a fully Grotthuss-shuttling excess proton (H⁺), a classical hydronium (H₃O⁺) model, and a potassium cation (K⁺). The force field for both the protein and the potassium cation (GROMOS87), the MS-EVB2 model for aqueous PT (and the related terminologies thereof), the construction and characteristics of the reduced LS2 system, and simulation protocols have been described in our previous work (15). This section therefore only focuses on relevant specifics for this study. The classical H₃O⁺ was described by constraining the MS-EVB2 model to one state while removing two diagonal repulsion potentials (Eqs. 2 and 3 in Day et al. (25)). These two terms were introduced to the MS-EVB2 model to correct the formation energy of the otherwise overbound protonated water clusters, and they are hereby not valid for a single-state scheme.

Using umbrella sampling (37,38), the free energies were calculated as functions of the z axis (channel axis). Use of this reaction coordinate reflects the fact that the ion conduction is a charge displacement parallel to an applied transmembrane electric field (22). The length of the reaction coordinate was chosen such that the free-energy profiles could asymptotically go flat into the bulk water phase, yielding a span roughly from −24 Å to 21 Å that encompasses the channel length from −16 Å (N-end) to 13 Å (C-end). For each cation, ∼70 umbrella-sampling windows were used. The biasing potentials were harmonic ones applied on the cation (for H⁺, the center of excess charge (CEC) as defined in Day et al. (25)) with force constants ranging from 2.0 to 16.0 kcal/mol⁻¹Å⁻². Each window's simulation time was to 3–8 ns. The convergence of the sampling was verified by doubling the simulation duration until no detectable difference was observed in the free-energy results. To obtain a meaningful PMF for the reaction coordinate segments outside the channel length (−16–13 Å) where the cation is unbounded, harmonic restraints with a force constant of 1 kcal/mol⁻¹Å⁻² were applied on both the x and y coordinates of the transporting species to confine them in a cylindrical region with a radius of ∼2.5 Å (22). The free-energy profiles were calculated from the simulation trajectories using the weighted histogram analysis method (39–41).

Block averaging was used to estimate the statistical uncertainty in the PMF results presented here. In this method, each long trajectory can be divided into the same number (two or more) of blocks, and using the data from one block for each window, a single measurement of the PMF can thus be calculated. Of course, the precision of each measurement may depend on the block size, especially when the total sampling volume is restricted by the available computational resources, which is not uncommon for expensive simulations. Generally the larger the block size (hence the fewer the blocks), the less statistical uncertainty a measurement will have. In this study, each trajectory after the equilibration period (300–600 ps) was divided into two blocks, thus two PMFs were obtained for the same system. The two PMFs for each system were shifted toward each other until the root mean-square deviation between them was minimized; then the averages and the corresponding standard deviations were calculated and shown in Fig. 2.

The maximal ion conductance can be estimated from the simulations using the following equation (22):

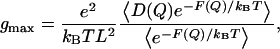(1)

where e is the electron charge, k_B is the Boltzmann constant, T is the temperature, L is the pore length, and D(Q) and F(Q) are the diffusion constant and free-energy profile at the point Q on the reaction coordinate, respectively, and finally the brackets denote spatial averaging over the length L. Following Roux and co-workers (22), the diffusion constants of the cations were calculated as a function of the reaction coordinate (Fig. 3). The equation for position-dependent diffusion constants in the original method (42) can be considerably simplified as recently shown by Hummer to the following form (43):

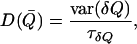(2)

where 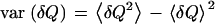is the variance and 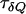is the characteristic time of the correlation function 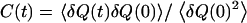with 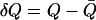as the deviation from the average position ( 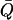). The advantage of this method is to allow for convenient estimation of position-dependent diffusion constants from the same umbrella-sampling simulations that employ harmonic biasing potentials. This equation is, however, only exact for overdamped harmonic oscillators. For more complicated systems that do not behave like an overdamped harmonic oscillator on the dimension of the reaction coordinate, the result can have considerable errors. For example, for the bulk water phase, where the result derived from Eq. 2 can be justified with one from the standard Einstein equation, up to 100% relative errors were observed for several models (data not shown). Despite this inaccuracy, it should be noted that the maximal conductance from Eq. 1 is normally dominated by the free-energy term.

The effects of the uncertainty of the PMFs on the errors of the ion conductance results have been analyzed by the bootstrapping method. For the PMFs here, the relatively error is ∼100%, which, together with the error from the diffusion constant, suggests that the maximal ion conductance results should be trusted at the level of the order of magnitude.