Multipoint Linkage Analysis with Many Multiallelic or Dense Diallelic Markers: Markov Chain–Monte Carlo Provides Practical Approaches for Genome Scans on General Pedigrees

Abstract

Computations for genome scans need to adapt to the increasing use of dense diallelic markers as well as of full-chromosome multipoint linkage analysis with either diallelic or multiallelic markers. Whereas suitable exact-computation tools are available for use with small pedigrees, equivalent exact computation for larger pedigrees remains infeasible. Markov chain–Monte Carlo (MCMC)–based methods currently provide the only computationally practical option. To date, no systematic comparison of the performance of MCMC-based programs is available, nor have these programs been systematically evaluated for use with dense diallelic markers. Using simulated data, we evaluate the performance of two MCMC-based linkage-analysis programs—lm_markers from the MORGAN package and SimWalk2—under a variety of analysis conditions. Pedigrees consisted of 14, 52, or 98 individuals in 3, 5, or 6 generations, respectively, with increasing amounts of missing data in larger pedigrees. One hundred replicates of markers and trait data were simulated on a 100-cM chromosome, with up to 10 multiallelic and up to 200 diallelic markers used simultaneously for computation of multipoint LOD scores. Exact computation was available for comparison in most situations, and comparison with a perfectly informative marker or interprogram comparison was available in the remaining situations. Our results confirm the accuracy of both programs in multipoint analysis with multiallelic markers on pedigrees of varied sizes and missing-data patterns, but there are some computational differences. In contrast, for large numbers of dense diallelic markers, only the lm_markers program was able to provide accurate results within a computationally practical time. Thus, programs in the MORGAN package are the first available to provide a computationally practical option for accurate linkage analyses in genome scans with both large numbers of diallelic markers and large pedigrees.

Linkage analysis is widely used in human gene mapping. Choices involved in the design of such studies include selection of large versus small pedigrees and genotyping with multiallelic versus diallelic markers, as well as mixtures of these possibilities. Each of these choices induces analytical constraints, with a trade-off between the number of markers and the size of the pedigrees that can feasibly be analyzed with exact, deterministic computational methods. The Lander-Green algorithm¹ permits exact computation for large numbers of markers but only on relatively small pedigrees, whereas the Elston-Stewart algorithm² permits exact computation on large pedigrees but only for a relatively small number of markers analyzed jointly. Exact computation remains infeasible for the case of large numbers of markers combined with large pedigrees. Since large pedigrees can be particularly informative for gene mapping,³ these limitations create problems for the efficient use of commonly used multiallelic STR markers and are particularly problematic with the increasing use of large numbers of diallelic SNPs.⁴

The difficulty of using all available multilocus marker data on general pedigrees has led to the development of methods based on sampling rather than on exact computation. The goal of these Monte Carlo (MC)–based approaches is to sample rather than to enumerate possible missing-data configurations and then to average a mapping statistic over many such samples. Implementations based on dependent samples obtained with Markov chain–MC (MCMC) approaches have been under development for >15 years; the primary publicly available linkage-analysis packages are SimWalk^5,6 and MORGAN.^7–10 Both of these packages represent long-term development and evolution of the MCMC approach and can be used for a variety of linkage-analysis approaches, including the classic model-based LOD score.¹¹ Both are sufficiently useful that they are increasingly being used for routine real-data analyses of STR markers.^12–16 Other MCMC-based linkage-analysis programs also exist^17,18 but are either not yet publicly available or still in early development.

The operating characteristics of MCMC-based programs for use with multiallelic markers have not been systematically evaluated. Although the development of both SimWalk2,^5,6 and MORGAN,^15,19–21 has included comparison of results from MCMC and deterministic analyses, these examples have been limited to a small number of pedigrees analyzed under, at most, a few conditions. There has been only one larger-scale evaluation: analysis of results from simulated multiallelic genotypes showed that marker identity-by-descent (IBD) estimates obtained with SimWalk2 appear to be accurate compared with results obtained with exact computation.⁶ However, this study was based on results for only a single pair of individuals in generally small pedigrees and did not include large pedigrees with large amounts of missing data—a situation that occurs in many real data sets. There has also been almost no comparison between MCMC programs. Previous direct comparison of programs is limited to IBD estimates obtained with Loki²² and SimWalk2 for a single real-data set analyzed as part of Genetic Analysis Workshop (GAW) 13²³: there was strong overall concordance between pairwise IBD estimates obtained by the two programs, but with considerably longer computation times for SimWalk2 than for Loki. Since Loki and MORGAN both use the same locus²² and meiosis sampler,²⁴ it is reasonable to expect that the general conclusions obtained should extend to programs in the MORGAN package. However, this was only a single data set with well-sampled and shallow pedigrees, and the outcome might not be typical of those for other data sets. Also, some individual IBD estimates differed considerably between the two programs, and the impact of these discordant estimates on linkage analysis was not evaluated.

There also has been no systematic evaluation of the accuracy or operating characteristics of MCMC-based linkage-analysis programs for use with large numbers of SNPs. The few available reports of use of these programs suggest that analysis of large numbers of SNPs can be particularly challenging, even with MCMC-based methods. For example, three studies with large pedigrees (of up to 93 individuals) noted that, for practical reasons, SimWalk2 was restricted to a maximum of 35–45 SNPs.^14,25,26 Others have noted that the computational burden of MCMC-based programs for analysis of dense SNPs is very high, effectively limiting the number of SNPs that can be feasibly analyzed or requiring substantially increased computer investment.^4,27,28 Finally, one analysis of a real data set, which used the MORGAN program lm_markers as part of GAW 14, noted that linkage-analysis results obtained with SNPs appeared to be unexpectedly “noisy” compared with results from STR markers on the same pedigrees.²⁷ This noise raises the possibility that alternative run conditions could affect the quality of the results. All of these reports are limited to comments provided as part of specific real-data analyses and do not provide a more extensive investigation of relevant issues.

Here, we provide an evaluation of the performance of two MCMC-based linkage-analysis programs with a range of pedigree structures and markers. We use SimWalk2 and the program lm_markers from the MORGAN package, and we focus on the LOD score as a linkage statistic. The program lm_markers combines the block-Gibbs MCMC locus sampler²² with the meiosis sampler,²⁴ with sampling conditional on the marker data.²⁹ Once marker inheritance indicators have been obtained, lm_markers and SimWalk2 both use the same approach for estimation of the LOD score.⁵ Our results confirm the accuracy of both programs for use with multiallelic markers on pedigrees of varied sizes and missing-data patterns, but with some computational differences. One important outcome of this investigation is the demonstration that lm_markers provides an accurate and computationally practical option for use with large numbers of dense SNPs in linkage analysis of large pedigrees.

Methods

Overview

We had two goals that we addressed by analysis of simulated data. First, we wanted to compare and quantify the effects of the two main user-specified choices for the MCMC-based LOD score program lm_markers: the method for providing starting configurations and the effect of the number of total MCMC scans used for the analysis, where a scan is one cycle of obtaining new realizations of the missing data. Second, we wanted to compare analysis results obtained with lm_markers with those obtained with SimWalk2 and with those obtained with exact deterministic computation. Most of the analysis conditions also allowed deterministic computation to provide a “gold standard” for comparison. In addition, a few analysis conditions involve situations for which a gold-standard result is computationally infeasible but for which alternative results that would provide useful comparisons could be obtained. Toward these goals, we investigated the outcome of analyses with (1) large numbers of dense SNPs on small pedigrees, (2) small numbers of sparsely spaced STR markers on large pedigrees, (3) larger numbers of sparsely spaced STR markers on large pedigrees, and (4) large numbers of dense SNPs on large pedigrees.

Pedigrees

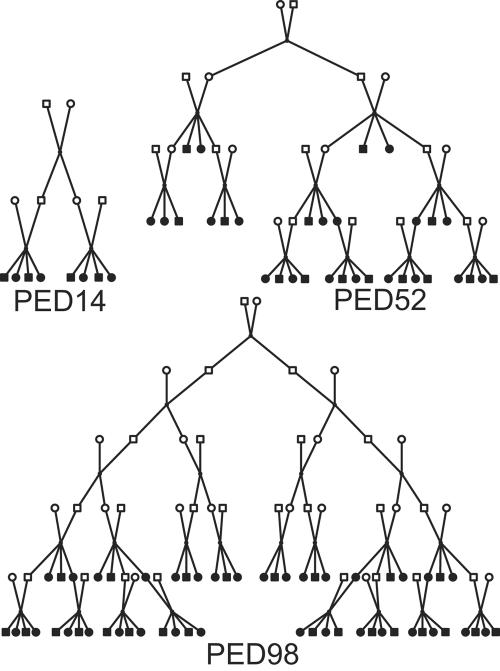
We simulated data on three pedigree structures (fig. 1). Trait and marker data used for all linkage analyses were treated as either observed or missing, in accordance with the data availability indicated in figure 1. We used a small, 14-member pedigree (PED14) primarily for use with large numbers of densely spaced SNPs. For such small pedigrees, analysis with an exact method, as is needed for a gold-standard comparison, is possible with a program that uses the Lander-Green algorithm¹ for likelihood computation. PED14 was close to the maximum pedigree size that could be analyzed using this algorithm with our available computer memory. We used a moderately large, 52-member pedigree (PED52) with no data in the top two generations and a large, 98-member pedigree (PED98) with no data in the top four generations, primarily for use with multiallelic markers that are typical of STR mapping panels. Both large pedigrees are representative of pedigrees used in many studies, with PED98 representing a particularly difficult analytic challenge. In addition to the versions of the pedigrees shown in figure 1, we also used these pedigrees to explore the effects of particular missing-data patterns. PED52_R was obtained through reduction of the available observed data, by the elimination of all observed data in generation 3. PED98_A had augmented data, achieved by adding observations on all nonfounder males in generation 4. Exact computation for a gold-standard comparison of both of these larger pedigrees can be achieved only with the Elston-Stewart algorithm,² which limits the number of markers that can feasibly be analyzed in an exact multipoint analysis. Finally, we performed two additional sets of analyses under conditions for which no gold-standard analysis could be produced and only cross-program comparisons or comparisons with an easier-to-compute alternative were possible. For these, we used PED52, both for analysis of a larger number of multiallelic markers and for analysis of a large number of SNPs.

Figure  1. .

Pedigree structures used for analysis. Blackened symbols represent sampled individuals.

Markers and Trait Models

We simulated 100 replicates of data for each pedigree configuration. Marker genotypes were generated at uniform intervals on a 100-cM chromosome with the program Genedrop from the MORGAN package. Diallelic SNP genotypes were simulated at 0.5-cM intervals, and, in the same simulations, multiallelic STR genotypes were simulated at 10-cM intervals. In both cases, the markers were simulated under the assumptions of no interference and of linkage equilibrium among loci, since, currently, the MCMC-based programs cannot incorporate linkage disequilibrium (LD). A diallelic trait locus was simulated that was at approximately the midpoint between markers 105 and 106 on the SNP map and between markers 5 and 6 on the STR map. These choices of marker spacing approximate current mapping panels, including several current ∼10-cM density STR mapping panels and, for SNPs, the density is between the densities of the ∼10K Affymetrix³⁰ and ∼5K Illumina SNP panels.³¹ Allele frequencies for simulated markers were based on a sample of markers used to construct The SNP Consortium's clustered-SNP map³² and on STR markers used for a recent linkage analysis of five chromosomes.³³

Founder-genome labels (FGLs) were retained at the trait locus for later use, to provide a standard for comparison, as further described in the “Analysis Configurations” and “Comparison of LOD Scores” subsections. These FGLs consist of a unique label for each founder chromosome and identify the specific founder chromosome from which each descendant chromosome is derived.³⁴ FGLs are equivalent to a perfectly informative marker at the location of such an FGL, given the available phenotype and pedigree information.

The trait model used for both data simulation and linkage analysis involved a diallelic locus with a minor-allele frequency and three penetrance values characterizing a reduced-penetrance, partially dominant trait with sporadic cases. Since the MCMC sampling of the programs evaluated here involves only the marker loci and not the trait locus, with LOD scores from both programs computed as suggested by Lange and Sobel,⁵ details of the model are not important for interpreting relative performance of the two programs. However, the trait models are provided for completeness. For simulations involving PED14, the allele frequency, p_D, for minor allele D, was 0.1, and the trait penetrances were 0.95, 0.8, and 0.05 for trait genotypes DD, Dd, and dd, respectively. For simulations involving PED52 and PED98, p_D=0.2, and penetrances were 0.8, 0.7, and 0.05, respectively. An ascertainment criterion based on rejection sampling was imposed after trait and marker simulation, with the simulations repeated until 100 data sets per pedigree structure were obtained. For PED14, a retained pedigree was required to have at least one affected and one unaffected individual in each of the two sibships in the final generation of the pedigree. For PED52 and PED98, each pedigree was required to have at least one affected member in each sibship with no further descendants.

Analysis Configurations

SNP markers were used for analysis of PED14 in three different configurations (table 1). All 200 diallelic markers (PED14-200) were used to mimic an analysis involving a complete set of dense SNPs on a small chromosome. Two additional data sets were produced by starting with the complete 200-SNP data set and reducing it to a data set consisting of 67 SNPs (PED14-67). To evaluate the effect of marker density, we thinned SNP markers to a sparser panel of 67 markers spanning the chromosome, by retaining every third marker (PED14-67s). To evaluate the effect of the number of SNPs used for analysis, we retained the 67 densely spaced markers in the center of the map (PED14-67d), since this provides the same density of markers as does PED14-200 but with the same reduced total number of markers as PED14-67s.

Table 1. .

Data Configurations

	No. of			Marker
Data Set	Pedigree Members	Missing Generations	Markers	Type	Spacinga (cM)
PED14-FGL	14	2	1	FGL	NA
PED14-67s	14	2	67	SNP	1.5
PED14-67d	14	2	67	SNP	.5
PED14-67	14	2	67	SNP	.5 or 1.5
PED14-200	14	2	200	SNP	.5
PED52-FGL	52	2	1	FGL	NA
PED52-3	52	2	3	STR	10
PED52R-3	52	3	3	STR	10
PED52-10	52	2	10	STR	10
PED52-67d	52	2	67	SNP	.5
PED98-3	98	4	3	STR	10
PED98A-3	98	3	3	STR	10

^aNA = not applicable.

Exact computation with PED14 was also used to evaluate use of FGLs as a standard of comparison. The goal was to determine whether the use of computationally practical single-marker analysis of FGLs could serve as an adequate baseline analysis in situations for which exact computation would normally be impossible. Exact analysis is possible for PED14 under both conditions, eliminating discrepancies that might result from use of an MC approach. For this purpose, one analysis configuration consisted of the trait-locus FGLs used in a single-marker exact analysis (PED14-FGL), with PED14-67d used for an exact multipoint analysis. Since use of either the FGLs or a large number of dense SNPs should extract virtually all information, it was expected that LOD scores for these two situations would be very similar.

Analysis of PED52 and PED98 also involved several configurations (table 1). For analyses of STR markers that were used for a gold-standard computation, only markers 5–7 surrounding the trait locus were used (PED52-3 and PED98-3), because of the computational burden of using more than three STR markers for the exact analysis. Two additional analyses that do not have gold-standard comparisons were also performed for PED52. One analysis compared the results of the two MCMC-based programs, using data from all 10 STR markers (PED52-10). A second analysis compared results from 67 dense SNPs (PED52-67d) with results obtained from a single-marker exact analysis based on only the FGLs at the trait locus (PED52-FGL).

LOD-Score Computations

MCMC-based LOD scores were obtained with SimWalk2 version 2.91^6,35 and a prerelease of lm_markers version 2.7 from the MORGAN package. Both programs use MCMC-based implementations to obtain samples from the posterior distribution of inheritance indicators conditional on marker data.^{6,8,29,35–37} File setup for SimWalk2 was performed with MEGA2³⁸ because of strict file format requirements; file setup for lm_markers and programs used for exact analysis was performed with shell scripts because of their more flexible format requirements. For a given realization of inheritance indicators, both SimWalk2 and lm_markers use the same approach for computation of LOD scores⁵ for a specified trait-locus position and trait model, with the final LOD score representing the logarithm of an average over many iterations of the MCMC process. For analysis of STR data sets, we used the distributed binary file for SimWalk2. Because the distributed version of the program that can be used with large numbers of SNPs required more free memory (>1 GB) than we had available, we rebuilt a version of the program with a limit of 200 markers for analysis of SNP data, using version 3.35 of MENDEL,³⁹ which is needed for LOD-score computations.

Run conditions for the MCMC-based programs were as follows. Analyses with lm_markers used a hybrid sampler consisting of an equal proportion of a locus and a meiosis sampler,³⁷ on the basis of earlier work that indicated insensitivity of results to the exact proportions of the two samplers when the proportions are in the range of 0.2–0.8.^34,40 Of the final number of scans, 10% (1/11 of the total run) was discarded for burn-in. For evaluation of its effect on accuracy, the run length, N, excluding burn-in, was varied by factors of 10, from 300 to 3,000,000 scans. Not all run lengths were used for all analysis configurations. Both starting configurations that are the only current options were also evaluated: initial realizations obtained with (1) an independent-locus (IL) setup,²² which ignores the effects of linkage among multiple loci, and (2) sequential imputation (SI),²⁹ to allow for dependence among loci. SI is an MC approach that uses independent realizations of missing data but that allows for effects of linkage.⁴¹ For brevity, we refer to these two options as “lm_markers-IL” and “lm_markers-SI,” respectively. Except where explicitly stated, we present results for lm_markers-SI because it gave more-accurate results under otherwise equivalent conditions. The number of initial SI realizations for lm_markers-SI was the minimum of 10⁵ and N/3. Run lengths were limited to N=3,000 and N=30,000 for lm_markers-IL. For SimWalk2, default parameter values were used for all analyses, since modification of run conditions involves a large number of potentially interacting parameters with little published advice regarding choice of such parameters and because the default values have been chosen to work well under a variety of conditions.⁶

LOD scores were also obtained with deterministic methods for all conditions where such computations were practical. MERLIN version 1.0-alpha⁴² was used to compute multipoint LOD scores for PED14-200, PED14-67d, and PED14-67s and for single-marker analysis of PED14-FGL. VITESSE version 2.0.1⁴³ was used to compute multipoint LOD scores for PED52-3 and PED98-3 and for single-marker analysis of PED52-FGL. VITESSE analysis of PED52 and PED98 with more than three STR markers was not computationally practical, given our goal of performing 100 simulations under each data configuration and analysis. The correct trait model, marker model, and map model were used in the analysis, with the exception of analyses with FGLs, for which a very low allele frequency (0.001) was used for each FGL to approximate unique alleles.

LOD scores were computed at different points along the map, depending on the data configuration and analysis program. For all analyses of PED52 and PED98 with the MCMC-based programs and STR markers, LOD scores were computed at or very close to each marker and at multiple points in each intermarker interval and outside the map, which were chosen to match the fixed conditions used in LOD-score computations by SimWalk2. Analysis of PED52-3 with VITESSE matched that of the MCMC programs in the region spanning the markers. Analysis of PED98-3 with VITESSE was restricted to a single point at the position of the trait locus, because of the excessive required computation time. For analysis of PED14-200 and PED14-67d with lm_markers and MERLIN, LOD scores were computed at the markers and at the midpoint of each interval, whereas, for analysis of PED14-67s, LOD scores were computed at the markers and at four additional equally spaced points between each successive pair of markers. For analyses of these dense markers, we did not try to match the number of points at which LOD scores were computed with the nine points per interval required by SimWalk2, since this would not normally be a reasonable choice for such densely spaced markers. For analyses of FGL data, computations with exact programs were performed only at the position of the trait locus. For MCMC-based analyses only, a small number of points flanking both ends of the map were also computed, because of the standard defaults of the programs; since contribution to the computation time for these flanking points is small, relative to the rest of the analysis for SNPs, this has, at most, a minor effect on the comparison of central-processing-unit (CPU) requirements.

Comparison of LOD Scores

We treated each pedigree replicate as a unit, providing 100 independently and identically distributed replicates for each analysis configuration. For most situations, we computed two single-number summaries to measure accuracy of the MCMC-estimated results. The measure of discrepancy at the position of the trait locus is the absolute error of the estimated LOD score at the trait locus: Δ₁=|LOD_t,M-LOD_t,E|, where LOD_t,M and LOD_t,E are the LOD scores computed at the position of the trait locus, t, with the MCMC (M) and exact (E) approaches, respectively. A measure of the worst-case discrepancy, Δ₂, is the maximum pointwise absolute error, or Δ₂=max|LOD_i,M-LOD_i,E|, where the maximum is taken over all positions, i, for which LOD scores were computed, excluding the marker positions. The marker positions were excluded because both lm_markers and SimWalk2 realize inheritance vectors at marker locations, conditional on only the marker data. At a marker location, therefore, the trait information is likely to be in strong disagreement with the inheritance vector, resulting in high MC variance and poor MCMC LOD-score estimates. We computed only Δ₁ for PED98-3, since we computed exact LOD scores only at the position of the trait locus.

For analysis of PED52-10, we compared MCMC-based results from lm_markers-SI with those from SimWalk2, as an empirical comparison. For this 10-marker data configuration, exact computation was not feasible. For practical reasons of obtaining a summary measure of similarity, we compared the LOD scores computed only at the position of the trait locus.

We also evaluated results obtained with MCMC-based analysis for dense SNPs and PED52-67d. It was computationally impractical to perform extensive simulations for PED98 and SNPs with SimWalk2. For PED52-67d, we compared LOD scores at the position of the trait locus obtained with both lm_markers-SI and SimWalk2 with LOD scores obtained with exact methods for PED52-FGL. To evaluate accuracy of the MCMC-based analyses, using the FGLs as a comparison standard, we computed, at the trait locus, a comparison measure that is similar to Δ₁ but that is based on the LOD score for the FGLs rather than on the LOD score for the 67 markers: Δ₃=|LOD_S-LOD_F|, with subscripts S and F indicating computations performed with SNPs or with FGLs, respectively.

Results

SNPs and PED14: lm_markers Run Conditions

Run length

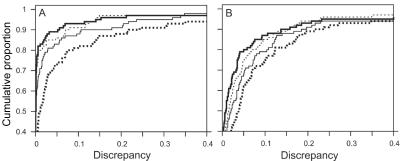
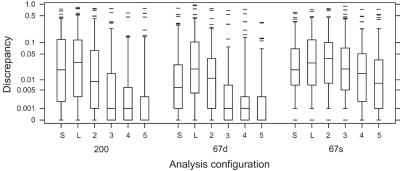
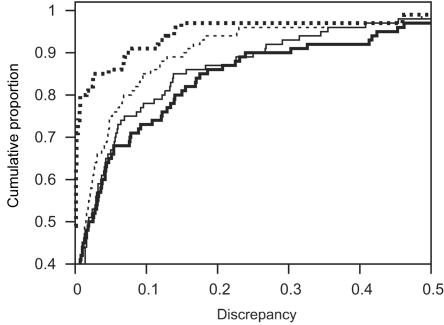
As expected, accuracy of LOD-score estimates improved with the number of scans. Because accuracy was so much higher for lm_markers-SI than with lm_markers-IL (see the “Starting Configuration” subsection), we focus here primarily on the results of lm_markers-SI, although the qualitative results were similar for lm_markers-IL (table 2). Figure 2 shows the cumulative distribution of Δ₁ for both PED14-200 (fig. 2A) and PED14-67s (fig. 2B) obtained with lm_markers-SI and several run lengths: the fraction of PED14-200 data sets for which Δ₁<0.1 increased from 82% to 93% as the number of scans increased from 300 to 300,000, with large gains in accuracy in the increase from 300 to 3,000 scans and smaller gains thereafter. Results for PED14-67s were similar, although the overall accuracy was somewhat lower overall than for the 200-SNP configuration. Results for PED14-67d were similar to the 200-SNP configuration (not shown). Table 2 provides more detail for both Δ₁ and Δ₂ and for the effect of run length on accuracy: depending on the data set, the mean for Δ₁ for 30,000 scans with lm_markers-SI was between one-third and one-half that of runs of 300 scans, with similar gains in accuracy for Δ₂. Figure 3 shows the steady improvement in the distribution of Δ₁ obtained with increasing run lengths with lm_markers-SI, with the improvement manifested in increasingly lower medians, lower upper quartiles, and reduction in the most-extreme points with increasing run length. Figure 3 also shows that, for the two dense-SNP configurations, the median of Δ₁ was ⩽0.001 for runs of ⩾3,000 scans, indicating that at least half the replicates provided extremely accurate results.

Table 2. .

Characteristics of Analyses of PED14 with SNP Markers^[Note]

		Mean Discrepancy Value or Time, by Program and Starting Configuration
		lm_markers-SI Scans				lm_markers-IL Scans
Metric and SNPs	LODa	3×102	3×103	3×104	3×105	3×103	3×104	SimWalk2b	MERLIN
Δ1:
200	.294	.074	.043	.029	.029	.142	.108	.089	NA
67d	.283	.055	.028	.027	.015	.159	.095	.051	NA
67s	.234	.093	.074	.055	.053	.115	.104	.075	NA
Δ2:
200	NA	.379	.293	.212	.185	.573	.484	.508	NA
67d	NA	.216	.115	.082	.067	.417	.310	.220	NA
67s	NA	.345	.288	.188	.196	.429	.323	.299	NA
Timec:
200	NA	.084	.839	8.40	64.9	.615	6.164	683.0	.289
67d	NA	.021	.218	2.19	17.9	.176	1.776	66.42	.072
67s	NA	.031	.306	3.07	26.8	.292	2.919	66.00	.190

Note.— Values are shown as means across 100 replicates. NA = not applicable.

^aMean LOD score obtained at the trait locus with exact computation by MERLIN.

^bDefault setting used.

^cIn CPU min per pedigree on an AMD 1.8-GHz Opteron computer.

Figure  2. .

Cumulative distributions of discrepancy of LOD scores at the trait locus. Discrepancy is measured by Δ₁ and is obtained with lm_markers with the SI startup configuration for PED14-200 (A) and PED14-67s (B), for runs of 300 (heavy dotted line), 3,000 (thin solid line), 30,000 (thin dotted line), and 300,000 (thick solid line) scans. For emphasis of the most important part of the distributions, both the horizontal and vertical scales have been truncated.

Figure  3. .

Discrepancies of LOD scores at the trait locus, measured by Δ₁, computed with lm_markers and SimWalk2 for PED14-200 (200), PED14-67d (67d), and PED14-67s (67s) and shown on a log scale. Discrepancies are shown for runs with SimWalk2 (S), with lm_markers with the IL starting configuration (L) and 30,000 scans, and with lm_markers with the SI starting configuration for 300 (2), 3,000 (3), 30,000 (4), and 300,000 (5) scans. To avoid problems with taking the logarithm of 0, we added 10⁻³ to the discrepancy scores before taking the logarithm.

Starting configuration

The choice of starting configuration had a strong impact on the resulting accuracy of LOD scores obtained with lm_markers. We focus here on dense SNP markers for which the effect was strongest. For the two run lengths evaluated, the results for lm_markers-SI were considerably more accurate for a given run length, as measured by both Δ₁ and Δ₂, than were the equivalent lm_markers-IL runs. In fact, the shortest runs with lm_markers-SI (N=300 scans) were faster and also had median and mean Δ₁ and Δ₂ values that were approximately equal to or better than those obtained with the much longer runs (N=30,000 scans) based on lm_markers-IL (fig. 3 and table 2). Similarly, for the same run length (e.g., N=30,000), the accuracy obtained with lm_markers-SI was much better than that obtained with lm_markers-IL (fig. 3). For the looser scan (PED14-67s), the starting configuration had less effect on accuracy, but there was still an improvement in the accuracy under lm_markers-SI (fig. 3). Similar trends with less dramatic results were also obtained with STR markers (results not shown). The generally poorer performance of lm_markers-IL for the SNP markers led us to perform all other comparisons with only the lm_markers-SI configuration.

SNPs and PED14: lm_markers versus SimWalk2

Computational requirements

The two MCMC-based programs had different computational requirements for analysis of SNPs. Memory requirements were considerably different. Fixed memory allocation made it necessary to rebuild SimWalk2 to enable it to run with up to 200 SNPs within the memory and swap space available to us: with this reduction in the number of SNPs, the program required ∼425 MB of virtual memory and used ∼15 MB of memory for analysis of PED14-200. In contrast, lm_markers uses very little memory, and dynamic-memory allocation prevents the need for tailoring program parameters to a particular project: for PED14-200, lm_markers required ∼2.5 MB of virtual memory and ∼1.5 MB of memory for analysis. Overall computation times were also very different (table 2): for similar accuracy in LOD scores, SimWalk2, running with default settings, required at least 3 orders of magnitude more CPU time than did runs with 3,000 scans with lm_markers-SI. For analysis of the small PED14 pedigree, both programs required more CPU time than did exact computation, although lm_markers-SI provided reasonable results with 3,000 scans, with only 1.5–3× as much computation time as MERLIN required. In contrast, SimWalk2 required between ∼250 and ∼2,400× as much computation time. There were also differences in the relative time needed for analysis of different data configurations, although, in both cases, run length was essentially constant over replicates, within a specified set of run conditions. Computation time with lm_markers was linear in the number of scans and was approximately proportional to the number of markers, given a specified number of MCMC scans (table 2). In contrast, although computation time with SimWalk2 was also independent of marker density for the two different 67-SNP data sets, computation time increased faster than linearly with larger data sets, with analysis of 200 SNPs requiring >10× as much CPU time as analysis of 67 SNPs.

Accuracy

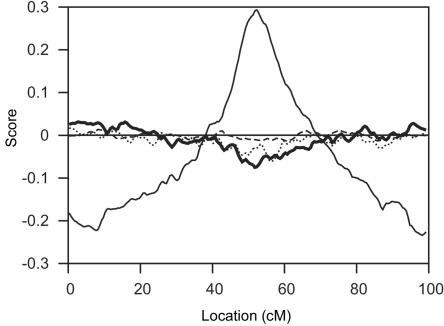
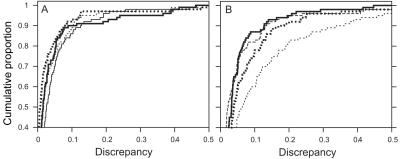
LOD scores produced by SimWalk2 were less accurate than those obtained with lm_markers-SI for most run lengths. Table 2 and figure 3 show that values for Δ₁ and Δ₂ that were obtained with SimWalk2 were less accurate than values obtained with only 300–3,000 scans for PED14 analyzed with lm_markers-SI. SimWalk2 gave slightly more-accurate results than those obtained with lm_markers-IL and N=30,000 scans for all three configurations, as measured by Δ₁, and for the two 67-SNP configurations, as measured by Δ₂. Use of 30,000 scans with lm_markers-IL yielded accuracy that was similar to that obtained by SimWalk2, but both conditions gave markedly less accurate results than did use of lm_markers-SI run for 30,000 scans (fig. 4). Figure 5 shows the cumulative distributions of Δ₁ for runs with SimWalk2 and lm_markers-SI with 30,000 scans, showing that ∼91% of PED14-200 data sets yielded Δ₁<0.1 for lm_markers-SI, compared with only 73% from SimWalk2. The difference in accuracy was less extreme, although still evident, for analysis of PED14-67s: Δ₁<0.1 for lm_markers-SI and for SimWalk2 85% and 78% of the time, respectively. Other comparisons yield similar conclusions (fig. 3).

Figure  4. .

LOD scores obtained for PED14-200. Mean LOD scores are shown across 100 replicates, obtained by exact computation with MERLIN (thin solid line). Remaining lines show mean differences between MCMC-based LOD scores and exact LOD scores for lm_markers with SI startup and 30,000 scans (dashed line), lm_markers with IL startup and 30,000 scans (thick solid line), and SimWalk2 (dotted line). The horizontal line represents no difference.

Figure  5. .

Cumulative distributions of discrepancy measured by Δ₁ for PED14-200 (thick lines) and PED14-67s (thin lines) with lm_markers and 30,000 scans (dotted lines) and SimWalk2 (solid lines). For emphasis of the most important part of the distributions, both the horizontal and vertical scales have been truncated.

Density and number of markers

The two MCMC-based programs showed different sensitivities to number and density of SNP markers in analysis of PED14. For data sets with the same number of SNPs, both programs showed reduced accuracy in the analysis of sparse (PED14-67s) compared with dense (PED14-67d) SNPs. The two MCMC programs differed in their relative accuracies in analysis of dense SNPs when the difference was the total number of markers (PED14-200 vs. PED14-67d), with the larger number of SNPs having an adverse effect on the accuracy of results obtained from SimWalk2. Median accuracy obtained with lm_markers-SI for a given number of scans was essentially independent of the number of SNPs in the analysis, whereas the median accuracy with SimWalk2 for analysis of PED14-67d was higher than that for PED14-200 (fig. 3).

Large-Pedigree Analyses: STR Markers

Analysis of PED52-3 was accurate and computationally fast with both SimWalk2 and lm_markers-SI (fig. 6A and table 3). The mean discrepancy at the trait locus of Δ₁=0.049 for SimWalk2 was only slightly higher than that of the 30,000-scan run with lm_markers (Δ₁=0.042), with the maximum discrepancy across the map of Δ₂=0.077 for SimWalk2 also only slightly higher than that for lm_markers for this same run length (Δ₂=0.061). Accuracy of the shorter lm_markers runs was only modestly lower than accuracy of the longest runs, with short runs of only 3,000 scans still providing mean Δ₁ that was ∼10% of the mean LOD score of 0.5, computed with exact methods. The CPU time for analysis was very similar and modest across programs: 2.078, 2.529, and 2.23 min for SimWalk2, VITESSE, and lm_markers, respectively, run with 30,000 scans.

Figure  6. .

Cumulative distributions of discrepancy measured by Δ₁ for analysis of three markers on PED52 (A) and PED98 (B). Thick solid line represents SimWalk2, thin solid line represents lm_markers and 3,000 scans (A only), thin dotted line represents lm_markers and 30,000 scans, thick dotted line represents lm_markers and 300,000 scans, and dashed line represents lm_markers and 3,000,000 scans (B only). For emphasis of the most important part of the distributions, both the horizontal and vertical scales have been truncated.

Table 3. .

Characteristics of Analyses with Large Pedigrees^[Note]

	Mean Discrepancy Value or Time,by Program and Starting Configuration
	lm_markers-SI Scans
Data Set (LODa) and Metric	3×103	3×104	3×105	3×106	SimWalk2	VITESSEb
PED52-3 (.500):
Δ1	.052	.042	.034	ND	.049	NA
Δ2	.080	.061	.050	ND	.077	NA
Timec	.255	2.529	23.43	ND	2.078	2.23
PED52R-3 (.403):
Δ1	ND	.055	ND	ND	.037	NA
Time	ND	2.774	ND	ND	1.902	227
PED52-10 (ND):
Time	ND	5.71	ND	ND	14.13	ND
PED52-67d (.788d):
Δ3	ND	.153	ND	ND	.493	ND
Time	ND	11.57	ND	ND	694.4	ND
PED98-3 (.989):
Δ1	.171	.132	.077	.058	.053	NA
Time	.818	8.070	72.64	716.1	5.203	4,836e
PED98A-3 (1.148):
Δ1	ND	.080	ND	ND	.063	NA
Time	ND	7.474	ND	ND	5.533	811e

Note.— Values are shown as means across 100 replicates. ND = not done.

^aMean LOD score computed by VITESSE at the trait locus with exact methods.

^bNA = not applicable.

^cIn CPU min per pedigree on an AMD 1.8-GHz Opteron computer.

^dExact LOD score obtained from exact single-marker analysis of the FGLs.

^eTime extrapolated to that required for analysis of the same number of points used by the other programs, including external positions outside the marker map.

There were greater differences in the results obtained for PED98-3 with SimWalk2 compared with lm_markers-SI (fig. 6B and table 3). For this data configuration, SimWalk2 gave more-accurate results with shorter computation times than lm_markers. For lm_markers, there was a greater loss in accuracy, resulting from the use of shorter runs, than was observed for PED52-3. For a given number of scans with lm_markers, the increased CPU requirement for PED98-3 compared with PED52-3 was similar (2.91–2.99-fold time difference, depending on the number of scans) to that for SimWalk2 (2.74-fold). However, the achievement of accuracy comparable to that obtained with SimWalk2 required 3×10⁶ scans for PED98-3, with a corresponding increase in required CPU time.

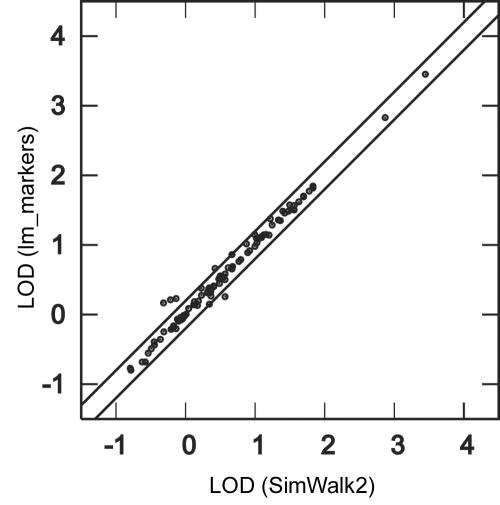
LOD scores obtained with SimWalk2 and lm_markers-SI for analysis of 10 STR markers on PED52 were similar (fig. 7), which is what would be expected if both programs gave accurate results, although, for the 10-marker comparison, exact computation for comparison was not computationally feasible. The correlation over data replicates in LOD scores at the trait locus was 0.99 between the two programs, and the mean absolute difference between results for the two programs was only 0.051, or <10% of the mean LOD score of 0.57 across all replicates obtained by lm_markers-SI. Results were similar for the maximum LOD score obtained anywhere on the chromosome (not shown). Similar to results obtained for PED14 analyzed with the two different numbers of SNPs (table 2), computational requirements increased faster with the number of markers for SimWalk2 than for lm_markers (table 3).

Figure  7. .

LOD scores computed for PED52 analyzed with 10 STR markers (PED52-10) obtained from 100 data sets with SimWalk2 and with lm_markers, with use of 30,000 scans. Lines indicate differences of 0.2 from the diagonal. See table 3 for mean run times.

The effect of changes to the missing-data patterns differed between the two programs. SimWalk2 gave more-accurate results with increasing amounts of missing data, as measured by lower values of Δ₁, for analyses performed on PED52_R-3 compared with PED52-3 and for analyses performed on PED98-3 compared with PED98_A-3 (table 3). The opposite result was obtained for lm_markers, which was more accurate in the presence of more data constraints, with Δ₁ increasing with increasing amounts of missing data for both data sets (table 3).

Large-Pedigree Analyses: SNPs

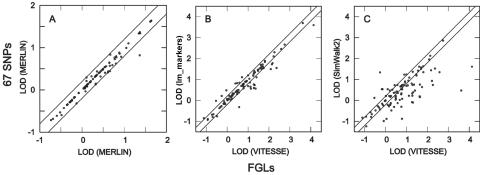
FGLs and dense SNPs gave highly similar results in exact computation, when exact computation was possible for both cases. In the case of PED14-67d versus PED14-FGL, there was a strong correlation, of 0.99, between LOD scores at the trait locus, with a difference >0.2 for the two LOD scores obtained in only 1 of 100 replicates (fig. 8A). The mean (±SD) discrepancy, Δ₃, relative to use of the FGLs was 0.04 (±0.078). This demonstrates that use of the FGLs provides a reasonable standard of comparison in situations where exact computation with SNPs is not possible, and it encourages the use of FGLs to evaluate use of SNPs on large pedigrees, where exact results cannot be obtained for comparison.

Figure  8. .

LOD scores obtained with FGLs with use of an exact analysis (horizontal axes) or with 67 SNPs (vertical axes). A, Exact analysis with MERLIN of both 67d SNPs and single-marker analysis of FGLs on PED14. B, PED52-67d analyzed with lm_markers versus PED52-FGL analyzed with VITESSE. C, PED52-67d analyzed with SimWalk2 versus PED52-FGL analyzed with VITESSE. Lines indicate differences of 0.2 from the diagonal.

Analysis of PED52-67d with lm_markers-SI gave accurate results in a reasonable amount of computation time, as measured against exact results for PED52-FGL. A strong correlation of 0.96 was obtained between LOD scores obtained with exact computation with FGLs and those obtained with MCMC computation with dense SNPs (fig. 8B). The overall mean LOD score for PED52-67d analyzed with lm_markers and 30,000 scans was 0.724, which is only slightly less than the mean of 0.788 for PED52-FGL analyzed with VITESSE. The discrepancy in LOD scores at the trait locus, Δ₃, had a mean of 0.15 (±0.21). Finally, computation time was not onerous, requiring a mean of 11.57 CPU min/pedigree for 30,000 scans (table 3).

In contrast, SimWalk2 gave considerably lower accuracy for the dense SNPs and required considerably more computation time than did lm_markers-SI. For SimWalk2, the correlation in LOD scores obtained with exact versus stochastic computation in LOD scores was only 0.73. The overall mean LOD score of 0.429 for PED52-67d was considerably lower than the score of 0.788 obtained with exact computation for PED52-FGL, and the discrepancy—Δ₃=0.493 (±0.65)—was considerably larger than that for lm_markers. In addition, computational requirements for SimWalk2 were considerable, requiring ∼60× more CPU time than the 30,000-scan runs with lm_markers (table 3). Finally, relative to results for lm_markers, many more points fell outside the 0.2-LOD window around equality of the two approaches, with the discrepancies of these points considerably higher than that obtained with lm_markers (fig. 8B and 8C).

Discussion

Here, we have presented an evaluation and comparison of two MCMC-based programs, SimWalk2 and lm_markers, for use in linkage analysis based on SNP or STR markers. To the best of our knowledge, this is the first systematic comparison of such MCMC-based programs that evaluates performance under a variety of pedigree sizes, missing-data patterns, and marker types that typify the range of data available to many real studies. Our results identify both similarities and differences in the operating characteristics of these two programs. Both performed well for multipoint analysis of STR markers spaced at densities that are typical of a genome scan: in both cases, LOD scores were accurately estimated under a range of pedigree sizes and missing-data configurations with relatively modest computational requirements, even for full-chromosome analyses. In contrast, for dense SNPs, only lm_markers provided results that were both sufficiently accurate and computationally practical to provide useful analysis with current genome-scan panels of SNP markers. One general conclusion that can be derived is that accuracy of results from lm_markers is positively affected by increasing data constraints produced by both increasing marker density and data availability, whereas accuracy of results from SimWalk2 is negatively influenced by these same conditions. Finally, our results lead to suggestions for guidelines for the use of MCMC-based analysis programs in genome-scan linkage analyses.

Differences in the performance of the two MCMC-based programs for analysis of STR markers were relatively minor. For small numbers of markers and midsized pedigrees, measures of both accuracy and computation time were essentially identical for the two programs, whereas, for the largest pedigree analyzed, SimWalk2 achieved accurate results faster than did lm_markers for the small number of markers tested. However, the relative computation time needed for the two programs changes with increasing numbers of markers. Since most chromosomes contain >10 STR markers, the time needed to perform a first-pass genome scan will generally be less for lm_markers than for SimWalk2 on pedigrees similar to those analyzed here. However, since both programs perform computations relatively rapidly, even for fairly large pedigrees, the total time needed to perform a genome scan with STR markers is unlikely to provide a significant bottleneck for either program.

The accurate results obtained with STR markers for both programs suggests an approach for validating the strongest linkage signals in a MCMC-based genome scan. A persistent challenge for MCMC-based analyses has been to determine whether a particular result is reliable when a gold-standard result is unobtainable, as would normally be the case when a MCMC-based approach is used for real data analysis. The reliability of results obtained with both programs for STR markers suggests that, in this context, use of SimWalk2 to check the results of lm_markers or the reverse provides a useful check, with agreement between results providing additional confidence in accuracy of the results. Also, since such checks would presumably be limited to a small number of regions of high interest, the computational overhead needed would be relatively minimal. This approach of comparing results from the two programs may be extended to additional situations for which accuracy of these methods has not yet been thoroughly investigated. One such possibility is use on complex pedigrees, for which evaluation of performance is a topic of future investigation.

Demonstration that accurate LOD scores can now be obtained with lm_markers for dense SNPs on large pedigrees is important. The difficulty of performing multipoint computations has, until now, prevented widespread use of SNPs for analysis of large pedigrees, but the results here show that analysis of such markers is now feasible with the MORGAN package. The accuracy of results obtained for SNPs is likely to result from two features of this package: (1) the use of an MCMC sampler for the inheritance indicators that combines²⁹ the advantages of both a locus²² and a meiosis sampler²⁴ and (2) recent implementation of an SI procedure to obtain a good starting configuration, which, as we showed here, provides significant advantages over the starting configuration used earlier.²⁷ Even though these improvements now make it possible to perform analyses with large numbers of SNPs, approaches for modeling LD are as yet unavailable in the context of MCMC-based linkage analysis.

Effective use of current MCMC programs with dense SNP marker panels will require some care. Until modifications can be made to these programs to incorporate information about LD, preprocessing of markers will be needed to eliminate markers with strong evidence of LD to avoid inflated evidence of linkage, as has already become commonplace for analysis of smaller pedigrees.^44–46 For linkage detection, as well as for initial fine mapping, such thinning of markers may be all that is needed for MCMC as well as standard approaches, since, beyond the use of a density that captures the most information about the inheritance vector, there is little advantage in using markers that are more densely spaced than the recombinant events that are being captured, with such events rarely found even at 1-cM resolution in typical data sets.⁴⁷ Past investigation also suggests that thinning SNPs to 1 per cM has no measurable effect on the results obtained.⁴ Such thinning also reduces computational time, since adding markers incurs increased computational time. Nevertheless, there will almost certainly be situations for which marker thinning is not desired. It may be possible in the future to incorporate into the MCMC programs a haplotype model similar to that used by MERLIN,⁴² or haplotype-inference approaches,^48–51 to deal with the LD for such densely spaced markers.

Analysis of SNPs with MCMC-based programs introduces the challenge of determining necessary run-time conditions, since conditions needed for reliable results vary among data sets. SimWalk2 has a default that has been tuned to provide reliable results for STR markers, but our simulation studies here suggest that the current defaults are not adequate for use with the large numbers of dense SNPs that are needed for analyses associated with a genome scan. The MORGAN package uses a different philosophy and expects the user to provide run-time parameters. To address these issues, two observations suggest that it may be possible to use a simulation-based approach to determine the analysis conditions before performing a genome scan with lm_markers: first, computation time for a particular set of analysis conditions and amount of data is essentially constant, and, second, use of FGLs provides a reasonable measure against which accuracy with dense SNPs can be estimated. Thus, it should be possible to simulate multiple data sets consisting of SNPs and the FGLs at a trait locus, with use of a single-trait model and one example of each of the pedigree structures and missing-data patterns to be used in the analysis. This simulation could be followed by a single-locus analysis of the FGLs to provide a standard for comparison with MCMC analysis of each of the SNP-based simulated data sets. The average accuracy of each of those sets of run-time conditions could then be used to establish the necessary conditions for a genome scan.

Future work to further improve MCMC analysis of both SNP and STR marker data is still needed. One issue identified as part of the current study is that of the method of selecting a starting configuration of underlying genotypes or inheritance indicators, which influences the accuracy of the results in the presence of a fixed amount of computer time. Of course, a long run would compensate for a poor starting configuration, and, not surprisingly, we found that the accuracy of runs improved with run length, regardless of the starting configuration. However, because real-data analysis requires computationally practical decisions, in many cases, a long run that is sufficient to overcome a poor starting configuration may not be practical, especially for large data sets. Thus, it may be useful to continue to evaluate additional procedures that might lead to rapid identification of good starting configurations. Finally, although we focused here on LOD-score analysis with a discrete trait, both programs compute other linkage statistics; for example, as illustrated elsewhere,^15,16 lm_markers can easily perform analyses with quantitative trait models, and other programs in the MORGAN package provide additional linkage statistics, as well as additional trait models for LOD-score linkage analysis.²¹