Abstract
The modest correlation between mRNA expression and protein abundance in large-scale data sets is explained in part by experimental challenges, such as technological limitations, and in part by fundamental biological factors in the transcription and translation processes. Among various factors affecting the mRNA–protein correlation, the roles of biological factors related to translation are poorly understood. In this study, using experimental mRNA expression and protein abundance data collected from Desulfovibrio vulgaris by DNA microarray and liquid chromatography coupled with tandem mass spectrometry (LC–MS/MS) proteomic analysis, we quantitatively examined the effects of several translational-efficiency-related sequence features on mRNA–protein correlation. Three classes of sequence features were investigated according to different translational stages: (i) initiation, Shine–Dalgarno sequences, start codon identity, and start codon context; (ii) elongation, codon usage and amino acid usage; and (iii) termination, stop codon identity and stop codon context. Surprisingly, although it is widely accepted that translation initiation is the rate-limiting step for translation, our results showed that the mRNA–protein correlation was affected the most by the features at elongation stages, i.e., codon usage and amino acid composition (5.3–15.7% and 5.8–11.9% of the total variation of mRNA–protein correlation, respectively), followed by stop codon context and the Shine–Dalgarno sequence (3.7–5.1% and 1.9–3.8%, respectively). Taken together, all sequence features contributed to 15.2–26.2% of the total variation of mRNA–protein correlation. This study provides the first comprehensive quantitative analysis of the mRNA–protein correlation in bacterial D. vulgaris and adds new insights into the relative importance of various sequence features in prokaryotic protein translation.
HIGH-THROUGHPUT postgenomic technologies such as microarray and proteomics analyses have provided powerful methodologies to study patterns of gene expression and regulation at the genome scale (Horak and Snyder 2002; Smith et al. 2002). Given the fact that no single approach can fully unravel the fundamental biology that is typically quite complex, an integrative approach of multiple levels of information is necessary and valuable to fully elucidate the complex biological system being studied. In several recent studies, integrative analyses of transcriptomic and translatomic data have helped researchers better understand the global regulatory processes and complex metabolic networks in living organisms (Gygi et al. 1999; Greenbaum et al. 2002, 2003; Hegde 2003; Mootha et al. 2003a,b; Alter and Golub 2004).
Early large-scale analyses of mRNA expression and protein abundance data showed that the correlation between mRNA and protein abundance was typically weak (Futcher et al. 1999; Gygi et al. 1999; Ideker et al. 2001; Greenbaum et al. 2003; Washburn et al. 2003). It has been proposed that three potential reasons for the lack of a strong correlation between mRNA and protein expression levels are: (i) translational regulation, (ii) differences in protein in vivo half-lives, and (iii) the significant amount of experimental error, including differences with respect to the experimental conditions (Greenbaum et al. 2003; Beyer et al. 2004). We recently performed a quantitative analysis of the contributions of various biochemical and physical sources to the correlation of mRNA and protein abundance in Desulfovibrio vulgaris. The results showed that analytic variations in mRNA expression and protein abundance contributed to 34–44% of the total variation of mRNA–protein correlation, and protein and mRNA stabilities contributed to 5 and 2% of the total variation of mRNA–protein correlation, respectively (Nie et al. 2006a). However, since more than half of the variation remains unexplained, quantitative investigation of other factors, such as sequence features related to regulation at the translational level, will be important for further understanding of the mRNA–protein correlation.
Efficiency of protein biosynthesis depends on many factors. First, initial anchoring of ribosomes onto the mRNA depends on complementary binding of the Shine–Dalgarno (SD) sequence ∼10 bases upstream of the start codon (Shine and Dalgarno 1974) and a sequence close to the 3′ end of the 16S rRNA in the 30S ribosomal subunit (McCarthy and Brimacombe 1994; Stenstrom et al. 2001). In this process, the short SD sequence motif serves as the ribosomal binding site (RBS). The ribosomal binding to this purine-rich SD region is of prime importance to locate the ribosome at the proper initiation codon (Stenstrom et al. 2001). The strength of this interaction has been used to estimate the efficiency of translation initiation (Schurr et al. 1993; Osada et al. 1999) or to predict the actual start sites (Suzek et al. 2001). Second, nonrandom use of synonymous codons in the coding region of highly expressed Escherichia coli genes indicates that sequences further downstream of the start codon could be of importance for translation efficiency (Faxen et al. 1991; McCarthy and Brimacombe 1994; Collins et al. 1995). A difference in translation rate in the order of 6-fold was found when infrequent and common codons were compared (Sorensen et al. 1989). The 12 codons could impose a 15-fold difference in gene expression in studies using a lacZ-based fusion system preceded by a canonical Shine–Dalgarno sequence (Looman et al. 1987; Stenstrom et al. 2001). Third, translation efficiency also depends on the availability of various amino acids. Among 20 amino acids, costs of synthesis vary from 12 to 74 high-energy phosphate bonds per molecule (Akashi and Gojobori 2002). The selective advantage of using a cost-efficient amino acid in a highly expressed protein can be great. The evidence of natural selection of amino acid usage to enhance metabolic efficiency has been found in the proteomes of E. coli and Bacillus subtilis (Akashi and Gojobori 2002). Fourth, translation termination depends upon the attachment of a release factor (RF) in the place of a tRNA in the ribosomal complex (Rocha et al. 1999; Kisselev et al. 2003). While release factors might exhibit different recognition efficiency to different stop codons, the pattern of stop codon usage changes more considerably than the start among prokaryotes (Poole et al. 1995; Rocha et al. 1999; Ozawa et al. 2002). In addition, the use of the stop codon was found to be correlated significantly with the G + C content of the genome, e.g., negatively for TAA and positively for TGA in B. subtilis (Rocha et al. 1999). Moreover, cases have been reported in which the trinucleotides (stop codons) are not sufficient to terminate translation effectively (Tate et al. 1995, 1996). Studies showed that nucleotide distribution around the stop codons, especially the base following the stop codon, is significantly biased and is related to translation termination efficiency (Brown et al. 1990; Cavener and Ray 1991; Poole et al. 1995, 1997; Tate et al. 1996).
D. vulgaris belongs to a group of obligate anaerobic microorganisms, sulfate-reducing bacteria (SRB) (Voordouw 1996). Research interest in the SRB has been due to their corrosion of pipes and their ability to precipitate heavy metals (e.g., Cr6+, Fe3+, and U6+) and radionuclides (e.g., U6+) from solution via bacterial metal reduction (Heidelberg et al. 2004). The genome of D. vulgaris was recently finished (Heidelberg et al. 2004). Our group has been using a whole-genome microarray and liquid chromatography coupled with tandem mass spectrometry (LC–MS/MS) to investigate gene expression and protein abundance in D. vulgaris under various growth conditions (Zhang et al. 2006a,b,c,d). Taking advantage of these experimental data, we attempted to determine the relative effects of various sequence features related to translational efficiency on mRNA–protein correlation in D. vulgaris in a single unified framework with a multiple-regression approach. Sequence features considered in this study can be categorized into three classes with regard to the three stages of protein translation: (1) translation initiation, Shine–Dalgarno sequences, start codon identity, and start codon context; (2) translation elongation, codon usage and amino acid usage; and (3) translation termination, stop codon identity and stop codon context. The results provided the first systematic quantitative analysis of the effects of translational efficiency-related sequence features on the mRNA–protein correlation and will help improve the understanding of mRNA–protein correlation, as well as regulation of gene expression at the translational level.
METHODS
Data sets:
Three transcriptomic and translatomic data sets used for model construction and verification were collected from D. vulgaris DSM 644 grown on lactate- or formate-based chemically defined media. To minimize experimental variations between microarray and proteomic measurements, for each growth condition, identical cell samples were used as starting materials to isolate RNA and proteins for analyses. The complete description of experimental design and cultivation conditions can be found in our previous study (Zhang et al. 2006a).
Microarray data: An oligonucleotide microarray was used to obtain gene expression data (Zhang et al. 2006a). To minimize variations between microarray measurements, for each growth condition, at least two replicate cell samples were used as starting materials to isolate RNA for analyses. In addition, each replicate sample used for RNA profiling was a pool of three individual biological replicates. Microarrays containing 3548 ORFs of D. vulgaris were designed by NimbleGen System (Madison, WI), using its maskless array synthesizer (MAS) technology (Nuwaysir et al. 2002; Heidelberg et al. 2004). Arrays were designed with JazzSuite software and the MAS units were used to manufacture the custom arrays. For each ORF, 13 unique 24-mer oligonucleotides from throughout the ORF were printed onto glass microscope slides (Nuwaysir et al. 2002). The complete description of data acquisition and analysis can be found in our previous study (Zhang et al. 2006a).
Proteomics data: The D. vulgaris samples were analyzed by LC–MS/MS on a Finnigan model LTQ ion trap mass spectrometer (ThermoQuest, San Jose, CA). Mass spectrometry (MS) analysis was performed using a Finnigan model LTQ ion trap (ThermoQuest) with electrospray ionization (ESI) (Zhang et al. 2006c). Peptide identification was performed using SEQUEST Version 2.7 (ThermoQuest) (Eng et al. 1994; Yates et al. 1995) to search the D. vulgaris protein sequence database (Heidelberg et al. 2004). The relative protein abundance was estimated on the basis of the number of peptide hits (Gao et al 2003; Qian et al 2005). The peptide hits for a given protein were the average of three LC–MS/MS measurements. The complete description of proteomic data acquisition and analysis can be found in our previous study (Zhang et al. 2006c,d). In this study, to further remove the possible systematic errors caused by gene length and amino acid composition, we normalized the peptide hit by dividing it with a correction factor: “effective number of peptides.” The effective number of peptides is derived as follows: (i) First, we used the “PeptideCutter” program (http://ca.expasy.org/tools/peptidecutter/) to analyze every protein in the D. vulgaris genome and determined the possible cleavage sites by trypsin; (ii) second, we wrote a perl script to determine the number of peptides of all sizes after trypsin cleavage (the perl script is available upon request); and (iii) finally, we added up the number of peptides of length 7–25 amino acids as the effective number of peptides because the mass (m/z) detection range can pick up peptides only of this size range (Zhang et al. 2006c,d). The normalized peptide hits were then used as the protein abundance for all statistical analyses performed in this study.
In addition, to exclude the possibility that sequence features are surrogate measures of mRNA levels when there was a correlation between sequence features and measurement errors of mRNA, a regression model was trained to predict the mRNA abundance in one replicate with that in other replicates plus sequence features. We gradually lowered the threshold (fold of change) in the training sets of replicates until sequence features no longer contributed to the prediction. Thus the sequence features were completely independent of mRNA abundance of genes used in the following statistical analysis. The threshold values were determined as 3.5, 4.2, and 4.3 (fold change among replicates) for lactate-exponential (LE), formate-exponential (FE), and lactate-stationary (LS) conditions, respectively. Using this method, 349, 395, and 357 genes/proteins that satisfy the quality control criteria for LE, FE, and LS conditions, respectively, were used in the following multiple-regression analyses.
Quality of microarray and proteomic data and their correlation:
The quality of the microarray data was evaluated with the Pearson correlation coefficient analysis among multiple measurements. Pearson correlation coefficients of the microarray experiments are from 0.97 to 0.99 among replicate samples (Nie et al. 2006a), and Pearson correlation coefficients of LC–MS/MS measurements normalized by amino acid composition are >0.86–0.92 among replicates, indicating good reproducibility. Correlation of mRNA expression and normalized protein abundance of cells grown was modest, of ∼0.54–0.63 (P-value <0.001) by Pearson correlation coefficient for all conditions. The correlation levels were close to that previously reported for yeast (Ideker et al. 2001).
Cellular functional category:
The cellular functional categories of all genes in the D. vulgaris genome are downloaded from the comprehensive microbial resource (CMR) of TIGR (http://cmr.tigr.org) (Heidelberg et al. 2004). On the basis of the original annotation, the genes/proteins are classified into 19 cellular functional categories.
Identification and analysis of Shine–Dalgarno sequences:
Two different methods were used to identify the SD sequences in D. vulgaris genes:
Free energy-based method (Schurr et al. 1993; Osada et al. 1999): This method aligned the 3′ end of 16S rRNA and 5′-UTR of an mRNA and then used a dynamic programming algorithm to find the minimum free energy of a window of specific size (Osada et al. 1999). Initially, we performed an analysis similar to what was described by Osada et al. (1999), where the base-pairing potentials between the 3′ tail of 16S rRNA and 5′-UTR of all genes were calculated and averaged by positions to view the overall trend in the whole genome. Sequences cctgcggctggatcacctccttt and cctgcggttggatcacctcctta from the 3′ end of 16S rRNA were used in D. vulgaris (NC_002937 and NC_005863) (Heidelberg et al. 2004) and E. coli (U00096) to calculate the free energy values in these two species, respectively. The C programs used to perform the calculation were kindly provided by Y. Osada of the Institute for Advanced Biosciences of Keio University. To determine the effects of SD sequence during protein translation, we calculated the free energy for base pairing of 16S rRNA with SD sequence for each gene. To do this, we extracted the 25-base and 50-base nucleotide sequence immediately upstream of the start codon of each gene. Each extracted sequence was aligned with the 3′ tail of 16S rRNA to compute the minimal free energy (MFE) with the Java Applet at http://www.mag.keio.ac.jp/%7Ersaito/Research/BasePAP/BasePAP.html (implemented by Y. Osada. A modified JAVA code to batch calculate MFE is available upon request). Since it is possible that various lengths of 16S rRNA tails used in the calculation might affect the accuracy of the MFE values, three lengths (13, 20, and 23) were used, which corresponded to sequences gatcacctccttt, gcggctggatcacctccttt, and cctgcggctggatcacctccttt, respectively.
Probabilistic method (Suzek et al. 2001): This method used a “seed” sequence to train a probabilistic model of SD sequences, which was then used to find the SD sequences in regions upstream of start codons of all genes. A good seed sequence is the 3′ end of the 16S rRNA (Suzek et al. 2001). Five copies of 16S rRNA genes have an identical 3′ tail in D. vulgaris (notably the annotated sequences were incomplete and missing the sequence ctggatcacctccttt at the 3′ end; however, this sequence does exist in all five copies of D. vulgaris 16S rRNA genes). Interestingly, although D. vulgaris is a GC-rich species, the sequence of the 16S rRNA 3′ tail is highly similar to that of most other prokaryotes (compared with other species described by Ma et al. 2002) and it contains the typical anti-SD sequence ctcct, which complements with the default seed sequence aggag used in the RBSFinder program (downloaded at ftp://ftp.tigr.org/pub/software/RBSfinder/). Two window sizes, 25 and 50, were used to search for SD sequences. The RBSFinder code was slightly modified to output the maximal RBS score (the modified perl code is available upon request).
Start codon, stop codon, and their contexts:
The identity of each start codon and stop codon was treated as a categorical variable during multiple-regression analysis. The start codon context was defined as the upstream 30 bases and downstream 9 codons of the start codon. Therefore, each sequence of start codon context is 60 bases long, including the start codon. To evaluate the potential of each start codon context to form a stable mRNA secondary structure, the minimum free energy of this region was computed with the Vienna package RNAfold (Hofacker 2003; Hofacker and Stadler 2006). The stop codon and the base immediately downstream of the stop codon were regarded as the stop codon context. Each combination was treated as a categorical variable in multiple-regression analysis described below.
Analyses of the overall codon usage and amino acid usage:
The major trends in codon usage and amino acid usage were revealed with a correspondence analysis. The relative synonymous codon usage (RSCU) was used in the correspondence analysis to remove the effects of amino acid usage. For amino acid usage, the raw codon counts were added up for each amino acid and used as input in the correspondence analysis. The CodonW software (http://codonw.sourceforge.net) was used for the correspondence analysis, generating four major axes accounting for most of the variations in codon usage or amino acid usage of D. vulgaris genes or proteins, respectively (Wu et al. 2006).
Analyses of the preferences in codons and amino acids:
D. vulgaris is a GC-rich species (GC, 64%; GC3, 77%) (Heidelberg et al. 2004). Therefore, the unequal usage of amino acids or synonymous codons can be simply a result of mutational bias (Knight et al. 2001). To examine the preferences for certain codons or amino acids, we used the “percentage of differences” (POD) to indicate the preferences (positive values) and avoidance (negative values), which takes the mutational bias into account. The POD is defined as
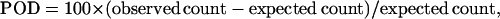 |
(1) |
where observed count is the actual number of each codon or amino acid in a set of genes, and expected count is the expected number of that codon or amino acid when codon usage and amino acid usage are solely results of base composition due to mutational bias. The base composition was estimated with the frequency of each base at the third codon position with the whole-genome data because this position is the most neutral (Sueoka 1988). The absolute expected frequency of each codon is calculated as the product of the mutational bias of each base that composes the codon. The relative expected frequency of each codon equals the absolute expected frequency of this codon divided by the sum of absolute expected frequencies of all codons in the same codon family, which contains all synonymous codons coding for the same amino acid. As a result, the relative expected frequency of codon ATG is 1 because there is only one codon coding for methionine. The same thing happens to codon TTG. Finally, the expected number of a codon equals the product of its relative expected frequency and the observed total number of codons of its codon family.
Preferences in amino acid usage were measured in a similar way. For a particular amino acid, the observed number is the sum of the number of codons coding for it. Its absolute expected frequency is the sum of the absolute expected frequency of its coding codons. Its relative expected frequency equals its absolute expected frequency divided by the sum of absolute expected frequencies of all amino acids (essentially 61 codons, because 3 termination codons were excluded). Finally, the expected count of this amino acid is the product of its relative expected frequency and the total number of amino acids observed in a set of genes.
The significance of the POD was evaluated with the following method: The observed count for a particular codon was assumed to follow a binomial distribution 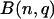 , in which n is the total number of codons in its codon family, and q is the relative expected frequency of the codon within its synonymous codon family. The significance is based on testing whether the observed relative frequency equals the expected relative frequency of this codon in its synonymous codon family. Since the number n is a large number here, a normal approximation has been used to approximate the binomial distribution (Ott and Longnecker 2001; Devore and Farnum 2005). Because multiple tests were involved, a Bonferroni procedure has been implemented to adjust the P-values obtained from multiple tests (Ott and Longnecker 2001). For an amino acid, P-values were computed in a similar way to test whether an amino acid count follows the distribution
, in which n is the total number of codons in its codon family, and q is the relative expected frequency of the codon within its synonymous codon family. The significance is based on testing whether the observed relative frequency equals the expected relative frequency of this codon in its synonymous codon family. Since the number n is a large number here, a normal approximation has been used to approximate the binomial distribution (Ott and Longnecker 2001; Devore and Farnum 2005). Because multiple tests were involved, a Bonferroni procedure has been implemented to adjust the P-values obtained from multiple tests (Ott and Longnecker 2001). For an amino acid, P-values were computed in a similar way to test whether an amino acid count follows the distribution 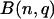 , where n is the total number of amino acids and q equals the relative expected frequency of this amino acid.
, where n is the total number of amino acids and q equals the relative expected frequency of this amino acid.
Correlation and regression:
Correlation coefficients, such as Pearson's correlation coefficient and Spearman's rank correlation coefficient, were computed (Devore and Farnum 2005). Furthermore, single-regression and multiple-regression analyses were performed to measure the correlation pattern between mRNA and protein abundance as described before (Ott and Longnecker 2001; Nie et al. 2006a). To obtain a reliable correlation between mRNA and protein abundance, only proteins with variations among measurement replicates less than threefold were included. Fold change in original scale is equivalent to the arithmetic difference in the log scale, also called range of samples (Montgomery 2001). For instance, max( )/min(
)/min(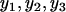 ) = 3 is equivalent to log[max(
) = 3 is equivalent to log[max(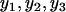 )] − log[min(
)] − log[min(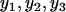 )] = log(3). Previously, we reported the proteomic–mRNA correlation through
)] = log(3). Previously, we reported the proteomic–mRNA correlation through 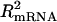 from a simple regression,
from a simple regression,
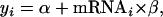 |
(2) |
where mRNAi is the log of mRNA expression level for the ith gene (Nie et al. 2006a). In this study, we included the quantitatively measured sequence features into a multiple regression,
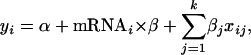 |
(3) |
where xij refers to the jth covariate (measuring a sequence feature such as codon usage, k is the number of covariates of a particular sequence feature) of the ith gene, and βj represents the slope for the jth covariate (Nie et al. 2006a). Particularly, we reported the 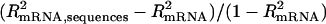 as the adjusted
as the adjusted 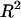 for the mRNA–protein correlation. For each covariate, we used the standard F-test to examine whether they were significant (P-value of the F-test reported) (Ott and Longnecker 2001). Finally, since the contribution from each of these effects may not be additive, we investigated their joint effects on the mRNA–protein correlation in a single multiple-regression analysis by using the equation
for the mRNA–protein correlation. For each covariate, we used the standard F-test to examine whether they were significant (P-value of the F-test reported) (Ott and Longnecker 2001). Finally, since the contribution from each of these effects may not be additive, we investigated their joint effects on the mRNA–protein correlation in a single multiple-regression analysis by using the equation
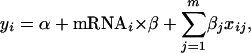 |
(4) |
where all sequence features were included as covariates (m is the total number of all covariates). P-values associated with each covariate were measured.
RESULTS
Sequence features related to translation initiation:
Shine–Dalgarno sequences:
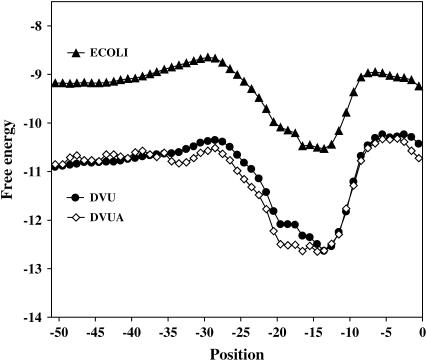
To determine the effects of SD sequences, we need to be certain that the same mechanism of translation initiation also exists in D. vulgaris. To confirm this, we systematically calculated the average free energy of the potential base pairing of 16S rRNA 3′ tail and upstream of D. vulgaris genes with the free-energy-based method (Osada et al. 1999). A sharp drop of the free energy was observed in the region of −25– ∼ −5 in all genes in the D. vulgaris chromosome and megaplasmid (Figure 1). This trend is highly similar to what has been observed in E. coli (Osada et al. 1999), suggesting that Osada's method works very well in D. vulgaris as well. It also indicates that the same mechanism of translation initiation is employed in D. vulgaris as in most prokaryotes. Interestingly, the average free energy by position is lower in D. vulgaris than in E. coli (Figure 1), which could be due to the high GC composition of the D. vulgaris genome.
Figure 1.—
Sharp decreases in free energy around positions −25 and −5 (relative to the start codon) are observed in D. vulgaris (DVU) and the metaplasmid of D. vulgaris (DVUA) and in E. coli (ECOLI). The free energy of all genes on each chromosome was averaged by position.
Using the same free-energy-based method (Osada et al. 1999), we calculated the MFE of 16S rRNA–SD base pairing for all D. vulgaris genes. As one might expect, the length of the 16S sRNA 3′ tail and upstream sequences might affect the free energy value calculated. To test this effect, we chose three lengths (13, 20, and 23) of 16S rRNA 3′ tail and two lengths (25 and 50) of mRNA upstream sequences and calculated the MFE for various combinations. In addition to the free-energy-based method, we also employed a probabilistic method to quantify the strength of RBS (Suzek et al. 2001). The putative SD sequence was found with a RBS score higher than the threshold value (Suzek et al. 2001). The result showed that the contribution varied considerably among various methods of SD MFE calculations, with MFE20_50 (20 refers to the length of 16S rRNA 3′ tail and 50 refers to the length of the upstream sequence of genes) explaining the highest variations in mRNA–protein correlation (up to 1.9–3.8% among various data sets, P-value <0.001; Table 1, supplemental Table 1 at http://www.genetics.org/supplemental/). This result also showed that the SD effect calculated by the probabilistic method does not seem to explain much of the variation in mRNA–protein correlation (mostly ∼1.0%, supplemental Table 1). In addition, only a weak correlation between RBS score and MFE20_50 was observed (r = −0.27, P < 0.0001), suggesting that these two methods may be different in evaluating SD sequences. In this study hereafter, MFE20_50 was used in all analyses involved.
TABLE 1.
Contribution of various features to the total variation of mRNA–protein correlation
| Variables | Partial R2 (lactate-log) | Partial R2 (formate-log) | Partial R2 (lactate-stationary) |
|---|---|---|---|
| mRNA expression | 0.384 (P < 0.0001) | 0.278 (P < 0.0001) | 0.394 (P < 0.0001) |
| SD sequence | |||
| MFE20_50 | 0.038 (P = 0.0003) | 0.031 (P = 0.0005) | 0.019 (P = 0.0095) |
| Start codon | |||
| ATG | 0.002 | 0.000 | 0.003 |
| TTG | 0.002 | 0.001 | 0.003 |
| GTG | 0.002 | 0.000 | 0.001 |
| Sum of start codona | 0.006 (P = 0.5660) | 0.001 (P = 0.9175) | 0.007 (P = 0.4733) |
| Start codon context | 0.018 (P = 0.0131) | 0.026 (P = 0.0014) | 0.003 (P = 0.3016) |
| Codon usage | |||
| CR1 | 0.001 | 0.003 | 0.001 |
| CR2 | 0.003 | 0.029 | 0.011 |
| CR3 | 0.000 | 0.002 | 0.000 |
| CR4 | 0.049 | 0.123 | 0.056 |
| Sum of codon usagea | 0.053 (P = 0.0011) | 0.157 (P = 0.0000) | 0.067 (P = 0.0001) |
| Amino acid usage | |||
| AA1 | 0.030 | 0.021 | 0.011 |
| AA2 | 0.017 | 0.000 | 0.017 |
| AA3 | 0.023 | 0.063 | 0.026 |
| AA4 | 0.003 | 0.035 | 0.005 |
| Sum of amino acid usagea | 0.073 (P = 0.0000) | 0.119 (P = 0.0000) | 0.058 (P = 0.0003) |
| Stop codon | |||
| TGA | 0.020 | 0.020 | 0.008 |
| TAG | 0.001 | 0.003 | 0.001 |
| TAA | 0.003 | 0.000 | 0.004 |
| Sum of stop codona | 0.023 (P = 0.0422) | 0.023 (P = 0.0292) | 0.013 (P = 0.2095) |
| Stop codon context | |||
| TAAA | 0.004 | 0.000 | 0.005 |
| TAAT | 0.000 | 0.005 | 0.001 |
| TAAC | 0.000 | 0.000 | 0.000 |
| TAAG | 0.002 | 0.000 | 0.002 |
| TAGA | 0.000 | 0.000 | 0.009 |
| TAGT | 0.000 | 0.008 | 0.000 |
| TAGC | 0.001 | 0.004 | 0.000 |
| TAGG | 0.001 | 0.004 | 0.001 |
| TGAA | 0.005 | 0.001 | 0.012 |
| TGAT | 0.001 | 0.000 | 0.001 |
| TGAC | 0.016 | 0.018 | 0.017 |
| TGAG | 0.007 | 0.000 | 0.002 |
| Sum of stop codon context a | 0.037 (P = 0.3669) | 0.041 (P = 0.1916) | 0.051 (P = 0.1079) |
| Sum of all features aboveb | 0.249 | 0.398 | 0.218 |
| Totalc | 0.169 (P < 0.00001) | 0.262 (P < 0.00001) | 0.152 (P < 0.00001) |
All scores are partial scores after mRNA, i.e., explanation of protein variations after taking away mRNA effects. The “sums” listed for each group are sums of “partial R2's” that have removed the overlapping effect among various variables.
P-value measurements are from the standard F-test.
Not including mRNA expression.
The results are from multiple-regression analyses that include all features.
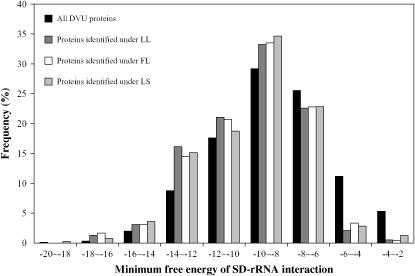
A recent study of E. coli showed that the SD MFE values in highly expressed genes (defined as genes whose protein product can be detected on 2D gels) were lower than in other genes (Lithwick and Margalit 2003). We previously found that the D. vulgaris proteins detected by LC–MS/MS represented the highly expressed genes (supplemental Figure 1 at http://www.genetics.org/supplemental/; Zhang et al. 2006c). When the MFE20_50 value of the detected proteins was compared with that of all proteins in the D. vulgaris genome, a similar frequency distribution pattern was found (Figure 2), suggesting that overall there was no strong evidence for lower MFE in proteins identified in LC–MS/MS.
Figure 2.—
Frequency distribution of SD–rRNA interaction minimum free energy for all D. vulgaris proteins and proteins identified in three growth conditions. LL, lactate-log phase; FL, formate-log phase; LS, lactate-stationary phase.
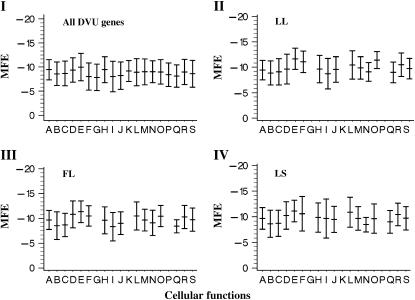
We previously found that mRNA–protein correlation may be different among various functional categories (Nie et al. 2006a). Given the fact that MFE values may be related to mRNA expression and protein abundance, one immediate question is whether MFE values also varied among functional categories of a given gene/protein. The results showed that while most of the functional categories shared similar levels of MFE values, genes from several functional categories, such as amino acid biosynthesis, central intermediary metabolism, energy metabolism, protein fate, and protein synthesis, had lower MFE values (Figure 3, category I). This pattern appears to be consistent when we used corresponding genes of the proteins identified under the three growth conditions examined in this study (Figure 3, categories II, III, and IV).
Figure 3.—
Minimum free energy of SD–rRNA interaction of genes belonging to various functional categories: (I) all genes, (II) lactate-log condition, (III) formate-log condition, and (IV) lactate-stationary condition. The cellular functional categories are: A, amino acid biosynthesis; B, biosynthesis of cofactors and carriers; C, cell envelope; D, cellular processes; E, central intermediary metabolism; F, DNA metabolism; G, disrupted reading frame; H, energy metabolism; I, fatty acid and phospholipid metabolism; J, hypothetical proteins; K, other categories; L, protein fate; M, protein synthesis; N, biosynthesis of purines and pyrimidines; O, regulatory functions; P, signal transduction; Q, transcription; R, transport and binding proteins; and S, unknown function. The functional categories without any proteins detected are left blank in II, III, and IV. The central, top, and bottom horizontal lines in the plots represent the mean, plus and minus the standard deviation for each function category.
Start codons:
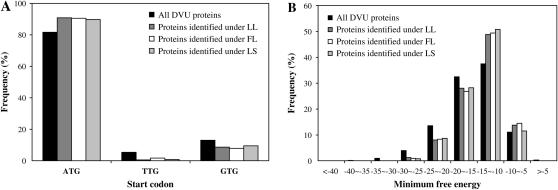
In the D. vulgaris genome, the start codon ATG is the most frequent start codon, consistent with the early conclusion that ATG is a preferred start codon, independent of the G + C content (Rocha et al. 1999). Approximately 82% of the D. vulgaris genes start with this codon, while the less frequently used TTG and GTG codons are found in 5.4 and 13% of the genes (Figure 4A). This strong bias in start codons was also observed in the proteins detected in various growth conditions (Figure 4A). This observation confirms that the canonical start codon ATG is more translationally optimal than noncanonical start codons. However, overall, the start codon identity explained only 0.1–0.7% of the total variation in mRNA–protein relationship under the three growth conditions as indicated by regression analyses (Table 1).
Figure 4.—
(A) Frequency distribution of start codon usage in all D. vulgaris proteins and proteins identified from three growth conditions. (B) Frequency distribution of minimum free energy of predicted mRNA secondary structure at start codon context of all D. vulgaris proteins and proteins identified from three growth conditions.
Start codon context:
Studies showed that stem–loop structures formed at the start site can affect the accessibility of the SD sequence or start codon for ribosomal binding (de Smit and Van Duin 1990, 1994; Rocha et al. 1999). To determine the potential effects of these mRNA secondary structures on protein translation, we computed the minimum free energy for the 60-base sequences spanning the start codon with RNAfold (Hofacker 2003; Hofacker and Stadler 2006). We found that proteins detected in our study tend to have relative high MFE values compared with all proteins in the D. vulgaris genome (Figure 4B), suggesting that avoidance of mRNA secondary structure might be a strategy for genes to achieve a high translation rate. Overall, the start codon context explains 0.3–2.5% of the variation in mRNA–protein correlation under the three growth conditions (Table 1), which is larger than that by start codons alone.
Sequence features related to translation elongation:
Codon usage pattern:
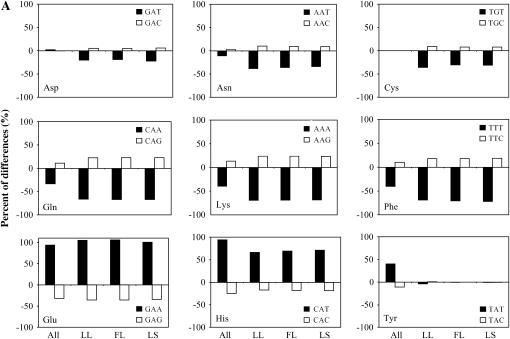
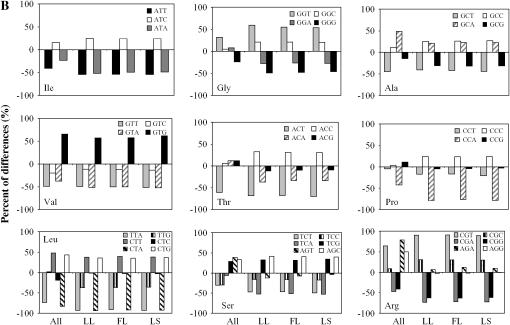
The codon usage in the G + C-rich D. vulgaris genome has not been fully investigated before (Heidelberg et al. 2004). In this study, two approaches have been employed to investigate the unequal codon usage in D. vulgaris. The first approach is to compare the extent of codon usage deviated from the expected frequency between detected proteins and all proteins to determine which codon is associated with protein translation. Due to the high GC composition of the D. vulgaris genome, the observed unequal frequency of synonymous codons can be simply a result of biased base composition due to mutational bias (Knight et al. 2001). Therefore, we used POD to measure how much the observed codon frequency deviated from the expected frequency determined on the basis of the base composition alone. Briefly, a positive POD value suggests an overrepresentation of the codon, whereas a negative POD indicates an underrepresentation. If the codon usage is associated with gene expression level, we would expect to see significantly different POD values between detected proteins and all proteins. Indeed, we found that except for Glu and Val codon families, the POD values of at least 1 codon within all the other 16 sense codon families (Met and Trp are excluded because they have only 1 codon) were significantly different (P-values <0.0001) between detected proteins and all proteins (Figure 5, A and B). In most cases, the absolute values of POD are greater in detected proteins than in all proteins, suggesting a stronger bias for these codons in detected proteins. This observation is consistent with previous findings in E. coli and Saccharomyces cerevisiae (Ikemura 1981, 1982, 1985). Taken together, it is obvious that codon usage in D. vulgaris is strongly associated with protein expression.
Figure 5.—
Comparison of the preferences of synonymous codon usage between all D. vulgaris proteins and proteins identified from three growth conditions. (A) Twofold codon families. (B) Multifold codon families.
The second approach is a correspondence analysis of the RSCU. The first four major trends in codon usage (CR1 to -4) determined by correspondence analysis accounted for 17.1, 4.4, 3.9, and 3.7% of the total variations in RSCU of all D. vulgaris genes (Wu et al. 2006). We included the first four major axes in codon usage of the D. vulgaris genome in a multiple-regression analysis. The result showed that codon usage alone contributed to 5.3–15.7% of the total variation in mRNA–protein correlation under the three conditions (P-value <0.001) (Table 1).
Amino acid usage:
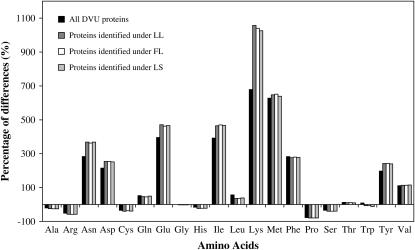
It was observed that the usage of some amino acids was correlated with gene expression (Akashi 2003; Chanda et al. 2005; Schaber et al. 2005). To determine whether it is the same case for amino acid usage in D. vulgaris, we applied a similar approach to the one used for codon usage, as described in the previous section. The only difference was that this time the frequencies of all synonymous codons were summed. Therefore, if the usage of an amino acid is associated with protein expression, we expect the POD value of this amino acid in detected proteins to be different from that in all proteins. As expected, the POD values of amino acids Asn, Asp, Glu, Ile, Tyr, and Lys in detected proteins are significantly higher than those in all proteins (P-values <0.0001 for all these amino acids) (Figure 6), suggesting that these amino acids are preferred in more abundant proteins.
Figure 6.—
Comparison of the preferences of amino acid usage between all D. vulgaris proteins and proteins identified from three growth conditions.
Given the fact that amino acid usage in D. vulgaris does associate with protein expression, we employed a multiple-regression analysis to determine its relative contribution to mRNA–protein correlation. A correspondence analysis of the deduced protein sequences of 3522 genes in D. vulgaris was performed to reveal the major trends. The first four trends (AA1 to -4) identified by correspondence analysis explain 18.6, 11.5, 9.7, and 7.0% of the variability in D. vulgaris amino acid usage, respectively (Wu et al. 2006). When we included the first four major axes in amino acid usage of the D. vulgaris genome in a multiple-regression analysis, the result showed that amino acid usage alone contributed to 5.8–11.9% of the total variation in mRNA–protein correlation under the three growth conditions (P-value <0.001) (Table 1).
Sequence features related to translation termination:
Stop codons:
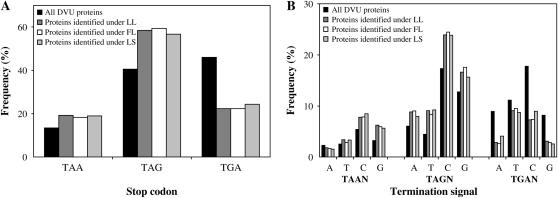
In D. vulgaris, three types of stop codons are all commonly used, with ∼45, 41, and 14% among all genes for TGA, TAG, and TAA, respectively (Figure 7A). However, among the proteins detected under our three growth conditions, TAG seems to be the most preferred stop codon: ∼56–59% of protein-encoding genes use TAG as a stop codon (Figure 7A). Regression analysis showed that stop codon identity was an important feature affecting mRNA–protein correlation. It alone explained 1.3–2.3% of total variation in mRNA–protein correlation under the three growth conditions (Table 1).
Figure 7.—
(A) Frequency distribution of stop codon usage in all D. vulgaris proteins and proteins identified from three growth conditions. (B) Frequency distribution of tetranucleotide termination signals in all D. vulgaris proteins and proteins identified from three growth conditions.
Stop codon context:
The base immediately downstream of the stop codon was also investigated for its role in translation termination. In D. vulgaris, “C” appears to be preferred after all three stop codons (Figure 7B). The most frequent stop signal is TAGC, which is even higher in proteins identified under the three conditions, suggesting that it might be the optimal stop signal. Simple regression analysis confirmed that stop codon context was an important feature affecting mRNA–protein correlation. It alone contributed 3.7–5.1% of total variation in mRNA–protein correlation under the three growth conditions (Table 1).
Multiple-regression analysis:
To quantitatively determine the relative contribution of each translation efficiency-related feature on mRNA–protein correlation, all sequence features studied above were integrated into a multiple-regression analysis. The results showed that these features together accounted for ∼15.2–26.2% of the total variation in mRNA–protein correlation (Table 1). The P-values of this regression model, for all three conditions, are all <0.00001, which indicates that contribution of these features to the mRNA–protein variation is significant. In addition, the result is very consistent under all three growth conditions.
To further evaluate the multiple-regression model itself, and to verify the sincerity of the contribution resulting from this multiple regression, we ran two bootstrap tests by keeping sequence features unchanged for all genes, while randomly permuting their proteomic abundance among the genes so that the proteomic abundance of a given gene is randomly assigned to a different gene. The bootstrap tests were run by randomly selecting 1000 permutations for each test. For each permutation, a multiple regression was fitted and 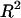 was reported as we did for the real data. The bootstrap P-value is reported as the probability that the simulated
was reported as we did for the real data. The bootstrap P-value is reported as the probability that the simulated 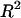 is larger than the
is larger than the 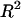 associated with the real data. A smaller P-value suggests that the
associated with the real data. A smaller P-value suggests that the 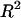 obtained for the real model is statistically more significant. The two null models for the bootstrap tests were that (1) the contribution by mRNA levels and all sequence features is not larger than the mRNA level alone and (2) the contribution by mRNA levels and all sequence features is no larger than that by mRNA levels and initiation-related sequence features (excluding elongation- and termination-related sequence features), respectively. The results showed that the P-values from the first bootstrap analysis are 0 for the contributions computed under all three growth conditions, and the P-value for the second null hypothesis is <0.0001 for all three conditions. The results demonstrated that correlation of mRNA expression and protein abundance was affected at a fairly significant level by multiple sequence features related to translational efficiency in D. vulgaris. Among them, the amino acid usage and codon usage are the top two factors, followed by stop codon context and SD sequences (Table 1).
obtained for the real model is statistically more significant. The two null models for the bootstrap tests were that (1) the contribution by mRNA levels and all sequence features is not larger than the mRNA level alone and (2) the contribution by mRNA levels and all sequence features is no larger than that by mRNA levels and initiation-related sequence features (excluding elongation- and termination-related sequence features), respectively. The results showed that the P-values from the first bootstrap analysis are 0 for the contributions computed under all three growth conditions, and the P-value for the second null hypothesis is <0.0001 for all three conditions. The results demonstrated that correlation of mRNA expression and protein abundance was affected at a fairly significant level by multiple sequence features related to translational efficiency in D. vulgaris. Among them, the amino acid usage and codon usage are the top two factors, followed by stop codon context and SD sequences (Table 1).
DISCUSSION
It is widely accepted that gene regulation in prokaryotes occurs mainly at the transcription level and secondarily at the level of translation (Lange and Hengge-Aronis 1994; Chhabra et al. 2006). Nevertheless, so far no systematic quantitative analysis has been performed on the effects of various translation-related sequence features on mRNA–protein correlation, and it remains unclear how strong the translation control is. In this study, we exploited the whole-genome mRNA expression and LC–MS/MS proteome abundance data from D. vulgaris grown under three conditions to gain insights into how the mRNA–protein correlation may be affected by various sequence features related to translation efficiency (Zhang et al. 2006a,c). The major sequence features in each translational stage were quantified and their effects on mRNA–protein correlation were investigated. Multiple-regression analyses of all sequence features showed that they together contributed up to 15.2–26.2% of the total variation of mRNA–protein correlation, suggesting that regulation at the translational level is indeed involved in determining mRNA–protein correlation in D. vulgaris. The result provides a valuable estimate of the contribution of translation-related sequence features to protein synthesis. It may be worth noting that although several previous studies have been performed to determine the contribution of some of these sequence features to mRNA or protein abundance (Poole et al. 1995; Rocha et al. 1999; Lithwick and Margalit 2003), these sequence features were not examined in a unified framework. To our knowledge, our analysis represents the first attempt to address the relative contribution of these sequence features to the mRNA–protein correlation with a single statistical model.
This investigation also benefited from the expression data sets we used. First, mRNA expression and protein abundance were determined for a pair of samples prepared in parallel to minimize the variations across experiments; second, the data set is relatively large (>400 proteins and their corresponding genes); and third, three individual data sets were collected independently for three growth conditions (Zhang et al. 2006a,c,d). All of these have substantially contributed to the reliability of our analyses; therefore, the results from our analyses may represent a general phenomenon in D. vulgaris.
The traditional view on the contribution of SD sequences to mRNA–protein correlation was that the competition between the ribosome–RBS interaction and the mRNA structure results in nearly “all-or-none” expression, leaving almost no room for regulation at the translation level (De Smit and Van Duin 1994; Rocha et al. 1999). Therefore, all moderately or highly expressed genes should have a good combination of a good RBS and an efficient start codon. In contrast, some other findings suggested that the SD sequence has little influence on protein expression, as the binding of the 16S ribosomal subunit has been found not to be essential for translation initiation (Calogero et al. 1988). In fact, there exist mRNAs without SD sequences (Boni et al. 2001). In a recent study with E. coli and Haemophilus influenzae genomes, it was also proposed that the base-pairing potential of the mRNA SD sequence and the rRNA seemed to have a negligible effect on protein expression (Lithwick and Margalit 2003). However, our study with D. vulgaris indicates that differential MFE values for SD sequences were present among genes/proteins of different abundance levels. Moreover, regression analysis showed that SD sequences contributed to 1.9–3.8% of the total variation of mRNA–protein correlation, suggesting that SD sequences do play a role in translational control.
It has been suggested that translation initiation is a rate-limiting step when compared with the elongation and termination stages of protein biosynthesis (Vellanoweth and Rabinowitz 1992; De Smit and Van Duin 1994; Rocha et al. 1999; Romby and Springer 2003). However, our study showed that features related to translation initiation (start codon and start codon context) play only a minor role in determining mRNA–protein correlation in D. vulgaris. To the contrary, the sequence features involved in translation elongation, such as codon usage and amino acid usage, may be more important in determining mRNA–protein correlation in D. vulgaris. This result is consistent with the conclusion by Lithwick and Margalit (2003), who found that codon bias had the greatest influence on protein expression levels, and also consistent with a recent study that estimated that codon bias accelerates translation in E. coli by no more than 60% in comparison to microbes with very little codon bias (Dethlefsen and Schmidt 2005).
Translation elongation can be retarded or stalled by the use of rare codons and the availability of various amino acids as building blocks (Varenne et al. 1989; Rocha et al. 1999; Akashi and Gojobori 2002). The second major sequence feature that influences the mRNA–protein correlation was identified as the amino acid usage of the proteins in D. vulgaris. Metabolic cost of amino acids has been previously proposed to explain the preferences in amino acid usage (Akashi and Gojobori 2002); abundant proteins tend to use more cost-efficient amino acids. However, no obvious correlation was found between amino acid preferences and metabolic cost in our study. For instance, amino acids (Asn, Asp, Glu, Ile, Tyr, and Lys) preferred in detected proteins are not of low metabolic cost (Akashi and Gojobori 2002). Instead, we observed a strong correlation between protein hydrophobicity and AA2 (Pearson correlation coefficient 0.78), suggesting that selection for protein structure remains as the major determinant of amino acid usage in D. vulgaris.
It has been shown that the identity of the stop codon and stop codon context influence the rate of translation termination (Poole et al. 1995). Several recent studies showed that the average gene expression level among the three stop codon groups in the five model organisms and humans does not differ significantly (P > 0.05) (Sun et al. 2005), and the association of stop codons with high expression as reflected by the Φ-coefficient was found to be weak (Lithwick and Margalit 2003). Our analysis indicated that, while the contribution by stop codons was not dramatic (1.3–2.3% to the total variation of mRNA–protein correlation), the contribution by stop codon context was found to be the third greatest sequence feature affecting mRNA–protein correlation, contributing 3.7–5.1% of the total variation. Therefore, the stop codon context may be more important in affecting the translation efficiency than previously suggested.
It might be noteworthy that while our previous study addressed the effects of experimental challenges and various physical properties of mRNA or proteins, such as analytic variation, stability of mRNAs and proteins, and the cellular functional category of genes/proteins, etc. (Nie et al. 2006a), this article focuses on the impact of the sequences to the proteomic and mRNA correlation pattern. An attempt has also been made to integrate all the features tested in this work and our previous article into one multiple-regression model. Consequently we found that >71% of mRNA–protein correlation variation can be accountable (L. Nie, G. Wu and W. Zhang, unpublished data), suggesting that we have identified most of the factors that can potentially affect mRNA–protein correlation. In addition, through an F-test the results showed that the contributions by translation-level factors are significantly independent of the contributions by errors and protein stability with a P-value <0.0001 (Ott and Longnecker 2001; L. Nie, G. Wu and W. Zhang, unpublished data). Although the model could be further improved if other related features, such as mRNA and protein degradation rate, can be included or larger proteomic data sets and their corresponding gene expression data become available, the results obtained here have greatly enhanced our understanding of correlation between mRNA expression and protein abundance. The results also lay down an important foundation for developing statistical tools in integrating microarray and proteomic data (Nie et al. 2006b). In addition, the study extended the concept of integrated genomics by including experimental genomics data and other quantitative properties that are sequence dependent. Without much modification, the methodology described in this article can also be applied to the analysis of other model organisms such as E. coli and S. cerevisiae.
As a complicated biological process, many details of translation still need further investigation; for example, highly expressed proteins may not necessarily require a high abundance of mRNA if they have a translation rate higher than average. In this study, we made the initial attempt to use postgenomic data to analyze a translation process in a simplified framework; it will be more informative to include other experimental parameters, such as RNA decay and protein degradation, into the model once they become available in the future. We point out that the conclusions reached were also subject to the limitations of the data sets (e.g., quality of data and size of data set). For example, the lack of a significant contribution of start codons to variations in the mRNA–protein correlation may be due to the fact that most proteins used in this analysis already have a good start codon. In addition, this study was also subject to the limitations of our methods to quantify sequence features, such as minimal free energy or SD computation. Because of all these reasons, caution needs to be taken in further interpreting these conclusions as general rules in all prokaryotic cells. Nevertheless, our study provides the first comprehensive quantitative analysis of various sources of contribution to the variation in mRNA–protein correlation and sheds some light on the translation process in bacterial D. vulgaris.
Acknowledgments
We thank the Environmental Molecular Sciences Laboratory (EMSL) at the Pacific Northwest National Laboratory (PNNL) for use of the proteomic instrumentation in generating data used in this research (EMSL proposal 15891). The EMSL is a national scientific user facility sponsored by the Department of Energy's Office of Biological and Environmental Research. We are grateful to three anonymous referees for many constructive suggestions and comments, which greatly improved the quality of this article. We are grateful for the valuable comments from Stephen J. Freeland, Philip Farabaugh, Janice Zengel, David Carlini, and Marie desJardins. We are also grateful to Bryan Mackay for a critical reading of the manuscript. The research described in this article was conducted under the Laboratory-Directed Research and Development Program (to W.Z.) at the PNNL, a multiprogram national laboratory operated by Battelle for the U.S. Department of Energy under contract DE-AC05-76RLO1830. G. Wu was supported by award 0317349 (to S.J.F.) from the National Science Foundation Division of Biological Infrastructure program Biological Databases and Informatics.
References
- Akashi, H., 2003. Translational selection and yeast proteome evolution. Genetics 164: 1291–1303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akashi, H., and T. Gojobori, 2002. Metabolic efficiency and amino acid composition in the proteomes of Escherichia coli and Bacillus subtilis. Proc. Natl. Acad. Sci. USA 99: 3695–3700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alter, O., and G. H. Golub, 2004. Integrative analysis of genome-scale data by using pseudoinverse projection predicts novel correlation between DNA replication and RNA transcription. Proc. Natl. Acad. Sci. USA 101: 16577–16582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beyer, A., J. Hollunder, H. P. Nasheuer and T. Wilhelm, 2004. Post-transcriptional expression regulation in the yeast Saccharomyces cerevisiae on a genomic scale. Mol. Cell Proteomics 3: 1083–1092. [DOI] [PubMed] [Google Scholar]
- Boni, I. V., V. S. Artamonova, N. V. Tzareva and M. Dreyfus, 2001. Non-canonical mechanism for translational control in bacteria: synthesis of ribosomal protein S1. EMBO J. 20: 4222–4232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown, C. M., P. A. Stockwell, C. N. Trotman and W. P. Tate, 1990. Sequence analysis suggests that tetra-nucleotides signal the termination of protein synthesis in eukaryotes. Nucleic Acids Res. 18: 6339–6345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calogero, R. A., C. L. Pon, M. A. Canonaco and C. O. Gualerzi, 1988. Selection of the mRNA translation initiation region by Escherichia coli ribosomes. Proc. Natl. Acad. Sci. USA 85: 6427–6431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cavener, D. R., and S. C. Ray, 1991. Eukaryotic start and stop translation sites. Nucleic Acids Res. 19: 3185–3192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chanda, I., A. Pan and C. Dutta, 2005. Proteome composition in Plasmodium falciparum: higher usage of GC-rich nonsynonymous codons in highly expressed genes. J. Mol. Evol. 61: 513–523. [DOI] [PubMed] [Google Scholar]
- Chhabra, S. R., Q. He, K. H. Huang, S. P. Gaucher, E. J. Alm et al., 2006. Global analysis of heat shock response in Desulfovibrio vulgaris Hildenborough. J. Bacteriol. 188: 1817–1828. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collins, R. F., M. Roberts and D. A. Phoenix, 1995. Codon bias in Escherichia coli may modulate translation initiation. Biochem. Soc. Trans. 23: 76. [DOI] [PubMed] [Google Scholar]
- de Smit, M. H., and J. van Duin, 1990. Secondary structure of the ribosome binding site determines translational efficiency: a quantitative analysis. Proc. Natl. Acad. Sci. USA 87: 7668–7672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Smit, M. H., and J. van Duin, 1994. Translational initiation on structured messengers. Another role for the Shine-Dalgarno interaction. J. Mol. Biol. 235: 173–184. [DOI] [PubMed] [Google Scholar]
- Dethlefsen, L., and T. M. Schmidt, 2005. Differences in codon bias cannot explain differences in translational power among microbes. BMC Bioinformatics 6: 3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Devore, J., and N. Farnum, 2005. Applied Statistics for Engineers and Scientists. Thompson Learning, Belmont, CA.
- Eng, J. K., A. L. McCormack and J. R. Yates, III, 1994. An approach to correlate tandem mass spectral data of peptides with amino acid sequences in a protein database. J. Am. Soc. Mass Spectrom. 5: 976–979. [DOI] [PubMed] [Google Scholar]
- Faxen, M., J. Plumbridge and L. A. Isaksson, 1991. Codon choice and potential complementarity between mRNA downstream of the initiation codon and bases 1471–1480 in the 16S ribosomal RNA affects expression of glnS. Nucleic Acids Res. 19: 5247–5251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Futcher, B., G. I. Latter, P. Monardo, C. S. McLaughlin and J. I. Garrels, 1999. A sampling of the yeast proteome. Mol. Cell. Biol. 19: 7357–7368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao, J., G. J. Opiteck, M. S. Friedrichs, A. R. Dongre and S. A. Hefta, 2003. Changes in the protein expression of yeast as a function of carbon source. J. Proteome Res. 2: 643–649. [DOI] [PubMed] [Google Scholar]
- Greenbaum, D., R. Jansen and M. Gerstein, 2002. Analysis of mRNA expression and protein abundance data: an approach for the comparison of the enrichment of features in the cellular population of proteins and transcripts. Bioinformatics 18: 585–596. [DOI] [PubMed] [Google Scholar]
- Greenbaum, D., C. Colangelo, K. Williams and M. Gerstein, 2003. Comparing protein abundance and mRNA expression levels on a genomic scale. Genome Biol. 4: 117.1–117.8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gygi, S. P., Y. Rochon, B. R. Franza and R. Aebersold, 1999. Correlation between protein and mRNA abundance in yeast. Mol. Cell. Biol. 19: 1720–1730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hegde, P. S., 2003. Interplay of transcriptomics and proteomics. Curr. Opin. Biotechnol. 14: 647–651. [DOI] [PubMed] [Google Scholar]
- Heidelberg, J. F., R. Seshadri, S. A. Haveman, C. L. Hemme, I. T. Paulsen et al. 2004. The genome sequence of the anaerobic, sulfate-reducing bacterium Desulfovibrio vulgaris Hildenborough. Nat. Biotechnol. 22: 554–559. [DOI] [PubMed] [Google Scholar]
- Hofacker, I. L., 2003. Vienna RNA secondary structure server. Nucleic Acids Res. 31: 3429–3431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hofacker, I. L., and P. F. Stadler, 2006. Memory efficient folding algorithms for circular RNA secondary structures. Bioinformatics 22: 1172–1176. [DOI] [PubMed] [Google Scholar]
- Horak, C. E., and M. Snyder, 2002. Global analysis of gene expression in yeast. Funct. Integr. Genomics 2: 171–180. [DOI] [PubMed] [Google Scholar]
- Ideker, T., V. Thorsson, J. A. Ranish, R. Christmas, J. Buhler et al., 2001. Integrated genomic and proteomic analyses of a systematically perturbed metabolic network. Science 292: 929–934. [DOI] [PubMed] [Google Scholar]
- Ikemura, T., 1981. Correlation between the abundance of Escherichia coli transfer RNAs and the occurrence of the respective codons in its protein genes: a proposal for a synonymous codon choice that is optimal for the E. coli translational system. J. Mol. Biol. 151: 389–409. [DOI] [PubMed] [Google Scholar]
- Ikemura, T., 1982. Correlation between the abundance of yeast transfer RNAs and the occurrence of the respective codons in protein genes. Differences in synonymous codon choice patterns of yeast and Escherichia coli with reference to the abundance of isoaccepting transfer RNAs. J. Mol. Biol. 158: 573–597. [DOI] [PubMed] [Google Scholar]
- Ikemura, T., 1985. Codon usage and tRNA content in unicellular and multicellular organisms. Mol. Biol. Evol. 2: 13–34. [DOI] [PubMed] [Google Scholar]
- Kisselev, L., M. Ehrenberg and L. Frolova, 2003. Termination of translation: Interplay of mRNA, rRNAs and release factors? EMBO J. 22: 175–182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knight, R. D., S. J. Freeland and L. F. Landweber, 2001. A simple model based on mutation and selection explains trends in codon and amino-acid usage and GC composition within and across genomes. Genome Biol. 2: RESEARCH0010. [DOI] [PMC free article] [PubMed]
- Lange, R., and R. Hengge-Aronis, 1994. The cellular concentration of the σS subunit of RNA polymerase in Escherichia coli is controlled at the levels of transcription, translation, and protein stability. Genes Dev. 8: 1600–1612. [DOI] [PubMed] [Google Scholar]
- Lithwick, G., and H. Margalit, 2003. Hierarchy of sequence-dependent features associated with prokaryotic translation. Genome Res. 13: 2665–2673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Looman, A. C., J. Bodlaender, L. J. Comstock, D. Eaton, P. Jhurani et al., 1987. Influence of the codon following the AUG initiation codon on the expression of a modified lacZ gene in Escherichia coli. EMBO J. 6: 2489–2492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma, J., A. Campbell and S. Karlin, 2002. Correlations between Shine-Dalgarno sequences and gene features such as predicted expression levels and operon structures. J. Bacteriol. 184: 5733–5745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCarthy, J. E. G., and R. Brimacombe, 1994. Procaryotic translation: the interactive pathway leading to initiation. Trends Genet. 10: 402–407. [DOI] [PubMed] [Google Scholar]
- Montgomery, D. C., 2001. Introduction to Statistical Quality Control (Wiley Series in Statistics and Probability). John Wiley & Sons, New York.
- Mootha, V. K., P. Lepage, K. Miller, J. Bunkenborg, M. Reich et al., 2003. a Identification of a gene causing human cytochrome c oxidase deficiency by integrative genomics. Proc. Natl. Acad. Sci. USA 100: 605–610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mootha, V. K., J. Bunkenborg, J. V. Olsen, M. Hjerrild, J. R. Wisniewski et al., 2003. b Integrated analysis of protein composition, tissue diversity, and gene regulation in mouse mitochondria. Cell 115: 629–640. [DOI] [PubMed] [Google Scholar]
- Nie, L., G. Wu and W. Zhang, 2006. a Correlation between mRNA and protein abundance in Desulfovibrio vulgaris: a multiple regression to identify sources of variations. Biochem. Biophys. Res. Commun. 339: 603–610. [DOI] [PubMed] [Google Scholar]
- Nie, L., G. Wu, F. J. Brockman and W. Zhang, 2006. b Integrated analysis of transcriptomic and proteomic data of Desulfovibrio vulgaris: zero-inflated Poisson regression models to predict abundance for undetected proteins. Bioinformatics 22: 1641–1647. [DOI] [PubMed] [Google Scholar]
- Nuwaysir, E. F., W. Huang, T. J. Albert, J. Singh, K. Nuwaysir et al., 2002. Gene expression analysis using oligonucleotide arrays produced by maskless photolithography. Genome Res. 12: 1749–1755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Osada, Y., R. Saito and M. Tomita, 1999. Analysis of base-pairing potentials between 16S rRNA and 5′ UTR for translation initiation in various prokaryotes. Bioinformatics 15: 578–581. [DOI] [PubMed] [Google Scholar]
- Ott, R. Y., and M. Longnecker, 2001. An Introduction to Statistical Methods and Data Analysis. Thompson Learning, Pacific Grove, CA.
- Ozawa, Y., S. Hanaoka, R. Saito, T. Washio, S. Nakano et al., 2002. Comprehensive sequence analysis of translation termination sites in various eukaryotes. Gene 300: 79–87. [DOI] [PubMed] [Google Scholar]
- Poole, E. S., C. M. Brown and W. P. Tate, 1995. The identity of the base following the stop codon determines the efficiency of in vivo translational termination in Escherichia coli. EMBO J. 14: 151–158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poole, E. S., R. Brimacombe and W. P. Tate, 1997. Decoding the translational termination signal: the polypeptide chain release factor in Escherichia coli crosslinks to the base following the stop codon. RNA 3: 974–982. [PMC free article] [PubMed] [Google Scholar]
- Qian, W. J., T. Liu, M. E. Monroe, E. F. Strittmatter, J. M. Jacobs et al., 2005. Probability-based evaluation of peptide and protein identifications from tandem mass spectrometry and SEQUEST analysis: the human proteome. J. Proteome Res. 4: 53–62. [DOI] [PubMed] [Google Scholar]
- Rocha, E. P., A. Danchin and A. Viari, 1999. Translation in Bacillus subtilis: roles and trends of initiation and termination, insights from a genome analysis. Nucleic Acids Res. 27: 3567–3576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Romby, P., and M. Springer, 2003. Bacterial translational control at atomic resolution. Trends Genet. 19: 155–161. [DOI] [PubMed] [Google Scholar]
- Schaber, J., C. Rispe, J. Wernegreen, A. Buness, F. Delmotte et al., 2005. Gene expression levels influence amino acid usage and evolutionary rates in endosymbiotic bacteria. Gene 352: 109–117. [DOI] [PubMed] [Google Scholar]
- Schurr, T., E. Nadir and H. Margalit, 1993. Identification and characterization of E. coli ribosomal binding sites by free energy computation. Nucleic Acids Res. 21: 4019–4023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shine, J., and L. Dalgarno, 1974. The 30-terminal sequence of Escherichia coli 16S ribosomal RNA: complementarity to nonsense triplets and ribosome binding sites. Proc. Natl. Acad. Sci. USA 71: 1342–1346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith, R. D., G. A. Anderson, M. S. Lipton, C. Masselon, L. Pasa-Tolic et al., 2002. The use of accurate mass tags for high-throughput microbial proteomics. OMICS 6: 61–90. [DOI] [PubMed] [Google Scholar]
- Sorensen, M. A., C. G. Kurland and S. Pedersen, 1989. Codon usage determines translation rate in Escherichia coli. J. Mol. Biol. 207: 365–377. [DOI] [PubMed] [Google Scholar]
- Stenstrom, C. M., H. Jin, L. L. Major, W. P. Tate and L. A. Isaksson, 2001. Codon bias at the 3′-side of the initiation codon is correlated with translation initiation efficiency in Escherichia coli. Gene 263: 273–284. [DOI] [PubMed] [Google Scholar]
- Sueoka, N., 1988. Directional mutation pressure and neutral molecular evolution. Proc. Natl. Acad. Sci. USA 85: 2653–2657. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun, J., M. Chen, J. Xu and J. Luo, 2005. Relationships among stop codon usage bias, its context, isochores, and gene expression level in various eukaryotes. J. Mol. Evol. 61: 437–444. [DOI] [PubMed] [Google Scholar]
- Suzek, B. E., M. D. Ermolaeva, M. Schreiber and S. L. Salzberg, 2001. A probabilistic method for identifying start codons in bacterial genomes. Bioinformatics 17: 1123–1130. [DOI] [PubMed] [Google Scholar]
- Tate, W. P., E. S. Poole, J. A. Horsfield, S. A. Mannering, C. M. Brown et al., 1995. Translational termination efficiency in both bacteria and mammals is regulated by the base following the stop codon. Biochem. Cell. Biol. 73: 1095–1103. [DOI] [PubMed] [Google Scholar]
- Tate, W. P., E. S. Poole, M. E. Dalphin, L. L. Major, D. J. Crawford et al., 1996. The translational stop signal: codon with a context, or extended factor recognition element? Biochimie 78: 945–952. [DOI] [PubMed] [Google Scholar]
- Varenne, S., D. Baty, H. Verheij, D. Shire and C. Lazdunski, 1989. The maximum rate of gene expression is dependent on the downstream context of unfavourable codons. Biochimie 71: 1221–1229. [DOI] [PubMed] [Google Scholar]
- Vellanoweth, R. L., and J. C. Rabinowitz, 1992. The influence of ribosome-binding-site elements on translational efficiency in Bacillus subtilis and Escherichia coli in vivo. Mol. Microbiol. 6: 1105–1114. [DOI] [PubMed] [Google Scholar]
- Voordouw, G., 1996. The genus Desulfovibrio: the centennial. Appl. Environ. Microbiol. 61: 2813–2819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Washburn, M. P., A. Koller, G. Oshiro, R. R. Ulaszek, D. Plouffe et al., 2003. Protein pathway and complex clustering of correlated mRNA and protein expression analyses in Saccharomyces cerevisiae. Proc. Natl. Acad. Sci. USA 100: 3107–3112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu, G., L. Nie and W. Zhang, 2006. Relation between mRNA expression and sequence information in Desulfovibrio vulgaris: combinatorial contributions of upstream regulatory motifs and coding sequence features to variations in mRNA abundance. Biochem. Biophys. Res. Commun. 344: 114–121. [DOI] [PubMed] [Google Scholar]
- Yates, III, J. R., J. K. Eng, A. L. McCormack and D. Schieltz, 1995. Method to correlate tandem mass spectra of modified peptides to amino acid sequences in the protein database. Anal. Chem. 67: 1426–1436. [DOI] [PubMed] [Google Scholar]
- Zhang, W., D. E. Culley, J. C. M. Scholten, M. Hogan, L. Vitiritti et al., 2006. a Global transcript analysis in Desulfovibrio vulgaris grown on different carbon sources. Antonie Leeuwenhoek 89: 221–237. [DOI] [PubMed] [Google Scholar]
- Zhang, W., D. E. Culley, M. Hogan, L. Vitiritti and F. J. Brockman, 2006. b Oxidative stress and heat-shock responses in Desulfovibrio vulgaris by genome-wide transcriptomic analysis. Antonie Leeuwenhoek 90: 41–55. [DOI] [PubMed] [Google Scholar]
- Zhang, W., M. A. Gritsenko, R. J. Moore, D. E. Culley, L. Nie et al., 2006. c Proteomic view of the metabolism in Desulfovibrio vulgaris determined by liquid chromatography coupled with tandem mass spectrometry. Proteomics 6: 4286–4299. [DOI] [PubMed] [Google Scholar]
- Zhang, W., D. E. Culley, M. A. Gritsenko, R. J. Moore, L. Nie et al., 2006. d LC-MS/MS based proteomic analysis and functional inference of hypothetical proteins in Desulfovibrio vulgaris. Biochem. Biophys. Res. Commun. 349: 1412–1419. [DOI] [PubMed] [Google Scholar]