Spurious spatial periodicity of co-expression in microarray data due to printing design

Abstract

Global transcriptome data is increasingly combined with sophisticated mathematical analyses to extract information about the functional state of a cell. Yet the extent to which the results reflect experimental bias at the expense of true biological information remains largely unknown. Here we show that the spatial arrangement of probes on microarrays and the particulars of the printing procedure significantly affect the log-ratio data of mRNA expression levels measured during the Saccharomyces cerevisiae cell cycle. We present a numerical method that filters out these technology-derived contributions from the existing transcriptome data, leading to improved functional predictions. The example presented here underlines the need to routinely search and compensate for inherent experimental bias when analyzing systematically collected, internally consistent biological data sets.

INTRODUCTION

Microarray technology has emerged as a viable and indispensable tool in cell biology, offering information on the simultaneous activity of virtually all genes within a given organism (1). Consequently, gene expression profiling is used in a variety of applications, from uncovering gene function (2,3) to the molecular classification of cancer phenotypes (4–12). Owing to the widespread use of microarray technology, it is of great importance to ensure that the measured gene expression levels reflect the number of specific mRNA molecules in the cell (13). Two main types of errors contribute to inaccuracies in measured gene expression levels: systematic and non-systematic errors. Systematic errors arise reproducibly as a result of the experimental procedure (14,15), while non-systematic errors originate from the inherent biological variability of cells (16–18). Normalization methods have been widely used to correct for systematic errors (19–22), but the source of the corrected biases remains largely unexplored.

Here, using publicly available microarray data on synchronized Saccharomyces cerevisiae cell cultures traversing through the cell cycle (23,24), we uncover a strong technical component imposed over the gene expression values measured by microarray. In particular, we show that the printing of the probes on the microarray results in a major and systematic contribution to the observed gene expression levels that has a significant impact on the interpretation of gene expression measurements. The generality of our results is demonstrated by the presence of the observed effects in microarray data that were collected by two different techniques in different laboratories, one using custom built cDNA arrays and the other using Affymetrix oligoarrays. We reproduce the observed experimental bias by computer simulation and by a simple theoretical model. Based on this model, we develop a method to filter out the observed bias from the existing microarray data, thereby improving the classification of genes into functional categories.

MATERIALS AND METHODS

Data sets

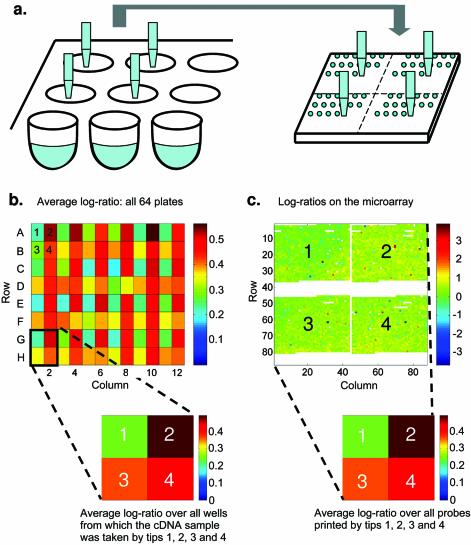
The complete microarray data on synchronized S.cerevisiae cell cultures traversing through the cell cycle (23,24), which we refer to as combined data (CD), were downloaded from http://genome-www.stanford.edu/cellcycle/data/rawdata/combined.txt. Individual array data (IAD) for three of the four experiments, available online at http://genome-www.stanford.edu/cellcycle/data/rawdata/individual.html, contain additional information about the experimental technology, including the location of all cDNA samples on the 96-well microtiter plates, as well as the location of the corresponding probes on the microarray slides. Moreover, the location of the spots on the scanned fluorescence images used to calculate the expression ratios are also provided and the images are available for download. In the α-factor experiment, unique probe spots corresponding to 6145 genes were printed from plates 1 through 64 onto the microarray slide (24). The cDNA samples were arranged on the 64 microtiter plates according to their chromosomal order (from the centromere to the left telomere and then from the centromere to the right telomere). The probe locations on the microarray and the four blocks of 44 × 44 spots apparent on the scanned fluorescence images indicate that the cDNA samples were printed via a four tip print head from the 96-well plates onto the microarray two rows at a time (see also Figs 1 and 2). Therefore, each of the four print tips deposited 44 × 44 = 1936 probe spots on each microarray.

Figure 1.

Spatial periodicity of temporal mRNA expression profiles correlates with cDNA probe locations on the microarray chip. (a) Average cross-correlation coefficient of the temporal expression profiles as a function of the inter-gene distance along the chromosomes for the combined data (CD). The average spatial cross-correlation coefficient C(D) for each of the 16 yeast chromosomes (A–P) following α-factor arrest-induced synchronization are shown. The inset displays a portion of C(D) obtained for chromosome B to demonstrate the short period (2 gene) spatial periodicity of gene expression. (b) Average distance of the spotted cDNA probes on the microarray chip as a function of the chromosomal distance D. The inset shows in detail this dependence for the same portion of chromosome B, as in (a). (c) Spatial arrangement of deposited cDNA probe spots on the microarray chip. As an example, a set of 264 consecutive genes (in chromosomal order) is considered. Spots of the same color are printed on the slide by the same print tip. The gradually darker shades indicate simultaneous printing of 24 spots from two consecutive rows on the 96-well plate. The numbers in this table correspond to both the spatial order on the chromosome and the position on the 96-well plates from left to right and from top to bottom. (d) The 2 gene and 24 gene periodicities appear as a consequence of the arrangement of cDNA probes on the microarray chip.

Figure 2.

The microarray printing procedure as a source of experimental bias. (a) The location of the printing head with four tips as it transfers samples from 96-well plates onto the microarray slide. The resulting printing pattern defines four groups of spots, labeled 1–4. Each well of a 96-well plate can be labeled according to the print tip that took the sample from it. (b) The average log-ratio of measured expression levels calculated from the individual array data (IAD) is shown for each position within the 96-well plates, for time point 10 (i.e. 70 min after release from α-factor arrest). Note the regularity of the pattern within this 8 × 12 matrix. It can be approximately constructed from the repetition of 2 × 2 matrices (corresponding to print tips 1–4, shown in the bottom left corner). Averaging over all wells labeled 1–4 results in the 2 × 2 matrix shown under the 8 × 12 matrix. (c) All samples printed on the microarray yield four spatially distinct groups of 44 × 44 spots, corresponding to print tips 1–4. Averaging the log-ratios of measured expression levels from the IAD within each of the four groups of spots results in the 2 × 2 matrix shown below the microarray. The numbers that appear within the 2 × 2 matrices on the left and right are identical, indicating that printing was performed with a four-tip print head, and each tip contributed a significant bias to the measured expression data.

Average spatial cross-correlation coefficient

To study the spatial properties of the gene expression data for each of the 16 yeast chromosomes we rearranged the CD set based on the sequential order of genes on the individual chromosomes from the left to the right telomeres. For each chromosome the expression log-ratios are organized as a matrix E(i,t) of N_G rows and N_T columns, where N_G is the number of genes on the chromosome, while N_T represents the total number of experiments (the number of sampling times). We define the spatial distance D between genes G_i and G_j as the difference between their row numbers within the matrix E(i,t) (see also Supplementary Material).

The co-expression of any two genes G_i and G_j is characterized by the cross-correlation coefficient of their temporal expression profiles E(i,t) and E(j,t), defined as

C(i,j) = C(E(i,t),E(j,t)) = = [〈E(i,t)E(j,t)〉 – 〈E(i,t)〉〈E(j,t)〉] × × {〈[E(i,t) – 〈E(i,t)〉]²〉〈E(j,t) – E(j,t)〉]²〉}^–1/2     1

where 〈〉 denotes the temporal average of the quantity within the angle brackets. To determine how co-expression depends on the distance between genes, we averaged the cross-correlations C(i,j) for all genes G_i and G_j located at distance D = |i – j| from each other. For a chromosome containing N genes, the average spatial cross-correlation coefficient C(D) was calculated for distances ranging from D = 1 to D = N/2:

Spatial arrangement of the probe spots on the microarray

As described above, during the printing procedure the cDNA probes are placed on the microarray in a particular pattern, in accordance with their order on the chromosome. The generic printing procedure can be best illustrated if we consider 246 consecutive genes from three 96-well microtiter plates (see Fig. 1c). The four-tip print head takes samples from two consecutive rows of the plate and prints them on the slide. Therefore, if G₁, G₂, G₃, … are consecutive genes on the microtiter plate, genes G₁, G₂, G₁₃, and G₁₄ will be printed simultaneously on the microarray by print tips 1, 2, 3 and 4, respectively. The next quadruplet of genes printed on the slide will be G₃, G₄, G₁₅ and G₁₆, followed by G₅, G₆, G₁₇ and G₁₈, etc. Due to this procedure, genes G₁, G₃, G₅, … G₁₁; G₂₅, G₂₇, … G₃₅; G₄₉, G₅₁, … G₅₉; … will be printed by tip 1 and affected by the same tip-dependent bias. At the same time, genes G₂, G₄, … G₁₂; G₂₆, G₂₈, … G₃₆; G₅₀, G₅₂, … G₆₀; … will be printed by tip 2 and affected by the same tip-dependent bias (specific to tip 2, and different from the bias characterizing tip 1). One can similarly create the list of genes printed by tips 3 and 4.

To characterize the dependence of cDNA probe position on the microarray as a function of the chromosomal location of the corresponding genes, we define the average intergenic distance on the scanned fluorescence images as

δ(D) = 〈(x_i – x_{i + D})² + (y_i – y_{i + D})²〉^–1/2     3

where x_i and y_i denote the horizontal and vertical coordinates (in pixels) of the probe spot corresponding to gene G_i on the microarray, and the average is taken over all possible gene pairs located at distance D from each other on the chromosome.

Simulation of the printing procedure

We generated four groups of time-dependent ‘log-ratios’ [ξ₁(i,t), ξ₂(i,t), ξ₃(i,t), and ξ₄(i,t), i = 1, 2, 3, …, N_G/4] by choosing uncorrelated random values from a Gaussian distribution. The total number of ‘genes’ in this simulation was N_G = 400 and the four groups of 100 simulated ‘log-ratios’ corresponded to the four groups of genes printed by each of the print tips. Additionally, to model the contribution of the four printing tips to the measured expression, four independent random values, η₁(t), η₂(t), η₃(t) and η₄(t), were added to each gene in the four groups at each time. In the α-factor experiment, the order of genes in the data table is a function of the physical location of their corresponding probes on the microarray. The order of genes in our simulated data table was determined using the same function, selecting genes from the four groups as follows: G₁¹, G₂², G₃¹, G₄², …; G¹_{P– 1}, G_P², G³_{P+ 1}, G⁴_{P + 2}, G³_{P + 3}, G⁴_{P + 4}, …; G³_{2P – 1}, G⁴_2P, G¹_{2P + 1}, G²_{2P + 2}, …; where P = 10 represents the number of wells within one row on the ‘plate’. The superscripts and subscripts represent the group (1, 2, 3 or 4) to which the gene belongs and the number of the gene in the list, respectively. Finally, we calculated the average cross-correlation of the genes in the list, depending on the distance D, defined as the difference of their subscripts [D(G_i^m,G_jⁿ) = |i – j|]. See Supplementary Material for a theoretical understanding of the observed spatial periodicity of co-expression.

Correction of the bias introduced by the print tips

To correct for the bias introduced by the print tips, we applied the method described in Yang et al. (21), i.e. at each time t we subtracted the average expression (4/N_G)∑_iξ_g(i,t) from all the ‘log-ratios’ within each group g, g = 1, 2, 3, 4:

ξ_g*(i,t) = ξ_g(i,t) – [(4/N_G)∑_iξ_g(i,t)]     4

where the asterisk denotes the corrected values.

We applied the same correction method to the experimental data, replacing ξ_g(i,t) with E_g(i,t) in equation 4. However, for the experimental data, the bias within an experiment is not constant, but has a trend as the experiment proceeds (see Fig. 3a). Therefore, for each of the 64 microtiter plates used in an experiment, we improved the method described in Yang et al. (21) by calculating the average log-ratios

Figure 3.

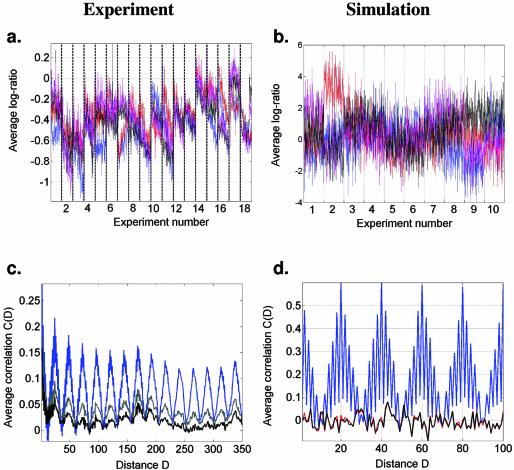
Print tip-related bias across all experiments and the corresponding simulation. (a) Average log-ratios of expression levels of the features printed by each of the four tips within each 96-well plate used in each experiment (IAD). Blue, red, black and magenta correspond to print tips 1–4, respectively (the numbers define the spatial position within the print head and not the actual print tip). The abrupt changes of the average log-ratios between experiments are likely to correspond to cleaning and interchanging the print heads. Notice how the bias gradually changes within each experiment, until the tips are cleaned or changed. (b) The corresponding simulation: four groups of 10 × 10 uncorrelated Gaussian random numbers were generated in 18 in silico experiments. Additionally, four independent random numbers were added to each of the four groups within each experiment. The log-ratios of simulated expression levels of all spots within each ‘experiment’ are shown. To correct for the tip-related bias, the mean log-ratio for tips 1–4 within each experiment is subtracted from the corresponding group of spots. (c) The result of the correction: average cross-correlation calculated as in Figure 1, but using all genes instead of those residing on the same chromosome. The blue, gray and black lines correspond to the original data, the first degree and the second degree correction, respectively. In the second degree correction, a linear trend of the log-ratios is subtracted within each experiment instead of simply subtracting the mean log-ratio. Notice that the 2 gene and 24 gene periodicities nearly disappear, but a 176 gene periodicity is revealed. (d) Correction of the computationally generated data. The red, blue and black lines correspond to the original, bias-affected and corrected data, respectively. Notice that the correction algorithm almost completely recovers the original in silico data after the correction.

corresponding to tip g and plate p at time t. Next, we approximated the increasing trend of the bias at time t by using a least squares linear fit. Finally, we obtained the corrected E_g**(i,t) as follows:

E_g**(i,t) = E_g(i,t) – [a(t)p + b(t)]     5

where a(t) and b(t) are the coefficients obtained from the linear fit at time t.

Hierarchical clustering and functional classification

We used the algorithms Cluster and TreeView developed by Eisen et al. (25) to hierarchically cluster the genes based on the similarity of their expression profiles, both for the original and the corrected data. Next, we developed our own software to color the dendrogram produced by the program Cluster based on the functional classes to which the genes belong (see Supplementary Material). The 19 functional classes of S.cerevisiae gene products (see Supplementary Material) were downloaded from the MIPS database (26): http://mips.gsf.de/proj/yeast/catalogues/funcat/.

We define the distance of two genes on the dendrogram as the minimum number of steps needed to walk from one node to the other as follows. For each pair of nodes, the list of superior nodes is determined. If the numbers of steps to the first superior node common to both are s₁ and s₂, respectively, then the distance of the nodes on the dendrogram is s₁ + s₂. The closest neighbor of a gene within a functional class is the gene from the same functional class located at minimum distance from it. The average minimum distance is the arithmetic mean of the distances between all closest neighbors within a functional class.

RESULTS

Spurious spatial periodicity of co-expression during the S.cerevisiae cell cycle

We examined the similarity of temporal expression profiles of individual genes as a function of their spatial separation along the individual yeast chromosomes. We rearranged the microarray expression data such that all genes followed their natural order along the 16 yeast chromosomes. Next, we calculated the average spatial cross-correlation coefficient C(D) of the temporal expression profiles of genes located at a distance D from each other (see Materials and Methods). If the expression level of neighboring genes did not correlate, C(D) should be approximately 0 for any D ≠ 0. As gene expression requires a locally permissive chromatin structure (27), we expected C(D) to gradually decay with the distance due to the fact that neighboring genes have a higher likelihood to be simultaneously accessible for transcription than those that are far from each other along the chromosome. In contrast, we found that C(D) exhibited an unexpected and remarkable periodicity. As shown in Figure 1a for α-factor synchronized yeast cells (24), on average the temporal expression profiles of genes located at distances that are multiples of 24 have an increased tendency to correlate in all chromosomes. At higher resolution (Fig. 1a, inset) the presence of a second spatial periodicity with smaller amplitude is also evident with a remarkably regular 2 gene period superimposed on the 24 gene periodicity.

The observed spatial periodicity was not unique to yeast cells synchronized by α-factor arrest. Yeast cultures synchronized by elutriation or by arrest of a cdc15 temperature-sensitive (ts) mutant displayed a similar periodicity to that seen for α-factor arrest (24). In contrast, the period for cdc28^ts mutants (23) was shorter, involving genes located at distances that are multiples of 13 (see Supplementary Material). The source of this difference was not immediately apparent, since both the synchronization protocols and the yeast strains were different from the other experiments. However, the data for cdc28^ts mutants were collected on Affymetrix oligoarrays (23), while all others were collected on cDNA microarrays in a different laboratory (24), suggesting a possible systematic experimental bias as the source of the observed periodicity.

To assess whether the 2 gene and 24 gene periodicities correspond to true biological activity or to consistent experimental biases, we examined the properties of the spotted cDNA microarrays utilized in the α-factor experiment. As the cDNA probes are deposited on the microarray slides in a highly regular pattern (see Materials and Methods and Fig. 1c), we studied how the average distance of the cDNA probe spots on the scanned images depends on the chromosomal distance of their corresponding genes. The average inter-spot distance δ(D) on the scanned fluorescence images for all genes separated by a chromosomal distance D is shown in Figure 1b, with an enlarged section in the inset. It is evident that the double periodicity present in these graphs is virtually identical to that seen for the average spatial cross-correlation coefficient C(D) in Figure 1a. This indicates that the observed spatial periodicity of the average spatial cross-correlation coefficient C(D) in spotted cDNA arrays arises as a consequence of the experimental technology (Fig. 1c and d). A similar analysis for the Affymetrix oligoarrays was not possible, because the scanned fluorescence images and the location of the oligonucleotide groups on the array are not publicly available.

The experimental source of the spurious periodicity of co-expression

To uncover the cause of the observed spatial periodicity, we calculated the average log-ratio of expression for each of the 96 wells on the 64 microtiter plates from which the deposited cDNA probes originated (Fig. 2a). The images that we obtained following this calculation displayed a surprising regularity for all 18 time points of the α-factor experiment, i.e. they can be viewed as a repetition of a block of four wells (Fig. 2b). This, together with the arrangement of the features on the scanned slide images into four distinct blocks, implies that the observed regularity is a result of tip-specific biases introduced by the four-tip printing head, as previously suggested (21).

To further demonstrate this, we averaged the log-ratios corresponding to each of the four positions within the 4-well blocks in all α-factor experiments (Fig. 2b). At the same time we calculated the average log-ratio of all the spots located within one of the four blocks on the slide (Fig. 2c). The average log-ratios calculated in these two ways were identical, allowing us to label each well on the 96-well plates and each spot on the microarray slide with 1, 2, 3 or 4, corresponding to the four printing tips. (The indices 1–4 characterize the position of the tips within the print head, and not the actual print tips.)

In Figure 3a we plotted the average log-ratio of all genes printed by tips 1–4, with blue, red, black and magenta, respectively, for plates 1–64 progressively used in each of the 18 α-factor experiments. There are three conclusions that can be drawn from investigating Figure 3a. First, the systematic difference between the average log-ratios corresponding to different print tips demonstrates the tip-specific contribution to the measured gene expression. Second, the experimental contribution to the measured log-ratio gradually changes as each of the 18 experiments progresses (from plate 1 through plate 64). Finally, the abrupt changes of average log-ratio at the borders between two experiments most likely reflect the fact that the print tips were manipulated (cleaned and replaced in the print head in random order) between experiments.

Next we examined if the observed periodicity can arise as the result of four random, additive time-dependent biases η₁(t), η₂(t), η₃(t) and η₄(t), which identically affect all genes labeled 1, 2, 3 and 4, respectively. To this end, we simulated the printing procedure (see Materials and Methods) and calculated the average cross-correlation of the genes in the list, depending on the distance D between them. The results of this simulation, shown in Figure 3b and d, were very similar to those observed in the actual experimental data (Fig. 3a and c). Thus, it is evident that the print tips introduce a significant bias to the experimental data. The average standard deviation of a time series during the α-factor experiment is σ_ξ = 0.268 ± 0.14, while the average standard deviation of the bias introduced by a print tip is σ_η = 0.095 ± 0.0067 (i.e. 36% of σ_ξ). Due to such a contribution, the cross-correlation coefficient of any two time series will typically be altered (see Supplementary Material) by a value up to

ΔC ≈ [1 + (σ_ξ/σ_η)²]^–1 = 0.1116.

For example, the average cross-correlation coefficient of all pairs of genes within groups 1 and 2 are 0.1442 ± 0.3085 and 0.1338 ± 0.3006, respectively. However, the average cross-correlation of all possible gene pairs between groups 1 and 2 is only 0.0111 ± 0.2903. Moreover, the actual value of the increase in cross correlation could be much greater, depending on the standard deviations and the cross-correlation coefficient of the two time series before correction.

The source of the observed periodicity of C(D) in Affymetrix oligoarrays remains unclear. However, most probably the source of this periodicity is not biological either. To understand it, detailed information is needed about the manufacture of oligoarrays used in the cdc28^ts experiment.

Correction of technical bias in microarray data

An obvious approach to correct for the uncovered systematic bias is to calculate the average expression within each of the four groups of genes at each time point and subtract it from all genes in that group. As shown in Figure 3d, this method results in the complete elimination of the spurious periodicity in the simulated data. However, when we apply the same technique to the experimental data (Fig. 3c), the periodicity is reduced in amplitude, but it does not completely disappear. The explanation for this is that in the experimental data the four bias values are not constant throughout an experiment. Instead, they gradually change from the first to the last (64th) microtiter plate used within each of the 18 α-factor experiments, i.e. they are characterized by a trend as a function of the plate number. If we correct for this trend as well (using a linear fit to the expression data within each α-factor experiment), the 2 gene and 24 gene periods disappear almost completely (Fig. 3c). However, at this time a 176 gene periodicity, which was initially masked by the other two periods, is revealed. This 176 gene period is not related to the printing tips. Rather, it indicates the existence of a location-dependent bias for each spot on the microarray, as it takes 176 = 4 × 44 spots to arrive back near a given printing position on the slide (Fig. 2a). The remainders of the 2 gene and 24 gene periodicities are due to deviations of the trend from linearity.

Average linkage clustering of the original and corrected microarray data

To determine the biological implication of these data correction techniques, we studied whether the result of average linkage clustering (25) is different for the original and the corrected data sets in the α-factor experiment. For chromosome A the resulting dendrograms are qualitatively similar, but also show local differences (see Fig. 4a and b). To examine whether the correction technique improved the biological significance of the results, we assigned functional classes to the genes based on the functional classification of their products in the MIPS database (26). Next, we iteratively colored all nodes of the dendrogram according to the functional classes to which they belong (see Materials and Methods). From Figure 4a and b it is apparent that genes within the same functional class are closer on the dendrogram when the corrected gene expression data is used. To quantify this improvement, we calculated the average minimum distances within each functional class on the dendrogram (see Materials and Methods). The average minimum distance in the original dataset was greater for the majority of functional classes (Fig. 4c): it decreased from 13.3369 to 12.4067 after the correction.

Figure 4.

The consequence of the correction on subsequent analyses. Average linkage clustering of the (a) original and (b) corrected data for chromosome A in the α-factor experiment (CD). The colors correspond to functional classes downloaded from the MIPS database (http://mips.gsf.de/proj/yeast/catalogues/funcat/). Notice the visible change in the resulting dendrogram and the closer clustering of genes within the same functional classes. (c) The average minimum distance among genes within the same functional class for the original (black bars) and corrected (red bars) data. The minimum distances averaged over all functional classes are 13.3369 and 12.4067 for the original and corrected data, respectively.

DISCUSSION

The large amount of microarray data that has been collected over the last several years promises to revolutionize our understanding of the global transcriptional organization of cells as well as the classification of clinical entities, such as various tumor types. A key requirement of this goal, however, is to examine biological information rather than technology-derived systematic bias. Despite the fact that bias introduced by printing tips within one repeated experiment has been known and has been corrected before (21), the importance of this problem in the context of multiple experiment protocols has never been previously realized. Here we have identified the source of the systematic technical bias for spotted cDNA arrays in great detail, and developed an improved method to correct for the changes in bias as each experiment progresses. The source of the spatial periodicity for Affymetrix oligoarrays is not clear, since the details of oligoarray manufacture (e.g. the location of oligonucleotide groups) are not publicly available.

The generality of our results suggests that in addition to the transcriptome profiles of the yeast cell cycle, many previously published microarray datasets may be affected by the same systematic biases. Thus, there is a need to computationally correct both existing and future microarray data along the lines suggested here, and to make the corrected data available to the scientific community. Also, if the outcomes of microarray experiments are expected to be quantitatively reliable, it will be necessary to modify the printing protocols, repeat the experiments several times and take the average as a result. In particular, care has to be taken that the set of genes printed on each slide by one printing tip be as different as possible in each experiment, because two genes printed by the same tip in all experiments will have a greatly increased cross-correlation coefficient. Moreover, in multiple experiment protocols the effect of print tips on the cross-correlation coefficient becomes increasingly dominant at the expense of biological information as the number of experiments increases (see Supplementary Material).

Several recent studies indicate that genes with similar expression profiles spatially cluster within the genomes of several organisms (28–33). This information, taken together with the evidence for a connection between gene expression and chromatin dynamics (34), underlines the need to search for the effect of spatial chromatin organization on gene expression in space and time. Temporal microarray data could provide the means to uncover the potential spatio-temporal organization of gene expression. However, the systematic print tip related bias that we have uncovered indicates that currently available time series (or multiple experiment) data on gene expression are not suitable to answer such questions. Thus, extreme care has to be taken when interpreting microarray data to uncover the relationship between relative chromosomal position and co-expression of genes (28,29,31), since the observed effects are likely to arise due to the printing procedure and the arrangement of probes on the microarray.

Based on our results, it should be easy to develop a computer program to serve as a sensitive test and compare the printing quality across different sets of experiments. For multiple experiment protocols, the program would calculate and compare average cross-correlations between a large set of probe pairs printed by the same tip and probe pairs printed by different tips. If the average cross-correlation for probe pairs printed by the same tip is found significantly higher than for probe pairs printed by different tips, the microarray data have to be corrected. For single experiment (or repeated experiment) protocols, the mean and standard deviation of probes printed by each tip have to be calculated and compared (21). If the values obtained for probe sets printed by different tips are significantly different, the microarray data have to be corrected.

Microarray technology has greatly improved our understanding of biological processes and disease entities. However, the example presented here demonstrates the indispensability of a routine search for systematic experimental biases in the analysis of systematically collected, large-scale biological datasets.

SUPPLEMENTARY MATERIAL

Supplementary Material is available at NAR Online.