Structural details (kinks and non-α conformations) in transmembrane helices are intrahelically determined and can be predicted by sequence pattern descriptors

Abstract

One of the promising methods of protein structure prediction involves the use of amino acid sequence-derived patterns. Here we report on the creation of non-degenerate motif descriptors derived through data mining of training sets of residues taken from the transmembrane-spanning segments of polytopic proteins. These residues correspond to short regions in which there is a deviation from the regular α-helical character (i.e. π-helices, 3₁₀-helices and kinks). A ‘search engine’ derived from these motif descriptors correctly identifies, and discriminates amongst instances of the above ‘non-canonical’ helical motifs contained in the SwissProt/TrEMBL database of protein primary structures. Our results suggest that deviations from α-helicity are encoded locally in sequence patterns only about 7–9 residues long and can be determined in silico directly from the amino acid sequence. Delineation of such variations in helical habit is critical to understanding the complex structure–function relationships of polytopic proteins and for drug discovery. The success of our current methodology foretells development of similar prediction tools capable of identifying other structural motifs from sequence alone. The method described here has been implemented and is available on the World Wide Web at http://cbcsrv.watson.ibm.com/Ttkw.html.

INTRODUCTION

The relationship between a protein amino acid sequence and its three-dimensional structure (1,2) is at the very core of structural biology and bioinformatics. Although primary and tertiary structural data on proteins have accrued at a very fast pace, a general purpose algorithm for deducing the fold of a polypeptide (i.e. its three-dimensional structure) from its sequence remains elusive. This is particularly true for polytopic membrane protein superfamilies, such as the G-protein-coupled receptors, for which a high-resolution structure has thus far been determined for only bovine rhodopsin, one of the family’s 1000+ members.

Some of the most successful approaches to three- dimensional structure and function prediction are based on the fact that the large numbers of currently known primary structures are organized, by their similarities, into far fewer protein families presumed to share the same fold.

Physical characteristics of natural polypeptides, i.e. amphiphilic polymers containing a mixture of polar and non-polar side chains, are such that there is an upper limit on the size of a single, compact, folded protein domain, i.e. approximately 300–400 residues. In such domains, only a few thousand unique folds are expected to occur in nature (3,4) (by ‘fold’ we mean a polypeptide chain with secondary structure elements, i.e. α-helices, β-sheets and loops, assembled in space with a defined topology and tightly packed into a compact domain).

At the one-dimensional sequence space of amino acids, conservation of the three-dimensional structures of polypeptides is typically reflected by conservation of selected residues at defined positions of amino acid sequence alignments. The specific amino acid choices and their relative arrangement in the sequence correspond to sequence patterns that constitute ‘signatures’ representative of protein folds (5).

Determination of conserved sequence patterns often employs similarity search software programs that carry out direct pair-wise comparisons of a query with every sequence present in a large database, e.g., FASTA (6), BLAST/PSI-BLAST (7), Smith–Waterman (8), etc. An alternative approach identifies conserved sequence patterns in a set of multiply aligned sequences (9). If enough sequences are available, they can be used to build a Markov model and an engine suitable for searching databases for more instances of similar patterns [see, for example, Karplus et al. (10)].

In earlier work, the Teiresias pattern discovery algorithm (11) was used to identify and build a very large collection of sequence patterns by processing the GenPept database as a whole (12); this computation has been routinely repeated at regular intervals on the increasingly larger releases of the SwissProt/TrEMBL database (13). The patterns contained in this collection have been shown to capture functional and structural signals that extend beyond protein family boundaries, not an unexpected result considering the manner in which the collection is produced. Additionally, and since this collection nearly completely covers the currently known sequence space of natural proteins, it can be used in lieu of the original processed sequence database to solve a gamut of problems, which among others include protein annotation (14), gene finding (15), etc. In an analogous manner, in the work described herein, we have replaced the original input database, i.e. a small training set of transmembrane ‘non-canonical’ conformations, by an equivalent set of amino acid patterns and have derived from it pattern descriptors with unique predictive power.

Transmembrane helices of polytopic proteins are common building elements of many large, biologically important structures such as tissue- and/or ligand-specific receptors and enzymes (16). It has been reported that non-canonical conformations occur frequently in these proteins and are critical determinants of their structure and function (17,18). As such, they are frequently conserved, and sequence patterns encoding them represent a convenient point of departure for the potential generation of pattern descriptors for other structural elements within complex proteins.

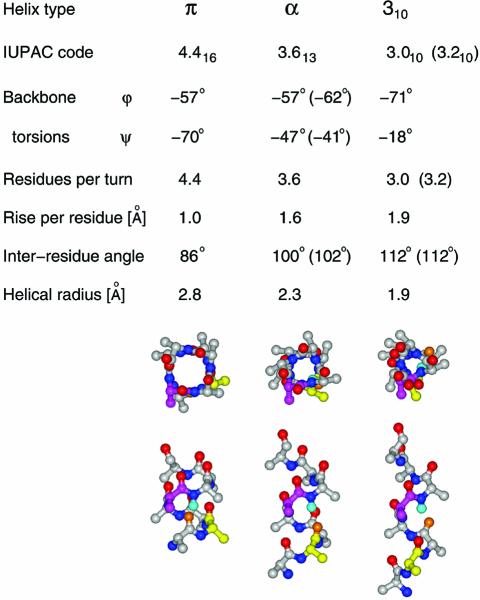
Helical conformations have most often been described by their backbone torsional values, φ and ψ. However, the relationship of these torsions to chain geometries is complex and degenerate, i.e. many different combinations of φ, ψ angles are compatible with a single C_α trace. Geometric descriptors of different helical habits with increased discriminating power include C_α–C_α distances (plotted as differences from the corresponding values in a canonical α-helix), inter-residue or spoke angle plots, rise per residue plots, and H-bond connectivity plots. Table 1 summarizes the geometric properties of these three types of non-α-helical elements; the latter evidently occur in relatively short sequence runs, typically not exceeding the length of two α-helical turns (7–8 amino acids).

Table 1. Parameters characterizing non-canonical conformations.

See Pauling et al. (19) and Barlow and Thornton (20) for explanations of theoretical (–57, –47) and natural (–62, –41) α-helical backbone torsions, and the theoretical (3.0) and the actual (3.2) ‘3.0’ helix. Backbone stick diagrams are those of nonaalanine peptide in π, α and 3₁₀ conformations, with residues 2 and 5 color coded yellow and magenta. The amide hydrogen of residue 6 is shown in cyan and the closest carbonyl oxygen that can form a backbone hydrogen bond is shown in orange.

Here we report on the development of sequence-based descriptors for the three ‘non-canonical’ conformations important for the structure and function of transmembrane α-helices, namely the π-like helices, 3₁₀-like helices, and the proline- and non-proline-induced kinks. To the best of our knowledge, the identification of such non-α-helical structures directly from sequence has not been attempted previously. It should be noted that approaches based on sequence similarity tools or Markov models are not well suited for this task due to the short length of the involved peptides; the same holds true for the traditional secondary structure prediction methods. On the other hand, as outlined below, pattern discovery carried out at the primary structure level can effectively tackle this problem.

MATERIALS AND METHODS

Although no definite non-canonical sequence patterns have been described previously, characteristic ‘fuzzy’ sequence features have been known to associate with the non-canonical structures in which we are interested. In fact, in the π-helices, residues with large aromatic or hydrophobic side chains often precede the proline residues; the 3₁₀-helices contain β-branched side chains N-terminal to proline residues and, in proper kinks, aromatic residues are frequent, with glycine near, and sometimes outside, the kinks (17).

In brief, we began with a small and carefully constructed set of amino acid sequence fragments corresponding to instances of the three non-canonical conformations. Then, employing an approach whose underpinnings can be traced to the work described in Rigoutsos et al. (12,14), we computed separately for each of the three categories an exhaustive set of sequence patterns with two or more instances in each of the three input sets.

A complete collection of all instances of non-canonical conformations was constructed and kept up to date by manually analyzing new membrane protein structures deposited with the Protein Data Bank and categorizing the sequences of the corresponding transmembrane helices into each of the three groups of non-canonical conformations. Within each group, the individual fragments were right-aligned, i.e. terminated at the ‘signature’ residue of each instance (e.g. the proline in proline-induced kinks). As reported previously (17), in all cases, it is the residues N-terminal but not C-terminal to the signature residue involved in a non-canonical element which are responsible for the deviations from α-helicity. The right-aligned 5–9 residues [the exact number used being determined from deviations in i→i-4 backbone hydrogen bonding, cf. (17)] responsible for each occurrence of each non-canonical element were then tabulated to develop training sets for each type of non-canonical element; examples for π-helical segments are shown in Figure 1. If an entry under consideration identically agreed with an entry already existing in the repository over the extent of the non-canonical element at hand (i.e. 5–9 residues), then the new entry was considered a duplicate and discarded.

Figure 1.

Instances of proline- and non-proline-induced π-helical segments determined from the X-ray crystallographic structures of various proteins (PDB codes followed after the first colon by a letter designation for the protein chain and transmembrane helix numbering are indicated in the left most column). The residues N-terminal to the perturbing residue that form the π-helical segments are shown in bold, and the 10 residues on either side of the set of perturbing residues are shown with the numbering of the most N-terminal residue indicated on the left and that of the perturbing residue on the right.

Our training set consists of our latest collection of non-redundant entries: it was determined as described above and contains 33 instances of π-helical motifs, 34 instances of 3₁₀-helical motifs, and 55 instances of proline- and non-proline-induced kink motifs. In Table 2, we list the Protein Data Bank entries together with the protein chain and number of the transmembrane helix which contained each of the training instances.

Table 2. For each of the three categories of deviations from the α-helical habit, we list the Protein Data Bank entries together with the protein chain and number of the transmembrane helix which contained each of the training instances.

Instances of tight turns	Instances of true kinks	Instances of wide turns
2OCC:A8	2OCC:A2	2OCC:A2
1AR1:A8	2OCC:A5	2OCC:G1
1PRC:L3	2OCC:A6	1AR1:A2
1C3W:A6	2OCC:A6	1BE3:C8
1E12:A6	2OCC:A10	1AIJ:L3
1EHK:A8	2OCC:B2	1AIJ:M3
1EZV:C6	2OCC:B2	1PRC:L3
1JGJ:A6	2OCC:M1	1PRC:M3
1JB0:L1	1AR1:A2	1F88:A5
1JB0:M1	1AR1:A5	1EHK:A5
1M56:A8	1AR1:A6	1EYS:L3
2OCC:D1	1AR1:A6	1EYS:M3
1AR1:A11	1AR1:B2	1JB0:A3
1BE3:D9	1AR1:B2	1JB0:B7
1AIJ:L3	1BE3:D9	1JB0:I1
1AIJ:M3	1C3W:A2	2OCC:A2
1AIJ:M5	1C3W:A3	2OCC:A10
1PRC:L5	1E12:A2	2OCC:I1
1PRC:L5	1E12:A3	1AR1:A2
1PRC:M3	1EUL:A11	1AR1:A10
1PRC:M5	1F88:A4	1C3W:A7
1E12:A3	1F88:A6	1E12:A5
1F88:A3	1F88:A7	1E12:A7
1F88:A7	1F88:A7	1EUL:A1
1EHK:A4	1FX8:A7	1F88:A2
1EHK:A5	1FX8:A8	1FX8:A8
1EHK:A6	1EHK:A2	1EHK:A2
1EHK:A10	1EHK:A3	1EHK:A10
1EYS:L3	1EHK:A6	1JGJ:A5
1EYS:M3	1EHK:A6	1JGJ:A7
1EYS:M5	1EHK:A9	1JB0:A3
1EYS:M5	1EHK:A13	1JB0:A7
1JB0:A10	1EZV:G1	1JB0:B3
1JB0:B10	1JGJ:A3
	1JB0:I1
	1M56:A5
	1M56:A6
	1M56:B2
	1KQF:C2
	2OCC:A10
	2OCC:C3
	2OCC:C6
	2OCC:K1
	2OCC:L1
	1AR1:A10
	1EUL:A1
	1F88:A3
	1FX8:A8
	1EZV:D1
	1JGJ:A2
	1JGJ:A4
	1JB0:A9
	1JB0:B9
	1JB0:L1
	1M56:A9

The entries above (resp. below) the horizontal line in each column have proline (resp. a residue other than proline) as their signature residue.

We subsequently applied the Teiresias algorithm (11) to each of the three categories of our training set and discovered patterns that described the corresponding category in its entirety and were specific enough to identify instances of each non-canonical element in a database of protein sequences. During the pattern discovery process, we took into account the following 12 classes of equivalent residues: (a) {A,G}, {D,E}, {K,R}, {I,L,M,V}, {S,T}, {Q,N}, {F,Y}, and (b) {A,S}, {F,L}, {S,N}, {I,V,T}, {A,T,G,S}. Group (a) comprises traditionally accepted equivalence classes that preserve the chemical nature of a residue. On the other hand, group (b) was derived from observing typically occurring substitutions within class-1 of the G-protein-coupled receptors. Allowing the amino acids within each class to replace one another is expected to increase the sensitivity of the discovered patterns, but at the same time is bound to result in a larger number of patterns with decreased specificity. Less specific patterns can in general give rise to cross-talk and to false-positive hits but, as shown below, this did not become an issue in our work.

From the generated set of patterns, we subselected only those whose right-most literal coincided with the ‘signature residue’. All wild cards were subsequently replaced by a regular expression of the type [X₁X₂ … X_M] where each X_i was an amino acid choice that the wild card was representing; those patterns for which the regular expression required that M be ≥4 were discarded. We retained only those patterns that included the signature residue and an additional 6–8 positions to its left and which had an estimated log-probability ≤–23 of being accidental occurrences. (The log-probability estimate for each pattern was computed using a second-order Markov chain built from the contents of the SwissProt/TrEMBL database.) The N_i patterns that satisfied the above properties were included in a composite descriptor C_i for the ith category (with i being one of {3₁₀-helix, kink, π-helix}). Clearly, the number of patterns that effectively comprise each composite descriptor can be controlled by the user-defined LogProb_thres, e.g. when LogProb_thres = –25, the composite descriptors for the 3₁₀-helix, kink and π-helix classes consist of 7697, 21 167 and 10 032 patterns, respectively. By design, the patterns in each collection completely, unambiguously and redundantly characterize each non-canonical structure as captured by the category’s respective training instances. It should be noted that, although we could identify and remove from each composite descriptor C_i those of its patterns that matched training sequences of the other two descriptors, we did not do so. Instead, we opted to let the composite descriptors compete with one another as explained below. This would not have been a good design choice had the patterns comprising each composite descriptor been degenerate.

The three non-canonical composite descriptors were combined into a single engine that could process an amino acid query sequence and annotate various regions of the sequence as being instances of non-canonical conformations. The patterns from composite descriptor C_i that had a user-defined log-probability of random appearance ≤LogProb_thres (clearly, LogProb_thres ≤–23) and matched over the same region of the query, contributed to the right-most R_i positions of the region ‘an amount’ equal to 1/N_i: this simple weighted scheme allows us to account for the fact that each descriptor comprises a different number of patterns. We set the value of R_i to 6 for 3₁₀-helices, 5 for kinks and 7 for π-helices. A query position would be considered further if, and only if, it was matched by at least P patterns.

Let now x₁, x₂ and x₃ denote the contributions a position receives from each composite descriptor, respectively; we use the unit vector (u₁, u₂, u₃) = (x₁, x₂, x₃)/||(x₁, x₂, x₃)|| to determine the position’s membership in a category. Note that in the online implementation of this engine (http://cbcsrv.watson.ibm.com/Ttkw.html), we plot this vector as a function of position.

The following represent typical thresholding choices that can be used to label positions which are matched by at least P patterns: (i) if for a given position, u_i ≥ 2.5 u_j and u_i ≥ 2.5 u_k, the position should be labeled by category i (similarly for the other categories); (ii) if, on the other hand, u_i ≥ 2.5 u_k and u_j ≥ 2.5 u_k, the position should be labeled as a hybrid between categories i and j (similarly for the other pairs of categories; an example of such a situation is an amino acid that is the signature residue for one non-canonical conformation but also participates in an instance of a second non-canonical conformation that immediately follows its position); and (iii) otherwise, the position would be labeled as a hybrid between all three categories.

RESULTS

First, we evaluated the sensitivity of each of the three descriptors as well as the potential of each descriptor to erroneously recognize as its own instances of non-canonical elements belonging to any of the other two categories. In fact, the composite descriptor for each category correctly characterized all of the training sequence fragments of its own category. Under the assumption that our training sets provide a representative sample of these non-canonical elements, this last result indicates that the sensitivity of each composite descriptor was at 100% for the instances of the respective class. Given that the patterns comprising each composite descriptor do not include any of the training sequences in its original form, correct recognition of all of these sequences is a non-trivial event. Indeed, by definition, the computed patterns correspond to amino acid combinations that appear twice or more in the training sequences from each category; moreover, any duplicate entries have been removed from the training sets.

In an effort to gauge the potential for ‘cross-talk’ situations, each composite descriptor was used to interrogate the training instances of the other two categories. Cross-talk, if present, would demonstrate itself when one or more patterns from the composite descriptor for a type i non-canonical conformation matched training set instances for a type j conformation, with i ≠ j (here, i and j assume values from the set {3₁₀-helix, kink, π-helix}). Clearly, as the value of LogProb_thres increases, so does the potential for cross-talk. By processing the training sequences and carrying out the 6 (=3 × 2) tests using LogProb_thres = –23, we verified that no composite descriptor generates hits outside of its own class. Thus, there is no cross-talk between the composite descriptors, as this can be assessed by using the training sets as a collection of true positives.

Next, we evaluated the rate at which our scheme generated false positives by interrogating a database of non-transmembrane protein sequences using all three composite descriptors simultaneously. The target database consisted of the union of all full-length sequences that are contained in the ‘all alpha’ and ‘all beta’ classes of the SCOP database (21), and comprised 120 sequences with a total of 18 885 amino acids. The goal of this experiment was to determine whether the composite descriptors would result in erroneous conclusions if presented with (i) helical structures that were not membrane spanning; and (ii) non-helical structures. If the result of our pattern discovery phase was the generation of descriptors that simply recognized helices, then non-membrane-spanning α-helical queries would give rise to false positives. Similarly, if our descriptors were not specific enough, then amino acid sequences corresponding to non-helical structures would also generate false hits. Finally, if the result of training was the creation of descriptors which recognized transmembrane elements, then non-transmembrane α-helical and β-sheet queries should generate no false positives.

For the purposes of this evaluation, any region in the processed input that was claimed by a composite descriptor to be an instance of the descriptor’s category gave rise to R_i mislabeled amino acid positions; naturally, an ideal composite descriptor should find no instances of non-canonical conformations in the ‘all alpha’ and ‘all beta’ input we described above. We counted the total number of mislabeled positions and used it to calculate the ratio of correctly labeled positions for various combinations of LogProb_thres and P. Table 3 shows the results of this analysis. As can be seen therein, for several choices of P and LogProb_thres, we can correctly exclude 99.97% of the processed positions (= an equivalent false-positive rate of 0.03%). These results corroborate our proposal that the original sequence elements as well as the composite descriptors that were derived from those elements are uniquely restricted to non-canonical structures within transmembrane regions. Clearly, the least restrictive combination of P and LogProb_thres values for which this rate is achieved, i.e. P = 7 and LogProb_thres = –26, makes an ideal choice for default settings.

Table 3. Ratio of correctly labeled amino acid positions when processing the union of the full-length sequences in the ‘all alpha’ and ‘all beta’ SCOP classes.

		LogProbthres choices for the patterns forming the composite descriptors
		–23	–24	–25	–26	–27	–28
Minimum number P of patterns required to match a region before it can be reported	4	99.28%	99.45%	99.75%	99.92%	99.95%	99.95%
	5	99.38%	99.52%	99.80%	99.92%	99.95%	99.95%
	6	99.59%	99.75%	99.87%	99.95%	99.95%	99.95%
	7	99.64%	99.76%	99.89%	99.97%	99.97%	99.97%
	8	99.69%	99.82%	99.89%	99.97%	99.97%	99.97%

See also text for a discussion.

Using these default settings, we ‘interrogated’ the bovine rhodopsin primary structure for the presence of various types of non-canonical elements. Although sequence elements from rhodopsin were included in the original sequence sets, by virtue of having replaced the entire training set by a collection of patterns, the composite descriptors did not include any of rhodopsin’s original sequence inputs per se. For P = 7 and LogProb_thres = –26, our search engine identified all non-canonical elements that could be manually recognized in the crystal structure of rhodopsin and correctly determined their nature and spatial extent. Figure 2 is a color-coded depiction of the search engine’s output. Within helix 1 of the bovine rhodopsin, there is a kink with proline as the signature residue (xxxLLI-MLGFP-INFxxx). A proline occurs at this position in only 8.2% of the class-1 G-protein-coupled receptors. However, this kink is included in a segment of sequence that, in the majority of the class-1 receptors, exhibits similarity to sequences in our training set for a wide turn with asparagine as the signature residue (xxxGGFGNxxx). In 50.1% of class-1 receptors, a glycine is present at position N-4, i.e. xxxGgfgNxxx, whereas 75.2% have a glycine at position N-1, i.e. xxxggfGNxxx. An examination of this helical region in the crystal structure of rhodopsin shows properties of both a kink and a wide turn. Given this complexity, this segment was not included in the initial training set and is, thus, not shown in Figure 2.

Figure 2.

Non-canonical conformations identified by the descriptor search engine in the bovine rhodopsin primary structure: helical regions are shown in red letters and non-helical regions in black. For this run, LogProb_thres was set to –26 and P was set to 7; see text for a description of the parameters. For this choice of parameters, the search engine correctly identified all the non-canonical elements that can be identified in the bovine rhodopsin crystal while generating no false hits. The identified non-canonical features are shown by color-coding: green, π-helix; pink, 3₁₀-helix; yellow, proline- or non-proline-induced kink. See also text for a discussion.

We also examined the impact that the values for P and LogProb_thres have on the non-canonical conformations that our pattern-based search engine identifies, using again the bovine rhodopsin sequence as our test input. As it turns out, from among the various P and LogProb_thres combinations listed in Table 3, the only one which gives rise to a false prediction is the least stringent P = 4 and LogProb_thres = –23. Figure 3 is a color-coded depiction of the search engine’s output in this case: a falsely predicted kink (shown in blue) appears, in addition to the correctly predicted non-canonical conformations.

Figure 3.

Examining the impact of the parameter settings on the non-canonical conformations identified by the descriptor search engine in the bovine rhodopsin primary structure: helical regions are shown in red letters and non-helical regions in black. As shown in Table 3, reducing the system’s stringency increases the expected average amount of mislabeling. This is demonstrated here, again using the bovine rhodopsin sequence as the test input: for the least stringent combination of values in Table 3 (LogProb_thres = –23 and P = 4), a kink is falsely predicted (shown in blue color), in addition to the correctly predicted non-canonical conformations. Notably, this is the only combination of values from Table 3 which will give rise to a false positive when processing the bovine rhodopsin sequence. See also text for a discussion.

Finally, we used the program to evaluate a number of other G-protein-coupled receptors, including the three α₁- and three β-adrenergic receptor subtypes. Based on detailed biophysical studies (22), these proteins are all predicted to have a proline-induced kink in their sixth transmembrane domain (their sequences in this region are shown in Fig. 4), and this kink was correctly identified by the program.

Figure 4.

Amino acid sequences of bovine rhodopsin and the α₁, α₂ and β-adrenergic receptor subtypes. Residues that form a proline-induced kink in TMVI of bovine rhodopsin, and the homologous residues in the other receptors are indicated in bold.

Interestingly, when a less closely related helix-6 sequence, that of chick rhodopsin (AYCFCWGP), was evaluated, a kink was not predicted. However, if the first cysteine of this sequence is changed to leucine (the residue that is found in this position in bovine rhodopsin), a kink is predicted. None of the equivalence classes that we have used permit {L,C} substitutions. This is because of the approximately 2300 members of the class-1 G-protein-coupled receptors, only 2.0% contain a cysteine at that position, whereas 24.9% contain a leucine, thus indicating that a C to L substitution is probably tolerated but occurs extremely infrequently. (Note that percentages quoted here are calculated after correcting for the over-representation bias from the different numbers of subtype entries.) In contrast, a cysteine at the second position of the above sequence is present in 68.0% of the 2300 G-protein-coupled receptors sequences, with only 5.7% having a leucine at this position; this indicates that a C to L substitution can occur, but very uncommonly.

DISCUSSION

Based on an analysis of all available high-resolution structures of polytopic membrane proteins, we showed in earlier work that ∼50% of their transmembrane domains contain short segments that deviate in their structure from that of a regular α-helix (17). Three different types of deviation were delineated: kinks that were most commonly induced by proline, but could also be due to other residues; runs of π-helical character (π bulges); or one or two turns of 3₁₀ helix. In all cases, these deviations from the canonical α-helical structure terminate at a signature residue (e.g. proline in the case of proline-induced kinks), after which the transmembrane segment returns to being α-helical. Thus, the residues forming the deviations from α-helical structure are always located N-terminal to the signature residue, and can be readily identified from variations in the C_α–C_α distances from those found in canonical α-helices, and from deviations in the i→i-4 backbone hydrogen bonding that is characteristic of the residues in an α-helix.

Given that non-canonical elements alter the direction (e.g. kinks) of a transmembrane segment or its radius (e.g. π- and 3₁₀-helices), they can perturb, in some cases markedly, interhelical contacts and/or the side chain orientations. Accurate delineation of such non-canonical elements is thus critical if valid macromolecular models are to be developed for polytopic proteins, most of which have not been characterized at atomic resolution. Moreover, an understanding of the determinants of these non-canonical regions may provide important insights into polytopic protein folding and stability, and potentially allow prediction of their three-dimensional structure from primary sequence information.

The result of our analysis is that descriptors for the short peptide sequences forming non-α-helical elements can be effectively generated, despite the very small number of currently available unique sequence instances. In light of the small cardinality of the training sets and the limited spatial extent of the corresponding non-α-helical elements, the ability to compute specific patterns that correspond to non-canonical elements and to exploit them in the context of a search engine is both a non-trivial event and a testimony to the power of the methodology.

Our study suggests that the occurrence and conservation of non-canonical conformations is a ‘local’ phenomenon, i.e. the non-canonical structural signals are encoded intra-helically by short peptidic sequences (nonapeptides at most). This result bodes well for further development of descriptor-based ‘search engines’ aimed at the elucidation of fine conformational details in protein structures. The patterns that we discovered for each of the three training sets of non-canonical elements were data driven and derived in an automated manner. In general, each instance of a non-canonical element gave rise to multiple, distinct patterns resulting in a very desirable redundancy of representation. Subselecting from among the patterns discovered in each category, and combining them, we built a composite descriptor for the category. Pooling together patterns capturing the same feature into a composite descriptor permitted us to maintain high sensitivity and specificity levels while, at the same time, greatly boosting the resulting signal-to-noise ratio. We anticipate further improvements in the sensitivity and specificity of our composite descriptors, as more non-canonical conformations become known with the availability of newly crystallized protein structures.

Taken together, our findings can be interpreted to indicate that simple physical rules govern the occurrence and conservation of non-canonical conformations. Most importantly, the ability to generate discriminating patterns and composite descriptors suggests that the non-canonical nature of a helical segment is largely encoded intra-helically by a very limited set of residues, rather than being the result of long range or even intermolecular interactions.