Mathematics of quantitative kinetic PCR and the application of standard curves

Abstract

Fluorescent monitoring of DNA amplification is the basis of real-time PCR, from which target DNA concentration can be determined from the fractional cycle at which a threshold amount of amplicon DNA is produced. Absolute quantification can be achieved using a standard curve constructed by amplifying known amounts of target DNA. In this study, the mathematics of quantitative PCR are examined in detail, from which several fundamental aspects of the threshold method and the application of standard curves are illustrated. The construction of five replicate standard curves for two pairs of nested primers was used to examine the reproducibility and degree of quantitative variation using SYBER® Green I fluorescence. Based upon this analysis the application of a single, well- constructed standard curve could provide an estimated precision of ±6–21%, depending on the number of cycles required to reach threshold. A simplified method for absolute quantification is also proposed, in which quantitative scale is determined by DNA mass at threshold.

INTRODUCTION

Kinetic PCR (kPCR) allows quantification of a target DNA within a sample, with the advantage that sensitivity is independent of copy number (1–4). The key aspect differentiating kPCR from previous quantitative PCR methodologies is that target copy number is determined from the fractional cycle at which a threshold amount of amplicon DNA is reached (threshold cycle or C_t), set at a point where amplicon DNA just becomes detectable, but is still within the exponential phase of the amplification (5–7). This approach ensures that interfering factors associated with the late stages of amplification are minimized, and provides the potential for unprecedented precision for quantitative determinations.

Although several methods have been developed to measure C_t, all are based upon fluorescent monitoring of amplicon DNA generation (8–10). Absolute quantification can be achieved using a standard curve, constructed by amplifying known amounts of target DNA in a parallel group of reactions run under identical conditions to that of the sample (7,11). Standard curve preparation is both labour intensive and error prone, with quantitative accuracy being dependent on both the accuracy of DNA standard quantification and the quality of standard curve construction (1,12,13).

In this study, a detailed examination of the mathematics governing PCR yielded insights into the process of quantitative kPCR and into some of the fundamental aspects of the threshold method. This provided a foundation from which to examine the reproducibility of standard curve construction. Assessment of intra- and inter-run variation indicates that a substantial degree of precision can be achieved, even with the application of a single standard curve to multiple runs. An alternative approach is also proposed in which quantitative scale is determined by DNA mass at threshold, such that absolute quantification would only require determination of amplification efficiency.

MATERIALS AND METHODS

The DNA standard consisted of a 218 bp amplicon produced by the K3/K2 primer pair (forward K3: GGCACCTC AGGAATGGGCTATTACAA and reverse K2: AGAATA ACACAGAAATCTGTAGGTGGAATTGAA) that was purified by chloroform extraction followed by isopropanol precipitation, and quantified by averaging three replicate A₂₆₀ absorbance determinations conducted on two spectrophotometers. A second 102 bp amplicon was produced by pairing of K2 with another primer (forward K1: TCCTATGAGATTATGACGCATTTCTCCAAA) located near the center of the K3/K2 amplicon. The primer pair combinations of K3/K2 and the nested K1/K2 thus allowed the production of two different-sized amplicons (218 and 102 bp, respectively) using the same DNA standard dilution series.

PCR amplifications were conducted using QuantiTect™ Syber® Green PCR Kit (Qiagen Inc.) according to the manufacturer’s instructions, with 0.25 µM primers and a variable amount of DNA standard in a 35 µl final reaction volume. Thermocycling was conducted using an Opticon2 DNA Engine (MJ Research Inc.) initiated by a 15 min incubation at 94°C, followed by 45 cycles (90°C, 1 s; 62°C, 120 s) with a single fluorescent reading taken at the end of each cycle. Each run was completed with a melting curve analysis to confirm the specificity of amplification and lack of primer dimers. C_t values were determined by the Opticon2 software using a fluorescence threshold manually set to 0.0160 for all runs and exported into a MS Excel workbook (Microsoft Inc.) for analysis (available as Supplementary Material).

RESULTS

Mathematics of quantitative kPCR

The basic equation describing PCR amplification is:

N_C = N₀·(E + 1)^C1

where C is the number of thermocycles, E is amplification efficiency (also expressed as %E = E ×100%), N_C is the number of amplicon molecules and N₀ is the initial number of target molecules.

In simple terms, each thermocycle produces an increase in N_C in proportion to amplification efficiency, such that 100% efficiency produces a doubling in the number of amplicon molecules. Additionally, the quantity of N_C present after any specific number of thermocycles is dependent on N₀. Rearrangement of equation 1 provides the mathematical relationship upon which quantitative kPCR is based:

N₀ = N_C/(E + 1)^C2

Quantification of N_C thus allows N₀ to be calculated if amplification efficiency is known. A major breakthrough for quantitative PCR came with the use of DNA fluorescence to monitor amplicon accumulation (3,5). Based upon this technique Higuchi et al. (5) developed an elegant method that simplifies N_C determination, such that individual amplification reactions are compared at the point at which they contain identical amounts of amplicon DNA. This is accomplished by selecting a fluorescent threshold (F_t) from which the fractional thermocycle (C_t) is calculated that defines the theoretical point at which each amplification reaction reaches fluorescence threshold.

Under this ‘threshold’ method, N_C becomes a constant such that equation 2 becomes:

N₀ = N_t/(E + 1)^Ct3

where C_t is the threshold cycle and N_t is the number of amplicon molecules at fluorescent threshold.

Absolute quantification can be achieved using a standard curve constructed by amplification of known amounts of target DNA and plotting the resulting C_t values against target DNA concentration. The mathematical basis of a standard curve can be derived by taking the logarithm of equation 3:

Log(N₀) = Log(N_t) – Log[(E + 1)^Ct]

Log(N₀) = Log (N_t) – Log(E + 1)·C_t

Log(N₀) = –Log(E + 1)·C_t + Log (N_t)4

Assuming E and N_t are constants, equation 4 has the general structure of a line (y = mx + b) such that plotting Log(N₀) versus C_t produces a line with:

Slope = –Log(E + 1)

E_S = 10^–Slope – 15

and

Intercept = Log(N_t)

N_t = 10^Intercept6

where E_S is the slope-derived estimate of amplification efficiency.

Although the ability to derive amplification efficiency from the slope of a standard curve has been widely reported, it has not been generally recognized that the number of amplicon molecules at threshold can be directly determined from the intercept. It must also be stressed that these derivations are valid only if all PCR reactions have identical amplification efficiencies, and only if amplification efficiency is invariant over the number of thermocycles required to reach C_t.

Another important but often overlooked aspect of the threshold method is the interdependency of C_t and N_t on F_t, which has two important implications. First, C_t values generated from different amplification runs can be directly compared only if an identical F_t is used for each run. Second, the relationship between N_t and F_t is dependent on amplicon size. This is due to the fact that the underlying determinant of F_t is DNA fluorescence, which in turn has a linear relationship with DNA mass. As such F_t directly reflects DNA mass at threshold, which is related to N_t as described by:

M_t = (N_t·A_S)/9.1 × 10¹¹7

where M_t is the DNA mass at threshold in nanograms, A_S is the amplicon size in base pairs and 9.1 × 10¹¹ is the number of single base pair molecules per nanogram.

A less obvious but potentially significant extension of this is that if M_t is known, N_t can be predicted for any amplicon of known size, if it is assumed that amplicon size and base pair composition do not significantly influence DNA fluorescence. To test the general utility of PCR mathematics for standard curve evaluation and to examine the effectiveness of M_t for predicting N_t, a series of replicate standard curves was constructed for two amplicons that differ significantly in size.

Experimental design for constructing replicate standard curves

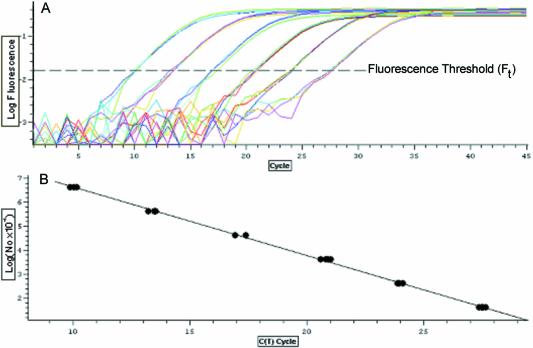
Figure 1 is an example of the two types of graphic output generated by the instrument used in this study, and illustrates the two basic steps in quantitative kPCR using the threshold method, i.e. the selection of a fluorescent threshold from which C_t values are generated (Fig. 1A), followed by linear regression analysis of a Log(N₀) versus C_t plot, from which E_S and N_t are estimated (Fig. 1B).

Figure 1.

Output of a typical amplification run used for construction of the standard curves in this study. Four replicate amplification reactions were conducted for each concentration of DNA standard, covering six magnitudes of target DNA concentration. (A) Plot of the log of reaction fluorescent versus thermocycle that provides a graphic representation for each amplification reaction, in which the linear region represents the exponential phase of the amplification. Fluorescent threshold provides the reference point from which the threshold cycle (C_t) is calculated. (B) The resulting standard curve generated by plotting the log of target DNA concentration versus threshold cycle. Linear regression analysis is used to determine the slope and intercept, which correspond, respectively, to the amplification efficiency and the number of amplicon molecules at threshold, as described by equation 4.

The major consideration for F_t selection is that it falls within the exponential phase of the amplification reaction, best illustrated by plotting log fluorescence versus cycle number (Fig. 1A). As long as F_t is within this log-linear region, the absolute value of F_t was found to have only a modest impact on the slope-derived estimate of amplification efficiency (data not shown). However, as outlined above, F_t does have a direct impact on both C_t and N_t such that F_t must be fixed if data from multiple runs are to be directly compared.

To evaluate the reproducibility and quantitative variation of the threshold method, five replicate standard curves were generated from two pairs of nested primers (K3/K2 and K1/K2, see Materials and Methods for additional details) using a DNA standard dilution series covering six magnitudes of target DNA concentration. The use of nested primers allowed two different-sized amplicons (218 and 102 bp, respectively) to be amplified side-by-side within the same run, using the same DNA standard dilution series. Intra- and inter-run variation could then be examined for each of the two amplicons, free of errors caused by variations in the DNA standard. Using an identical F_t for all runs, the average C_t of four replicate amplifications for each DNA concentration were used in the analysis (Table 1). A spreadsheet containing the individual C_t values and the calculations used for their analysis is provided as Supplementary Material.

Table 1. C_t data from five replicate amplification runs using two pairs of nested primers.

K1/K2 (102 bp)
N0	Run 1	Run 2	Run 3	Run 4	Run 5	Combined
4.17 × 107	9.470 ± 0.112	10.178 ± 0.178	9.907 ± 0.181	9.892 ± 0.136	10.006 ± 0.161	9.893 ± 0.279
4.17 × 106	13.503 ± 0.338	13.519 ± 0.214	13.535 ± 0.137	13.556 ± 0.195	13.573 ± 0.347	13.537 ± 0.232
4.17 × 105	17.422 ± 0.119	17.257 ± 0.206	16.972 ± 0.159	17.105 ± 0.280	17.346 ± 0.093	17.220 ± 0.234
4.17 × 104	21.362 ± 0.097	20.882 ± 0.146	20.863 ± 0.145	20.815 ± 0.250	21.302 ± 0.156	21.045 ± 0.284
4.17 × 103	24.112 ± 0.205	24.150 ± 0.036	23.998 ± 0.126	24.247 ± 0.147	24.353 ± 0.256	24.172 ± 0.196
4.17 × 102	27.912 ± 0.221	27.660 ± 0.076	27.608 ± 0.130	27.884 ± 0.264	28.190 ± 0.226	27.851 ± 0.275
Average SDa	±0.182	±0.143	±0.146	±0.212	±0.207	±0.250
%Molb	±12.4	±9.6	±9.8	±14.6	±14.2	±17.4
K3/K2 (218 bp)
N0	Run 1	Run 2	Run 3	Run 4	Run 5	Combined
4.17 × 107	8.602 ± 0.235	8.491 ± 0.140	8.444 ± 0.099	8.752 ± 0.127	8.841 ± 0.309	8.626 ± 0.235
4.17 × 106	12.349 ± 0.141	11.979 ± 0.137	12.291 ± 0.083	12.539 ± 0.367	12.312 ± 0.258	12.294 ± 0.271
4.17 × 105	15.794 ± 0.138	16.049 ± 0.155	16.089 ± 0.227	16.106 ± 0.194	15.644 ± 0.177	15.936 ± 0.248
4.17 × 104	19.701 ± 0.171	19.549 ± 0.209	19.828 ± 0.261	19.715 ± 0.319	19.203 ± 0.184	19.599 ± 0.305
4.17 × 103	22.574 ± 0.184	22.904 ± 0.182	22.920 ± 0.269	23.311 ± 0.163	23.388 ± 0.151	23.019 ± 0.351
4.17 × 102	26.114 ± 0.113	26.447 ± 0.065	26.436 ± 0.215	27.039 ± 0.122	27.006 ± 0.223	26.608 ± 0.395
Average SDa	±0.164	±0.148	±0.192	±0.215	±0.217	±0.301
%Molb	±11.1	±10.0	±13.0	±14.8	±14.9	±21.3

Average C_t values (runs 1–5, ± standard deviation, n = 4) for six target DNA concentrations (N₀), in addition to the average of all C_t values for each concentration from all runs (combined, ± standard deviation, n = 20). The average standard deviation in C_t for each run is also used to estimate the corresponding percentage of molecules.

^aAverage of the standard deviations from each data set.

^bAverage standard deviation converted into percent molecules using equation 8.

Intra- and inter-run variation in C_t

As an initial step for evaluation of quantitative precision, the reproducibility of amplification under our experimental conditions was estimated, based upon the standard deviation in C_t values generated from replicate amplifications. Moreover, due to the exponential scale of C_t, the impact of its variation can be difficult to assess, and thus the standard deviations in C_t were also used to estimate the variation in percent molecules based upon the equation:

±%Molecules = [(E + 1)^SD – 1] ×100%8

where SD is the standard deviation in C_t generated from replicate amplifications.

Overall the standard deviation in C_t of replicate amplifications ranged from 0.036 to 0.367 cycles, with an average of 0.183 cycles (Table 1 and Supplementary Material). This corresponds to an estimated variation in molecules that ranges from ±2.3 to ±26.6% with an average of ±12.4%, using an amplification efficiency of 90% taken from the slope-based estimate of amplification efficiency determined below.

Based upon the average standard deviation produced from each individual run, estimates of the intra-run variation were similar for both amplicons, ranging from ±9.6% to 14.9% of molecules (runs 1–5, Table 1). When combined with inter-run variation, this increased to ±17.4 and ±21.3% of molecules for each amplicon, respectively, based upon averaging the standard deviation in C_t for each DNA concentration from all runs (‘Combined’, Table 1). These variations, although significant, indicate that C_t values have an acceptable level of reproduciblity over the six magnitudes of target DNA concentration that were examined.

Standard curve construction and evaluation

Evaluation of the quantitative variation between replicate standard curves was conducted by generating N_t and %E_S values for each amplification run listed in Table 1. This was done by exporting the C_t values into a spreadsheet, and calculating the slope and intercept for each run using linear regression analysis of log(N₀) versus C_t. Two methods were then used to assess the quantitative variation between the five replicate standard curves constructed for each of the two amplicons (Table 2).

Table 2. Summary of the linear regression analysis conducted for each amplification run listed in Table 1 and an evaluation of inter-curve variation.

K1/K2 (102 bp)
Regression analysis summarya				Evaluation of inter-curve variationb
	r2 c	%Es	Nt	Ct = 10	Ct = 15	Ct = 20	Ct = 25	Ct = 30
Run 1	0.9971	87.4%	1.96 × 1010	3.67 × 107	1.59 × 106	6.88 × 104	2.98 × 103	1.29 × 102
Run 2	0.9997	92.6%	3.27 × 1010	4.64 × 107	1.75 × 106	6.59 × 104	2.48 × 103	9.36 × 101
Run 3	0.9995	91.7%	2.74 × 1010	4.08 × 107	1.58 × 106	6.09 × 104	2.35 × 103	9.09 × 101
Run 4	0.9999	89.8%	2.43 × 1010	4.00 × 107	1.62 × 106	6.59 × 104	2.67 × 103	1.08 × 102
Run 5	0.9992	88.3%	2.39 × 1010	4.26 × 107	1.80 × 106	7.59 × 104	3.21 × 103	1.35 × 102
	%CVd	±2.2%	±19.0%	±8.7%	±6.0%	±8.2%	±12.8%	±18.1%
	Average	90.0%	2.56 × 1010	4.13 × 107	1.67 × 106	6.75 × 104	2.74 × 103	1.11 × 102
Combined	0.9994	90.0%	2.52 × 1010	4.13 × 107	1.67 × 106	6.74 × 104	2.72 × 103	1.10 × 102
	Mte	2.83 ng
K3/K2 (218 bp)
Regression analysis summarya				Evaluation of inter-curve variationb
	r2 c	%Es	Nt	Ct = 10	Ct = 15	Ct = 20	Ct = 25	Ct = 30
Run 1	0.9987	93.3%	1.36 × 1010	1.87 × 107	6.95 × 105	2.58 × 104	9.55 × 102	3.54 × 101
Run 2	0.9992	89.4%	9.88 × 109	1.66 × 107	6.81 × 105	2.79 × 104	1.14 × 103	4.69 × 101
Run 3	0.9987	89.8%	1.09 × 1010	1.80 × 107	7.29 × 105	2.96 × 104	1.20 × 103	4.87 × 101
Run 4	0.9999	88.3%	1.10 × 1010	1.97 × 107	8.31 × 105	3.51 × 104	1.49 × 103	6.28 × 101
Run 5	0.9987	87.9%	9.49 × 109	1.73 × 107	7.39 × 105	3.15 × 104	1.35 × 103	5.75 × 101
	%CVd	±2.1%	±14.7%	±6.6%	±8.0%	±11.9%	±16.4%	±21.0%
	Average	89.7%	1.10 × 1010	1.81 × 107	7.35 × 105	3.00 × 104	1.23 × 103	5.03 × 101
Combined	0.9999	89.8%	1.10 × 1010	1.81 × 107	7.35 × 105	2.98 × 104	1.21 × 103	4.92 × 101
	Mte	2.63 ng

The spreadsheet used for this analysis is available as Supplementary Material.

^aLinear-regression analysis of the data sets from Table 1 based upon equations 5 and 6.

^bN₀ calculated using equation 3, for the specified C_t values using the E_S and N_t from each run.

^cPearson correlation coefficient.

^d(SD/Average) ×100%.

^eDNA mass at threshold calculated for the ‘combined’ N_t using equation 7.

Examination of the absolute values of N_t and %E_S revealed similar trends for both amplicons, with an inter-curve variation in %E_S of ±2.2 and ±2.1%, and variation in N_t of ±19.0 and ±14.7%, respectively, as based upon their standard deviations (Table 2). Taken individually, the magnitude of variation in %E_S and N_t suggests the resulting variation in N₀ determination could be large. For example, for a C_t of 25 cycles, a ±2.2% variance in the estimate of amplification efficiency would produce an approximate ±33% variation in N₀ that, when combined with the apparent ±19% variance in N_t, could produce an overall variation of about ±52% for N₀. It must be noted, however, that further examination suggests that these estimates of variance are most certainly erroneous, due to an apparent intra-curve correlation between slope and intercept.

Comparing the %E_S and N_t values generated from each individual standard curve reveals that for both amplicons, the curve that produced the highest %E_S also produced the highest N_t (Table 2, K1/K2, run 2 and K3/K2, run 1). Similarly, the standard curves producing the lowest %E_S also had the lowest N_t (Table 2, K1/K2, run 1 and K3/K2, run 5). Taken together, these trends suggest that variations in intercept and slope are not solely caused by inter-run variation in instrumentation and/or amplification, but also reflect an innate characteristic of linear regression in which variations in slope can be compensated for to some degree by a corresponding variation in intercept.

This can be best illustrated through an alternative approach to evaluating quantitative differences produced by replicate standard curves. As illustrated in Table 2, inter-curve variation can be estimated by comparing the calculated N₀ for a series of simulated C_t values using equation 3. Thus, for the five standard curves constructed from the K1/K2 amplicon, the calculated N₀ for C_t=10 cycles ranges from 3.67 × 10⁷ to 4.64 × 10⁷ molecules, with an average of 4.13 × 10⁷ molecules and a standard deviation corresponding to ±8.7% of molecules (Table 2). Furthermore, a general increase in variation is observed with increasing C_t such that for C_t = 30 cycles, a variation of ±18.1% of molecules is produced. Very similar results were produced by the larger K3/K2 amplicon (Table 2).

Overall, this analysis demonstrates that quantitative variations produced by replicate standard curves can be relatively small, ranging in this study from a low of about ±6% to a high of about ±21% depending on the number of cycles needed to reach threshold. The observed inter-curve variation in the absolute values of slope and intercept also suggests that curve-based estimates of amplification efficiency and N_t require a larger data set than would normally be used for construction of a single standard curve. Indeed, the relative accuracy of the N_t estimates for each of the two amplicons can be tested through the correlation of their respective M_t values, as described by equation 7. Based upon the N_t values derived from each respective ‘combined’ data set, the estimated M_t values differ by 7.3% (Table 2). This provides support for both the optical precision of the instrumentation and similarity in the SYBER® Green I fluorescent characteristics of these two amplicons.

DISCUSSION

Despite the extensive use of the threshold method for absolute quantification, there exists a paucity of studies that have examined the utility of the underlying mathematics. Furthermore, the general simplicity and widespread use of standard curves has led to the automation of quantitative determinations, which can obscure the mathematical principles upon which the analysis is based. Familiarity with the fundamentals of PCR mathematics cannot only yield important insights, but as well provide a foundation from which to address some of the major limitations of quantitative kPCR.

At the most basic level, the threshold method does not generally provide an effective indication of quantitative precision or accuracy. Although the standard deviation in C_t produced from replicate amplifications can provide an estimate of reproducibility, there is a general deficiency in reporting the errors associated with standard curve construction. This makes it difficult to evaluate the effectiveness of any specific quantitative determination, or of comparing results produced by different studies. As was demonstrated in this study, a basic assessment of standard curve construction can be conducted, if it is understood that slope and intercept are directly correlated to amplification efficiency and the number of amplicon molecules at threshold (N_t), respectively.

In this study, comparison of replicate standard curves revealed potentially large inter-curve variations, based upon the absolute values of slope and intercept. This initially led to the conclusion that this was caused by substantial inter-run variations in amplification and/or instrumentation. However, upon closer examination, an intra-curve correlation between slope and intercept became apparent, such that differences in slope are compensated for to a significant degree by corresponding differences in intercept.

This can be demonstrated through simple mathematical modeling, in which the initial number of target molecules (N₀) is calculated for a series of simulated C_t values (equation 3, Table 2). This showed that despite the differences in the absolute values of amplification efficiency and N_t, the resulting N₀ values generated by each standard curve were unexpectedly similar. Based upon this analysis the application of a single, well-constructed standard curve could provide an estimated precision of ±6–21% of molecules, depending on the number of cycles required to reach threshold.

Notwithstanding the interrelationship of slope and intercept, it must be stressed that the mathematics of PCR dictate that amplification efficiency and N_t are independent entities. In reality N_t is determined solely by the fluorescent threshold (F_t), and as such its value is independent of the parameters impacting PCR amplification. Indeed, this interrelationship between N_t and F_t has important practical implications, based on the principle that F_t does not directly reflect the number of amplicon molecules, but rather DNA mass at fluorescent threshold (M_t). This in turn dictates that M_t could be used to predict N_t for any amplicon of known size, if it is assumed that amplicon size and base composition do not significantly impact DNA fluorescence. Support for the validity of this assumption was provided by the N_t estimates generated from the two amplicons used in this study, for which the predicted M_t values differ by 7.3% (equation 7, Table 2).

The practical significance of this becomes apparent if it is noted that N_t is the sole determinant of scale (equation 3), the accuracy of which is dependent on the quantitative accuracy of the DNA standard used for standard curve construction. If, however, M_t can be used to predict N_t with sufficient precision, a common quantitative scale could be applied to all amplicons. In addition to circumventing the necessity of preparing a quantified DNA standard for each individual amplicon, the major source of variation in quantitative scale would become the optical precision of the instrument. Equally significant is that absolute quantification would be simplified, requiring only determination of amplification efficiency once M_t has been established.

SUPPLEMENTARY MATERIAL

Supplementary Material is available at NAR Online.