The Generalized Matching Law in Elite Sport Competition: Football Play Calling as Operant Choice

Abstract

A mathematical model of operant choice, the generalized matching law was used to analyze play-calling data from the 2004 National Football League season. In all analyses, the relative ratio of passing to rushing plays was examined as a function of the relative ratio of reinforcement, defined as yards gained, from passing versus rushing. Different analyses focused on season-aggregate data for the league as a whole, game-by-game data for the league as a whole, and game-by-game data for individual teams. In all analyses except those for a few individual teams, the generalized matching law accounted for a majority of variance in play calling. The typical play-calling pattern reflected undermatching (suggesting imperfect sensitivity of play calling to yardage-gained reinforcers) and a bias for calling rushing plays. Bias was found to be a function of both the relative risk of turnovers and the relative variability in yards gained associated with passing versus rushing plays. The external validity of the matching analyses was supported by significant correlations between parameters of the generalized matching law and team success on offense and season winning percentage. These results illustrate the broad applicability of the generalized matching law to problems outside of the laboratory.

The matching law (Herrnstein, 1961) states that individuals tend to divide their time and effort between two or more simultaneously available behavior options proportional to the reinforcement that is contingent on each. A small family of mathematical models based on this maxim accounts well for performance under concurrent reinforcement schedules in the laboratory (e.g., Baum, 1979), and has also provided insights into a variety of socially important problems such as employee absenteeism (Redmon & Lockwood, 1986), teen pregnancy (Bulow & Meller, 1998), and classroom behavior (Billington & DiTommaso, 2003). Collectively, these analyses are noteworthy for suggesting that principles of operant choice operate robustly, even amid the complexity of everyday environments.

Few everyday environments are as complex and multiply determined as those in which elite sport competition occurs. Among the many variables believed to influence sport performance are coaching strategies and coach personalities; rules of a sport and the extent to which they are enforced by officials during a given contest; the location in which competition occurs and the behavior of spectators; weather (for outdoor sports) and the condition of the playing surface; the skills of individuals who participate on the team; and the mental and physical well-being of those players at the time of competition. Any lawful principle or functional relation found to cut through all of these variables to reliably predict sport performance would be noteworthy indeed.

Vollmer and Bourret (2000) provisionally identified the matching relation as one such predictor when they showed that the generalized matching law (Baum, 1974, 1979) provided a good account of shot selection in two college basketball teams. The generalized matching law predicts that, given two behaviors, B₁ and B₂, and rates of reinforcement contingent on them, R₁ and R₂, respectively, relative effort investment in the behaviors varies linearly with relative reinforcement rates. This relation is expressed as

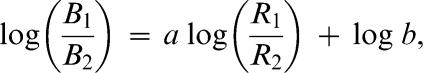1

in which the behavior and reinforcement ratios are logarithmically transformed to yield an easy-to-evaluate linear function in which, if behavior matches reinforcement perfectly, the slope  =  1 and the intercept  =  0. The two fitted parameters of the equation describe obtained estimates of slope and intercept, which usually deviate from the ideal values. The slope of the function, a, is viewed as a measure of sensitivity to reinforcement differentials, that is, of how much behavior ratios change given one unit of change in reinforcement ratio. The intercept, log b, indicates bias, or systematic preference not accounted for by reinforcement rates.

In Vollmer and Bourret's (2000) analysis of players on two college basketball teams, behaviors were two-point and three-point shots attempted, and reinforcers were succesful shots made of the same two types. Graphic analyses suggested that the generalized matching law provided a good fit to the shot-selection data, and based on raw data in Table 1 of the report, it can be estimated that the generalized matching law accounted for about 90% or more of shot-selection variance across players on both teams. Players showed near-perfect reinforcement sensitivity (slope ∼1), and a bias for three-point shots was evident (intercept ∼0.12) (i.e., three-point shots were taken more often than frequency of shot making predicted, presumably because of their higher point value).

Table 1. Fitted Parameters of Equation 1 for Each National Football League Team for the 16 Games of the 2004 Regular Season.

Team	Reinforcement sensitivity (a  =  slope)	Bias (log b  =  intercept)	Variance accounted for (%) by Equation 1
Arizona Cardinals	0.567	−0.080	67.0
Atlanta Falcons	0.413	−0.109	28.9
Baltimore Ravens	0.528	−0.054	51.9
Buffalo Bills	0.391	−0.086	40.9
Carolina Panthers	0.608	−0.129	61.6
Chicago Bears	0.489	−0.022	62.8
Cincinnati Bengals	0.473	−0.034	40.5
Cleveland Brownsa	0.366	−0.078	22.7
Dallas Cowboys	0.502	−0.082	59.6
Denver Broncos	0.620	−0.165	61.6
Detroit Lions	0.415	0.004	57.7
Green Bay Packers	0.615	−0.105	64.1
Houston Texans	0.470	−0.132	46.8
Indianapolis Colts	0.585	−0.150	85.3
Jacksonville Jaguars	0.486	−0.044	54.1
Kansas City Chiefs	0.652	−0.122	73.3
Miami Dolphins	0.399	0.025	23.7
Minnesota Vikings	0.645	−0.109	57.6
New England Patriots	0.575	−0.167	85.3
New Orleans Saints	0.591	−0.092	62.1
New York Giants	0.343	−0.017	38.1
New York Jets	0.537	−0.149	65.7
Oakland Raiders	0.419	0.046	53.1
Philadelphia Eagles	0.716	−0.105	59.6
Pittsburgh Steelers	0.635	−0.256	57.9
San Diego Chargers	0.900	−0.232	57.8
San Francisco 49ers	0.695	−1.00	77.6
Seattle Seahawks	0.588	−0.076	43.9
St. Louis Rams	0.575	−0.077	74.4
Tampa Bay Buccaneers	0.663	−0.136	78.6
Tennessee Titans	0.726	−0.058	79.6
Washington Redskins	0.776	−0.097	70.2

^aAnalysis based on 15 games. Cleveland accrued negative net passing yards in one game. Because logarithmic transformations can be performed only on positive numbers, this game was omitted from analysis.

In the present study, we used the generalized matching law to evaluate choice in a different sport, American-rules professional football (as contrasted with rugby football, Australian-rules football, or soccer; see McCorduck, 1998). In applying Equation 1, we assumed that the relative rate of calling pass versus rush plays would vary as a function of relative reinforcement, which we operationalized as average yards gained for passing and rushing plays.

Football was chosen for examination for several reasons. First, play calling can be conceptualized as individual behavior. Typically in American-rules professional football (hereafter referred to simply as football), each team has one individual, usually an offensive coordinator working in conjunction with a head coach, who decides what kind of play, passing or rushing (running), will take place on each down or opportunity (McCorduck, 1998). Offensive coordinators are typically highly skilled (and highly paid) professionals with considerable football experience and whose play-calling behavior leads to high-stakes outcomes (e.g., team success, continued employment). Second, in calling plays, coaches routinely consider the success (i.e., reinforcement) of previously attempted plays (Edwards, 2002), suggesting a general sensitivity of play calling to reinforcement. Third, individual differences in play-calling patterns may be anticipated. As a function of coaching staff, player skill, and other factors, teams often adopt specific offensive styles for which they become known over time. For example, during 2004 the Indianapolis Colts were regarded as a passing team, with Peyton Manning, who threw for a league record 49 touchdowns for the season, as quarterback (Clayton, 2005). By contrast, the Atlanta Falcons were regarded as a rushing team with Michael Vick, a strong runner but inconsistent passer, as quarterback (Winkeljohn, 2005). We wondered whether such differences would be apparent in the fitted parameters of the generalized matching law. Fourth, there are situation-specific patterns in play calling. For example, during 2004, National Football League (NFL) teams rushed on 52% of first-down plays but on only 24% of third-down plays (data provided by Roland Beech of twominutewarning.com). It is reasonable to suggest that yardage gains associated with rushing and passing vary across game situations, and thus situational patterns might manifest as changes in the generalized matching law's fitted parameters. Finally, rushing and passing statistics for every team in the NFL are readily available from their Web site and other sources, making possible analyses based on the generalized matching law.

Vollmer and Bourret's (2000) analyses of basketball focused primarily on aggregate outcomes in which each individual player on a team contributed one data point. We employed a similar level of analysis by using each team (and its associated play caller) in a league as one observation in aggregate analyses. It should be noted, however, that this approach deviates from the typical analysis of laboratory performance based on the generalized matching law, in which one individual is observed across a variety of relative-reinforcement conditions (Baum, 1979). To better evaluate how well the generalized matching law predicts individual functional relations, we also undertook analyses in which a single team (or play caller) was the focus, using each game in a season as an observation.

General Method and Analytical Strategy

Data were retrieved from archival sources between July 20 and September 10, 2005. Unless otherwise noted below, data were retrieved from http://www.nfl.com. The primary data consisted of the number of passing and rushing plays executed and net yards gained from those plays for each of the 32 NFL teams during each game of the 16-game 2004 regular season. Several aspects of this data set should be noted. First, plays are categorized as rushing or passing based on what actually occurred rather than what was called, and these may differ in the case of “audibles” (i.e., when a quarterback calls a different play than originally planned). Second, “sacks” (i.e., when a quarterback is tackled behind the line of scrimmage) are treated as failed rushing plays even though the quarterback's original intention may have been to pass the ball. Because yards lost as well as the intention of the quarterback to pass or not during each play that resulted in a sack are not specified, we could not apply a correction for this feature of the data. Third, although it is possible for a player to receive a pass and subsequently fumble the ball, yards gained from the pass are still recorded.

Least squares linear regression was used to fit Equation 1 to the data. Specifically, the ratio of yards gained through passing versus rushing was used as a predictor of the ratio of pass plays versus rushing plays called. Play-calling (behavior) and yardage-gained (reinforcement) ratios were expressed in the form of pass or rush. In this application, Equation 1 yields three values of interest. First, variance accounted for is a measure of the amount of between-observation changes in play calling that can be explained via reference to reinforcement, as defined here in terms of yards gained through passing and rushing. Second, the estimate of a, or slope, describes the sensitivity of changes in play calling to changes in relative reinforcement rate. Third, the estimate of log b indicates a systematic preference, or bias, for passing (positive values) or rushing (negative values) that is not attributable to the relative yards gained ratio.

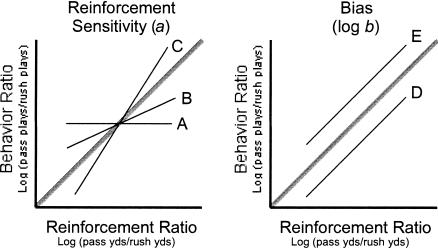
Figure 1 illustrates some possible outcomes of applying Equation 1 to football play-calling data. Each panel shows several lines of best fit, with perfect matching (slope  =  1, and zero bias) shown as a thick gray line. In the left panel, when slope  =  0 (A), no reinforcement sensitivity exists, and play-calling patterns do not shift with changes in relative yards gained for passing versus rushing. When 0 < slope < 1 (B), play calling is positively correlated with yardage gained but, moving left to right across the panel, the play-calling ratio changes relatively little as the yardage ratio changes. When slope > 1, the play-calling ratio changes relatively more than the yardage ratio. In the right panel, when log b > 0 (E), although play calling shifts systematically with yardage gained, pass plays are called consistently more often than the yardage ratio predicts. When log b < 0 (D), rush plays are called consistently more often than the yardage ratio predicts.

Figure 1. Some potential outcomes of applying Equation 1 to football play-calling data. See text for explanation.

Study 1: Season-aggregate League Outcomes

Initial analyses concentrated on NFL play calling with each team's season-aggregate statistics treated as one case, or data point. This analysis is analogous to the analysis by Vollmer and Bourret (2000) in which each individual player on a basketball team contributed one data point.

Results and Discussion

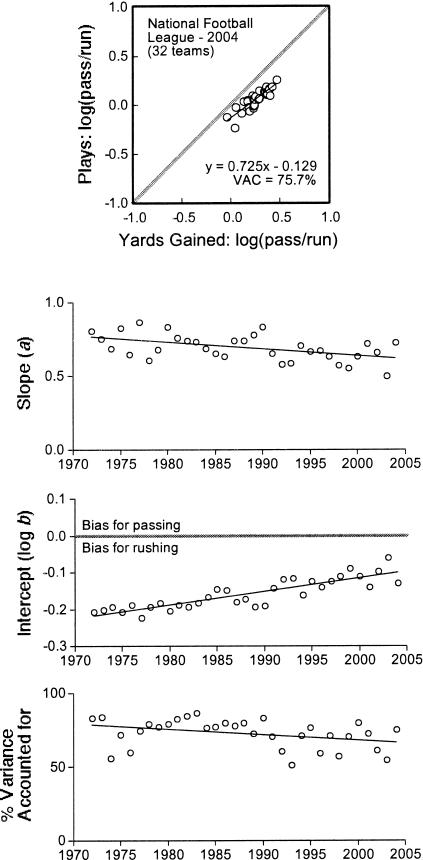
As shown in Figure 2, the generalized matching law accounted for a majority of variance in play calling (75.7%). This, in combination with the positive slope of the matching relation (a  =  0.725), indicates that especially successful passing teams tended to call many pass plays per opportunity, and those that were especially successful rushing tended to call many rushing plays per opportunity. Such undermatching is typical of individuals who work on concurrent schedules of reinforcement in the laboratory (Baum, 1979) but, interestingly, undermatching was not observed by Vollmer and Bourret (2000) in their analysis of two basketball teams. The present data do not explain this apparent between-sport difference. In addition, there was a bias in favor of rushing (log b  =  −0.129). Thus, although play calling varied systematically with yardage gained, teams tended to call more rushing plays than predicted based on yardage statistics.

Figure 2. Top: results of applying the generalized matching law (Equation 1) to 2004 regular-season play calling by NFL teams.

Each data point represents one team. Heavy diagonal lines indicate perfect matching. Bottom three panels: slope, intercept, and variance accounted for by Equation 1 when applied to the 1972 through 2004 NFL regular-season data. Trend lines were determined using least squares linear regression. See text for further explanation.

Historical Comparisons

Because the present analyses focus primarily on the 2004 season, it is important to know whether this is a representative season in the NFL. The analysis shown in Figure 2 was repeated for each season in the NFL from 1972 (the earliest year for which team statistics were available; see http://www.pro-football-reference.com/years/index.htm) to 2003. The fitted parameters obtained from applying Equation 1 to these data are also shown in Figure 2. Outcomes from 2004 fell within historical ranges and were especially similar to those of approximately the past decade. It is clear, however, that NFL play-calling patterns are not static. Across the 32 years, the variance accounted for by Equation 1 has decreased by an average of about 0.4% per year. In general, yardage gained is becoming a less reliable predictor of play calling. Slopes of matching relations are growing shallower at an average rate of about −0.005 per year, indicating that play callers' sensitivity to yardage gained as reinforcement is decreasing. Finally, log b estimates show gradual erosion of bias for rushing, at an average rate of change of about 0.004 log units per year.

A variety of factors that are considered common knowledge in football circles might contribute to these historical trends. Passing offenses have become more sophisticated, perhaps contributing to a shift away from rushing bias. In addition, the NFL has implemented a series of rule changes (especially in 1974, 1976, and 1978) designed to favor passing because it is popular with fans (National Football League, n.d.). As the NFL has become more profitable and expensive to operate over the past several decades, the pressure for teams to win has increased, causing coaches and players to be replaced more frequently than in the past. Also contributing to player turnover have been changes in free-agency rules, which address a player's ability to change teams when a contract expires, and in the salary cap, a team's limit on total salary that can be paid to players in a year. These factors may help to explain why the variance accounted for by Equation 1 has decreased over the years.

Comparison with Other Leagues

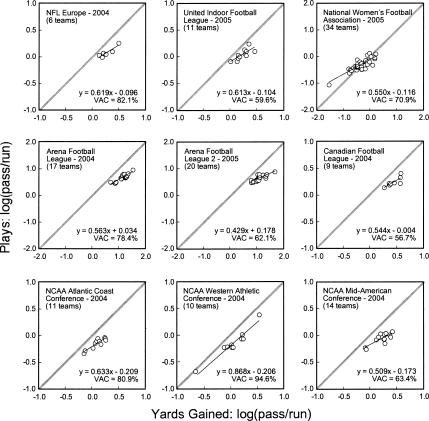
As a test of the generality of NFL outcomes, the analysis shown in Figure 2 was repeated (Figure 3) for six other professional leagues that employ rules similar to those of the NFL: NFL Europe, the Canadian Football League (2004 season; http://www.cfl.ca), Arena Football League (2004; http://www.arenafootball.com), Arena Football League 2 (2005 season; http://www.af2.com), United Indoor Football League (2005 season; http://www.unitedindoorfootball.com), and National Women's Football Association (2005 season; http://webgamestats.com/nwfa.aspx). To assess the extent to which NFL outcomes are specific to professional football, Figure 3 also shows data from three randomly chosen Division I leagues of the National Collegiate Athletic Association Conference (2004 season; http://sports.espn.go.com/ncf/standings).

Figure 3. Results of applying the generalized matching law (Equation 1) to season-aggregate play calling of teams in nine leagues.

Heavy diagonal lines indicate perfect matching.

The generalized matching law accounted for the majority of variance in season-aggregate play calling in all eight leagues (range, 57% to 95%), indicating that Equation 1 provides a good description of this behavior in all leagues examined. Just as in the NFL, slopes of the matching relation were positive but less than 1 (range, 0.429 to 0.868). Each unit of variance in relative yardage gained was accompanied by less than one unit of variance in relative play calling. In six of the nine leagues shown in Figure 3, log b estimates indicated a bias for calling rushing plays, just as in the NFL. The remaining leagues showed a bias for passing or essentially no bias. This pattern could be related, in part, to rule differences among leagues. For example, Canadian Football League teams are allowed only three downs to gain at least 10 yards and thereby retain offensive possession, whereas four downs are allowed in other leagues. This may put special pressure on CFL teams to throw the ball to gain as many yards per attempt as possible.

The rushing bias also might be related to the relative risk of losing offensive possession through a turnover involved in rushing versus passing (McCorduck, 1998). Complete turnover data were available for five of the leagues shown in Figures 2 and 3. In three leagues for which a rushing bias was evident, turnovers were less likely when rushing than when passing (National Football League: approximately one fumble lost for every 38 rushes and one interception for every 31 passes; NFL Europe: once every 37 and 27 plays, respectively; United Indoor Football League: once every 44 and 20 plays, respectively). By contrast, in two leagues that showed little bias or a passing bias, turnovers were more likely when rushing than when passing (Canadian Football League: once every 20 and 31 plays, respectively; Arena Football League 2: once every 8 and 31 plays, respectively).

The present analysis cannot explain league differences in turnover risk, but across the five leagues for which data were available, the relative risk (per-play fumble rate/per-play interception rate, logarithmically transformed) was strongly correlated with bias (r  =  .921, p  =  .0247). As relative risk of a fumble increased, league-aggregate bias shifted from rushing to passing. It seems reasonable to propose that bias in play calling reflects, in part, an aversion to turnover risk. If turnovers can be thought of as intermittent negative punishment for calling certain kinds of offensive plays, then this finding is consistent with a proposal by basic researchers that punishment, when superimposed on operant choice, contributes to bias (e.g., Bradshaw, Szabadi, & Bevan, 1979). It should be noted, however, that the role of punishment in operant choice is not well understood, and currently only very limited laboratory data bear on the bias hypothesis (Critchfield, Paletz, MacAleese, & Newland, 2003). Thus, while demonstrating the relevance of basic behavioral principles to elite sport competition, the present study also provides clues about how to think about punishment generally.

Conditional Play Calling

If play calling in football is behavior under environmental control, then it should vary with the circumstances. NFL rules allow for four opportunities, or downs, to gain 10 yards, which earns a team continued possession of the ball, although the fourth down is usually reserved for punting, which delivers the ball to the opponent away from one's goal line (McCorduck, 1998). Functionally, then, three chances are provided to gain sufficient yardage. Logic suggests that teams have the greatest flexibility in how they call plays on first down; thus, it might be predicted that on first down, teams are maximally sensitive to the relation between play calling and yards gained, with this sensitivity tempered, perhaps, by the fact that the risk of a turnover is low for rushing plays. Thereafter, play calling may become more constrained by game situations. For example, if yards are lost on first down, a team has only two downs remaining to gain substantial yardage, perhaps putting a premium on passing. By contrast, a sizable gain on first down allows a team to run the ball for remaining yardage, which may be an advantage because fumbles are less probable than interceptions.

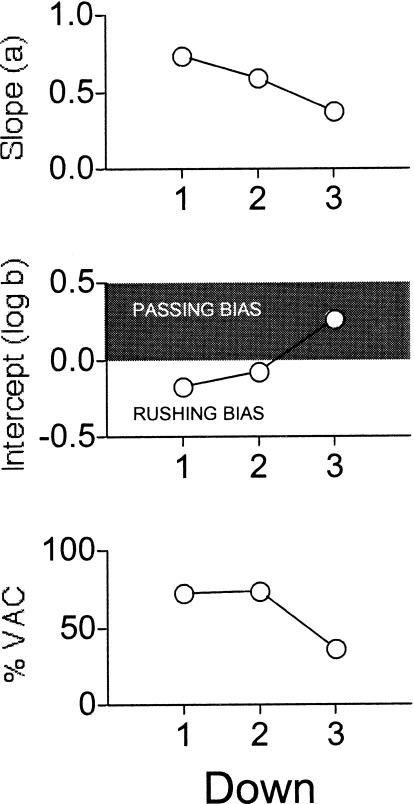
As a partial test of this conditionality hypothesis, Figure 4 summarizes the results of fitting Equation 1 separately to regular season play-calling data for first downs, second downs, and third downs, for all NFL teams combined. Three patterns are evident. First, as predicted above, the slope of the matching relation was highest for first-down plays and declined for subsequent downs. Second, as predicted above, there was a strong rushing bias on first-down plays. Consistent with the notion that teams sometimes become more desperate for yardage on subsequent downs, the rushing bias decreased for second-down plays and became a passing bias for third-down plays. Finally, the variance in play calling accounted for by Equation 1 was low for third-down plays. This might be expected if third-down play calling is conditional on yardage gained on previous downs (e.g., Westerling, 2002). In a sense, our analysis may have fitted a single mathematical function to an aggregate of heterogeneous functional relations. The data available to us did not permit a separate analysis of third downs on which teams faced long versus short yardage needs, but we predict that such an analysis would show better fits, as well as a passing bias in the former case and a rushing bias in the latter case.

Figure 4. Fitted parameters of the generalized matching law (Equation 1) when applied to play calling in the NFL on first-, second-, and third-down situations during the 2004 regular season.

In the analysis of each down, each of 32 teams served as an individual observation. Raw data were provided by twominutewarning.com.

Study 2: Game-by-game League Outcomes

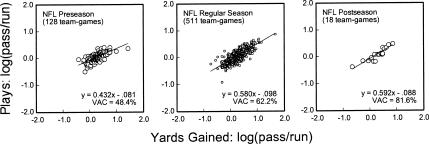
By focusing on season-aggregate statistics, the preceding analyses might obscure considerable game-by-game variability in play calling. Moreover, Figures 2 and 3 show only regular-season outcomes, leaving open the question of whether the generalized matching law also accounts for play calling during preseason games, when teams are still developing their strategies and evaluating personnel, or for postseason games, when contingencies on winning are considerably more acute than during the regular season. We therefore examined game-by-game statistics for all 32 teams in the NFL during the 2004 preseason, regular season, and postseason.

Results and Discussion

Figure 5 shows the aggregate of all teams, with each data point representing single-game statistics from one team. In a sense, each game for each team was regarded as an experimental condition in which factors such as weather, injuries to key players, and defensive strategies of the opposition might create a unique relative yardage-gained ratio for passing and rushing.

Figure 5. Results of applying the generalized matching law (Equation 1) to the game-by-game data of all NFL teams during three phases of the 2004 season.

A linear trend is obvious in all three panels of Figure 5. During the preseason, the linear fit was relatively poor, indicating that yardage gained was a relatively weak predictor of play calling in the sense predicted by Equation 1. In addition, the slope of the function was relatively flat, indicating that game-by-game changes in yardage earned were accompanied by fairly small adjustments in play calling. The variance accounted for by Equation 1, and the slope of the function, increased in the regular season and again in the postseason.

These effects might be explained in terms of accumulated contingency exposure. Laboratory research with pigeons suggests that sensitivity to reinforcement increases with experience on concurrent schedules (Todorov, Olivera Castro, Hanna, de Sa, & Barreto, 1983). As teams move from preseason to regular season to (for some teams) postseason competition, play callers gain experience with the yardage-gained contingencies assumed in the present analysis to affect play calling.

Play calling also might vary across different phases of a season (Figure 5) because the circumstances under which games are played differ (e.g., http://www.twominutewarning.com/gt8.htm). During the preseason, some players may be in early stages of physical conditioning and mastery of the team's offensive system. Coaches are testing the capabilities of the players, including some players who ultimately will not be on the regular-season roster. Thus, it is not surprising to find more variable performances during the preseason. In many outdoor venues, weather changes progressively from the preseason (late summer) to regular season (fall) to postseason (winter). Moreover, the cost of losing a game increases as the three phases of the season progress. Preseason outcomes have no bearing on the rest of the season. Regular-season wins, in the aggregate, affect playoff eligibility, but no single game dictates this outcome. During the playoffs, a loss ends a team's season, making each win pivotal. Overall, play callers are influenced by different factors at different points of the season.

Both of the preceding accounts of the data in Figure 5 should be considered with some caution, for two reasons. First, the playoffs do not encompass a random sample of teams. Because it is logical to predict that teams succeed by adapting to reinforcement variables (a proposition that receives further attention below), the relatively high sensitivity and variance accounted for seen in the playoffs could simply reflect the exclusion of unsuccessful teams. It is also worth noting that the stakes of winning and losing are much higher for teams that participate in postseason play, because a loss would terminate the team's season. Second, the contingency-exposure account is challenged by the fact that, when we fitted Equation 1 to data from successive four-game blocks of the regular season (across which contingency exposure accumulates), we found no systematic changes in sensitivity, bias, or variance accounted for (data not shown). We address this finding further in the General Discussion.

Study 3: Game-by-game Individual Team Outcomes

The preceding analysis aggregates data from different teams and play callers. To focus as much as possible on the behavior of individual play callers, Equation 1 was fitted separately to the data of each team, with each data point representing one of 16 regular-season games (preseason games were excluded from this analysis due to factors described above, and too few postseason games occur in the NFL to support a meaningful analysis of individual team outcomes).

Results and Discussion

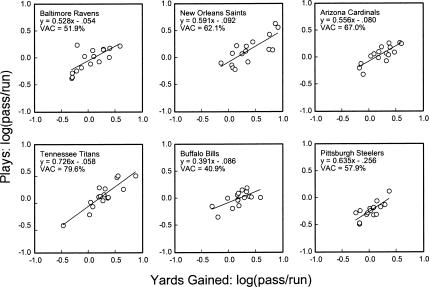
Table 1 summarizes the results and Figure 6 shows illustrative cases. Equation 1 accounted for a substantial amount of variance in play calling in most cases; at least 40% of the variance for 28 of 32 teams. These fits are modest compared to those typically seen when matching equations are applied to laboratory performance (e.g., Pierce & Epling, 1983), although they compare favorably to those obtained from some other descriptive studies of behavior in more complex settings outside the laboratory (e.g., Martens, Halperin, Rummel, & Kilpatrick, 1990).

Figure 6. Illustrative instances of applying the generalized matching law (Equation 1) to the game-by-game data of specific teams.

See text for explanation.

Overall, most teams were broadly similar to the regular-season league-aggregate outcomes described previously. The top row of panels in Figure 6 shows results for three teams that approximated the median slope (0.575), intercept (−0.0945), and variance accounted for by Equation 1 (60%). Some obvious between-team differences also were found, as the bottom row of panels in Figure 6 illustrates. Tennessee and Buffalo showed unusually steep and flat slopes, respectively, indicating that the Tennessee play caller adapted play calling to yardage gained more sensitively than did the Buffalo play caller. New England (not shown) and Pittsburgh showed unusually strong biases for calling rushing plays.

Serious football fans will notice immediately that the data in Table 1 bear no obvious correspondence to lay descriptions of the team offenses involved. For instance, during 2004, Indianapolis, which was known as a passing team (Oates, 2005), showed a stronger rushing bias than Atlanta, which was known as a rushing team (Polzer, n.d.). This apparent contradiction may be resolved simply by noting that lay descriptions may focus on the number of passing versus rushing plays called by a team, or perhaps the relative success of passing versus rushing plays, whereas the generalized matching law focuses on the relation between play calling and success. The generalized matching law does not, for instance, take issue with the fact that Indianapolis called many passing plays during 2004. It merely clarifies that this team called more rushing plays than would be predicted by the ratio of passing yards gained to rushing yards gained. Thus, an analysis of play calling based on the generalized matching law reveals patterns that are not apparent in more casual inspections of offensive performance.

Bias

As discussed previously, one possible influence on bias in play calling is the risk of a turnover. Turnovers are low-frequency events, making the calculation of turnover rates for individual teams meaningful only at the season-aggregate level. For each NFL team, turnover rate was defined as the logarithmically transformed ratio of fumbles per rushing play to interceptions per passing play for the entire regular season. This relative turnover rate was significantly correlated with bias in play calling, r  =  .360, p  =  .0431. Thus, across teams, as the relative risk of a fumble increased, bias for rushing decreased or shifted toward a bias for passing.

Most NFL teams showed a bias for calling rushing plays even though passing plays netted more yardage on average than rushing plays (for all games and teams combined, 6.69 and 4.14 yards per play called, respectively). This may reflect the fact that, during the 2004 regular season (as in most seasons) more than 40% of passes were not completed. Thus, pass plays net big yardage gains given a completion (more than 11 yards per completion on average in 2004), but none at all given an incompletion. In previous analyses, play calling was shown to be averse to risk in the form of turnovers. It seems reasonable, therefore, to suggest that an additional appeal of rushing plays is that they yield more certain yardage outcomes than passing plays.

If so, then the extent to which rushing plays are preferred should vary with the consistency of yardage outcomes associated with them. Ideally, variability in yardage outcomes would be assessed on a play-by-play basis, but NFL data are not readily available in this form. Instead, for each team, we determined the mean yards earned per rushing play for each game and calculated the standard deviation of these measures. The same was done for mean yards gained per passing play. At the team level, the standard deviation of yards gained per rushing play (median for 32 teams  =  1.13) was smaller than that for passing play (median  =  1.77), suggesting a greater degree of uncertainty in passing outcomes on any given play. In a multiple regression analysis evaluating the conjoint relation between team variance in rushing and passing yards per play and bias (log b), a statistically significant overall correlation, F(2, 29)  =  3.86, p  =  .0308, incorporated a significant relation between variance in rushing yards and bias (b  =  0.104, SE  =  0.039, β  =  .445, t  =  2.672, p  =  .0125). Specifically, as variance in rushing yardage increased, rushing bias became less pronounced or shifted toward a bias for passing.

Multiple Influences on Play Calling

An important constraint on the capacity of Equation 1 to account for play calling is the fact that football play distribution statistics are not a pure measure of play calling. Although a coach usually designates the plays, most football quarterbacks are charged with a certain amount of improvising, either by using an audible to change the play assigned by the coach just before it is executed (Westerling, 2002) or by modifying a play once it is in progress (e.g., on a play called and initially executed as a pass, a player might decide to rush if an opportunity presents itself). NFL statistics designate a play as pass or rush according to what actually took place, not what was called originally, and thus some of the primary play caller's intentions are lost in every data set. In this context, it may be noteworthy that Atlanta, one of the teams for which Equation 1 provided a poor fit, was led in 2004 by quarterback Michael Vick, who is known as an especially prolific improviser. Perhaps the Atlanta data reflect an unusual degree of blending of influences from two individuals, coach and player, although we know of no obvious way to test this notion quantitatively.

At least some play-calling statistics may be impure in the sense that different coaches on the same team call different plays (e.g., a head coach may overrule an offensive coordinator in some situations), and it stands to reason that different individuals will have different play-calling tendencies. Unfortunately, no public records are kept of who called what plays for a given team. Occasionally, however, a specific event will highlight the differential influence of two coaches on play calling. During 2004, two NFL teams replaced head coaches during the season, allowing a comparison of play calling under two coaching regimes working with the same roster of players. As Table 2 shows, both Miami and Cleveland showed different play-calling patterns under different coaches (these fits must be regarded with some caution given the small number of games involved). These cases bolster the assumption that matching in NFL play calling reflects the offensive strategies of individuals, even if, in other cases, the available data do not always indicate clearly which individuals.

Table 2. Fitted Parameters of Equation 1 for Two National Football League Teams That Experienced a Change of Head Coach During the 2004 Regular Season.

Team	Head coaches (games)	Reinforcement sensitivity (a  =  slope)	Bias (log b  =  intercept)	Variance accounted for (%) by Equation 1
Miami	Wannstedt (1–9)	0.451	−0.340	30
	Bates (10–16)	−0.066	0.240	<1
Cleveland	Davis (1–11)	0.194	−0.027	7
	Robiskie (12–16a)	0.640	−0.174	62.3

^aGame 13 was excluded from the analysis because Cleveland registered negative passing yards in this game, and the logarithmic transformations required to apply Equation 1 are suitable only for positive numbers.

General Discussion

Sports fans often attribute success to a player's unusual talents, as in a recent writer's observation that the presence of Atlanta quarterback Michael Vick on the field “just picks up the intensity of the whole team. There's a certain feeling that just spreads throughout the team” (Shell, 2003). Many observers also believe that a coach's inspiration lifts teams to success. For instance, Schembechler (2002) has written that “Ordinary men make promises to achieve excellence. Motivated men are fearless. … They make commitments, and they never compromise. … A man must commit himself to that degree of passion before he truly earns the title coach” (p. 18). Such sentiments reflect a special case of the Great Individual versus the Zeitgeist hypotheses of historical events (Boring, 1950; Diamond, 1999). According to Diamond, lay explanations of important human events tend to focus on the will and character of individuals involved and thereby ignore the influence of unexotic, though powerful, situational variables. Based on the present findings and those of Vollmer and Bourret (2000), the matching law may help to identify some of those variables in sport environments.

The matching law has now been applied successfully to a variety of situations outside the laboratory, including choices made during competition by highly skilled basketball players (Vollmer & Bourret, 2000). The present study extends that track record to play calling by football teams. One contribution of the present study was the inclusion of supplemental analyses showing that estimated matching parameters varied as might be expected across different conditions (i.e., team ranking, down of play, regular-season vs. playoff games). These results provide support for the external validity of matching outside the laboratory.

In applying a simple quantitative model to play calling, the present analysis overlooks much that is regarded as important to football success. For instance, a cornucopia of strategies exist for deciding what type of play is most suitable to call depending on the down, the plays that a team has executed recently, the type of defensive strategy employed by an opponent, the game situation, the weather conditions, the abilities of key players, and so forth (Westerling, 2002). Furthermore, it is reasonable to assume that strategies may also shift as the magnitude of the reinforcer, or yardage gained, varies across games situations. For example, although a 1-yard gain may not seem as salient of a reinforcer as a 20-yard gain, it may be the case that only 1 yard was needed to obtained a first down or even a touchdown. Future research into this subject may benefit from the analysis of two-point conversion play calling, because these plays hold the reinforcement value constant. In addition, research using video-game simulation technology with coaches may address some of the situational confounding effects (e.g., weather) to create a more controlled investigation of choice in a sports context. However, despite ignoring most of these factors, the present analysis revealed a global association between play calling and relative success of passing and rushing plays.

Cause-and-effect Questions

Although Equation 1 accounted for less variance in football play calling than laboratory performance, the present findings are noteworthy in that a fairly simple quantitative model predicts behavior under the complex circumstances of elite sport competition. This may be possible because the generalized matching law, although not devised with football in mind (Baum, 1974), anticipates a central maxim of football play calling, that offensive success depends on some strategy for intermingling passing and rushing plays. According to football lore, mixing the two types of plays prevents a defense from concentrating fully on either type of play, thereby increasing the odds of the offense encountering an inadequately prepared defense on a given play (Westerling, 2002). From this perspective, play calling influences yardage gained, but the generalized matching law makes clear that the reverse also may be true. Although the generalized matching law is mute about what kind of play should be called on a given down, as a model of choice (behavior allocation) it predicts that, as long as both passing and rushing yield yardage gains, both types of plays will be called occasionally.

Nevertheless, the reader is cautioned that other variables outside matching relations may influence play calling. For example, one traditional view of football play calling is that the “run sets up the pass.” That is, after several rushing attempts, regardless of yardage gained, the offensive coordinator may call for a passing play to test the defense. Thus, calling a passing play amid a chain of rushing plays creates a sense of uncertainty in the defense during future play series. This view that a series of plays becomes contingent on one another begins to deviate from our analogy of concurrent schedules as more plays are called in succession. Therefore, it may not be surprising that the variance accounted for by Equation 1 was higher during first and second downs than during third downs.

Analyses based on the generalized matching law assess covariation between reinforcement conditions and behavior allocation but, as the preceding discussion implies, do not establish cause–effect relations. In the laboratory, reinforcement conditions are manipulated systematically, promoting strong inferences about the influence of these conditions on behavior allocation. In the present analysis, it is tempting to conclude that yardage gained influences play calling, but other mechanisms could create matching. Imagine, for example, that for each NFL team mean yards gained per rushing or passing play were constant across games. Imagine, too, that some factor not evaluated in the present study caused the number of rushing versus passing plays called to vary across games. Total yards gained through rushing and passing would vary directly with the number of plays called, producing matching at a descriptive level, but not because yardage-gained reinforcement influenced play-calling behavior. The data presented thus far cannot rule out such a possibility.

Two points argue against the preceding as a satisfactory explanation of play calling. First, the constant-yardage account does not anticipate systematic team differences in reinforcement sensitivity or bias (Table 1). Indeed, this account predicts perfect matching for each team. Interteam variations might, perhaps, be attributed to measurement error resulting from limited behavior samples, but, as will be discussed below, some of these variations appear to be related to important team outcomes, suggesting that they are in fact systematic variations. Second, for many teams there was considerable game-by-game variation in mean yards gained per rushing and passing play. If the constant-yardage account is accurate, then as variability in yardage gained through passing and rushing increases (i.e., variability not due to number of plays called), the variance in play-calling data for which Equation 1 accounts should decrease. To test this prediction, we calculated, for each NFL team in the 2004 regular season, the standard deviation of both mean per-game yards gained per rushing play and mean per-game yards gained per passing play. A multiple regression analysis was conducted to determine the conjoint relationship between these predictor variables and the percentage of variance in individual teams' play calling for which the generalized matching law accounted (Table 1). The overall correlation was not statistically significant, F(2, 29)  =  1.82, p  =  .1801. Although it is possible to rule out a constant-yardage hypothesis, doing so does not, of course, directly support the reinforcement interpretation normally encompassed by the generalized matching law.

In the laboratory, matching usually emerges gradually after extended contingency exposure, and something similar was apparent in Vollmer and Bourret's (2000) basketball data. Shot-selection patterns tended to converge on matching-law predictions as experience accumulated across many games. As noted previously, however, we found no evidence that NFL play calling better approximates yardage-based predictions of the generalized matching law as the regular season progresses. What, then, accounts for the game-by-game correspondence of NFL play calling and yardage outcomes?

A single NFL game appears to provide little opportunity for acquisition based on contingency exposure alone. Yet some laboratory data suggest that, given experience with frequently changing reinforcement conditions, individual behavior can adapt quite rapidly in the fashion predicted by the matching law (Davison & Baum, 2000). Here it may be relevant that, unlike many laboratory subjects, NFL coaches and offensive coordinators are not novices. Both groups of individuals have worked previously for many teams at many levels of competition and for high-stakes outcomes, possibly rendering them extremely sensitive to reinforcement variables.

It is also worth noting that subjects in the preponderance of laboratory studies on concurrent reinforcement schedules are nonhumans. By contrast, some experimentally naive human subjects show steady-state performance after less than an hour of contingency exposure (e.g., Critchfield, et al., 2003; Magoon & Critchfield, in press). Given this standard of comparison, game-by-game changes in NFL play calling do not seem remarkable.

Finally, it seems likely that antecedent stimuli play an important role in NFL play calling. For example, prior to a game, coaches study opponents' behavior tendencies by viewing game films and examining detailed statistics (Fulmer, 2002). Speaking loosely, these may provide vicarious experience that obviates the need for an extended learning curve. More specifically, rules about play calling may be derived that substitute for contingency shaping (Skinner, 1969). Presumably, antecedent control exists over both pass-play calling and rush-play calling, and these forms of control compete. There is precedent for this view both within behavior analysis and elsewhere. In the former case, contingency discriminability theories (Davison & Nevin, 1999) assume that operant choice is affected by both consequences and the discriminative stimuli that are correlated with them. In the latter case, taking inspiration directly from the matching law, some proponents of value-expectancy theory hold that multiple expectancies, which are defined as “anticipations of consequences for a given action” (Borders, Earleywine, & Huey, 2004, p. 539), compete just as do current contingencies. To wit: “Individuals may make a behavioral decision based on anticipated reinforcement for that behavior as well as anticipated reinforcement for competing, alternative, behaviors” (Borders et al., p. 540). Although we can suggest no obvious means of quantifying the relative contributions of contingency exposure and antecedent stimuli, it seems reasonable to assume that NFL play calling is affected by both.

Matching and Team Success

If matching is an important component of sport behavior, then it is reasonable to ask whether team accomplishments might be improved by taking note of it. The present analysis cannot demonstrate cause and effect, but potential connections between matching outcomes and team success can be examined descriptively. Table 3 shows means of the fitted parameters of the generalized matching law for the 10 most and least successful NFL teams in terms of total offense (yards gained from all sources; see http://sports.espn.go.com/nfl/statistics) during the 2004 regular season. Successful offensive teams tended to show steeper matching slopes and more pronounced rushing biases than unsuccessful ones, and the generalized matching law tended to fit their offensive data better.

Table 3. Mean (SD) of Fitted Parameters of Equation 1 for National Football League Teams Ranked in the Top 10 and Bottom 10 in Total Offense for the 2004 Regular Season.

	Teams		t test for unpaired scores
	Top 10	Bottom 10	t(18)	p
Slope	0.685 (0.098)	0.486 (0.133)	3.287	.0041
Intercept	−0.133 (0.046)	−0.048 (0.043)	4.314	.0004
Variance accounted for (%)	69.7 (10.9)	47.9 (16.9)	3.419	.0031

Simple correlations were examined between team winning percentage for the 2004 regular season and the fitted parameters of Equation 1, with Atlanta excluded from the analysis as an unusual case due to questions about who selects the plays. The amount of variance accounted for by Equation 1 was a statistically reliable predictor of winning (r  = .409, p  =  .0225), but the slope of the matching relation was not (r  =  .281, p  =  .1252). Taken at face value, this finding suggests that play callers must adjust their play calling from game to game to reflect yards gained for passing and rushing (they must match), but the sensitivity of that relation is not important. This conclusion should be considered with caution, however, due to the restricted range of slope estimates in the data set (all slopes were positive and less than 1). It is reasonable to anticipate a curvilinear relation between slope and winning percentage. Slopes approaching zero, and negative slopes, indicate poor matching of play calling to yards gained, and should be associated with poor winning percentages. Exceptionally steep slopes (>1) indicate a tendency toward exclusive use of rushing or passing plays, and this predictability also should be associated with poor winning percentages (e.g., Westerling, 2002).

The intercept of the matching relation also was a significant predictor of season winning percentage (r  =  −.579, p  =  .0007). In a pool of NFL teams that adjusted play calling to yardage gained, therefore, those that showed a strong bias for calling rushing plays tended to win more games than teams with a weaker rush bias or with a passing bias. Three caveats are offered concerning this finding. First, it is typical for the team leading in points near the end of the game to “run down the clock” in an attempt to decrease the opportunity of a turnover. This is traditionally done by calling a series of rushing plays because they, when kept in bounds, do not result in stopping the game clock. Thus, it may not be surprising that successful teams (teams presumably in the lead near the end of the game) demonstrated a bias towards rushing. Second, recalling that, across leagues, bias was linked to turnover risk, this pattern may turn out to be conditional. In a league with high fumble risk, like Arena Football League 2, a strong tendency to rush the ball might be associated with poor outcomes. Team-level matching analyses for a variety of leagues would be needed to test this suggestion. Third, because the present study employed descriptive methods, it should not be assumed that NFL win percentage can be improved simply by increasing the number of rushing plays called. The latter caution notwithstanding, in sport contexts the association between rushing bias and winning percentage appears to be fairly strong. In the present data set the association was stronger than that between winning and 25 of 30 offensive statistics reported by a commercial service for people interested in football wagering (http://www.twominutewarning.com/correlations.htm). Interestingly, all of those 30 statistics (e.g., average yards gained per offensive play and average points scored per drive, or offensive possession) focus on the success of offensive efforts and say little about the behavior of those who select offensive plays. The present matching-law analysis, by contrast, places the emphasis on a functional relation between play calling and the offensive outcomes that result. As shown by considerable experience in applied behavior analysis, such relations are likely to be important foundations for identifying strategies of change.