Health Insurance and Health at Age 65: Implications for Medical Care Spending on New Medicare Beneficiaries

Abstract

Objectives

To investigate the consequences of endogeneity bias on the estimated effect of having health insurance on health at age 63 or 64, just before most people qualify for Medicare, and to simulate the implications for total and public insurance (Medicare and Medicaid) spending on newly enrolled beneficiaries in their first years of Medicare coverage.

Data

The longitudinal Health and Retirement Survey of people who were 55–61 years old in 1992, followed through biannual surveys to age 63–64 or until 2000 (whichever came first), and those who were 66–70 years olds from the Medicare Current Beneficiary Surveys, 1992–1998.

Study Design

Instrumental variable (IV) estimation of a simultaneous equation model of insurance choice and health at age 63–64 as a function of baseline health and sociodemographic characteristics in 1992 and endogenous insurance coverage over the observation period.

Findings

Continuous insurance coverage is associated with significantly fewer deaths prior to age 65 and, among those who survive, a significant upward shift in the distribution of health states from fair and poor health with disabilities to good to excellent health. Treating insurance coverage as endogenous increases the magnitude of the estimated effect of having insurance on improved health prior to age 65. The medical spending simulations suggest that if the near-elderly had continuous insurance coverage, average annual medical spending per capita for new Medicare beneficiaries in their first few years of coverage would be slightly lower because of the improvement in health status. In addition, total Medicare and Medicaid spending for new beneficiaries over their first few years of coverage would be about the same or slightly lower, even though more people survive to age 65.

Conclusions

Extending insurance coverage to all Americans between the ages of 55 and 64 would improve health (increase survival and shift people from good–fair–poor health to excellent–very good health) at age 65, and possibly reduce total short-term spending by Medicare and Medicaid for newly eligible Medicare beneficiaries, even though more people would enter the program because of increased survival.

Several recent studies have examined the consequences of uninsurance in a near-elderly population using data from the longitudinal Health and Retirement Survey (Heeringa and Conner 1995). Baker et al. (2001, 2002) found that those who were continuously or intermittently uninsured, or lost their insurance coverage over a 2–4 year period, experienced greater health declines than those who were continuously insured. McWilliams et al. (2004, 2003) found that lack of insurance was associated with significantly increased mortality, and that previously uninsured near-elderly adults who survived to age 65 increased their use of basic clinical services after they obtained Medicare coverage more than those who had been fully insured.

These research findings raise two important questions. Does lack of insurance prior to age 65 result in people qualifying for Medicare in worse health than if they had been insured? If so, is public insurance spending through Medicare and Medicaid on newly enrolled beneficiaries greater than it would be if people had continuous insurance coverage prior to age 65?

Our analysis extends these previous studies in several ways. As the prior studies were not specifically interested in the question of health status at entry to Medicare, they included changes in health for people as young as 57, as well as people who were older than 65 and had already aged into Medicare coverage. If attaining Medicare coverage improves health (Lichtenberg 2002), then the previous results may understate the impact of lack of insurance on health status at age 65. We also analyze data from the Health and Retirement Survey (HRS), but define our endpoint as health status at the last survey before turning 65.

Second, Baker et al. (2001, 2002) did not adjust for possible bias in the estimation of the health insurance effect because of the selection of people into insurance states based on their unobserved health. This bias could occur through a combination of mechanisms. People who are uninsured at this age and in good health may forego insurance coverage, especially nongroup coverage, because of its very high cost for older people. At the other extreme, people in poor health who are unable to work may qualify for Medicaid and/or Medicare coverage because of a work-limiting disability. Similarly, people in less than perfect health with employer-sponsored insurance may be more likely to continue working to keep their insurance coverage, as opposed to taking early retirement without coverage. These behaviors raise the possibility that unobserved health, which affects future health, may be better among the uninsured and worse among the insured than if people were randomly assigned to alternative insurance states in an experiment.

McWilliams et al. (2004) used a propensity score method based on health insurance status in 1992 to adjust for the effects of observable differences associated with insurance coverage. However, this adjustment may not fully account for the effects of unobserved factors. We use instrumental variable (IV) analysis (McClellan and Newhouse 2000) to adjust for possible biases because of unobserved factors, focusing on the percentage of time a person was insured over the entire observation period prior to turning 65. (McWilliams et al. [2004] adjust only for insurance status at baseline, 1992.)

Third, Baker et al. (2001, 2002) measured the change in health by two categorical variables: a “major decline in health,” defined as a change in self-reported health status between baseline and endpoint either (1) from excellent, very good, or good health to fair or poor, or (2) from fair to poor, and a “new difficulty with mobility,” defined from specific questions asking whether the person had “no difficulty” with an activity at baseline, but was unable to perform the activity at the endpoint. Consequently, people already in poor health or unable to perform the mobility activities at baseline, as well as people who died, were excluded from the analysis. McWilliams et al. (2004) analyzed only mortality, ignoring changes in health status among survivors. We analyze a broader and more detailed measure of health prior to age 65, taking into account mortality, self-reported health status, and the presence of instrumental activities of daily living (IADL) or activities of daily living (ADL) limitations.

Finally, we use the results from our analysis of the relationship between insurance coverage and health prior to age 65 to simulate whether medical spending by newly enrolled, aged Medicare beneficiaries might be affected by extending continuous insurance coverage to all people between the ages of 55 and 64. We use data on health and medical care spending from the Medicare Current Beneficiary Survey (MCBS) to simulate the effects of a change in the distribution of initial health states on both total and public (Medicare plus Medicaid) medical care spending by 66-70-year olds.1

METHODOLOGY

Data and Sample

Analysis of Health Prior to Age 65: The HRS

The HRS is a nationally representative longitudinal survey of a sample of people who were between the ages of 51 and 61 in 1992. The HRS is sponsored by the National Institute of Aging (grant number NIA U01AG09740) and conducted by the University of Michigan. The initial sample was interviewed approximately every 2 years to obtain information on health, insurance coverage, and work status of respondents and their spouses. Detailed information on education, demographic characteristics, and work history was collected at baseline. The most recent year for which data were available is 2000.

The analysis sample is a subset of the 9,761 people who were age-eligible in 1992. (Older and younger spouses are also surveyed, but they were excluded because no weights are available for them.) We excluded 5,598 people who did not turn 65 until 2002 or later and 396 people who were covered by public insurance (Medicare or Medicaid) in 1992. Medicare and Medicaid coverage of nonelderly adults in this age range is due almost entirely to the presence of a disability, end-stage renal disease, or blindness. As these are clear-cut cases where preexisting chronic poor health determines insurance coverage, they were not appropriate observations for an analysis of the effect of lack of insurance on subsequent health. An additional 169 cases did not respond to subsequent surveys, and 34 cases were missing key information on at least one survey. People were followed until the last survey before they turned 65. The final analysis sample consisted of 3,564 people (including 259 decedents) who were between the ages of 55 and 61 in 1992; were followed for 4, 6, or 8 years; and, if still alive, were 63 or 64 at their last interview.

Simulation of Medicare and Total Health Spending for New Aged Medicare Beneficiaries: The MCBS

We use the MCBS to obtain data on medical care spending by initial health status for recently enrolled Medicare beneficiaries. The MCBS is a continuous survey of a representative sample of the Medicare population, including elderly and disabled persons living in the community and in institutions (Adler 1994). We use the “Cost and Use” files from 1992 to 1998 to estimate total and Medicare health spending for new aged beneficiaries. In all, 2,081 sample persons who entered the survey at age 66 or 67 in the 1992–1995 waves were followed for 3 calendar years after their initial year in the survey. We restricted the sample to persons not residing in institutions at their first interview (as the HRS is a noninstitutionalized survey), but followed respondents if they entered an institution during the 3-year observation period.

Conceptual Framework

Analysis of Health Prior to Age 65

Our conceptual model postulates that health at age 65 depends on prior health, health behaviors, basic sociodemographic characteristics at baseline, and the extent of insurance coverage over the observation period. We also assume that insurance coverage over the observation period depends on baseline health and on intermediate or expected changes in health. For example, someone in only fair to good health or expecting a possible health decline may be more likely to continue working in order to retain employer-sponsored insurance (or to purchase individual insurance or to apply for public insurance coverage) than someone who is in excellent health and contemplating early retirement. This hypothesized relationship between health and health insurance is a possible source of bias if there is a systematic difference in underlying or unobservable health that is related to whether a person chooses to have or is able to retain insurance coverage over the observation period.

Ideally, we would like to estimate an explicitly dynamic intertemporal model of the relationship between health insurance coverage and health in successive periods. As this is beyond the scope of this analysis, we make the simplifying assumption that health prior to age 65 depends on the percentage of time a person has health insurance coverage over the entire observation period.

This conceptual framework implies a two-stage empirical approach to adjust for possible bias because of the effects of unobservable health and other differences on insurance status. First, we estimate a model of the percentage of time the person has insurance coverage over the observation period including several factors hypothesized to affect insurance coverage but not health outcome. Then we use the insurance model to generate an estimate of predicted insurance coverage, which becomes the primary independent variable in the model for health status at age 65.

The exogenous identifying variables are critical to the validity of the IV approach, since they create the variation in predicted insurance coverage that is used to identify the true effect of insurance on health. However, the conceptual framework can only suggest what those variables might be. Therefore, we test that they satisfy the statistical criteria for a valid IV and explore the sensitivity of the estimated insurance effect to variations in the set of exogenous identifying variables.

Simulation of Health Spending for New Aged Medicare Beneficiaries

We use the results of the analysis of health prior to age 65 to generate a probability distribution, P_ji, of the likelihood of being in j distinct health states at age 65 for individual i. We combine these probabilities with estimates from the MCBS of public spending, MP_J, and total spending, MT_j, for the same j initial health states, to simulate alternative distributions of total and public medical spending using equations (1) and (2) for total spending and public (Medicare and Medicaid) spending, respectively:

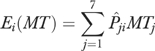(1)

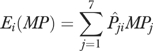(2)

As described below, we use an ordered logistic model to calculate a predicted probability for each of j health states for i individuals in the HRS sample of the form

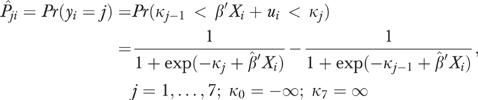(3)

These predictions are done in three ways: first, by combining the coefficients from the model not adjusted for endogeneity bias with the actual data (X_i) reported by the individual; second, by setting the insurance coverage variable to 1 (100 percent of the observation period); and third, by using coefficients from the IV model and assuming 100 percent coverage.

The mean levels of spending for each health state come from MCBS data for beneficiaries entering the survey at age 66 or 67. Their actual expenditures were summed over three calendar years (or until death if it occurred within these 3 years).2 (The MCBS does not provide data for 65-year olds.) Beneficiaries were then stratified into j discrete initial health states (described below) to calculate the mean spending levels, MP_j and MT_j.

Variables

Health Status

Health status is measured by a combination of self-reported general health status (excellent, very good, good, fair, or poor) and reported inability to perform basic activities of daily living. In the HRS and the MCBS, people who report being unable to independently (1) walk several blocks, (2) do heavy housework, or (3) do light housework were classified as “IADL disabled.” Those who report being unable to independently (1) get dressed, (2) bathe, (3) get into and out of bed or chairs, (4) walk across a room, or (5) feed themselves were classified as “ADL disabled.” Disability status is thus defined as a trichotomous variable having the values: Not Disabled, IADL Disabled, and ADL Disabled.

We combined the disability measure with self-rated health status to create a health index based on multiattribute utility theory (Keeney and Raiffa 1976). In the terminology of this theory, self-rated health and disability status are attributes that affect utility. A scale is created where the best outcome (excellent health without limitation) is assigned an index value of 1.0 and the worst outcome (dead) is assigned a value of 0.0. The assignment of index values for intermediate health states is based on correspondence analysis (Greenacre and Hastie 1987) that estimates the “distance” between categorical health states. We follow Erickson, Wilson, and Shannon (1995) in using the results of such an analysis to assign index values to each of the 15 possible health outcome pairs for living sample persons.3 The continuous index allows us to estimate both linear and, by ranking the index values, ordered models of health status. Table 1 shows the distribution of health status at baseline and at exit for those aged 63 or 64 and the index values corresponding to each category derived by Erickson et al. (1995).

Table 1.

Percentage Distributions of Baseline and Exit Health Status (Health and Retirement Survey Sample, N=3,564)

Health Status	Disability Status	Health Status Index*	Baseline (Ages 55–61 in 1992)	Exit (Ages 63–64 or Death Prior to Age 65)
Excellent	None	0.995	23.1%	13.2%
Very good	None	0.908	29.0	29.2
Good	None	0.813	24.8	26.6
Excellent	IADL	0.570	0.5	0.6
Fair	None	0.563	9.0	11.4
Very good	IADL	0.510	1.2	1.6
Excellent	ADL	0.471	0.2	0.1
Good	IADL	0.450	2.5	3.1
Very good	ADL	0.410	0.3	0.0
Good	ADL	0.360	0.7	0.1
Poor	None	0.347	1.3	3.2
Fair	IADL	0.290	2.8	2.2
Fair	ADL	0.210	0.8	0.2
Poor	IADL	0.170	2.2	1.6
Poor	ADL	0.100	1.7	0.2
Death		0.000	0.0	6.9

Note:

^*Derived from Erickson, Wilson, and Shannon (1995).

ADL, activities of daily living; IADL, instrumental activities of daily living.

Insurance Status

Insurance information was collected at each biannual survey and referred to coverage at the time of the survey. In the absence of information about changes in insurance status (insured or uninsured) between interviews, we assumed that the coverage reported at each survey applied to the entire time since the last survey. Those who reported being insured at all interviews were coded as having coverage for 100 percent of the observation period, while those who were uninsured at all interviews were coded as having coverage for 0 percent of the time. All other cases were given values based on the percentage of observation points they reported having insurance coverage. (For example, a person who was insured for one of three rounds was assigned a value of 33 percent, and a person insured for four of five rounds, a value of 80 percent.)

Table 2 shows the distribution of cases over the range of 0–100 percent coverage. While only 6.8 percent were uninsured across all interviews, another 22.6 percent reported being uninsured at least once during the observation period. The majority, 70.6 percent, were continuously insured.4

Table 2.

Distribution of Cases by Percentage of Time Covered by Insurance, 1992–2000 (Health and Retirement Survey Sample, N=3,564)

Percentage of Time Insured*	Percentage of Cases
0	6.8
20	0.7
25	1.1
33	1.9
40	1.0
50	2.5
60	1.6
66	4.5
75	4.8
80	4.3
100	70.6

Note:

^*Based on proportion of survey rounds with insurance coverage between 1992 and 2000.

Other Independent Variables in the Health Model

In addition to baseline health status and insurance coverage, the model for exit health includes dichotomous measures for the presence of any of six major chronic conditions at baseline: hypertension, diabetes, cancer, pulmonary disease, heart disease, stroke, or arthritis. We use three dichotomous measures to indicate health behaviors: light-to-moderate or heavy alcohol consumption, relative to none, and whether the person smoked. Education is measured by a set of dichotomous variables for educational attainment relative to less than 9 years of education: some high school, high school graduate, some college, college graduate, and postgraduate degree. We also include dichotomous variables for gender and for race/ethnicity: African American, Hispanic, or other race relative to white, non-Hispanic. Age at baseline is measured by a set of dummy variables.

Exogenous Identifying Variables in the Insurance Model

We assume that spouse's prior union membership (if married), immigrant status and years in the U.S. if foreign born, and involuntary job loss within the last 5 years influence insurance status but are not correlated with unobservable factors that affect future health. These factors are hypothesized to influence insurance coverage mainly through access to employer-sponsored insurance and retiree insurance (for people who retire early) coverage. Recent immigrants are less likely to know about or be eligible for public insurance coverage and, in this age range, may be less likely to work or to work in a job that provides insurance. Immigrant status and spouse's union membership are measured at baseline. Involuntary job loss (laid off, let go, company closed) within the last 5 years is measured at each interview and represented by a dichotomous variable that takes the value 1 if the person reported experiencing any involuntary job loss during the observation period. Table 3 reports the mean values of the independent variables used to estimate the multivariate regression models of insurance coverage and health prior to age 65.

Table 3.

Mean Values of Independent Variables, 1992 (Health and Retirement Survey, N=3,564)

Variable	Mean
Baseline health status index	0.79
Baseline HS7 (excellent) (%)	23.1
Baseline HS6 (%)	29.0
Baseline HS5 (%)	24.8
Baseline HS4 (%)	10.7
Baseline HS3 (%)	4.9
Baseline HS2 (poorest health) (%)	7.5
Hypertension (%)	38.9
Diabetes (%)	10.5
Cancer (%)	6.6
Pulmonary disease (%)	8.3
Heart disease (%)	13.1
Stroke (%)	2.0
Arthritis (%)	40.6
Light or moderate drinker (%)	59.7
Heavy drinker (%)	5.0
Smoker (%)	24.3
Female (%)	52.4
Married (%)	77.0
African American (%)	9.0
Hispanic (%)	4.3
Other race (%)	2.1
Some high school (%)	13.2
High school graduate (%)	40.5
Some college (%)	18.9
College graduate (%)	11.3
Postgraduate degree (%)	8.0
Age 55 in 1992 (%)	4.7
Age 56 in 1992 (%)	18.6
Age 57 in 1992 (%)	17.7
Age 58 in 1992 (%)	18.8
Age 59 in 1992 (%)	17.5
Age 60 in 1992 (%)	18.8
Foreign born (%)	7.5
Years in U.S. (foreign born only)*	2.0
Spouse union member (%)	9.0
Involuntary job loss in last 5 years (%)	8.5

Note:

^*Years in the U.S. were missing for a small number of cases and are represented by a dichotomous variable indicating missing years. This variable was not statistically significant in the insurance model.

Statistical Analysis

We use IV analysis to adjust for possible bias because of the influence of health on insurance status (McClellan and Newhouse 2000) and apply established statistical tests of the validity of the IV approach (Bound, Jaeger, and Baker 1995; Staiger and Stock 1997). First, the exogenous identifying variables hypothesized to influence insurance coverage but not future health should be significant determinants of health insurance coverage. This condition is tested by an F-statistic for the joint hypothesis that the coefficients of all the exogenous identifying variables are equal to 0. An F-value greater than 10 is recommended.

Second, all the variables used to predict both health and insurance coverage should be independent of any unobserved factors, represented by the residual term of the regression model, that influence health prior to age 65. This condition is tested by regressing the residuals from the exit health model against all the exogenous independent variables in the system. The test statistic is calculated as N × R² from this regression and is distributed as a χ² (Greene 1990, pp. 538–539). The hypothesis of no correlation is accepted if the test statistic is smaller than the appropriate critical value.

We recognize that even if the exogenous identifying variables we use satisfy these tests collectively, there may still be concern that the IV coefficient is sensitive to this particular combination of exogenous variables. Therefore, to gauge the robustness of the estimated coefficient, we also estimate the model using instruments constructed from each of the identifying exogenous variables individually and in pairs. Finally, since the IV tests were developed for linear models, we estimate both the insurance and health models as linear functions for the purpose of conducting the tests. In other words, we treat exit health status as a cardinal scale ranging in value from 0 (death) to 1 (excellent health with no IADL/ADL limitations).

For the purpose of simulating medical care spending using the MCBS data, however, we convert the health measure into an ordered categorical scale and estimate the health model using ordered logistic analysis. The categorical scale collapses the 16 distinct values in the continuous scale (Table 1) into seven ordered categories: 1 (death), 2 (scale values 0.1−0.3), 3 (scale values 0.3−0.5), 4 (scale values 0.5−0.8), 5 (scale value 0.81), 6 (scale value 0.91), and 7 (scale value 0.995). The last three values correspond to good, very good, and excellent self-reported health with no IADL or ADL limitations. We use the ordered logistic model to estimate the probabilities of being in each of these health states just prior to Medicare coverage at age 65 [equation (3)].

We use the ordered categorical scale in the simulation for two reasons. First, assigning death a value of 0 on the linear health status scale is arbitrary, since the scale values for the other health states were all based on information provided by living people. Converting the measure to an ordered categorical scale preserves the ranking of the different health states, but does not impose an arbitrary scale value to measure the distance between death and the poorest health state for someone alive. Second, the relatively small sample of newly eligible aged beneficiaries in the MCBS does not provide enough cases to generate reliable estimates of health spending in a more detailed breakdown of the poorer health states.

RESULTS

Statistical Tests for IV Validity

The complete tests for the validity of the IV analysis are available in the appendix tables, which report the linear first-stage insurance equation, the linear observational, and IV health status equations, and the regression of the residuals from the health status equation against the model's exogenous variables. Each of the exogenous identifying variables is statistically significant, and the F-test for their joint significance is 15.9. Having a spouse who belonged to a union has a positive effect on insurance coverage, while involuntary job loss has a negative effect on coverage. People who were foreign born also have less coverage, although this effect diminishes the longer the time has passed since the person entered the U.S. The partial R² for the additional variables is 0.021, which accounts for 12.3 percent of the variance explained by the first-stage model for insurance coverage.

In the second test, the R² from the regression of all the independent variables against the residuals from the health model is 0.0008, which produces a test statistic of 2.85. The corresponding critical value of the χ² distribution is 7.78 at the 10 percent level of significance. Thus, we accept (cannot reject) the null hypothesis that the exogenous variables are uncorrelated with the residuals. These results indicate that the insurance IV satisfies the standard tests for identifying a weak instrument.

The OLS estimate of the coefficient for insurance coverage is highly significant with a value of 0.219, meaning that a person with complete insurance coverage would have a health status score 0.219 greater than a person who had no insurance coverage. The IV estimate of this coefficient is 0.381, which is 75 percent larger, and also highly significant. To test the sensitivity of the IV estimate to the specification of the exogenous identifying variables, we re-estimated the model with each of the identifying variables individually and in pairs. The resulting IV coefficients ranged from a low value of 0.285 (p=.12) to a high value of 0.461, with the others clustered between 0.363 and 0.426. Although we do not test other possible instruments, this set produces relatively similar coefficient estimates individually and in various combinations.

Analysis of Health Prior to Age 65: Ordered Logistic Regression Results

Table 4 reports the observational and IV estimates of the effects of insurance coverage on health prior to age 65 from the ordered logistic regression model that we use to construct the predicted probabilities for the spending simulation. As with the linear models reported in the online only appendix, the IV coefficient is substantially larger in magnitude than the observational coefficient, 2.67 compared with 1.35. The other variables in the model suggest that poor baseline health status and the presence of particular chronic conditions at baseline are all associated with poorer health at the endpoint. Smokers have significantly poorer health outcomes in both models. Highly educated people have better outcomes in the observational model, but these effects are diminished in the IV model, suggesting that some of the effect of education works through insurance coverage.

Table 4.

Ordered Logistic Regression Coefficients, Health Status Prior to Age 65^*, by Estimation Method (Health and Retirement Survey Sample, N=3,564)

	Estimation Method
	Observational		Instrumental Variable
Independent Variable	β	(p-value)	β	(p-value)
Pct. time insured	1.35	(<.01)	2.67	(<.01)
Baseline health status category†
HS6 (very good health)	−0.95	(<.01)	−0.95	(<.01)
HS5	−1.76	(<.01)	−1.74	(<.01)
HS4	−2.31	(<.01)	−2.17	(<.01)
HS3	−2.24	(<.01)	−2.15	(<.01)
HS2 (poorest health)	−3.22	(<.01)	−3.07	(<.01)
Hypertension	−0.29	(<.01)	−0.30	(<.01)
Diabetes	−0.71	(<.01)	−0.64	(<.01)
Cancer	−0.41	(<.01)	−0.34	.01
Pulmonary disease	−0.25	.05	−0.23	.08
Heart disease	−0.30	(<.01)	−0.30	(<.01)
Stroke	−0.33	.12	−0.20	.39
Arthritis	−0.22	(<.01)	−0.23	(<.01)
Light or moderate drinker	−0.01	.91	−0.04	.62
Heavy drinker	0.01	.97	0.05	.73
Smoker	−0.53	(<.01)	−0.42	(<.01)
Married	0.16	.05	0.05	.60
Female	0.14	.05	0.11	.11
Race and ethnicity‡
African American	−0.15	.13	−0.06	.56
Other race	−0.10	.48	0.12	.50
Hispanic	−0.07	.77	0.06	.80
Education§
Some high school	−0.19	.18	−0.31	.04
High school graduate	−0.06	.66	−0.24	.13
Some college	0.16	.26	−0.08	.69
College graduate	0.11	.49	−0.15	.46
Postgraduate	0.52	(<.01)	0.24	.27
Age in 1992¶
55	0.12	.63	0.14	.58
56	0.07	.74	0.10	.65
57	0.20	.36	0.16	.45
58	0.14	.53	0.08	.71
59	0.46	.04	0.37	.09
60	0.45	.04	0.31	.17
Cut points
Cut 1	−3.71		−2.80
Cut 2	−2.99		−2.12
Cut 3	−2.29		−1.45
Cut 4	−1.28		−0.46
Cut 5	0.24		1.05
Cut 6	2.27		3.07

Notes:

^*Dependent variable is categorical measure for health status at exit with seven ordered categories, from death to excellent health with no IADL/ADL limitations.

^†Omitted reference category is excellent health with no ADL/IADL limitations.

^‡Omitted reference category is white, non-Hispanic.

^§Omitted reference category is less than 9 years of education.

^¶Omitted reference category is age 61.

ADL, activities of daily living; IADL, instrumental activities of daily living.

To illustrate the difference between the observational and the IV coefficient estimates, we use the ordered logistic models to predict the distribution of health states prior to age 65 assuming complete insurance coverage for the entire observation period. We compare these distributions with the predicted distribution assuming actual insurance coverage and the coefficients from the observational model.

Table 5 shows that the percentage predicted to die before reaching age 65 is 6.7 percent assuming actual coverage, with 29.8 percent in very good health and 13.3 percent in excellent health (with no IADL or ADL limitations). Assuming full coverage under the observational model reduces the predicted mortality rate to 4.9 percent, and increases the percentages in very good and excellent health to 31.7 and 14.6 percent. Using the coefficients from the IV model reduces the mortality rate even further, to 3.9 percent, and increases the percentages predicted to be in very good and excellent health to 33.9 and 16.6 percent.5,6

Table 5.

Simulated Health Care Outcomes, Health Prior to Age 65 (Health and Retirement Survey Sample, N=3,564)

	Predicted Percentage Distribution of Health Outcome, by Insurance Coverage
		Simulated Full Insurance Coverage (%)
Health Status Categories	Actual Insurance Coverage (%)	Observational*	Instrumental Variable†
7 (excellent)	13.3	14.6	16.6
6	29.8	31.7	33.9
5	26.5	27.0	26.6
4	13.4	12.8	11.6
3	6.3	5.6	4.7
2 (poorest)	4.0	3.3	2.7
1 (death)	6.7	4.9	3.9
Total	100.0	100.0	100.0

Notes:

^*Based on observational ordered logistic regression model, Table 4.

^†Based on instrumental variable ordered logistic regression model, Table 4.

Simulation of Health Spending for New Aged Medicare Beneficiaries

Tables 6 and 7 report the spending simulations for new Medicare beneficiaries. (Estimates are expressed in $2001 dollars.) In Table 6, we report average annual spending levels (over the 3 years a person is followed by the MCBS) by initial health status for the sample of 66–67-year olds from the MCBS. Both public and total medical spending by “young” Medicare beneficiaries show a clear health gradient. Persons in excellent health at the initial interview had average annual spending of $3,466 over the subsequent 3 years. Medicare and Medicaid account for less than half of this total spending, $1,705. Total spending increases in successively larger increments as initial health status deteriorates. Those in the poorest initial health state spent an average of $19,901 per year over the subsequent 3 years, with public spending covering almost 80 percent of the total. Private insurance and out-of-pocket payments increase much less than Medicare and Medicaid payments as health status declines, presumably because these expenses cover Medicare deductibles, which do not increase with declining health status, and because institutional care typically does not impose coinsurance or copayments.

Table 6.

Average Annual Medical Care Spending (over 3 Years), by Baseline Health Status Category (Medicare Current Beneficiary Survey, Ages 67–70^*)

		Average Annual Spending (over 3 years)
Health Status Category	Sample Size	Medicare & Medicaid	Private Insurance	Out-of-Pocket	Total
7 (excellent)	434	$1,705	$791	$826	$3,466
6	555	2,330	814	1,018	4,363
5	492	3,401	1,168	1,049	5,803
4	202	5,786	1,320	1,268	8,733
3	148	8,106	2,004	1,814	12,123
2 (poorest)	250	15,991	1,678	1,786	19,901
1 (death)	0	0	0	0	0
Total	2,081	–	–	–	–

Note:

^*Medical care spending is tracked for 3 years for people who enter MCBS at age 66 or 67, starting the year after initial entry into survey sample.

Table 7.

Simulated Medical Care Spending for New Medicare Beneficiaries under Three Alternative Initial Health State Distributions

	Initial Health State Distribution
		Simulated
Simulated Spending*	Actual†	Observational Method‡	Instr. Var.Method§
Average annual spending (over 3 years) per beneficiary (2001 $s)
Medicare and Medicaid	3,899	3,768	3,560
Private insurance	1,027	1,027	1,010
Out-of-pocket	1,046	1,051	1,042
Total	6,022	5,921	5,712
Total spending¶ (billions, 2001 $s)
Medicare and Medicaid	7.15	7.04	6.72
Private insurance	1.88	1.92	1.91
Out-of-pocket	1.92	1.96	1.97
Total	11.05	11.06	10.78

Notes:

^*Based on equations (1) and (2) combining mean spending from Table 6 and distributions of initial health status from Table 5.

^†From Table 5, column 1.

^‡From Table 5, column 2.

^§From Table 5, column 3.

^¶Annual spending for a single age cohort (e.g., 66-year olds) of new aged Medicare beneficiaries.

We use equations (1) and (2) to combine the estimates of mean spending by initial health state (Table 6) with the three alternative distributions of initial health states generated from the health outcome models estimated with the HRS data (Table 5). Using data on actual insurance coverage to predict the distribution of initial health states from the HRS sample, the figures in Table 7 show that simulated average annual total spending per new Medicare beneficiary is $6,022 and public (Medicare and Medicaid) spending is $3,889.

When we simulate spending assuming complete insurance coverage, the estimates from the observational model suggest that total and public spending per new beneficiary actually decline slightly, even though more people are projected to survive to age 65 because of the complete coverage. The lower spending occurs because more people are projected to be in the excellent and very good health states, which have relatively low average spending, compared with the poorest health states.

Using the distribution of health states from the IV insurance estimates magnifies this effect. Total spending per beneficiary falls by 5.1 percent to $5,712 and public spending falls by 8.7 percent. Even after adjusting for the prediction that 2.8 percent more people will survive to age 65, these estimates of per beneficiary spending imply that total annual medical care spending for each new group of 65-year olds who become Medicare beneficiaries would fall from $11.05 to $10.78 billion per year over the first few years of Medicare coverage, and public insurance spending (Medicare and Medicaid) would fall from $7.15 billion to $6.72 billion per year.7

DISCUSSION

These calculations assume that there are no changes in spending behavior and health at ages 65 and 66, which precede the first MCBS observations of medical spending at age 67. It has been suggested that behavior at age 65 is most sensitive to insurance coverage prior to Medicare eligibility, as previously uninsured individuals seek services they were unable to afford in the preceding years (Lichtenberg 2002; McWilliams et al. 2003). Since the MCBS sample does not include beneficiaries in their first year of coverage, we are unable to estimate this effect. If it exists, our estimates may understate future cost savings of universal insurance coverage of the near-elderly. Similarly, because we are only able to observe behavior for a 3-year period in the MCBS, we assume that after age 70, the effects of universal insurance under Medicare “wear off.” If the health benefits continue, our estimates again understate future cost savings of universal insurance.

On the other hand, other researchers have suggested that increased longevity may not result in lower lifetime Medicare expenditures (Miller 2001), but will only delay them. More recently, Lubitz et al. (2003) found that Medicare beneficiaries with no functional limitations at age 70 had a life expectancy of 14.3 years and spent $136,000 over their remaining lifetime, while beneficiaries with at least one ADL limitation had a life expectancy of 11.6 years and slightly higher cumulative spending of $145,000. To the extent that health improvements produced by insurance are not “permanent,” but only constitute a delay of the onset of disease and death, our estimates may overstate lifetime cost savings. However, if end-of-life care is less costly as people age, then increased longevity may not lead to greater lifetime spending. Without a longer follow-up period, however, we are unable to evaluate these possibilities.

Limitations

Our analysis is subject to a number of qualifications that could affect the precise magnitudes of the coefficients estimated and the subsequent simulation results. First, we were only able to measure insurance at 2-year intervals without knowing the exact times when insurance status may have changed. To some extent, however, measurement error in insurance coverage as an independent variable is mitigated by the fact that our IV estimation method replaces observed insurance status with predicted insurance status (Kmenta 1971, p. 309). We were also unable to estimate our two-stage nonlinear model using a joint estimation routine, which may have caused some bias in the estimated standard errors. However, given the high significance levels of the key variables, it is unlikely that a joint estimation routine would have altered the findings substantially.

Another measurement limitation of our analysis is that exit health was not measured exactly at the time of or just before the respondent's 65th birthday. Since the HRS is conducted approximately every 2 years, respondents were either 63 or 64 at the date of their last interview before turning 65. As we controlled for age in the analyses, we do not believe that the estimates of the effect of insurance coverage on health prior to turning 65 were likely to have been biased because of the variation in the exact age at the time of the last interview.

A similar age qualification applies to the simulation sample from the MCBS, since it begins data collection for elderly beneficiaries at age 66, after people have been covered for a year. This may bias our estimates of spending downward, since it has been hypothesized that many newly eligible beneficiaries experience a spike in medical spending because of improved insurance coverage relative to their pre-65 insurance state. However, this bias would presumably affect both the baseline and simulated spending patterns for ages 67–70, and is thus unlikely to create a substantial error in the estimates of the differences in spending associated with the change in the distribution of initial health status.

As noted above, our analysis did not attempt to estimate an explicitly dynamic model of the intertemporal relationship between insurance status and health. Nor were we able to account for the possibly differential effects associated with variations in the timing of periods of uninsurance prior to turning 65. Future work, which will have the advantage of larger eligible samples, as more of the initial set of age-eligible people turns 65, may be able to address these limitations. We do not believe, however, that our simplified approach to measuring insurance coverage resulted in significant upward bias of the results.8 For example, if someone lost insurance coverage, experienced a subsequent deterioration in health, regained coverage, and had health return to the initial level, we would be likely to understate the effect of insurance on health as we measured the loss of coverage over the observation period, but not the health decline.

Finally, our analysis makes no attempt to quantify the value of the additional years of healthier life projected by our model. Recent calculations (Vigdor 2003) of the value of improved health accruing from universal coverage for the entire nonelderly population suggest that they can be substantial. Depending on whether it is assumed that insurance affects only mortality or both mortality and morbidity, the annual value of improved health from universal health coverage was estimated to range from $65 to $130 billion, compared with an estimated annual cost of providing coverage of $34 to $69 billion (IOM 2003, pp. 69, 104). Thus, valuing the improved health gained by the near-elderly from complete coverage would only add to the estimate of Medicare and Medicaid savings for new Medicare beneficiaries.

Implications for Policy

The primary policy implication of our research is that extending insurance coverage to all Americans between the ages of 55 and 64 would improve health (increase survival and shift people from good–fair–poor health to excellent–very good health) at age 65, and possibly reduce total short-term spending by Medicare and Medicaid for newly eligible Medicare beneficiaries, even though more people enter the program because of increased survival. The various sensitivity tests we conducted suggest that the precise magnitudes of these effects are somewhat sensitive to the choice of functional form, exogenous identifying variables for the IV estimation, and the measurement of insurance coverage. However, all of the estimates indicate that insurance coverage has a statistically significant effect on health and that accounting for endogeneity bias increases the magnitude of the insurance effect.

The illustrative simulation of the impact of improved health at age 65 on the health care spending of new Medicare beneficiaries estimated that the potential savings to public insurance programs would be $270 million per year (in 2001 dollars) for each new group of 65-year-old Medicare beneficiaries over the first few years they are in the program. If these savings persist over the first 5 years in the program, Medicare and Medicaid would spend about $1.35 billion less for each cohort of new beneficiaries.

This estimate is significant because it represents a potential offset against the cost of expanding insurance coverage to the nonelderly uninsured. Even if our estimate of potential savings is too high, the fact that there are any savings at all is significant, because it is often thought that reducing mortality increases morbidity, with the implication that not only would more people survive to qualify for Medicare, but that they would also be in poorer health, causing Medicare expenditures to increase.

Our analysis suggests that the increased medical care use that presumably accompanies expanded insurance coverage also improves morbidity as well as reduces mortality. Fewer people reach age 65 in fair or poor health with a disability. As people in these health states are much more costly to care for under Medicare, even small reductions in the number of people in these health categories can offset higher spending because of increased numbers of people in better health states.

If expanding health insurance coverage of the nonelderly or near-elderly improves the health of those who ultimately qualify for Medicare coverage, then anticipated savings in Medicare and Medicaid spending on the elderly could provide some of the funds to cover the cost of expanding insurance coverage to the uninsured. One policy option to consider might be to lower the age of eligibility for Medicare, perhaps to age 55, and allow people to buy Medicare coverage on an actuarially fair basis, but with premium subsidies for lower income people. Potentially, some of the cost of subsidizing coverage for low-income near-elderly would be offset by lower medical spending in the years after age 65.

SUPPLEMENTARY MATERIAL

The following supplementary material is available online:

APPENDIX TABLE 1. First-Stage Equation for Insurance coverage.

APPENDIX TABLE 2. Health Status Prior to Age 65 by Estimation Method.

APPENDIX TABLE 3. OLS Regression of Residuals against All Exogenous Variables.