Three-dimensional Numerical Modeling and Computational Fluid Dynamics Simulations to Analyze and Improve Oxygen Availability in the AMC Bioartificial Liver

Abstract

A numerical model to investigate fluid flow and oxygen (O₂) transport and consumption in the AMC-Bioartificial Liver (AMC-BAL) was developed and applied to two representative micro models of the AMC-BAL with two different gas capillary patterns, each combined with two proposed hepatocyte distributions. Parameter studies were performed on each configuration to gain insight in fluid flow, shear stress distribution and oxygen availability in the AMC-BAL. We assessed the function of the internal oxygenator, the effect of changes in hepatocyte oxygen consumption parameters in time and the effect of the change from an experimental to a clinical setting. In addition, different methodologies were studied to improve cellular oxygen availability, i.e. external oxygenation of culture medium, culture medium flow rate, culture gas oxygen content (pO₂) and the number of oxygenation capillaries. Standard operating conditions did not adequately provide all hepatocytes in the AMC-BAL with sufficient oxygen to maintain O₂ consumption at minimally 90% of maximal uptake rate. Cellular oxygen availability was optimized by increasing the number of gas capillaries and pO₂ of the oxygenation gas by a factor two. Pressure drop over the AMC-BAL and maximal shear stresses were low and not considered to be harmful. This information can be used to increase cellular efficiency and may ultimately lead to a more productive AMC-BAL.

Introduction

Acute liver failure (ALF) is a severe disease with high mortality rates (60–90%). At present, the only efficient therapy is orthotopic liver transplantation (OLT).11 To bridge ALF patients to liver transplantation or to regeneration of the native liver, liver support systems are needed. The most promising bridging method for the treatment of ALF patients are bioartificial liver (BAL) support systems. These systems are extracorporeal devices that are generally comprised of a bioreactor in which living hepatocytes are seeded. In a clinical setting, toxic plasma of ALF patients is perfused through a BAL system and detoxified by viable hepatocytes. A major advantage of BAL systems, as compared to other non-biological liver support systems, is the capacity to provide a full range of metabolic functions to compensate for the complex metabolic disorders seen in ALF. Although many BAL systems have demonstrated their detoxifying capacity or liver-specific functions in in vitro, ex vivo and in phase I clinical studies, no BAL system has shown to significantly improve survival in ALF patients bridged to transplantation in a controlled trial (for review:40).

Important issues for the development of an effective BAL system are local plasma flow and oxygen transport. Optimal cell function, i.e. detoxifying capacity, is only obtained when a BAL system is adequately perfused with plasma to enable efficient mass transfer. In this situation, sufficient nutrients (e.g. glucose, fatty acids) and oxygen are supplied, whereas unwanted metabolites (e.g. ammonia) are efficiently detoxified and metabolic end products (e.g. urea, CO₂) subsequently removed. In principle, oxygen (O₂) transfer is the main limitation in the efficiency of a BAL,3 because of the low solubility of oxygen in plasma and high demand for oxygen of functionally active hepatocytes.

The AMC-Bioartificial Liver (AMC-BAL; Academic Medical Center, Amsterdam, The Netherlands, patent No: WO 97/12960) was developed with a special design for on-site oxygenation of hepatocytes and direct contact of plasma to the cells to enhance bidirectional solute exchange. The AMC-BAL has shown promising results in in vitro set-ups, small and large animal ALF models, and finally in a phase I clinical study with ALF patients.13,39 But to increase the efficiency of the AMC-BAL, further optimization of plasma perfusion and oxygenation of hepatocytes may be useful.

Numerical techniques and Computational Fluid Dynamics (CFD) simulations are useful tools to gain insight in local flow field and oxygen transport in hollow fiber BALs19,27,30 as well as in other types of hepatocyte systems.16,23,25 These numerical techniques can also be used to determine the optimal working parameters and to further optimize the design of a BAL system. In this respect, we used CFD simulations as a methodological approach to analyze the configuration of the AMC-BAL. We constructed three-dimensional computer models of two representative unit volumes – micro models – of the laboratory-scale AMC-BAL. Fluid flow and oxygen transport and consumption were simulated in these micro models to gain insight in the flow field and local cellular oxygen availability. Numerical parameter studies were performed to assess possible improvements in local oxygen availability of hepatocytes. Several parameters were tested: (1) effect of the internal oxygenator system, (2) pO₂ of the oxygenation gas, (3) culture medium flow rate, (4) incorporation of an external oxygenator in the extracorporeal circuit, (5) the number of oxygen capillaries, (6) the effect of plasma perfusion versus normal culture medium, and (7) the effect of changes of hepatocyte oxygen consumption characteristics in time. Finally, we discuss the implication of this information for the optimization of the AMC-BAL into a more efficient bioartificial liver.

Materials and methods

The internal geometry of the laboratory-scale AMC-BAL is schematically drawn in Fig. 1 in a longitudinal and transverse cross-section. The bioreactor is built from a cylindrical polycarbonate housing (Fig. 1l) in which two pieces of three-dimensional (3D) non-woven polyester matrix mat (Fig. 1e, g) are spirally wound around a massive inner core (Fig. 1i). A space between the two mat segments (Fig. 1f) is left open for an additional hepatocyte seeding port (not shown). In the hydrophilic matrix, high-density hepatocyte culture is possible. Between the matrix windings, hydrophobic gas capillaries (Fig. 1m) are positioned in parallel along the entire bioreactor as an internal oxygenator system to supply additional oxygen to the hepatocytes. Culture gas (95% air, 5% CO₂) is perfused through these capillaries. Plasma enters the bioreactor through an inlet port (Fig. 1b) and flows through the inflow zone (Fig. 1j) further passes the hydrophilic matrix mat and through the void inter-capillary space (Fig. 1n). Plasma exits the bioreactor via the outflow zone (Fig. 1k) through the outlet port (Fig. 1d). Plasma and culture gas are counter-current flows.

Figure 1.

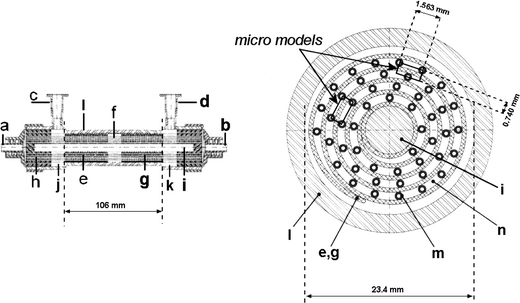
Longitudinal (left) and transverse (right) view of the internal geometry of the AMC-BAL with a – gas outlet; b – gas inlet; c – plasma inlet port; d – plasma outlet port; e – first mat segment; f – interspace; g – second mat segment; h – polyurethane potting to separate gas and fluid compartment; i – inner core; j – inflow zone; k – outflow zone; l – polycarbonate housing; m – gas capillaries; n – inter-capillary space through which plasma flows. The inline and triangular micro models are designated.

Computer Model

Since the entire BAL geometry is too large and complex to model, three-dimensional unit volumes – micro models – were isolated from the geometry (Fig. 1). Each three-dimensional micro model (Fig. 2) consists of 2 pieces of mat (thickness = 400 μm, height = 1563 μm, length = 50 mm; Fig. 1e, g) separated by a void interspace section (length = 6 mm; Fig. 1f). At both sides of the mat, gas capillaries (outer diameter = 380 μm) and an inter-capillary space are present. The two micro models differ only in their gas capillaries’ position. Either the capillaries are in a rectangular (inline micro model – Fig. 2) or in a triangular (triangular micro model – Fig. 2) pattern. These two configurations are the most distinct that could be isolated as the position of the capillaries relative to each other changes continuously along the course of the spiral mat (Fig. 1). These two micro models were therefore considered to be representative for the entire AMC-BAL. Simulations on both models will allow us to assess the influence of the capillary arrangement.

Figure 2.

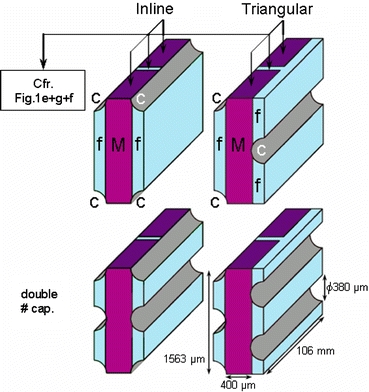
AMC-BAL micro models. Upper left, inline micro model; upper right, triangular micro model (c – capillary wall, M – non-woven matrix mat, f – inter-capillary space); lower left, inline micro model with double number of capillaries; lower right, triangular micro model with double number of capillaries.

Both models were created in the modeling software Gambit 2 (Fluent Inc., Sheffield, UK). All dimensions were derived from a laboratory-scale AMC-BAL or were supplied by the manufacturer. The curvature of the mat was neglected and the inflow and outflow zones before and after the mat segments in the AMC-BAL were not included in the micro models. Each standard micro model contains the equivalent capillary wall surface of 1 whole capillary. Since the entire laboratory-scale AMC-BAL contains 300 capillaries, each micro model can thus be considered as 1/300th part of AMC-BAL. Consequently, one AMC-BAL can be regarded as a combination of 300 separate micro models in parallel.

Modeling Fluid Flow

Theoretical Model

To simulate fluid flow, the commercial CFD package Fluent 6.2 (Fluent Inc., Sheffield, UK) was used to numerically solve the steady-state Navier–Stokes equations. Standard pressure discretization scheme and second order upwind momentum discretization scheme were used. Pressure–velocity coupling scheme was SIMPLE. Fluid properties were set to those of culture medium to allow future validation with in vitro experiments. Culture medium was modeled as an incompressible, isothermal, Newtonian fluid composed of 90% water (ρ = 998 kg/m³) and 10% serum (ρ = 1030 kg/m³) with a resulting density of 1001.2 kg/m³. Dynamic viscosity μ of culture medium with 5 g/l bovine serum albumin (BSA) at 37°C was set to 0.691 mPa s.26 Plasma viscosity at 37°C was set to 1.3 mPa s.31

Resistance to Flow of the Non-woven Polyester Mat

The non-woven polyester matrix was modeled as an isotropic homogeneous porous zone. A measure for the viscous resistance of the non-woven polyester matrix used in Fluent 6.2 was determined in an experimental set-up by establishing the pressure drop – flow rate relationship. A sample of this matrix fabric sheet was clamped between two connecting tubes. These tubes were placed in a closed circuit with an overflow reservoir, which provided a constant static pressure load over the matrix sample. Pressure difference over the matrix sheet was measured using a calibrated differential pressure transducer (Fuji Electrics FCX, Japan). Flow rate was measured gravimetrically. De-ionized water was used. Static pressure load was set so average velocities in the experiment were in the same order of magnitude as could be expected in the AMC-BAL (1–7 mm/s). A viscous resistance factor of 2.7 ± 0.2 × 10¹⁰ m⁻² was calculated as an average of 10 measurements. Resistance to flow of hepatocyte cell layers (section “Modeling oxygen transport and consumption”) was modeled using the same viscous resistance factor.

Boundary Conditions

We assumed that total flow rate (15 ml/min) inside the research scale AMC-BAL is homogenously distributed. In this way, each micro model has the same flow rate of 0.05 ml/min, i.e. 1/300th of the total flow rate. Pressure inlet boundary conditions were used; outlet boundary condition was a zero pressure outflow; the capillary walls were ‘no-slip’ walls and symmetry boundary conditions were used at the side walls of the model.

Modeling Oxygen Transport and Consumption

Theoretical Model

To simulate oxygen transport and consumption, Fluent 6.2 solves the steady-state convection–diffusion-reaction equation (Eq. 1). Discretization scheme was set to QUICK.

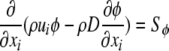1

The transported scalar φ is the local oxygen concentration (vol.%), which is also the product of the oxygen solubility α and the local oxygen partial pressure (pO₂) according to Henry’s Law (φ = α*pO₂). Oxygen solubility α is 3.1385 × 10⁻⁵ ml O₂/mmHg*ml fluid in culture medium and 2.855 × 10⁻⁵ ml O₂/mmHg*ml fluid in plasma. D is the oxygen diffusion coefficient, which is 2.92 × 10⁻⁹ m²/s in culture medium and 2.18 × 10⁻⁹ m²/s in plasma.2,17,33,44 Oxygen consumption by the primary porcine hepatocytes in the AMC-BAL was modeled by an additional source term S_φ, which was only implemented in regions that were designated to contain hepatocytes.

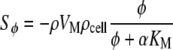2

This source term (Eq. 2) was based on the Michaelis–Menten kinetics of O₂ consumption by hepatocytes. As such, O₂ uptake is dependent on the local hepatocyte density ρ_cell and in a non-linear way dependent on the local O₂ availability.

Michaelis–Menten parameters of primary porcine hepatocytes were obtained from Balis et al.1 Values of culture day 2 were taken as they are characterized by a highly demanding O₂ uptake (V_M = 0.7286 nmol/s*10⁶ cells; K_M = 2 mmHg). These values were measured in 2D culture, whereas hepatocyte culture in the AMC-BAL is three-dimensional and at high density. For this reason, a lower O₂ consumption may be expected as the specific O₂ uptake rate per cell is reported to decrease at increasing cell densities.30 On the other hand, O₂ consumption may rise significantly when a metabolic load is applied to the cells.4 As such, the proposed consumption characteristics are justified by assuming these values to represent the most limiting case for oxygen availability. Consequently, attention must be paid when comparing simulation results to other numerical studies.19,23,25

Hepatocyte Distribution in the Micro Models

In an in vitro setting, the laboratory scale AMC-BAL is seeded with 1 billion porcine hepatocytes via three different loading ports, while gently rotating the bioreactor to assure a homogeneous cell distribution. As we assumed that one micro model is one 300th part of an entire laboratory scale AMC-BAL, one micro model contained 3.33 million cells.

Since no detailed information on the internal hepatocyte distribution in the AMC-BAL is available, two cell distributions are hypothesized. In cell distribution 1, all hepatocytes are homogeneously distributed in the non-woven matrix (resulting hepatocyte density ρ_cell of 53.7 × 10⁶ cells/ml). In previous macroscopic and microscopic studies of an early prototype AMC-BAL, the majority of the hepatocytes were immobilized within the three-dimensional matrix.14 However, given the undifferentiated method of hepatocyte seeding, it is possible that hepatocytes also adhere to the surface of gas capillaries. Therefore, in cell distribution 2, 50% of the hepatocytes are located in the matrix (ρ_cell = 31.7 × 10⁶ cells/ml) and 50% in a hepatocyte layer around the capillaries. The hepatocyte layer was set to be 122 μm, with a ρ_cell of 81.7 × 10⁶ cells/ml. This cell layer thickness is in the range of what is used in other numerical studies19,20 and is consistent with the size of primary porcine hepatocyte 3D cell clusters found in vitro.15 All proposed cell densities were also considered to be realistic.8,21,37

The complete AMC-BAL cannot be modeled by using only one cell distribution or only one micro model. Therefore, each cell distribution was applied to both micro models, leading to four basic configurations in total. All four micro model configurations were assessed independently. With a combination of these micro models, the entire AMC-BAL can be modeled in future studies.

O₂ Diffusion Constant Through Non-woven Matrix

Free O₂ diffusion through the mat zone is hindered by the non-woven arrangement of hydrophilic polyester fibers, which are considered to be impermeable to O₂. To compensate for this hindered diffusion, a correction factor for the O₂ diffusion coefficient in the mat volume was determined.

On a microscopic view of the non-woven matrix, the mat porosity was determined to be 91%. A modified two-dimensional inline micro model was constructed with 250 polyester fiber circles randomly located within the boundaries of the mat volume. On this modified inline micro model, the pO₂ distribution was simulated using hepatocyte distribution 1 (Fig. 3A). Standard boundary conditions were used and culture flow rate was zero. O₂ diffusion coefficient in the mat zone of the modified micro model was the same as for free culture medium, since culture medium occupies the void spaces between the polyester fibers. Subsequently, an analogous simulation was performed on a regular inline micro model, i.e. with the mat modeled as homogeneous medium, with an adjusted O₂ diffusion coefficient in the mat zone to match the results of the ‘modified’ model (Fig. 3B). A correction factor of 0.85 (D_mat = 2.48 × 10⁹ m²/s) for O₂ diffusion was necessary to take into account the presence of the non-woven polyester matrix mat. This correction factor is in accordance with the equation of Rayleigh (correction factor ∼ 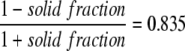), which has been experimentally verified for various sheets of porous media.29,32,34

Figure 3.

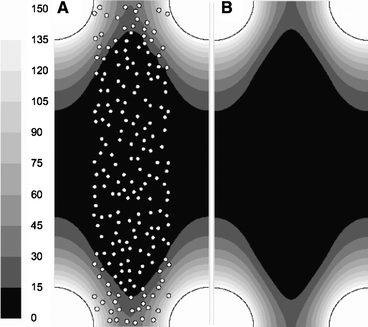
Determination of the correction factor for O₂ diffusion through the non-woven polyester mat. (A) pO₂ distribution [mmHg] on modified inline micro model (polyester fibers drawn) under standard boundary conditions, no medium flow; (B) identical pO₂ distribution [mmHg] obtained with identical simulation settings, but with mat as homogeneous medium with an adjusted diffusion constant (with a factor of 0.85) to account for hindered diffusion.

O₂ Diffusion Constant Through Zones Containing Hepatocytes

Oxygen can diffuse through both continuous fluid spaces as well as through hepatocytes. In regions seeded with hepatocytes, the resulting “effective” diffusion coefficient D_eff will be lower than in free medium, since O₂ diffuses more slowly through hepatocytes. The extent to which the diffusivity is reduced will logically depend on the local hepatocyte density. Since experimental data on O₂ diffusion constants through hepatocyte cell layers with different cell densities is not readily available, a theoretical approach was chosen.

Riley et al.35 developed an empirical relation (Eq. 3) that relates the effective diffusion coefficient D_eff to the local free diffusion coefficient D₀, the intracellular diffusion coefficient D_cell and the cell volume fraction φ. This equation, based on Monte Carlo simulations, shows a good agreement with available data throughout a wide range of cell volume fractions (0.04 < φ < 0.95).

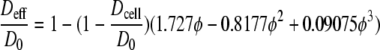3

D_cell was set to 0.25 × 10⁻⁹ m²/s, which is an average of intracellular O₂ diffusion constants in hepatocytes reported by Jones.22 Cell volume fraction φ is the local volume percentage of space that is occupied by hepatocytes and was calculated as the product of the local hepatocyte cell density and the average hepatocytes cell volume.9 Local free diffusion coefficient D₀ is dependent on the perfusion fluid, e.g. culture medium or plasma, and on the location of hepatocytes in the model; either in the inter-capillary space or in the mat zone. O₂ diffusivities in different regions of both micro models are presented in Table 1.

TABLE 1.

O₂ diffusion constants in different zones of the micro models.

Region in the micro model	D0 [10−9 m2/s]		ρcell [106 cells/ml]	φ		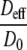Deff [10−9 m2/s]
	Cult. med.	Plasma				Cult. med.	Plasma
No hepatocytes
Inter-capillary space	2.92	2.18	0	0	1	2.92	2.18
In mat	2.48	1.85	0	0	1	2.48	1.85
Cell distribution 1
In mat	2.48	1.85	53.7	0.172	0.75	1.87	1.41
Cell distribution 2
In mat	2.48	1.85	31.7	0.102	0.85	2.11	1.59
In hepatocyte cell layer around capillaries – part in mat zone	2.48	1.85	81.7	0.262	0.64	1.59	1.22
In hepatocyte cell layer around capillaries – part in inter-capillary space	2.92	2.18	81.7	0.262	0.64	1.86	1.41

The ratio of the effective diffusion constant to the free diffusion constant D_eff/D₀ is calculated from the local free oxygen diffusion constant D₀ and the local cell volume fraction φ using Eq. 3. The local effective diffusion coefficients D_eff in culture medium and plasma per region are presented in the last column.

The obtained local diffusion coefficients are in the range of reported values for hepatocytes and other cell types.6,16,18,41,43

Boundary Conditions

Oxygen partial pressure (pO₂) of incoming culture medium was set to 146.5 mmHg, which was an average of three culture medium pO₂ measurements using an ABL505 blood-gas analyzer (Radiometer Copenhagen). Axial and radial O₂ transport resistances in gas capillaries were neglected, since the culture gas flow rate through the gas capillaries and their O₂ permeability are high.5 As such, O₂ supply through gas capillaries was modeled by imposing a constant 150 mmHg pO₂ on the capillaries’ outer walls, which corresponded to the pO₂ of culture gas used in vitro (95% air, 5% CO₂). All other boundary faces have no-flux boundary conditions.

Grid Dependency

One micro model mesh contained approximately 3.75 million finite volume mesh elements. Further increase in the number of cells rendered identical simulation results.

Simulations Overview and Assessment

As previously stated, four micro model configurations were used: (a) the inline micro model with cell distribution 1, (b) the inline micro model with cell distribution 2, (c) the triangular micro model with cell distribution 1, and finally (d) the triangular micro model with cell distribution 2. Fifteen case studies (Table 2) were performed on each configuration.

TABLE 2.

Overview of simulations.

Case	Fluid	pO2 gas (mmHg)	pO2 medium (mmHg)	Qmedium (ml/min)	# capillaries	KM (mmHg)
Reference case
(1) Standard boundary conditions	Culture medium	150	146.5	0.05	1	2
Effect of the internal oxygenator
(2) pO2 gas = 0	Culture medium	0	146.5	0.05	1	2
(3) pO2 gas = 0; pO2 medium × 2	Culture medium	0	293	0.05	1	2
Increasing oxygen availability
(4) pO2 gas × 2	Culture medium	300	146.5	0.05	1	2
(5) pO2 gas = carbogen	Culture medium	722	146.5	0.05	1	2
(6) pO2 medium × 2	Culture medium	150	293	0.05	1	2
(7) pO2 medium = carbogen	Culture medium	150	722	0.05	1	2
(8) Fluid flow rate Qmedium × 2	Culture medium	150	146.5	0.10	1	2
(9) Fluid flow rate Qmedium × 10	Culture medium	150	146.5	0.50	1	2
(10) No. capill.  × 2	Culture medium	150	146.5	0.05	2	2
(11) No. capill.  × 2; pO2 gas × 2	Culture medium	300	146.5	0.05	2	2
Clinical versus experimental setting
(12) Plasma	Plasma	150	146.5	0.05	1	2
(13) Plasma; pO2 gas × 2	Plasma	300	146.5	0.05	1	2
Changes of hepatocyte O2 consumption in time
(14) KM day 4	Culture medium	150	146.5	0.05	1	4.75
(15) KM day 5	Culture medium	150	146.5	0.05	1	7.5

Each case is applied to the four basic micro model configurations (inline and triangular micro model each with cell distribution 1 or 2).

The first case study was simulated using standard boundary conditions as described in previous paragraphs. This ‘reference case’ study (1) is the internal control for all other case studies with the same micro model configuration. The effect of the internal oxygenation system was assessed by disabling culture gas flow (2), and by assessing the effect of an external oxygenator that oxygenates incoming medium to a doubled pO₂ as an alternative for internal oxygenation (3). To increase oxygen availability to the hepatocytes, different strategies were assessed. First, by using a more oxygen rich culture gas, i.e. a doubled pO_{2 gas} (4) or carbogen gas (95% O₂) (5). Second, by incorporating an external oxygenator to increase incoming medium pO₂ to a doubled (6) or carbogen (7) level. Third, by changing culture medium flow rate to a doubled (8) or 10-fold (9) flow rate. Finally, by doubling the number of capillaries (10) or by combining the double number of capillaries with a doubled culture gas pO₂ (11). In cases with a doubled number of capillaries, cell density in the hepatocyte layer around the capillaries was kept constant. This lead to a cell layer thickness of 68 μm, keeping the number of hepatocytes around all capillaries equal to 50% of total, as was initially proposed. In micro models with double number of capillaries the distance between the capillaries is halved (see Fig. 2).

In the next case studies, we studied the effect of plasma versus culture medium, since this is the main difference in perfusion in a clinical setting as compared to an experimental setting. Standard boundary conditions (12) and a doubled pO_{2 gas} (13) were used and compared with cases (1) and (4). Finally, time-related changes in oxygen consumption characteristics of hepatocytes were investigated by varying K_M values. K_M values of culture day 4 (14) and 5 (15) were compared to the reference case (1). According to Balis et al.,1K_M values change remarkably throughout the first 5 days, whereas V_M values remain constant. We therefore kept V_M constant in these simulations.

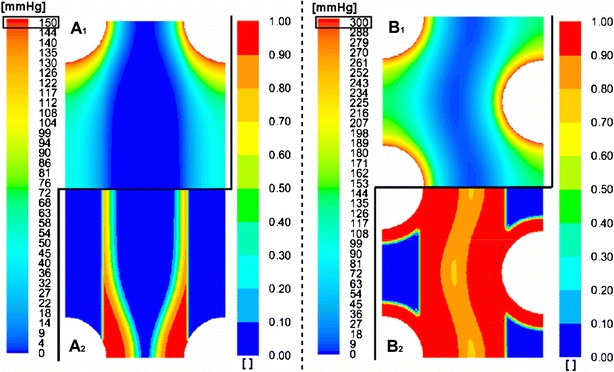
The proposed simulation cases on the four different micro model configurations were assessed by examining pO₂ distributions. However, not every simulated pO₂ profile can be shown due to brevity reasons. To evaluate the effect of the parameters discussed in the parameter study, the local effective hepatocyte utilization ratioV_ratio (Eq. 4) was studied.30

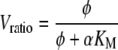4

V_ratio is the ratio of the observed oxygen consumption rate to the maximal hepatocyte oxygen consumption rate, i.e. V_M, and ranges between 0 and 1 (asymptotically). A threshold for V_ratio of 0.9 was chosen as introduced by Patzer30 and corresponds with a minimal pO₂ level of 18 mmHg when K_M = 2 mmHg. Consequently, oxygen availability in the AMC-BAL was quantified by determining the percentage of hepatocytes with V_ratio > 0.9.

Results

Fluid Flow and Shear Stress Distribution

Figure 4 represents an example of colorimetric contour plots of fluid flow and shear stress distributions in two different micro models with different hepatocyte distributions. In the upper part, velocity magnitudes (m/s, left legend) in a transverse plane midway through the first mat segment are shown for the reference case (case 1) of an inline micro model with hepatocyte distribution 1 (Fig. 4A1) and for a triangular micro model with hepatocyte distribution 2 and with a double number of capillaries (case 10–11) (Fig. 4B1). The contour plots can be mirrored with respect to the horizontal axis as micro models are symmetrical.

Figure 4.

Colorimetric contour plot of velocity magnitudes (m/s, left legend, upper part 1) and shear stress levels (Pa, right legend, lower part 2) in a transverse plane midway through the first mat segment, in the reference case (case 1) of an inline micro model with hepatocyte distribution 1 (A1 and A2 resp.) and in a triangular micro model with hepatocyte distribution 2 and with double number of capillaries (case 10–11) (B1 and B2 resp.).

Fluid flows in the non-woven matrix mat zone and in the hepatocyte cell layers were orientated axially and are uniform in size (approx. 8 μm/s in Fig. 4A1 and 37 μm/s in Fig. 4B1). In the inter-capillary space, flow velocities have a poiseuille-like (parabolic) profile with maximal velocities of approx. 3.6 mm/s in Fig. 4A1 and 7.8 mm/s in Fig. 4B1. In the interspace between two mat segments, flow lines expand radially due to the sudden increase in local cross-sectional area. However, these flow lines reconverge when entering the second mat segment, where the velocity profile was identical compared to the first mat segment (not shown). Static pressure drop over the entire micro model was 15.7 Pa in the reference case of the inline micro model with hepatocyte distribution 1 (Fig. 4A) and 69.3 Pa for the triangular micro model with hepatocyte distribution 2 and double number of capillaries (Fig. 4B). The lower parts of Fig. 4 (A2 and B2) show corresponding shear stress distributions (Pa, right legend). Maximal shear stresses were generally located near the mat side surfaces and also – in case of cell distribution 2 – at the boundary between the hepatocyte cell layer and inter-capillary space.

In Table 3, an overview is given of maximum velocity magnitudes in the inter-capillary space, uniform velocity magnitudes in the mat/hepatocyte layer zone, as well as static pressure losses over the entire micro model and maximal local shear stresses for all simulation cases. Maximum velocities in the inter-capillary space ranged between 3.6 and 45 mm/s, whereas uniform velocities in the mat/hepatocyte layer ranged between 8 and 110 μm/s. Simulation results showed that velocities in the mat zone and in hepatocyte layers were consistently two orders of magnitude smaller than in the inter-capillary space. Velocity profiles and shear stress profiles were similar for the different simulation cases, but differed in magnitude between cases when flow rate was altered or when the internal geometry had been changed, e.g. due to additional gas capillaries and/or hepatocyte layers around the capillaries. Static pressure loss over the entire micro model and local shear stress levels were additionally influenced by the type of fluid, e.g. plasma or culture medium. Static pressure loss over the entire micro model ranged from approx. 16 to 203 Pa. Maximum shear stress ranged between approx. 0.03 and 0.40 Pa. Largest maximum values were reached in hepatocyte distribution 2 with a 10-fold flow rate.

TABLE 3.

Overview of the maximum velocity in the inter-capillary space, the uniform velocity in the mat/hepatocyte layer zone, the static pressure loss over the entire model and the maximal shear stress for all simulation cases and for different hepatocyte distributions.

Cases	Hepatocyte distr. 1	Hepatocyte distr. 2
Velocity in mat/hepatocyte cell layer (mm/s) – Maximum velocity in inter-capillary space (mm/s)
(1,2,3,4,5,6,7,14,15) Standard flow rate	0.0085 – 3.59	0.011 – 4.60
(8) Qmedium × 2	0.017 – 7.17	0.022 – 9.20
(9) Qmedium × 10	0.084 – 35.7	0.11 – 45.0
(10,11) No capillaries × 2	0.0195 – 5.69	0.037 – 7.75
(12,13) Plasma	0.0085 – 3.59	0.011 – 4.60
Static pressure loss over micro model (Pa)
(1,2,3,4,5,6,7,14,15) Standard flow rate	15.7	20.6
(8) Qmedium × 2	31.4	41.1
(9) Qmedium × 10	155.7	203.3
(10,11) No capillaries × 2	36.1	69.3
(12,13) Plasma	30.0	39.3
Maximum shear stress (Pa)
(1,2,3,4,5,6,7,14,15) Standard flow rate	0.032	0.041
(8) Qmedium × 2	0.064	0.083
(9) Qmedium × 10	0.31	0.40
(10,11) No capillaries × 2	0.056	0.083
(12,13) Plasma	0.057	0.073

Values for the inline and triangular micro model are identical.

Importantly, both the inline and triangular micro model had the same flow field, static pressure loss and shear stress distributions within a simulation case with certain boundary conditions and hepatocyte distribution (comparison not shown).

Oxygen Transport and Consumption

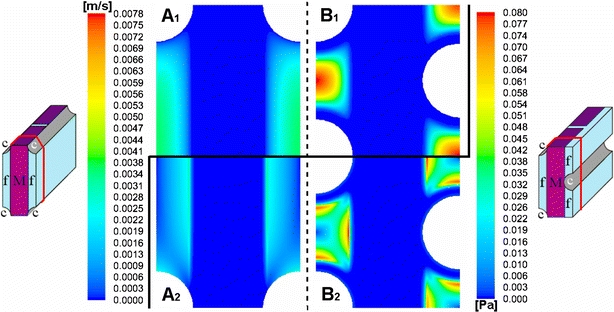
Results of oxygen transport and consumption simulations are presented by means of two contour plots of pO₂ and V_ratio distributions (Fig. 5). Also, Table 4 presents detailed information for each simulated case and micro model configuration on the percentage of hepatocytes that consume oxygen at a minimal V_ratio level of 0.9.

Figure 5.

Colorimetric contour plot of pO₂ (mmHg, left legend, upper part 1) and effective hepatocyte utilization ratio V_ratio (dimensionless, right legend, lower part 2) in a transverse plane midway through the first mat segment, in the reference case (case 1) of an inline micro model with hepatocyte distribution 1 (A1 and A2 resp.) and in a triangular micro model with hepatocyte distribution 2 and with double number of capillaries and doubled culture gas pO₂ (case 11) (B1 and B2 resp.) (Note: B1 different scale compared to A1).

TABLE 4.

Percentages of total hepatocyte cell amount that attain a V_ratio > 0.9.

% Hepatocytes with Vratio > 0.9
Case	Hepatocyte distribution 1		Hepatocyte distribution 2
	Inline (%)	Triangular (%)	Inline (%)		Triangular (%)
			Mat (%)	Capill. (%)	Mat (%)	Capill. (%)
Reference case
(1) Standard boundary conditions	15.7	15.8	28.8		28.6
			3.3	54.1	3.3	53.5
The effect of the internal oxygenator
(2) pO2 gas = 0	1.7	1.7	1.7		1.7
			3.1	0.4	3.1	0.4
(3) pO2 gas = 0; pO2 medium × 2	6.2	6.2	6.3		5.9
			11.0	1.7	10.3	1.7
Increasing oxygen availability
(4) pO2 gas × 2	30.4	30.2	50.3		50.3
			5.1	95.1	5.0	94.9
(5) pO2 gas = carbogen	62.4	64.5	80.7		88.3
			61.2	100.0	76.3	100.0
(6) pO2 medium × 2	20.1	20.2	34.5		33.9
			11.8	57.0	11.0	56.5
(7) pO2 medium = carbogen	35.5	35.1	54.2		53.4
			40.6	67.7	37.5	69.1
(8) Qmedium × 2	17.9	18.1	31.6		31.4
			6.6	56.4	6.5	56.0
(9) Qmedium × 10	28.4	28.6	45.7		45.6
			22.2	68.9	22.1	68.9
(10) No capillaries × 2	31.8	31.8	56.7		56.8
			14.1	100.0	14.3	100.0
(11) No capillaries × 2; pO2 gas × 2	61.0	59.9	87.5		84.8
			75.3	100.0	69.9	100.0
Clinical versus experimental setting
(12) Plasma	12.0	12.0	22.9		23.0
			2.6	43.0	2.6	43.0
(13) Plasma; pO2 gas × 2	22.8	22.9	40.8		40.9
			2.9	78.4	2.9	78.3
Changes in hepatocyte O2 consumption in time
(14) KM day 4	8.7	8.7	18.9		18.9
			1.1	36.4	1.1	36.4
(15) KM day 5	5.0	5.1	12.9		13.0
			0.3	25.3	0.3	25.5

In the case of hepatocyte distribution 2, distinction is made between the percentage of the total number of hepatocytes in the mat and the percentage of total number of hepatocytes in the cell layers around the capillaries.

Reference Case Simulations (Case 1)

Figure 5A1 illustrates the pO₂ distribution in a transverse plane midway through the first mat segment in the reference case (case 1) for the inline micro model with hepatocyte distribution 1. Highest pO₂ (150 mmHg) was found close to the capillary wall. A large pO₂ gradient extended radially from the capillary and was steeper at the side of the capillary in the mat zone. At a radial distance of 86 μm from the capillary, pO₂ in the mat zone dropped already below 20 mmHg. A region where oxygen was depleted (0 mmHg) is present in the center of the hepatocyte-seeded mat throughout both mat zones. Analogous pO₂ distributions were found in cross-sections of the micro model further downstream to the plane of Fig. 5A1, but with overall decreasing average oxygen level. Oxygen content of the perfused culture medium in the inter-capillary space dropped from its initial value of 146.5 mmHg to approx. 60 mmHg midway the first mat segment and further decreased downstream to 28 mmHg at the end of the first mat segment. At the start of the second mat segment, culture medium pO₂ in the inter-capillary space was increased to 40 mmHg and again decreased to 22 mmHg at the end of the mat segment.

As a standard for cellular oxygen availability, the effective hepatocyte utilization ratio V_ratio was calculated (Fig. 5A2). Complying with pO₂ distribution, hepatocytes in the center of the mat zone cannot consume oxygen at all (V_ratio ∼ 0), whereas hepatocytes closest to the capillaries have enough oxygen available to consume oxygen at near maximum capacity (V_ratio ∼ 1). Approximately 16% of all hepatocytes in the model consumed oxygen with V_ratio > 0.9 (Table 4). A change to hepatocyte distribution 2 was characterized by a larger radial pO₂ gradient around the capillaries and a more extended zone of zero oxygen content in the mat segments. Due to the additional presence of a dense hepatocyte layer around the capillary, pO₂ dropped below 20 mmHg from a radial distance of 65 μm from a capillary (compare to 86 μm in hepatocyte distribution 1). Nevertheless, 29% of all hepatocytes attained a V_ratio of more than 0.9. Fifty four percent of the hepatocytes in cell layers around the capillaries reached the threshold of V_ratio > 0.9, whereas 3% of the hepatocytes in the mat zone.

pO₂ and V_ratio distributions for the reference case of the other three micro model configurations are not shown for brevity reasons.

Simulation results also showed that inline and triangular micro models, using the same hepatocyte distribution, showed qualitative and quantitative identical pO₂ distributions.

The Effect of the Internal Oxygenator (Case 2,3)

Disabling culture gas flow (∼pO_{2 gas} = 0 – case 2) led to a reduction of cells with V_ratio > 0.9 to approximately 2% for all micro model configurations. Replacing the internal oxygenator by an external oxygenator, which doubles culture medium pO₂ (case 3), led to a “V_ratio > 0.9” fraction of approx. 6% for all micro model configurations. More specifically, in cell distribution 2, this was true for only 1% and 2% of the hepatocytes around the capillaries, and for 3% and11% of the hepatocytes in the mat zone, for case 2 and 3, respectively.

Increasing Oxygen Availability (Case 4–11)

Doubling culture gas pO₂ (case 4) almost doubled “V_ratio > 0.9” percentages (Table 4) from approximately 16% to 30% in micro models with hepatocyte distribution 1; an increase of 93%. A 75% increase (29–50%) was obtained in micro models with cell distribution 2. This increase mainly occurred in the hepatocyte layer around capillaries, i.e. 55% in case 1 to 95% in case 4. A further pO_{2 gas} increase to carbogen level (case 5) led to an approximate quadruple and triple “V_ratio > 0.9” fraction compared to the reference case for distribution 1 and 2, respectively. In the latter, hepatocytes in both the mat zone as well as in the cell layers have increased threshold percentages. Furthermore, about 7% more hepatocytes attained the threshold in the triangular capillary arrangement compared to inline when using hepatocyte distribution 2. In distribution 1, inline and triangular configurations rendered quasi-identical results.

Doubling culture medium pO₂ (case 6) led to a 28% and 20% increase in V_ratio percentages for cell distribution 1 and 2, respectively. In the latter, the relative increase was higher in the mat zone as compared to the hepatocyte layers. Further increase of pO_{2 medium} to carbogen level (case 7) led to a 125% and 88% increase in “V_ratio > 0.9” percentages compared to the reference case for distribution 1 and 2, respectively. Inline and triangular models rendered identical results under the same hepatocyte distribution.

Doubling culture medium flow rate (case 8) resulted in a 14% and 10% increase in “V_ratio > 0.9” fraction for distribution 1 and 2, respectively. Further increase of culture medium flow rate up to a 10-fold (case 9) resulted in an 81% and 59% increase for distribution 1 and 2, respectively. Typically in cases with increased flow rate in cell distribution 2, V_ratio percentages in the mat zone changed remarkably, whereas in the hepatocyte layers there was only a minor increase. Again, inline and triangular models rendered identical results under the same hepatocyte distribution.

A 2-fold increase in the number of capillaries (case 10) resulted in a doubled percentage of cells that attain the V_ratio > 0.9 threshold in cell distribution 1 (+102%) and 2 (+98%). In the latter, this increase occurred in the mat zone as well as in the cell layer around the capillaries. The combination of a double number of gas capillaries and a doubled pO_{2 gas} (case 11) increased the threshold percentages to almost quadruple (+280%) for cell distribution 1 and triple (+200%) for cell distribution 2. Again, only minor differences existed between inline and triangular micro models.

Figure 5B1 shows the pO₂ distribution in a transverse plane midway through the first mat segment in the triangular micro model with cell distribution 2 (case 11). In this case, highest pO₂ levels (∼300 mmHg) were only found close to the capillary walls. A very steep radial gradient was noted in the hepatocyte cell layer around the capillaries. pO₂ in the center of the mat zone was 7 mmHg. As in the reference case, pO₂ distributions of cross-sections further downstream showed analogous results as compared to Fig. 5A1, but with overall decreasing average oxygen level. The distribution of V_ratio corresponding to the pO₂ distribution of case 11 is depicted in Fig. 5B2. The entire hepatocyte layer (100%) around the capillaries and large parts of the mat zone (70%) had a V_ratio of at least 0.9. Consequently in case 11, 85% of all hepatocytes had a V_ratio higher than 0.9 (Table 4).

Clinical Versus Experimental Setting (Case 12,13)

Changing fluid properties from culture medium to plasma resulted in a 24% decrease in V_ratio > 0.9 percentages in micro models with cell distribution 1 and a 20% decrease in cell distribution 2 (case 12). Doubling pO_{2 gas} in the clinical setting (case 13) showed a relative rise of 91% and 78% compared to the clinical reference case (case 12) in cell distribution 1 and 2, respectively. Compared to the analog case in in vitro settings (case 4), the change of fluid properties also corresponds with a respective 25% and 19% decrease of the “V_ratio > 0.9” fraction.

Changes in Hepatocyte O₂ Consumption in Time (case 14,15)

Changing K_M values to the situation on day 4 (case 14) or 5 (case 15) causes slight increases in absolute pO₂ level. Also, pO₂ gradients are less steep and the oxygen depleted zone in the center of the matrix is slightly smaller (not shown). However, “V_ratio > 0.9” fractions decreased 45% and 68% for cell distribution 1 and 34% and 55% for distribution 2 compared to day 2 (case 1) for day 4 and 5, respectively.

Discussion

Fluid Flow and Shear Stress Distribution

Perfusion of a micro model was largely influenced by the presence of the non-woven mat. Although the cross-sectional area of the inter-capillary space and the non-woven mat are roughly the same size, fluid flow in the mat zone was generally two orders of magnitude smaller as compared to the flow in the inter-capillary space. This effect is caused by the higher resistance to flow of the non-woven mat, forcing the majority of fluid flow through the inter-capillary spaces, which have a negligible flow resistance. This also causes the overall pressure loss to be minimal. Since the same hydraulic permeability is used for the hepatocyte layers, fluid velocities there are also in the range of micrometer per second. Consequently, apart from the incorporation of additional gas capillaries (case 10–11), also the presence of hepatocyte layers around the capillaries (cell distribution 2) increased flow velocities and pressure loss in the model as the free cross-sectional area of the inter-capillary space is reduced. Fluid flow simulations for the inline and triangular variant of the different case studies render identical results for velocity profiles, pressure loss and shear stress distributions. This was expected as the micro models consist of the identical geometrical entities, which are only changed in location relative to each other. From a fluid dynamical point of view, we conclude that the change in capillary arrangement along the course of the spiral mat in the AMC-BAL does not influence fluid flow, pressure drop or shear stress distribution.

The static pressure loss over one micro model can be regarded as the total pressure drop over the entire AMC-BAL without the inflow and outflow zone (Fig. 1e–g), since the AMC-BAL can be represented by 300 micro models in parallel. This pressure drop, i.e. max. 200 Pa ∼ 1.5 mmHg, is negligible when compared to the pressure losses in the extracorporeal circuit. These low pressure gradients are in accordance with the in vivo situation in the liver lobule, in which pressure drops of approximately 3 mmHg over the sinusoids are normal.7,28 This is considered advantageous for cell culture inside the AMC-BAL.

Shear stress was also assessed as it is a possible determinant of cellular damage and reduced metabolic function. Shear stress is directly proportional to the local velocity gradient and the fluid viscosity. Consequently, shear stresses are generally more elevated in cases with higher velocity magnitudes in the inter-capillary space (e.g. in case of increased flow rate, doubled number of capillaries, cell distribution 2) and where fluid viscosity is increased (e.g. when plasma was used instead of culture medium – ‘clinical setting’ – case 12–13). Results show that only hepatocytes located at the side of the mat and at the border of the hepatocyte layers with the inter-capillary space are subjected to a certain level of shear stress.

In vivo values of hepatocyte wall shear stress are difficult to obtain, and comparison is therefore difficult. In human, liver sinusoid wall shear stress τ can be calculated as 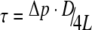 ∼ 1Pa (with static pressure drop Δp ∼ 3 mmHg; sinusoid diameter D ∼ 9 μm; length L ∼ 1 mm;7,28 and considering laminar flow and a cylindrical shape of the sinusoid). In mice sinusoids, shear stress was calculated to be 0.55 Pa.24,27 However, in vivo, hepatocytes are not directly subjected to this shear stress as they are shielded by the sinusoid endothelial lining. As a result, the maximal tolerable level of shear stress is lower than 1 Pa. Tilles et al.38 showed in in vitro studies on rat hepatocytes that hepatocyte function, measured as albumin and urea synthesis rates, was significantly decreased (resp. 2.6- and 1.9-fold) when hepatocytes were directly exposed to shear stresses higher than 0.5 Pa compared to low shear stresses (<0.033 Pa). Under standard conditions, maximum shear stress values in the AMC-BAL do not exceed 0.04 Pa. Additionally, the majority of the hepatocytes are not subjected to significant shear stresses. Small zones with increased shear stress exist but maximal values are considered to be acceptable and not detrimental for the viability and function of hepatocytes. However, shear stresses may increase up to 0.4 Pa when flow rate is increased 10-fold (case 9). Moreover, should plasma be used in this case, instead of culture medium, maximal shear stress values may then reach up to 0.71 Pa (not simulated; obtained by data extrapolation), which is in the critical range (>0.5 Pa38). Additionally, very high flow rates, e.g. 10-times the normal culture flow rates, may cause detachment of hepatocytes and therefore should not be used in spite of any possible increase in local O₂ availability. Subsequently, case 9 (culture medium flow rate × 10) can already be discarded in the search for optimal O₂ availability, based on fluid dynamical grounds.

Oxygen Transport and Consumption

We assessed the oxygen availability in different case studies and in different micro model configurations. In this paragraph, the results are discussed per case.

Reference Case Simulations (Case 1)

Highest oxygen concentrations in the mat zone are located near the gas capillaries and near the border of the mat and the inter-capillary space. In zones with limited flow velocities, cellular oxygen supply is clearly dependent on diffusion, which causes large radial pO₂ gradients. On the other hand, diffusive O₂ transport from the culture medium towards the hepatocytes also causes an axial gradient in culture medium oxygen content. As a consequence, culture medium only oxygenates the mat near the very start of the first mat segment and near the side of the mat. The depth of O₂ penetration into the mat decreases rapidly further downstream, since as the majority of oxygen content in the convective flow is already consumed in the first part of the micro model. Nevertheless, oxygen level in the culture medium is not totally depleted at the end of the micro model as the fluid transit time is not sufficiently long for all oxygen to diffuse to the hepatocytes.

In contrast, the O₂ concentration in the gas capillaries remains constant along the micro model axis, so the zone around the capillaries, which is oxygenated has a constant radius throughout the entire micro model. This pattern of oxygenation leads to about 80% higher V_ratio percentages in hepatocyte distribution 2 as compared to 1, since more hepatocytes are close to the gas capillaries in cell distribution 2. So despite steeper pO₂ gradients near the gas capillaries and consequently a larger zone of depleted oxygen in the mat zone in case of hepatocyte distribution 2, this cell distribution leads to significantly higher V_ratio percentages. However, this effect is related to the maximal oxygen diffusion distance, which is limited by the Michaelis–Menten oxygen consumption parameters, local hepatocyte density and local diffusion coefficient in general and by the specific local gas capillary and culture medium pO₂ in this reference case.

Since regions which are oxygenated by one gas capillary in particular do not overlap or influence each other in the reference case simulations, diffusive oxygen supply by the capillaries is independent of relative capillary location. Convective oxygen transport is also identical as flow distribution is irrespective of capillary placement (section “Fluid flow and shear stress distribution”). Consequently, inline and triangular capillary pattern give identical results concerning oxygen transport and consumption in these reference cases when the same hepatocyte distribution is used, as is confirmed by simulation results.

Concerning oxygen transport, we can conclude that the oxygen supply in the AMC-BAL is not fully adequate to provide all hepatocytes with sufficient oxygen to maintain O₂ consumption at minimally 90% of the maximal uptake rate (V_ratio > 0.9). Given that the AMC-BAL can be modeled as a combination of micro model configurations, 16–28% of the hepatocytes in the AMC-BAL are adequately oxygenated. In other words, between 72% and 84% of the hepatocytes are subjected to a pO₂ of less than 18 mmHg under the current conditions. Normal physiological pO₂ values in the liver sinusoids are between 70 mmHg in the periportal area and 20 mmHg in the pericentral area.42 But it is difficult to determine the effect on viability and function of hepatocytes below this threshold. Studies indicate that hepatocyte respiration becomes impaired below 1–2 mmHg pO₂.10 With respect to these values, further investigation of simulation results showed that under current conditions 67% and 52% of the hepatocytes in cell distribution 1 and 2 have a pO₂ below 2 mmHg and will suffer from hypoxia. The remaining 17–20% of the hepatocytes are likely to be characterized by shifts to more anaerobic metabolic processes.36 However, it should be noted that the low “V_ratio > 0.9” percentages are largely influenced by the very stringent hepatocyte oxygen consumption ratios used in this numerical model. Also, hepatocytes which are subjected to low oxygen levels for a prolonged period of time might show changes in oxygen consumption characteristics (V_M, K_M) to compensate for the lack of oxygen. This could account for account for higher oxygen availability in vitro. The use of different (V_M, K_M)-values throughout the model to address this behavior can be implemented in future work. Nevertheless, further increase in O₂ availability may prove useful to increase the cell viability and subsequently the efficiency of the AMC-BAL.

The Effect of the Internal Oxygenator (Case 2,3)

Disabling the internal oxygenator leads to detrimental results and reduces the percentage of adequately oxygenated hepatocytes to virtually zero. This confirms the importance of the internal oxygenator and illustrates the small contribution of the incoming convective oxygen flux by culture medium. Incoming culture medium flow adds only 0.17 nmol O₂ per second to the micro model, while maximal oxygen uptake V_M equals 0.7286 nmol/s*10⁶ cells. As such, theoretically no more than 0.2 × 10⁶ cells, i.e. 6% of the total amount of hepatocytes per micro model, would be able to consume at maximal uptake rate. In reality, only 1.7% of the hepatocytes can consume at a V_ratio > 0.9 due to the presence of pO₂ gradients. Replacing the internal oxygenator by an external oxygenator, which doubles the flow pO₂ and thus the convective oxygen flux, will only increase the “V_ratio > 0.9” percentage to about 6%. Since this is still considerably less than in the reference cases, external oxygenation – even at elevated pO₂ levels – is a not suitable replacement for the internal oxygenation system as the gas capillaries constitute the main oxygen supply. As such, the internal oxygenator is an essential part of the AMC-BAL.

Increasing Oxygen Availability (Case 4–11)

In the reference case models, merely 16–28% of the hepatocytes are adequately supplied with oxygen to consume at a V_ratio > 0.9, depending on hepatocyte distribution. We therefore assessed several strategies to increase overall oxygen availability.

Culture medium flow rate (case 8,9) does not have a considerable effect on cellular oxygen availability. A 2-fold increase in flow rate resulted in an increase in regions with V_ratio > 0.9 of only 14%. This was expected as the convective oxygen supply is only a minor contributor to the overall oxygen supply. Consequently, doubling the medium pO₂ (case 6) does not greatly increases the amount of regions with sufficient oxygen either. As already discussed, changes in culture medium properties are reflected in a small increase of regions with V_ratio in the mat zone, and more specifically in the first mat segment as oxygen content of the fluid is rapidly decreased downstream. It is interesting to note that doubling the flow rate and doubling the medium pO₂ both supply exactly the same amount of oxygen to the micro model: in the latter, oxygen is supplied at increased pO₂, whereas in the former oxygen is supplied at standard level but with a higher flow rate. Nevertheless, doubling pO_{2 medium} is preferred compared to increasing flow rate when aiming at a better effective hepatocyte utilization ratio since the doubled flow rate does not give the oxygen enough time to diffuse to the hepatocytes as the residence time before oxygen exits the micro model is cut in half. However, a disadvantage of increasing pO₂ in the medium is the requirement of an external oxygenator, which makes the extracorporeal circuit more complex and costly and increases the extracorporeal plasma volume in a clinical setting.

Doubling the pO₂ of the oxygenation gas (case 4) is much easier to achieve in practice. Importantly, the “V_ratio > 0.9” percentage increases significantly to almost a doubled level as compared to the reference case. In comparison, culture medium flow rate has to be increased more than 10-fold (case 9) to achieve similar results as with a 2-fold increase in pO₂ of the oxygenation gas. This illustrates how oxygen supply is only minor dependent on fluid flow rate. However, saturation of “V_ratio > 0.9” percentages with increased flow rate is not yet achieved at 10-fold flow rate. Nevertheless, a 10-fold flow rate is not preferred because of possible detachment of the hepatocytes and an increased risk of possible shear stress damage to the hepatocytes.

The effective hepatocyte utilization ratio can even be further improved. Culture medium pO₂ can be set to carbogen level (case 7) or the number of capillaries can be doubled (case 10). On average and for both hepatocyte distributions, these two methods lead to a 2-fold increase in the amount of hepatocytes consuming oxygen at V_ratio > 0.9 as compared to the reference case. When both approaches are compared for hepatocyte distribution 1, the results are slightly better when using the carbogen medium pO₂. But for hepatocyte distribution 2, the double number of capillaries leads to better results. An increase in the number of capillaries is preferred over carbogen medium perfusion, since carbogen medium perfusion leads to extremely high and possible toxic12pO₂ values of almost 720 mmHg. Carbogen medium perfusion also requires an additional external oxygenator. Therefore, increasing the number of capillaries by 2-fold is a more easy and safe method to increase the effective hepatocyte utilization ratio.

The results obtained with double capillary numbers are also better when compared to the doubling of the oxygenation gas pO₂. In cell distribution 2, this is mainly caused by the redistribution of the hepatocytes located around the capillaries. By increasing the number of capillaries, the hepatocyte layer thickness decreased (section “Modeling oxygen transport and consumption”). As a consequence, the region that a gas capillary can sufficiently oxygenate now spans the entire hepatocyte layer so 100% of the cell layer (Table 4) is sufficiently oxygenated. In cell distribution 1, the total region with V_ratio > 0.9 has also increased by two, as each additional capillary supplies an additional (constant) volume of hepatocytes with V_ratio > 0.9. In contrast, doubling the oxygenation gas pO₂ increases the region surrounding a single capillary with V_ratio > 0.9 with a factor of less than two.

The ultimate results in improving cellular oxygen availability and effective hepatocyte utilization ratio are found when oxygenation gas is set to carbogen level (case 5) or when a double number of capillaries is used in combination with a doubled oxygenation gas pO₂ (case 11). V_ratio > 0.9 percentages have quadrupled for cell distribution 1 and tripled for cell distribution 2 as compared to the reference case for both approaches.

Simulation results show that in case 11, the respective gains in V_ratio > 0.9 regions are cumulated when the case of a double number of capillaries and a doubled pO_{2 gas} are combined. It can also be noted that there is a small but significant difference between the inline and triangular capillary pattern in case 5. When carbogen oxygenation gas is used, the region with V_ratio > 0.9 surrounding a capillary has grown to such an extent that it could overlap with the region of surrounding capillaries. If a capillary is present straight opposed to another (inline pattern), this overlap is present. Consequently, the intersection of the two regions only contributes once to the amount of region with V_ratio > 0.9. In contrast, when capillaries are in a triangular pattern, the region surrounding the capillary can extent to its fullest, thus increasing the percentage V_ratio > 0.9 more compared to the inline micro model. This effect is more pronounced in the cell distribution 2 compared to distribution 1.

Given the possible toxicity of the hyperoxic oxygen levels when carbogen oxygenation gas is used (case 5), the preferred method to optimally and maximally increase oxygen availability in the AMC-BAL is to double the number of gas capillaries together with a 2-fold increase in culture gas pO₂. We note, however, that the calculated improvements in O₂ availability and V_ratio > 0.9 percentages do not necessarily translate into identical increases in cell viability or functional activity. Nevertheless, similar trends between simulation results and the in vitro situation are expected, but have to be validated.

Clinical Versus Experimental Setting (Case 12,13)

An important 20–25% decrease in the amount of hepatocytes with V_ratio > 0.9 is caused by the lower diffusion coefficient (−9%) and oxygen solubility (−25%) in plasma as compared to culture medium. As in reference case 1, results are independent of capillary pattern and are higher in cell distribution 2 as compared to cell distribution 1. Doubling the oxygenation gas pO₂ in the clinical setting leads to approximately the same relative increase in V_ratio percentages as it does in the experimental setting. As such, we conclude that any relative increase in oxygen availability found in the experimental setting by any possible strategy can also be applied to the clinical setting, taking into account that the absolute V_ratio > 0.9 fractions are decreased with a constant percentage depending on hepatocyte distribution.

Changes in Hepatocyte O₂ Consumption in Time (Case 14,15)

Higher K_M values of day 4 and 5 cause the decrease in oxygen consumption to start at higher oxygen levels compared to lower K_M values of day 2. Consequently, pO₂ gradients are less steep and oxygen penetrates further into the mat zone or into hepatocyte layers because of the reduced local O₂ uptake. Paradoxically, “V_ratio > 0.9” fractions have decreased. This is understood when converting the V_ratio threshold to the minimal cellular pO₂ to which the hepatocytes must be subjected to, using Eq. 4. Whereas in the reference case, hepatocytes are considered to be sufficiently oxygenated when cellular pO₂ reaches at least 18 mmHg, threshold values are now approximately 43 and 68 mmHg for day 4 and 5, respectively. Since the overall pO₂ level in the latter cases is not equally elevated, V_ratio > 0.9 fractions are strongly reduced. Conversely, when applying an identical pO₂ threshold instead of V_ratio, hepatocyte percentages in case 14 and 15 are increased with 3% and up to 20% compared to day 2. As such, an increase in K_M causes average cellular pO₂ to increase, but whether there is also an increase in the number of hepatocytes that are sufficiently oxygenated is difficult to determine based on computer simulations, as this depends on the criteria, i.e. minimal V_ratio versus minimal pO₂, used.

Conclusions

A numerical model to investigate fluid flow and oxygen transport and consumption in the AMC-BAL was developed and applied to two representative micro models of the AMC-BAL. Two different gas capillary patterns, i.e. ‘inline’ and ‘triangular’, were used and combined with two proposed hepatocyte distributions, leading to four basic configurations in total. Fifteen case studies were performed on each of the configurations in order to gain insight in the fluid flow, shear stress distribution, oxygen availability and effective hepatocyte utilization ratio V_ratio of the AMC-BAL and to assess possible strategies to further improve cellular oxygen availability. We found that the AMC-BAL does not provide sufficient oxygen to all hepatocytes to allow them to consume oxygen at 90% of their maximal uptake rate under standard operating conditions. The internal oxygenator is an essential part of the AMC-BAL. Doubling the number of gas capillaries together with a 2-fold increase in the oxygenation gas pO₂ was found to be the optimal method to maximally increase O₂ availability. Additionally, pressure drop over the AMC-BAL and cellular shear stress levels were found to be low and advantageous to cell culture. The developed model also allowed us to assess the effect of the transition from the in vitro to the clinical setting and the effect of the change of hepatocyte O₂ consumption characteristics in time. Since large variations in simulation results between hepatocyte distributions are shown, an assessment of the in vitro hepatocyte distribution in the AMC-BAL is useful. Subsequently, an attempt to validate the numerical model with in vitro experiments should be made. Eventually, adoption of this information may lead to a more efficient and productive AMC-BAL in the near future.