Dynamic reorganization of the functionally active ribosome explored by normal mode analysis and cryo-electron microscopy

Abstract

Combining structural data for the ribosome from x-ray crystallography and cryo-electron microscopy with dynamic models based on elastic network normal mode analysis, an atomically detailed picture of functionally important structural rearrangements that occur during translocation is elucidated. The dynamic model provides a near-atomic description of the ratchet-like rearrangement of the 70S ribosome seen in cryo-electron microscopy, and permits the identification of bridging interactions that either facilitate the conformational switching or maintain structural integrity of the 50S/30S interface. Motions of the tRNAs residing in the A and P sites also suggest the early stages of tRNA translocation as a result of this ratchet-like movement. Displacement of the L1 stalk, alternately closing and opening the intersubunit space near the E site, is observed in the dynamic model, in line with growing experimental evidence for the role of this structural component in facilitating the exiting of tRNA. Finally, a hinge-like transition in the 30S ribosomal subunit, similar to that observed in crystal structures of this complex, is also manifest as a dynamic mode of the ribosome. The coincidence of these dynamic transitions with the individual normal modes of the ribosome and the good correspondence between these motions and those observed in experiment suggest an underlying principle of nature to exploit the shape of molecular assemblies such as the ribosome to provide robustness to functionally important motions.

The ribosome synthesizes proteins by translating the genetic information residing on the mRNA into a specific sequence of amino acids. Binding of elongation factor G and subsequent GTP hydrolysis promotes the translocation process (1). This process is accompanied by large conformational rearrangements of the ribosome (2, 3). In particular, a ratchet-like relative rotation of the two ribosomal subunits has been observed, and proposed as a key mechanical step in the translocation of the mRNA·tRNAs complex (4). Other motions, such as a large displacement of the L1 stalk region (5–7, 37), rearrangement of the L7/L12 stalk (2), and domain movement in the 30S subunit (8), have also been observed and implicated as functionally relevant for protein synthesis (9).

Cryo-electron microscopy (cryo-EM) and x-ray crystallography have provided glimpses of functionally important conformational changes occurring during protein synthesis in the ribosome (2–4, 9–11). However, these static structural models provide key information mostly about the endpoint states of such large-scale conformational transitions and do not directly probe the conformational transitions. Theoretical techniques (modeling and simulation) can be used to augment this information, to lend an understanding of the dynamics at a close-to-atomic level. Recent atomic-resolution structures of the ribosome (12–14) make simulation methods based on atomic or near-atomic theories possible. However, studies of such large assemblies, like the ribosome, with molecular dynamics simulations are beyond the scope of current methodologies. An alternative is the use of normal mode analysis (NMA), which describes mechanical displacements and their associated time scales within an analytical framework (15, 16). NMA provides information on the preferential direction of collective movements that occur during large conformational changes. In particular, the extent and direction of functionally important large-scale rearrangements of molecular structures and assemblies are often well represented by a small number of the lowest-frequency normal modes (17). The size of the ribosome limits the application of atomically detailed NMA with conventional molecular force fields. However, NMA based on simplified elastic representations of the potential energy can be used to overcome this limitation (18). In elastic network NMA, the structure is described as a set of pseudoatoms, to capture its mass distribution, which are coupled via harmonic springs forming an elastic network (17–20). This approach has been shown to reproduce the intrinsic motional properties of complex biological systems based on their equilibrium structures quite well (21, 22), relatively independently of the underlying resolution of the structural data (23, 24).

Linking observed and inferred functional transitions in the ribosome to atomic or near-atomic descriptions of structural rearrangements is the goal of the present work, and is anticipated to provide a deeper understanding of the interactions that facilitate the large-scale movements associated with translocation. To approach this objective, elastic network NMA (20) is carried out on the ribosome at near-atomic resolution to explore the dynamic motions that are closely coupled to function. In what follows, we demonstrate that motions deduced from comparisons of cryo-EM maps of functional complexes, such as the ratchet-like rotation, are well reproduced by the NMA using a simplified representation of the ribosome as an elastic network of pseudoatoms. In particular, we will illustrate how two peripheral bridges connecting the 30S and 50S subunits act as flexible connections to facilitate the relative ratchet-like motion observed in cryo-EM studies (4). Helix 27 of 16S RNA is found to lie on the axis of rotation of the 30S subunit, a fact that provides an explanation for its critical role in the functional rearrangement of the ribosome (10, 25). We also find displacements of the L1 stalk, which implicate this region in the binding and shuttling of tRNA at the E site, and a hinge-like domain rearrangement in the 30S subunit, supporting suggestions that motion is involved in the binding of IF1 (8). The robust character of motional properties emerging from the simplified elastic model used here suggests that nature exploits the gross “shape” of molecular machines and the connectivity of its components to achieve key functional motions.

Methods

An elastic network model was constructed based on the atomic structure from the 5.5-Å x-ray map of the 70S ribosome from Thermus thermophilus (14), and NMA was performed to explore its functionally important rearrangements. In our calculations, the ribosome is described as a three-dimensional elastic network of pseudoatoms based on the Cα and phosphate (P) atomic positions from the crystal structure (the only atoms present in the PDB structure files 1gix.pdb and 1giy.pdb; ref. 26). We slightly modified the x-ray structure of the ribosome by adjusting the position of the L9 protein to provide better agreement with the molecular envelope of the EM map (4). The tRNAs in the A and P sites were included in our analysis. The pseudoatoms based on this structural model constitute the junctions within the network; the junctions are connected in a pair-wise manner by a simple harmonic restoring force for pairs separated by less than some cutoff distance, R_C (18). We use a cutoff of 20 Å for the P–P and Cα–P pairs and 16 Å for the Cα–Cα pairs, based on their pair–pair distribution functions (20). Thus, in regions of the structure where the density of surrounding neighbors is greater, pseudoatoms will experience a greater restoring force associated with local distortions. Conversely, regions of atomic structure with a low density of neighboring atoms will be freer to move. The physical realization of this model is the elastic network Hamiltonian for the system, given by

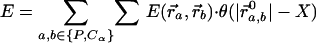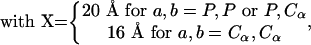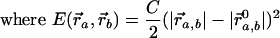[1]

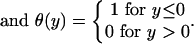For a range of choices of the cutoff distance around those given above, the nature of the normal mode displacements for the lowest frequency modes is not altered dramatically (see additional comments in Supporting Text, which is published as supporting information on the PNAS web site, www.pnas.org) (23). Finally, we note that the phenomenological constant describing the strength of the restoring force, C, is taken to be the same for all interacting pairs. This choice distorts detailed time- and energy-scale information for individual displacements along the elastic modes, but does not affect the character (direction) of the motions. Both energy- and time-scale features, and some aspects of nonlinearity in the energy cost of the distortion, can be restored with additional information about the magnitude of thermal fluctuations from experiment or other theoretical considerations (27). However, for our purposes of “annotating” the structural rearrangements at a near-atomic level, the amplitude of displacements along particular modes was adjusted to approximate the displacements suggested by the cryo-EM maps.

Given the Hamiltonian from the elastic network description of the ribosome as just described, the normal modes are computed by diagonalizing the Hessian matrix (matrix of second derivatives of the elastic energy function) by using the rotation–translation block (RTB) method (28, 29). This approach projects out the elements of the Hessian associated with the translation and rotation of rigid blocks of atoms, e.g., residues or nucleic acid bases, elements of rigid secondary structure, etc., to reduce the size of the matrix required for diagonalization while retaining flexibility of key structural elements. It has been demonstrated in previous applications of this approach that the choice of rigid blocks of up to five consecutive residues in enzyme systems does not degrade significantly the description of functionally relevant atomic displacements (29), and even the use of rigid blocks containing entire proteins provides useful information in exploring the swelling processes in icosahedral virus particles (21). In the present study, the RTB approach was used to project the Hessian into blocks comprising five consecutive Cα or P atoms; the block boundaries were constructed such that atoms from different subunits were not included in the same blocks. From the diagonalization of this reduced Hessian, both frequencies (eigenvalues) and directions (eigenvectors) for collective displacements of the system are constructed. The nature of atomic displacements in the framework of the normal mode representation is given by the expression

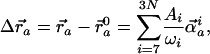[2]

where A_i/ω_i is an arbitrary amplitude for displacement along normal mode i with eigenvector component (direction) 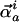for atom a; if the atoms are undergoing thermal excursions along each mode then A_i is given by 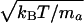, with T being the absolute temperature, k_B is the Boltzmann constant and m_a is the atomic mass of atom a. From this expression it should be evident that the lowest frequency modes generally provide the largest contribution to the atomic displacement of any atom. Although not obvious from the equation above, the lowest-frequency eigenvectors also represent the most distributed, or collective motions, i.e., the components of 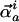are significant for the largest number of atoms, a (30). In the present study we have used only the directions of these motions (the eigenvectors), because these are well documented to provide a robust description of large-scale (and often functionally relevant) molecular motions in proteins and protein/DNA systems (31). We explore the displacement of the ribosomal complex along individual modes of motion computed from our elastic network NMA.

Results and Discussion

The lowest-frequency modes show a number of motions with potential functional significance, such as a change from an open to a more closed conformation of the ribosome, and motions of major subunit domains and protuberances and other rearrangements that have been implicated in functional roles. Among these motions, two are chosen to comprise the primary focus of this report because of their functional significance and earlier elucidation by means of experimental techniques (see Fig. 1). Other modes are described in Supporting Text and Fig. 5, which is published as supporting information on the PNAS web site.

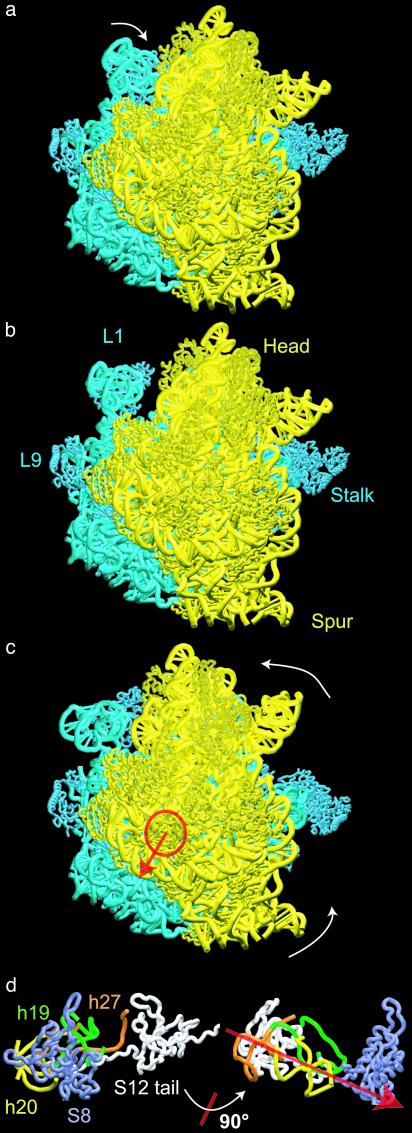
Fig. 1.

Structural rearrangements of the 70S ribosome obtained from elastic network NMA (30S subunit in yellow, 50S in blue). The ribosome is shown from the 30S solvent side. (a) The ribosome after a rearrangement along the first mode. The primary motion observed for this mode is displacement of the L1 protein to a position away from, or close to, the intersubunit space (also see Fig. 4b and Movies 1–3, which are published as supporting information on the PNAS web site). (b) The modified x-ray structure representing the equilibrium conformation of the ribosome. (c) The ribosome after displacement along mode 3. The primary motion is a rotation of the 30S subunit relative to 50S around the axis indicated in red. The amplitude of the displacement along this mode was adjusted to match the change due to the ratchet-like motion as observed in the cryo-EM maps of the structure during translocation; however, the direction of this displacement arose as a natural consequence of the NMA (see Supporting Text and Movies 1–3). (d)(Left) 30S RNA and protein components lying along the axis of rotation, viewed down that axis (close-up corresponding to the region indicated by the circle in c). (Right) Lineup of these components, viewed perpendicular to the axis (obtained from Left by a 90° rotation around an axis in the plane as indicated).

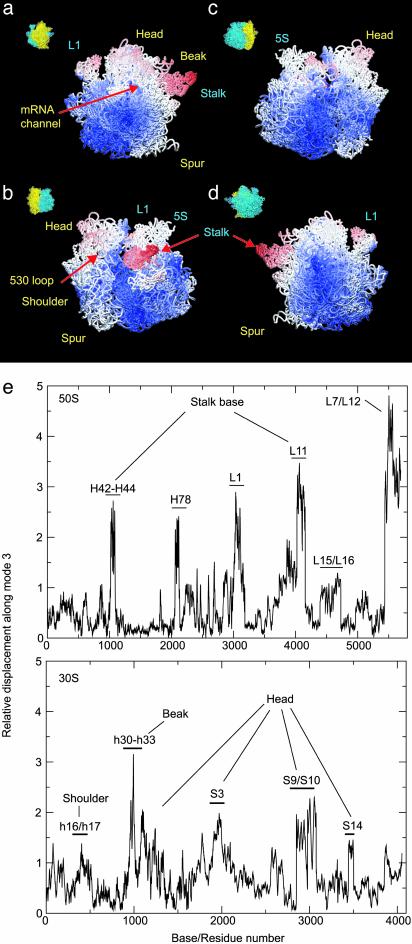
The lowest mode (mode 1, after the six trivial translation and rotation modes are removed) describes the motion of the L1 protein and another (mode 3) captures a rotation of the 30S relative to 50S subunit. The latter agrees with a complex motion previously described as a ratchet-like reorganization of the ribosome in response to the binding of elongation factor G (4). By combining the magnitude of this rearrangement deduced from cryo-EM with the direction of motion from our theoretical analysis, the local atomic displacements occurring during this functional motion are analyzed to yield information about the regions of the ribosome that are significantly involved in the internal structural reorganization (summarized pictorially in Fig. 2 a–d and more graphically in Fig. 2e). On the whole, the 30S subunit shows a larger internal rearrangement than the 50S subunit (Fig. 2 a–c). Only small motions are observed for domain III of the 50S subunit. The 30S subunit undergoes a rotation around an axis that involves proteins S8, S12, and helices h19, h20, h24, and h27 (Fig. 1d; the convention h for helices of 16S rRNA and H for those of 23S and 5S rRNA are used throughout the text). The overall rotation of the 30S subunit displaces primarily the head (h33 to h40), shoulder (Fig. 2b), and spur (Fig. 2a). It also affects the topology of the entrance channel for mRNA, defined by loop 530 and the 1,050/1,200 region of the 16S rRNA (see ref. 4). In contrast, the platform, which is tightly connected to the 50S subunit, appears to be relatively stable. In the 50S subunit, the L7/L12 stalk and stalk base are very mobile. An outward motion of the L7/L12 stalk is observed. Helices H42 to H44, which form the RNA portion of the stalk base, and protein L11 also show relatively large conformational changes. The 5S rRNA and the L1 stalk exhibit significant mobility, as well. Fig. 2 b and c reveals that, except for the peripheral bridges connecting the 30S subunit head with the 50S central protuberance (see below), the topology of the interface is relatively stable.

Fig. 2.

Atomic motion in the ribosome arising from displacements along mode 3. (a–d) Four different views are presented, as indicated by thumbnails (yellow = 30S, blue = 50S). The atoms are colored according to the amplitudes of their displacement from the equilibrium positions during the ratchet-like motion. The scale runs from red, representing the largest conformational change, to blue, indicating regions showing very little motion. Parts of the structure colored white represent intermediate-scale displacements during excursions along the ratchet-like mode. (e) Base/residue mapping of atomic displacements from normal mode 3 is shown. Labels indicate the regions of structure corresponding to base/residue numbers. The displacement amplitudes are given in arbitrary units.

NMA clearly indicates that those regions of the ribosome interacting directly with elongation factor G, e.g., the stalk base of the 50S subunit and the head and shoulder of the 30S subunit (2), undergo large conformational rearrangements during the ratchet-like motion. The displacements observed in our NMA indicate that helix h27 of 16S RNA, which is known to switch between a high- and a low-fidelity state of the decoding center (25) and to promote large conformational rearrangements in the whole ribosome (10), is located on the axis of rotation of the 30S subunit (Fig. 1 c and d). This finding provides rationalization for the dramatic effects of conformational switching, i.e., the base pairing rearrangement in helix 27, on the conformation of the ribosome.

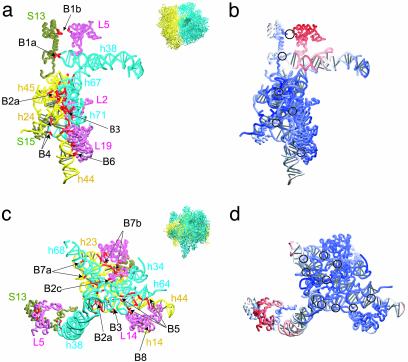
The bridges between subunits are important for maintaining the overall architecture of the ribosome (32–34). The structures forming the interface between the 30S and 50S subunits are shown in two different views in Fig. 3, along with relative amplitudes of the local rearrangements predicted from the NMA. Even though the interface appears to be well conserved during the ratchet-like motion, two of the bridges behave differently. Bridge B1b is strongly affected by the rotation resulting from mode 3. Protein L5 shows a large displacement compared with the rest of the interface. Helix H38 is also affected by the rotation, leading to a rearrangement in the region of bridge B1a. These two bridges must either play an important role in the control of the ratchet-like motion or in stabilizing the two extreme positions. In contrast, no significant rearrangements are seen for the other bridges, although small local changes occur in the RNA elements leading to these bridges. Helices h44 and H68 show local rearrangements (not shown). Interestingly, h44 of 16S RNA forms several bridges and, on the 50S side, H68 is located between the two helices H67 and H69 that are both involved in bridges. This placement suggests that these bridges preserve the integrity of the architecture of the ribosome during the ratchet-related conformational change.

Fig. 3.

The nature of motions at the interface between 50S and 30S ribosomal subunits as viewed from two different directions, indicated by thumbnails. (a and c) Components of the interface region. The 23S RNA is shown in blue, the proteins of the 50S subunit are shown in pink, the 16S RNA is shown in yellow, and the proteins of the 30S subunit are shown in tan. Bridges are indicated with red coloring. (b and d) Mapping of the displacements. Here the ribbons representing the structural components shown in a and c are colored according to the amplitude of their displacement on rotation associated with the ratchet-like mode 3 (color scheme as in Fig. 2). Black circles are used to indicate the locations of the bridges.

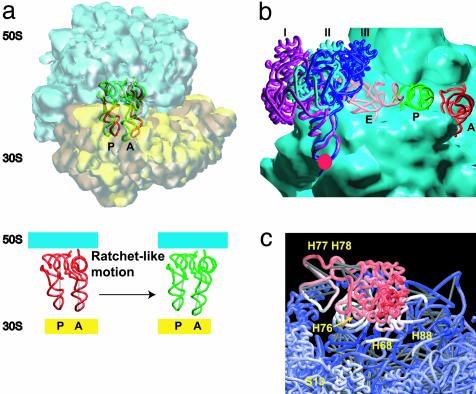
The positions of the tRNAs are also affected by the ratchet-like rotation arising from displacements along mode 3. After the conformational change, the majority of the contacts between the tRNA molecules, especially in the A site, and the ribosome are weakened, indicated by increasing distance between pairs of atoms that are interacting (Fig. 4a). Contacts made by the A-site tRNA with helix H38, the A-site finger, or with H89, are strongly affected by the rotation. For the P-site tRNA, contacts are not changed as much as those in the A site. However, new contacts emerge between this tRNA and H69 as a result of this motion The change in the interaction between the tRNA molecules and the two subunits suggests that the rotation may facilitate the movement of the tRNAs through the intersubunit space.

Fig. 4.

Local rearrangements within the ribosome as a result of displacement along the elastic normal modes. (a) Motions of tRNAs in the A and P sites as a result of the ratchet-like motion from mode 3. (b) Motion of the L1 stalk as a result of elastic mode 1. The displacements of this structural component occur around the pivotal point denoted by the red circle and are of the extent illustrated by the outer (I) and inner (III) positions. Position II represents the state observed in the x-ray model of Yusopov et al. (15), taken to be the equilibrium in the NMA, whereas the magnitude of displacements are taken from the structural work of Harms et al. (7). (c) The magnitude of motions in the L1 protein arising from mode 1 is shown by coloring the atoms according to the amplitude of their displacements along this mode (color scheme as in Fig. 2: red, large motion; white, intermediate-scale motion; blue, little or no motion). All graphics were produced by using the visualization program vmd (37).

The first normal mode corresponds to the displacement of the L1 stalk, which consists of helices H76–79 and protein L1, in a manner which opens/closes the inter-subunit space (Figs. 1a and 4b). This stalk has been observed to be mobile (5–7, 37) and it may be important for E-site tRNA function (7, 35, 37). Additional rearrangements related to the movement of the L1 stalk are seen in the head and the central protuberance of the 50S subunit, on the L1 side. The most interesting rearrangements are small conformational changes in H88 and H68 (Fig. 4c). H68 is connected with H69, which is known to interact with the tRNA at the A, P, and E sites (14). Thus, the motion of L1 is correlated with small rearrangements near the A, P, and E sites. The existence of such a coupling would add plausibility to the suggestion that the L1 stalk may play a role in affecting or regulating the removal of the E-site tRNA.

Conclusions

NMA using an elastic network model of the ribosome has revealed coordinated mechanical rearrangements and deformations that appear to be related to the functioning of this assembly. The character of these rearrangements agrees with experimental studies based on cryo-EM and x-ray crystallography of the ribosome and its components. Moreover, the displacements along specific normal modes provide detailed information on the way large-scale changes observed during the elongation cycle are coupled to local rearrangements, demonstrating that deeper interpretation of the experimental data can arise when coupled with the theoretical analysis of dynamics using such models. It is important to note that the essential properties captured by this model are the shape of the macromolecular assembly and the connectivity of its underlying structural framework. Thus, the key to the understanding of ribosomal function, which involves concerted movements of distant parts, appears to lie in the shape-dependent dynamic properties of its complex architecture. This is accessible by NMA of relatively simple mechanical models. These observations support the suggestion that nature may employ shape as a means to provide robust mechanical motions to be used in key biological functions.