Femtosecond broadband stimulated Raman spectroscopy: Apparatus and methods

Abstract

The laser, detection system, and methods that enable femtosecond broadband stimulated Raman spectroscopy (FSRS) are presented in detail. FSRS is a unique tool for obtaining high time resolution (<100 fs) vibrational spectra with an instrument response limited frequency resolution of <10 cm^–1. A titanium:Sapphire-based laser system produces the three different pulses needed for FSRS: (1) A femtosecond visible actinic pump that initiates the photochemistry, (2) a narrow bandwidth picosecond Raman pump that provides the energy reservoir for amplification of the probe, and (3) a femtosecond continuum probe that is amplified at Raman resonances shifted from the Raman pump. The dependence of the stimulated Raman signal on experimental parameters is explored, demonstrating the expected exponential increase in Raman intensity with concentration, pathlength, and Raman pump power. Raman spectra collected under different electronic resonance conditions using highly fluorescent samples highlight the fluorescence rejection capabilities of FSRS. Data are also presented illustrating our ability: (i) To obtain spectra when there is a large transient absorption change by using a shifted excitation difference technique and (ii) to obtain high time resolution vibrational spectra of transient electronic states.

I. INTRODUCTION

Time-resolved Raman spectroscopy is a valuable tool for revealing structural dynamics in ultrafast chemical and biological reactions.^1–6 Spontaneous Raman scattering can be used to obtain spectra over a ∼1500 cm^–1 spectral window, but requires picosecond or longer duration pulses to obtain adequate spectral resolution.⁷ A significant benefit of Raman scattering is resonance enhancement, which allows observation of the vibrational spectrum of a specific chromophore in a complex system;⁸ however, electronic resonance is often accompanied by fluorescence backgrounds that can easily overwhelm the spontaneous Raman signal. To overcome these problems of time resolution and spectral quality, we have been developing the technique of femtosecond stimulated Raman spectroscopy (FSRS).^9–17 FSRS can obtain Raman spectra over a 1500 cm^–1 window free from fluorescence backgrounds, with simultaneous high time and frequency resolution. The system we have developed is unique in its ability to obtain high signal-to-noise spectra in seconds with <100 fs temporal resolution and <10 cm^–1 spectral resolution, producing an instrument response product of <1 cm^–1 ps, more than an order of magnitude better than the transform limit of spontaneous Raman (15 cm^–1 ps) and five or more times better than other FSRS systems, whose products have ranged from 5 to 60 cm^–1 ps.^14,16,17 Here, we present a detailed technical description of the apparatus and methods we are using to produce FSRS spectra with visible and near-infrared (NIR) laser pulses generated from a femtosecond titanium:Sapphire laser.

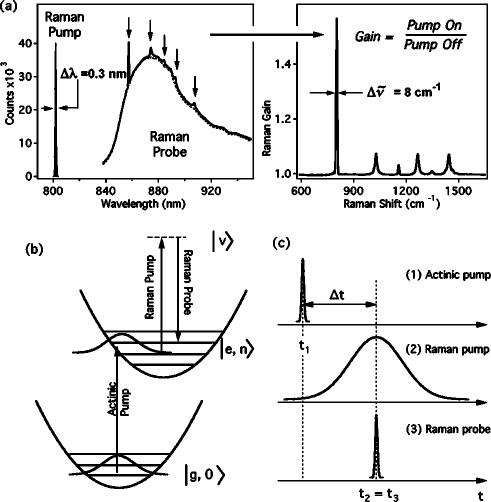
A schematic of the FSRS experiment is presented in Fig. 1. The stimulated Raman effect occurs when two coherent optical fields, the Raman pump at ω_p and the Raman probe at ω_S, propagate through a system with a vibrational resonance at ω_vib=ω_p-ω_S. Coherent excitation of the vibration produces amplification of the probe beam and attenuation of the pump beam. Stimulated Raman spectroscopy has traditionally been performed by scanning the Stokes frequency, ω_S, and plotting the gain of the probe intensity versus ω_p-ω_S.^18–20 In femtosecond broadband stimulated Raman spectroscopy, the Raman pump field is provided by a narrow bandwidth picosecond pulse at ∼800 nm and the Raman probe by a femtosecond NIR continuum pulse to the red of 800 nm. The broadband probe allows simultaneous observation of a large range of Stokes frequencies. Measurement of the probe spectrum with and without the Raman pump and then calculation of the pump-on:pump-off ratio generates a Raman gain spectrum in which the amplification of the probe at Raman resonances from the pump frequency is readily apparent [Fig. 1(a)]. The instrumental resolution of the gain spectrum is determined by the resolution of the spectrograph (∼6 cm^–1) and the bandwidth of the Raman pump (3–17 cm^–1). Time resolution is produced by introducing a ∼50 fs actinic pump pulse to initiate a photochemical reaction [Fig. 1(b)]. Depending on the actinic pump–probe time delay, Δt, the gain spectrum displays the vibrational spectrum of the excited electronic states or photoproducts generated by the actinic pump. The time resolution of the experiment can be <100 fs, and is determined by the ability to resolve the delay between the excitation by the actinic pump and the initiation of the Raman transition by the probe, although the specific dynamics and spectral linewidth observed in an experiment will also depend on the molecule being studied.

FIG. 1.

Illustrative diagrams of FSRS. (a) The spectra of the Raman pump and probe pulses for a typical FSRS experiment on cyclohexane. In the presence of the Raman pump pulse, the stimulated Raman effect amplifies the probe continuum at Raman frequencies (arrows) shifted from the Raman pump wavelength. The gain spectrum is obtained by dividing the Raman-pump-on probe spectrum by the Raman-pump-off probe spectrum. The frequency resolution of the spectrum is determined primarily by the bandwidth of the Raman pump pulse and is generally less than 10 cm^–1 . (b) Energy level diagram showing the electronic and vibrational resonances of the three laser pulses. (c) Timing diagram for FSRS. Time resolution is obtained by optically delaying the femtosecond duration actinic pump pulse (1) relative to the Raman probe (3). The temporal instrument response is limited only by the cross correlation of the actinic pump and Raman probe pulses and is typically <100 fs.

The temporal and spectral resolution limits of FSRS can be understood by examining the evolution of the quantum system using the Feynman diagram shown in Fig. 2.^21,22 Here, the system evolves temporally from bottom to top and dipole couplings are described by diagonal arrows that produce a transition in either the bra (right-hand side) or ket (left-hand side) part of the wave function. The molecular system initially in the ground state, ǀg,0〉. is excited by the actinic pump pulse at t₁ by the first two ω₁ dipole couplings to a vibrational state of the upper electronic surface, ǀe,n〉. After a delay, Δt, the Raman transition is initiated at t₃ by sequential couplings with the Raman pump (ω₂) and the broadband probe (ω₃). The system then propagates in a vibrationally coherent state ǀe,n〉〈e,n+1ǀ which decays with a characteristic dephasing time, ${\mathit{T}}_2^{\mathrm{vib}}$. In the homogeneous broadening limit, the dephasing time determines the inherent spectral line shape of the vibrational transition, as $\Delta \overline{v}$. The Raman transition is completed by a coupling of the ket with the Raman pump field and emission at the Stokes frequency, ω₃, placing the system in the final vibrationally excited state ǀe,n+1〉. It is important to note that the final emission at ω₃ along the probe wave vector k₃ can occur long after the probe pulse has left the sample.

FIG. 2.

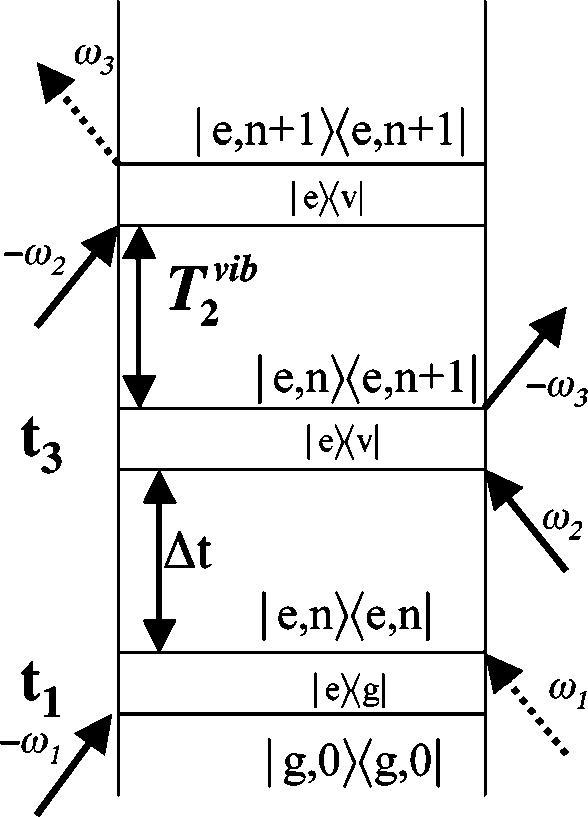
Feynman diagram describing the evolution of the density matrix for FSRS. The time delay, Δt, between the actinic pump (ω₁) and probe (ω₃) beams determines the delay between the electronic excitation of the sample and the initiation of the Raman transition. The vibrational dephasing time ${\mathit{T}}_2^{\mathrm{vib}}$ determines the linewidth of the Raman peaks. Use of a picosecond duration Raman pump (ω₂) allows the Raman spectrum to sample the full T₂ time of the vibrational transition and thereby produces lineshapes determined by the intrinsic molecular limits.

The time resolution in FSRS is primarily determined by the ability to resolve the time delay between the electronic excitation at t₁ and the initiation of the Raman transition at t₃ by sequential couplings with ω₂ and ω₃. The FSRS vibrational peak width is determined by the convolution of the Raman pump pulse with the decaying vibrational coherence. In the long-pulse limit, this convolution is determined solely by the dephasing time of the molecule and the observed peak width will be the minimum possible. However, if a short duration Raman pump pulse is used, the convolution will be truncated by the ω₂ pulse envelope, leading to a broader Raman line shape.

Furthermore, since the final detected signal represents an average over the vibrational dephasing time after the initial coupling of the vibrational states, changes in the vibrational frequency or phase during the dephasing time will affect the final FSRS line shape. In a spontaneous Raman experiment, the Raman transition is initiated at any time during the Raman pump pulse by ω₂ and the zero-point radiation field at ω₃. The resultant frequency and time resolution are both determined by the Raman pump pulse envelope and therefore subject to the transform limit. In contrast, FSRS maintains high time and frequency resolution by "gating" the initiation of the Raman transition with a short probe pulse and then completing the transition with a long Raman pump pulse.

In this article, we present an effective optical configuration for performing FSRS with <10 cm^–1 spectral resolution and <100 fs time resolution using a femtosecond titanium:Sapphire laser. The important characteristics of the laser system, detection apparatus, and data collection methods for obtaining stable spectral baselines and shot-noise-limited detection are described. FSRS spectra of rhodamine 6G, chlorophyll a, and 3,3’-diethylthiatricarbocyanine iodide (DTTCI) highlight the unique fluorescence rejection and rapid data acquisition times possible in a variety of resonance conditions. FSRS spectra of bacterial reaction centers obtained using shifted excitation Raman difference spectroscopy (SERDS) illustrate an effective method for removal of large transient absorption backgrounds. Finally, our femtosecond time-resolved spectra of diphenyloctatetraene illustrate the capabilities of FSRS to perform femtosecond time-resolved structural studies of excited states and chemical reaction intermediates.

II. EXPERIMENTAL DESIGN

A. Laser system

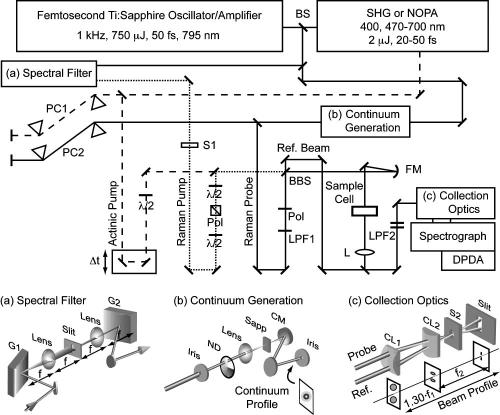
The femtosecond stimulated Raman laser system (Fig. 3) is based on a home-built Kerr lens mode-locked titanium:Sapphire oscillator²⁵ amplified by a regenerative amplifier (BMI alpha 1000/us). The 1 kHz amplifier produces a pulse train of 750 μJ pulses at ∼795 nm with a 24 nm bandwidth that are compressed to 45 fs sech² pulses. The pulse energy stability (±<0.3%) is critical for stable probe intensity, which determines the stability of the spectral baseline.

FIG. 3.

Laser and detection system for FSRS. The actinic pump (dashed) is generated by second harmonic generation or by the NOPA. The Raman pump (dotted) is produced by spectrally filtering the output of the Ti: Sapphire amplifier, as shown in (a). The Raman probe is produced by continuum generation in a sapphire plate (b) and split into a probe and reference beam for shot-to-shot normalization of the continuum intensity. The collection optics (c) image the probe and reference beams onto the slit as vertically displaced lines, before they are dispersed by the spectrograph and detected by a DPDA. Abbreviations: BS, 20%R beamsplitter; PC1, SF10 prism compressor; PC2, fused silica prism compressor; λ/2, half-wave plate; Pol, polarizer; LPF1, gradual cutoff long pass filter; BBS, broadband 50:50 beamsplitter; FM, 150 mm fl concave focusing mirror; LPF2, sharp cutoff long-pass filters; L, lens; S1, Raman pump shutter; S2, detector exposure shutter; CM, 100 mm fl concave mirror; CL1, 152 mm fl cylindrical lens; CL2, 100 mm fl cylindrical lens.

The actinic pump pulse is generated by a noncollinear phase-matched optical parametric amplifier (NOPA) that is pumped by 150 μJ of the amplifier output.²⁶ The NOPA input is split into a seed beam (15 μJ) and a pump beam (135 μJ). The seed beam is apertured to ∼2 mm and attenuated to ∼2 μJ before being focused into a 3 mm sapphire plate to generate a white-light continuum extending from 475 to 1100 nm. The pump beam is frequency doubled in a 1 mm beta-barium-borate (BBO) crystal to generate ∼30–35 μJ pulses at 397 nm. The seed and pump beams are focused and overlapped in a 2 mm BBO crystal to amplify a portion of the white-light continuum. The NOPA can generate ∼3 μJ pulse energies from 470–650 nm, with linear chirp and sufficient bandwidth to allow compression to 25–35 fs in an SF10 prism compressor (PC1).²⁷ For 397 nm excitation, the amplifier output is frequency doubled in a 1 mmBBO crystal just before the sample and the pulse width (50 fs) is minimized by precompensation in the prism compressor. The intensity of the actinic pump beam is varied by a circular variable neutral-density filter (Edmund) and the polarization is rotated by a broadband half-wave plate (Special Optics).

The Raman pump pulse is produced by spectrally filtering the amplifier output with either two narrow bandpass filters (NBPF, CVI laser), or by a custom grating filter [Fig. 3(a)]. The NBPFs had a combined 1.0 nm bandwidth transmission at ∼793 nm, producing an 800 fs pulse. However, the NBPFs are hampered by a low damage threshold and their transmission maximum is only tunable through a ∼5 nm range. Also, the 1.0 nm bandwidth limits the spectral resolution of the system to ∼17 cm^–1. The grating filter was designed to give a completely tunable filter with variable wavelength and bandpass.

The Raman pump spectral filter [Fig. 3(a)] is a synthesis of a double subtractive spectrograph²⁸ and a traditional grating-based pulse stretcher.²⁹ The femtosecond duration amplifier pulse is dispersed by a grating (1200 grooves/mm, 750 nm blaze) and focused onto an adjustable slit by a 100 mm focal length lens. The lateral position of the slit determines the wavelength and the slit width determines the bandwidth of the Raman pump pulse. After the slit, a 100 mm fl lens collimates the beam and a second grating removes the angular dispersion and spatial chirp. Placing the gratings and slit a single focal length away from the lenses ensures that the group-velocity dispersion (GVD) of the overall filter is negligible, and consequently that the output pulse is unchirped.²⁹ The output power is proportional to the spectral intensity of the original amplified pulse and can be >200 nJ/pulse from 780–820 nm. The pulse duration is inversely proportional to the slit width and typically varies from 2.1 ps for a 0.16 mm slit to 8.7 ps for a 0.02 mm slit, as measured by optical Kerr effect (OKE) crosscorrelation with the actinic pump. At large slit widths, it is necessary to align both grating angles and lens distances precisely in order to produce negligible GVD across the full transmitted bandwidth. The Raman pump power at the sample is adjusted by a polarization-rotator/cube-polarizer. A second half-wave plate rotates the polarization of the beam, allowing collection of either perpendicular or parallel Raman spectra.¹⁰ We have found that vibrating the Raman pump retroreflector with a small motor (∼80 μm total displacement at ∼110 Hz) greatly improves the baseline stability of the system. The cause of this improvement is most likely due to averaging out the cross-phase modulation (CPM) artifacts in the baseline.^10,11 Vibrating the Raman pump mirror will cause the collected spectra to be averaged over many slightly different Raman pump–probe time delays and phases and thereby produce a smooth average baseline. However, this has no effect on the experimental time resolution, which is determined by the actinic pump:probe time delay.

The probe is produced by continuum generation in a 3 mm thick sapphire plate. A small portion of the amplifier output (∼11 μJ) is picked off and conveyed by reflective optics to the continuum generation apparatus shown in Fig. 3(b). The mode of the beam is improved by aperturing it to a ∼2–3 mm diameter and the pulse energy is attenuated to 2 μJ with a circular variable neutral-density filter. The pulse is focused into the sapphire by a 100 mm fl BK7 singlet lens and the white light is collimated afterward by a 100 mm fl concave mirror (CM). Reflective collimation greatly decreases the GVD acquired by the NIR continuum. The day-to-day variation in the chirp of the continuum is stabilized by positioning the sapphire as close to the focusing lens as possible while maintaining continuum generation. This ensures that self-focusing of the input beam only generates filaments at the very back side of the sapphire plate, limiting the GVD that the continuum can acquire as it propagates through the material. A spectrally smooth and stable continuum appears as a 6–8 mm diameter white or yellow central spot surrounded by a red ring. The probe is compressed to a ∼30 fs chirp-free pulse using a fused silica prism compressor with a 50 cm separation between the prisms (PC2). In the absence of the compressor, the pulse is chirped by material dispersion, producing a 30 fs group delay between 950 and 840 nm.

The smooth spectral shape and stability of the probe spectrum are critical for obtaining stable Raman gain spectra. Any sharp features in the probe spectrum will produce an oscillating baseline from the CPM with the Raman pump. The red edge of the continuum naturally decays smoothly, but the blue edge is determined by the choice of long-pass filter (LPF1) used to remove the residual wavelengths <800 nm in the beam. We use a Wratten NIR cutoff filter (Kodak No. 87c) to produce a gradual increase of the continuum intensity around 830 nm. All thin transmissive optics in the probe path are set at Brewster’s angle to eliminate etaloning, which will produce strong baseline oscillations when the sample exhibits a NIR absorption or stimulated emission band. Rotating the sample cell 34° from normal is sufficient to remove etaloning from its thin windows. The polarization of the probe is improved to reduce background in the cross-correlation signal (see below) by placing a polarizer (Melles-Griot, Pol, Fig. 3) in the probe beam before the broadband beamsplitter. However, the poor transmission (43%) of this polarizer requires longer detector exposure times, increasing data acquisition times by more than a factor of 2. All spectra presented here were collected with the polarizer in place, producing a probe energy of 2.6 nJ/pulse at the sample point.

The temporal instrument response is measured using the OKE cross-correlation technique.^30,31 To perform OKE, the polarization of the actinic pump is rotated to 45° and a crossed polarizer is placed in the probe beam after the sample, aligned to completely extinguish the horizontally polarized probe. When the probe is spatially and temporally overlapped with the actinic pump, the OKE will rotate the polarization of the probe and allow transmission through the crossed polarizer. Dispersing and measuring the transmitted probe intensity as a function of actinic pump delay produces a cross-correlation trace for every wavelength in the continuum. The spatial overlap of the actinic pump and probe is optimized by maximizing the OKE signal at the Δt=0 position determined by the cross correlation. The temporal and spatial overlap of the Raman pump and probe is optimized by maximizing the Raman signal from a solvent. Consistent with theoretical predictions, the maximum signal arises when the probe slightly precedes the Raman pump pulse by about one-half the Raman pump duration.^32,33

In the geometry shown in Fig. 3, the actinic pump, Raman pump and probe are all made collinear with a broadband 50:50 beamsplitter (BBS). The continuum beam transmitted through the BBS is used as the reference to normalize for changes in the intensity and shape of the continuum. At the sample point, the beams are focused by a 150 mm fl concave mirror (FM) and pass through the sample with beam diameters of ∼60 μm at the focus before being collimated by a 150 mm fl lens. Using collinear pump and probe beams maximizes the spatial overlap of the beams as they propagate through the sample and allows the use of any pathlength sample cell; however, it is then necessary to remove the Raman pump with sharp cutoff LPFs (LPF2, Schott RG830 or RG850) before the spectrograph. Difficulties extinguishing the Raman pump while maintaining adequate intensity in the bluest portion of the continuum limit the usable spectrum in this configuration to Raman shifts greater than ∼600 cm^–1 .

In a crossing geometry, the actinic and/or Raman pump beams are displaced to the side of the beamsplitter and the three beams cross at the focus in the sample. Bypassing the beamsplitter approximately doubles the available power in the pump beams, allowing the Raman pump wavelength to be shifted further to the red. Additionally, the crossed beam geometry can improve the low-wave number region of the spectrum by minimizing scattering background caused by the Raman pump entering the spectrograph. This configuration allows the collection of Raman spectra down to ∼200 cm^–1 but the limited beam overlap at the crossing region reduces the usable sample pathlength to ∼1 mm.

B. Sample cell

For time-resolved experiments, the sample is contained in a short-pathlength flow-cell (Harrick Scientific) between 0.15-mm thick glass windows and recirculated by a peristaltic or micro-gear pump. The pulsed flow from the peristaltic pump is damped by flowing through a small glass bulb that contains ∼3 cm³ of air before the sample cell. The flow-cell pathlength can be adjusted from 0.5–3.5 mm using Teflon spacers. The thin windows of the flow cell allow for cross-correlations to be measured directly in the sample cell using the OKE technique with only minimal distortion from group-velocity mismatch (GVM) in the glass between the actinic pump and the probe. Even with the 0.5 mm cell, however, GVM of the sample limits the time resolution of the experiments. Hence, the temporal resolution can vary from 40–170 fs for actinic pump wavelengths from 650–397 nm, respectively, despite the fact that the pump pulses are 30–50 fs in duration. If highly concentrated samples are available, then use of a thin liquid jet would eliminate this problem.³⁴ A cuvette mixed with a micro stir bar is used if a longer pathlength is necessary.

C. Detection

The probe and reference beams are combined after the sample so that they travel to the spectrograph collection optics vertically displaced from one another. The spectrograph (ISA HR320) disperses the beams with a 600 grooves/mm grating and images them onto a dual-photodiode array detector (DPDA-1024, Roper Scientific) consisting of two 1024 pixel arrays of 25×2500 μm² photodiodes vertically separated by 1 mm. The collection optics [Fig. 3(c)] consist of two cylindrical lenses (CLs) that separately control the focusing of the beams in the horizontal plane and the vertical displacement of the beams at the entrance slit of the spectrograph. The first lens (CL1) is a 152 mm fl vertical focusing lens set 198 mm from the slit. This images the 8 mm diameter probe and reference beams (that are separated by 4 mm) onto the detector strips as two 2.4 mm tall stripes separated by 1.2 mm. The second lens (CL2) is separated from the slit by its 100 mm focal length and focuses the probe and reference beams to 100 μm full width at half maximum (FWHM) vertical lines at the slit. This effective slit width corresponds to a resolution of 5–7 cm^–1 after dispersion. Closing the slit so that the beams are clipped slightly improves the spectrograph resolution, but produces large fluctuations in the spectral profiles of the pump and probe. Because of this, experiments are performed with the slit ∼2 mm wide to prevent any beam clipping. The focal lengths of the collection lenses were chosen to be the minimum possible, while underfilling the 68 mm optics of the spectrograph. Use of conventional lenses instead of fiber optics, as used by others,¹⁷ to couple the probe and reference beams into the spectrograph avoids the high losses at the entrance and exit faces of the fibers and difficulties in matching the numerical apertures of the fiber to the spectrograph. This allows for faster readout of the detector and much higher signal-to-noise ratio (SNR) spectra. A synchronized shutter (Uniblitz VMM-T1, LS6S2) placed in front of the spectrograph slit controls the number of pulses integrated on the detector.

The DPDA is the ideal detector for these types of measurements because it has a very large full-well capacity (80 Me^- per pixel) and can be readout very quickly (10 ms). This allows for high SNR detection of small changes on top of a large background by maximizing the total detected photoelectrons. A spectrographic charge coupled device (CCD) can be used as a detector;^16,17 however, CCDs have several characteristics that make them less than ideal for these measurements. Primary among these are readout rate and full-well capacity, which together limit the CCD duty cycle when measuring high light levels. The DPDA is read out in ∼10 ms with a 200 kHz analog-to-digital converter (ADC). Reading out a complete CCD will take ∼300 ms with a 1 MHz ADC or ∼150 ms with a state-of-the-art 2 MHz ADC. Since the CCD will typically saturate with ∼20–50 pulses, the duty cycle of the experiment is limited to 12%–25%. Faster readout rates (∼10 ms) are possible using vertical binning on the CCD, but then the saturation level, limited by the shift register capacity, is reached much more quickly. In this case, readout will be necessary with every pulse and the duty cycle will be reduced to ∼9%. With the DPDA, 50–100 pulses (500–1000 counts/pulse at 1300 e^– /ct) are integrated on the detector and then read out, producing an 83%–91% duty cycle. The DPDA SNR is limited at long exposure times (>10¹⁰ photoelectrons or ∼100 exposures of 100 ms each) by systematic noise from the pixel-to-pixel variations in linearity. This systematic noise is reproducible and easily removed when a solvent or buffer spectrum is subtracted.

D. Data collection

The Raman pump beam is turned on and off by an electronic shutter in alternate exposures of the detector. This corrects for variations in the probe/reference ratio that occur on the time scale of seconds, caused by pointing instability in the probe beam. The Raman gain spectrum is calculated by dividing the Raman-pump-on probe spectrum by the Raman-pump-off spectrum after normalizing each exposure with the reference spectra:

$$\begin{array}{cc}\hfill & \text{Raman}\text{gain}\hfill \\ & \hfill & =\frac{{[(\text{probe}-\text{bkgnd})÷(\text{ref}-\text{bkgnd})]}_{\text{Raman pump on}}}{{[(\text{probe}-\text{bkgnd})÷(\text{ref}-\text{bknd})]}_{\text{Raman pump off}}},\hfill \end{array}$$ 1

where bkgnd refers to the detector background measured with the probe and reference blocked. The calculated spectrum is analogous to a transmission measurement in absorption spectroscopy. The spectrograph and Raman-pump shutters (Uniblitz) are triggered by the detector controller, which is synchronized to the 1 kHz laser pulse train. This ensures that the array is read out only after the exposure shutter (S2) is completely closed and that an integer number of pulses have been integrated on the detector. The spectra are collected on a personal computer by a data collection program written in labview (National Instruments) that performs automatic calculation, display, and averaging of Eq. (1). Systematic noise caused by the residual mismatch of the odd and even pixels in the DPDA is removed with a three-point binomial smoothing applied to the probe and reference spectra. The software also synchronizes: (1) The movement of the delay stage (Melles-Griot nanomover) that controls the optical delay of the actinic pump pulse, allowing automated collection of a series of varying time-delay spectra, (2) the state of the actinic pump shutter, allowing for automatic collection of ground-state spectra (actinic pump off) periodically throughout the experiment to monitor sample degradation, and (3) the position of the slit in the Raman pump spectral filter, which can be moved between two positions to collect shifted excitation Raman difference spectra (SERDS, see below) in rapid succession.

III. SYSTEM PERFORMANCE

A. Dependence on experimental parameters

For strongly Raman active solvents and Raman pump energies >200 nJ, the stimulated Raman features are clearly visible in the probe spectrum [Fig. 1(a)]. For more dilute solutes and smaller Raman pump powers, the gain features are typically not visible in the raw data, but only become apparent upon calculation of the gain spectrum via Eq. (1). Neglecting transient Raman effects, the Raman gain features should be exponentially dependent on the Raman scattering cross section, σ_R, sample concentration, c, intensity (photons /cm²/s) of the Raman pump pulse, I_pu, and sample pathlength, z:

$$\text{Raman}\text{gain}=\frac{\mathit{I}}{{\mathit{I}}_0}=\mathbf{exp}(\mathit{a}\cdot {\sigma }_{\mathit{R}}{cI}_{\mathbf{pu}}z),$$ 2

where a is a constant with units of cm² s, that subsumes several physical constants.^13,35–38 This equation is analogous to Beer’s law for absorption spectroscopy. In most cases the gain is small, meaning e^γ≈1+γ, with $\gamma =a\sigma c{I}_{\mathrm{pu}}z\ll 1$, in which case the Raman gain (RG) ratio will be linear in these variables. At very large gains, the linear approximation to the exponential breaks down and spectra should be calculated as the logarithm of Eq. (1).

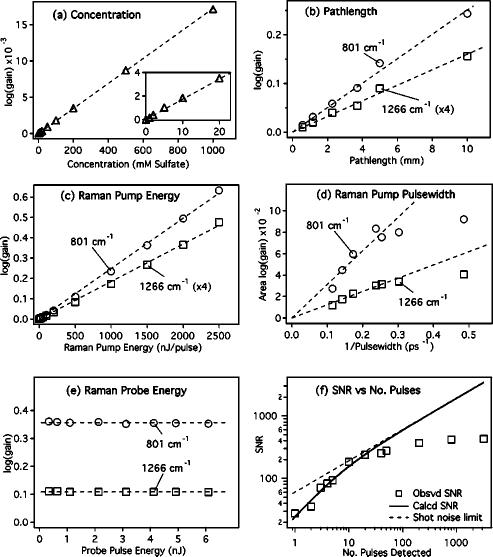
Figure 4 presents the dependence of the stimulated RG signal on the key experimental parameters. To probe the concentration dependence, aqueous sodium sulfate solutions were prepared from 0.001–1 M. Spectra were collected using a 10 mm pathlength cell, 0.5 μJ/pulse, 3.2 ps duration Raman pump pulses and by averaging 100 80 ms exposure spectra (total acquisition time =18 s). Difference spectra were calculated by subtracting a pure water spectrum which removes the systematic noise. The 981 cm^–1 sulfate peak was visible in the 1 mM sample with a gain, or amplification [RG-1, where Raman gain (RG) is the ratio calculated in Eq. (1)], of 3×10^–5 and a SNR of ∼2. The 1 M sample produced a gain of 4% and the signal increased exponentially between these two limits.

FIG. 4.

Dependence of the stimulated Raman gain intensity on experimental parameters. The Raman gain of the 981 cm^–1 sulfate peak increases exponentially with concentration (a). The intensities of the 801 and 1266 cm^–1 peaks of cyclohexane increase exponentially with changes in pathlength (b), Raman pump pulse energy (c), and 1/pump pulse duration [FWHM^–1 (d)]. In (e), the gain is shown to be independent of Raman probe energy. The observed SNR (f) for the 1266 cm^–1 peak of cyclohexane follows the theoretical limit for exposures of ∼20 pulses. With longer exposures, the systematic noise of the detector limits the SNR.

Figure 4(b) presents the pathlength dependence of the cyclohexane gain signal. The sample pathlength was varied from 0.5 to 3 mm by using the sample flow cell and the 5 and 10 mm pathlength data were taken using a stationary cuvette. The Raman pump had a pulse energy of 500 nJ/pulse with a ∼4 ps duration. The gain increases linearly with pathlength, though there is some evidence of a plateau at long pathlengths because of the increase in the diameter of the beam away from the focal spot. The Raman pump is typically ∼60 μm in diameter within ∼3 mm of the focus, diverging to ∼100 μm 5 mm from the focus. The exponential increase in the gain with changes in pathlength will be valid only in regions where the beam diameters are constant.

The dependence of the gain signal on Raman pump intensity, I_pu, is explored in two different experiments [Figs. 4(c) and 4(d)]. We can approximate I_pu=E_pu/(A τ_pu), where E_pu is the energy per pulse, A is the cross-sectional area of the beam at the focus, and τ_pu is the duration (FWHM) of the pulse. This implies an exponential dependence of the gain on the pulse energy, E_pu, or on the inverse of the pulse duration, τ_pu. The pulse energy dependence of the gain of the 801 and 1266 cm^–1 cyclohexane peaks using a 3.2 ps pump pulse and a 10 mm pathlength cell is presented in Fig. 4(c). The logarithm of the 801 cm^–1 cyclohexane gain amplitude increased linearly from 2.2×10^–3 (RG=1.0051, 0.5% amplification) at 10 nJ/pulse (0.17 GW/cm²) to 0.63 (RG=4.28, 328% amplification) at 2500 nJ/pulse (0.63 GW/cm²), where the RG is defined by Eq. (1). Over this same range, the logarithm of the 1266 cm^–1 peak amplitude increased linearly from 4.6 ×10^–4 (RG=1.0011) to 0.12 (RG=1.31). Aperturing the 6 mm diameter pump beam to 2.6 mm produced better overlap with the probe throughout the focal region and increased the gain an additional 30% for a given power; however, the maximum pulse energy was then limited to 700 nJ.

The effect of Raman pump duration on the gain intensity is shown in Fig. 4(d). The pulse width was varied from 2 to 9 ps by changing the slit width in the Raman pump spectral filter while maintaining a constant pulse energy of 150 nJ/pulse at the sample, a 5 mm cuvette of cyclohexane. To remove the effect of spectral broadening when using short pulses, the plotted intensity is the integrated area of the peak rather than simply the peak amplitude. For pulse durations longer than 4 ps (${\tau }_{\mathrm{pu}}^{-1}$< 0.25), the gain grows exponentially with ${\tau }_{\mathrm{pu}}^{-1}$ as expected. At shorter pulse durations (${\tau }_{\mathrm{pu}}^{-1}$< 0.25), transient effects limit the gain and the pulse width dependence levels off. Transient effects become important when the pulse duration approaches or is less than the vibrational dephasing time and have been treated extensively in studies of traditional stimulated Raman spectroscopy.^36–38

The gain intensity as a function of probe power is displayed in Fig. 4(e). As expected from Eq. (2), the gain is completely independent of the intensity of the probe. Instead, the intensity of the probe just limits the SNR of the spectra for a given exposure time.

Figure 4(f) shows the increase in the SNR with the number of detected pulses, n_p. The extremely fast acquisition rates possible for FSRS are apparent by noting that the SNR for an exposure of the sample to only a single Raman pump pulse (n_p=1) is >20. The ability to obtain single-pulse Raman spectra potentially opens up new areas in real-time observation of chemical dynamics. The observed SNR levels are calculated as the gain of the cyclohexane 1266 cm^–1 peak (15% using a 3.8 ps, 1 μJ Raman pump pulse, and a 1 cm pathlength) divided by the standard deviation of the baseline around 1600 cm^–1. The theoretical noise level is calculated as the baseline noise in the double division of Eq. (1), and includes contributions of shot noise and readout noise added in quadrature. The shot noise is the minimum possible noise for any measurement of N_e photoelectrons and is equivalent to $\sqrt{{\mathbf{N}}_{\mathbf{e}}}$ for any single measurement. Our gain spectra are produced by four measurements (probe and reference spectra with Raman pump on and off) in which, at a Raman shift of 1600 cm^–1, we observe 250 counts/pulse at a detector gain of 1300 e^– /count. Readout noise is 1 count/readout, or $\sqrt{2}$ counts for a single spectrum that measures pump-on and pump-off exposures sequentially. The effect of readout noise is only observable for very short exposures, with n_p <10. For longer exposure times, the theoretical noise is determined entirely by the shot noise. The observed SNR matches the theoretical noise for n_p <20; however for a very large number of pulses, n_p>50, the detector systematic noise dominates and the observed SNR levels off. The shot-noise-limited SNR is completely recoverable if a difference spectrum is taken between two samples.¹⁰ Using a CCD for detection would limit the effect of readout noise at low exposure levels and would likely improve the systematic noise at high light levels, but these benefits would come at the expense of a five to ten times increase in the acquisition time.

B. Fluorescence rejection

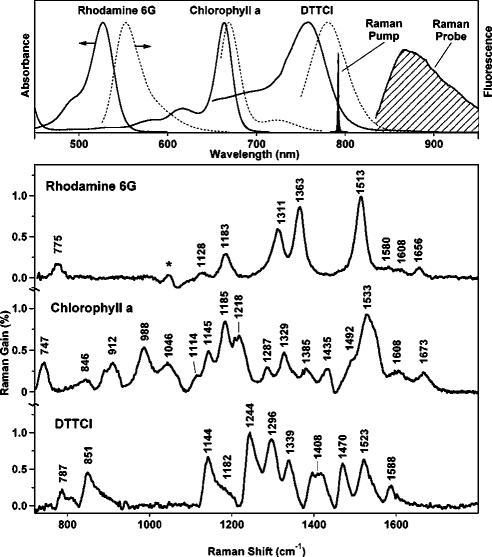
FSRS makes it possible to collect high-quality Raman spectra from samples that are highly fluorescent. For example, in Fig. 5, we present spectra collected from rhodamine 6G, chlorophyll a, and DTTCI (3,3’-Diethylthiatricarbocyanine Iodide).¹⁰ These compounds were chosen because they provide a range of resonance conditions and fluorescence backgrounds. The rhodamine 6G (λ_max =530 nm) and chlorophyll a (λ_max=670 nm) spectra were collected in 11 s and the DTTCI (λ_max=760 nm) spectrum was collected in 2.2 s using an 800 fs 1.5 μJ/pulse Raman pump. The observed noise levels are within 50% of the shot-noise limit because the systematic noise is removed by the subtraction of the pure solvent spectra. The largest peaks have gains of ∼1%, producing SNRs of 50 and 100 for the 2.2 and 11 s spectra, respectively. The stimulated Raman peak frequencies agree with spontaneous Raman spectra of these species obtained using a variety of more difficult fluorescence rejection techniques.^39–41

FIG. 5.

Absorption (top, solid), fluorescence (top, dashed), and stimulated Raman spectra (bottom) of rhodamine 6G, chlorophyll a, and DTTCI showing that stimulated Raman spectra are obtained easily from molecules with high fluorescence backgrounds. The rhodamine 6G (1.3 mM in methanol) and chlorophyll a (0.6 mM in ethanol) spectra were each collected in 11 s, while the DTTCI (2 μM in methanol) spectrum was collected in 2.2 s. In each Raman spectrum the solvent peaks have been subtracted; the asterisk (*) indicates an artifact from this subtraction. Experimental conditions: Raman pump =793 nm, 1.5 μJ/pulse, 800 fs; pathlength =1 cm.

The FSRS detection format dramatically eliminates the spontaneous emission background in these fluorescent samples. Most dramatically, this allows the observation of the resonance Raman spectrum of DTTCI directly in resonance with this laser dye’s 760 nm absorption. The DTTCI stimulated emission produces a smooth gain background across the Raman window of ∼1%, but its smooth shape did not interfere with observation of the stimulated Raman spectrum. No fluorescent background interference was observed in the FSRS spectra of chlorophyll a and rhodamine 6G, despite the visible yellow fluorescence in the rhodamine 6G solution arising from two-photon excitation by the Raman pump. It would be nearly impossible to obtain spectra of chlorophyll a and DTTCI using spontaneous Raman. The large fluorescence background would require signal averaging for 8 days (chlorophyll a) or ∼1 year (DTTCI) to obtain equivalent SNR spectra using spontaneous techniques.¹⁰

C. Shifted excitation Raman difference techniques

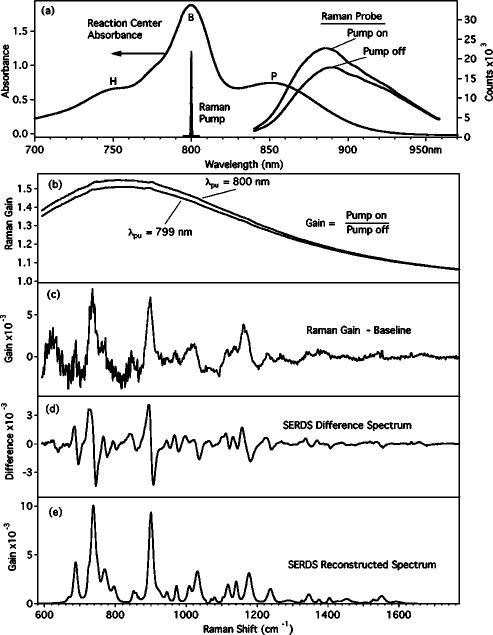
Stimulated emission or transient absorption may produce a large offset in the FSRS gain spectrum from the baseline value of 1.0. A detailed examination of the effect of electronic resonance on FSRS is beyond the scope of this article, but we present here an empirical methodology to remove the baseline offsets that are generated by the Raman pump-induced transient bleach. This effect is highlighted in Fig. 6, where we present FSRS studies of a mutant bacterial reaction center from Rhodobacter capsulatus. The reaction center consists of the special pair bacteriochlorophylls (BChls) absorbing at ∼870 nm (P), a pair of accessory bacteriochlorophylls absorbing at 800 nm (B), and two bacteriopheophytins absorbing at 740 nm (H).⁴² In this mutant, the bacteriopheophytins have been replaced by BChls and two mutations at the accessory BChl positions have been made to inhibit A-side electron transfer.^43,44 The absorption band of the special pair (P) is quite strong within the probe spectral window, leading to a 50% attenuation of the probe intensity. When the 800 nm Raman pump is turned on, excitation of the accessory BChls is followed by rapid energy transfer to the special pair, producing a transient bleach of the P band that dramatically increases the transmitted intensity of the probe. When the gain spectrum is calculated, the spectrum [Fig. 6(b)] has a very large offset from 1. After baseline subtraction, the resultant Raman spectrum [Fig. 6(c)] contains very large systematic noise, due to pixel-to-pixel variations in linearity, that hides many of the smaller Raman features. One way to remove this systematic noise is to perform SERDS.⁴⁵ In this case, a second spectrum is collected in which the Raman pump has been shifted to 799 nm [Fig. 6(b)]. The baseline offset from the electronic spectra will be exactly the same, but the Raman features will be shifted by ∼15 cm^–1. Subtracting the first spectrum from the second removes the large offset and the systematic noise, revealing the clear shot-noise-limited SERDS difference spectrum [Fig. 6(d)] in which each Raman peak is observed as a derivative like feature. The original spectrum, in which the smaller peaks are now apparent [Fig. 6(e)], can be reconstructed by band fitting or integration of the SERDS difference spectrum.^45,46

FIG. 6.

Femtosecond stimulated Raman spectra of the bacterial reaction center YFH mutant provided by Bocian and Chen (see Ref. 44). Shown in (a) is the absorption spectrum of the reaction center and the spectra of the Raman pump and probe pulses. The 800 nm Raman pump produces a large transient bleach of the P band and an increase in the transmitted intensity of the probe, causing the large baseline offset in the gain spectrum (b). When a polynomial baseline is subtracted, the resultant Raman gain spectrum (c) contains a very high systematic noise level. To remove this noise, a second gain spectrum is collected in which the Raman pump has been shifted to 799 nm. Taking the difference of the 799 and 800 nm Raman gain spectra removes the baseline and the systematic noise to produce the shot-noise-limited SERDS (d) (see Ref. 45). From the SERDS spectrum, the Raman spectrum can be reconstructed (e) by integration or by fitting to a predetermined peak shape.

D. Femtosecond time-resolved vibrational spectroscopy

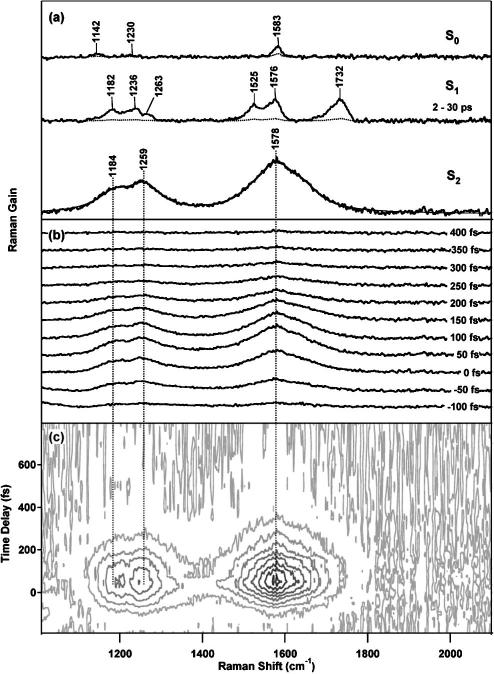
Femtosecond time-resolved stimulated Raman spectra of diphenyloctatetraene (DPO) are presented in Fig. 7 to demonstrate the unique ability of FSRS to perform time-resolved structural measurements. The FSRS spectra were taken in 25 fs steps, using an 800 fs, 30 nJ Raman pump at 793 nm, and a 50 fs, 30 nJ actinic pump pulse at 397 nm.¹¹ Spectra were acquired as the average of 400 100 ms exposures, giving rise to acquisition times of 90 s per time point. The solvent and ground-state DPO peaks have been subtracted, as well as the baseline due to Raman pump-induced bleach of the S₂ NIR absorption band. This pump-induced bleach produces a sloping baseline with maximum offset of ∼0.5% that must be carefully fit and subtracted. To avoid inconsistencies in the baseline that would affect the observed kinetics, we compare the baselines of different time points to ensure that the shape is consistent and that the baseline amplitude follows the excited state population kinetics. Estimated uncertainty in the baseline is the major contributor to the 10%–20% error bars of the integrated area of the Raman peaks.^11,12 Very strong Raman peaks (0.1%) attributable to the short-lived ${\mathrm{S}}_2\left(1{\mathrm{B}}_{\mathrm{u}}^{+}\right)$ state are visible at 1578, 1259, and 1184 cm^–1 which grow in at Δt=0 and decay completely by 300 fs. At longer times, the distinctive high-frequency ${\mathrm{S}}_1\left(2{\mathrm{A}}_{\mathrm{g}}^{-}\right)$ bond grows in at 1732 cm^–1, along with peaks at 1576, 1525, 1263, 1236, and 1182 cm^–1. It is interesting to note that the S₂ vibrational peaks are broadened to ∼105 cm^–1 FWHM by the electronic lifetime of S₂ rather than by a purely vibrational dephasing time. Although we have not observed any features attributable to resonance fluorescence,²⁴ they are easily distinguished from Raman by changing the Raman pump wavelength slightly.

FIG. 7.

(a) Femtosecond time-resolved spectra of the ground and S₁ and S₂ excited electronic states of DPO. The evolution of the spectra over time in the individual traces (b) and in the contour plot of (c), reveal the growth of the large Raman features attributed to S₂, their disappearance with a ∼100 fs time constant, and the lack of any spectral shift over this time period.

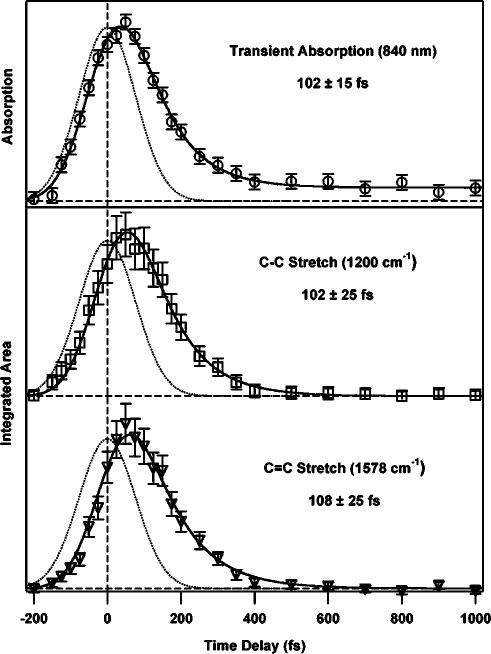
The short acquisition times of these time-resolved Raman spectra allow for the collection of very detailed kinetic traces. Spontaneous Raman acquisition times are usually on the order of 20 min or longer per pump–probe time delay, which limits the number of time points that can be acquired in a reasonable length of time, especially for photosensitive samples.^5,47 FSRS spectra are acquired in 90 s or less, allowing the acquisition of many more time points to determine kinetics with greater precision. This capability is exemplified in Fig. 7(c), which presents a contour plot of the evolution of the DPO spectrum from –200 to 800 fs in 25 fs steps. From the contour plot, it is clear that the vibrational peaks do not exhibit any spectral shift during the ∼100 fs S₂ lifetime, indicating that negligible structural changes or vibrational cooling occurs on this time scale. There is no evidence for an intermediate electronic state between S₂ and S₁. A quantitative kinetic analysis (Fig. 8) shows that the integrated areas of the S₂ Raman peaks rise and fall with the same kinetics as the S₂ NIR transient absorption, growing in with the 170 fs instrument response and decaying with a 100 fs time constant. The instrument response limited rise time clearly indicates that the time resolution of the experiment is determined by the actinic pump–probe cross correlation.

FIG. 8.

Transient absorption kinetics (○) of diphenyloctatetraene’s S₂ state and the kinetic evolution of the integrated area of the C–C stretching region at 1200 cm^–1 (□) as well as the C=C stretching region at 1578 cm^–1 (▽) from –200 to 1000 fs. All fits are a convolution of the instrument response (dotted line, 170 fs) and an exponential lifetime resulting in three similar decay times: 102±15 fs (transient absorption), 102±25 fs (1200 cm^–1), and 108±25 fs (1578 cm^–1).

In conclusion, the rapid data acquisition, fluorescence rejection, and broad spectral window of FSRS make it uniquely valuable for time-resolved vibrational structural studies. The high peak intensity of the Raman pump combined with the broad bandwidth of the fs probe allow the acquisition of high SNR spectra using extremely short acquisition times over a 1500 cm^–1 spectral window. By adding a femtosecond actinic pulse, we have shown that it is possible to perform time-resolved structural studies of photochemical systems with 100 fs time resolution. The independence of temporal and spectral resolution intrinsic to FSRS, in combination with its inherent insensitivity to fluorescence, provides a valuable new tool for vibrational structural studies of ultrafast photochemical reaction dynamics.