Intra- and interpopulation genotype reconstruction from tagging SNPs

Abstract

The optimal method to be used for tSNP selection, the applicability of a reference LD map to unassayed populations, and the scalability of these methods to genome-wide analysis, all remain subjects of debate. We propose novel, scalable matrix algorithms that address these issues and we evaluate them on genotypic data from 38 populations and four genomic regions (248 SNPs typed for ∼2000 individuals). We also evaluate these algorithms on a second data set consisting of genotypes available from the HapMap database (1336 SNPs for four populations) over the same genomic regions. Furthermore, we test these methods in the setting of a real association study using a publicly available family data set. The algorithms we use for tSNP selection and unassayed SNP reconstruction do not require haplotype inference and they are, in principle, scalable even to genome-wide analysis. Moreover, they are greedy variants of recently developed matrix algorithms with provable performance guarantees. Using a small set of carefully selected tSNPs, we achieve very good reconstruction accuracy of “untyped” genotypes for most of the populations studied. Additionally, we demonstrate in a quantitative manner that the chosen tSNPs exhibit substantial transferability, both within and across different geographic regions. Finally, we show that reconstruction can be applied to retrieve significant SNP associations with disease, with important genotyping savings.

The recent common ancestry of the human species provides a tool for the identification of genes that are involved in the susceptibility to, or protection from, common disease. However, the implementation cost of exhaustive genetic association studies comparing all human genetic variation in a very large number of cases and controls remains prohibitive. On the other hand, it has become apparent that common genetic variants such as single nucleotide polymorphisms (SNPs) contain a lot of redundant information due to the linkage disequilibrium (LD) structure of the genome (Daly et al. 2001; Goldstein and Weale 2001; Jeffreys et al. 2001; Patil et al. 2001; Stumpf 2002). This observation suggests the possibility of identifying a small set of SNPs that capture the genetic information within a specified genomic region and enables the design of cost-efficient genetic association studies. Such SNPs are commonly designated as tagging SNPs or tSNPs.

This notion motivated the HapMap project, which in phase I has released a public database of 1,000,000 SNPs, typed in four populations from three geographic regions (Africa, Europe, and East Asia) (The International HapMap Consortium 2003, 2005). It has been suggested that the populations studied in the HapMap project will serve as reference populations that will guide the selection of tSNPs for the design of genetic association studies by investigators around the world. However, the extent to which tSNPs selected in one of the HapMap populations will be predictive of unassayed SNPs in individuals from an unstudied population is an important question that has only recently been addressed by a number of studies (Ke et al. 2004; Mueller et al. 2005; Ramirez-Soriano et al. 2005; De Bakker et al. 2006; Gonzalez-Neira et al. 2006; Magi et al. 2006; Montpetit et al. 2006; Willer et al. 2006).

At the same time, a large number of methods identifying an “optimal” set of tSNPs has recently been introduced in the literature (for review, see Halldorsson et al. 2004b). Early methods necessitate haplotype inference—which is, from a computational time viewpoint, prohibitive for whole-genome studies for a large number of individuals—or rely on definitions of haplotype block boundaries, namely regions of high association between SNPs. Such methods subsequently select tSNPs based on these blocks (Johnson et al. 2001; Patil et al. 2001; Gabriel et al. 2002; Wang et al. 2002; Zhang et al. 2002, 2005; Ke and Cardon 2003; Sebastiani et al. 2003; Stram et al. 2003). No consensus “block” definition has been reached thus far, and recent studies have demonstrated marked differences in the number and length of blocks generated by different methods (Ding et al. 2005; Zeggini et al. 2005). Finally, no formal metric has been agreed upon for the quantification of the coverage provided by existing approaches and the tSNP selection problem in general (Schwartz et al. 2003; Wall and Pritchard 2003a, b). In most recent studies in the literature, this is implemented by estimating the r² coefficient between tagging SNPs and tagged SNPs (Chapman et al. 2003; Weale et al. 2003; Carlson et al. 2004; De Bakker et al. 2005). Although a high r² relationship might be a good indicator that a genetic association study will be effective, it is not clear whether such a relationship is sufficient. On the other hand, if tSNPs can be used to accurately reconstruct unassayed genotypes (or haplotypes), then it will be possible to retrieve the information retained in the data set, including r² relationships. The reconstruction of genotypes based on preselected tSNPs has received considerably less attention, and there is currently a dearth in methods that can efficiently address the reconstruction problem in a quantitative manner (Evans et al. 2004; Halldorsson et al. 2004a; Lin and Altman 2004).

In this study, we define the tSNPs selection problem as a reconstruction problem. Within this framework, we study a sample of ∼2000 individuals from 38 populations from around the world typed for four genomic regions (Yale data set). To test our methods on a denser marker map, HapMap data from the four corresponding genomic regions were also included in our study. The data may be viewed as a table (one for each genomic region and each population) consisting of ∼2000 rows, one for each individual, and a number of columns, one for each SNP site. We use a simple linear algebraic algorithm to select columns (and thus tSNPs) from this table, and we characterize the extent to which major patterns of variation of the intrapopulation data are captured by a small number of tSNPs. Next, we test the accuracy of prediction of unknown SNPs within a single population using only the tSNPs by splitting our sample into training and test sets for each of the populations. Next, we investigate the transferability of tSNPs across populations in a quantitative manner by testing the feasibility of reconstructing unknown SNPs in a previously unstudied target population using tSNPs determined in an available reference population. Finally, we test the impact of these methods on an association study using a publicly available data set (Daly et al. 2001; Rioux et al. 2001). Our algorithms are greedy, heuristic variants of recently developed randomized algorithms for extracting structure from large matrices. These randomized algorithms have provably good computational-time performance, and they are, in principle, scalable to whole-genome data analysis. Our analysis of the worldwide SNP data with these novel algorithmic tools provides an initial characterization of (1) the feasibility of intrapopulation unassayed SNP reconstruction using tSNPs, and (2) the transferability of tSNP selection for the reconstruction of unassayed SNPs for populations within and between diverse geographic regions.

Results

Data sets and characterization of linear structure in the populations

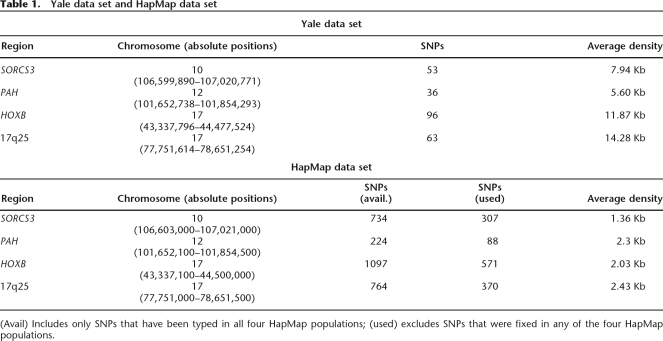
We analyzed four different genomic regions, using data both from 38 populations from around the world (Yale data set) as well as the HapMap populations (HapMap data set). For our Yale data set, a total of 248 SNPs were genotyped on ∼2000 unrelated individuals (Supplemental Fig. 1; Table 1). HapMap data from the four corresponding genomic regions were also included in our study (Table 1). This provided us with the opportunity to test our methods on a denser marker map. We noticed that many of the available HapMap SNPs were actually monomorphic in at least one population. Since our aim was genotype prediction, we excluded from the analysis of the HapMap data set SNPs that were fixed in any one of the HapMap populations in order to avoid distortion of the reported errors. (Prediction for a monomorphic site will always be accurate.) This reduced the data set substantially from a total of 2731 SNPs to 1336 for all four populations, Yoruba (YRI), Europeans (CEU), Chinese (CHB), and Japanese (JPT) (Table 1).

Table 1.

Yale data set and HapMap data set

(Avail) Includes only SNPs that have been typed in all four HapMap populations; (used) excludes SNPs that were fixed in any of the four HapMap populations.

Prior to applying our algorithms, we converted the SNP genotype data for each population and region studied to numeric data in order to process them with linear algebraic methods. Since only genotypic and not haplotypic data were available, each entry in the original data is a pair of bases that may be assumed to be ordered alphabetically. The data are converted without any information loss to numeric matrices. The (i, j)-th entry of any of these matrices is set to −1, 0, or +1, depending on whether, respectively, the i-th individual is homozygous (for one allele arbitrarily chosen of the two alleles) in the j-th SNP site, heterozygous at that site, or homozygous (for the other allele) at that site. A careful implementation of our linear algebraic algorithms allows the existence of missing entries. However, for simplicity and clarity of presentation of our algorithmic techniques, we chose to report results on matrices with no missing data. In the Yale and HapMap data sets, a small number (≤5%) of genotypes were missing, and we filled them in using the technique described in Alter et al. (2000); see Methods and the Supplemental material for details.

Linear structure in a data set is equivalent to the fact that the columns (rows) of the matrix can be expressed as linear combinations of a small number of left (resp. right) singular vectors with a small loss in accuracy (Golub and VanLoan 1989). We shall call these vectors eigenSNPs (Lin and Altman 2004). Recent results in the computer science and applied mathematics literature (Frieze et al. 2004; Drineas and Mahoney 2005, 2007; Drineas et al. 2006a, b) demonstrate that instead of using left (right) singular vectors, which are linear superpositions of all the columns (rows) of the matrix, a small number of actual columns (rows) might be used without any significant loss in accuracy. Since we hope to identify a small number of tSNPs that efficiently describe most of the data and also rely on a small number of individuals to do so (i.e., the HapMap subjects), this is precisely the type of structure that we hope to identify.

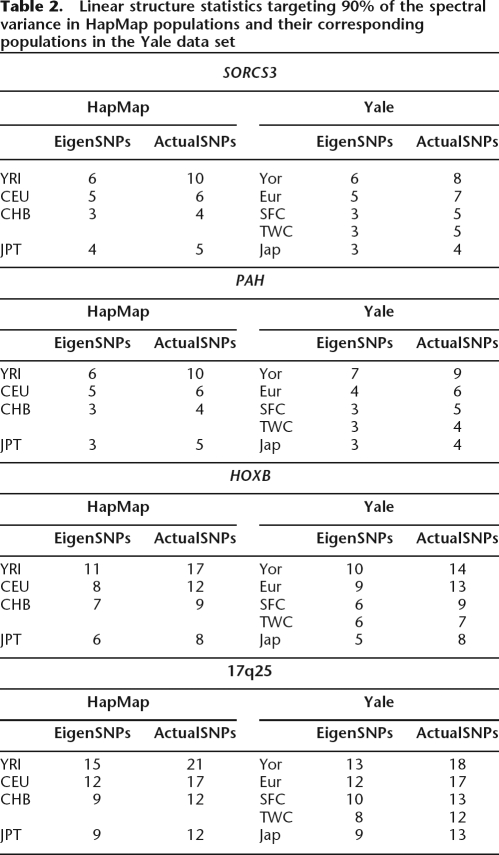
For each of the populations and the regions studied we computed the Singular Value Decomposition in order to determine the number of left singular vectors (eigenSNPs) that were needed to capture 90% and 99% of the spectral variance of the SNP data matrix for that population; see Methods for details. Results for each of the four genomic regions targeting 90% of the population’s spectral variance are presented in Table 2 for the HapMap data set and Figure 1 for our sample of worldwide populations. (See Supplemental Table 1 and Supplemental Fig. 2 for the respective results targeting 99% of the population’s spectral variance.) These data demonstrate that there exists a substantial amount of linear structure within each of the studied populations and data sets. Analysis of the HapMap genotypes in all four regions shows, as expected, that the Yoruban sample requires the highest number of eigenSNPs to capture the data, followed by the European and East Asian samples (Chinese and Japanese). For example, for the HOXB region (571 SNPs spanning ∼1 Mb), only 11 eigenSNPs are enough to capture 90% of the spectral variance in the Yoruba and as few as six eigenSNPs suffice for the Japanese. When targeting 99% of the spectral variance of each data set, the number of eigenSNPs needed to capture the structure of the data increases on average two to three times, but still remains quite low.

Table 2.

Linear structure statistics targeting 90% of the spectral variance in HapMap populations and their corresponding populations in the Yale data set

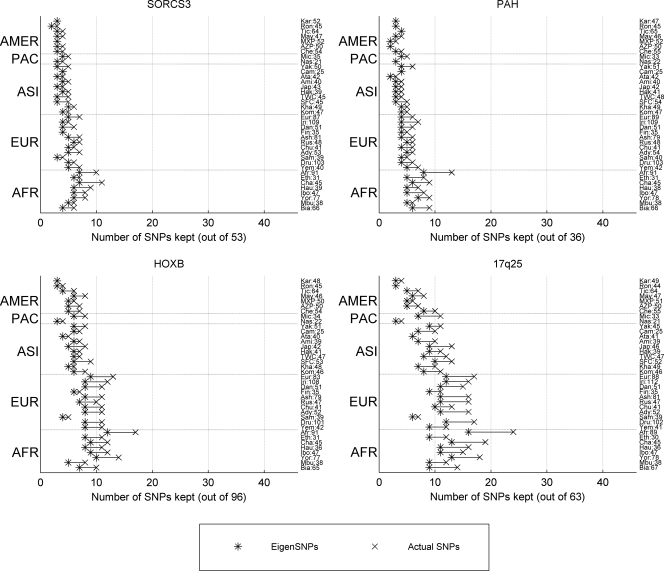
Figure 1.

Number of eigenSNPs (computed with the SVD) and actual SNPs (computed with the tSNPsMultiPassGreedy algorithm) explaining 90% of each population’s spectral variance. The number of individuals in each population sample is denoted next to the population’s abbreviation. Populations are ordered (bottom to top) based on geographic regions (abbreviations used are shown in parentheses). Africa: Biaka (Bia), Mbuti (Mbu), Yoruba (Yor), Ibo (Ibo), Hausa (Hau), Chagga (Cha), Ethiopian Jews (Eth), African Americans (Afr), South-west Asia and Europe: Yemenites (Yem), Druze (Dru), Samaritans (Sam), Adygei (Ady), Chuvash (Chu), Russians (Rus), Ashkenazi Jews (Ash), Finns (Fin), Danes (Dan), Irish (Iri), European Americans (Eur), Asia: Komi (Kom), Khanty (Kha), Chinese Han-San Francisco (SFC), Chinese-Taiwan (TWC), Hakka (Hak), Japanese (Jap), Ami (Ami), Atayal (Ata), Cambodians (Cam), Yakut (Yak), Pacific: Nasioi (Nas), Micronesians (Mic), America: Cheyenne (Che), Pima-Arizona (AZP), Pima-Mexico (MXP), Maya (May), Ticuna (Tic), Rondonian Surui (Ron), Karitiana (Kar).

The Yale data set, including 38 worldwide populations, has considerable linear structure as well. Five of our 38 populations correspond to the HapMap populations (Yoruba, European Americans, Chinese from San Francisco and Taiwan, and Japanese). Interestingly, although the four genomic regions we studied were typed at a much lower density for the 38 populations, almost the same number of eigenSNPs is needed in each case for the HapMap and our own “HapMap corresponding” populations (Table 2; Supplemental Table 1). This seems to suggest that the fundamental structure of the studied regions is accurately captured by the SNPs assayed for the Yale data set. However, testing such hypotheses further is difficult, mainly due to the fact that there is very little overlap between the SNPs typed in the Yale and HapMap samples.

In general, the amount of linear structure, as measured by the (decreasing) number of left singular vectors (eigenSNPs) required to capture the spectral variance within a population, increases as we move out of Africa to Europe, East Asia, and finally, the Americas. This is more pronounced for the two longest regions that we studied, HOXB and 17q25. The African Americans appear to be the most diverse population for all of the regions studied, requiring the greatest number of eigenSNPs.

Selecting tSNPs from a single population

We demonstrated that the major axes of variation in the SNP data matrices for each population could be covered with a small number of left singular vectors or eigenSNPs, which are linear combinations of the actual SNPs. We now seek to identify within each population a set of nonredundant real SNPs (tSNPs) that can retain most of the information contained in the original data matrix. Toward that end, we use the tSNPsMultiPassGreedy Algorithm (see Methods), which selects tSNPs by performing multiple passes over the data. In a pass, the “most informative” SNP (in a linear algebraic projection sense) is selected, its contribution to data is extracted, and the procedure is repeated. This algorithm is a greedy variant of a provably accurate randomized algorithm (Drineas and Mahoney 2007).

Results are presented in Table 2 and Supplemental Table 1 for the HapMap data and Figure 1 and Supplemental Figure 2 for our 38 populations. In our linear algebraic framework, the number of eigenSNPs determined by SVD corresponds to a lower bound for the number of actual tSNPs that capture the same spectral variance in the data. We emphasize that this lower bound may not be achievable. Nevertheless, our results demonstrate that for most populations in both the HapMap and Yale data sets, a large fraction of their spectral variance can be covered by a number of actual SNPs that is not much larger than the number of eigenSNPs. We also found that the data sets that could be reconstructed from the selected tSNPs using standard least squares regression manage to retain the LD properties of each region as well as the allele frequencies for the common “tagged” SNPs (see Supplemental note and Supplemental Tables 2 and 3). We did notice, however, that in general rare SNPs appeared even less polymorphic in the reconstructed data set (data not shown). The difficulty in capturing rare variation may prove to be a general limitation of the tSNPs approach.

It is important to emphasize that at this stage tSNPs have been selected after having seen all of the genotypes for all individuals in each population. We have not performed any actual prediction in “unknown” samples, but simply established the fact that, in principle, redundancy does exist in the data, and thus it is possible to pick tSNPs that cover a certain percentage of the variance of the data.

Using tSNPs to reconstruct unassayed SNPs within a single population

We now address whether it is possible to reconstruct untyped genotypic information in individuals within a population given only a few tSNPs. For each of the populations and for each region, we split the data into training sets and test sets of three different sizes. The different training set sizes corresponded to 90%, 70%, and 50% of the population size, and the remainder of the population was used as a test set. (To get statistically significant results, 100 random splits were performed for each denomination and the results were averaged over all repetitions.) We then selected different numbers of tSNPs using the tSNPsMultiPassGreedy algorithm on the training sets. We considered these tSNPs to be assayed (known) in the training sets and reconstructed the unassayed (unknown) SNPs on the test set using the ReconstructUnassayedSNPs algorithm (see Methods for details).

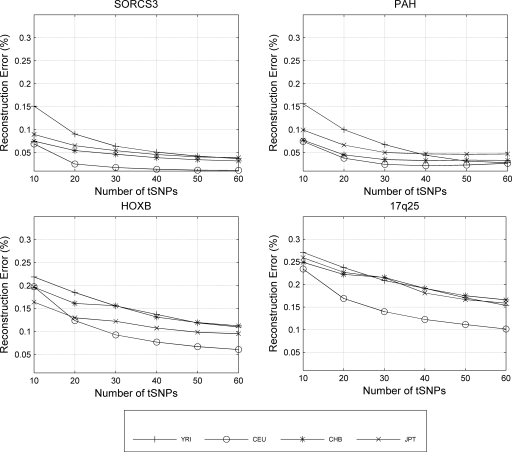
The reconstruction error curve for the HapMap populations, using 10–60 tSNPs (in increments of 10) is shown in Figure 2. We would have expected the HapMap East Asian samples to be the easiest to predict. However, in all four regions, the highest reconstruction accuracy is achieved for the European sample. This may be due to the fact that the European sample consists of trios, while the Chinese and Japanese HapMap samples consist of unrelated individuals. As shown later in this section, in the Yale data set, where all populations consist of unrelated individuals, prediction is generally more accurate for the East Asian samples than the European samples. In most cases, the HapMap Yoruban sample is the most resistant to prediction. We discuss here our results (Fig. 2) using 70% of each population as the training set and trying to reconstruct the remaining 30%; see Supplemental Figure 3 for results using 90% of each population as the training set and trying to reconstruct the remaining 10% (results using 50% of the population as the training set were similar and are not shown). For the relatively short regions studied, PAH and SORCS3, the reconstruction error quickly drops below 10% using information from as few as 20 tSNPs of 88 and 307 SNPs, respectively. At around 40 tSNPs, in each case, the curve levels off and continues to drop with a slower rate. More tSNPs are needed for the 1-Mb regions we studied, HOXB and 17q25. The data set for the 17q25 region appears to be the least structured one. This may be due to the LD structure of the region or the lower density of the reference map used.

Figure 2.

Intrapopulation reconstruction error (ratio of erroneously predicted entries over total number of predicted entries) for each of the four HapMap populations. The training set size is 70% of the total population size.

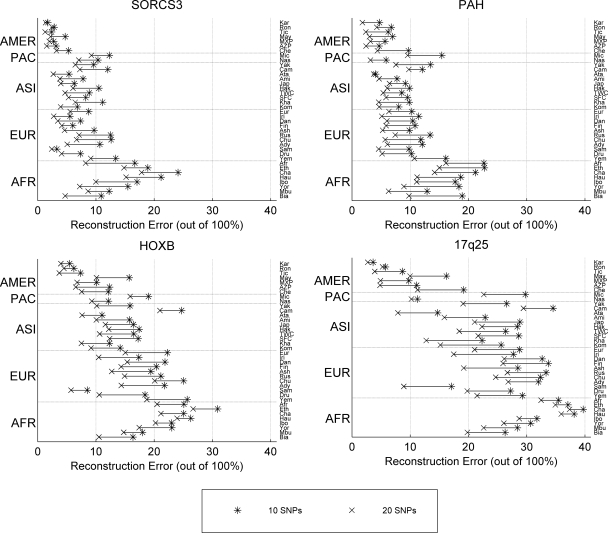
For clarity of presentation, we only show here reconstruction errors when keeping 10 or 20 SNPs for the 38 populations of the Yale data set (Fig. 3, using 70% of each population as the training set, and Supplemental Fig. 4 using 90%). A gradient is again observed, with the smallest reconstruction errors achieved for the same number of tSNPs in the American Indian populations (<5%–10%) and the error increasing as we move through Asia and Europe back to Africa. This seems to follow the general pattern of migrations during human expansion out of Africa and the increasing amount of LD toward the Americas. In general, we achieve higher reconstruction accuracy in PAH and SORCS3, the shorter and more densely typed regions that we studied (reconstruction error around 10% or less for most populations, using 20 tSNPs), while 17q25, the longest and more sparsely typed region, proves to be the most difficult to reconstruct. In all four regions, the African populations show a high degree of heterogeneity and are more resistant to prediction than other populations.

Figure 3.

Intrapopulation reconstruction error (ratio of erroneously predicted entries over total number of predicted entries) for each of the 38 Yale data set populations. The training set size is 70% of the total population size. Populations are ordered (bottom to top) based on geographic regions (Africa, Europe, Asia, Micronesia, Americas).

Using tSNPs to reconstruct unassayed SNPs across populations

Finally, we explore the feasibility of predicting untyped SNPs in one population based on tSNPs selected on another population. Consider the following situation. We are given individuals from a reference population, typed over n SNPs. Now, a new, previously unstudied target population becomes of interest, and we seek to type a small number (say c ≪ n) of tSNPs for this new target population and reconstruct the unassayed n − c SNPs. We seek (1) tSNP selection algorithms to pick the SNPs to be assayed on the target population, given only the genotypes of all n SNPs in the reference population, and (2) tSNP reconstruction algorithms to reconstruct the unassayed SNPs, given only the genotypes of the c tSNPs in the target population and the genotypes of all n SNPs in the reference population (see Supplemental Fig. 5).

This situation represents the realistic scenario of an investigator designing a study based only on a reference population, e.g., a population studied in the HapMap project. To address this question in the Yale data set, we first assigned each of the 38 populations in turn as a reference. We then identified a set of tSNPs using the tSNPsMultiPassGreedy algorithm targeting 90% and 99% of the spectral variance of the reference population and assumed that (for each of the remaining 37 populations) these tSNPs were known. Finally, we reconstructed the unknown SNPs for all available individuals in each of the remaining 37 populations by using the ReconstructUnassayedSNPs algorithm. The same experiment was performed using the HapMap populations in the four regions that we studied. Transferability between the HapMap populations and the ones in the Yale data set could not be evaluated due to the very small overlap of the assayed SNPs in the two data sets.

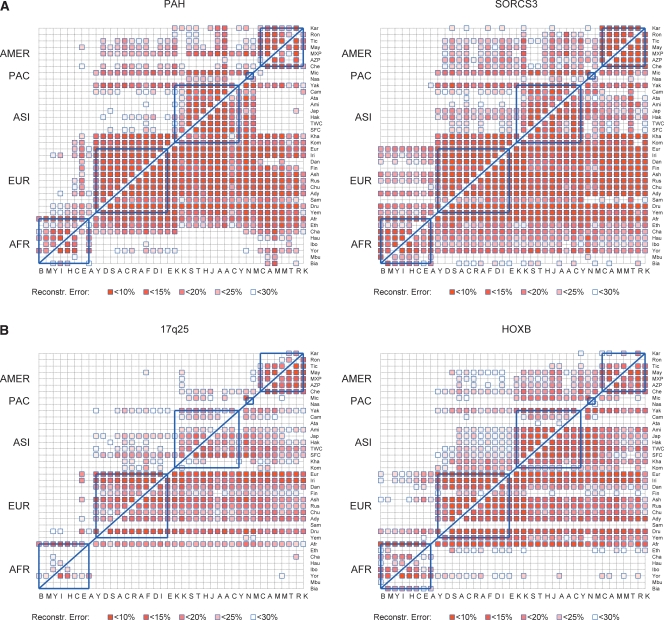
Our findings for the Yale data set (Fig. 4A,B, targeting 99% of the reference population spectral variance and Supplemental Fig. 6a,b targeting 90%) suggest that there exists considerable transferability of tSNPs, mainly within the geographic boundaries of continents, but to a great extent also across them. What is particularly striking is the fact that the European populations in all four regions can be used here to predict, often with an error <10%, the majority of the Asian, Pacific, and American Indian populations. In general, moving out of Africa from West to East, populations can be used as a reasonably good reference for their more eastern neighbors, with the exception of those that are known to have remained isolated for many years, like the Samaritans or the Pacific Islanders. Interestingly, our very diverse sample of African Americans is the only one that can be used to predict unknown SNPs in almost all other populations in this study. This does not seem to be an artifact of the large number of selected tSNPs, since our analysis shows that even when the same number of tSNPs is selected in two reference populations from different continents, different populations will be captured in each case.

Figure 4.

(A,B) Interpopulation reconstruction error (ratio of erroneously predicted entries over total number of predicted entries) for all pairs of populations. Populations are ordered (bottom to top and left to right) based on geographic regions (Africa, Europe, Asia, Micronesia, Americas). The (i, j)-th entry in the plot (i-th row, j-th column) corresponds to the reconstruction error for the j-th population, using the i-th population as reference. The SNPs to be assayed in the j-th population are determined by running the tSNPsMultiPassGreedy algorithm on the i-th population, seeking to explain 99% of the population's spectral variance. Blank entries correspond to reconstruction errors larger than 30%. The five geographic regions of our study are delimited by the blue boxes. (A) PAH and SORCS3; (B) 17q25 and HOXB.

Although similar patterns are observed in all four genomic regions that we studied, the portability of tSNPs seems to be more pronounced in the short and more densely typed regions (PAH and SORCS3). The SORCS3 region is 200 Kb longer than PAH. However, the structure of the region appears to be extremely homogeneous around the world. On the other hand, the 17q25 region has the least amount of tSNP transferability among populations. It has approximately the same length as the HOXB region that we analyzed (1 Mb), but was typed at a lower density (14.3 Kb vs. 11.9 Kb). It is not clear whether our results reflect the relatively poor marker resolution that we have for this region or the LD structure. As discussed in the next paragraph, our analysis of the HapMap genotypes for the same regions seems to support the first hypothesis.

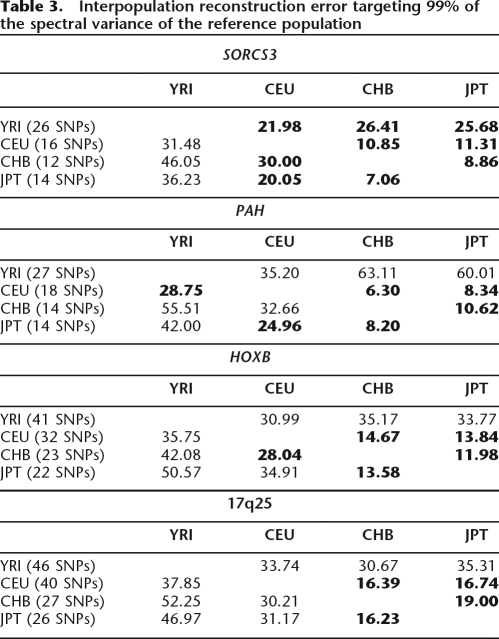
The transferability of tSNPs among the HapMap populations (Table 3; Supplemental Table 4) seems to follow the same general principles as those shown from the analysis of the 38 populations. All four regions have been typed with markers at comparable spacing (between, on average, 1.3–2.4 Kb) and the reconstruction errors are also comparable for the same population pairs across the four regions. This depicts the effect of marker density on reconstruction accuracy.

Table 3.

Interpopulation reconstruction error targeting 99% of the spectral variance of the reference population

The entries in boldface represent reconstruction error <30%.

Searching for association in a reconstructed data set

In order to further validate our methods and investigate their impact on the outcome of a real association study we used a publicly available data set previously studied for association with Crohn disease (Daly et al. 2001; Rioux et al. 2001). The data set consisted of 103 SNPs typed over 500 Kb on 5q31 for 139 family trios with one child affected with Crohn disease. First, we reproduced the results of the original study using the transmission test for linkage disequilibrium (TDT) as implemented by Haploview (Barrett et al. 2005). We chose P ≤ 2 × 10⁻⁴ as the threshold of significance, to conform to the results reported in the original study. Eight markers were found to be associated with the disease in the original data set (see Supplemental material for association study). We then performed 100 random splits of the data in the training set (50% of the families) and the test set (the remaining families). In each trial, the training set was used as a reference for the selection of tSNPs targeting 90%–99% of its spectral variance in increments of 1%. The selected tSNPs were subsequently used to reconstruct the “unassayed” set of genotypes in the test set. We then performed the TDT for each of the reconstructed data sets, and we report here the average results over 100 runs for each target spectral variance.

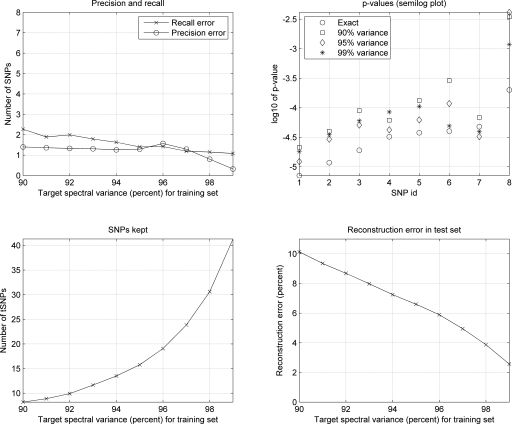
As it is shown in Figure 5, using only eight of 103 SNPs, we achieve 90% reconstruction accuracy, while 41 SNPs are needed to reach 2.5% reconstruction error. As a reference for our savings success, we note here that an LD-based tSNP method, as implemented in Tagger (De Bakker et al. 2005), chooses 43 tSNPs for the same data set (capturing SNPs with r² threshold ≥0.8). We considered the eight markers found to be associated with Crohn disease in the original data set (P ≤ 2 × 10⁻⁴) as ground truth, and we compared the results of our association experiments with this set of markers. Figure 5 shows the number of SNPs for which the TDT on the reconstructed data set erroneously exceeded (false positives, precision curve) or failed to reach the set threshold of significance (false negatives, recall curve). Remarkably, using only eight SNPs of 103 (10% reconstruction error) only two of the eight significant markers are missed and less than two (on average) erroneously exceed the set threshold of significance. When choosing 30 or 40 tSNPs (4% and 2.5% reconstruction error, respectively) one false negative and virtually no false positive results are found. It is true that some power is lost, however, the “false negative” SNPs of our test runs miss the mark only by very little, as revealed when plotting the TDT P-values for each of the eight significant SNPs using the original and the reconstructed data sets (Fig. 5). Interestingly, in almost every case, the P-values from the analysis of the reconstructed data sets are very close to those produced in the original tests. Furthermore, the one or two SNPs that appear as “false positives” are actually correlated to the SNPs reported in the original paper as significantly associated with the disease (data not shown). In any case, even with a 10% reconstruction error, which translates to 90% genotyping savings, the investigator would (in this example) retrieve the significant association in this chromosomal region, and could proceed to more focused genotyping in order to refine the findings of the analysis on the reconstructed data set.

Figure 5.

Genotype reconstruction for association analysis (50% training set). (Top, left) Number of SNPs for which the TDT on the reconstructed data set erroneously exceeded (false positives, precision curve) or failed to reach (false negatives, recall curve) the set threshold of significance P ≤ 2 × 10⁻⁴. (Top, right) P-values for each of the SNPs that were significantly associated with the disease in the original data set (SNP id 1: IGR2063b_1, 2: IGR2060a_1, 3: IGR2055a_1, 4: IGR2096a_1, 5: IGR3081a_1, 6: IGR3096a_1, 7: IGR2198a_1, 8: IGR3236a_1), and the corresponding TDT P-values in reconstructed data sets targeting 90%, 95%, and 99% of the training set spectral variance (log₁₀ 2 × 10⁻⁴ ≈ −3.7). (bottom left, right) Number of tSNPs selected targeting 90%–99% of the training set spectral variance and reconstruction error in the test set.

Discussion

Most existing tSNP selection methods are either based on the arbitrary definition of haplotype block boundaries, or in the currently most common block-free approaches; tSNPs are picked based on correlations using the r² metric. A block-free method like the one we are using circumvents problems such as the arbitrary nature of block-length definitions and takes advantage of all existing associations, even across rigid block boundaries. If the occurrence of haplotype blocks is solely due to recombination hotspots, then SNP correlations will exist only within blocks (Goldstein and Weale 2001; Jeffreys et al. 2001). However, the formation of blocks may also be the result of the concurrent acting forces of recombination and population-specific demographic history (Wang et al. 2002; Zhang et al. 2002, 2004). On the other hand, methods that rely on r² estimations in order to set some SNPs (tSNPs) as proxies for others also depend on the inherent assumption that if SNP A is in LD with SNP B and SNP B is associated with a disease-causing variant, then SNP A will also be associated with the disease variant. This may not always be the case because of heterogeneity and confounding factors (Pritchard and Cox 2002; Montpetit et al. 2006; Terwilliger and Hiekkalinna 2006). Therefore, we suggest that instead of performing analysis on a set of tSNPs, one can use the next best alternative to actually having the entire data set available: an accurately reconstructed data set.

A few results (Evans et al. 2004; Halldorsson et al. 2004a; Lin and Altman 2004) in the genetics literature make an explicit attempt to evaluate their algorithms by reconstructing the “unknown” SNPs. Building upon recent results in the Computer Science and Applied Mathematics literature (Drineas and Mahoney 2005, 2007; Drineas et al. 2006a, b), we propose novel, scalable, linear algebraic algorithms that are useful in this context. In doing so, we show in a very large and diverse population sample that genotype reconstruction based on tSNPs is feasible and, even more interestingly, that it is possible to select tSNPs in one population in order to accurately predict unknown SNPs in a different population. Furthermore, we test the use of these algorithms in the setting of a real association study and find that significant associations with disease can be recovered in a reconstructed data set with important genotyping savings. An interesting direction for future research is to use LD tSNP selection methods and attempt reconstruction using these SNPs. Nevertheless, with this study we attempt to set the general mathematical framework for principled genotype reconstruction.

Our algorithm for tSNP selection can be readily applied to the genotypic data that current SNP typing technologies generate, without the need for the intermediate step of haplotype inference. Algorithms for tSNP selection that rely on EM-based algorithms (Excoffier and Slatkin 1995) or other haplotype inference techniques (Clark 1990; Hawley and Kidd 1995; Stephens et al. 2001; Niu et al. 2002) are computationally expensive and unlikely to be scalable to very large or whole-genome data sets. On the contrary, given n SNPs and m individuals, our algorithm for tSNP selection scales linearly with the number of SNPs and individuals in the data. Using standard Computer Science notation, the running time of our algorithms is O(mn). For reference, our algorithms ran in under 30 sec in a 2.5-GHz Pentium with 1 GB of RAM for each of the largest runs presented here, thus suggesting that extensions to much larger genome-wide SNP data sets are possible.

A few other methods motivated by linear algebra considerations, and in particular the SVD and the related Principle Components Analysis (PCA), have been previously applied to the tSNP selection problem (Meng et al. 2003; Horne and Camp 2004; Lin and Altman 2004). Lin and Altman claimed that PCA-based methods will likely be very difficult to apply on whole-genome data sets. Recent approximation algorithm results (Drineas et al. 2006b) suggest otherwise if the data are very large and if approximate solutions are adequate for the particular application.

The transferability of tSNPs among populations is a question that is beginning to be addressed by recent studies, which have either studied only a few populations or a single genomic region. Common sets of tSNPs have been defined based on the evaluation of correlations between “known” SNPs and “unassayed” ones (Ke et al. 2004; Mueller et al. 2005; Ramirez-Soriano et al. 2005; De Bakker et al. 2006; Gonzalez-Neira et al. 2006; Magi et al. 2006; Montpetit et al. 2006; Willer et al. 2006). Gonzalez-Neira et al. (2006) have recently presented a study of a worldwide sample of populations (1055 individuals) and one genomic region (1 Mb at ≈ 7 Kb density) and concluded, like we do in this study, that portability of tSNPs does exist among populations within each continental group and that tSNPs defined in Europeans are often efficient for Middle/Eastern and Central/South Asian populations. We take this kind of study one step further by studying a much larger worldwide sample (2000 individuals) and four genomic regions. Furthermore, by attempting to reconstruct untyped genotypes in our very large and diverse set of populations, we are able to quantify the amount of tSNP transferability that exists within geographic boundaries of continents, but also across them. The observed patterns of tSNP transferability reflect population relationships, histories, and migrations of ancient populations.

Even at the cost of typing extra SNPs, our study indicates that the populations used in the HapMap project will most likely serve as a good reference for extrapolation of results in other populations, especially Europeans and East Asians. Our results quantify the rather intuitive observation that given a target unstudied population, it is always better to pick a reference population from the same geographic region, since the transferability of tSNPs is significantly higher. However, we would like to note that although the tSNP selection concept in general will likely be very efficient for the analysis of common SNPs, rare variants will most probably be overlooked and different approaches should perhaps be pursued if such variants are of interest. To the extent that the common disease/common variant (Lander 1996; Chakravarti 1999) hypothesis is valid, the HapMap project and tSNP selection will prove to be powerful tools for the design of association studies.

In conclusion, we explored the extent of linear algebraic structure of genotypic data in four regions of the genome and illustrated the value of linear structure extrapolation techniques for the selection of tSNPs and reconstruction of untyped SNPs. A MatLab implementation of our algorithms and the data studied here are available at http://www.cs.rpi.edu/~javeda/ CUR_ tSNPs.htm. Our results indicate that reconstruction accuracy increases with reference map density and LD of the studied region. The pattern of linear structure in our sample of worldwide populations is reminiscent of the observed LD patterns around the world and it seems possible that similar forces may have acted to shape both the LD and linear structure in such data. Further study should shed more light on the degree of correlation between the linear structure observed in a data set and the underlying LD patterns and haplotype structures. It is also possible that nonlinear structure extraction techniques will prove to be the most promising in order to elucidate in a more refined manner the genomic architecture of extremely diverse or richly structured populations.

Methods

Data sets

We present data on a total of 1979 unrelated individuals from 38 populations from around the world (Supplemental Fig. 1). ALFRED (http://alfred.med.yale.edu/), the allele frequency database, contains descriptive information and literature citations for these population samples. A total of 248 SNPs in four genomic regions were typed in all 38 populations. We also investigated the same four genomic regions (SORCS3, PAH, HOXB, and 17q25) using the available genotypes from the HapMap database on the four HapMap populations. We only included in our analysis data from SNPs that were polymorphic in all four populations (a total of 1336 SNPs; see Table 1 for details). Since we had selected the SNPs to be typed in the Yale samples well before the publication of the HapMap results, there was little to no overlap between the SNPs that we studied in the Yale samples and those typed in the HapMap populations. Finally, the data set that we used for validation of our algorithms in an association study is publicly available at http://www.broad.mit.edu/humgen/IBD5/ and has been described in detail (Daly et al. 2001; Rioux et al. 2001).

Encoding our data and evaluating linear structure

We transformed the raw data to numeric values, without any loss of information, in order to apply our linear algebraic algorithms. See Algorithm Encode in the Supplemental material for a precise statement of this procedure. For clarity of presentation, we filled in a (very small) number of missing entries in the Yale and HapMap data sets using the procedure described in Alter et al. (2000); for the association study data set, we did not fill in the missing data.

Our algorithms for tSNP selection and tSNP transferability take advantage of and extract linear structure in the SNP data matrix. In order to determine the extent to which the SNP data matrix has this structure, we shall use the Singular Value Decomposition (SVD) (Horn and Johnson 1985; Golub and VanLoan 1989). The SVD is a commonly used tool from Linear Algebra to extract linear or low-rank structure in data represented by a matrix. For example, it provides the mathematical foundation for the commonly used method of Principal Components Analysis (PCA). We emphasize that the SVD is used in this work only to determine the extent of linear structure in the data matrix. Our algorithms for tSNP selection and tSNP transferability will extract linear structure, but will not use the SVD.

Given an m × n matrix A, the SVD returns m pairwise orthogonal unit vectors uⁱ that form a complete basis for the m-dimensional Euclidean space, n pairwise orthogonal unit vectors vⁱ that form a complete basis for the n-dimensional Euclidean space, and ρ = min{m,n} singular values σ_i such that σ₁ ≥ σ₂ ≥ . . . σ_ρ ≥ 0. The matrix A may be written as a sum of outer products (rank-one components) as A = 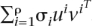. We notice that when applied to a SNP data matrix the uⁱ are associated with the columns (SNPs) of this matrix and are called eigenSNPs (Lin and Altman 2004). Notice that the i-th singular vector corresponds to the i-th singular value, and thus, there exists a natural ordering of the singular vectors. One interpretation of the SVD is that keeping the top k ≤ ρ left singular vectors we can express all of the columns of the matrix A as linear combinations of these k left singular vectors with a small loss in accuracy. More precisely, for all i = 1, . . . , n, A⁽ⁱ⁾ ≈ Σ^k_j=1 z_iju^j; where A⁽ⁱ⁾ denotes the i-th column of A as a column vector and the z_ij are real numbers. The z_ij are computed by solving least squares regression problems to minimize the Euclidean norm of the difference vector A⁽ⁱ⁾ – Σ^k_j=1 z_iju^j. Overall, using the top k left singular vectors we can approximate A by A ≈ A_k = U_kZ; where Z is the k × n matrix whose entries are the z_ij. Standard methods from Linear Algebra can be used to show that Z = 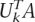. If the difference A – A_k is small, then we say that A is well-approximated by a rank- k matrix, and if k ≪ min{m, n}, then we say that A is approximately low-rank or has good linear structure. Intuitively, this means that there is significant redundancy of information in the columns of A. Algorithm 2 in the Supplemental material describes in detail how we evaluate the linear structure in our populations.

Selecting tSNPs and reconstructing genotypes

Via the SVD, we can compute a set of vectors u¹, . . . , u^k such that every column of A^X (the matrix encoding SNP data from population X) may be expressed as a linear combination of these k vectors with a small, fixed loss in accuracy. Since the columns of A^X are the SNPs that were assayed on X, one might be tempted to call the u¹, . . . , u^k tSNPs for population X. Unfortunately, the u¹, . . . , u^k are not actual SNPs (columns of A^X). Instead, they are linear combinations of actual SNPs, and in general, have no biological interpretation.

An obvious next step is to wonder whether we can find a small number of columns of A^X (namely, actual SNPs) such that expressing every column of A^X as a linear combination of these columns by solving least squares regression problems and subsequently rounding the result would return an approximation to A^X with a small number of erroneous entries. Toward that end, we slightly modified the SelectColumnsMultiPass algorithm of Drineas and Mahoney (2007). The resulting tSNPsMultiPassGreedy algorithm does not come with a provable performance guarantee, but differs from most algorithms in current genetics literature in that it is guided by strong theoretical evidence regarding its performance. See the Supplemental material for an exact description of the algorithm.

We now describe our interpopulation reconstruction algorithm. Consider the matrix A^X corresponding to the m₁ subjects of population X, and assume that we seek to predict the SNPs for all m₂ subjects of a different population Y. Assume that the subjects of X are fully assayed. We will assay a small number (say c ≪ n) of SNPs for the subjects in Y and predict the remaining n − c SNPs for every subject in Y. In order to determine which c SNPs to assay for the subjects in Y we use the tSNPsMultiPassGreedy algorithm on A^X. After assaying the selected SNPs for the subjects of Y we will get an m₂ × c matrix C^Y. The ReconstructUnassayedSNPs algorithm (which implements a CUR-type decomposition of a matrix) essentially performs a least-squares regression fit for the subjects of Y (Drineas et al. 2006c). See the Supplemental material for an exact description of the algorithm. The same algorithm may be used to reconstruct unassayed SNPs of individuals within a population. More specifically, given a population X, we split the individuals into two sets: a training set X₁ and a test set X₂. The ReconstructUnassayedSNPs algorithm is used with X₁ instead of X and X₂ instead of Y.