Bounds for cell entries in contingency tables given marginal totals and decomposable graphs

Abstract

Upper and lower bounds on cell counts in cross-classifications of nonnegative counts play important roles in a number of practical problems, including statistical disclosure limitation, computer tomography, mass transportation, cell suppression, and data swapping. Some features of the Fréchet bounds are well known, intuitive, and regularly used by those working on disclosure limitation methods, especially those for two-dimensional tables. We previously have described a series of results relating these bounds to theory on loglinear models for cross-classified counts. This paper provides the actual theory and proofs for the special case of decomposable loglinear models and their related independence graphs. It also includes an extension linked to the structure of reducible graphs and a discussion of the relevance of other results linked to nongraphical loglinear models.

1. Introduction

Upper and lower bounds on cell counts in cross-classifications of positive counts given certain marginal totals play important roles in a number of the disclosure limitation procedures, e.g., see the various papers in the 1998 special issue of The Journal of Official Statistics (1). In that context, if a cell count is small and the upper bound is “close” to the lower bound, the intruder knows with certainty that there is only a small number of individuals possessing the characteristics corresponding to the cell and this may pose an undo risk of disclosure of the identity of these individuals. Similarly, such bounds also arise in a variety of other contexts including mass transportation problems (2), computer tomography (3), ecological inference in the social sciences (4), causal inference in imperfect experiments (5), and are the focus of the probabilistic literature on copulas (6). Much of the work on this problem has been focused on bounds in the case when the marginal totals are nonoverlapping.

The class of bounds we describe is a generalization of bounds usually attributed to Fréchet (7), whose original presentation was in terms of cumulative distribution functions (c.d.f.) for a random vector (D₁, D₂, … , D_m) in R^m:

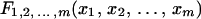1

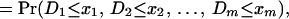which are essentially equivalent to contingency tables when the underlying variables are categorical. For example, suppose we have a two-dimensional table of counts, {n_ij} adding up to the total n₊₊ = n. If we normalize each entry by dividing by n and then create a table of partial sums, by cumulating the proportions from the first row and first column to the present ones, we have a set of values of the form [1]. Thus, Fréchet bound results for distribution functions correspond to bounds for the cell counts where the values {x_i} in [1] represent “cut-points” between categories for the ith categorical variable. Bonferroni (8) and Hoeffding (9) independently developed related results on bounds.

We are interested in the following generalization of the Bonferroni–Fréchet–Hoeffding bounds. Consider a k-dimensional contingency table n_K arranged as a linear list of m counts. The random variable assigned to the ith cell will be denoted Y_i. Let 𝒮 be a system of nonempty subsets of {1, 2, … , m}, such that ∪_S∈𝒮 S = {1, 2, … , m}. The Fréchet class ℱ(𝒮) (6) is the class of m-variate distributions with fixed marginals {F_S : S ∈ 𝒮}, where F_S is the joint c.d.f. of random variables {Y_i : i ∈ 𝒮}. Because the indices of the margins being fixed might be overlapping, we have to impose a consistency constraint, namely

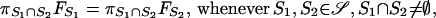where π_S means integrating out the variables that do not appear in S. Following Rüschendorf (10), for a measurable function φ: R^m → R, we define M(φ) = sup {∫ φdF : F ∈ ℱ (𝒮)} and m(φ) = inf {∫ φdF : F ∈ ℱ (𝒮)}. Our goal is to determine M(φ) and m(φ) in the particular case when φ is the identity function on the set R × … × (− ∞,y_i] × … × R. This is equivalent to determining sharp upper and lower bounds for the ith cell in the cross-classification n_K, given the marginals {n_S : S ∈ 𝒮}.

Fienberg (11) noted that there is an intimate link between bounds for non-negative cell entries in a cross-classification subject to marginal constraints, and maximum likelihood estimates for the same cell entries under the loglinear model whose minimal sufficient statistics are the margins. This link seems especially clear in the special case of cross-classifications of non-negative counts and loglinear models for their expectations that are decomposable, i.e., for tables where estimated expected values can be explicitly written as a function of the marginal totals (e.g., see refs. 12–14). Such models are a special subclass of the graphical loglinear models (e.g., see refs. 14 and 15), and these models are representable in terms of graphs that display conditional independence relationships. We present the results here in terms of graphs and explain how they apply to the more general situation. In the next section, we introduce some basic notation for the corresponding theory of decomposable graphs. Then, in Section 3, we give results on Fréchet bounds when the margins correspond to those that characterize decomposable loglinear models. Sections 4 and 5 extend the approach to reducible graphs and provide some explicit examples. In the final section, we present some conjectures on how these bound results can be extended to cases corresponding to bounds for cross-classifications that are not quite representable in graphical form but that utilize our results for reducible graphs.

2. Basic Graph Theory Results

In this section, we begin with some basic definitions and notations for graphs and then define decomposable graphs and present some results that characterize them.

2.1. Graph Terminology.

A graph is a pair 𝒢 = (V, E), where V is a finite set of vertices and E ⊆ V × V is a set of edges linking the vertices. Our interest is in undirected graphs, for which (u, v) ∈ E implies (v, u) ∈ E. For any vertex set A ⊆ V, we define the edge set associated with it as

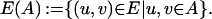Let 𝒢(A) = (A, E(A)) denote the subgraph of 𝒢 induced by A. The section graph 𝒢\A := 𝒢(V\A) is the subgraph of 𝒢 obtained by removing a set of vertices A ⊂ V from the graph. Two vertices u, v ∈ V are adjacent (neighbors) if (u, v) ∈ E. A set of vertices of 𝒢 is independent if no two of its elements are adjacent. The boundary bd(A) of a subset of vertices A ⊂ V is the set of vertices in V\A adjacent to at least one vertex in A:

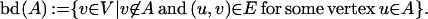The closure of A ⊂ V is cl(A) = A ∪ bd(A). An induced subgraph 𝒢(A) is complete if the vertices in A are pairwise adjacent in 𝒢. We also say that A is complete in 𝒢. A complete vertex set A in 𝒢 that is maximal is a clique.

Let u, v ∈ V. A path (or chain) from u to v is a sequence u = v₀, … , v_n = v of distinct vertices such that (v_i−1, v_i) ∈ E for all i = 1, 2, … , n. The path is a cycle if the end points are allowed to be the same, u = v. If there is a path from u to v we say that u and v are connected. The sets A, B ⊂ V are disconnected if u and v are not connected for all u ∈ A, v ∈ B. The connected component of a vertex u ∈ V is the set of all vertices connected with u. A graph is connected if all the pairs of vertices are connected.

The set C ⊂ V is an uv-separator if all paths from u to v intersect C. The set C ⊂ V separates A from B if it is an uv-separator for every u ∈ A, v ∈ B. C is a separator (cut-set) of 𝒢 if two vertices in the same connected component of 𝒢 are in two distinct connected components of 𝒢\C or, equivalently, if 𝒢\C is disconnected. In addition, C is a minimal separator of 𝒢 if C is a separator and no proper subset of C separates the graph. Unless otherwise stated, the separators we work with will be complete.

Consider a connected graph 𝒢 = (V, E) having a clique separator C, and let V₁, … , V_s be the vertex sets of the connected components of 𝒢\C. The subgraphs 𝒢(V₁ ∪ C), … , 𝒢(V_s ∪ C) are the leaves of 𝒢 produced by C. A graph is bipartite if its set of vertices can be partitioned into two disjoint subsets V₁ and V₂ such that every edge of the graph connects between a vertex of V₁ and a vertex of V₂, i.e. V₁ and V₂ are independent sets. A tree is a connected graph with no cycles. It has n vertices and n − 1 edges. In a tree, there is a unique path between any two vertices.

2.2. Decomposable Graphs.

Decomposable graphs possess the special property that allows us to “decompose” them into components or subgraphs and work directly with these components. They also allow us to make use of divide-and-conquer techniques to solve any type of problem associated with such a graphical structure. The idea is to decompose the graph 𝒢 in two possibly overlapping subgraphs 𝒢′ and 𝒢" so that no structural information of the graph is lost when transforming 𝒢 into 𝒢′ and 𝒢". Furthermore, by “correctly” decomposing 𝒢′ and 𝒢", and so on, one ends up with a set of subgraphs of 𝒢 that allow for no further decompositions. A set of subgraphs of 𝒢 generated in this way is called a derived system of 𝒢, while its elements are called atoms (16). If one does not lose any information along the way in the decomposition, then one can solve problems for each atom and then put together the component solutions to solve a combined problem for the initial graph 𝒢. But first we need to define what we mean by “correct” decomposition.

Definition 1: The partition (A₁, A₂, A₃) of V is said to form a decomposition of 𝒢 if A₂ is a minimal separator of A₁ and A₃.

In this case (A₁, A₂, A₃) decomposes 𝒢 into the components 𝒢(A₁ ∪ A₂) and 𝒢(A₂ ∪ A₃). The decomposition is proper if A₁ and A₃ are not empty. If A₂ is empty, A₁ and A₃ form two nonoverlapping connected components.

Throughout the remainder of this section, we will assume that the graphs we work with are connected. No loss of generality is incurred because all the results can be applied to a disconnected graph by applying them successively to each connected component. We follow closely Blair and Barry (17) and Lauritzen (18).

Definition 2: The graph 𝒢 is decomposable if it is complete or if there exists a proper decomposition (A₁, A₂, A₃) into decomposable graphs 𝒢(A₁ ∪ A₂) and 𝒢(A₂ ∪ A₃).

Because we require a proper decomposition of the graph at every step, the components 𝒢(A₁ ∪ A₂) and 𝒢(A₂ ∪ A₃) have fewer vertices than the original graph 𝒢, hence the procedure will stop after a finite number of steps. The smallest nondecomposable graph is a cycle with four vertices.

Definition 3: A vertex v ∈ V is simplicial in 𝒢 = (V, E) if bd(v) is a clique.

If v ∈ V is simplicial in 𝒢 and 𝒢 is not complete, ({v}, bd(v), V\cl(v)) is a proper decomposition of 𝒢. Simplicial vertices have very nice and useful properties:

Lemma 1. (i) A vertex is simplicial if and only if it belongs to precisely one clique. (ii) Any decomposable graph has at least one simplicial vertex.

The importance of simplicial vertices in describing the structure of decomposable graphs will soon become apparent. Assume that the graph 𝒢 has n vertices. An ordering of 𝒢 is a bijection from the vertex set V to a set of labels {1, 2, … , n}. Let v₁, v₂, … , v_n be an ordering of the vertex set V. The monotone adjacency set of v_i is given by:

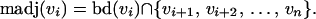2

There is a special class of orderings of 𝒢 that plays a central role in the characterization of decomposable graphs.

Definition 4: The ordering v₁, v₂, … , v_n is a perfect elimination ordering (PEO) if v_i is simplicial in the graph 𝒢 ({v_i, v_i+1, … , v_n}) for every i = 1, 2, … , n.

Any decomposable graph is characterized by the possession of a PEO, as the next result shows.

Theorem 1. A graph 𝒢 is decomposable if and only if 𝒢 has a perfect elimination ordering.

The maximum cardinality search algorithm (MCS) is a linear-time procedure for generating a perfect elimination ordering. It starts with an arbitrary vertex v ∈ V for which it sets v = v_n. The next vertex will be labeled n − 1 and will be one of the unlabeled vertices with the maximum number of labeled neighbors. The ordering v₁, v₂, … , v_n generated by continuing in this way will always be a PEO if the input graph is decomposable.

Let 𝒞(𝒢) = {C₁, C₂, … , C_p} be the set of cliques of a decomposable graph 𝒢 and v₁, v₂, … , v_n be a PEO obtained by applying the MCS algorithm. We will refer to v_iq as the representative vertex of C_q whenever C_q = {v_iq} ∪ madj(v_iq). The following result shows how MCS can efficiently generate the cliques in 𝒞(𝒢) by identifying their representative vertices.

Theorem 2. [Blair and Barry (17).] Let v₁, v₂, … , v_n be a PEO obtained by applying the MCS algorithm to a connected decomposable graph 𝒢. Then 𝒞(𝒢) contains precisely the following sets: {v₁} ∪ madj(v₁) and {v_i+1} ∪ madj(v_i+1), 1 ≤ i ≤ n − 1, for which | madj(v_i)| ≤ | madj(v_i+1)|.

Because MCS labels the vertices of 𝒢 in decreasing order, the cliques also will be generated in a decreasing order with respect to the labels of their representative vertices. More explicitly, assume that v_i1, v_i2, … , v_ip are the representative vertices of the cliques C₁, C₂, … , C_p, respectively, where i₁ > i₂ > … > i_p. The MCS algorithm finds the cliques in 𝒞(𝒢) in the order C₁, C₂, … , C_p. We need to introduce one additional class of sets.

Definition 5: Let V₁, … , V_k be a sequence of subsets of the vertex set of a graph 𝒢 = (V, E). Let H_j = V₁ ∪ … ∪ V_j, S_j = H_j−1 ∩ V_j, and R_j = V_j\H_j−1. The sequence is said to be perfect if (i) for all j > 1, there is an i < j such that S_j ⊆ V_i, and (ii) the sets S_j are complete for all j.

The first condition in Definition 5 is known as the running intersection property. The sets S_j are called the separators of the sequence.

Theorem 3. [Lauritzen (14).] Let V₁, … , V_k be a perfect sequence of sets that contains all cliques of a graph 𝒢. Then for every j, S_j separates H_j−1\S_j from R_j in 𝒢(H_j) and hence (H_j−1\S_j, S_j, R_j) decomposes 𝒢(H_j).

A total ordering C₁, C₂, … , C_p of the cliques in 𝒞(𝒢) generated by the MCS algorithm will always have the running intersection property (17). Because C₁, C₂, … , C_p are complete in 𝒢, the vertex sets S_j = (C₁ ∪ … ∪C_j−1) ∩ C_j will also be complete, and consequently C₁, C₂, … , C_p is a perfect sequence of sets. By recursively applying Theorem 3, we obtain that 𝒞(𝒢) is a derived system of 𝒢, whereas S_j (j = 2, … , p) is the corresponding sequence of separators [c.f. the recursive result described by Rüschendorf (10)]. We note that, although a clique can appear only once in 𝒞(𝒢), a separator can appear more than once in 𝒞(𝒢). Therefore, 𝒮(𝒢) is not really a set, but a “multiset” of separators (17).

3. Generalized Fréchet Bounds for Decomposable Loglinear Models

Let X = (X₁, X₂, … , X_k) be a vector of discrete random variables. Denote K = {1, 2, … , k} the index set associated with X₁, X₂, … , X_k. The random variable X_j can take the values x_j ∈ {1, 2, … , I_j}, for j = 1, 2, … , k. Let J_K = I₁ × I₂ × … × I_k and x = (x₁, x₂, … , x_k) ∈ J_K.

Consider the k-way contingency table n_K := {n_K(x)}_x∈JK. We let a = {i₁, i₂, … , i_p} denote an arbitrary subset of K, and we define X_a as the ordered tuple X_a = (X_i; i ∈ a). Similarly, we denote J_a = J_i1 × J_i2 × … × J_ip. The marginal table of counts n_a := {n_a(x_a)}_xa∈Ja corresponding to X_a is given by

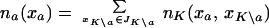We write n_ab instead of n_a∪b, where a, b ⊆ K. The grand total of the complete table is n_∅.

Assume we are given m possibly overlapping marginal tables n_C1, n_C2, … , n_Cp such that C₁ ∪ C₂ ∪ … ∪ C_p = K. Moreover, C₁, C₂, … , C_p are the cliques of a decomposable graph 𝒢 = (K, E). Let S₂, … , S_p be the separators associated with (C_j)_j. Every S_j is included in some clique C_i, hence the marginals n_S2, … , n_Sp will also be fixed.

The class of Fréchet bounds we present is linked with the theory of decomposable loglinear models. We think of every vertex i ∈ K of 𝒢 as being associated with a variable X_i. The structural information embedded in 𝒢 might be interpreted in the following way: If S separates A₁ and A₂ in 𝒢, then X_A1 is conditionally independent of X_A2 given X_S. The loglinear model with minimal sufficient statistics C₁, C₂, … , C_p will be decomposable because its independence graph 𝒢 is decomposable, and consequently the maximum likelihood estimates (MLEs) will exist and can be expressed in a closed form (14, 15). We develop explicit formulas for the tightest upper and lower bounds for the cell counts in the cross-classification n_K provided that the marginals n_C1, n_C2, … , n_Cp are known by employing a similar machinery to the one used for developing formulas for MLEs for a decomposable loglinear model. This machinery provides us with the tools we need for extending the usual Fréchet bounds to more complicated graphical structures.

We begin with a slightly more general statement of the original Fréchet bound result (2, 11).

Theorem 4. (Fréchet). (i) Let a₁, a₂ ⊆ K such that (a₁\a₂, a₁ ∩ a₂, a₂\a₁) is a proper decomposition of the graph 𝒢 (a₁ ∪ a₂). Then the following inequality holds:

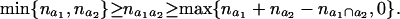3

(ii) The above inequality provides sharp bounds for the cells in the contingency table n_a1∪a2 given the marginals n_a1 and n_a2.

If two vertex sets are in two distinct connected components, they are separated by the empty set. It is not hard to see that Theorem 4 implies the following result.

Corollary 1. (i) If a₁ and a₂ are two disjoint subsets of K, we have

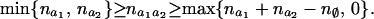(ii) The above inequality provides sharp bounds for the cells in the contingency table n_a1∪a2 given the marginals n_a1 and n_a2.

This immediately generalizes to a graph with any number of connected components.

Theorem 5. (i) Let {a₁, a₂, … , a_m} denote the set of connected components of the graph 𝒢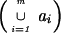. Then the following is true:

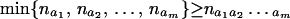4

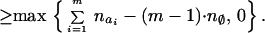(ii) The above inequality provides sharp bounds for the cells in the contingency table 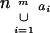given the marginals n_a1, n_a2, … , n_am.

We are now ready to explore the situation when the minimal sufficient statistics of a decomposable loglinear model define a connected graph.

Theorem 6. Suppose 𝒢 = (K, E) is connected and decomposable. Let 𝒞(𝒢) = {C₁, C₂, … , C_p} the set of cliques of 𝒢 ordered in a perfect sequence and 𝒮(𝒢) = {S₂, … , S_p} the corresponding set of separators. Then

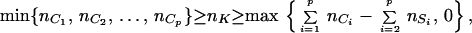5

and these are sharp bounds for the cells in the contingency table n_K given the marginals n_C1, … , n_Cp.

Proof: By induction. If 𝒢 decomposes in p = 2 cliques, then Eq. 5 is a direct consequence of Theorem 4. Suppose we know that Eq. 5 holds for any connected decomposable graph with p − 1 cliques. We want to prove Eq. 5 for a graph with p cliques.

Theorem 3 tells us that (H_p−1\S_p, S_p, R_p) is a decomposition of the graph 𝒢(H_p) = 𝒢. By using Theorem 4, we obtain

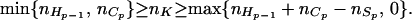6

The cliques of 𝒢(H_p−1) are C₁, C₂, … , C_p−1, and this is a perfect sequence in 𝒢(H_p−1). From the induction assumption that we made, we have

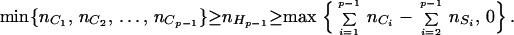7

By combining Eqs. 6 and 7, we obtain the desired Eq. 5. Again, because the bounds in Eq. 6 are the tightest possible for the counts in table n_K, and the same is true for the bounds in Eq. 7 for the cell counts in table n_Hp−1, we conclude that the bounds in Eq. 5 are also the tightest bounds for the counts in table n_K.

Buzzigoli and Giusti (18) proposed an algorithm, which they call the shuttle algorithm, that alternates iteratively between upper and lower bounds, and that when applied to decomposable structures appears to indirectly exploit the structure implicit in Theorem 6. But it does not achieve the sharp bounds in as computationally efficient fashion as we can by using the formula directly.

At this point we succeeded in developing formulas for the sharpest bounds when the sets of indices defining the known marginals define a connected decomposable graph. However, the connectivity assumption is not by any means essential. We can extend the definition of decomposable graphs to include disconnected graphs with all their connected components decomposable. By employing the maximum cardinality search algorithm sequentially for every connected component, we can determine the set of cliques of such a disconnected decomposable graph as the union of the sets of cliques associated with the connected components. The corresponding set of separators can be obtained in the same way.

The next result provides an explicit formula for the generalized Fréchet bounds associated with an arbitrary decomposable graphical structure. We emphasize that the generalized Fréchet bounds are sharp bounds given the information that we assumed we have.

Theorem 7. (i) Let 𝒢 = (K, E) be a decomposable graph. Then the following inequality is true:

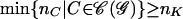8

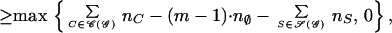where 𝒞(𝒢) is the set of cliques of 𝒢, 𝒮(𝒢) is the set of separators associated with 𝒞(𝒢), and m is the number of connected components of the graph 𝒢. (ii) The above inequality provides sharp bounds for the cells in the contingency table n_K given the marginals {n_C|C ∈ 𝒞(𝒢)}.

Proof: We apply Lemma 6 for each connected component of 𝒢, then Theorem 5 to combine the resulting inequalities. All the bounds for the marginal tables involved are tight, hence the bounds in Eq. 8 will also be tight.

4. Reducible Graphs

By exploiting decomposability in an appropriate manner, we have been able to find sharp bounds for cell counts when some special sets of marginals characterizing decomposable loglinear models are given. It is natural to ask ourselves whether we could develop similar results for reducible graphs, as described in refs. 16 and 19.

Definition 6: A graph 𝒢 is reducible if 𝒢 admits a proper decomposition, otherwise 𝒢 is a prime graph.

Any complete graph is prime, whereas any disconnected graph is reducible. By definition, the atoms contained in a derived system of a graph are all prime. Given that every reducible graph 𝒢 might have several derived systems (16), we would like to be able to isolate one of them that could fully characterize the input graph 𝒢.

Definition 7: A subgraph 𝒢(A) is a maximal prime (mp-) subgraph of 𝒢, if 𝒢(A) is prime and 𝒢(B) is reducible for all B with A ⊂ B ⊆ V.

The set of mp-subgraphs of 𝒢 is contained in every derived system of 𝒢. Moreover, the set of mp-subgraphs of 𝒢 is always a derived system of 𝒢 (19), and consequently it is the unique minimal derived system. If 𝒢 is decomposable, the mp-subgraphs of 𝒢 are complete, hence the unique minimal derived system of a decomposable graph contains only its cliques (19).

Section 2 describes a procedure for finding the mp-subgraphs of a decomposable graph. The order in which the MCS algorithm identifies the mp-subgraphs along with the set of separators are needed to reconstruct the original graph from its minimal derived system. We would like to devise a similar decomposition algorithm for the more general case when the input graph is reducible, not necessarily decomposable.

It is easy to see that any decomposable graph is reducible, but the converse is not true, as we will prove next. Gavril (20) introduced the family of clique separable graphs in the following recursive manner.

Definition 8: 𝒢 = (V, E) is a clique-separable graph if (i) 𝒢 is a Type 1 or Type 2 graph, or (ii) 𝒢 has a separator C, and the leaves of 𝒢 produced by C are clique-separable graphs.

A graph 𝒢 is a Type 1 graph if its vertex set can be partitioned in two subsets V₁, V₂, such that |V₁| ≥ 3, 𝒢(V₁) is a connected bipartite graph, V₂ is complete, and every vertex of V₁ is adjacent to every vertex of V₂. In addition, 𝒢 = (V, E) is a Type 2 graph if there exists a partition V₁, … , V_k of V, such that V₁, … , V_k are independent sets in 𝒢, and every vertex of V_i is adjacent to every vertex of V_j, for i ≠ j.

By definition, any decomposable graph is also clique-separable, and any clique-separable graph is reducible. However, Type 2 graphs are clique-separable but obviously they are not necessarily decomposable, hence the class of reducible graphs is much richer than the class of decomposable graphs.

Tarjan (16) has proposed an O(nm)-time method for decomposing a reducible graph with n vertices and m edges. The downside of Tarjan's algorithm is that it generates an arbitrary derived system of prime graphs. Leimer (19) has adapted this algorithm so that the input graph is decomposed exactly into its mp-subgraphs. A reducible graph 𝒢 might have several separators that would induce a proper decomposition of 𝒢. If we could select the “right” separator at every step of the decomposition procedure, then we would manage to avoid including nonmaximal prime subgraphs in the final derived system.

Definition 9: [Leimer (19).] Let (A₁, A₂, A₃) be a decomposition of 𝒢 into the subgraphs 𝒢′ = 𝒢(A₁ ∪ A₂) and 𝒢" = 𝒢(A₂ ∪ A₃). If the mp-subgraphs of 𝒢′ and 𝒢" are pairwise different and if they are all mp-subgraphs of 𝒢, then (A₁, A₂, A₃) is called a P-decomposition and A₂ is called a P-separator.

Moreover, a decomposition (A₁, A₂, A₃) is a P-decomposition if and only if 𝒢(A₂) is not an mp-subgraph of any of the graphs 𝒢(A₁ ∪ A₂) and 𝒢(A₂ ∪ A₃) (19). If a graph has a decomposition, then it also has a P-decomposition. Therefore it is possible to decompose a reducible graph by means of P-separators, and in this case we are guaranteed to obtain the minimal derived system of maximal prime subgraphs.

Assume that we somehow managed to order the vertex sets of the mp-subgraphs 𝒢(V₁), … , 𝒢(V_k) of a graph 𝒢 in a perfect sequence. By using the same notations as before, we have the following result.

Theorem 8. [Leimer (19).] (H_k−1\S_k, S_k, R_k) is a P-decomposition of 𝒢 into 𝒢′ = 𝒢(H_k−1) and the prime graph 𝒢" = 𝒢(V_k). 𝒢(V₁), … , 𝒢(V_k−1) are the mp-subgraphs of 𝒢′ and V₁, … , V_k−1 is a perfect sequence of sets in 𝒢′.

Theorem 8 can be applied recursively to generate a derived system of 𝒢. Because the decompositions performed along the way are P-decompositions, the minimal derived system of 𝒢 will be generated.

We are interested in the existence of a perfect sequence of the mp-subgraphs of a graph only for proving the correctness of our results. The ordering of the mp-subgraphs is not relevant when computing the generalized Fréchet bounds, and consequently, in an actual implementation of our algorithms, we would only have to obtain the set 𝒱(𝒢) of mp-subgraphs along with the corresponding sequence 𝒮(𝒢) of separators.

Leimer (19) has suggested an alternative approach that would allow us accomplish this task by taking advantage of the MCS algorithm we previously presented. The first step would be to transform a connected reducible graph 𝒢 = (V, E) in a closely related decomposable graph by adding extra edges in E. We would like to keep the number of edges added to a minimum, so that a minimal decomposable graph is derived.

Definition 10: [Tarjan (16).] Let π be an ordering of the vertex set of a graph 𝒢 = (V, E). The fill-in F_π caused by the ordering π is the set of edges:

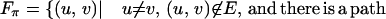9

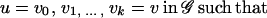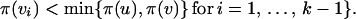The graph 𝒢_π = (V, E ∪ F_π) is called the minimal fill-in graph if there does not exist a numbering π′ of 𝒢 with F_π′ ⊂ F_π. It can be shown that the fill-in graph 𝒢_π is decomposable for any numbering π of 𝒢. Algorithms for generating a minimal fill-in graph can be found in Ohtsuki and Cheung (21).

The second step consists of applying the maximum cardinality search algorithm to the minimal fill-in graph 𝒢_π associated with the input graph 𝒢. However, we will not employ the “original” maximum cardinality search algorithm. We will make use instead of an expanded version (17) that can find the set 𝒞(𝒢_π) = {C₁, C₂, … , C_r} of cliques of 𝒢_π along with the associated system 𝒮(𝒢_π) = {S₂, … , S_r} of separators by constructing a tree 𝒯_π = (𝒞(𝒢_π), ℰ_τπ). We assume that the sequence C₁, C₂, … , C_r is perfect. For every clique C_j, j > 1, we choose a “parent” clique C_i, i < j such that S_j ⊂ C_i, and include the edge (C_j, C_i) in ℰ_τπ. Because the parent of a clique might not be unique, more than one tree could be constructed on 𝒞(𝒢_π). Moreover, C₁ cannot have a parent and will be called the root of the tree. This is certainly not a restriction because every clique can be C₁ in some perfect sequence. The tree 𝒯_π generated by the MCS algorithm has the additional property that S ⊂ V is a minimal vertex separator of 𝒢_π if and only if S = C_j ∩ C_i for some edge (C_j, C_i) ∈ ℰ_τπ. Consequently, the set of separators associated with 𝒞(𝒢_π) will be given by 𝒮(𝒢_π) = {C_i ∩ C_j : (C_i, C_j) ∈ ℰ_τπ}. Then S ∈ 𝒮(𝒢_π) will also be a minimal separator in 𝒢 if S is complete in 𝒢.

The last step of the algorithm is presented below in pseudo-code. With every clique C ∈ 𝒞(𝒢_π), we associate a vertex set Δ(C). Initially we set Δ(C) ← C for all C ∈ 𝒞(𝒢_π). A clique C is terminal in 𝒯_π if C is not the parent of any other clique, i.e., if there is no such C′ with (C′, C) ∈ ℰ_τπ.

• •  𝒱(𝒢) ← ∅; 𝒮(𝒢) ← ∅;

• •  while ℰ_τπ ≠ ∅ do

1.

Identify a terminal clique C_j;

2.

𝒞(𝒢_π) ← 𝒞(𝒢_π)\{C_j};

3.

ℰ_τπ ← ℰ_τπ\{(C_j, C_i)};

4.

if C_j ∩ C_i is complete in 𝒢 then

𝒱(𝒢) ← 𝒱(𝒢) ∪ {Δ(C_j)};

𝒮(𝒢) ← 𝒮(𝒢) ∪ {C_j ∩ C_i};

else

Δ(C_i) ← Δ(C_i) ∪ Δ(C_j);

end while

• •  𝒱(𝒢) ← 𝒱(𝒢) ∪ {Δ(C₁)}.

This algorithm provides a computational approach for identifying the maximal prime subgraphs 𝒱(𝒢) of an arbitrary connected reducible graph 𝒢, along with its associated system 𝒮(𝒢) of separators. We utilize it in the following section.

5. Generalized Fréchet Bounds for Reducible Loglinear Models

In Section 3, we showed that we can explicitly determine the tightest bounds for the cells in a table of counts n_K given a set of marginals when that set of marginals define a decomposable graph 𝒢 = (K, E). When the graph associated with some set of marginals is not decomposable, we have no choice but to employ iterative methods such as the simplex algorithm. Generally speaking, linear programming methods are computationally expensive and might yield results that are very difficult to interpret, so they should be used with care. The natural question to ask is whether we could reduce the computational effort needed to determine the tightest bounds by employing the same strategy used for decomposable graphs, i.e., decompositions of graphs by means of complete separators.

To be more specific, assume we want to determine the bounds for a contingency table n_K given the marginals n_C1, n_C2, … , n_Cp. In addition, C₁, C₂, … , C_p are the cliques of the graph 𝒢 = (K, E). 𝒢 is assumed to be reducible, not necessarily decomposable. Let V₁, V₂, … , V_q be the maximal prime subgraphs of 𝒢 ordered in a perfect sequence, and let S₂, S₃, … , S_q be the sequence of separators associated with V₁, V₂, … , V_q. Suppose we could compute tight bounds for the marginals n_V1, n_V2, … , n_Vq given n_C1, n_C2, … , n_Cp, i.e., we know n_V1^U, n_V2^U, … , n_Vq^U and n_V1^L, n_V2^L, … , n_Vq^L such that

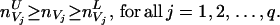10

Because S_j is complete in 𝒢, there will exist an i ∈ {1, 2, … , p} such that S_j ⊆ C_i. Hence n_Sj is a marginal table of n_Ci. Therefore, once we fixed n_C1, n_C2, … , n_Cp, the marginals n_S2, … , n_Sq will also be fixed. With the notations introduced above, we develop explicit formulas for sharp bounds for the cells counts in table n_K.

Theorem 9. Suppose 𝒢 = (K, E) is connected and reducible. The tightest bounds for the cell counts in the contingency table n_K given the marginals n_C1, n_C2, … , n_Cp are given by

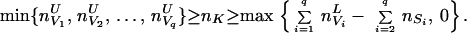11

Proof: Because V₁, V₂, … , V_q is a derived system of 𝒢, we could think about the subgraphs 𝒢(V₁), … , 𝒢(V_q) as being the cliques of a connected decomposable graph 𝒢′. Moreover, S₂, … , S_q will be the system of separators associated with V₁, V₂, … , V_q in 𝒢′. By employing Theorem 6, we obtain

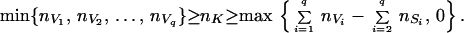12

Then Eq. 11 follows immediately from Eqs. 12 and 10. The bounds for the marginal tables involved are all sharp, hence the bounds in Eq. 11 will also be tight.

Once again, we will point out the link with maximum likelihood estimation in loglinear models. We define a reducible loglinear model as one for which the corresponding minimal sufficient statistics are margins that characterize the maximal prime subgraphs of a reducible graph. Assuming that one has calculated maximum likelihood estimates for the loglinear models determined by the independence graphs 𝒢(V₁),𝒢(V₂), … ,𝒢(V_q), then one can easily derive explicit formulae for the maximum likelihood estimates in the reducible loglinear model with independence graph 𝒢. By employing results of Lauritzen (14), we find that

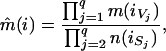13

(c.f. the special cases given in ref. 12).

We continue the analogy with the decomposable case we previously discussed by considering a reducible disconnected graph. We know how to find the maximal prime subgraphs (along with the corresponding sequence of separators) successively for every connected component. The set of mp-subgraphs for the complete graph is defined as the union of the sets of mp-subgraphs of every connected component. The set of separators can be determined in a similar way. We are now ready for the main result of the paper. However, we are going to postpone presenting it for the moment.

5.1. Example.

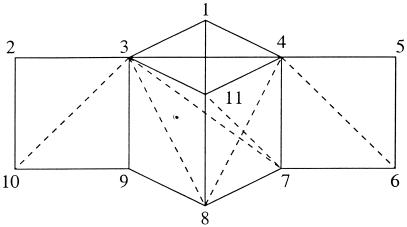
To clarify the concepts and the results presented so far, we use an example similar to the one proposed by Tarjan (16). The graph 𝒢 in Fig. 1 has 11 vertices and 17 edges represented by continuous lines. We want to determine the mp-subgraphs of 𝒢. The edge {3, 9} is a separator for {1, 3, 4, 5, 6, 7, 8, 9, 11} and {2, 3, 9, 10}. The latter is a four-cycle, hence cannot be further decomposed, and because it is not a complete, 𝒢 cannot be decomposable. Similarly, {4, 7} separates {1, 3, 4, 7, 8, 9, 11} and {4, 5, 6, 7}. Again, the latter is a four-cycle, hence it is a prime subgraph. Now the clique {1, 3, 4, 11} is separated from {3, 4, 7, 8, 9, 11} by the triangle {3, 4, 11}. The subgraph 𝒢({3, 4, 7, 8, 9, 11}) does not have a separator, therefore we have finished decomposing 𝒢. The set of mp-subgraphs is 𝒱(𝒢) = {{2, 3, 9, 10}, {4, 5, 6, 7}, {1, 3, 4, 11}, {3, 4, 7, 8, 9, 11}}, whereas the sequence of separators is 𝒮(𝒢) = {{3, 9}, {4, 7}, {3, 4, 11}}.

Figure 1.

A graph and its minimal fill-in set of edges.

Next we illustrate how to obtain 𝒱(𝒢) and 𝒮(𝒢) by using the decomposition algorithm from Section 4. The minimal fill-in graph 𝒢_π is obtained by adding six new edges to 𝒢. These edges are represented with dotted lines in Fig. 1. The cliques of 𝒢_π are C₁ = {1, 3, 4, 11}, C₂ = {3, 4, 7, 11}, C₃ = {3, 7, 8, 11}, C₄ = {4, 6, 7}, C₅ = {4, 5, 6}, C₆ = {3, 8, 9}, C₇ = {3, 9, 10}, and C₈ = {2, 3, 10}. The tree 𝒯_π constructed by the MCS algorithm on 𝒞(𝒢_π) = {C₁, C₂, … , C₈} has edges

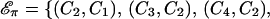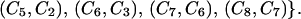We proceed to the last step of the algorithm. The clique C₅ is terminal, but C₅ ∩ C₄ = {4, 6} is not complete in 𝒢, hence we set Δ(C₄) = {4, 5, 6, 7}. After eliminating C₅ from the clique tree, C₄ becomes terminal. Because S₁ = C₄ ∩ C₂ = {4, 7} is complete in 𝒢, we identified the first mp-subgraph V₁ = Δ(C₄) and its associated separator S₁. We eliminate C₄ from 𝒯_π, and the algorithm proceeds in a similar manner.

The set 𝒞(𝒢) of cliques is essentially the set of edges of 𝒢 from which we take out {1, 3}, {1, 4}, {1, 11}, {4, 11}, {3, 4}, {3, 11}, and then add {1, 3, 4, 11}. Assume we want to determine upper and lower bounds for a cross-classification n_K with 11 dimensions. Given the marginal tables {n_C : C ∈ 𝒞(𝒢)}, it is possible to compute sharp bounds for the marginal tables corresponding to the mp-subgraph of 𝒢. Because the separators in 𝒮(𝒢) are subsets of some cliques, they will define marginals of some tables in {n_C : C ∈ 𝒞(𝒢)}, hence it is possible to make use of Theorem 9 to calculate sharp bounds for the cell counts in table n_K.

5.2. Bounds for Reducible Loglinear Models.

The foregoing example indicates that Theorem 9 is applicable in a more general setting than the one we previously suggested. Determining bounds for cell counts in a cross-classification given the marginals defined by the set of cliques is equivalent to the problem of calculating the MLEs of a graphical loglinear model. The minimal sufficient statistics of a graphical log-linear model define a graph, and the cliques of this graph are exactly the minimal sufficient statistics. If the minimal sufficient statistics are not cliques in the associated graph, the model is not graphical.

For example, suppose we have a table n_K corresponding to the graph in Fig. 1. Now assume we don't have access to the marginal n_[1,3,4,11], but instead we do know n_[1,3], n_[1,4], n_[1,11] and also n_[3,4,11]. These marginals no longer correspond to the cliques of a graph. Yet it is still possible to compute sharp bounds for the marginals determined by the mp-subgraphs of 𝒢, and then to combine these bounds using Theorem 9 to obtain tight bounds for the complete table n_K.

To be more explicit, suppose we are provided with a set of marginals n_D1, n_D2, … , n_Dr that define a graph 𝒢 = (K, E). We have K = 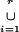D_i and E = {(u, v) : {u, v} ⊂ D_j, for some j = 1, … , r}. The mp-subgraphs of 𝒢 are 𝒱(𝒢) = {V₁, V₂, … , V_q}, whereas the corresponding sequence of separators is 𝒮(𝒢) = {S₂, … , S_q}. We emphasize that (D_j)_j do not have to be the set of cliques of 𝒢 and that 𝒢 is not necessarily connected. However, we need to impose one additional constraint, namely for every S_i, there is a j ∈ {1, 2, … , r} such that S_i ⊂ D_j. This implies that the marginals n_S2, … , n_Sq will be fixed once n_D1, n_D2, … , n_Dr are fixed. With these notations, we announce a more general version of Theorem 9.

Theorem 10. Let 𝒢 = (K, E) be a reducible graph. Then the following inequality is true:

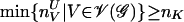14

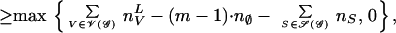where 𝒱(𝒢) is the set of maximal prime subgraphs of 𝒢, 𝒮(𝒢) is the set of separators associated with 𝒱(𝒢), and m is the number of connected components of the graph 𝒢. In addition, {n_V^U|V ∈ 𝒱(𝒢)} and {n_V^L|V ∈ 𝒱(𝒢)} are the tightest upper and lower bounds for the marginal tables {n_V|V ∈ 𝒱(𝒢)}, respectively.

Proof: Because 𝒱(𝒢) is a derived system of the graph 𝒢, we can think about the subgraphs {𝒢(V)|V ∈ 𝒱(𝒢)} as being the derived system of cliques of a graph 𝒢′. In this case 𝒮(𝒢) will be the set of separators associated with 𝒱(𝒢) in 𝒢′, hence Eq. 14 follows immediately from Eq. 8.

6. Conclusions

The results described in this paper are part of a programmatic effort to understand and operationalize the computation of upper and lower bounds for non-negative entries in cross-classifications subject to a set of marginal constraints. From research on mass transportation and other versions of this problem, we know that the computational problem is typically characterized as being NP-complete, and thus we cannot expect to find a simple approach that will deal effectively with the bound calculation problem, especially in high dimensions. Thus, instead of attempting to utilize a general computational approach such as linear programming or the simplex algorithm (22) or network methods (23, 24), we have opted to exploit the structure of the underlying probability structures based on statistical and mathematical theory.

In particular, we have worked with the graphical representation of probability distributions subject to conditional independence relationships and utilized existing results on decomposable graphs to derive explicit bounds for cell entries when the given marginals correspond to the maximal cliques of a decomposable graph. Our approach was motivated by the more specialized results for decomposable loglinear models for tables of counts where the minimal sufficient statistics are marginals and the expected cell values are explicit functions of them.

We also have extended the bound results from the decomposable to the reducible case, and this allows us to exploit other results and computational approaches for bounds applied to subtables corresponding to the reducible components that are not cliques. The results of Section 5 focus on the cases where tables still have a graphical representation representing conditional independence relationships. But there are many other probability structures where we would like to be able to calculate bounds but are not graphical in this sense. For example, a k-dimensional probability distribution given all (k − 1)-dimensional marginals is not graphical, but we are still able to exploit statistical theory to compute upper and lower bounds in this case. Fienberg (11) outlines an approach for doing this in the k = 3 case, and Dobra and Fienberg (25) provide detailed algorithms for k > 3. Suppose that one wants to compute bounds for a cross-classification that has a structure similar to that in the reducible case, except that we replace a d-dimensional nonclique by a d-dimensional probability distribution given all (d − 1)-dimensional marginals. Then we can combine the bounds computed for this nongraphical distribution using the reducible representation of Section 5.

Cox (26) raised a very interesting question, namely, whether one can actually construct a feasible table with a prescribed set of possibly overlapping margins. The solution to the feasibility problem is straightforward if the marginal tables constitute the maximal cliques of a decomposable graph. In this case, the explicit formulas for calculating the MLEs of the associated loglinear model provide us with a feasible table. In addition, if the set of margins are the minimal sufficient statistics of a reducible loglinear model, Eq. 13 tells us how to construct a feasible table given a consistent set of marginals associated with the maximal prime subgraphs of the induced independence graph. Therefore, the results substantially reduce the computational effort needed to solve the feasibility problem by reducing it to a number of smaller and hopefully easier-to-solve problems.

These results represent only a small part of those needed to allow the computation of upper and lower bounds for high-dimensional cross-classifications of the sort that arise in disclosure limitation and other practical problems.

Abbreviations

c.d.f.

cumulative distribution function

PEO

perfect elimination ordering

MCS

maximum cardinality search

MLE

maximum likelihood estimate

mp-

maximal prime

Appendix

We give below a proof of Theorem 4.

Proof: Let a₁ = {1, … , p} and a₂ = {q, … , m} where 1 ≤ q ≤ p ≤ m. Let n_i1⁰ … i_m⁰ be an arbitrary cell in the table n_a1∪a2. To avoid confusion, the marginals n_a1, n_a2, n_a1∩a2 will be denoted by A¹, A², A¹², respectively. The following equalities should hold:

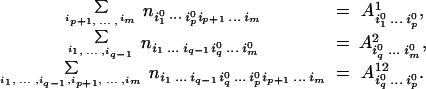Consider the sums:

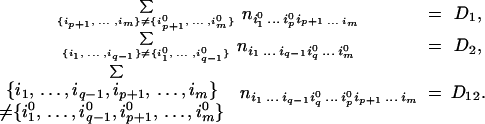With these notations, we have

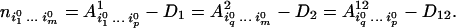15

We can write D₁₂ = D₁ + D₂ + D₃, where

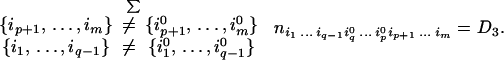It follows that

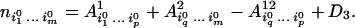16

Clearly D₁, D₂, D₃ ≥ 0. From Eqs. 15 and 16, we deduce

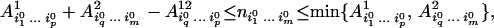which concludes the proof.