How important are entropic contributions to enzyme catalysis?

Abstract

The idea that enzymes accelerate their reactions by entropic effects has played a major role in many prominent proposals about the origin of enzyme catalysis. This idea implies that the binding to an enzyme active site freezes the motion of the reacting fragments and eliminates their entropic contributions, (ΔS_cat^‡)′, to the activation energy. It is also implied that the binding entropy is equal to the activation entropy, (ΔS_w^‡)′, of the corresponding solution reaction. It is, however, difficult to examine this idea by experimental approaches. The present paper defines the entropic proposal in a rigorous way and develops a computer simulation approach that determines (ΔS^‡)′. This approach allows us to evaluate the differences between (ΔS^‡)′ of an enzymatic reaction and of the corresponding reference reaction in solution. Our approach is used in a study of the entropic contribution to the catalytic reaction of subtilisin. It is found that this contribution is much smaller than previously thought. This result is due to the following: (i) Many of the motions that are free in the reactants state of the reference solution reaction are also free at the transition state. (ii) The binding to the enzyme does not completely freeze the motion of the reacting fragments so that (ΔS^‡)′ in the enzymes is not zero. (iii) The binding entropy is not necessarily equal to (ΔS_w^‡)′.

Many prominent proposals (e.g., see refs. 1 and 2) and textbooks that consider biochemical systems (e.g., refs. 3 and 4) invoke entropic contributions as major factors in enzyme catalysis. These proposals, which are intuitively very appealing (e.g., see ref. 5), have assumed that the large configurational space available for the reacting fragments in water would be drastically restricted in the enzyme active site. It has been thus deduced that this should lead to large entropic contributions to the difference between the activation barrier in the enzyme and in the reference solution reaction. However, the validity of these proposals is far from being obvious (6, 7). For example, the very influential proposal introduced by Page and Jencks (1) reflects the assumption that the formation of the transition state in a bimolecular reaction in solution involves complete loss of three translational and three rotational degrees of freedom. However, two or more of these degrees of freedom are usually almost free in the transition state (see below). More serious is the implicit assumption that the entropic contribution to catalysis is given approximately by the negative of the binding entropy (see below). Other problems with simple estimates of the entropic contribution will be mentioned in the next section.

The main stumbling block for determining the validity of the entropic proposal is the absence of direct experimental information about the corresponding contribution of the reacting fragments to the activation entropy in the enzyme and in solution. In this respect it is interesting to note the recent analysis of cytidine deaminase by Wolfenden and co-workers (8). This study found that the entropies of activation in the enzyme and in water are very similar and that the overall catalysis is due to enthalpic effects. Interestingly, it was found that the activation entropy in water and the binding entropy are significant. However, it is not known what parts of these entropies are associated with the restriction of the motion of the reacting fragments and what parts are associated with solvation entropies.

Intramolecular cyclizations of model compounds were used as “proofs” that enzyme catalysis involves large entropic contributions (e.g., ref. 2). However, recent simulations of Bruice and co-workers (9) indicated that the rate acceleration associated with smaller ring size is not necessarily associated with entropic contributions. Furthermore, our studies (6) have challenged the direct relevance of these model compounds to enzyme catalysis.

The entropic contributions to enzyme catalysis can be determined in principle by computer simulation approaches, but the development of the proper method is far from trivial because of enormous convergence problems. Nevertheless, some encouraging progress has been made in studies of related problems. This includes the progress in evaluating solvation entropies (10) and in evaluating binding entropies (11). Yet, no attempt has been made in evaluating activation entropies by simulation approaches. Note in this respect that the recent interesting studies reported by Kollman and co-workers (12, 13) have not provided ways for consistent evaluation of activation entropies or binding entropies.† At any rate, it is clear that calculations of activation entropies in enzyme active sites and in the corresponding reference solution reactions are essential for a quantitative understanding of entropic contributions to enzyme catalysis (6).

The present work introduces an approach for evaluating the contribution from the motion of the reacting fragments to the activation entropies of enzymatic reactions and uses this approach in assessing the importance of entropic effects to enzyme catalysis.

Defining the Problem

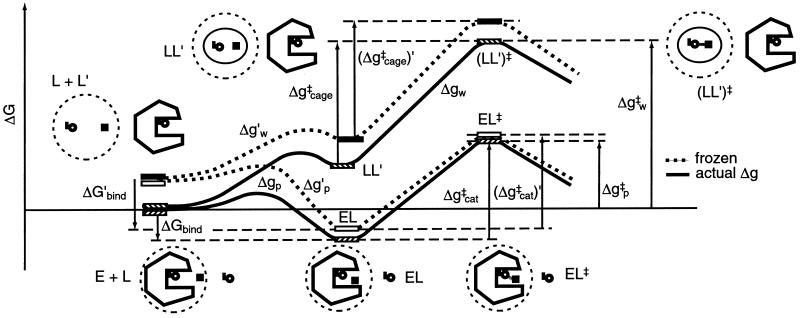
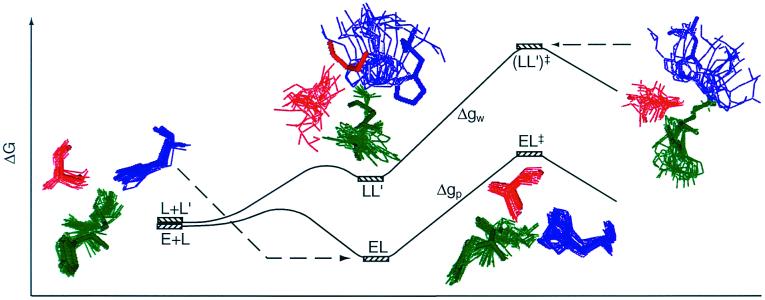
To evaluate the importance of a specific contribution to catalysis it is essential to define the relevant thermodynamic cycle. This is particularly important in considering entropy contributions, whose definition and estimates involve in many cases incomplete thermodynamic cycles. The starting point of the present study is the free energy diagram of Fig. 1. This diagram compares the activation free energies Δg_p^‡ and Δg_w^‡ for a given reaction in a protein (p) and in water (w) and also compares the corresponding activation free energies (Δg^‡)′ when the reacting fragments are frozen (see below). As shown in Fig. 1, Δg_p^‡ is given by ΔG_bind + Δg_cat^‡, and thus reflects the binding energy ΔG_bind, whose nature is quite clear and is not involved in the catalytic puzzle (see also ref. 7). The main open question is the relationship between Δg_cat^‡ (which corresponds to k_cat) and the activation barrier of the reaction in water, Δg_w^‡. It is also interesting, although not essential, to compare Δg_cat^‡ to the barrier Δg_cage^‡ obtained by correcting Δg_w^‡ for the free energy associated with bringing the reactants to a solvent cage, where each of the (n − 1) reactants (from an overall n reactants) is at a relatively small distance from the central reactant (the nth reactant). At this distance the interaction with the central ligand is small and each reactant moves almost freely. In a case of small reactant molecules we can define the cage volume by requiring that the central reactant will have a standard 1 M concentration and the other reactants will have a concentration that is less than or equal to 55 M. In other words, taking into account the free energy contribution associated with confining a molecule that occupies a molar volume v₀ (1,660 ų at 300 K) (6) to a volume v_cage we may write

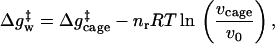1

where Δg_w^‡ is the activation barrier in solution at a standard state concentration, and v_cage is the volume of the solvent cage, which is taken to be larger than 1,660 ų/55. Here n_r is the number of the ligands that become bound to the substrate at the transition state. This number is equal to (n − 1) in a fully concerted reaction, whereas it reduces to 2 in a stepwise reaction. The seemingly arbitrary definition of Δg_cage^‡ (which will not change our final evaluation of Δg_w^‡) reflects two considerations. First, early workers (e.g., refs. 1 and 2) implied or stated correctly that the free energy price associated with bringing the reacting fragments to a distance of a weak interaction is given by simple concentration considerations and is given approximately by −RTln 55. Thus the real puzzle was (and is) why Δg_cat^‡ is much smaller than the barrier obtained by considering the small volume correction to Δg_w^‡. And second, comparing Δg_cat^‡ and Δg_cage^‡ provides conceptually and computationally closely related quantities, the activation barrier in the enzyme active site and the activation barrier in a solvent cage, where the reactants are in close proximity. It should also be stated that our cage system is very different than the system used by Jencks and others, where the reactants in solution are frozen in a space similar to that available in the enzyme active site. This traditional definition makes it rather difficult to define a simple thermodynamics cycle for the comparison of Δg_cat^‡ and Δg_w^‡.

Figure 1.

Comparison of the free energy profiles Δg for a given reaction in a protein (Δg_p^‡) and in water (Δg_w^‡). The figure represents these free energy profiles in the absence (Δg) and presence (Δg′) of constraints for the movement of the reacting fragments. Note that Δg_p^‡ corresponds approximately to k_cat/K_m (it is given by ΔG_bind + Δg_cat^‡). The figure uses the notation of L for ligand rather than S for substrate to prevent confusion with the symbol S used for entropy.

Now, the major question one has to address is related to the entropy contribution associated with the restriction of the motions of the reacting fragments by the enzyme active site, relative to the corresponding contribution in the solvent cage. This effect does not include the contribution from the change in the entropy of the environment (e.g., solvent), since the early proposals were defined clearly in terms of the substrate entropy rather than the entropy of the surroundings. Thus, we are not addressing here the change in the so called cratic entropy (11) that includes the overall change in entropy upon binding, but rather the changes in the contribution, ΔS′, from the configurational space of the reacting fragments. The factors involved in the catalytic effect of ΔS′ are illustrated in Fig. 1. The figure compares the free energy profile Δg_w and the corresponding (Δg_w)′, obtained by freezing the degrees of freedom of the substrate that are perpendicular to the reaction coordinate. Similarly, the figure compares Δg_p and (Δg_p)′. As clarified above, we are interested in the contribution of ΔS′ to (Δg_cat^‡ − Δg_w^‡) or to (Δg_cat^‡ − Δg_cage^‡). Using Fig. 1, we obtain:

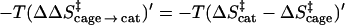2

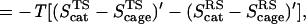where RS and TS, respectively, designate the corresponding contributions from the reactants state and transition state in the protein or in the solvent cage. Of course we can also obtain easily (ΔΔS_{w → cat}^‡)′.

The first point to note from Eq. 2 is that one must consider the entropy contributions from the RS and TS both in the enzyme and in the solvent cage. To the best of our knowledge all previous estimates, with the exception of ref. 6, have not considered both the RS and TS and have not defined the catalytic effect in a rigorous way. Probably the most systematic attempt was made by Jencks (page 720 of ref. 2), who defined the problem by considering the hypothetical case with identical ΔH^‡ in the enzyme and in water. He assumed that ΔS_cat^‡ is zero and estimated ΔS_w^‡ by considering the process of bringing the reactants in water to the same frozen position that they have in the enzyme. Furthermore, the TS in water was also assumed to be frozen in the same way. Basically, it was assumed implicitly that S_w^TS = S_p^TS ≃ 0, and that the activation entropy in water can be approximated by the binding entropy of the protein. In other words, Jencks as well as most other workers implied that we can freeze the motion of the reactants in solution in the same restricted space available for these motions in the protein and that the free energy that should be invested in this configurational restriction is the entropic contribution to the difference between Δg_w^‡ and Δg_cat^‡. This (apparently incorrect assumption) can be formulated by the more accurate terms of Fig. 1 as:

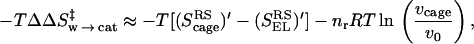3

where S_cage^RS is the hypothetical frozen RS of the solution reaction. Here we subtract −T(S_EL^RS)′ from −T(S_cage^RS)′, because the substrate is not completely frozen in the protein. However, as seen from Fig. 1, this is a problematic assumption in large part because of the fact that S′ is not zero at the TS of the solution reaction. Or in other words because of the fact that many of the motions that are free in the RS in the solvent cage are also free in the TS in this cage.

To further clarify this point we can consider the hypothetical case when all the motions are frozen in the enzyme in both the RS and the TS (so that (ΔS_cat^‡)′ = 0) and all the motions are free in solution in the RS and in the TS (so that (ΔS_cage^‡)′ = 0). In this case we have (ΔΔS_{cage → cat}^‡)′ = 0 and ΔΔS_{w → cat}^‡ ≃ 8 entropy units. On the other hand, if we only consider the RS in water and in the protein site we may obtain a large (ΔΔS_{cage → cat}^‡)′.

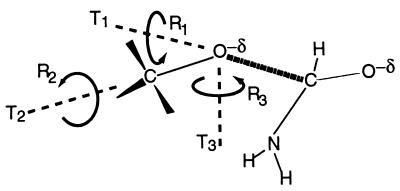
Finally, it might be useful to comment on the inherent assumption of Page and Jencks (1) that the formation of a bimolecular complex involves the loss of three translational and three rotational degrees of freedom. This model was based on considering two spherical fragments. However, in actual formation of the cage complex we still retain between one to three of these degrees of freedom. For example, in the attack of a CH₃O⁻ group on an amide we do not lose the rotation around the C–O axis, and two of the translational motions of the CH₃ group are almost free (see Fig. 2).

Figure 2.

Schematic representation of the translational and rotational degrees of freedom in the nucleophilic attack of a CH₃O⁻ group on an amide. The figure depicts only the transition state, but the corresponding RS picture can be obtained by stretching the C ⋯ O distance. For simplicity we place the rotation axes on the attacking oxygen. As illustrated, R₂ remains a free rotation in the TS, R₁ becomes a low-frequency torsional oscillator, while T₁, T₂, and T₃ become bending motions.

The above discussion should not be viewed as a list of problems with previous estimates but as a reminder that the problem of evaluating entropic contributions to enzyme catalysis has not been solved. It seems to us that this challenging problem cannot be resolved without some form of computer simulation approach.

Methods

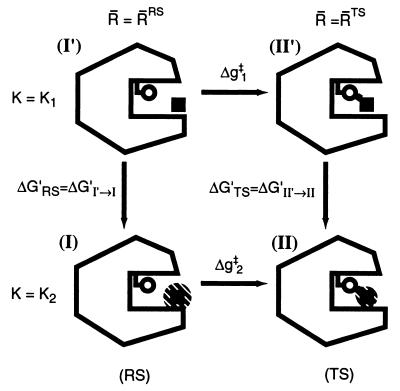
As clarified in the previous section, our task is to evaluate the entropic contribution of the reacting fragments to ΔΔg_{w → cat}^‡. To do so we developed a restrain–release approach (RRA) which is related in some aspects to the approach developed by Hermans and co-workers (11) for studies of binding entropies. Our approach has been described in detail in ref. 14, where it was used for studies of the activation entropy of amide hydrolysis in water. Here we discuss only the main points of this approach, which is based in the thermodynamic cycle of Fig. 3. This cycle considers the activation free energy, Δg^‡, for the given reaction in the given system (the enzyme or solvent cage) in two limiting conditions. In the first case (the upper part of the cycle) the reacting system is transformed from the RS to the TS along a (unspecified) reaction coordinate while a restraint is used to minimize the available configuration space in the direction perpendicular to this reaction coordinate. In this case the activation free energy, Δg₁^‡, does not involve the entropic contributions of the solute, (ΔS₁^‡)′ = 0, since the corresponding motions are frozen. In the second case (the lower part of the cycle) the reacting fragments are free to move so that the corresponding activation barrier, Δg₂^‡, includes the entropic contributions of the solute. Thus, the difference between the two Δg^‡ values gives the desired −T(ΔS^‡)′. The possible enthalpic contribution can be minimized with the proper selection of the initial conditions for the simulation (see below). Using the thermodynamic cycle, we can obtain (Δg₂^‡ − Δg₁^‡) from ΔG′_RS and ΔG′_TS. This can be done by imposing a strong position restraint in both states I′ and II′ and evaluating the corresponding free energies ΔG′_RS = ΔG′_{I′ → I} and ΔG′_TS = ΔG′_{II′ → II} associated with the release of these constraints (see below). In this way we can write

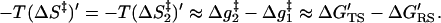4

The enthalpic contribution to ΔG′ will be discussed below. Now, the practical evaluation of the ΔG′ values involves the introduction of restrain potentials of the form

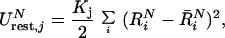5

where i runs over the substrate coordinates and R̄^N are reference coordinates that define the minimum of the restrain potential (see below) at the given state (N = I, or N = II for the RS and TS, respectively). The reference coordinates R̄^N are evaluated by running molecular dynamics (MD) relaxation runs on the RS and the TS with K = 0 (see also below). Different conditions for the MD runs can generate different values of R̄^N, and the selection of the optimal coordinates as well as the implications of this selection will be discussed below.

Figure 3.

Thermodynamic cycle used for the evaluation of the entropy contribution to the activation free energy of the reaction. The fragments are fixed in (I′) and (II′) and allowed to move (as indicated by the shaded area) in (I) and (II). The same circle is also used for the reaction in water (see figure 1 of ref. 14).

The constraint release free energies (ΔG′) are evaluated by a free energy perturbation (FEP) approach, where we use a mapping potential of the form

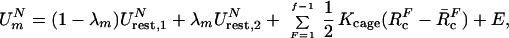6

where λ_m is changed from 0 to 1 in n increments and E designates the unconstrained potential surface of the system. R_c^F is the distance between an atom of the central fragment F = 1 and an atom of the Fth fragment. The K_cage term is needed to prevent divergence when K₂ → 0. The value of R_c^F is chosen in a way that the Fth fragment can move freely around the central ligand while still being close to this ligand. K_cage is chosen so that v_cage will correspond to 55 M concentration.

Now we can write

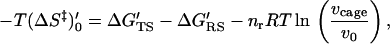7

where (ΔS^‡)′₀ designates the entropic contribution in the 1 M standard state and the last term in Eq. 7 gives the free energy associated with the change of the cage volume from v_cage to v₀.

The results of the thermodynamic cycle of Fig. 3 depend in principle on the chosen R̄ and may involve, in addition to ΔS′, contributions from the enthalpy of the reacting fragments and from their solvation by the surrounding environment. To extract ΔS′ from the total ΔG′ we have to formulate the cycle of Fig. 3 in a more rigorous way. This is done by the approach presented in the appendix of ref. 14, which considers the free energy ΔG′(R̄) of the system as a function of the restraint coordinates of the solute. Using the quadratic expansion of this potential of mean force (PMF) and evaluating the corresponding contributions has established that ΔG′(R̄₀) (where R̄ = R̄₀ is the R̄ that minimizes the PMF) gives the desired ΔS′ without additional enthalpic contributions. Although the minimization of this PMF is impractical at present, we can estimate the exact result for ΔS′ by performing several random simulations with different R̄^N and selecting the one that gives the minimum value of |ΔG′|. In other words, we can use the lower bound (14)

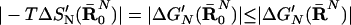8

and estimate the value of |−TΔS′_N(R̄₀^N)| by finding the smallest |ΔG′_N(R̄^N)|. With ΔS′_N(R̄₀^N) we can obtain (ΔS^‡)′ by using (see appendix of ref. 14)

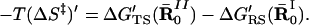9

Eqs. 8 and 9 and the treatment in ref. 14 outline the formal requirements for rigorous evaluation of (ΔS^‡)′. However, because the evaluation of ΔS′ with random R̄ is very expensive we confine the present study to the evaluation of the values of ΔS′_N at several values of R̄, obtained by running MD simulations on the corresponding potential surface with zero restrain potential. We then use the R̄ values that give the lowest |ΔG′| in evaluating ΔS′.

To evaluate activation entropies it is essential to perform long MD or Monte Carlo (MC) samplings of the corresponding potential surfaces. Such potential surfaces should provide a reliable representation of the relevant reactions and also allow for sufficient sampling at a reasonable computer time. At present, it is impossible to satisfy this requirement with a high-level ab initio potential surface because this would require an enormous amount of computer time. Approaches that obtain the solute potential surface by fitting it to the corresponding ab initio gas phase surface and then consider the interaction of the gas phase charges with the solvent can provide reasonable estimates of the solvent contribution to the activation entropies in reactions that involve relatively small charge separation. However, it is hard to use such approaches for evaluation of the solute contribution to the activation entropy. This is particularly true when the solute is constrained to move along the gas phase reaction coordinate (e.g. ref. 15) and the substrate fluctuations in the directions perpendicular to the reaction coordinate are not taken into account. In our opinion the optimal strategy is to use empirical valence bond (EVB) potential surfaces (6). These surfaces can be fitted to reliable ab initio surfaces and to relevant experimental information and then to provide a consistent and reliable description of the solution reaction. This description includes a consistent incorporation of the solvent in the solute Hamiltonian, consistent description of the motion of the reacting fragments, and an analytical representation of the given surface that allows one to perform very extensive MD simulations. The EVB method was described extensively elsewhere (6) and has been used by many other groups (see ref. 14 and references therein). Thus we will mention here only several crucial points.

The EVB approach describes the reacting system by mixing several diabatic states that represent the reactants, products, and crucial intermediates. The energy of each diabatic state i (ɛ_i) is described by a force-field like potential function and the off-diagonal terms (H_ij) are described by simple analytical functions. The parameters in the ɛ_i and H_ij values are determined by using both experimental information and ab initio calculations. To perform our RRA calculations we have to confine the reactants to the specified region of the potential surface (e.g., RS and TS). Here we limit our discussion to the common case where the system is represented by three diabatic states. In the case of a stepwise mechanism it is reasonable to use (14)

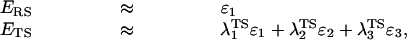10

where the λs are the values of the FEP mapping parameters that bring the system to the TS region.

Results and Discussion

The present study considered as a test case the catalytic reaction of subtilisin. The potential surface of this reaction was evaluated by the previously developed EVB potential surface (16). The three resonance structures that roughly correspond to the three states in the mechanism of action of subtilisin (reactants, intermediate, and products) are described in figure 6 of ref. 16. The parameters for this EVB potential energy surface are similar to those used in ref. 16. The rate-limiting step of the reaction is the attack of the O_γ of Ser-221 on the carbonyl carbon of the substrate. Thus, the entropy calculations have been done considering the RS and the TS, whose ground state energies E_g^RS and E_g^TS were obtained, respectively, by using Eq. 10 and λ_m^TS = (0.0, 0.4, 0.6), as described above. Within this model the system is divided into several regions (see ref. 17 for a detailed discussion). The reaction region (region I) is surrounded by a protein + solvent sphere (region II, with a radius r_a) that is surrounded by external regions with special polarization and position boundary conditions (17). The protein atoms in these external regions are held by strong constraints. All the calculations were done with the enzymix package (17).

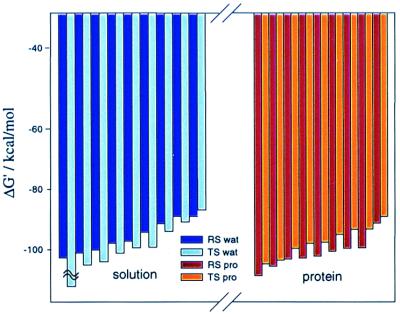
The simulations involved the release of the position restrains in 5 FEP stages, changing K_j from 100 to 30, from 30 to 3, from 3 to 0.3, from 0.3 to 0.03, and from 0.03 to 0.003, where all the values of K are given in kcal/(mol⋅Ų). Each of these stages involved 11 mapping steps, and each of these steps followed an initial relaxation of the given system. The total simulation time for these five stages was 1,100 ps for both the water and protein runs. K_cage was taken as 0.4 kcal/mol (which corresponds to v_cage of 1,660/55 ų) and R_c^F were taken as 3.0 and 3.1 for the O_γ–C distance and the O_γ–N_ɛ2 distance, respectively. To generate the different R̄s needed for obtaining the optimal ΔG′ we use different relaxation runs with different constraints on region I and II. Overall, we generated nine different R̄s for the RS and nine for the TS. Next we performed RRA calculations for the different R̄s. Table 1 gives the results of the simulations with r_a = 14 Å. Additionally, we depict in Fig. 4 the values of the ΔG′ in an increasing order. As is apparent from the figure, we obtain a reasonable convergence in the selection of minimal values of |ΔG′|. The differences between ΔG′_TS and ΔG′_RS (plus the volume correction of Eq. 7) yield the final values of −T(ΔS^‡)′₀ that are given in the last column of Table 1. As seen from the table, the entropic contribution of the reacting fragments is not so different in the enzyme and in the solvent cage. More specifically, the simulations give a difference of (2.5 − (2.6 + 2.4)) = −2.5 for −T((ΔS_cat^‡)′ − (ΔS_w^‡)′). This estimate already includes the effect of K_cage (≈−2.4 kcal/mol). Note that in this volume correction n_r is taken as 1, because the solution reaction has been found to involve a stepwise mechanism (18). The present estimate of −T(ΔΔS^‡)′ involves a few kcal/mol error and is likely to change with a more complete convergence (see footnote §). The main point is, however, that |T(ΔΔS^‡)′₀| is much smaller than previously thought. The reason for this exciting finding is rationalized in Fig. 5, which shows snapshots of the last FEP frame of the simulation where K changes from 0.003 to 0.0003 kcal/(mol·Å²). As seen in the figure the degree of movement for each system (cage and protein) is similar in RS and in TS. If this conclusion will hold in other systems, which is likely (see below), then entropic effects do not contribute in a major way to the reduction of Δg_cat^‡.

Table 1.

ΔG′ (in kcal/mol) for the hydrolysis of the Tyr-Gly dipeptide in water and in the active site of subtilisin

System	ΔG′RS			ΔG′TS			−T(ΔS‡)′0
Water	−91.9,	−103.7,	−89.6,	−95.7,	−87.0,	−99.3,	2.6 + 2.4
	−90.0,	−98.6,	−93.8,	−134.1,	−91.7,	−101.7,
	−98.9,	−96.0,	−100.2	−105.0,	−99.2,	−102.7,
Protein	−102.3,	−103.8,	−113.0,	−103.5,	−98.6,	−96.6,	2.5
	−100.6,	−100.1,	−92.9,	−90.4,	−95.9,	−100.0,
	−103.0,	−106.6,	−103.4	−95.4,	−98.4,	−105.3

The calculations were done with r_a = 14 Å, and the results reported were evaluated with different R̄ values, obtained by the nine relaxation runs described in the text. The underlined values in boldface are the lowest absolute values obtained in each case and thus the optimal estimate of the corresponding −TΔS′ (see text). −T(ΔS^‡)′₀ is obtained from Eq. 7 with the optimal ΔG′ and a 2.4 kcal/mol volume correction for the water case. 

Figure 4.

ΔG′ values at different initial conditions: in water (Left), and in the protein site (Right). Black and gray bars correspond to ΔG′ in the reactant state and in the transition state, respectively. The figure represents the results of Table 1 for the simulations with region II radius of 14 Å, and the calculated values have been plotted in decreasing order of |ΔG′|.

Figure 5.

Superposition of snapshots of the trajectories propagated at the last point of the FEP protocol where K changes from 0.003 to 0.0003 kcal/mol for the RS and the TS of the water surface (solid curve) and the protein surface (dashed curve). The free energy profiles are given in a schematic way. The 20 snapshots for each system were taken at equal time space during 50-ps runs. L designates ligand as in Fig. 1.

Concluding Remarks

This work examined the importance of the entropic contribution of the reacting fragments in enzyme catalysis. This was done by developing a computer simulation method capable of evaluating (ΔS^‡)′ in enzyme and in solution, and using this method in calculations of (ΔΔS^‡)′ for the catalytic reaction of subtilisin. It was found that (ΔΔS^‡)′ is much smaller than commonly assumed and should not be approximated by T(ΔS_bind)′.

Our finding of a rather small (ΔΔS^‡)′ is consistent with a study (19) of nucleophilic displacements on phenyl esters in water. It was shown that dividing −TΔS_w^‡ by the kinetic order of the reaction (first, second, and third) gives 4 to 5 kcal/mol. This finding was interpreted to indicate that bringing each species to the TS does not involve more than 5 kcal/mol entropic contribution (19, 20). Since the solvent contributions (14) to both −TΔS_w^‡ and −T(ΔS_cat^‡)′ are positive, |−T(ΔΔS^‡)′| should be quite small.

Obviously one may wonder what is the origin for the difference between the present results and previous estimates. One of the reasons that were alluded to in the Introduction is the fact that many of the motions that are free at the RS are also free at the TS. Another important factor is associated with the fact that (ΔS_cat^‡)′ is not zero in the protein. Finally, as was noted in the Introduction (see Fig. 2), the early estimate of Page and Jencks (1) provides an overestimate of the entropy loss upon binding, where some rotational and translational motions remain free even in the solvent cage.

The importance of entropic effects in enzyme catalysis has been frequently deduced from the trend in the rates of intramolecular cyclization reaction, where the formation of smaller rings is associated with larger rate constants. Recent studies (9) have suggested, however, that this trend may be due to RS destabilization enthalpic effects. This does not mean that such enthalpic effects play a significant role in enzyme catalysis. In fact, it is not clear that intramolecular cyclization reactions are directly relevant to most enzymatic reactions (6). At any rate, the present approach may provide a powerful way of exploring RS enthalpic contributions. That is, if instead of using the optimal R̄ for both the enzyme and the solution reaction we use the R̄ of the enzyme reaction for the water reaction we should be able to evaluate the enthalpic contribution associated with the distortion of the structure of the substrate by the enzyme.

The present work is an attempt to obtain a quantitative estimate of the entropic contribution of the reacting fragments to enzyme catalysis. The finding that these contributions are much smaller than previous estimates as well as simulations of many enzymatic reactions is consistent with the view that electrostatic effects are the major factor in enzyme catalysis. As argued repeatedly before (e.g., refs. 6 and 7), the electrostatic effects are due to the preorganized polar environment of the enzyme active site and to the relatively small reorganization free energy of this environment. The ability of the enzyme to provide smaller reorganization free energy than water does involves, of course, some entropic effects. These effects are not, however, the entropic effects introduced in all early proposals of entropic contributions to enzyme catalysis. That is, previous proposals were based on the assumption that the enzyme decreases the entropy of the reacting fragments. On the other hand, our electrostatic proposal involves the reduction of the reorganization free energy (which includes some entropic contributions) by folding the enzyme to its catalytic configuration. This contribution of the enzyme–enzyme rather than the enzyme–substrate interaction is the most important factor in enzyme catalysis.

Abbreviations

EVB

empirical valence bond

MD

molecular dynamics

FEP

free energy perturbation

RS

reactant state

TS

transition state

RRA

restrain–release approach