Replication by a single DNA polymerase of a stretched single-stranded DNA

Abstract

A new approach to the study of DNA/protein interactions has been opened through the recent advances in the manipulation of single DNA molecules. These allow the behavior of individual molecular motors to be studied under load and compared with bulk measurements. One example of such a motor is the DNA polymerase, which replicates DNA. We measured the replication rate by a single enzyme of a stretched single strand of DNA. The marked difference between the elasticity of single- and double-stranded DNA allows for the monitoring of replication in real time. We have found that the rate of replication depends strongly on the stretching force applied to the template. In particular, by varying the load we determined that the biochemical steps limiting replication are coupled to movement. The replication rate increases at low forces, decreases at forces greater than 4 pN, and ceases when the single-stranded DNA substrate is under a load greater than ≈20 pN. The decay of the replication rate follows an Arrhenius law and indicates that multiple bases on the template strand are involved in the rate-limiting step of each cycle. This observation is consistent with the induced-fit mechanism for error detection during replication.

DNA polymerases (DNAPs) are responsible for the synthesis of a new DNA strand on a single-stranded (ss) template (1). They play a key role in the replication, repair, and proofreading of DNA by catalyzing the addition of a complementary dNTP to the 3′ end of the growing strand. The rate of replication of a DNAP, its fidelity, and its processivity (its uninterrupted association with the template) are related to the enzyme's function in vivo.

Typically, fast and processive enzymes are associated with quick replication. The simplest example of such an enzyme is T7 DNAP coupled to Escherichia coli thioredoxin (2), which may incorporate several thousand nucleotides at a rate of ≈300 bases per second (b/s) without dissociating from its template (3). A mutant of T7 DNAP (Sequenase), lacking 28 amino acids and the associated exonuclease activity, retains these properties (4) and was studied in this report.

Slower, less processive enzymes are usually responsible for repair (and have an auxiliary role in replication). Possessing 5′→3′ as well as 3′→5′ exonuclease activity, DNAP I from E. coli is representative of this group of DNAPs (1). The 5′→3′ exonuclease activity is situated on the smaller fragment of the tri-domain enzyme and may be eliminated by proteolysis. The remaining large (Klenow) fragment, which was also studied here, has a low processivity (1−100 bases) and a slow replication rate (15 b/s) (5). As with T7 DNAP, the 3′→5′ exonuclease activity of the Klenow fragment may be abolished by a mutation without significantly altering its polymerase activity (6, 7).

Although T7 DNAP and E. coli DNAP I have different functions and replication rates, they are structurally similar: they resemble a right hand with the active polymerization site in the palm, the dNTP-binding region in the fingers, and the processivity factor on the thumb (8). The rate-limiting step in replication is thought to involve a conformational change (4, 5), from an open to a closed conformation of the fingers, where the bound dNTP is matched to its homologous base on the template (9).

Despite this similarity, recent structural and kinetic studies suggest that the different characteristics of these enzymes (rate, fidelity, and processivity) depend on subtle conformational differences within the enzyme/template complex (10, 11). X-ray and footprinting studies have shown that different polymerases make subtly different contacts with the minor groove of the double-stranded (ds) DNA (2, 12). T7 DNAP appears to interact with three bases, whereas the Klenow fragment has been reported to contact four bases. Whether these differences have direct functional implications, for example in the fidelity or processivity of the enzymes, is not known.

In this paper we will address this issue by using single molecule experiments to study the replication on a template under tension of two functionally different polymerases: Sequenase and Klenow. We shall see that the aforementioned structural differences appear to correlate with movement of the enzymes during the rate-limiting step of their cycle. That motion is coupled to a displacement of at least n bases on the template (n = 2 for Sequenase and n = 4 for Klenow). The requirement, at the rate-limiting step of replication, of complementarity between the last n bases of the two strands provides a mechanism for error detection during replication (should one of these n bases not match).

Single molecule experiments have been used to study a number of molecular motors [kinesin (13, 14), myosin (15), F1-ATPase (16), RNA polymerase (17), topoisomerase II (18), and DNAP (19)]. In these studies, the variation of the enzymatic rate with load has been instrumental in providing a unique insight into biochemical steps that are coupled to movement. It is important to note that even though single turnover resolution was not always achievable, it was nevertheless possible to gain insight into the constituent steps of the enzymatic cycle. For example, with RNA polymerase the fact that the transcription rate is constant at low template tension indicates that the rate-limiting biochemical step does not generate movement (17). In the case of topoisomerase II, the exponential decay with load of the rate of supercoil removal suggests that the rate-limiting step in the reaction involves a movement of the enzyme by about 1 nm, presumably during closure of the DNA gate (18). Finally, recent experiments (19), although lacking single base resolution, were able to show from an analysis of the rate vs. force dependence that T7 DNAP organizes two template bases in the polymerization site during each catalytic cycle (19). In the experiments reported here we use the distinct mechanical properties of ssDNA and dsDNA to follow the replication by a single DNAP of a ssDNA template under external load. While we have obtained independently the same results as Wuite et al. [that Sequenase organizes two template bases (19)], the different rate vs. force dependence for Klenow DNAP suggests that this enzyme has to organize at least four template bases during each catalytic cycle.

Materials and Methods

DNA and Sample.

dsDNA [17-kb pXΔII a gift of J.-F. Allemand, Ecole Normale Supérieure (20); 11-kb charomid a gift of O. Hyrien, Ecole Normale Supérieure (21)] was differentially end-labeled by ligating DNA fragments (about 800 bp long), multiply labeled with either biotin or digoxigenin, to its extremities (22). This DNA construct was denatured by heating in 2 mM NaOH at 100°C for 5 min. The resulting ssDNA was immediately bound to streptavidin-coated superparamagnetic beads (4.5 μm; Dynal, Oslo) by a 5-min incubation in PBS. The beads were then diluted 20-fold in the incubation buffer [10 mM phosphate buffer (pH 8)/0.1% Tween 20/0.1 mg/ml fish sperm DNA/1 mM NaN₃] and incubated for about 20 min on an anti-digoxigenin-coated square glass capillary (1 × 1 × 50 mm; Vitrocom, Rockaway, NJ) placed on top of a 63× immersion objective of an inverted microscope. The unbound beads were washed by flushing the capillary tube with a few milliliters of incubation buffer.

Force and Extension Measurement.

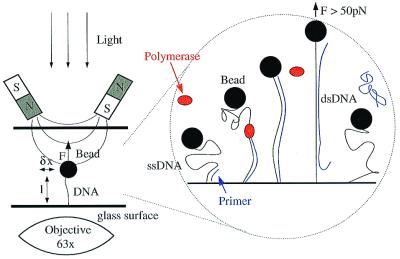
A strong magnetic field gradient was generated on the sample by focusing the field (≈0.5 tesla) of two small NdFeB magnets with appropriate pole pieces separated by ≈1.5 mm. By varying the distance between the magnets and the capillary tube, a force of up to 100 pN can be exerted on the magnetic bead and its tethered DNA molecule (22) (see Fig. 1). The molecule's extension, 〈z〉 = l, is measured by real-time video analysis of the bead's image (22). Mechanical drifts of the microscope are corrected by the simultaneous differential tracking of two beads: the bead attached to the DNA and an identical reference bead immobilized on the surface. To measure the force, F, we monitor the transverse Brownian fluctuations 〈δx²〉 of the DNA-tethered bead and use the equipartition theorem to determine F = k_BT l/〈δx²〉 (23). To replicate the ssDNA, an 18-base primer specific to a single locus of the DNA template (pXΔII) is first hybridized to the template, and DNAP is then injected. Because ssDNA and dsDNA have different extensions for a given force, measuring the length of the chain allows for monitoring of the synthesis of the second strand in real time. Once replication is complete, the newly synthesized strand may be displaced from the duplex by stretching the DNA with a force F > 50 pN [in 10 mM phosphate buffer (pH 8)]. The force vs. extension curve after ejection of the new strand matches the initial curve before replication (see Fig. 2b). This step breaks the link between the bead and the surface about 50% of the time.

Figure 1.

Sketch of the experimental system and the replication experiment. (Left) The setup, consisting of a ssDNA bound at one extremity to a small magnetic bead and at the other to the surface of a capillary tube. Small permanent magnets pull on the bead with a force F < 100 pN. F is monitored through the fluctuations δx² of the bead. The extension l of the molecule is monitored in real time. (Right) The steps during the synthesis of the complementary DNA strand. For small stretching force, the ssDNA has a small extension. Hybridization of a specific primer near one end of the molecule allows the polymerase to start replication. The progression of the polymerase leads to an increase of the molecule's extension. When the entire molecule has been replicated, we increase the stretching force to 50 pN for a short time. This destabilizes the newly synthesized strand, which unpairs from the template and diffuses in the buffer. The ssDNA molecule is ready for a new run of replication.

Figure 2.

Force vs. extension curves F(l) for ssDNA. (a) Comparison of the elasticity of a charomid and pXΔII ssDNA in the polymerization buffer and the known dsDNA elasticity curve (WLC, worm-like chain). Length was normalized with respect to the dsDNA extension. (The error in this normalization is ≈10% for the charomid and ≈5% for pXΔII.) Notice that the elastic behavior of these two molecules is different below ≈ 10 pN, consistent with the difference in G+C content of the molecules which influences the stability of secondary structures at low forces. (b) Determination of the extent of polymerization. Extension vs. force curves in polymerization buffer for dsDNA l_ds(F) (⋄), ssDNA l_ss(F) before replication (○), partially replicated DNA (□), and ssDNA (+) produced by briefly pulling on the replicated template with a force F > 50 pN to eject the newly synthesized strand. The full line is the superposition l_p(F) = pl_ds(F) + (1 − p)l_ss(F) with percentage replication p = 0.7 which fits the measured points (□) remarkably well.

High Stringency Primer Hybridization.

A primer (5′-GTA CCG TTA AGT CAG GTG-3′; MWG-Biotech France) was chosen at 1,807 bases from the end of the pXΔII template. Hybridization was performed on a 6 pN-loaded template for 15 min in the polymerization buffer [10 mM Tris (pH 8)/5 mM MgCl₂/25 mM KCl/100 μM of each dNTP/1 mg/ml BSA/1 μM primer]. Note that hybridization on a template under tension (like hybridization at high temperature) selects against noncomplementary sequences and controls the stringency of hybridization. The capillary was then rinsed with 10 mM Tris (pH 8)/100 mM NaCl, after which Klenow fragment (Roche Molecular Biochemicals), Klenow fragment minus exo3′→5′ (New England Biolabs), or sequenase Version 2.0 (Amersham Pharmacia) was injected at ≈20 nM in the polymerization buffer. The hybridization stringency was assessed by using a nonspecific primer on the same molecule and checking that it did not initiate polymerization under the same conditions.

Low Stringency Hybridization.

Highly stringent priming requires time-consuming preparations on a template under tension. Because the ssDNA construct is fragile and the full replication of the 17-kb pXΔII DNA by Klenow may last up to 6 h (see Fig. 3a), a quicker protocol on a shorter molecule (an 11-kb charomid) with lower stringency of priming was generally used to determine the force dependence of the replication rate for Klenow. A primer (5′-ATG GAG GCG GAT AAA GTT-3′; MWG-Biotech France) was chosen at 1,000 bases from the end of the template. The hybridization was performed for 5 min in 10 mM Tris (pH 8)/5 mM MgCl₂/25 mM KCl/100 μM each dNTP/1 μM primer. Klenow was then injected without rinsing at a concentration of ≈10 nM. As the tension on the template was not high enough to ensure that no nonspecific priming occurred, it cannot be excluded that polymerization started at different sites. However we did check in a few cases that results in these conditions did not differ significantly from those in high stringency conditions. All experiments were performed at 25 ± 1°C.

Figure 3.

Time evolution of the replication on a pXΔII ssDNA under a tension of 1 pN (specific priming). (a) Number of bases N(t) replicated by Klenow minus exo3′→5′ as a function of time in two successive replication runs on the same template. Notice that pauses in replication occur at different positions in successive runs. The dots represents the raw data after low-pass filtering at ≈1 Hz. The extension of the DNA is converted into the number of added nucleotides N(t) as explained in the text. The full lines are polygon fits (see Materials and Methods) with an average time duration of 100 s. (b) N(t) for Sequenase in two runs on different molecules. The full lines are polygon fits with an average time duration of 10 s.

Data Processing.

Determination of the replication rate requires measuring the elongation of the molecule vs. time: l(t). The number of nucleotides added is then given by: N(t) = [l(t) − l(0)]N_tot/Δl(F), where N_tot is the total number of replicated bases and Δl(F) is the total change in extension at force F. The Brownian fluctuations of the DNA's extension σ₁ = 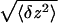(which vary between 70 nm at 1 pN and 25 nm at 19 pN) limit the resolution in a single replication run (to 500 bases at 1 pN and 175 bases at 19 pN). The absolute size of the replication domain (or the absolute position of the replication complex along the molecule) may be determined with an accuracy of δn ≈ 1,000 bases, set by the precision (ɛ ≈ 0.3 μm) in the absolute length measurements: δn/N_tot = ɛ/Δl(F).

To determine the local rate of replication v(t), the average over the fluctuations in extension must be determined. Because filtering l(t) would smear out pauses in replication and thus yield lower average replication rates, we chose to fit the elongation signal l(t) (0 < t < t_max) to a polygon of M vertices (see Fig. 4a). The rationale for that fit is that l(t) is a broken line: replication bursts correspond to rising segments, pauses to horizontal ones. The number of vertices M = t_max/Δt was chosen to tolerate for an error smaller than 5% on the average rate (Δt = 10 s for Sequenase, 100 s for Klenow). The coordinates {t_i, l_i} of the polygon vertices were adjusted to minimize the fitting error (χ² test) (24) while maintaining t_i − t_i−1 ≈ Δt. The average number of bases replicated between two adjacent vertices of the polygon is then Δn_i = (l_i − l_i−1)N_tot/Δl(F) and the replication rate is: v(t_i) = Δn_i/(t_i − t_i−1). In this paper the mean and standard deviations of measured replication rates are given with respect to the number of individual molecules studied K and the number of independent measurements J. The error in the estimate of the mean rate σ_〈v〉 (at a given force) has two contributions: (i) a statistical error equal to the spread in the measured rates σ_v divided by 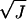(24) and (ii) a systematic error σ_s resulting from the precision ɛ = 0.3 μm in the conversion from measured lengths to number of replicated bases: σ_s = 〈v〉ɛ/Δl(F). (This contribution is significant near the point where the extensions of ss- and dsDNA are equal.) Thus σ_〈v〉² = σ_v²/J + σ_s². (For the case of F = 10 pN described in Fig. 4, we have 〈v〉 = 121 b/s, σ_v = 31 b/s, J = 12, σ_s = 13b/s, thus σ_〈v〉 = 16 b/s.)

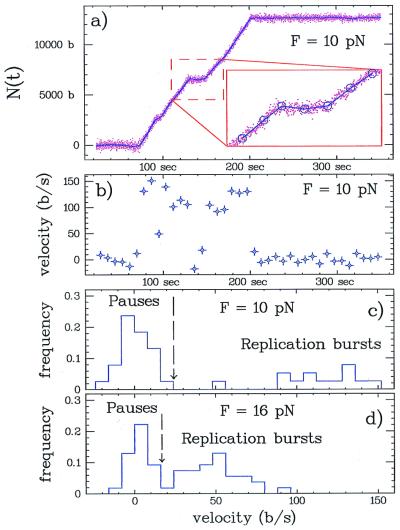
Figure 4.

Measurement of the replication rate by Sequenase. (a) Time course of replication after high stringency hybridization on pXΔII at 10 pN. The raw data (dots) were fitted by a polygon with M = 40 vertices (shown as ○ in the Inset) as explained in Materials and Methods. (b) Instantaneous replication rate (velocity) as determined from the slope of the polygon segments drawn in a. (c) The histogram of the velocities determined in b displays two peaks. The peak at v = 0 ± 8.6 b/s results from pauses in replication. The broad peak with positive rates results from replication bursts. The boundary between the two peaks is shown by the dashed line at thrice the standard deviation of the pauses peak, i.e., 26 b/s. (d) The instantaneous replication rate histogram at 16 pN (M = 56). The peak of replication bursts has a mean value of ≈50 b/s. The boundary between the pauses and replication peaks is at 20 b/s, lower than in c because of the smaller noise at this higher stretching force.

The replication rate versus force curves were fitted to the model described in the following discussion by using a Levenberg–Marquardt algorithm (24) to determine the two parameters of the model (v₀, n). Because of the nonlinearity of the fit and the likelihood that the probability distribution of the parameters of the model is non-Gaussian, we have used a Monte-Carlo bootstrap method (24) to estimate the error in the fitted parameters and the associated confidence levels.

Results and Discussion

The experiment is conducted in a small capillary placed above an oil immersion microscope objective. The inlet and outlet of the capillary are connected to small reservoirs permitting buffer changes. A ssDNA molecule is anchored at one end to the bottom surface of the capillary and at the other to a small magnetic bead. As shown in Fig. 1, magnets are placed just above the capillary and generate a vertical force F. Motion of the magnets on a millimeter scale in the vertical (z) direction is used to control the force F applied on the molecule. At a fixed magnet position, the force F is constant. A computer image analysis is used to track the bead's position x, y, z in real time. From these data we determine the extension of the molecule l and the stretching force F. The replication experiment is carried out by monitoring the extension l of the molecule while the polymerase is converting ssDNA to dsDNA.

The Difference in the Elastic Behavior of ssDNA and dsDNA Allows for Monitoring of the Activity of DNAP.

The extension vs. force curve for ssDNA in the polymerization buffer, l_ss(F), is shown in Fig. 2 and compared with the analogous curve for dsDNA, l_ds(F). The elasticity of the latter is well described by the worm-like chain model of a polymer with a persistence length ξ = 50 nm (22, 25, 26). ssDNA exhibits a more complex behavior dependent on the strength of the secondary structures formed. Thus l_ss(F) cannot be described by a simple statistical model, such as the modified freely jointed chain model proposed by Smith et al. (27). Although this model describes the experimental results obtained in 10 mM phosphate buffer at high forces reasonably well, it fails at low forces. Indeed, below 10 pN the elastic behavior of pXΔII (70% A+T) is significantly different from that of a charomid (50% A+T), as is evident in Fig. 2a. The crossing point between ssDNA and dsDNA, where l_ds = l_ss, is at F = 3.2 pN for a pXΔII DNA and at F = 4.9 pN for a charomid. Because the extension–force curves l_ss(F) for ssDNA exhibit a complex variation with ionic strength, the measurement of this curve in the enzymatic assay conditions is required before the study of replication.

Measurement of the Activity of a Single DNAP.

The replication of ssDNA into dsDNA as a function of time is measured by monitoring the relative change in either extension or rigidity of the system. Thus the extension vs. force behavior l_p(F) of a molecule which has been partially replicated, p being the percentage of replication, is intermediate between that of ssDNA l_ss(F) and dsDNA l_ds(F) as shown in Fig. 2b for p = 70%. A partially replicated molecule is well described by the superposition of dsDNA and ssDNA elastic behavior: l_p(F) = pl_ds(F) + (1 − p)l_ss(F). Inverting this expression allows us to determine the percentage of replication p(t) = (l(t) − l_ss(F))/Δl(F) with Δl(F) = l_ds(F) − l_ss(F). The number of incorporated nucleotides at time t, N(t), is then the total number of nucleotides times the percentage of replication N(t) = p(t)N_tot. When l_ds(F) ≈ l_ss(F) at F = 4 pN, the molecule's extension does not change noticeably on replication. However, as ssDNA is replicated into stiffer dsDNA, replication can still be measured by monitoring the increase in the system stiffness, ∂l_p(F)/∂z [which is inversely proportional to the longitudinal fluctuations of the bead (22): 〈δz²〉].

By using random primers, the ability of the enzymes to replicate a 17-kb ssDNA was checked. Initiating synthesis at arbitrary sites, the replication rate v(t) for Sequenase exhibited bursts of replication followed by pauses. Complete replication was confirmed by checking that the replicated molecule could be fit by a worm-like chain model with the persistence length of 50 nm expected for dsDNA. At the end of the replication cycle the newly synthesized strand may sometimes be ejected without rupturing the bonds binding the bead to the surface (see Figs. 1 and 2) by briefly pulling on the molecule with a force F > 50 pN (28). Complete ejection was confirmed by verifying that the force vs. extension curve of the molecule after this brief pull was identical to the one before replication, see Fig. 2. On hybridization of a new primer and addition of DNAP, a new round of replication can then be initiated on the same DNA molecule.

As previously reported (4), the polymerization rate is sequence-dependent. To verify this in our experiments, we set a unique starting point for replication by annealing a specific primer to the template under stringent hybridization conditions. Because of the intrinsic thermal fluctuations (see Materials and Methods) at low force or for a low processivity enzyme, it is difficult to ensure that the same polymerase is monitored throughout the experiment. However, with specific priming we can be certain that only a single enzyme is active at a given time. For the pXΔII template we achieved specific priming of an 18-base primer at 1,807 bases from the 3′ end by stretching the template with a 6-pN force (in 5 mM MgCl₂ and 25 mM KCl ionic conditions).

A striking feature of the replication by a single enzyme is the existence of long pauses of varying duration (up to hours) and position along the molecule. Fig. 3a shows the number of replicated nucleotides, N(t), in two successive replication runs on the same template under a 1-pN load for Klenow minus exo3′→5′. Notice that replication on the same molecule doesn't always pause at the same sites. Hence these long pauses are apparently not due to defective bases on the template (e.g., depurination). We believe that they are a result of fluctuating hairpins, which may act as road blocks for the proceeding polymerase (29). Although the duration of pauses was significantly shorter for Sequenase [hundreds of seconds; see Fig. 3b], than for Klenow (thousands of seconds), we do not have sufficient data to analyze these events more precisely, especially because pauses are comparable in duration to the lifetime of polymerase activity.

Fig. 3b shows N(t) for Sequenase under a 1-pN load, whereas Fig. 4a corresponds to a 10-pN stretching force. In all cases, N(t) displays a typical broken line shape with some added noise. We thus fitted N(t) to a broken line with slightly varying time intervals, corresponding to an average integration time Δt. While significantly reducing the noise, this algorithm allows for abrupt changes in replication rate as observed between burst to pause phases. The choice of the integration time, Δt, is a tradeoff between a large Δt ensuring low noise in the replication rate and a small Δt allowing for the observation of short pauses. As F is increased, the experimental noise decreases and consequently Δt can be reduced. The replication rates in Fig. 4b are obtained by plotting the slope of the fitted segments in Fig. 4a with Δt = 8 s. The histogram of these replication rates (at 10 pN) is shown in Fig. 4c. A peak is observed at v = 0 with a standard deviation σ₀ = 8.6 b/s corresponding to the pauses and end of replication. A second broad peak corresponds to the replication rates during burst activity. To measure the polymerase properties, we disregard pauses by considering only rates greater than 3σ₀ (here 26 b/s). σ₀ decreases when the template stretching force F is increased as may be seen in the histogram in Fig. 4d obtained at F = 16 pN.

To compare with bulk experiments, we have measured the mean replication rate at low forces (F ≈ 1 pN). As expected, the mean replication rate of Sequenase (210 ± 10 b/s; K = 3, J = 46) is higher than for Klenow (6 ± 1 b/s; K = 9, J = 114) and Klenow minus exo3′→5′ (7 ± 1 b/s; K = 4, J = 50). The value for Sequenase is consistent with its known activity (3). For Klenow, slightly higher values of 15 b/s have been reported in single turn-over experiments (5). These data are, however, similar to the maximal replication rates measured here: 13.5 ± 1.5 b/s for Klenow at a load of F ≈ 4 pN. This medium stretching force might help to suppress the possible secondary structures in the rather long ssDNA molecule used here.

Force Dependence of the Replication Rate.

To study the force dependence of the replication rate v(F), we used a high stringency hybridization protocol with Sequenase. The replication rates measured at 1 and 2 pN with low stringency priming were slightly lower than with the high stringency protocol (see Fig. 5c) which may be attributed to the different (G+C richer) template used.

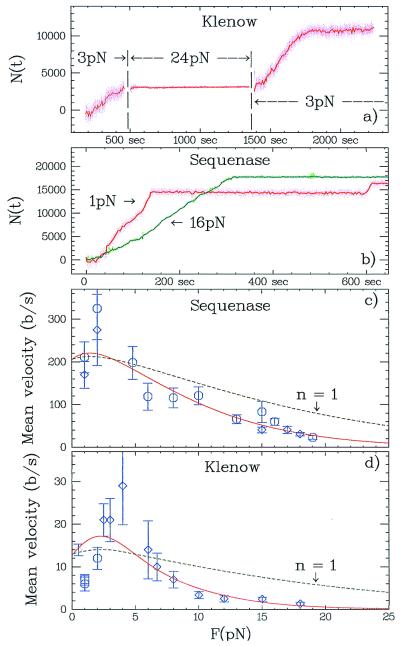
Figure 5.

Force dependence of the replication rate. (a) Replication by Klenow on a charomid is started at 3 pN. Increasing the force to 24 pN stops the replication. After reducing the force back to 3 pN, the polymerization degree, N, has not changed and the enzyme starts replicating again. (b) Number of bases N(t) replicated by Sequenase on pXΔII at two different forces: 1 pN and 16 pN. (c) Mean replication rate, 〈v〉, versus force for Sequenase: high stringency hybridization (K = 13, J = 154; ○) and random priming (K = 5, J = 82; ⋄). The error bars represent σ_〈v〉 estimated as explained in Materials and Methods. The full curve is a fit to the model described in the text 〈v(F)〉 = v₀exp(−nFΔh/k_BT), where v₀ = 200 b/s and n = 2.1 (only ○ were fitted). The dashed curve is obtained with the previously determined v₀ and n = 1 (as expected if only one base was rate determining). (d) Replication rate versus force for Klenow: low stringency hybridization (K = 24, J = 298; ⋄), high stringency hybridization (K = 9, J = 114; ○). Replication rate for Klenow minus exo3′→5′ high stringency hybridization (K = 4, J = 50; □). The full curve is a fit to ⋄, where v₀ = 13.5 b/s and n = 4.

The mean replication rate of the two studied polymerases is strongly affected by the stress on the template (Fig. 5). Klenow stalls at a template stretching force of about 20 pN. Thus, at an initial force of 3 pN, the enzyme exhibits normal activity (Fig. 5a). Increasing the force to 24 pN inhibits polymerization, which can be reinitiated by reducing the stress back to 3 pN. Note that exposing the molecule to a 24-pN strain does not eject the newly synthesized strand, as the number of incorporated nucleotides does not decrease. Below the stalling force, polymerase slows down as the load is increased: Sequenase, for example, works slower at 16 pN than at 1 pN (Fig. 5b) and stalls at a force of 26 ± 6 pN (K = 8, data not shown). For both enzymes, in the range of 0 < F < 4 pN, the mean rate increases with increased force, whereas above 4 pN it decreases exponentially with the force as the enzyme has to work against the load on the template (Fig. 5 c and d).

How can the exponential decay of the mean replication rate at high forces be explained? One might expect the load to interfere with the binding of the enzyme to its template or with a rate-limiting step of the enzymatic cycle. Because DNA is known to be bent by ≈80° to fit into the binding pocket of the polymerase (10, 12), stretching might indeed lower the affinity of the enzyme for its substrate and a higher enzymatic concentration might significantly increase the replication rate. To assess this effect, the mean replication rate was measured at 15 pN for two concentrations of Sequenase: 20 and 200 nM. The mean rate was v = 37 ± 5 b/s (K = 2, J = 54) at 20 nM and v = 59 ± 8 b/s (K = 2, J = 32) at 200 nM. As these rate are of the same magnitude despite a 10-fold difference in concentrations, we deduce that for the enzymatic concentration used in our experiments (≈20 nM) the binding efficiency was not significantly affected by the stretching force.

In the following we shall therefore assume that the enzyme performs an amount of work, Fδ, while contracting the template by a distance δ against the force. The work performed during a rate-limiting step of the enzymatic cycle reduces the replication rate by an Arrhenius factor exp(−Fδ/k_BT) (17, 30). Let Δh = (l_ss − l_ds)/N_tot be the difference in the distance (at a given force F) between successive bases in ssDNA and dsDNA (see Fig. 2b). As this represents the largest length change per base (i.e., contraction for F > 4 pN) in our experiment, we define by n = δ/Δh the minimum number of contracted bases during the polymerization rate-limiting step. We thus fit the measured mean replication rate to the following Arrhenius law: 〈v(F)〉 = v₀exp(−nFΔh/k_BT) and determine v₀ and n (Fig. 5 c and d). For Sequenase the best fit values (see Materials and Methods) are v₀ = 200 ± 20 b/s and n = 2.1 ± 0.5 (confidence level: P = 95%), whereas for the Klenow fragment: v₀ = 13.5 ± 1.5 b/s and n = 4.0 ± 0.7 (P = 95%). The values of v₀ are consistent with the published values for Sequenase and 15 b/s for Klenow (4, 5). Moreover, results for v₀ and n similar to the one for Sequenase were recently obtained on wild-type T7 DNAP by Wuite et al. (19).

The values obtained for n are interesting because they relate to the minimal number of bases implicated in the replication rate-limiting step. Obviously, when a new nucleotide is added to the growing strand, the ssDNA has to contract to fit into the dsDNA structure. Thus one might have expected n = 1 to come out naturally from a fit to the data. However, as can be seen from Fig. 5 c and d, the predicted decay of the replication in that case does not fit our data. The hypothesis that a single nucleotide (the one added) is singly participating in the rate-limiting step can be rejected with confidence P > 99% [Monte-Carlo bootstrap method (24)]. Moreover, notice that the values of n determined here are actually lower bounds as they assume the greatest possible conformational change: that between stretched ss- and dsDNA resulting from complete fraying of the dsDNA end over n bases. As this is unlikely to happen, the values of n imply that more nucleotides on the template strand than the one being replicated are involved in determining the replication rate.

This result is consistent with the induced-fit kinetic mechanism for error detection during DNA replication (4, 5). According to this mechanism, the rate-limiting step in replication is due to a conformational change in the enzyme–DNA complex characterized by a transition between a loose and tightly fit configuration of the two DNA strands. An error in the insertion of the last n bases skews the equilibrium to the “loose” configuration, slowing down replication and favoring error correction by the native DNAP exonuclease activity. Similarly in our experiment, by pulling on the template strand the equilibrium should be skewed to the “loose” configuration, thus reducing the forward rate. Structural data indeed show that the polymerase has a strong interaction with the dsDNA minor groove over a length of several base pairs [with respect to the 3′ end; refs. 2 and 31]. Thus, close interaction with 3 and 4 nucleotides of the template are reported for T7 DNAP and Klenow, respectively (2, 12), which is close to the values of n estimated in our experiments.

Conclusions

We have shown that the replication by a single DNAP can be followed due to the different elastic behavior of ssDNA and dsDNA. The enzyme can convert part of the energy gained from the hydrolysis of dNTP to work against an external force applied on the template (17). Both Sequenase (a replicase) and Klenow (a repair enzyme) show similar behavior when their template is stretched by an external force. The rate-limiting step in their enzymatic cycle involves more than just the one nucleotide being incorporated. Although they perform different functions, both enzymes belong to the DNAP I family and are thus structurally related. It will be interesting to see whether there is a correlation between n, the number of bases involved in the replication rate limiting step, and the number of bases in close interaction with the polymerase as seen in the structural data.

Abbreviations

DNAP

DNA polymerase

ss

single-stranded

ds

double-stranded

b/s

bases per second