Nonglassy kinetics in the folding of a simple single-domain protein

Abstract

Theory suggests that the otherwise rapid folding of simple heteropolymer models becomes “glassy”—dominated by multiple kinetically trapped misfolded states—at low temperatures or when the overall bias toward the native state is reduced relative to the depth of local minima. Experimental observations of nonsingle-exponential protein-folding kinetics have been taken as evidence that the protein-folding free energy landscape is similarly rough. No equivalent analysis, however, has been reported for a simple single-domain protein lacking prolines, disulfide bonds, prosthetic groups, or other gross structural features that might complicate folding. In an effort to characterize the glassiness of a folding free energy landscape in the absence of these potentially complicating factors, we have monitored the folding of a kinetically simple protein, peptostreptococcal protein L (protein L). We observe no statistically significant deviation from homogeneous single-exponential relaxation kinetics across temperatures ranging from near the protein's melting temperature to as low as −15°C. On the basis of these observations, we estimate that, if there is a glass transition in the folding of protein L, it occurs at least 45°C and possibly more than 145°C below the freezing point of water. Apparently the folding free energy landscape of protein L is extremely smooth, which may be indicative of a rate-limiting step in folding that is, effectively, a nonglassy process.

Proteins spontaneously fold to their unique native structures many orders of magnitude more rapidly than would be possible were the folding process an exhaustive random search of conformational space (1). This seemingly paradoxical behavior has led to numerous theoretical models of how naturally occurring proteins achieve their native structures on a biologically relevant time scale (2–5), many of which have emerged from studies of the simulated folding of simple protein-like lattice and off-lattice polymers (5–13).

A large body of theoretical work suggests that the otherwise rapid folding of lattice polymers (2, 6, 7) and simplified off-lattice polymers (12, 14) becomes “glassy”—dominated by multiple kinetically trapped misfolded states—at low temperatures or when the overall bias toward the native state is reduced relative to the depth of local minima. As nonsingle-exponential “stretched” or “heterogeneous” relaxation is a fundamental attribute of glasses (15), these studies have led to the prediction that the folding of real proteins will deviate from single-exponential kinetics as the temperature is reduced and multiple traps begin to retard the folding process (2, 6, 11, 12, 14). Provided a suitable experimental approach is adopted, this hypothesized temperature- and stability-dependent glass transition should provide a unique opportunity for evaluating the correspondence between theory and experiment in protein folding.

Recent reports of nonsingle-exponential kinetics in the refolding (16, 17) or unfolding (18) of several proteins have been taken as evidence in favor of this rough energy landscape. To obtain a more complete understanding of the effect, we have investigated the refolding of the IgG-binding domain of peptostreptococcal protein L (protein L). Similar to lattice polymers, but in contrast to several proteins previously reported to exhibit heterogeneous folding kinetics, protein L is a single-domain protein lacking proline residues, disulfide bonds, prosthetic groups, and other gross structural features that might induce heterogeneity unrelated to fine-scale roughness in the energy landscape (19). At 62 residues, protein L is only twice the size of the larger simulated polymers. The refolding of a tryptophan-containing protein L mutant can be homogeneously initiated and reproducibly monitored by using conventional stopped-flow fluorescence techniques. The refolding of this mutant is rigorously described as a two-state process across a wide range of experimental conditions (20–23), deviating only under conditions of significantly enhanced native stability (24). Neither fluorescence (20) nor small-angle x-ray scattering experiments (23) indicate the existence of significant kinetic phases occurring during the mixing dead time. Previous studies demonstrate that native fluorescence, far-UV ellipticity (20), hydrogen exchange protection (20), and radius of gyration (23) are recovered with identical kinetics, indicating that fluorescence reports on the rate-limiting step in folding. Here we detail the results of efforts to detect heterogeneous nonsingle-exponential kinetics in the folding of this simple protein.

Methods

Protein L was produced as previously described and was used without removal of the histidine affinity tag (20). Additional reversed-phase HPLC purification produced material of >99% purity (assayed via electrophoresis and mass spectrometry). Experiments were performed in 50 mM potassium phosphate, pH 7.0. Experiments performed at −3.5 and −15°C included 10% and 40% (vol/vol), respectively, of ethylene glycol.

Equilibrium chemical and thermal denaturation experiments were performed by using 2 μM protein L and were monitored via ellipticity at 220 nm on an Aviv 202 (Aviv Associated, Lakewood, NJ) circular dichroism spectrometer. Chemical unfolding curves were generated by using guanidine hydrochloride (GuHCl); denaturant concentration was varied by using an automatic titrator via stepwise addition of a high denaturant solution into a low denaturant solution. Equilibration was performed for 120 s at each concentration before data collection. Thermal denaturations were conducted by increasing temperature of the sample in 1°C intervals and equilibrating for 120 s per increment. Data from chemical and thermal denaturations were fitted to standard two-state transitions with linear baselines by nonlinear least regressions using kaleidagraph (Abelbeck Software, Reading, PA). Unfolding free energies (ΔG_u), m-values, and denaturation midpoints (C_m) were determined by assuming a linear dependence of ΔG_u on GuHCl concentration. Estimated fitting errors on ΔG_u and C_m are <6%. Melting temperature (T_m) values were extracted as has been described (25, 26); estimated fitting errors are <1°C.

Refolding kinetics were determined by using an Applied Photophysics model SX.18MV stopped-flow spectrometer (Leatherhead, U.K.) thermostated to ±0.5°C. Kinetic measurements were made at an excitation wavelength of 280 nm, and total emission was monitored at >305 nm. Refolding was initiated by 1:11 dilution of 2 μM protein L (10 μM at −15°C) in 2.5 to 5.3 M GuHCl into refolding buffer. For marginal stability measurements, refolding was initiated by 1:11 dilution into final GuHCl conditions that were equivalent to the experimentally determined C_m (Table 2). Data were collected for 5–15 kinetic lifetimes (when control experiments indicate refolding is complete) and fitted to the appropriate functions using kaleidagraph.

Table 2.

Folding kinetics and fitting statistics at marginal stability

Conditions		Single-exponential model				Stretched-exponential model
Temperature, °C	Cm, M	kobs (s−1)	Correlation coefficient, r2	Residuals		Heterogeneity, h	Correlation coefficient, r2	Residuals
				Mean amplitude, %	Serial correlation, r2			Mean amplitude, %	Serial correlation, r2
58	0.8	37.3  ± 4.1	>0.999	0.3	0.02	1.02  ± 0.03	>0.999	0.2	0.005
37	1.9	2.0  ± 0.5	0.994	1.2	0.0003	1.03  ± 0.03	0.994	1.2	0.0006
25	2.4	0.42  ± 0.01	0.997	0.9	0.02	0.95  ± 0.07	0.998	0.8	0.0007

The work reported here depends critically on our ability to homogeneously initiate and reproducibly monitor folding. Control experiments employing free tryptophan demonstrate that, under the conditions used, the SX.18.MV stopped-flow fluorimeter used is sufficiently stable for periods exceeding 50 s (data not shown). Above −4°C, dilution of free tryptophan in GuHCl into refolding conditions and fitting the data to linear relationships yield relative amplitude changes in the 0.5–1% range and minimal serial correlation of the residual over the time scales reported in this work (some of which is because of a sinusoidal phase at 50 Hz; see below). Slow but significant instrument drift precludes studies of the relatively slow refolding (rates <0.1 s⁻¹) that occurs under marginal stability conditions at lower temperatures. Control experiments also indicate a large mixing artifact before 10 ms and moderate linear drift in the instrument over 1–2 s at −15°C (data not shown). The early mixing artifact was avoided by excluding data from the first 10 ms of experiments conducted under the most extreme solvent and temperature conditions. Fittings of simulated data indicate this omission does not reduce our ability to observe kinetic heterogeneity.

Refolding rates and heterogeneity parameters were determined by fitting data from ≥9 independent replicates to single- and stretched-exponential models, respectively. Below 0°C, each replicate consisted of the average of five refolding experiments. Above 0°C, each replicate represented a single experiment. The reported rates and heterogeneity factors, and their estimated errors, represent the average and 1-σ confidence intervals of these replicates. Fitting statistics (including Patterson correlation coefficients, residual amplitudes, and serial correlation of the residuals) were determined by using an average of all data collected under a given set of conditions. The mean absolute value of the variance was normalized by the overall amplitude change to calculate mean residual amplitudes. Serial correlations of the fit residuals (the autocorrelation of residuals i and i + 1) were also monitored and reported. Significant serial correlation of the residuals is observed only for data collected at −15°C. As described below, however, much of this correlation arises because of linear instrument drift under these conditions. When this drift is accounted for, moderate (r² = 0.152) serial correlation of the residual remains. Approximately half of this residual amplitude arises, however, because of a significant sinusoidal phase with a frequency, 50.08 ± 0.12 Hz, suggesting that the remaining residual correlation arises due to electronic noise (instrument built to 50-Hz European electrical specifications).

Results

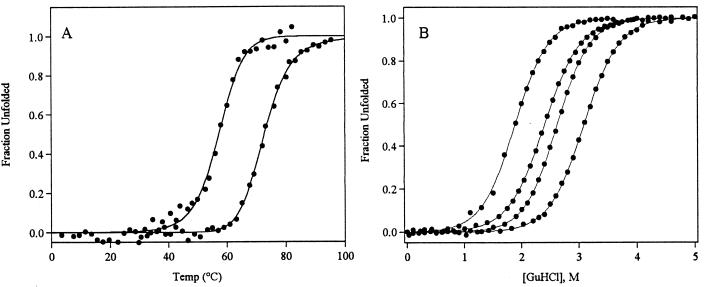
To understand the relationship between heterogeneous folding kinetics and native-state stability, we have monitored the equilibrium unfolding of protein L under a variety of temperatures and solvent conditions. The thermal unfolding of protein L is highly cooperative and is well fitted as a two-state process (Fig. 1a). These unfolding profiles provide an estimate of 75°C for the melting temperature, T_m, (usually denoted T_f in the theoretical literature) in buffer lacking denaturants or other cosolvents. Under the solvent conditions used here, melting temperatures below the T_m in water are observed, reaching 58°C in 40% ethylene glycol, 0.8 M GuHCl. The chemical denaturation of protein L is also well fitted as a two-state process (20–23) (Fig. 1b), with fits predicting a stability 4.5 kcal/mol in water and ranging from >9.1 kcal/mol to ≈0 kcal/mol under the conditions used.

Figure 1.

(A) The thermal unfolding of protein L is well fitted as a two-state process (solid lines) over the range of conditions used (25, 26). The melting temperature, T_m, is 75°C in buffer alone (rightmost curves). This is reduced to 58°C in 40% ethylene glycol, 0.8 M GuHCl (leftmost curve). (B) The equilibrium chemical unfolding of protein L is also well described as a two-state process (solid lines) across the range of conditions used. From left to right, the curves reflect unfolding at 37, 25, 5, and −5°C.

We have examined the refolding kinetics of protein L via traditional stopped-flow fluorescence techniques under conditions of moderate and marginal stability and at temperatures as low as −15°C. To test theoretical predictions of glassy folding kinetics, we fit experimentally observed refolding relaxation kinetics to single-exponential and stretched-exponential models:

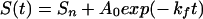1

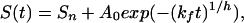2

where k_f is the folding rate, A₀ denotes the fluorescence amplitude change, and S_n and S(t), respectively, denote the fluorescence of the native state and that observed at time t. The heterogeneity factor, h, describes the degree of deviation of the relaxation from a single-exponential function. A heterogeneity factor of unity implies homogeneous single-exponential behavior. Values of h significantly greater than 1 reflect a complex glassy process dominated by multiple local minima. Heterogeneity factors of less than unity would be unrelated to glassy kinetics; glassy traps reduce rates and thus stretch, rather than accelerate, exponential decay curves.

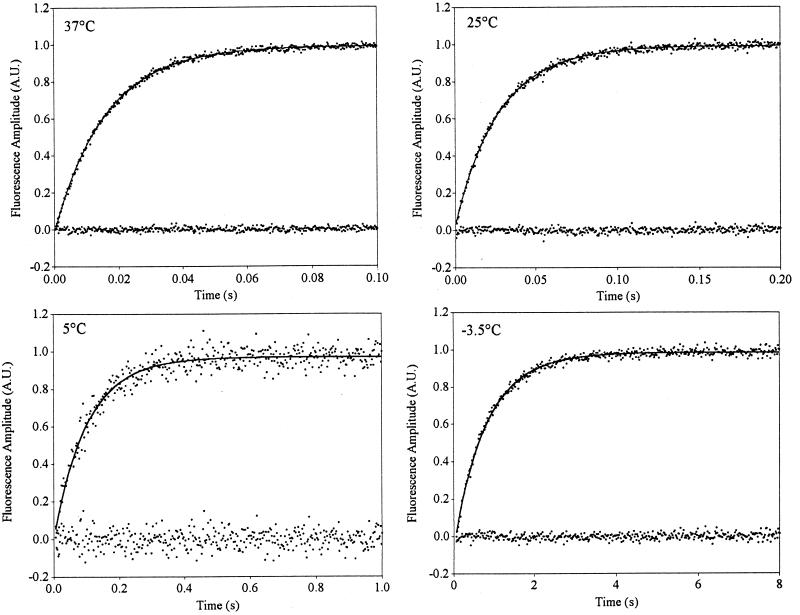
We have examined the refolding kinetics of protein L under conditions where there is a strong energetic bias toward the native state (Fig. 2). Across temperatures ranging from 37 to 5°C, we observe no statistically significant evidence of nonsingle-exponential kinetics under stabilizing conditions; single-exponential models produce excellent correlation coefficients (r² > 0.94), small mean residual amplitudes (a measure of the amplitude of any phases not captured by the model), and trivial serial correlation of the residual (a measure of the information content of the variance not captured by the model). The use of stretched-exponential models neither significantly improves the quality of the fits nor predicts heterogeneity factors differing significantly from unity (Table 1).

Figure 2.

The refolding kinetics of protein L under conditions of moderate stability are well fitted as a single-exponential process over a temperature range of 37°C to −3.5°C. Correlation statistics and the mean amplitude and serial correlations of the residuals all indicate that a single-exponential model accurately fits the observed data. Stretched-exponential models (Eq. 2) neither produce statistically significant improvements in the fit nor predict heterogeneity factors, h, differing significantly from unity (Table 1).

Table 1.

Folding kinetics and fitting statistics at moderate stability

Conditions		Single-exponential model				Stretched-exponential model
Temperature, °C	ΔGu, kcal/mol	kobs, s−1	Correlation coefficient, r2	Residuals		Heterogeneity, h	Correlation coefficient, r2	Residuals
				Mean amplitude, %	Serial correlation, r2			Mean amplitude, %	Serial correlation, r2
37	3.8	63.0  ± 2.0	0.996	1.6	0.003	0.98  ± 0.08	0.996	1.6	0.07
25	4.5	36.4  ± 2.2	0.996	1.0	0.001	1.07  ± 0.08	0.992	1.0	0.02
5.0	5.5	6.6  ± 0.4	0.941	3.6	0.0003	1.07  ± 0.17	0.942	3.6	0.0001
−3.5	6.7	1.3  ± 0.2	0.992	1.2	0.001	1.06  ± 0.08	0.992	1.1	0.001
−15	>9.1*	62.0  ± 3.4†	0.996	1.4	0.597	0.84  ± 0.06‡	0.997	1.2	0.481

^*Technical difficulties preclude the determination of stability under these conditions. Shown stability estimated from extrapolations of stability at higher temperatures. 

^† Rapid folding (despite low temperatures and high viscosity) because of significantly enhanced stability in the presence of ethylene glycol (data not shown). 

^‡ Heterogeneity factors <1 are unrelated to glassy kinetics and apparently arise because of a small linear instrument drift. Fitting these data to a stretched-exponential model with a linear baseline predicts a heterogeneity factor of 1.04 ± 0.07 (see Results). 

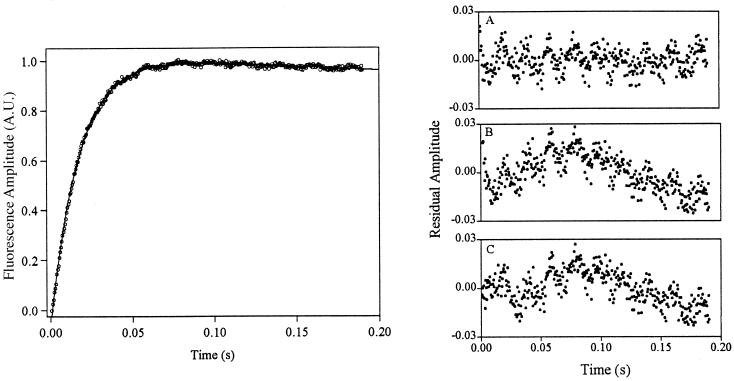
Kinetic experiments at temperatures below 0°C must be performed in the presence of cryoprotectants such as ethylene glycol to prevent sample freezing. Despite this potential complication, results obtained under these conditions are fully consistent with data obtained above 0°C. Kinetics observed at −3.5°C are well fitted as a single-exponential process (Fig. 2c; Table 1). Kinetic experiments performed at −15°C are particularly challenging because of the extremely high viscosity of cold, 40% ethylene glycol. Nevertheless, single- and stretched-exponential fits are effectively equivalently robust at this temperature (r² = 0.996 vs. 0.997, respectively, mean residual amplitudes ≈0.5%; Table 1). Moreover, fitting to a stretched-exponential model predicts a heterogeneity factor of less than unity, a value unrelated to glassy kinetic traps that would slow, rather than accelerate, folding. Both single- and stretched-exponential fits exhibit significant serial correlation of the residual (0.597 and 0.481, respectively) at −15°C, indicating that, despite their small magnitude, the information content of the residuals is considerable. Control experiments suggest this may arise because of linear instrument drift under the conditions used. Consequently, the inclusion of a linear baseline (A_b) in the single-exponential model,

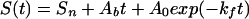3

produces statistically improved fits (r² = 0.999; mean residual amplitude, 0.3%; serial correlation of the residual, 0.152) over the single- and stretched-exponential models (Fig. 3). Fitting these data to a stretched-exponential model with a linear baseline predicts a heterogeneity factor, h = 1.04 ± 0.07, within error of unity. We observe no compelling evidence of nonsingle-exponential behavior at temperatures as low as −15°C.

Figure 3.

The refolding kinetics of protein L at −15°C are complicated by linear instrument drift under the conditions used. Thus, whereas single- and stretched-exponential models fit the data approximately equally well (residuals B and C Right), it is only with the inclusion of a linear baseline that all phases are accounted for (Right). Much of the remaining residual appears to arise because of sinusoidal electronic noise. Solid line indicates fit of single-exponential linear baseline model (Left).

Several authors have suggested that glassy kinetics will be most readily apparent when the overall bias toward the native state is minimized and thus the relative depths of local minima are most significant (7, 27, 28). Unfortunately, however, experimental conditions that destabilize the native state also destabilize the interactions that produce local minima; thus, in contrast to simulations, it is not possible to manipulate local well depths independently of the global free energy in vitro. Nevertheless, in an effort to address this issue, we have monitored refolding at or near the midpoint of the GuHCl-induced unfolding of protein L (C_m), where native-state stability is ≈0 kcal/mol (Table 2). Refolding data collected under these conditions over temperatures ranging from 58 to 25°C are well fitted as single-exponential processes (marginal stability folding is too slow to monitor accurately at lower temperatures because of instrument drift). Fitting these data to stretched-exponential models neither improves fit statistics nor predicts heterogeneity factors differing significantly from unity (Table 2).

Discussion

Under conditions of both moderate and marginal native-state stability, in water at temperatures near freezing and in cryosolvents at temperatures as low as −15°C the refolding kinetics of protein L are well described as a homogeneous single-exponential process. Consistent with this, stretched-exponential kinetic models produce heterogeneity factors well within experimental error of unity. We observe no statistically significant evidence of glassy heterogeneous refolding under any conditions accessible using our experimental approach.

The nonglassy folding kinetics of protein L contrast with previous reports of “strongly nonexponential,” heterogeneous, or “strange” kinetics in the folding or unfolding of several proteins at temperatures well above −15°C. Dual-exponential kinetics have been reported for the temperature jump-induced unfolding of cspA at 80°C (18), but no evidence for heterogeneous folding has been reported (29). Dobson and coworkers have reported that, as monitored by pulse labeling hydrogen exchange, the refolding of equine lysozyme at 25°C is best described by multiple stretched-exponential decays (17), which they have interpreted as multiple heterogeneous nucleation sites in this larger, disulfide-bonded, two-domain protein. More recently, Gruebele and coworkers, using temperature jump-initiated refolding, have reported “strange” kinetics in the refolding of cold denatured phosphoglycerate kinase (PGK) and ubiquitin at 20 and 8°C, respectively (16). At lower temperatures (2–5°C), however, the refolding kinetics of the latter two proteins are well fitted as single-exponential processes.

Rather than reflecting a general glassiness to the folding energy landscapes of all proteins, the heterogeneous refolding kinetics of equine lysozyme, PGK, and ubiquitin may reflect differing experimental conditions or gross structural differences between these proteins and protein L. In contrast to protein L, equine lysozyme and PGK are multidomain proteins that fold via well-populated partially structured intermediates (17, 30, 31). Ubiquitin also folds via a well-populated intermediate at moderate temperatures (32, 33), although this is absent in the mutant for which heterogeneous kinetics have been described. The nonsingle-exponential refolding of these proteins may specifically reflect heterogeneity in the discreet intermediates formed during their folding (17). The nonexponential refolding kinetics of ubiquitin and PGK may also reflect that the differing initial conditions used T-jump studies; cold denatured states, when rapidly transferred to folding conditions, may behave differently than chemically denatured states (16, 18). Last, sequence composition may be an important distinction between previous reports of heterogeneity and this work; ubiquitin and PGK contain 3 and 17 prolines, respectively. The relatively slow cis-trans isomerization of this residue can induce significant heterogeneity in the refolding of proline containing proteins when, for example, differing proline isomerization states give rise to different near-native folding intermediates (34–36). Such proline-induced heterogeneity is often abolished under conditions of reduced native-state stability, when only the correct isomeric state is stable enough to fold (34–36). This may also account for the apparent lack of heterogeneity in the refolding of these proteins at low temperatures (where stability is reduced), an observation otherwise at odds with predictions that reduced temperature and stability would increase, rather than decrease, glassiness. Protein L, which lacks both prolines and well-populated intermediates, also lacks statistically significant evidence of kinetic heterogeneity.

Does the refolding of protein L become glassy at temperatures below −15°C? Effectively all kinetics become glassy at arbitrarily low temperatures as normally trivial energetic barriers loom large relative to random thermal fluctuations. Comparison of our data with simulation results indicates, however, that the glass transition in the folding of protein L must occur at extremely low temperatures. Folding simulations suggest that heterogeneous strongly nonsingle-exponential kinetics (h > 1.25) will be observed at temperatures as high as 1.12- to 2-fold greater than the glass transition temperature (T_g) (11–13) (numerical simulations demonstrate that heterogeneity factors as low as 1.15 would be readily detected given observed signal-to-noise ratios). If these estimates are applicable to the folding of real proteins, the observation of single-exponential refolding kinetics at −15°C implies an upper limit on T_g of −45 to −145°C.

Straightforward comparison of theoretical predictions with the experimental observations reported here is hampered by differing estimates of how far above T_g nonsingle-exponential kinetics will first be observed. It has been suggested that, if evolutionary pressures have not completely optimized folding, naturally occurring proteins may be “frustrated” and exhibit glassy kinetics even at physiologically relevant temperatures (12). Clearly this suggestion is difficult to reconcile with single-exponential folding kinetics occurring at temperatures more than 50°C below those at which protein L evolved. On the basis of the results of lattice polymer studies, however, Onuchic, Wolynes, and coworkers have estimated that “good folders” are characterized by T_m/T_g ratios of 1.3–1.6 or higher. For protein L (with a T_m ranging from 75°C in water to 57°C under the conditions used here), this corresponds to a T_g of −5 to −66°C or lower. Similarly, a T_g of approximately −90°C has been inferred for the folding of real proteins on the basis of the experimentally observed kinetics of a ligand-induced conformational change in native myoglobin (2, 6, 7, 37). If nonsingle-exponential behavior, as theorized (11), is apparent at temperatures as high as 1.41⋅T_g to 2⋅T_g, we can definitively discount these predictions. If, instead, estimates that heterogeneous kinetic behavior does not appear above T = 1.12⋅T_g are correct (11, 12), we cannot positively discount a glass transition below −45°C. This suggests, however, that T_g in the lower half of the predicted range would lie beyond those that are addressable via current experimental approaches.

Alternatively, single-exponential relaxation kinetics may arise because the rate-limiting step in the folding of simple single-domain proteins is, in any real sense, a fundamentally nonglassy process (9, 38). This is consistent with a recent analysis of calorimetric protein-folding data by Kaya and Chan (39), which places an upper limit on T_g of significantly less than −200°C. Glassy kinetics will arise if misfolded states are local thermodynamic minima with relative stabilities of at least a few times k_BT (40). Equilibrium studies of peptides excised from single-domain two-state folding proteins demonstrate, however, that partially structured states are rarely more than 50% populated unless they comprise at least ≈90% of the full-length sequence (41, 42). If the majority of the polypeptide chain must be organized before the depth of the native well drops below a few k_BT, then perhaps the partially structured misfolded states of small single-domain proteins rarely achieve significant relative stabilities. Were this true, then escape from local minima would not define their folding kinetics. This suggestion is consistent with recent claims that a diffusive search for the correct overall topology is the dominant contributor to the rate-limiting step in the process (10, 43–45). This topomer search mechanism cannot be modeled via local-move simulation of a course lattice polymer; in these simulations, the formation of the native topology is synonymous with the formation of native interactions. For this reason, lattice polymer studies may overemphasize the role of local minima in defining folding kinetics. In addition to predicting single-exponential kinetics, the topomer search model is consistent with recent observations regarding the viscosity dependence of two-state folding—which suggest that the rate-limiting step is a diffusive process involving considerable motion through bulk solvent (22, 46, 47)—and the ability of a gross measure of native-state topology to accurately predict relative folding rates (48).

Protein L folds with single-exponential kinetics at the coldest temperatures accessible via our experimental approach. Whether this is because of selective pressures driving the glass transition more than 80–180°C below the temperature at which the protein evolved or whether it arises because the rate-limiting step in folding is, effectively, a fundamentally nonglassy process remains beyond the realm of direct experimental verification. Irrespective of their exact mechanistic interpretation, however, the results presented here demonstrate that the folding of protein L is not glassy at physiologically or experimentally relevant temperatures.

Abbreviations

GuHCl

guanidine hydrochloride

PGK

phosphoglycerate kinase

T_g, glass transition temperature

T_m, melting temperature