Negative hair-bundle stiffness betrays a mechanism for mechanical amplification by the hair cell

Abstract

Hearing and balance rely on the ability of hair cells in the inner ear to sense miniscule mechanical stimuli. In each cell, sound or acceleration deflects the mechanosensitive hair bundle, a tuft of rigid stereocilia protruding from the cell's apical surface. By altering the tension in gating springs linked to mechanically sensitive transduction channels, this deflection changes the channels' open probability and elicits an electrical response. To detect weak stimuli despite energy losses caused by viscous dissipation, a hair cell can use active hair-bundle movement to amplify its mechanical inputs. This amplificatory process also yields spontaneous bundle oscillations. Using a displacement-clamp system to measure the mechanical properties of individual hair bundles from the bullfrog's ear, we found that an oscillatory bundle displays negative slope stiffness at the heart of its region of mechanosensitivity. Offsetting the hair bundle's position activates an adaptation process that shifts the region of negative stiffness along the displacement axis. Modeling indicates that the interplay between negative bundle stiffness and the motor responsible for mechanical adaptation produces bundle oscillation similar to that observed. Just as the negative resistance of electrically excitable cells and of tunnel diodes can be embedded in a biasing circuit to amplify electrical signals, negative stiffness can be harnessed to amplify mechanical stimuli in the ear.

Uniquely among sensory receptors, the hair cells in the ears of tetrapod vertebrates use mechanical feedback to amplify their inputs. Mechanical amplification endows these animals with both exquisite auditory sensitivity and sharp frequency discrimination (reviewed in refs. 1–3). More specifically, by providing energy to compensate for that lost to viscous dissipation in the ear's fluids, the amplifier permits each receptor organ to act as a highly tuned resonator (4). The ear's active process is characterized by metabolic vulnerability, an intimation of powered amplification, and by the spontaneous emission of sounds in a quiet environment, a sign of excess feedback gain.

The mechanism by which mechanical energy is produced by the vertebrate inner ear remains uncertain. The active process of mammals is thought to involve electromotility, a voltage-induced change in the length of the outer hair cell (reviewed in refs. 5–7). In nonmammalian tetrapods, whose hair cells lack electromotility, amplification apparently involves active hair-bundle movements. In response to abrupt deflections, active hair bundles can twitch, performing work against an external load (8). Active bundles can exhibit spontaneous oscillations (9–11) that may underlie spontaneous otoacoustic emissions. Finally, spontaneously oscillatory hair bundles can amplify periodic mechanical stimuli (12). In the present work, we have examined the mechanical properties of active hair bundles under displacement-clamp conditions. By so doing, we have identified a mechanism by which hair bundles produce oscillations and effect amplification.

Materials and Methods

Saccular maculae were dissected from bullfrogs (Rana catesbeiana) and maintained at room temperature in a two-compartment experimental chamber as described previously (12). The solution in the upper compartment, which bathed the apical hair-cell surfaces including the hair bundles, was oxygenated N-methyl-d-glucamine (NMDG) endolymph consisting of 2 mM Na⁺, 3 mM K⁺, 0.25 mM Ca²⁺, 110 mM NMDG, 118 mM Cl⁻, 3 mM d-glucose, and 5 mM Hepes. The solution in the lower compartment, which contacted the basolateral cellular surfaces, was oxygenated standard saline solution containing 110 mM Na⁺, 2 mM K⁺, 4 mM Ca²⁺, 122 mM Cl⁻, 3 mM d-glucose, and 5 mM Hepes. Each solution had a pH of ≈7.3 and an osmotic strength of ≈230 mmol⋅kg⁻¹.

After removal of the otolithic membrane (12), the preparation was mounted on the stage of an upright microscope (MPS, Zeiss) and illuminated with a mercury lamp equipped with heat filters and a bandpass filter of 500 ± 40 nm (center wavelength ± range to half transmittance). While the macular epithelium was observed under a ×40 water-immersion objective lens of numerical aperture 0.75, the kinociliary bulb of an individual hair bundle was attached to the tip of a sputter-coated glass fiber ≈100 μm in length and ≈0.5 μm in diameter (8, 12). Each fiber had a stiffness of 70–310 μN⋅m⁻¹ and a drag coefficient of 25–105 nN⋅s⋅m⁻¹. An image of the fiber's tip was magnified ×1,000 and projected onto a dual photodiode, from whose output bundle displacements could be measured with a precision of ≈1 nm. Before each measurement of the fiber's motion, the system was calibrated by displacing the photodiode with a 20-μm pulse delivered by a piezoelectrical actuator.

In displacement-clamp experiments, the fiber's base was driven by a piezoelectrical stimulator connected to a negative-feedback system. The original clamp circuit (8, 13), which provided only proportional gain, was supplemented with differential and integral components to accelerate feedback responsiveness and improve steady-state tracking (14).

Stimuli and responses were filtered at 1 kHz with an eight-pole Bessel filter, sampled at 2.5 kHz, and acquired with labview (version 5.0, National Instruments, Austin, TX). Using kaleidagraph (version 3.0.9, Synergy Software, Reading, PA) to fit data from displacement-force relations to Eq. 2, we obtained values for the parameters Κ_∞, N, and z. We additionally combined Eqs. 2, 4, and 5 to independently fit the data and estimate the values of Κ_SP, κ, and d.

Hair-bundle oscillation was modeled by describing the mechanical forces on and within a hair bundle (8, 15), including that caused by adaptation. The adaptation motor was assigned a constant climbing rate of 0.1 μm⋅s⁻¹ and a slippage rate dependent on the stereociliary Ca²⁺ concentration and the tension in each gating spring (16). The Ca²⁺ concentration was calculated for three-dimensional diffusion, with a diffusion coefficient of 800 μm²⋅s⁻¹, to a binding site 10 nm from a transduction channel (17). In the presence of endolymph and at a resting potential of −60 mV, Ca²⁺ was specified to carry 3% of the transduction current (18) through a channel of conductance 90 pS (19) and of resting open probability 0.45. The Ca²⁺-binding site of the adaptation motor was characterized by an association rate constant of 10⁸ s⁻¹⋅M⁻¹ and a dissociation rate constant of 20⋅10³ s⁻¹. The slippage rate constant then depended hyperbolically on the binding site's probability of occupation; the maximal value was 560⋅10³ m⋅s⁻¹⋅N⁻¹. The model's differential equations were solved with mathematica (version 4.0.1.0, Wolfram Research, Champaign, IL).

Results

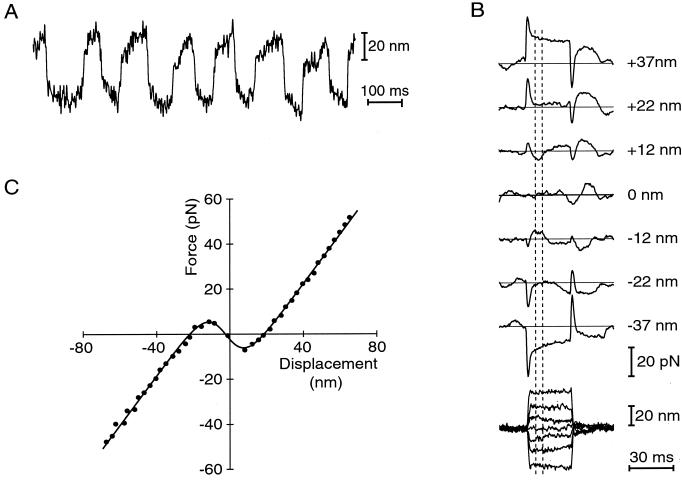
By mechanically characterizing active hair bundles from the bullfrog's sacculus, we sought to identify the basis of their spontaneous oscillation and amplification. We first simulated in vitro the ear's peculiar ionic environment, in which hair cells separate fluids of differing ionic composition. Hair bundles were immersed in low-Na⁺, low-Ca²⁺ NMDG endolymph, whereas the cells' basolateral surfaces were bathed in a high-Na⁺ ionic milieu resembling ordinary extracellular fluid (12). As measured by the motion of a tightly coupled glass fiber, a hair bundle under these circumstances routinely displayed spontaneous oscillation at 5–40 Hz with a peak-to-peak amplitude as great as 50 nm (Fig. 1A). Spontaneous hair-bundle oscillation often persisted through an hour or more of continuous recording. The bundle's motion resembled the relaxation oscillations encountered in many dynamical systems: in each half cycle, a slow excursion concluded with an abrupt stroke in the opposite direction (reviewed in ref. 20, pp. 211–215).

Figure 1.

(A) Spontaneous oscillation at ≈7 Hz of a hair bundle from the bullfrog's sacculus. Note the alternation between slow bundle movements and rapid strokes in the opposite direction. (B) Measurement of the relation between hair-bundle displacement (lower family of traces) and applied force (upper traces). Under displacement-clamp conditions, a bundle was deflected distances up to ±70 nm in steps of ≈5 nm. Seven typical responses are plotted, each an average of 20 repetitions; the corresponding hair-bundle displacements are given to the right. A step command initially evoked a viscous-force transient in the direction of bundle movement; the force then changed slowly as the bundle adapted to its new position. The elastic response of the hair bundle was measured soon after the viscous response had vanished but before adaptation had progressed significantly; the measurement window of 5–10 ms from the onset of the stimulus is enclosed by vertical dashed lines. For displacements of ±12 nm, the direction of bundle displacement was opposite in sign to the force applied; the bundle's chord stiffness, F_SF/X, was therefore negative. Almost no force was required to displace the bundle by ±22 nm. Finally, at ±37 nm, the bundle behaved as an ordinary spring with positive stiffness. (C) Displacement-force relation measured under displacement-clamp conditions. Each point represents a bundle displacement and the corresponding force exerted by the fiber, as averaged over the time window designated in B. The continuous curve is the best fit of the data by Eq. 2, for which Κ_∞ = 1,090 μN⋅m⁻¹, N = 65, z = 0.72 pN, F₀ = 25 pN, and X₀ = −2.2 nm. In this and the subsequent figure, as well as in all data analysis, the curve was not constrained to pass through the origin.

Displacement-Clamp Measurement of Bundle Forces.

Using a displacement-clamp circuit to control the position of the fiber's tip (8, 13), we effectively stiffened the fiber until we suppressed the bundle's spontaneous motion. We were then able to measure the forces required to displace the bundle by distances up to ±70 nm in its plane of symmetry. These responses were complex (Fig. 1B), for they included two components in addition to the instantaneous elastic restoring force of the hair bundle (21). The outset of each force record was marked by a transient caused by the hydrodynamic drag on the bundle and fiber as they rapidly approached their commanded displacement (8). This drag force reflected the viscous drag coefficients of the hair bundle and stimulus fiber, respectively ξ_HB and ξ_SF, as well as the rate of displacement:

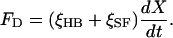1

The latter portion of each record was dominated by the force caused by adaptation, the process that resets a hair bundle's position of mechanosensitivity in response to an externally imposed deflection (22). We made force measurements 5–10 ms after the onset of a displacement step, as soon as the viscous-drag transient had concluded but before significant adaptation had occurred.

When displaced extensively along its axis of mechanosensitivity, an active hair bundle behaved as an ordinary spring of constant stiffness (Fig. 1C). Within ±20 nm of the resting position, however, the stiffness varied significantly with displacement. This nonlinearity was related to the gating of transduction channels, for blockage of channel gating with iontophoretically applied gentamicin (23) reversibly linearized the response (not shown). The striking feature of our recordings was that, for displacements in the range of ±10 nm, the hair bundle's slope stiffness actually became negative. Within this interval, in other words, displacement of the bundle in either direction required the application of force in the opposite.

Our data were well fit by a gating-spring model in which mechanoelectrical transduction channels operating in parallel adopt either an open or a closed state (reviewed in refs. 15 and 24). The force F_SF applied by the stimulus fiber to deflect the bundle a distance X is given by

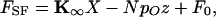2

in which the externally applied force is opposed by the bundle's linear stiffness Κ_∞ and includes a constant offset F₀ (15, 21). The negative term reflects gating compliance, a consequence of the direct mechanical gating of transduction channels (21). As they open or close, the N channels exert a force on average in the same direction as the hair bundle's displacement, resulting in an apparent softening of the bundle. This gating force increases in proportion to the single-channel gating force z and to the mean channel open probability p_O,

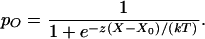3

Here X₀ is the position at which the open probability is one half, k the Boltzmann constant, and T the temperature. Our results are consistent with the idea (11, 24) that gating compliance can be so great over a range of displacements as to dominate the stiffnesses of other hair-bundle components and render the bundle's overall stiffness negative. Similar relations were measured for a total of 20 hair bundles that displayed spontaneous oscillations; the maximal negative stiffnesses lay in the range −93 μN⋅m⁻¹ to −993 μN⋅m⁻¹ and averaged −360 ± 240 μN⋅m⁻¹ (mean ± SD, n = 23 measurements). For the same set of measurements, the average values of the principal parameters were Κ_∞ = 680 ± 360 μN⋅m⁻¹, N = 47 ± 31, and z = 0.67 ± 0.26 pN. Negative stiffness was repeatedly demonstrable in a given cell; whenever the displacement-clamp circuit was disengaged, though, spontaneous bundle oscillation resumed.

Mechanical Biasing of the Hair Bundle.

Under displacement-clamp conditions, the fiber's effective stiffness countered the bundle's negative stiffness, rendering the combined system stable throughout the range of deflections. The negative-stiffness region was unstable, however, in that a free or weakly loaded bundle could not have settled there but would have been rejected to a position of force balance in a flanking region of positive stiffness. We reasoned that a hair bundle might become a mechanical oscillator or amplifier if some mechanically active element repeatedly biased the bundle—that is, forced it to operate—in its region of negative stiffness.

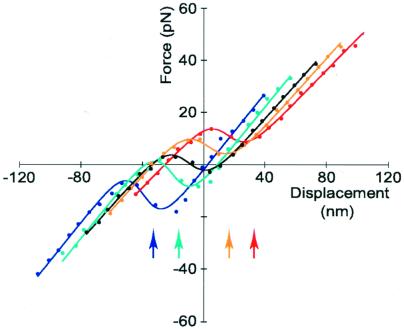
To demonstrate mechanical biasing of the hair bundle, we used the displacement clamp to offset the bundle by amounts in the range of ±40 nm. By bringing the bundle outside its region of negative stiffness, we mimicked a free bundle's movement to escape this unstable region. After allowing 70–100 ms for adaptation to conclude, we again measured the displacement-force relation. We found that the relation had indeed shifted along the displacement axis in the direction of the applied offset (Fig. 2), relocating the region of negative stiffness near the offset position. The shift was incomplete, however; for a sample of eight hair bundles offset by 10–63 nm in either direction, the displacement-force relation shifted on average by 82% ± 11% (mean ± SD, n = 32 measurements) of the imposed offset. This degree of shift agrees well with previous observations of the extent of adaptation, which for small displacements is ≈80% (10, 16, 22, 25, 26). The average slope along which the displacement-force relation shifted was 460 ± 300 μN⋅m⁻¹ (mean ± SD, n = 13 shifts, 8 cells). This result is not inconsistent with the expectation that adaptation should translocate the relation along a line of positive slope corresponding to the stereociliary pivots' stiffness (15).

Figure 2.

Migration of the displacement-force relation during adaptation. The central, black curve was obtained by measuring the forces necessary to displace the clamped hair bundle by the indicated distances from its initial position. The curves at the right resulted from similar measurements taken 100 ms after the bundle had been offset and held 16 nm (orange) or 33 nm (red) in the positive direction. The left curves (cyan and blue, respectively) stemmed from offsets of the same magnitude in the negative direction. The arrows at the illustration's bottom mark the offset positions. The five curves were fit with parameter values in the ranges Κ_∞ = 570–690 μN⋅m⁻¹, N = 44–56, and z = 0.53–0.64 pN. The maximal negative stiffnesses varied between −400 μN⋅m⁻¹ and −900 μN⋅m⁻¹. The relations shifted along a line of slope 400 μN⋅m⁻¹.

Discussion

Negative Stiffness in Hair Bundles.

In measurements of the mechanical properties of hair bundles under displacement-clamp conditions, we consistently observed that oscillatory bundles display negative stiffness. For each of the 20 hair bundles that we examined, the displacement-force relation resembled those illustrated (Figs. 1 and 2) and was fit by the two-state model (Eq. 2) with a regression coefficient of r > 0.99. In the simplest formulation of the gating-spring model for transduction (ref. 27; reviewed in refs. 15, 24), the single-channel gating force is given by

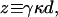4

in which γ is the geometrical gain between hair-bundle displacement and gating-spring extension, whose value is γ ≈ 0.14 (21), κ is the stiffness of a single gating spring, and d is the distance by which a gating spring shortens as a channel opens. From our results, the stiffness of a single gating spring is κ = 570 ± 250 μN⋅m⁻¹ (mean ± SD, n = 23 measurements), a value in accord with earlier determinations of 400–500 μN⋅m⁻¹ (13, 21). The bundle's linear stiffness includes components caused by the gating springs and the stereociliary pivots:

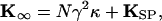5

in which Κ_SP is the combined stiffness of the stereociliary pivots. For the same sample, Κ_SP = 190 ± 130 μN⋅m⁻¹, a result in reasonable agreement with previous estimates of 180–650 μN⋅m⁻¹ (13, 21, 28).

Our data indicate that the distance by which a gating spring shortens as a channel opens is d = 8.2 ± 1.5 nm (mean ± SD, n = 23 measurements), a value well in excess of the prior estimate of 4 nm (ref. 21; see also ref. 19). The physical interpretation of this result is unclear. Although the distance seems too large to reflect the movement of a channel's pore-obstructing gate, the value would be plausible if the gating spring were attached to the gate by a molecular lever. The estimated movement could alternatively be an overestimate of the actual gating distance if the gating spring were nonlinear. Finally, the displacement-force relation could have been affected by the presence of significant compliance in the linkage between the fiber and bundle. The displacement-clamp system controlled the position of the series combination of the bundle and the linkage, whose combined stiffness, Κ_C, is given by

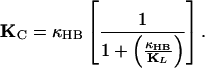6

Here K_HB is the hair bundle's actual stiffness, as given by Eq. 2, and Κ_L is that of the linkage. For large displacements, the hair bundle behaved as a spring of positive stiffness Κ_∞. In the presence of a compliant linkage, the measured stiffness would therefore have been less than the bundle's true stiffness. For small displacements, on the contrary, the measured stiffness was negative. Because successful clamping required the linkage's stiffness to exceed the hair bundle's negative stiffness in magnitude, the measured magnitude of the negative stiffness would have exceeded that of the bundle. As a result, we would have underestimated N and overestimated z and therefore d. Series compliance could not have produced negative stiffness, however, and does not alter the conclusion that a high value of d underlies the phenomenon.

It has been suggested that the estimated movement on channel opening would be halved if an identical channel occurred at each end of a gating spring (19). If z is great enough to produce negative stiffness in the displacement-force relation, however, negative cooperativity between each pair of channels should introduce a second region of negative stiffness, a phenomenon that we never observed. Our data are consistent with the presence of a channel at either end of each gating spring, for example at the upper or the lower end of each filament in a tip link, but suggest that most gating springs do not have equivalent channels at both ends.

A Model for Hair-Bundle Oscillation.

What is the utility of negative stiffness, of which we are aware of no previous demonstration in a biological system? Negative resistance, an electrical analog of negative stiffness that occurs in physical devices such as tunnel diodes, serves engineers in the design of electrical oscillators and amplifiers (29). The membrane voltage-current relations of neurons and other excitable cells also display negative resistance, which underlies these cells' ability to generate action potentials (reviewed in ref. 30). In both the physical and the biological examples, oscillation or amplification ensues when the relevant system is biased into its region of negative resistance.

Mechanical biasing of the hair bundle requires an active element that can exert force on the bundle. Two lines of evidence suggest that this biasing element is the myosin motor that mediates mechanical adaptation (reviewed in refs. 31–33), the process that partially restores the open probability of the transduction channels to its original value during a sustained stimulus. First, in NMDG endolymph containing 250 μM Ca²⁺, the adaptation motor reaches a steady state for a channel open probability near one-half (25, 27). As required for biasing of a hair bundle to an unstable position, this probability corresponds to a bundle position well within the negative-stiffness region. Second, computer modeling of the bundle's mechanical behavior using measured values for the rate of mechanoelectrical adaptation (22, 25) generates spontaneous hair-bundle oscillation at the observed frequency.

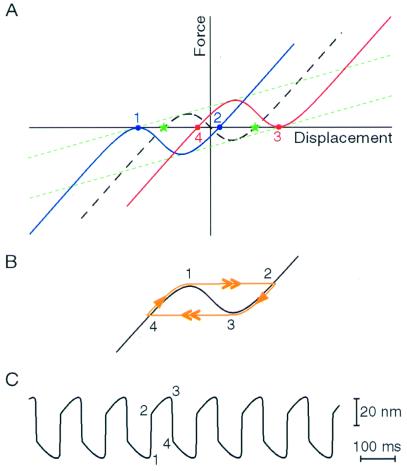
An interplay between adaptation and the hair bundle's negative slope stiffness explains the bundle's spontaneous oscillations. In this model (Fig. 3A), the slow component of each half cycle reflects the activity of the adaptation motors, which move the bundle toward the region of negative stiffness. The fast component, in which the hair bundle lurches across this unstable region, amounts to a first-order phase transition: the opening or closing of each transduction channel produces a force on the bundle that impels other channels to follow suit, resulting in a molecular avalanche during which most of the channels open or close cooperatively. If the position at which the adaptation motor would be at rest lies within the negative-slope region, a free or weakly loaded hair bundle cannot reside there. The bundle is therefore forced to oscillate (Fig. 3 B and C), perpetually frustrated in its attempt to find repose at a thermodynamically unstable position. The instability that underlies this oscillation persists so long as the magnitude of the bundle's negative stiffness exceeds the stiffness of the external load.

Figure 3.

A model of the hair bundle's spontaneous oscillation. (A) The channel open probability equilibrates with the tension in the gating springs on a time scale much faster than that of adaptation. Under this quasistatic condition, a free bundle must reside at a point of zero force. The region of negative slope stiffness in the initial displacement-force relation (dashed black curve) implies that the bundle is bistable: there are two such points (green stars). Assuming that the bundle first occupies the negative stable point, the transduction channels' low open probability causes adaptation to shift the displacement-force relation in the negative direction. The shift proceeds with a slope set by the stiffness of the stereociliary pivots (ref. 15; dotted green lines). When the relation's left-sided local maximum becomes tangent to the abscissa (at point 1 on the blue curve), however, the negative stable point vanishes, and the bundle must leap to the positive stable point (point 2) to maintain the zero-force condition. For the parameter values of Fig. 1C, this transition corresponds to an abrupt increase in the channel's open probability from 0.15 to 1.0. At the bundle's new position, the channels' high open probability promotes adaptation in the opposite direction until the bundle's position corresponds to the right-sided local minimum of the displacement-force relation (point 3 on the red curve) and the bundle jumps in the negative direction (to point 4). The channel's open probability correspondingly plummets from 0.85 to 0.0. Oscillation ensues from repetition of this sequence. (B) Trajectory (1 → 2 → 3 → 4) of the hair bundle along the displacement-force relation as this relation undergoes the adaptive shift depicted in A. The double arrows indicate the fast transitions across the unstable region of negative stiffness (1 → 2 and 3 → 4), whereas the single arrows demarcate the slow adaptive movements along the stable branches of the relation (2 → 3 and 4 → 1). C, Hair-bundle oscillation produced by a model of bundle mechanics that incorporates the parameter values for the cell whose response is depicted in Fig. 1A. The numbers relate phases of the oscillation to points on the displacement-force relations of A and B.

Although the present report concentrates on spontaneously oscillatory hair bundles, negative slope stiffness may occur in quiescent bundles as well. So long as the channel open probability at which the adaptation motor reaches a steady state lies outside the region of instability, even a bundle with negative stiffness has a stable resting position. If negative stiffness occurs in a hair bundle exposed to standard saline solution, for example, the resting open probability of ≈0.15 (25, 26, 34, 35) would correspond to a bundle position negative to the unstable region. Displacing such a bundle into the region of negative stiffness, however, should trigger movements resembling a single cycle of oscillation: after leaping in the positive direction, the bundle would experience adaptation until it jumped back to a steady-state position with a channel open probability near the original value. The correspondence between this expected trajectory and the twitch observed when an unclamped hair bundle is transiently displaced in the positive direction (8, 10, 21) suggests that negative stiffness underlies the twitch. Although the fact that hair bundles occasionally oscillate in standard saline solution (10) also implies that negative slope stiffness can occur in that medium, the rapidity of adaptation in high-Ca²⁺ conditions may have prevented the direct observation of negative stiffness to date.

Mechanism of Amplification by Active Hair-Bundle Movement.

The negative-stiffness instability can effect amplification of mechanical stimuli in two ways. First, when the hair bundle's negative stiffness dominates the load, the bundle undergoes large spontaneous oscillations. Because the bundle is buffeted by thermal noise, these mechanical oscillations are irregular (Fig. 1A) and display a diffuse power spectrum centered on a characteristic frequency. When even a tiny sinusoidal stimulus is applied near this characteristic frequency, however, entrainment occurs and the power expended by the hair cell is funneled into the stimulus frequency (12). As the strength of stimulation grows and bundle movements become more regular, the stimulus magnitude should be encoded first in increasing phase coherence of bundle motion, then in successively larger movements (36). The comparable behavior of neural responses in the avian auditory nerve (37) might stem from this amplification mechanism.

An alternative means of amplification operates when the bundle's negative stiffness almost exactly balances the load's stiffness. In this event, the slope of the combined displacement-force relation is nearly zero near the origin, so a very small stimulus force produces a large displacement and a correspondingly great change in channel open probability. The system is then poised on the verge of the oscillatory instability, at a Hopf bifurcation (reviewed in ref. 20, pp. 248–253). This situation is uniquely advantageous for sharply tuned, high-gain amplification of weak periodic stimuli, in which the frequency of spontaneous oscillation at the bifurcation defines the resonant frequency (36, 38, 39). Consistent with the relevance of this mechanism, the negative stiffness values reported here overlap the stiffness of the otolithic membrane that constrains hair bundles in vivo (40).

Domain of Amplification by Active Hair-Bundle Movement.

All of the major classes of tetrapod vertebrate display an aural active process characterized by high sensitivity, sharp frequency selectivity, metabolic vulnerability, and otoacoustic emissions (reviewed in ref. 3). The range of animals in which active hair-bundle movements play a role in amplification, however, remains uncertain. Although the hair bundles of fishes are capable of slow spontaneous and evoked motions (41, 42), the phenomenon has not been investigated in detail. Active bundle movements have been extensively documented in amphibians and reptiles; birds, too, possess mechanically active hair bundles (reviewed in ref. 43). Slow hair-bundle motions associated with adaptation have been observed in mammalian hair cells (44, 45), but rapid, active bundle movements have not been reported. Mechanical amplification by active hair-bundle motions may therefore be a widespread phenomenon, but it remains unclear whether this mechanism operates throughout the vertebrates.

The most important uncertainty about active hair-bundle movements is their potential utility for high-frequency hearing in mammals, whose hair cells can be tuned to stimulus frequencies exceeding 100 kHz (46) and can produce vigorous spontaneous otoacoustic emissions at frequencies up to ≈60 kHz (47). Because the extension of the hearing range to high frequencies coincides with the evolution of outer hair cells (reviewed in refs. 2, 3), it is generally believed that these cells' electromotility, or mechanical responsiveness to transmembrane voltage, constitutes the aural amplifier in mammals (reviewed in refs. 5–7, but see ref. 48). Although the physiological mechanism of high-frequency electrical stimulation remains uncertain, electromotility indeed operates with singular rapidity, displaying a high-frequency cutoff during direct electrical stimulation of 20–80 kHz (49–51). Active hair-bundle movements, by contrast, have not yet been shown to occur at frequencies above a few hundred hertz.

At the same time, a contribution of bundle motility to high-frequency amplification cannot be excluded. Active movements might be powered by additional processes faster than the stepping of myosin, for example by Ca²⁺-mediated channel reclosure (21, 38). Even if myosin's power strokes drive amplification, adjustment of the mechanoenzyme's ATP-hydrolytic rate constants for operation at mammalian body temperature suggests that myosin can participate in mechanical oscillation at frequencies of several kilohertz (reviewed in ref. 31). Moreover, coupling of the force production by an ensemble of myosin molecules to a hair bundle's passive mechanical properties can potentially yield oscillation at frequencies well in excess of the rate of ATP hydrolysis (36, 52). Only two ingredients are necessary to endow hair bundles with the ability to amplify their mechanical inputs by the mechanism described here: a region of negative stiffness in the displacement-force relation and a biasing element such as that provided by the adaptation motor. Because both gating compliance (53, 54) and adaptation (44, 45) have been demonstrated in mammalian hair cells, active bundle movements driven by the adaptation motor may provide an additional or alternative source of amplification in the mammalian cochlea as well.

Abbreviation

NMDG

N-methyl-d-glucamine