Anatomy of protein structures: Visualizing how a one-dimensional protein chain folds into a three-dimensional shape

Abstract

Here, we depict the anatomy of protein structures in terms of the protein folding process. Via an iterative, top-down dissecting procedure, tertiary structures are spliced down to reveal their anatomy: first, to produce domains (defined by visual three-dimensional inspection criteria); then, hydrophobic folding units (HFU); and, at the end of a multilevel process, a set of building blocks. The resulting anatomy tree organization not only clearly depicts the organization of a one-dimensional polypeptide chain in three-dimensional space but also straightforwardly describes the most likely folding pathway(s). Comparison of the tree with the formation of the hydrophobic folding units through combinatorial assembly of the building blocks illustrates how the chain folds in a sequential or a complex folding pathway. Further, the tree points to the kinetics of the folding, whether the chain is a fast or a slow folder, and the probability of misfolding. Our ability to successfully dissect the protein into an anatomy tree illustrates that protein folding is a hierarchical process and further validates a building blocks protein folding model.

How a one-dimensional (1D) polypeptide chain folds into a three-dimensional (3D) entity is a fascinating problem. Despite our increasing knowledge, and the considerable progress made in the improvement of the methodology for the prediction of a protein 3D structure from its sequence (1), the protein folding problem still presents a major hurdle. Part of the reason why the folding problem remains so difficult derives from a lack of a folding model that enables visualizing how a 1D protein chain folds into its 3D native state. To fill this gap, we have devised, based on the building block folding model (2, 3), a procedure for progressively dissecting native protein structures to reveal their anatomy. Here we show how, based on their structural anatomy, we may visualize their dynamic folding pathways.

The building block folding model is a “practical” model for protein folding (2, 3). The model postulates that protein folding is a hierarchical process (4) and that the basic unit from which a fold is constructed, i.e., the hydrophobic folding unit (HFU), is the outcome of a combinatorial assembly process of a set of building blocks. The hydrophobic folding units in turn associate to create intramolecular domains, which subsequently assemble to build either an intramolecular multidomain protein fold or an intermolecular quaternary structure. The “building block” itself is defined as a highly populated, contiguous fragment in a given protein structure. It may be composed of a single secondary structure element or a contiguous fragment consisting of interacting structural elements, such as observed in supersecondary structures (5, 6). On the other hand, a hydrophobic folding unit has been defined as an independent, compact, thermodynamically stable folding unit with a buried hydrophobic core (7, 8).

According to the building block folding model, if we were to splice out the building block from the protein chain, the most highly populated conformation of the resulting peptide in solution would very likely be similar to that of the building block when it is embedded in the native protein. Nevertheless, whereas the conformations of most building blocks are preserved in the final folded native structure, the mutually stabilizing association between the building blocks may still result in alternate conformations being selected in the combinatorial assembly. In such cases, the conformations of the building blocks that we observe in the native protein structure differ from their original stand-alone conformations.

The theoretical foundation of the building block folding model and the anatomy trees is implicit in the description of the protein folding process as being guided by a funnel shape free energy landscape. It is now realized that the landscape theory has its origins in the idea of minimal frustration, already shown to be valid for small fast-folding proteins. The minimal frustration theory foresees that protein folding is energetically minimally frustrated and is dominated by topological 3D interactions in a 1D polypeptide chain (9–11).

In this paper, we present an algorithm, similar to the methods used by Lesk & Rose (12) and Wodak & Janin (13) almost two decades ago, to locate building blocks in a given protein tertiary structure. However, we do not confine ourselves to binary cleavages of the polypeptide chain; instead, our algorithm allows multiple dissections at each iterative level, creating a descending hierarchy of contiguous fragments. Each node in the descending anatomy tree is a one-segment building block. The entire native structure of the protein is the starting root-node of this anatomy tree. The locations of the building blocks correspond to the end nodes of the top-down sprouting tree.

To be able to dissect the protein structure to create an anatomy tree, it is essential to have a scoring function that is independent of the fragment size. In this study, we have devised such a statistically based scoring function. The scoring function has been constructed to measure the relative conformational stability of all candidate building blocks. There are three ingredients in this, empirical fragment-size-independent scoring function. These relate to measurements of compactness, degree of isolation, and hydrophobicity. The first two correspond to the classical visual criteria of a domain via inspection of the 3D structure of the protein, whereas hydrophobicity is the dominant driving force in protein folding (14). We apply the multicut dissection progressively to sets of fragments with the highest stability score. Hence, after completion of the cutting procedure, inspection of the resulting anatomy tree straightforwardly yields the most likely folding micropathway. Whereas already the anatomy tree itself outlines the more probable folding routes, analysis of the minima among the cut-out fragments yields both the number of alternate routes, and a description of the less probable folding pathways gliding down the funnel slopes. Further, trapped intermediates are inferred, via misassociation of the highest population time, or alternate local-minima building blocks, present in our building-block map. These illustrate very good correspondence with experimental fragment CD and fluorescence spectra results (15).

Thus, the wealth of information contained in a correct dissection of a protein tertiary structure into highly populated or stable substructures has several biological implications. First, this information enables analysis and assessment of the folding complexity in terms of sequential/nonsequential folding in a more precise manner (16). In turn, the folding complexity yields the likelihood of misfolding, as well as the kinetic folding rate of a given protein. Second, the dissection yields a library of protein fragments, ranging from complete tertiary folds to short pieces of the chain, with their associated favorable conformations. These can provide an extremely rich and useful resource for secondary structure, or for ab initio tertiary structure prediction (17). Third, partial threading has proven very useful in protein fold recognition, when new folds are encountered. However, if such an approach is to be successful, the key ingredient is the availability of a complete, nonredundant library of known contiguous fragments, along with their likely conformations.

Methods

The Scoring Function.

The scoring function developed in this study is based on a previous scoring function that has been successfully applied to locate hydrophobic folding units (7). The HFU scoring function has four ingredients: compactness, hydrophobicity, degree of isolatedness, and number of segments. By definition, a building block has only one segment. Therefore, only the first three ingredients are used in the current scoring function for locating building blocks. The scoring function we have designed is fragment-size independent. The new function is expressed as a linear combination of the three measurements, with each quantity calculated as the deviation from the averaged value of known protein structures. The new building block scoring function, Score^B.B., is in this form:

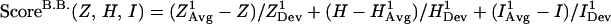1

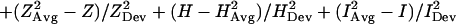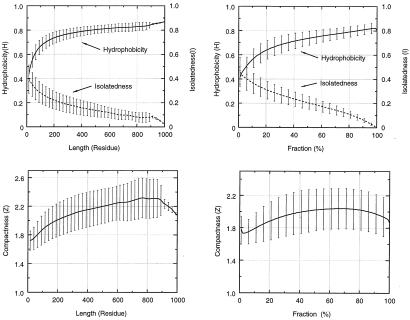
where Z, H, and I are, respectively, the compactness, the hydrophobicity, and the degree of isolatedness of a candidate fragment. (A brief description of their definitions is given in supplementary Methods, which are published on the PNAS web site, www.pnas.org.) The corresponding arithmetic average, X_Avg, and standard deviation, X_Dev, are determined from a nonredundant dataset of 930 representative single-chain proteins. Average and standard deviation with superscript 1 are calculated with respect to fragment size; average and standard deviation with superscript 2 are calculated as a function of the fraction of the fragment size to the whole protein. The plots of these twelve statistical values (six averages and six corresponding standard deviations) are depicted in Fig. 1.

Figure 1.

Plots of statistical values of hydrophobicity, isolatedness, and compactness based on fragments generated from a representative dataset of 930 single-chain proteins. For a chain with a size of N_e residues, and with a size limit of a building block set to N_s residues, the total number of sampled fragments is N_total = Σ(N_e − N_i + 1), where N_i runs the summation from N_s to N_e. The statistical values are derived from a large number of fragments. For example, the number of sampled fragments with sizes of 15, 400, and 900 residues are 194,127, 19,621, and 132, respectively. Two sets of statistical values are calculated here. A and C plot the data with respect to fragment sizes ranging from 15 to 1,000 residues. B and D draw the data calculated as a function of fraction of the fragment size with respect to the whole protein. These range from 0% to 100%. In these figures, the standard deviations are plotted as an error bar with their corresponding averaged values at the middle of the bar. The standard deviation bars are drawn only every 25 residues or 5%.

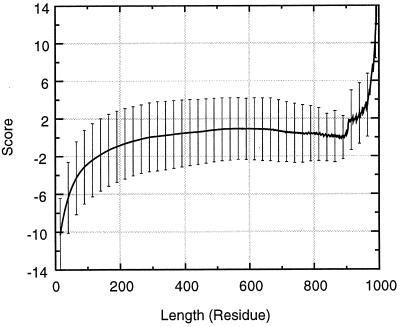
The size-independent stability form of the function assumes that fragments of different sizes have equal averaged conformational stability. However, the linearity of the hydrophobicity (H) and of the isolatedness (I) in the region of fragment size > 150 residues suggest that true fragmental stability should reflect this trend. Therefore, instead of using statistical values, the H_Avg and I_Avg in the scoring function are calculated from a fitted straight line, to reflect the relative size-dependent stability. Fig. 2 shows the average scores and their standard deviations for all fragments in the 930 representative chains as a function of fragment size, following the modification because of this relative stability concern.

Figure 2.

The averaged scores and their standard deviations for all fragments in the 930 representative chains with respect to the fragment size.

The Cutting Procedure.

The detailed description of the cutting procedure is given in supplementary Methods. It includes four sections: locating a basket of building blocks (relatively stable contiguous fragments), a recursive top-down splitting process, the multisplicing procedure, and assembly of hydrophobic folding units.

Results

The Anatomy Tree and Folding Pathways: the Actin Example.

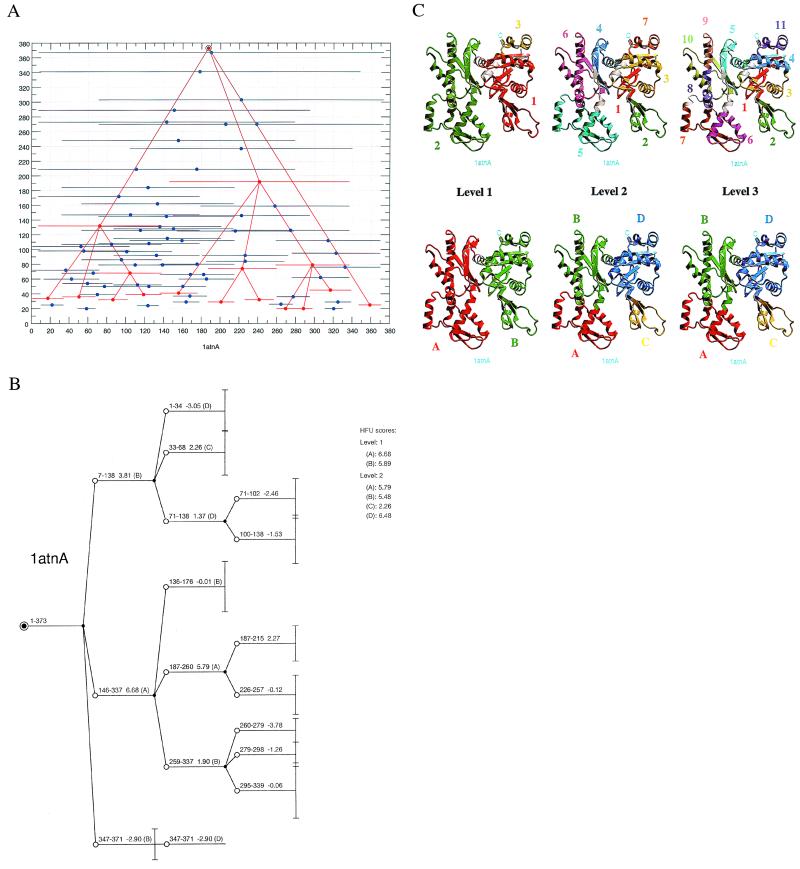
The structural anatomy of every single-chain protein in the PDB can be accessed via our web site at http://protein3d.ncifcrf.gov/tsai/anatomy.html. For each chain, the results of the dissection are summarized and presented in a number of useful ways. First, we provide a list of the fragments found in the first step of the anatomy process. These are the local minima in the fragment map. From this reservoir, any set of fragments that yields the entire protein via a combinatorial assembly is a plausible folding pathway. Table 1, which is published as supplemental material, presents the results for actin (PDB: 1atnA) as an example.

Second, the most likely folding pathway is depicted on the fragment map. Fig. 3A illustrates one example, for actin. Local minima are plotted in horizontal blue lines. The collection of building blocks that present the most likely folding pathway are in red lines. For actin, inspection of the plot reveals that no single route dominates the folding path. Building blocks assemble (the bottom half of the figure) to eventually form the entire native structure at the top.

Figure 3.

The actin example. (A) The two-dimensional fragment map of actin, 1atnA. The x and y coordinates represent the fragment location and size. Local minima in the fragment map are indicated by solid circles. The associated horizontal line for each minima reflects its size. The results of the anatomy (a collection of building blocks at each level) are highlighted in red color, to distinguish them from those in blue, which represent the local minima. Lines are drawn to indicate parent–child relationship. This representation shows clearly the most likely folding micropathway among many other plausible pathways. (B) The detailed anatomy information complementing A. Starting with the entire protein as a parent node (solid circle), the branches (empty circles) are linked to their parent node. At the next anatomy level, each child node becomes a new starting parent node. If a new parent node does not produce any children, it is an end node of the building block. A vertical bar is drawn to reflect the size of the end-node building block. In the figure, each building block (node) is labeled with its stability score and a letter in parenthesis. The letter indicates to which hydrophobic folding unit (A, B, C, or D) the building block belongs. The scores of the corresponding HFUs at each level are listed on the upper right hand side of the figure, next to the anatomy tree. (C) The graphical presentation at each anatomy level for actin (1atnA). The upper row depicts the results of the building block assignments for three dissecting levels, and the lower row depicts their corresponding hydrophobic folding unit assignments. In the assignments, each color represents a building block or an HFU. In the building block assignment, the chain goes from the N terminus to the C terminus with the following color order: (1) red, (2) green, (3) yellow, (4) blue, (5) cyan, (6) magenta, (7) orange, (8) purple, (9) pink, (10) light green, and (11) dark blue. In the HFU assignment, the color goes in alphabetical order: (A) red, (B) green, (C) yellow, (D) blue. Every combinatorial possibility of assembling fragments from the pool of local minima (generated in the first step) is a candidate in the cutting of the protein into building block fragments. To provide a specific example, the fragments centered near residues 90 (for the fragment 7–138), 258 (), and 360 () yield one of many candidates that fulfill two conditions. First, fragments of any combinatorial assembly must cover the entire node-fragment. (For the starting node, it is the whole protein.) Second, fragment overlap among the selected fragments must be at most 7 residues. Next, among all combinatorially assembled candidates, the average score of the best two fragments (if there more than two for this node-fragment in the pool) is used to judge the best cutting. The “best of two” is an ad hoc rule, simply because in our hands it works better than any other choice with the designed scoring function. In A, at the first cutting level, these three fragments centered near residues 90, 258, and 360 have the highest score among all other combinatorially assembled fragments from the local-minima pool. Hence, in the example here, the protein has been muli-spliced into three fragments at the first level based on the scores of the two fragments, 7–138 and 146–337.

Third, the results of the dissection can further provide the detailed anatomy of the step-by-step paths that follow the most likely building block assembly routes (Fig. 3B). The number of branches in each node indicates how many building blocks have been derived from the corresponding parent building block. Each building block is labeled with a score and with a letter in parenthesis. The letter indicates to which HFU (A, B, C, or D) the building block belongs. The scores of the corresponding HFUs at each level are listed on the upper right hand side of the figure, next to the anatomy tree.

Fourth, Fig. 3C depicts the anatomy at each level for the 1atnA example. The figure presents a step-by-step graphic illustration of the structural anatomy. In the figure, the upper row displays the anatomy of the building block cutting, and the lower row presents the HFU assignments, through a combinatorial assembly process of the building blocks. By going through the anatomy tree organization, we can clearly follow how the 3D fold formed from the 1D polypeptide chain. Moreover, actin is a complex, nonsequentially folding protein (3). If we compare the building blocks anatomy (Fig. 3C Upper) with the HFU assignments (Fig. 3C Lower), we can see how the nonsequential interactions between the building blocks have arisen during the folding of the actin chain. At level 1, we see three building blocks and two HFUs. With the head and tail interaction (building blocks 1 and 3 in HFU unit B) being excluded from the classification of a nonsequential interaction (3), the anatomy level 1 of actin is classified as belonging to the sequential folding category. At level 2, there are seven building blocks and four HFUs with two HFU units (unit B and unit D) illustrating a nonsequential interaction. The nonsequential interaction in unit B is between building blocks 4 and 6 and in unit D between building blocks 1 and 3. Hence, by going back from level 3 to level 1, we trace the major folding pathways: through a comparison of the top (dissection) building block row and the bottom (assembly to hydrophobic folding unit row), we can identify the building blocks as they progressively assemble to yield the units. For example, at level 3, i.e., at the bottom of the tree (right hand side of the figure), building blocks 1, 3, 4, and 11 assemble to yield HFU D, whereas 5, 8, 9, and 10 yield hydrophobic unit B, and 6 and 7 yield unit A. Misassembly of any of these, at this or at any other level, or of any other building blocks present in the fragment map (Fig. 3A, and supplementary Table 1), will result in trapped intermediates, nestling in their wells along the folding micropaths. Whereas in these intermediates the conformations of the building blocks themselves may be at their native states, their misassociations will inevitably result in nonnative contacts. These will yield populations of conformers, with different nonnative contacts.

The Case of α-Lactabumin.

Here we analyze the well studied α-lactalbumin (α-LA). We illustrate that the anatomy trees not only are consistent with visual domain and subdomain classification, but also are validated by experiments. α-LA is a critical regulatory component in lactose synthase in mammals. It contains two subdomains with substantial intersubdomain interactions. The α-subdomain contains four α-helices, and the β-subdomain consists of a small β-sheet and loops. The native structure has four disulfide bonds. One of these connects two helices in the helix–loop–helix structure responsible for calcium binding.

α-LA forms an equilibrium molten globule under a variety of mildly denaturing conditions. The best studied is the acid-denatured state (A-state). At neutral pH, the molten globule state can be obtained by depleting bound calcium, by abolishing four disulfide bonds (mutating cysteines to alanines, ref. 18), or by mixing with a denaturant. Further, a peptide model of the α-subdomain also forms a molten globule-like state (19). α-LA molten globule is compact, with significant native-like secondary structures in the α-subdomain. The β-subdomain is more disordered.

The folding picture emerging from different probing methods is that α-LA folds via a molten globule intermediate (20). The species formed in the early stages of refolding of the apo-protein have at least 85% of the α-helical content of the native state, and near-native compactness (21). A structure that persists in these transient species is located predominantly in the α-subdomain of the native protein and resembles that present in the partially folded A-state at low pH. Folding in the presence of Ca²⁺ is similar to that in its absence, although the rate increases by more than two orders of magnitude. The disulfide bonds stabilize the overall fold rather than drive folding. The rate-determining transition from the compact partially structured (molten globule) species to the native state is highly cooperative. In terms of thermodynamics, the entropy of dehydration is the dominant factor providing stability for the compact intermediate state on the folding pathway, whereas for the stability of the native state, the conformational enthalpy is the dominant factor (22).

Limited proteolysis, a complementary approach to common physiochemical methods, is useful for probing protein structure and dynamics (23–25). Local unfolding (chain flexibility) may be responsible for selective peptide bond fission of a protein substrate. Results deduced from limited proteolysis of partly folded states of α-LA are in good agreement with those derived from NMR and other probing methods (25).

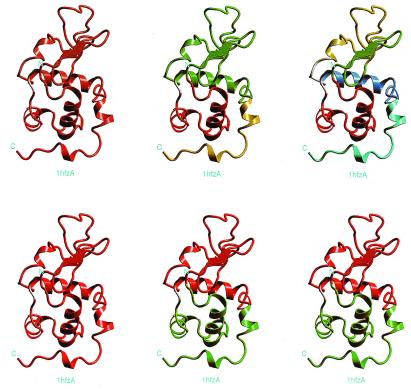
Fig. 4 gives a graphical illustration of the anatomy at each level for α-LA (123 residues). At the first anatomy level, the protein remains almost intact (), indicating it is a cooperative unit. At the next level, it is cut into three fragments (3–38, 39–105, and 106–123, respectively), with two assembled hydrophobic folding units. At the last level, the one-segment folding unit (fragment 39–105) is further divided into three fragments (39–55, 56–81, and 87–108). The most likely folding pathway is in general remarkably consistent with experiments that probe the folding mechanism, and especially the limited proteolysis of Fontana and coworkers (25). First, fragment 39–55 at the last level with the lowest score (−4.90) correlates nicely with the initial proteolytic cuts of α-LA in its A-state or apo form by three proteases. The experimental cleavages occur at the same 39–54 region, with the actual site(s) of the cuts depending on the protease used (25). Second, at the second level, the existence of the three fragments (two cleavage points, 38/39 and 105/106) also reflect nicely the limited proteolytic evidence, namely, that subsequent cleavages occur mostly at chain regions 31–35 and 95–105. Third, the two-segment folding unit (3–38 and 106–123) is supported by evidence that some structure is obtained for a two-chain species 1–40 and 104–123 (25). Fourth, fragment 53–103 is structured, as characterized by similar α-helical content as the corresponding chain segment in native α-LA. This 53–103 fragment corresponds to the association of two sequentially linked building blocks, 56–81 and 87–108. Consistently, there is a local minimum fragment 48–105 with a score of 2.94 in the complete list of 20 local minima of the fragment map (not shown). Fifth, the 111–120 peptide populates a nonnative structured conformation, in rapid exchange with a random coil state in aqueous solution (26). This further supports fragment 106–123 (with a score of −9.10 as compared with the score of fragment 3–38, −0.53) as being stabilized in its native conformation by associating with fragment 3–38. Sixth, the peptides, residues 72–100 from bovine α-LA (with or without Cys⁷³ and Cys⁹¹ replaced by alanines) are monomeric and unstructured in aqueous solution (20). This fact, along with the calculated score for fragment 87–108 (−2.95) and the local minimum fragment 70–105 (not shown) with a score of −2.38, reflect the ability of our scoring function in assessing fragment stability.

Figure 4.

The graphical representation at each anatomy level for α-LA (PDB code: 1hfzA). The results presented in this figure corresponds very nicely with the experimental results obtained by partial proteolysis (25). Note that, in this figure, a single helix constitutes a building block fragment. Because the scoring function is empirical, it is unclear above which threshold value a cut fragment is stable when isolated. According to the definition of the scoring function, if a fragment score is positive and the size is above 200 residues, the fragment will be more stable than at least half of the known conformations in the PDB for fragments with similar size (Fig. 2). A short helix assigned as a building block is not owing to its stability (score) but to its fragment size. If the size of an unassigned fragment is larger than the minimum size of a building block, it is assigned as a building block.

Discussion

The Anatomy Tree: Visualizing Dynamic Folding Pathways from Static, Native Folds.

In general, the anatomy of the protein tertiary structure is based on two simple criteria. First, the 3D structure is divided into domains. If individual compact entities stand out in a simple visual inspection, such a division should be feasible. Second, within the domain, recursive structural motifs are recognized as secondary structures (α-helices and β-strands) or are further recognized as supersecondary structures, e.g., as in the case of the helix–turn–helix motif. Richardson (27) devised a particularly nice representation of protein structural anatomy. However, when viewed in this traditional way of protein structural anatomy, no direct relationship can be derived between the recognized domains, supersecondary structures, and secondary structural elements.

Here, we show how from 1D protein chain one can visualize the dynamic folding pathways leading to the 3D fold. We do this by creating an anatomy tree, in terms of the protein folding process. The goals behind the development of an algorithm for dissecting the native protein structure to reveal its anatomy are 2-fold. First, at the lowest, final dissection level, we obtain a set of building blocks, the elements from which the native structure is constructed. However, additionally, by carrying out the dissection through a step-wise, multisplicing progressive procedure, our intention is to obtain the tree organization of the anatomy. And, it is the tree itself that immediately reveals the folding pathway(s) of the polypeptide chain. By following the anatomy tree, from the top down, choosing the routes of the highest scoring building blocks as the nodes sprout, we are able to gauge the more highly traversed routes.

In constructing such an upside-down anatomy tree starting with the native conformation, we make two assumptions. First, the conformations of the building blocks that we observe in the native structure are likely to be those that the building blocks inherently possess. That is, fragments with the same amino acid sequence in solution would most probably have similar conformations. And, second, the stability measurement of an isolated contiguous fragment in a particular conformation reflects its population time during the folding process. In practice, this implies that, in choosing the building blocks, we assume that the building blocks to which we assign high stability scores are the ones that have high population times in solution.

The first assumption appears to be valid. It is well known that protein folding is not a random search toward the native conformation (28). To avoid the huge random search time in the folding process, it is logical to assume that there are some favorable local structures with high population times. Experimental and theoretical studies have already implicitly considered their existence. To name a few, short peptides such as α-helices or β-strands have been observed in solution with substantial population times (29–31). Some secondary structures have been observed experimentally during the very early stages of the folding process (32–34). Peptide fragments have been considered as the model for an initiation of protein folding (35–37). In theory, both the initial formation of “microdomains” in protein folding in the collision-diffusion model (38) and the proposed “foldon” approach (39), where a protein is built from a collection of foldons, are consistent with the “building blocks” concept.

Our second assumption also appears valid. Peptides with high population times have been shown to have a strong hydrophobic core. A relevant example is the β-hairpin peptide. Our simulations of a 16-residue β-hairpin peptide fragment from protein G (40) have shown that it folds rapidly and cooperatively to a conformation with a defined secondary structure and a packed hydrophobic cluster of aromatic side chains. In experiments, this peptide has been observed to be very stable (41).

In practice, then, for our purpose here, the critical issue is the development of a scoring function that would be able to measure the stability of any fragment of the chain, in a fragment-size-independent way. Conforming to such rationale, our algorithm dissects the protein structure into high-population time fragments. The function that we have devised for measuring the stability of the candidate building blocks is statistically based. By including the two types of terms, with respect to both fragment size and as a function of the fraction of the fragment size to the whole protein, we obtain a balance for all fragment sizes. To validate the success of our fragment-size-independent scoring function will require a set of systematically carried out stability measurements either from experiments (25, 41) or from theoretical calculations (42) for protein fragments of different sizes. However, the consistency and the improvement of the HFU assignments via a combinatorial assembly of the assigned building blocks is an indirect evidence for its validity.

The Usefulness of the Anatomy Tree.

Being able to construct an anatomy tree for any protein structure is particularly useful. First, by inspecting the trees we are able to see whether proteins fold through multiple routes. In such a multiple-route case, building blocks at different locations assemble separately; only at later stages do these units combine to form larger structural elements and ultimately the entire fold.

Second, anatomy trees narrate a sequential versus a nonsequential folding pathway story of the protein. The fragment map (Fig. 3A) immediately suggests the likelihood that the protein is a sequential or a nonsequential folder. If more than two branches descend from a node, the protein is likely to be a nonsequential, folding already at that node-level. Third, inspection of the HFUs also illustrated the folding complexity.

Fourth, anatomy trees straightforwardly suggest which proteins are fast folding chains. Fast-folding proteins are likely to be sequentially folding proteins (16, 43). Fifth, here, we illustrate only the predominant pathway down the funnel slope. Hence, by weighing the relative scores at each node, we can choose alternate routes. Fast folders may be expected to have a predominant folding pathway. Sixth, through inspection of the building blocks in the fragment map, we may obtain an insight into folding intermediates trapped along the funnel walls. The conformers residing in these wells largely represent native building blocks in their native conformations. However, their associations involve nonnative contacts.

Recently the contact order, an average measurement of the sequential distance of residues that interact in the structure, has been devised (43, 44). The contact order correlates highly with measured folding rates for a set of single domain proteins with no detectable intermediate folding state. We expect that the contact order between building blocks in the anatomy tree and their stabilities (i.e., computed scores) together with a simple kinetic model will give at least as good a correlation.

Hence, the anatomy tree is rich in useful information, illustrating the actual pathways, the kinetics of folding, the type of folds, and the probability of misfolding. However, additionally, we have a collection of fragments along with their conformations that form the protein structure. Because we collect the fragments at each stage of the dissection process, at the end of the procedure, we are left with a large collection of fragments, ranging in sizes from shorter building blocks to the entire folds. This rich collection is very useful for the prediction of protein structures, whether through fold recognition or for ab initio calculations. Because along with the fragments their stability scores are also presented, these can also serve as a useful library for picking the more stable candidates for folding (unfolding) simulations. (A detailed discussion of these points is given in the supplementary material.)

Conclusions

The approach illustrated here is based on the notion that the native state is a critical determinant of the folding mechanism and of its rate. Rather than imagining that in the search for an optimal fold all potential contacts are tried, leading to a vast number of intermediates formed in the transition state, here we suggest that the native contacts predominate as the chain undergoes its folding process. This idea is implicit in viewing protein folding as being guided by a funnel-shaped free energy landscape. It is based on the idea of minimal frustration that has been shown to be valid for small, fast folding proteins (9–11). Furthermore, these native contacts are largely those existing relatively near each other on the linear chain. Hence, such native contacts are kinetically favored. Even if eventually longer range contacts prevail, the chain would still go through the trial-formation of nearby contacts first, because they are kinetically more favorable than the ones that are farther away. Further, the native contacts that are made early in the folding process are those involving intrabuilding blocks folding. Most building blocks have high population times, as is evident from their observation in solution when in a peptide-fragment form. This suggests that similar folds will manifest similar folding mechanisms, regardless of the variability in their sequences and in their stabilities. These points have been discussed recently (44). Consistently, we observe this situation when we compare the anatomy trees of a mesophilic (from Clostridium symbiosum) and a thermophilic (from Pyrococcus furiosus) glutamate dehydrogenases (not shown). These arguments further suggest that the breadth of the transition state is limited, because it largely involves misassociations of preformed building block conformations, rather than all hypothetical, potential contacts. This is consistent with the view that, in reality, the difference between the “old view” and the “new view” is not that large (10).

Here, we show how, through a dissection procedure of the native folds, we may visualize folding pathways. Based on a practical folding model, “the building block model,” we have designed a top-down multisplicing procedure and a fragment-size-independent scoring function to analyze the anatomy of protein structures. Given 3D protein coordinates, our approach is able to provide explicitly an outline of the most likely folding pathway, via a tree organization of building blocks. The results for any of the single-chain proteins are available via web browsing at http://protein3d.ncifcrf.gov/tsai/anatomy.html. The structural anatomy as generated by our algorithm clearly depicts the organization of a 1D polypeptide chain in 3D space. The success of the anatomy procedure itself further validates the hierarchical nature of protein folding and implies that the folding process is very likely not dominated by a single micropath. If we accept that protein folding is a hierarchical process, we can combinatorially assemble sets of building blocks to produce hydrophobic folding units. Consistently, by performing this procedure, we have obtained a significant improvement in the hydrophobic folding unit assignments, further illustrating the usefulness of this anatomy tree protein folding concept.

Abbreviations

HFU

hydrophobic folding unit

α-LA

α-lactalbumin

1D

one-dimensional

3D

three-dimensional