Discovering functional relationships between RNA expression and chemotherapeutic susceptibility using relevance networks

Abstract

In an effort to find gene regulatory networks and clusters of genes that affect cancer susceptibility to anticancer agents, we joined a database with baseline expression levels of 7,245 genes measured by using microarrays in 60 cancer cell lines, to a database with the amounts of 5,084 anticancer agents needed to inhibit growth of those same cell lines. Comprehensive pair-wise correlations were calculated between gene expression and measures of agent susceptibility. Associations weaker than a threshold strength were removed, leaving networks of highly correlated genes and agents called relevance networks. Hypotheses for potential single-gene determinants of anticancer agent susceptibility were constructed. The effect of random chance in the large number of calculations performed was empirically determined by repeated random permutation testing; only associations stronger than those seen in multiply permuted data were used in clustering. We discuss the advantages of this methodology over alternative approaches, such as phylogenetic-type tree clustering and self-organizing maps.

With the increasing availability of RNA expression microarrays, the current focus is now on elucidating networks of genomic regulation hidden in the large amounts of data. There have been four general techniques used to ascertain the functions of genes from expression data. One way is to list genes by fold-increase or decrease after an intervention. This method has been used to analyze gene expression patterns in human cancer and to find inflammatory disease-related genes (1, 2). Although important, this method typically elucidates only the one regulatory network examined.

A second method involves the assignment of each gene to a multidimensional point with coordinates equal to expression levels at various time points or experiments. Euclidean distances between points are calculated, then graphed by using phylogenetic-type trees. Related genes are thought to be closer to each other in the multidimensional space. This technique has been used to predict functional relationships between genes thought to be involved in central nervous system development (3, 4). The third method involves taking the same type of multidimensional space and constructing self-organizing maps to find clusters of points (5). However, there are problems with both of these methods using Euclidean distances, most notably the difficulty in finding genes negatively associated with each other.

Finally, a fourth method involves phylogenetic-type tree clustering using branch lengths proportional to the correlation coefficient calculated between gene expression levels (6). This methodology has been used to hierarchically cluster chemotherapeutic agents by mechanism of action (7, 8) and to cluster the genes involved in the fibroblast response to serum (9). A problem with this method is that it clusters genes into a single structure and pairs each gene with one other, when several regulatory pathways may be present in biological systems and expressed genes can participate in more than one pathway.

Our purpose here was to develop a methodology that distinguishes true biological associations from noise, generating hypotheses of putative functional relationships between pairs of genes. Specifically, we used baseline RNA expression levels measured from the NCI60, a set of 60 human cancer cell lines used by the National Cancer Institute Developmental Therapeutics Program to screen anticancer agents since 1989 (8). We joined the gene expression levels to a database with measures of cancer susceptibility to anticancer agents, to see how the baseline RNA expression levels in the cell lines correlated with the inhibition of growth of these same cell lines to thousands of anticancer agents. To be clear, RNA expression levels were measured without any exposure to anticancer agents. As shown below, this methodology, termed relevance networks, is able to form clusters without having the problems listed above that are inherent in other methodologies. A feature of a clustering technique such as relevance networks, is that it allows us to find correlations across disparate biological measures, such as RNA expression and susceptibility to pharmaceuticals.

Methods

Gene Expression Data.

RNA expression was measured at baseline in the NCI60 cell lines. Details of the steps needed to measure RNA expression levels in cells have been described (5). HU6800 arrays (Affymetrix, Santa Clara, CA) were used, containing probe sets for 6,416 human genes (5,223 known genes and 1,193 expressed sequence tags). The details of the expression data set are described elsewhere (T. R. Golub, personal communication), and the expression data are available in its entirety at http://www.genome.wi.mit.edu/MPR. Because probe sets for some genes are present more than once on the array, the total number on the array is 7,245. Affymetrix software was used to calculate the relative abundance of each gene from the average difference of intensities between matching and mismatched probe-pairs designed to hybridize a particular sequence.

Anticancer Agent Susceptibility Data.

We used a validated subset of the National Cancer Institute Human Tumor Cell Line Screen containing 5,084 anticancer agents tested against the NCI60 panel (7, 10, 11). The amount of growth inhibition compared with control was measured at several dosages for each chemical and cancer cell line. From this, the GI50, or dose needed to cause 50% growth inhibition, was calculated. For this analysis, susceptibility was expressed as the negative logarithm of GI50.

Although the susceptibility data and baseline RNA expression data were not measured simultaneously, these were both characteristics, or features, of the same cell lines. The data were concatenated together, making a total of 12,329 features measured on the 60 cell lines, or cases. The National Cancer Institute data set was not completely comprehensive, in that there were 18,616 missing anticancer agent susceptibility values.

Removing Features with Low Entropy.

Each feature in the data set was first analyzed to ascertain whether it contained a sufficient range of values. Outlier values in a feature will bias the correlation coefficient when that feature is compared with others; thus, we desired to minimize spuriously high correlation coefficients. To do this, we calculated the entropy of each feature by using

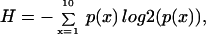where log2 is base 2 logarithm, and p(x) is the probability a value was within decile x of that feature. For example, a gene with the expression amounts 20, 22, 60, 80, and 90 would have deciles 7 units wide, with two values in the first decile, one in the sixth decile, and one in the ninth and 10th decile, making H = 1.92.

We excluded from further analysis the 5% of features that had the lowest entropy (i.e., the least uniformly distributed values) and were likely to bias the correlation coefficient, even though this meant we were unable to construct hypotheses with these features. Of the original 12,329 features, we excluded 544 RNA measurements and 93 anticancer agents, leaving 6,701 RNA expression levels and 4,991 measures of anticancer agent susceptibility. The genes and anticancer agents removed are listed at http://www.chip.org/genomics.

Relevance Networks.

We evaluate the similarity of features by comprehensively comparing all features with each other in a pair-wise manner over the same cases. Several similarity metrics have been previously used in this methodology, including mutual information (12, 13). In this experiment, we rate the similarity of patterns of features by using

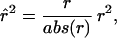where abs is the absolute value function and r² is the sample correlation coefficient. In effect, r̂ is the same as r², the pair-wise correlation coefficient around which a large statistical literature has been built, but retaining the original positive or negative sign of r. All features are connected to all other features with an r̂². We hypothesize that features with a high abs(r̂²) represent hypotheses of a biological relationship. We choose a threshold abs(r̂²), then display only the fraction of relationships at or above that threshold. Groups of features that are connected to each other with abs(r̂²) higher than the threshold will aggregate and form a cluster, or a relevance network. By changing the threshold abs(r̂²), one can tune the relevance networks to include or exclude hypothetical relationships. At lower thresholds, the hypotheses generated may represent novel and true functional relationships, but also will be harder to distinguish from random noise.

Results

Using this methodology, relevance networks were constructed from the 11,692 features (baseline expression of 6,701 genes and measures of susceptibility to 4,991 anticancer agents) in the 60 NCI60 cell lines. There were 68,345,586 pair-wise comparisons between features, of which roughly 22 million relationships were between a pair of genes, 12 million relationships were between two anticancer agents, and 33 million were between a gene and an anticancer agent.

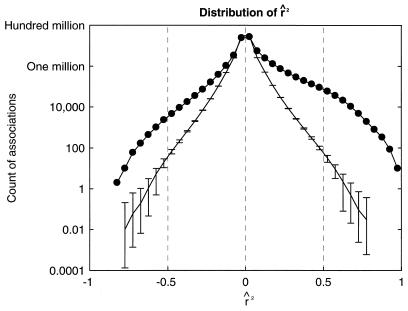
The distribution of r̂² is shown in Fig. 1. Overall, the distribution had a mode at zero and was skewed such that there were 32% more positive correlations than negative ones. Five percent of associations had abs(r̂²) above 0.17. For each gene and anticancer agent, measurements were randomly permuted 100 independent times. The average distribution of r̂² with standard deviations for these permuted data sets also is plotted in Fig. 1. Permutation was unable to create any associations with r̂² at or over 0.80 or under −0.85. Thus, associations found in the original data set with abs(r̂²) at 0.80 were reproduced by permutation in less than 1% of trials and were viewed as highly unlikely to be generated through random chance (i.e., a signal substantially stronger than noise). This was used to determine the threshold abs(r̂²), in that the threshold needed to be at or above 0.80 to maximize the signal strength over noise. We feel this use of permutation to guide the analysis was critical. For example, previously published reports on alternative analyses of this data highlighted associations with r² at 0.55, which is well within the attainable range through random permutation (14).

Figure 1.

A database of baseline expressed levels of 7,245 genes in 60 cancer cell lines was joined with a database containing the amounts of 5,084 anticancer agents needed to inhibit growth of those same cell lines. The joined database contained 12,329 features measured in 60 cell lines. The 637 features that did not contain a sufficient range of values were removed, using an entropy-based method described in the text. The remaining 11,692 features were compared against each other in a pairwise manner making 68,345,586 pairs, in an effort to find anticancer agent susceptibility patterns and gene expression patterns that were correlated with each other. The distribution of correlation coefficients is shown here (r̂² signifies r² retaining the sign, positive or negative, of r). For each feature, gene and susceptibility measurements were randomly permuted 100 times. The average distribution of r̂² for each permuted set is shown with error bars covering two standard deviations. Random permutation was unable to create an association with r̂² at or over 0.80 or lower than −0.85.

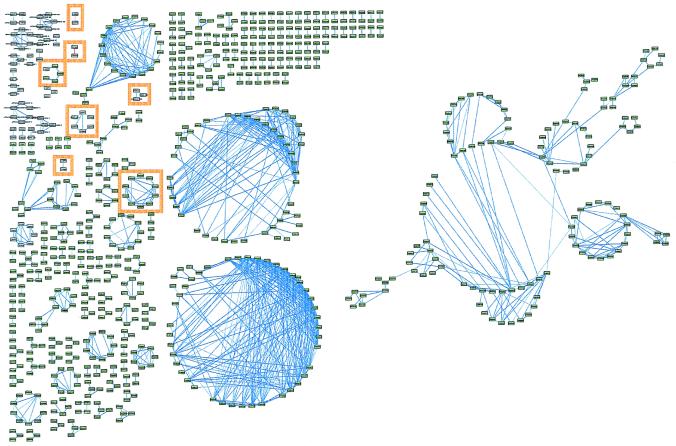
With the threshold abs(r̂²) set to 0.80, there were 202 constructed relevance networks, containing 834 features and 1,222 associations (Fig. 2). The majority of associations were between pairs of measures of anticancer agent susceptibility. Despite the large number of associations shown, this represents fewer than 0.002% of the 68,345,586 total pair-wise comparisons. The diagram is too small to make out specific details and enlarged versions of all of the figures along with the descriptions for each accession number are available at http://www.chip.org/genomics. The relevance networks were graphically displayed by using nodes to represent genes and anticancer agents, and links between nodes to represent hypothetical functional relationships between features. The graphical layout of relevance networks was automatically generated by using the graph editor toolkit (Tom Sawyer Software, Berkeley, CA). Seven specific networks are shown in Table 1.

Figure 2.

Relevance networks constructed from the joined databases of baseline gene expression in 60 cancer cell lines and measures of susceptibility of the same cell lines to anticancer agents. The pairs of features (anticancer agents in green boxes, genes in white boxes) with r̂² at or greater than ± 0.80 were drawn with line thickness proportional to r̂². Features without an association at ± 0.80 were removed. Associations with negative r̂² are in red. Seven networks are highlighted in orange and are in Table 1. Large versions of all figures and descriptions for each accession number may be found at http://www.chip.org/genomics.

Table 1.

Seven relevance networks of the 202 from Fig. 2

The first network is an example of derivative associations, where several of the anticancer agents are slightly modified from each other. Networks 2–7 represent those found that demonstrate or potentially contain biological relationships. Several anticancer agents have no names and were listed only by accession number. Nodes representing measures of susceptibility to a single anticancer agent are shaded green and have labels starting with P. These labels correspond to the agent's National Cancer Institute NSC number. Nodes representing the expression levels of a single gene are in white; labels drawn within each node correspond to the RNA's GenBank accession code. Specific genes may be found by using the index at http://www.ncbi.nlm.nih.gov/Entrez/nucleotide.html, and anticancer agents may be found by NSC number by using http://dtp.nci.nih.gov/docs/dtp_search.html. 

We categorized the associations we found in the 202 networks into a taxonomy of three types: identity or synonymy, derivation, and biologic relationship.

Specific Clusters Found Through Analysis of RNA Expression and Anticancer Agent Susceptibility.

Fifteen of the 202 networks demonstrated synonymy-type associations; 10 of these linked the expression of RNA used as endogenous or spiked controls in the Affymetrix HU6800 array. Four of these 15 networks linked genes that were listed under multiple GenBank accession numbers: SRP20 (L10838 and D28423), tropomyosin alpha chain (M19267 and Z24727), small nuclear ribonucleoprotein B (X17567 and X52979), and nicotinamide N-methyltransferase (U08021 and U51010). One network linked expression levels of laminin receptor precursor (M14199) and laminin receptor mRNA (U43901). These synonymy networks act as a positive control, in that measurements from similar sets of probe pairs should be similar, and the expression patterns should be highly correlated.

One hundred seventy eight of the 202 networks linked anticancer agents exclusively, one of which is shown as network 1 in Table 1. The majority of these associations were between one anticancer agent and another compound chemically related to or derived from the first. The larger networks had associations between many compounds with similar mechanisms of biological action (for example, the alkylating agents).

The remaining nine of the 202 networks showed associations of the third type: those suggesting potential biological relationships. Six of these are listed in Table 1 as networks 2–7. One network (not shown) linked melanoma-associated antigens 2, 3, and 12. These three genes are expressed in melanoma and several other malignant tumors and share a high degree of sequence similarity (15). Another network (not shown) linked caldesmon 1 and alternative splicing products 3 and 4; and a third (not shown) linked two related sequences from major histocompatibility class I (D32129 and X12432).

In Table 1, network 2 correctly linked keratin 8 and 18, two intermediate filament proteins. Keratin 18 is a type I (acidic) keratin and keratin 8 is a type II (neutral/basic) keratin (16), which are known to be coexpressed and function together to stabilize each other from degradation (17, 18). Keratins 8 and 18 do not have a significantly similar sequence.

Network 3 negatively linked glycoprotein Ib beta, which is a component of the platelet receptor for von Willebrand factor, and psd, which contains Sec7 and pleckstrin homology domains. Glycoprotein Ib beta is a component of a receptor involved in the early stages of hemostasis and is known to interact with signaling protein 14–3-3 zeta, which also contains pleckstrin homology domains (19, 20). This link represents a hypothesis that psd represents another protein involved in the signaling cascade from the von Willebrand factor receptor.

Putative Link Between a Single-Gene and Anticancer Agent Susceptibility.

At a threshold abs(r̂²) of 0.80, only one network contains an association between a gene expression and a measure of anticancer agent susceptibility, and this network is labeled 7 in Table 1. The association is between the gene coding for lymphocyte cytosolic protein-1 (LCP1, pp65, or L-plastin, UniGene Hs.198260), and the anticancer agent NSC 624044 (4-thiazolidinecarboxylic acid, 3-[(6-[2-oxo-2-(phenylthio)ethyl]-3-cyclohexen-1-yl]acetyl]-2 thioxo-, methyl ester, [1R-[1α(R*),6α]]-(9CI)). LCP1 is an actin-binding protein involved in leukocyte adhesion (21) whose regulation is steroid hormone receptor-dependent (22). A specific role for L-plastin in tumorogenicity has been postulated; low-level expression of L-plastin is thought to occur in most human cancer cell lines (23). It is hypothesized that phosphorylation of this protein may regulate lymphokine-activated killer cell adhesion to tumors (24). Prostate carcinoma invasion is decreased when levels of L-plastin are suppressed (25). Expression of T-plastin, a related gene, is increased in cisplatin-resistant cell lines (26). Although there is no known relationship between this specific anticancer agent and gene in the biomedical literature, other thiazolidine carboxylic acid derivatives are known to inhibit tumor cell growth (27).

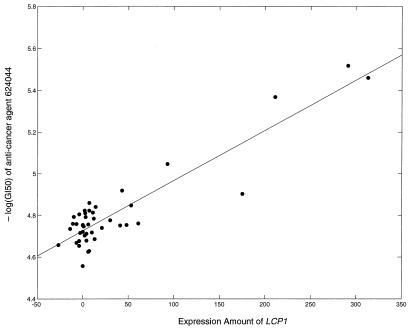
The GI50 of agent NSC 624044 was found to increase in cells expressing more LCP1. A scatterplot of the RNA expression of LCP1 versus the GI50 of cell lines against agent 624044 across cell lines is shown in Fig. 3; the calculated r̂² was 0.83.

Figure 3.

The highest r̂² between a baseline gene expression and measure of anticancer agent susceptibility was between lymphocyte cytosolic protein-1 (LCP1) and anticancer agent NSC 624044, a thiazolidine carboxylic acid derivative. Here, amount of LCP1 expression is plotted against the GI50 of the anticancer agent across the NCI60 cell lines. Line represents fitted linear model with r̂² of 0.83.

Discussion

Using relevance networks, a gene can be directly or indirectly linked to several genes as well as phenotypic measurements, such as measures of anticancer susceptibility. Relevance networks display nodes with varying degrees of cross-connectivity. In the extreme, these are cliques, where every node is cross-connected with every other node in a network. An example is in network 1 in Table 1, where five anticancer agents with similar mechanisms of action were highly cross-connected. These highly cross-connected networks of nodes represent features that are not only associated pair-wise, but also in aggregate. They represent the most trusted associations. Phylogenetic-type trees can only link each feature to one other feature, typically the one it is most strongly correlated with, and do not display additional links (6). In addition, phylogenetic-type trees cannot easily cluster disparate types of biological measures. Phylogenetic-type trees can be calculated to cluster genes and anticancer agents separately, but do not allow one to easily determine the associations between genes and anticancer agents (14).

Several proposed methodologies for functionally clustering genes involve calculating the Euclidean distance between clusters of cell states in expression space (3–6). However, clustering by this metric may ignore genes whose expression levels are highly negatively correlated across cell lines. During relevance network construction, negative correlations are discovered and treated the same as positive ones and are used in clustering.

Because several algorithms now exist to functionally cluster genes, we felt it important to test the significance of our discovered associations in a statistical and quantitative manner. Using permutations of the data, we calculated 100 distributions of pair-wise correlations and were able to highlight only those associations and clusters that were statistically significant in the original data, meaning those demonstrated to be unlikely to be caused by random chance. Although hypotheses representing true biological relationships may exist in associations with weaker strength, we felt they could not be statistically distinguished from random noise. It is possible that if additional experiments were performed or cell lines collected to “exercise” the expression space, the strength of these weaker associations could be enhanced.

The examples listed here show that relevance networks can successfully cluster baseline gene expression measurements in cancer cell lines and measures of anticancer agent susceptibility in those same cell lines. In addition to finding several hypothetical biological relationships between genes and between anticancer agents at the threshold abs(r̂²), we found a strong association between the gene LCP1 and anticancer agent NSC 624044, a thiazolidine carboxylic acid derivative. Other associations between baseline expression levels gene and anticancer agent susceptibilities can be found by setting the threshold strength lower. However, it is important to note that doing so would have increased the likelihood of finding a spurious association as demonstrated by permutation analysis. We feel computing analyses of permuted data should become a minimum standard for testing the statistical significant of a clustering methodology.

Given the paucity of “correct answers” in the literature and the poor annotations in human genome databases, it is difficult to fully evaluate the generated hypotheses without performing the necessary specific biologic experiments. Improving annotations in human genome databases eventually will allow for an automated testing of a hypothesized functional relationship against known information in the biomedical literature.

One limitation in this methodology is that we restrict the comprehensive pairwise comparisons to only those features that demonstrate a sufficient distribution of values across their dynamic range. Spikes, or outlying values in a nonuniform distribution, may be an indicator of the true biological range of a feature, such as a gene that acts as a step function (with only low or high measurements, and none in between). They also may be present when a gene or anticancer agent truly acts uniquely in a single cell line. Because we arbitrarily exclude 5% of features, this means that we did not generate hypotheses that used all of the collected features. We may have missed reporting a valid hypothesis, while trying to avoid reporting false-positive hypotheses.

A second limitation in the analysis is that there is no modeling of measurement noise. The reproducibility of RNA expression as detected on an oligonucleotide microarray is under analysis, and noise may be larger at lower expression values. We currently use raw expression values to compute correlation coefficients. Ideally, a correlation coefficient computed from low expression values should have a wider confidence interval than one constructed from higher, more accurate expression values. One way to address these issues is to compute the cross-entropy, or the amount of information gained about the pattern of one feature given another, instead of correlation coefficient (13).

There are several directions of research indicated. First, cases that violate the model association between two features may represent important exceptions that should be studied. Second, the analysis can be expanded more broadly to include clinical features, so that these may be associated with RNA expression patterns. Finally, the specific hypotheses linking genes to each other and to measures of anticancer agent susceptibility need to be tested, with the promise of discovering potentially new pretherapy markers and drug-resistance genes that could help suggest specific chemotherapeutic agents to use in patients.