Abstract
Perceptual studies make a clear distinction between sensitivity and decision criterion. The former is taken to characterize the processing efficiency of the underlying sensory system and it increases with stimulus strength. The latter is regarded as the manifestation of a subjective operation whereby individuals decide on (as opposed to react reflexively to) the occurrence of an event based on factors such as expectation and payoff, in addition to its strength. To do so, individuals need to have some knowledge of the internal response distributions evoked by this event or its absence. In a natural, behaviorally relevant multistimulus environment, observers must handle many such independent distributions to optimize their decision criteria. Here we show that they cannot do so. Instead, while leaving sensitivity unchanged, lower and higher visibility events tend to be reported respectively less and more frequently than when they are presented in isolation. This behavior is in quantitative agreement with predictions based on the notion that observers represent a multistimulus environment as a unitary internal distribution to which each stimulus contributes proportionally to its probability of occurrence. Perceptual phenomena such as blindsight, hemineglect, and extinction may be, at least in part, accounted for in such a way.
Keywords: decision making, psychophysics, criteria drift, unitary internal distribution
It is well established (1, 2) and by now common knowledge that humans (and nonhumans) can and do set the reference strength of an internal response beyond which internal events will be assumed to represent external events in relation to the probability and/or the payoff associated with the latter: equally energetic events will be reported more frequently if their occurrence is likely (or the payoff is high) than if it is not. Signal detection experiments also have established that, for a unique stimulus strength and occurrence probability, observers can simultaneously entertain a number of response criteria that translate into different levels of confidence as to the occurrence of that stimulus (1, 2). The literature remains silent, however, on the issue of whether or not humans can entertain multiple criteria based on different probabilities associated with a number of simultaneous, spatially distinct events. Common sense admits the proposition according to which the (yes/no) report of the occurrence of any among N distinct events can be biased by the a priori likelihood of that event (Fig. 1a). But is this still the case in an environment characterized by a variety of stimulus intensities? A multistimulus environment where different events differ in their likelihood is the typical milieu of most organisms. Characterizing decision making within such an ambience is, then, of critical significance for understanding how humans regulate (or adapt) the point on their sensory continuum they use as a reference for judging “reality” given the actual magnitudes and probabilities of the ongoing physical events (3). In the present study, this broad issue is scaled down to its most elementary form, whereby decision criteria are studied for only two stimuli at a time that may or may not differ in their strength. In one “baseline” condition, observers' capacity of adjusting their decision criteria to the occurrence probability of the signal was assessed for a number of different strength signals presented in isolation with one out of three occurrence probabilities. A second experimental condition was meant to check whether the performance above (i.e., both sensitivities and criteria) is maintained when two equal strength stimuli with different occurrence probabilities are displayed simultaneously. Potential context-related interactions between decision criteria (and sensitivities) were further studied in a third condition involving the simultaneous presentation of stimuli differing in both strength and occurrence probability.
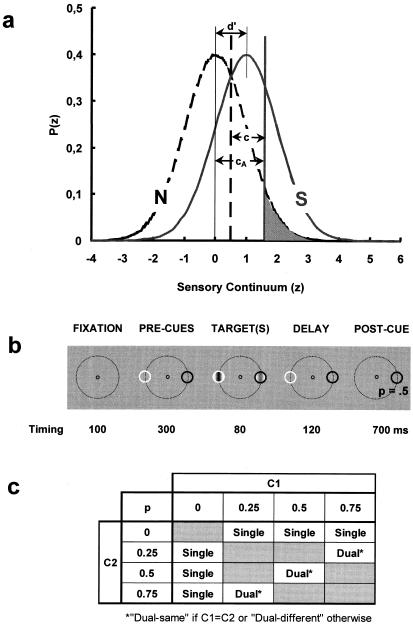
Figure 1.
(a) The Signal Detection Theory (1) framework for the dual-criterion experiment. Gaussian functions describe the probability density, P(z), of the internal response distributions (in standard z-scores; abscissa) for the noise [N: PN(z)] alone (dashed curve) and for the signal + noise [S: PS(z)]. Thin vertical lines show their means with sensitivity (d′ = zHit − zFA, with zHit and zFA the z scores for the observed correct target detection and false alarm rates) being the distance between these means (d′ = 1 in this case) measured in units of the noise standard deviation, σN, and assuming that N and S are normally distributed with σ = σN = σS. We define an “absolute” criterion as cA = −zFA. Defined in this way, criteria are independent of the univariance assumption (i.e., σS = σN), because they depend on the N distribution only. The corresponding values of the likelihood ratio criterion, β = Ps(z = cA)/PN(z = cA), characterize observers' response bias independently of d′. Error rate is minimized when β = PN/PS, (with PN and PS the a priori N and S probabilities) but experimental results show that observers adopt a more conservative behavior with βs closer to one (1). The vertical dashed and continuous heavy lines show optimal criteria for PS = 0.5 and PS = 0.25, respectively. The shaded area denotes the False Alarm (FA) rate for the latter case. (b) One trial sequence as detailed in the text. (c) The 12 experimental conditions as characterized by the combination of two distinct stimuli of contrast C1 and C2 and of four stimulus probabilities.
Experimental Design and Methods
Fig. 1b illustrates the sequence of events within one trial. In each block of trials and on each trial, observers were presented with, in sequence (i) a fixation white circle present during the whole trial; (ii) one white and one black “precue” circles; (iii) two 3 cycles/deg vertical Gabor targets of contrasts C1 and C2 presented within the precue circles with probabilities, P1 and P2; and (iv) after their offset (“delay” period), one of the precues randomly disappeared. Observers had to respond whether or not a target was presented inside the persistent (postcue) circle only. This experimental format combines partial report (4) and signal detection techniques. It requires that observers monitor both locations until the “appearance” of the postcue. The stimuli were presented on a 29 cd/m2 gray background. The fixation circle was 0.5° in diameter. The cue circles were displayed 1.6° to the left and to the right of fixation (on the dashed large circles absent in the actual trials; Fig. 1b) with their locations randomized across trials. The pairs C1,P1 and C2,P2 were consistently associated with the cue polarities, and observers were informed of this mapping before each block. A few blocks also were run with horizontal targets and/or with cues and targets displayed above and below fixation. Incorrect responses were signaled by a short tone (feedback).
For each experimental block, the contrasts of the two targets (C1 and C2) and their probabilities (P1 and P2) were fixed and systematically mapped on each of the two cue polarities with observers having full knowledge of this cue-color/stimulus-mapping at the start of each experimental block. C1 and C2 were in the range of 0.02 to 0.05. The specific values for each observer were chosen based on preliminary experiments with no other constrain than to yield d′s between 0.5 and 3.5 (i.e., most of the measurable d′ range) and d′ differences between 0.7 and 2 (see below). Probabilities of the targets could be 0, 0.25, 0.50, or 0.75. Stimulus characteristics were manipulated to yield three experimental conditions.
The “single” condition involved the presentation of one single target in each trial (obtained by setting one of the two probabilities, or equivalently, one of the two contrasts in a pair to zero). Stimulus characteristics (C and P) were fixed and announced at the beginning of each experimental block. The target was presented randomly across trials within a white or a black cue circle so that cue polarity yielded no meaning in this condition. For a given C, the probability of the signal (0.25, 0.50, or 0.75) was randomized across blocks so that three sensitivity (d′) and criterion (cA, β; Fig. 1a) values were assessed for each C. Signal contrasts also were randomized across blocks.
Under the “dual” conditions, two stimuli/signals were presented in each trial with their probabilities paired so as to yield a constant average signal probability of 0.5 (i.e., 0.25–0.75, 0.50–0.50, and 0.75–0.25). Thus, here again three d′ and cA values were assessed for each contrast in a pair. There were two sorts of dual conditions. Under the “dual-same” condition, the two stimuli in a pair were of identical contrasts (C1 = C2). Under the “dual-different” condition, the two contrasts were different (C1 < C2) and paired so as to yield d′ differences between 0.7 and 2. Fig. 1c displays the 12 stimulus pairings defined by the probabilities and contrasts of the stimuli. C-P pairings were randomized across blocks.
The most extensive data sets (three contrast pairs) were obtained from two naive, well-trained observers. An additional naive observer VR and the first author were run with only one contrast pair. Some critical points in the main experiment also were confirmed with the second author. Observer AG and additional naive observer VR also were run in a second experiment equivalent in all respects to the dual-different condition with the exception that one of the two stimuli never had to be reported and the observers were told so from the start. In all cases, one datum point was estimated from at least 312 trials but more typically from 416–832 trials.
Results
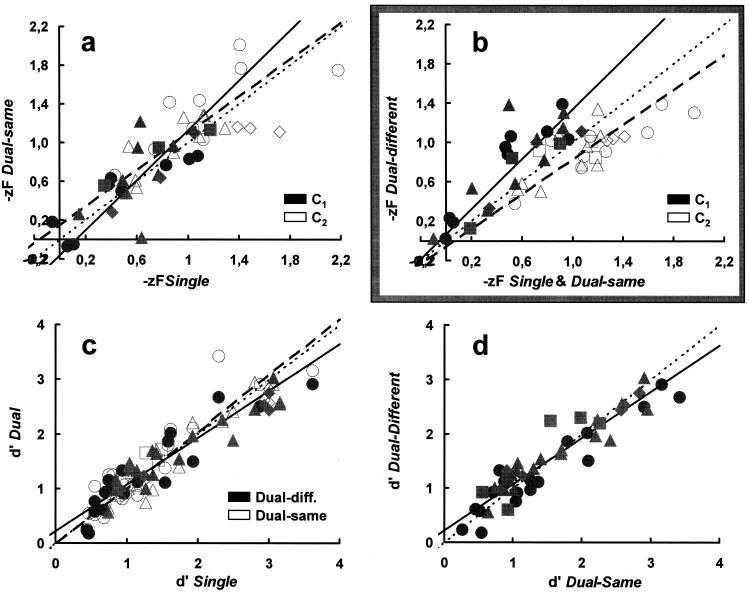
Operationally, the question raised here is whether or not the criteria for the paired stimuli remain unchanged when assessed under single and dual conditions. Fig. 2a shows that the absolute criteria (cA = −zFA, i.e., the standard z-score of false alarms; Fig. 1a) for single and dual-same conditions are scattered about the identity (slope 1, dotted) line for both the low (C1, solid symbols; paired t test = 0.3, df = 40, P = 0.38, not significant) and the high (C2, open symbols; paired t test = −1.05, df = 40, P = 0.15, not significant) contrasts used with each observer. The linear regression lines with errors in both coordinates (5) fit to each data subset (solid and dashed lines, respectively) are also close to this identity line. For both single and dual-same conditions, the average likelihood ratio criterion (β; Fig. 1a) for signal probabilities 0.25, 0.5, and 0.75 was (in agreement with the known conservative behavior of humans; ref. 1) 1.35, 1.05, and 0.75 and did not depend on d′. This is evidence that, for spatially distinct, equal strength stimuli, observers can and do entertain independent criteria in relation to the specified stimulus probabilities.
Figure 2.
Correspondence between criteria (a and b) and d′s (c and d) assessed under single, dual-same, and dual-different conditions. Different symbols are for different observers. Data points represented by identical symbols are for different stimulus probabilities and/or contrasts. (a and b) Solid and open symbols show the absolute criteria obtained for the low (C1) and high (C2) contrasts, respectively, in a stimulus pair. (a) cA[single] vs. cA[dual-same] comparison. The identity locus is shown as the dotted (slope 1) line. Solid and dashed regression lines are fits with errors in both coordinates (5) through the solid (C1 stimuli) and open (C2 stimuli) symbols, respectively. (b) As in a but for the cA[mean (single + dual-same)] vs. cA[dual-different] comparison. Note the upward and downward shifts of the dual-different criteria associated with low (solid symbols) and high (open symbols) contrasts, respectively, in a stimulus pair. (c) d′[single] vs. d′[dual] comparison with closed (solid regression line) and open (dashed regression line) symbols showing dual-different and dual-same data, respectively. The identity line is dotted. (d) d′[dual-same] vs. d′[dual-different] comparison. The identity and the regression line through all experimental points are dotted and solid, respectively.
In contrast with the above, cAs assessed under the dual-different condition are systematically different from the corresponding ones observed under the single and dual-same conditions (Fig. 2b). With very few exceptions, they lie above (solid symbols; paired t test = −5.03, df = 46, P < 0.00002) and below (open symbols; paired t test = 4.37, df = 46, P < 0.0001) the identity (slope 1, dotted) line for the low (C1) and high (C2) contrasts, respectively. This is to say that the cAs associated with the low and high contrasts in a dual-different pair “drift” as if “attracted” by the mean of the internal response distribution associated with the high and low contrast stimuli, respectively. This is so despite the fact that observers have full knowledge of the properties of the signals, that is, of their contrasts and probabilities.
Fig. 2 c and d shows that, unlike cAs, d′s remain insensitive to the experimental condition. They lie close to the slope 1 diagonal, whether assessed in single vs. the average of the dual-same and dual-different conditions (open and solid symbols, respectively, in Fig. 2c) or under dual-same vs. dual-different conditions (Fig. 2d).
The cA shifts observed under the dual-different condition are not entailed by the mere presence of two targets of different contrasts, but rather by the decisions taken on their occurrence. The dual-different condition was rerun with two observers (AG and VR) under conditions where one of the two stimuli (the “companion”) was never reported. The postcue was never presented for this stimulus, whereas the two cue polarities were randomized over the two stimulus contrasts. For a target stimulus of 4%, observer VR showed a slight but consistent criterion drop when the probability of either a 6% or 60% contrast companion (used in different blocks of trials) increased from zero to one. This is an effect opposite to the one observed in the main experiment. Observer AG showed no interaction whatsoever for either a 4% or 6% target in the presence of either a 5% or 60% companion (with each contrast pair run in different blocks). Thus, when one internal response distribution needs not to be estimated (because no related report is requested), the criteria used for the target stimuli do not drift toward the mean of that distribution (as in the main experiment). This observation goes against an interpretation of the main results reported here in terms of some sort of sensory adaptation (6).
Modeling the Data and Discussion
In a multistimulus environment where, potentially, decisions are to be made on the occurrence of any external event, the reliable representation of the internal response distributions associated with each external event is of critical importance for the efficiency of these decision processes. Decision criteria should be set so as to minimize some cost function, for example, the number of response errors (1). A failure to correctly represent the distinct distributions associated with the different targets would translate into criteria shifts. The presently observed criteria drifts may be regarded as the consequence of such a failure. More specifically, the present data are well fit by a model with no free parameters posing that observers have access to only one internal response distribution generated by the incoming stimuli. This unitary distribution is the weighted sum of the internal distributions evoked by each of these stimuli with weights equal to their respective occurrence probabilities. Observers decide on the occurrence of a signal in the standard way, that is, by reference to a given likelihood ratio criterion (β), a number that depends only on the signal probability as denoted by the associated precues, and for that matter, postcues. However, the likelihood ratios observers use for the comparison with this number are computed from the merged distribution. For equal strength stimuli, the unitary distribution will be identical to each individual distribution so that the predicted response criteria for such dual-same conditions should not differ from those observed under single conditions. Note that this model bears only on how observers use the internal response distributions in the decision process whereas leaving these distributions, and therefore, sensitivity, unaffected by the experimental manipulations. Indeed, the present data show no systematic d′ changes with these manipulations.
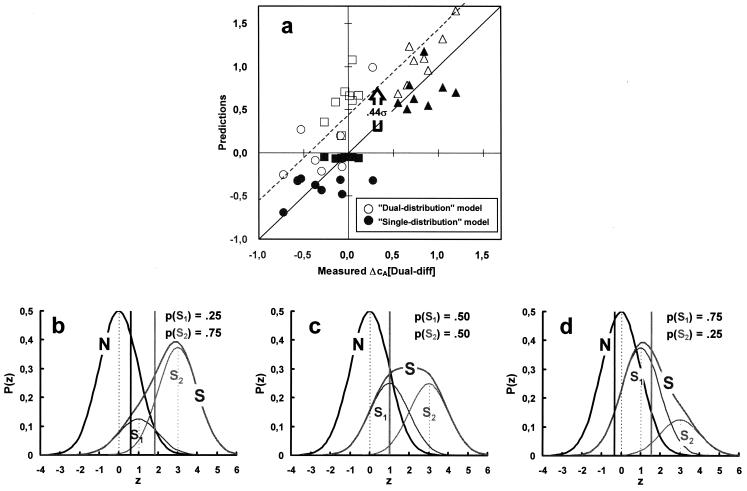
In Fig. 3a, the “unitary distribution” model is used to predict the cA differences (ΔcA) between the two stimuli in the dual-different pairs (closed symbols). This was achieved by using the observers' d′s and βs as assessed for the same stimuli and stimulus probabilities as under the single and dual-same conditions. Fig. 3 b and c provides an illustration of how this was accomplished (see legend). Predictions of the unitary distribution model lie very close to the line of perfect fit (the diagonal of slope 1) and account for 80% of the variance. On the alternative, standard Signal Detection Theory assumption that observers keep track of and independently use each of the two internal distributions associated with the two stimuli under the dual conditions, the dual-different case should yield the same criteria as those assessed under the single and/or dual-same conditions. The open symbols in Fig. 3a represent the actual ΔcAs between the same stimuli as measured in the single and/or dual-same cases. Overall, ΔcAs under the dual-different condition are smaller than those under the single and dual-same conditions (“attraction”; Fig. 2b) by an average of 0.44 (for an average Δd′ of 1.23).
Figure 3.
Correspondence between data and predictions by a dual and unitary internal distribution model. (a) cA differences (ΔcA) measured in the dual-different condition (abscissa) are compared with the corresponding ΔcAs averaged over the single and dual-same conditions (open symbols and dashed line; two-distribution model) and with the predictions of the unitary distribution model (closed symbols). ΔcAs were computed as cA(C2,P) − cA(C1,1 − P), that is between the criteria associated with the high contrast (C2) signal of probability P and the low contrast (C1) signal of probability 1 − P. Circles: cA(C2,0.25) − cA(C1,0.75); squares: cA(C2,0.50) − cA(C1,0.50); triangles cA(C2,0.75) − cA(C1,0.25); note that in the dual-different condition, the above predicted (unitary distribution) and measured ΔcAs are, in order, small and negative, close to zero, and large and positive. Symbols lying along the diagonal of slope 1 passing through the origin show perfect correspondence between data and predictions. The main assumption of the unitary model (b–d) is that, in a multistimulus environment, observers set, for a given stimulus probability, the same (nonoptimal) likelihood ratio criterion (β) as in a single-stimulus (or uniform) environment whereas the likelihood ratios they use for the comparison with this number are computed from the unitary internal response distribution (heavy continuous curves) generated by the ensemble of stimuli on which they have to decide. The unitary distribution is the weighted sum of the internal distributions evoked by each of these stimuli with weights equal to their respective occurrence probabilities (thin Gaussian curves). (b–d) The three contrast-probability pairings used in the experiments. The weaker and stronger signals in a pair are presented with probabilities 0.25, 0.75 (a), 0.5, 0.5 (b), and 0.75, 0.25 (c). Heavy vertical lines show where the criteria should be for each of these probabilities assuming that observers are optimal and use the same β as in the single and/or dual-same conditions. In practice, observers display a conservative behavior under all conditions so that these criteria are closer to each other than shown. Vertical dotted lines show the means of the N- and the two S-distributions. The actual internal response distributions (N and S) remain unchanged under all experimental conditions, so that a given target yields a constant d′ across all conditions.
In a multistimulus environment, precues (and for that matter, postcues) are helpful for optimizing performance when they are used to tag stimulus probabilities but not stimulus strengths. Observers decide on the presence/absence of a signal in relation to the internal response distribution associated with a given external event (7). Optimal decisions in the presence of more than one stimulus require the appraisal of the internal events distributions associated with each stimulus. The present data show that human observers cannot do so even though the different signals are spatially disjoint and unambiguously denoted by consistent precues. Instead, observers appear to use the composite distribution generated by the two simultaneously occurring stimuli and use it as a unitary distribution to set their criteria in accordance with the specified signal probabilities as (in)efficiently as in a single-stimulus environment. The global effect of this behavior is that, relative to the impoverished (single-strength) environments, the criteria they use in more ecological ones are displaced to higher values on the sensory scale (more misses) for the weaker signals, and to lower values (more false alarms) for the stronger ones, provided that the external events considered are behaviorally relevant. This fact generalizes to conditions where the paired stimuli are of orthogonal orientations or different spatial frequencies, or are presented at different eccentricities.§
The present results may bear on the well-known neuropsychological disorders of blind-sight (9), hemineglect (10), and extinction (11). Consequences of cortical injury, these conditions refer, respectively, to the relatively efficient behavior toward objects which the patients claim not to see, to their neglect of half of their sensory space, or of some simultaneously occurring stimuli. Presumably, patients of this kind are in a situation analogous to the one studied here. Given that they present a critical sensitivity drop contralateral to the injury, and on the assumption of a homogeneous physical world, such patients might displace their response criterion toward the mean of their internal responses along the nonaffected sensory space. They will then ignore the weaker internal responses generated in the affected areas. Criterion shifts under these neurological conditions have been invoked (12, 13) and actually observed (14).
The criterion shifts assessed in the present study depend on both the specific strengths (or d′s) and the probabilities of the stimuli involved in the detection task. They are quantitatively accounted for by a model whereby, for a given stimulus probability, observers use the same likelihood ratio criterion in a single-stimulus (uniform) or multistimulus environment but compute the current likelihood ratios needed for the comparison with this number from the unitary internal response distribution generated by the ensemble of stimuli on which they have to decide. This behavior is to be expected in detection (15) or scaling/classification experiments (6, 16) where nontagged, different strength signals are randomly mixed in one experimental block. Not knowing the specific signal (among many) to which an internal response distribution should be associated, observers have no means of keeping track of these distributions; as a consequence, they place their detection or classification criteria in relation to a global internal response distribution representing the ensemble of relevant stimuli. In the present experimental format, however, observers could and actually did keep perfect track of the stimulus identity by using the polarity of the precue and postcue circles. This is indicated by the fact that the criteria obtained under the single and dual-same conditions for the same signal probabilities are practically identical (Fig. 2a). Why then couldn't observers adjust their criteria in relation to each of the two distinct internal response distributions generated under the dual-different condition?
One may pose that, whatever the sampling resources of the system as a whole, it devotes them all to sampling one (intensive) reality at a time to reach a decision bearing on this reality. If equivalent criterion shifts were to be observed within the context of discrimination tasks along dimensions other than intensity (e.g., shape, color, and velocity), this could be regarded as a fundamental constraint imposed by the unity of action (or decision) on this reality (17). An alternative interpretation of the present results would be that the sampling resources of the brain are limited [e.g., to 7 ± 2 samples or chunks (18) or less (8)] and that they cannot be distributed across external events without a significant loss in accuracy. One way or another, the global use of a unitary internal response distribution in judging multiple simultaneously occurring events might account for the unity of the (visual) world as experienced and as acted on. Of course, the generality of this statement is subject to further studies of the present phenomenon in a variety of multidimensional environments.
Acknowledgments
We thank Randolph Blake, Patrick Cavanagh, Elliot Freeman, Avi Karni, Stanley Klein, Larry Maloney, and Joshua Solomon for valuable comments on earlier versions of this paper and Yoram Bonneh for providing the software. This work was supported in part by a joint French-Israeli Grant “Arc-en-ciel.”
Footnotes
This paper was submitted directly (Track II) to the PNAS office.
Gorea, A. & Sagi, D. (2000) Investig. Ophtal. Vis. Sci. Suppl., 41, S751 (abstr.).
References
- 1.Green D M, Swets J A. Signal Detection Theory and Psychophysics. New York: Krieger; 1974. [Google Scholar]
- 2.Macmillan N A, Creelman C D. Detection Theory: A User's Guide. Cambridge, U.K.: Cambridge Univ. Press; 1991. [Google Scholar]
- 3.Tversky A, Kahaneman D. Science. 1974;185:1124–1131. doi: 10.1126/science.185.4157.1124. [DOI] [PubMed] [Google Scholar]
- 4.Sperling G. Psychol Mono. 1960;74:1–29. [Google Scholar]
- 5.Press W H, Teukolsky S A, Vetterling W T, Flannery B P. Numerical Recipes in C. Cambridge, U.K.: Cambridge Univ. Press; 1992. pp. 666–670. [Google Scholar]
- 6.Helson H. Adaptation-Level Theory. New York: Harper & Row; 1964. [Google Scholar]
- 7.Vickers D. Decision Processes in Visual Perception. New York: Academic; 1979. p. 142. [Google Scholar]
- 8.Cowan, N. (2001) Behav. Brain Sci., in press. [DOI] [PubMed]
- 9.Weiskrantz L. Consciousness Lost and Found: A Neuropsychological Exploration. Oxford: Oxford Univ. Press; 1997. [Google Scholar]
- 10.Robertson I H, Marshall J C. Unilateral Neglect: Clinical and Experimental Studies (Brain Damage and Cognition) London: Robin Walker; 1994. [Google Scholar]
- 11.Humphreys G W, Romani C, Olson A, Riddoch M J, Duncan J. Nature (London) 1988;372:357–359. doi: 10.1038/372357a0. [DOI] [PubMed] [Google Scholar]
- 12.Campion J, Latto R, Smith Y M. Behav Brain Sci. 1983;3:423–448. [Google Scholar]
- 13.Klein S A. In: Toward a Science of Consciousness II: The Second Tucson Discussions and Debates. Hemeroff S R, Kaszniak A W, Scott A C, editors. Cambridge MA: MIT Press; 1998. pp. 361–369. [Google Scholar]
- 14.Azzopardi P, Cowey A. Consciousness Cognition. 1998;7:292–311. doi: 10.1006/ccog.1998.0358. [DOI] [PubMed] [Google Scholar]
- 15.Gescheider G A, Wright J H, Weber B J, Kirchner B M, Milligan E A. Percept Psychophys. 1969;5:18–20. [Google Scholar]
- 16.Parducci A. In: Handbook of Perception: Psychophysical Judgement and Measurement. Carterette E C, Friedman M P, editors. Vol. 2. New York: Academic; 1974. pp. 127–141. [Google Scholar]
- 17.Cotterill R M J. J Consciousness Studies. 1995;2:290–312. [Google Scholar]
- 18.Miller G A. Psychol Rev. 1956;63:81–97. [PubMed] [Google Scholar]