Greene SCPrimer: a rapid comprehensive tool for designing degenerate primers from multiple sequence alignments

Abstract

Polymerase chain reaction (PCR) is widely applied in clinical and environmental microbiology. Primer design is key to the development of successful assays and is often performed manually by using multiple nucleic acid alignments. Few public software tools exist that allow comprehensive design of degenerate primers for large groups of related targets based on complex multiple sequence alignments. Here we present a method for designing such primers based on tree building followed by application of a set covering algorithm, and demonstrate its utility in compiling Multiplex PCR primer panels for detection and differentiation of viral pathogens.

INTRODUCTION

Polymerase chain reaction (PCR) is a widely accepted method for clinical detection of pathogens due to its speed, sensitivity and specificity (1). PCR detection of viruses, especially RNA and retroviruses, is complicated by their high mutation rates. Thus, primers for virus detection are frequently designed to amplify highly conserved regions, where binding sites are most likely to be retained. By synthesizing primers with degenerate positions, all the possible variants of a target sequence can be covered. This method has been successfully applied to both pathogen detection and cloning of homologous genes (2–6).

Although the use of degenerate primers increases the flexibility of PCR applications it also increases the complexity of primer design. Degeneracy is a critical factor in the sensitivity of PCR because a highly degenerate primer will have few species that precisely match the template. In early rounds of PCR, the more homologous primers will likely be incorporated into products. The efficiency with which amplification proceeds in subsequent cycles is dependent on the similarity of the remaining primers in the pool. Hence, primers with the least number of degenerate positions have the greatest likelihood of success. The objective of degenerate primer design is to balance the coverage of variant sequences with the negative implications of degeneracy.

A consensus has emerged regarding appropriate GC content, acceptable hairpin lengths, melting temperature and maximum homopolymeric runs for primers (7). Based on these considerations, many software tools have been written for the design of non-degenerate primers (8–12). Degenerate and multiplex primer design has been classified as an optimization problem (13). Thus, heuristic algorithms have been particularly useful in addressing the challenge. Examples include the methods of Doi and Imai (14), GeneFisher (15), PRIMEGENS (11), CODEHOP (2), HYDEN (13), PROBEmer (12), MIPS (16), Amplicon (17), PDA-MS/UniQ (18) and MuPlex (19).

More sophisticated algorithms for primer design, coupled to intuitive public interfaces are becoming necessary to address the increase of sequence information in microbiology. Our work builds on the idea that primer design is an optimization problem that can be solved by adapting methods from computer science. The Set Covering Problem (SCP) has classically been used to describe an airline crew scheduling problem, wherein a group of crews must travel to a set of destinations with minimal cost. A brute force solution, which is an evaluation of all combinations of ‘schedules’, becomes computational intractable with only a few thousand possibilities. The SCP has been classified as NP Complete (20), meaning that no deterministic algorithm can solve it in polynomial time. A variety of approximation algorithms exist for solving the SCP (21–23); the most straightforward is a classical greedy method (24) [for a review, see Caprara et al. (25)]. SCP solving algorithms have been applied in HLA typing (26), identifying RNAi sequences (27), primer minimization in Multiplex PCR (18,28) and recently for creating oligonucleotide microarrays (29).

In this report we describe SCPrimer, a program that determines optimum primer pairs from multiple nucleic acid sequence alignments. The program first computes phylogenetic trees to identify candidate primers, and then uses a greedy SCP solving algorithm to identify the minimum set that will amplify all members of the alignment.

MATERIALS AND METHODS

Algorithm and implementation

Linhart and Shamir (13) provide an extensive description of the degenerate primer design problem and its complexity, which is summarized here. Fix an alphabet Σ = (A, T, G, C), and a primer P = p₁, … , p_k, where p_i ⊆ Σ. At any position, p_i may be more than one character, e.g. (A, G), which can be substituted for the corresponding IUPAC symbol for compact representation. The degeneracy of a primer is the product of the count of characters at each position, d(P) = ${\prod }_{i=1}^k$ ∣p_i∣. A primer P is considered to match a DNA string S = s₁, … , s_l, s_i ∈ Σ if it contains a substring of length k which can be generated from P by choosing a single letter at each position. The problem definition is: given a set of n strings (the templates), is there a primer P of length k and degeneracy of utmost d that matches m of the strings? The problem can be expanded to include a maximum number of mismatches, their positions and a variety of physical characteristics. The problem can be further extended to multiplex primers, by adding a constraint that any set of strings n is matched by only one set primers P*.

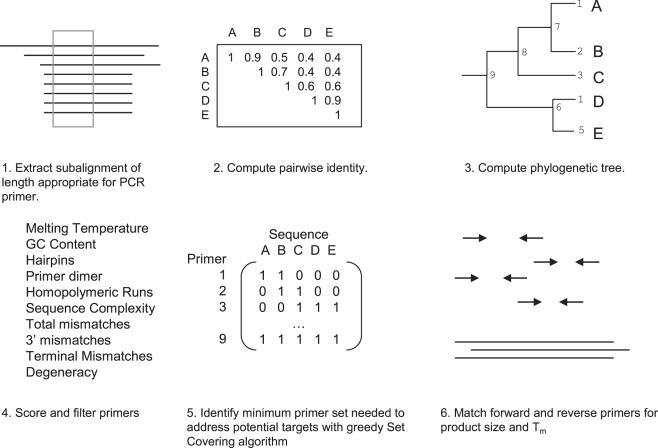
The SCPrimer algorithm consists of four steps, a tree building algorithm, a scoring function, the SCP solver and primer pair matching (Figure 1).

Figure 1.

Schematic diagram of SCPrimer design method. Sequences in a window the size of the desired primer (1) are compared to generate a similarity matrix (2), which is then used to build a phylogenetic tree (3). The consensus sequence for each branch of the tree is determined, then scored (4). Primers that do not pass the criteria are filtered out. A matrix corresponding to the ability of a primer to amplify a template is constructed, where 1 is true and 0 is false (5). The matrix is used by the set covering algorithm to determine the minimal set of primers required to amplify all sequences in the window. Primer pair candidates are matched for T_m and grouped by product size for user review.

Pairwise comparison and tree building

We will consider S to be a multiple alignment where each base can be addressed by row and column as S_i,j, the length of the alignment is ∣max j∣ = l. Sub-alignments S_j…j+k of the user specified k primer length are extracted from the entire alignment and filtered for uniqueness. An all-against-all, pairwise comparison is used to generate a similarity matrix for each sub-alignment. The matrix is used to generate a phylogenetic tree, using a hierarchical clustering algorithm based on Euclidean distance from the open source C Clustering Library (30) [Figure 1, (2)] A consensus which includes all nucleotides is computed at each node of the phylogenetic tree [Figure 1, (3)]. At this point the solution set contains 2n−1 primers of length k for l−k sub-alignments of S.

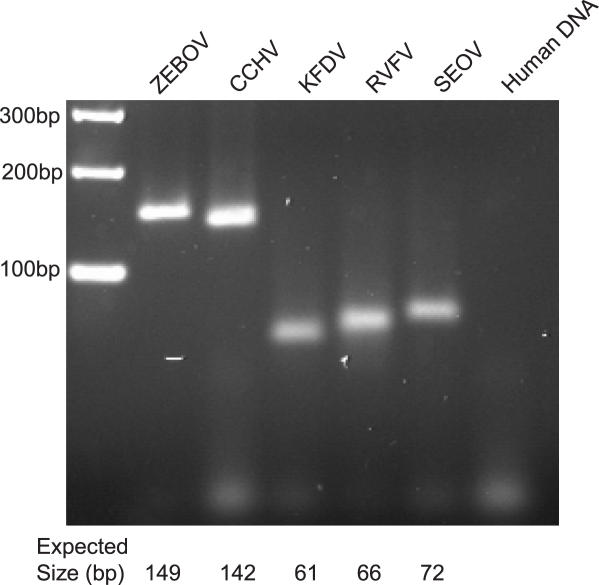
Figure 2.

Viral Hemorrhagic Fever Multiplex PCR primers were combined and used in a multiplex assay to amplify VHF standards at 10⁵ copies from a background of human DNA. Products were size fractionated by agarose gel electrophoresis and visualized by ethidium bromide staining. No products were identified in the absence of template.

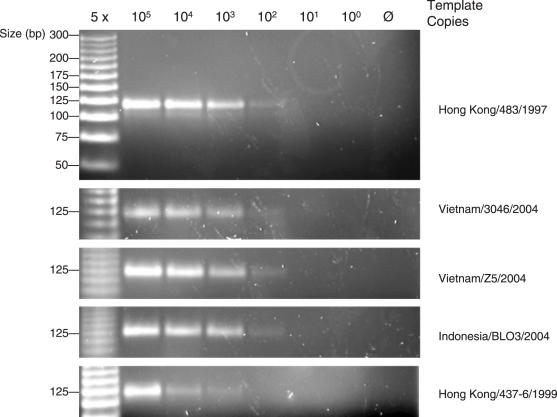
Figure 3.

Sensitivity of Influenza HA5 Primers Consensus primers were tested using linearized DNA standards. Products were size fractionated by agarose gel electrophoresis and visualized by ethidium bromide staining. All standards were amplified; no products were identified in the absence of template.

Scoring function and primer reduction

First, primers are checked for physical constraints, including T_m, GC content, homopolymeric runs, hairpin/primer–dimer formation and degeneracy. The remaining primers are compared to all sequences in the sub-alignment to determine if they are likely to hybridize and be extended complementary to the template. In this phase of the scoring, total mismatches to templates, 3′ mismatches and terminal 3′ mismatches are identified for each primer [Figure 1, (4)]. The output of the mismatch function is a binary value: 1 means the primer can be extended; 0 means it will not. In computational terms, it is an integer matrix that represents a set to cover (sequences, as columns) and elements that accomplish coverage (primers, as rows) [Figure 1, (5)].

Set covering algorithm

The primer extension matrix is the input for the greedy SCP approximation algorithm. The algorithm is implemented using the method described by Slavik (24) to solve the following minimization problem: for a sub-alignment of S_j…j+k which has matching primers P* = (P₁, P₂, … , P_n) find the set I ⊆ P* that minimizes Σc_i (where c_i is a cost function) and matches all substrings in S_j…j+k. In this formulation of the SCP, the primer count is used as the basic cost function for minimization. The cost function can be augmented to reflect primer quality, by adding a negative weight for deviation from ideal parameters. This allows the SCP to choose the better of two primers that cover the same sequences. The output of the algorithm is the minimal set of primers required to amplify all sequences in the sub-alignment S_j…j+k.

Primer matching

The final stage is to select the minimum number of forward and reverse primer sets that are optimized for product length, cross reactivity and T_m. An optional step that we pursue in our laboratory is to search GenBank for other than intended targets (microbial or host) that could confound assay performance by binding to candidate primers.

Algorithms were programmed in Perl, using modules from the BioPerl distribution for sequence manipulation (http://www.bioperl.org). The software is licensed under the GNU GPL (gnu.org), and is free for non-commercial, academic use. A web version is available at http://www.greeneidlab.columbia.edu/. A user may choose to implement heuristics for large alignments to reduce computational time. A fixed percentile of the most conserved sub-alignments can be evaluated (2, 10 or 50%) with the parameter Search Method. Alternatively, one can focus on specific regions that have many representative sequences (Coverage Requirement parameter). Finally, user can choose between two methods to calculate salt adjusted melting temperature; the Nearest Neighbor method (31) (slow, but accurate) or nucleotide frequency formula (32) (fast approximation).

Validation of the SCPrimer design algorithm

The speed of the SCPrimer design program was tested head-to-head with a brute force SCP search method. Speed was tested using an alignment of influenza A virus hemagglutinin 5 gene (HA5) sequences. The analysis was repeated 100 times to control for server load; execution times were averaged. Time trials were carried out on a Pentium 4 1.3 GHz, with 786 MB RAM running Redhat Linux FC3.

Primer design

Influenza HA5 sequences were downloaded from the Influenza Sequence Database (http://flu.lanl.gov) (33). At the time of analysis, the database comprises 449 full-length aligned sequences with isolation dates ranging from 1959 to strains of the recent avian influenza outbreak.

Viral hemorrhagic fever (VHF) virus sequences were extracted from the NCBI GenBank. The viral targets included Zaire Ebola Virus (ZEBOV, 7 sequences of the L polymerase), Crimean Congo hemorrhagic fever virus (CCHV, 32 sequences of the nucleocapsid), Seoul virus (SEOV, 26 sequences of the nucleocapsid), Kyasanur Forest disease virus (KFDV, 14 sequences of the NS5 gene) and Rift Valley fever virus (RVFV, 21 sequences of the NSs gene). Sequences were aligned using ClustalW (34) and then submitted to SCPrimer.

Design criteria for primers were as follows: 18–32 nt in length, Nearest Neighbor T_m 50–65°C (optimum 60°C) with sodium concentration of 50 mM, 40–60% GC, maximum allowed hairpins of 8 nt, a maximum homopolymeric run of 4 nt, maximum degeneracy of 16, no mismatches allowed in 3′ pentamer, maximum of three mismatches to any targeted template and an amplicon size of 60–150 nt. Primer pairs with melting temperatures within 3°C of each other were selected. The least degenerate primer pairs that fulfill those criteria were synthesized commercially (MWG Biotech, High Point, NC).

Standards and cycling protocol

To verify the sensitivity and specificity of the primers we created and cloned DNA standards for reference strains of VHF viruses by overlapping PCR. The influenza hemagglutinin gene (1.8 kb) was cloned for five strains of H5N1: Hong Kong/483/1997 (AF046097), Vietnam/3046/2004 (AY651335), Vietnam/Z5/2004, Indonesia/BL03/2004 and Hong Kong/437-9/1999 (AF216721). Clones of reference strains of HA1, three and seven were used as negative controls. Standards were generated by diluting linearized plasmid into 2.5 ng/μl human placental DNA (Sigma-Aldrich, St Louis, MO).

The HotStar Taq polymerase Multiplex PCR kit (Qiagen, Hilden, Germany), was used. Primers were used at a final concentration of 1.25 μM for singleplex and 0.5 μM each for Multiplex PCR with 2.3 mM MgCl₂ and 55 μM dNTP. Primers for the influenza HA5 PCR were mixed to a final concentration of 1.5 μM. The following touch-down cycling protocol was used: 95°C for 5 min; 95°C for 20 s, 20 s annealing from 65 to 57°C in −1°C increments, extension 72°C, 30 s for 7 cycles; then 38 cycles continuing with a cycling profile of 94°C for 20 s, 57°C for 20 s and 72°C for 30 s.

RESULTS

Computational complexity evaluation

SCPrimer processes an alignment in four steps: tree building, primer scoring, minimization with the greedy SCP solver and primer pair matching. At each step, the program is optimized to minimize analysis time (Figure 1).

The first step is building a tree using sequence similarity for sub-sections of the alignment; running time is proportional to the cube of the number of sequences, or O(n³) (35). In practice, the clustering subroutine completes in milliseconds, even with large alignments. The tree is then traversed from leaf to root, computing consensus sequences at each branch. Each consensus is a potential primer. Thus, the maximum number of primers to consider is the number of nodes on the tree. Primers are only designed in regions of the alignment with high conservation; the user can determine the threshold percentage for conservation that will be considered.

Step two is the scoring of each potential primer against all sequences in the alignment. A staged scoring function is used to minimize computation. Basic measures of primer quality are assessed first including GC content, single nucleotide repeats and terminal mismatches to templates.

Step three, potentially the most time consuming, minimizes the number of primers required to amplify a target set by using the SCP solver. Heuristic searches are currently the most efficient method to solve the SCP. The use of the greedy heuristic for the SCP guarantees nearly nlogn performance (24), where n is the number of primers to choose from.

The fourth step in the program is to identify primer pairs with matching T_m suitable for amplifying products of a specific size range. Using a lookup table, this step completes in linear time.

The computational time required to address a test alignment of 449 influenza HA5 sequences was minutes with SCPrimer, but ∼2 h using a brute force strategy. The brute force search method enumerates all combinations of primers and scores them all, returning the true minimum set. Greedy algorithms such as SCPrimer may not return the optimal solution for any problem (36); however, in this application both algorithms returned the same solutions for the HA5 alignment.

Application of SCPrimer to Multiplex PCR primer selection

Primers were designed for five VHF viruses to test performance of the program in creating Multiplex PCR panels. Nucleotide alignments were created for ZEBOV, CCHV, SEOV, KFDV and RVFV. The alignments comprised >30 sequences in most cases; thus, the processing time was negligible (Table 1).

Table 1.

Viral hemorrhagic fever primer panel

Virus	Reference strain	Gene	Direction	Sequence (5′–3′)	Tm (°C)	Amplicon length (nt)
Zaire Ebola Virus (ZEBOV)	NC_002549	L Polymerase	F	TTCCCTCCGTTGCCAATGATTAAAGAAC	59.5	149
			R	ACTGCATCCCAGCATGTCCTTTC	59.0
Crimean Congo hemorrhagic fever (CCHV)	U88412	Nucleocapsid	F	ACTYGTTGCAACWGGCCTTGC	59.4	142
			R	CATGYTGTCRGCACTTGCTTTRTCAAC	60.2
Seoul virus (SEOV)	NC_005236	Nucleocapsid	F	YGATGARYTGAAGCGCCARCTTGC	61.7	72
			R	GTAGGATCCCGRTCYTGCCC	57.8
Rift Valley fever virus (RVFV)	NC_002045	NSs	F	ACYGAGGCYATCCTMAGAGGGATTGAC	61.6	66
			R	AWYCTCATACATGASRTCAAAGCCTGGCAAC	62.2
Kyasanur Forest disease virus (KFDV)	NC_004355	NS5	F	CGTRTGGARGCCTGGCTGAAAG	59.6	61
			R	CRCTGACCAGCATRCGGGT	58.9

PCR primer performance was initially assayed in singleplex PCR using linearized DNA standards representing the respective virus reference strains. All target sequences were amplified resulting in products of the appropriate size (data not shown). Thereafter, primers were tested in multiplex assays comprising all 10 primers and an individual DNA standard. All VHF virus targets were successfully detected (Figure 2).

Validation of SCPrimer with large alignments

To assess the performance of primers selected from larger multiple sequence alignments, influenza HA5 primers were designed targeting all HA5 sequences described at the time of writing (449 sequences; 9/2005) (Table 2). Five isolates of H5N1 were detected at a sensitivity of 5000 molecules/PCR assay (Figure 3). HA5 primers were specific in that no products were obtained with HA1, 3 and 7 controls (data not shown).

Table 2.

Influenza hemagglutinin gene primers

Forward primer	5′–3′ Sequencea	Alignment percentageb	Mismatches to templatec	Reverse primer	5′–3′ Sequence	Alignment percentage	Mismatches to template
HA5F1	GTYACTGTBACACAYGCCCAAG			HA5R1	CCGAGGAGCCATCCAGCTACACTA
	GTtACTGTtACACAtGCCCAAG	85.0	0		CCGAGGAGCCATCCAGCTACACTA	93.8	0
	GTcACTGTtACACAcGCCCAAG	4.3	0		CCAAGGAGCCATCCAGCTACACTA	1.2	1
	GTcACTGTtACACAtGCCCAAG	3.2	0		CCGAGGAGCCATCCAGCTCCACTA	0.5	1
	GTtACTGTcACACAtGCCCAAG	2.0	0		CCGAGGAGCCATCCGGCTACACTA	0.5	1
	GTgACTGTcACACAcGCCCAAG	0.3	0		CCGAGGAGCCATCCAGCCACACTA	0.5	1
	GTtACTGTtACACAcGCCCAAG	0.3	0		CCGAGGGGCCATCCAGCTACACTA	0.2	1
	GTtACTGTcACGCAtGCCCAAG	0.3	0		CCCAGGAGCCATCCAGCTACACTA	0.2	1
	GTtACTGTgACACAtGCCCAAG	0.3	0		CCGAGAAGCCATCCAGCTACACTA	0.2	1
	GTtACTGCtACACAtGCCCAAG	0.3	0		CCGAGGAGCCACCCAGCTACACTA	0.2	1
	GTtACTGTtACACAtACCCAAG	0.3	1		CCGAGGAGCCAACCAGCTACACTA	0.2	1
HA5F2	GTGACGGTCACACATGCTCAGG				CCGAGGAGCCATCCAGCGACACTA	0.2	1
	GTGACGGTCACACATGCTCAGG	1.2	0	HA5R2	CCGAGGAGCCATCCAGCTACGCTA
HA5F3	GTTACTGTTACACATGCCCAAA				CCGAGGAGCCATCCAGCTACGCTA	1.0	0
	GTTACTGTTACACATGCCCAAA	1.2	0	HA5R3	CCAAGAAGCCATCCAGCCACACTG
HA5F4	GTTACTGTTACACATGCTCAAG				CCAAGAAGCCATCCAGCCACACTG	0.7	0
	GTTACTGTTACACATGCTCAAGd	1.4	0		CCAAGAAGCCACCCAGCTACACTG	0.2	2
					CCGAGGAGCCATCCAGCTACACTG	0.2	3

^aDegenerate positions are in lower case; primers are in boldface.

^bUnique template sequences and their representation in the alignment.

^cPrimer mismatches to each template sequence, nucleotide is indicated in boldface.

^dDark bar represents the 3′ pentamer where no mismatches are allowed.

DISCUSSION

The objective of SCPrimer is to provide a simple program for standardized consensus primer design that facilitates the development of multiplex assays and extracts the minimum primer set required to address complex alignments.

VHFs are triggered by an infection with filoviruses (Ebola Virus or Marburg virus), arenaviruses (Junin, Machupo or Lassa viruses), bunyaviruses (Congo-Crimean hemorrhagic fever or Rift Valley fever) or flaviviruses (Omsk hemorrhagic fever, Kyasanur Forest disease virus or Yellow Fever virus) (37,38). VHF agents pose a significant problem for public health because of high morbidity, mortality and the potential for rapid spread. Their evolution poses a continuous challenge to the utility of diagnostic PCR assays (39). SCPrimer enables the continuous update of diagnostic panels and is well suited to outbreak applications, as the reported VHF primers were designed in hours. By matching critical parameters like the T_m, 3′ clamp length and number of degenerate positions, primers designed for different viruses behave uniformly in PCR. Prediction of cross reactivity among primer sets is a feature which will be incorporated into later versions of SCPrimer. A different multiplex VHF primer panel, created with a beta-version of the program, was successfully applied in MassTag PCR detection of VHF agents in clinical specimens (40). MassTag PCR is a diagnostic platform wherein primers labeled with photo-labile unique mass signatures are used to identify the presence of genetic targets (41).

Influenza viruses have emerged as high-priority pathogens with global dissemination of H5N1 and appreciation of its pandemic potential. More than 4000 H5N1 sequences were deposited in GenBank through May 2006; thus, the design of HA5 consensus primers is a daunting task using a multiple alignment strategy. If the HA5 forward primer was designed using a standard consensus method, it would comprise 3072 species to cover all sequences without mismatches. This is not practical. One approach to the problem of reducing degeneracy in primer design is to split the alignment by genotype and then identify consensus sequences for each subgroup alignment. This strategy is time consuming; many combinations would be identified and each potential solution would have to be evaluated independently. The tree building and greedy heuristic employed in SCPrimer is a natural solution to such combinatorial problems. For example, SCPrimer identified a minimum set of four forward primers for the HA5 alignment that would address all known targets. A single degenerate primer covered 96.3% of sequences; three additional primers were needed to cover the remaining sequences.

CODEHOP has been used to identify new DNA viruses (42), and is therefore of particular interest for microbiologists working in pathogen discovery. CODEHOP is a program for degenerate primer design that is most similar to SCPrimer. However, the emphasis of CODEHOP is different from that of SCPrimer; CODEHOP performs exclusively at the amino acid level and tries to identify all theoretically possible nucleic acid coding variants resulting from the degenerate genetic code. Thereby it does not, and does not attempt to, minimize the degeneracy of the primer. SCPrimer restricts its scope to all variants represented in an alignment and attempts to provide the best solution for a user-defined maximum degeneracy per primer. In addition, the input for the web-based version of CODEHOP requires ungapped amino acid alignments of maximum width 55. Thus, it cannot address the comprehensive influenza HA5 alignment of width 600. We compared primers designed by CODEHOP for a 55 amino acid region which encompassed the HA5 primer-binding sites identified by SCPrimer. We executed CODEHOP with default settings and selected the least degenerate primer pair with a T_m near 60°C for analysis. The CODEHOP forward primer (CGTGACCCACGCCcarrayathyt) overlapped the 3′ end of the HA5F primer-binding site and had a degeneracy of 48. Upon comparison with the nucleic acid alignment, the primer had between three and five mismatches to every sequence. The reverse primer (ggntacacrctGCTCAAGTAGTTGCACGG) had degeneracy of eight, and between one and six mismatches to all sequences. Given that sensitivity decreases with increasing complexity of primer panels, the primers designed by CODEHOP may be sufficient for identifying known and novel sequences where transcripts are abundant, but may perform inefficiently in diagnostic PCR where sensitivity is critical.

SCPrimer was created to address the specific needs of virologists and bacteriologists in creating primers for pathogen detection. Although an ‘optimum’ sequence could be estimated by a more complicated scoring mechanism, this would not reflect the reality of experimental PCR. Investigators who wish to generate assays with highest sensitivity generally tune several potential primer pairs. Owing to the investment required to develop, optimize and validate diagnostic primers, an automated design program provides a reliable starting point for experimental evaluation.

CONCLUSION

We present a primer design program that uses the well-studied SCP, coupled with a tree building approach to select comprehensive primer sets. The program identifies sets which cover all sequences in multiple sequence alignments by a user-specified number of degenerate positions. The algorithm was tested with alignments of viral pathogens, and used to design primers that were sensitive and specific in singleplex and multiplex assays. Future versions of the program may incorporate secondary nucleic acid folding predictions to target only relaxed accessible regions, coverage of likely silent mutations with codon preference and use of structural information to identify highly conserved positions. Further, the output primers of SCPrimer conform to PrimerExpress™ (Applied Biosystems) parameters and implementation of a real-time probe design feature based on multiple sequence alignments would be a natural extension of our program.