A physical analogue of the Schelling model

Abstract

We present a mathematical link between Schelling‘s socio-economic model of segregation and the physics of clustering. We replace the economic concept of “utility” by the physics concept of a particle's internal energy. As a result cluster dynamics is driven by the “surface tension” force. The resultant segregated areas can be very large and can behave like spherical “liquid” droplets or as a collection of static clusters in “frozen” form. This model will hopefully provide a useful framework for studying many spatial economic phenomena that involve individuals making location choices as a function of the characteristics and choices of their neighbors.

At the end of the 1960s Tom Schelling (for a summary see refs. 1 and 2) introduced a model of segregation in which individuals, living on a lattice, chose where to live on the basis of the color of their neighbors. He showed that even if people only have a very mild preference for living with neighbors of their own color, as they move to satisfy these preferences, complete segregation will occur. This result is considered surprising and has generated a large literature. The structure of the segregated areas is known to be related to the free space available and the exact specification of the rules that govern how individuals move. However, no general analytical framework that encompasses all of the variants of the model has yet been proposed.

The original model was very simple. Take a large chess board, and place a certain number of black and white counters on the board, leaving some free places. A counter prefers to be on a square where half or more of the counters in his Moore neighborhood (his eight nearest neighbors) are of its own color (utility 1) to the opposite situation (utility 0). From the counters with utility 0, one is chosen at random and moves to a preferred location. This model, when simulated, yields complete segregation even though people's preferences for being with their own color are not strong.

We show that some simple physical theory can explain the segregation phenomena, which have been observed in the numerous variants on Schelling's original model. The variants involve modifying the form of the utility function used by Schelling, the size of neighborhoods, the rules for moving, and the amount of unoccupied space (see ref. 3 for a survey). One attempt to provide a formal structure has been made by Pollicott and Weiss (4). They, however, examine the limit of a Laplacian process in which individuals' preferences are strictly increasing in the number of like neighbors. In this situation it is intuitively clear that there is a strong tendency to segregation. Yet, Schelling's result has become famous precisely because the preferences of individuals for segregation were not particularly strong. Another related approach is that of Wolfram (5), who studies the evolution of clusters and strips in a 2D cellular automaton.

The Schelling result is of interest to economists because it illustrates the emergence of an aggregate phenomenon that is not directly foreseen from the individual behavior and because it concerns an important economic problem, that of segregation. Our analysis exhibits three features of the resultant segregation. The first is the organization of the system into “regions” or clusters, each containing individuals of only one color and the nature of these clusters. We explain the shape of the frontier between the regions. The second feature is the importance of the number of empty spaces in determining the final cluster configuration. We explain the role of the free space and how it winds up as a “no-man's land” between clusters. The third aspect concerns the rules that govern the movement of individuals. For example, we can decide to move agents only to empty spaces, allow agents to swap places, or allow only local movement as opposed to movement over any distance. We explain how and why these rules matter.

The Schelling model is based on the standard idea in economics that an individual agent makes decisions based on his preferences or utility function. This idea can be interpreted in physical terms as saying that decisions are driven by changes in the internal energy. Indeed there has been a long debate in economics over the use of this analogy (6). In our interpretation, the agent's satisfaction is equivalent to the energy stored in him. An increase in happiness is a decrease in internal energy. An agent, therefore, wants to minimize his energy, which is generated either by taking some action or through the interaction with his environment. The Schelling model assumes that the agent's utility depends on his local environment and that he moves if the utility falls below a certain threshold.

A Physical Model

Given this interpretation we can now switch completely to the physics analogy by treating agents as physical particles. In the Schelling model, utility depends on the number of like and unlike neighbors. In the particle analogue the internal energy depends on the local concentration (number density) of like or unlike particles. This analogue is a typical model description of microphysical interactions in dynamical physical systems of gases, liquids, solids, colloids, solutions, etc. Interactions between particles are governed by potential energies, which result in interparticle forces driving particles' dynamics.

The goal of such models is to study the collective behavior of a large number of particles. In the Schelling model the number of particles is conserved and the total volume in which they move is constant (that is, the underlying grid is fixed). Because particles do not gain or lose energy due to the movement itself, the pressure can be considered as constant. The system is not closed, however, because the energy lost by a particle is not transferred to other particles, but transmitted out of the system. Similarly, a particle can gain energy from outside the system when an unlike particle moves into the neighborhood and lowers the particle's utility. Hence, the system changes its energy only by emitting or absorbing radiation and not by changing its volume or pressure or number of particles.

The basic tendency of such a physical system is to minimize its total energy. Here, it can only achieve this goal by arranging particles into structures (clusters) that reduce the individual internal energy of as many particles as possible. In other words, interparticle forces induce particles to cluster and the formation and stability of a cluster is determined by these forces. Clearly, the only particles whose energy may change are those on the surface of a cluster. Hence, all we need to do is to look at the behavior of this force on the surface of a cluster to see whether the surface will be stable or if it will undergo deformations and ripping.

A preparatory step for the analysis of interparticle forces is to transform the discretized lattice of the Schelling model into a continuous medium. We replace the area ΔA of a lattice cell with a differential area dA. In the discrete case, this area is populated with only one agent or it is empty, but in general terms it is ΔN number of agents. In the continuous model this translates into dN, which then gives the number density of particles n(r⃗) = dN/dA at a point r⃗. The Schelling model does not allow for more than one particle at a lattice cell, hence n is constant across a cluster.

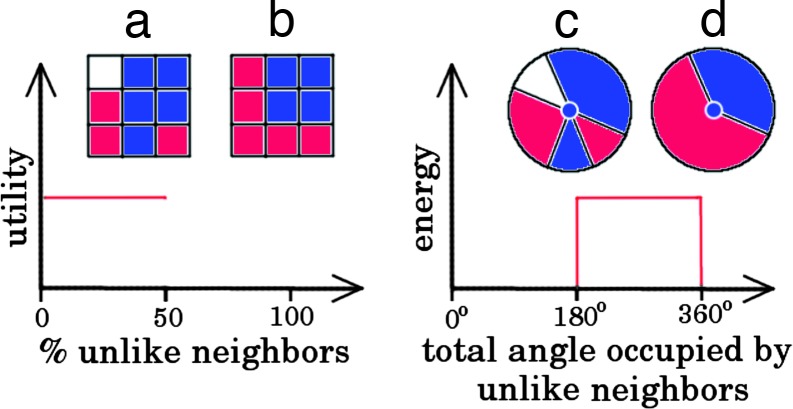
Next, we transform the utility function from counting the individuals in a neighborhood around an agent into the measurement of the total solid angle θ covered by different particles around a differential area dA (Fig. 1). Utility is replaced with energy ε(θ), with high utility corresponding to low energy and vice versa. We thus have the total energy dE = nε(θ)dA stored in dA or energy per unit area dE/dA = nε(θ). Because we are interested in the cluster surface, we take a differential length dL of the surface and write its energy per unit length as dΣ = nε(θ)dL. The total surface energy of a cluster is an integral of dΣ over the whole cluster surface. A cluster's dynamics is driven by its trying to minimize this surface energy. In physics, Σ is usually called surface tension. Notice that dΣ depends on the local surface curvature because we choose dL small enough to be a contact point of only two clusters (Fig. 1d).

Fig. 1.

Transition from a finite difference model into a continuous model. The Schelling model (Left) can be considered as a finite difference version of a more general continuous model (Right). Instead of counting neighboring individual grid cells, we can use angular coverage around a point where one neighboring grid cell on a rectangular grid corresponds to 45° angular coverage. In this way the cell configuration (a) is transformed into c and b into d. White represents empty space. Utility is the mirror of energy: high utility means low energy and vice versa. Energy is a function of the angle covered by unlike neighbors, and utility depends on the number, or proportion, of unlike neighboring cells. Now we have a complete description of the transformation from the Schelling model into its physics analogue.

If we take a local gradient along dL then we end up with the tension force

where L̂ is a unit vector along dL. The same force, but in the opposite direction can be derived for −L̂. Eq. 1 shows that specifying the utility function amounts to specifying the surface tension force of a cluster, where the force is a function of the local curvature θ(r⃗). We can then predict the behavior of a cluster, and, as a result, that of the whole system, for a given utility function. Schelling's model is, therefore, a finite difference version of a differential equation describing interparticle forces.

Cluster Formation

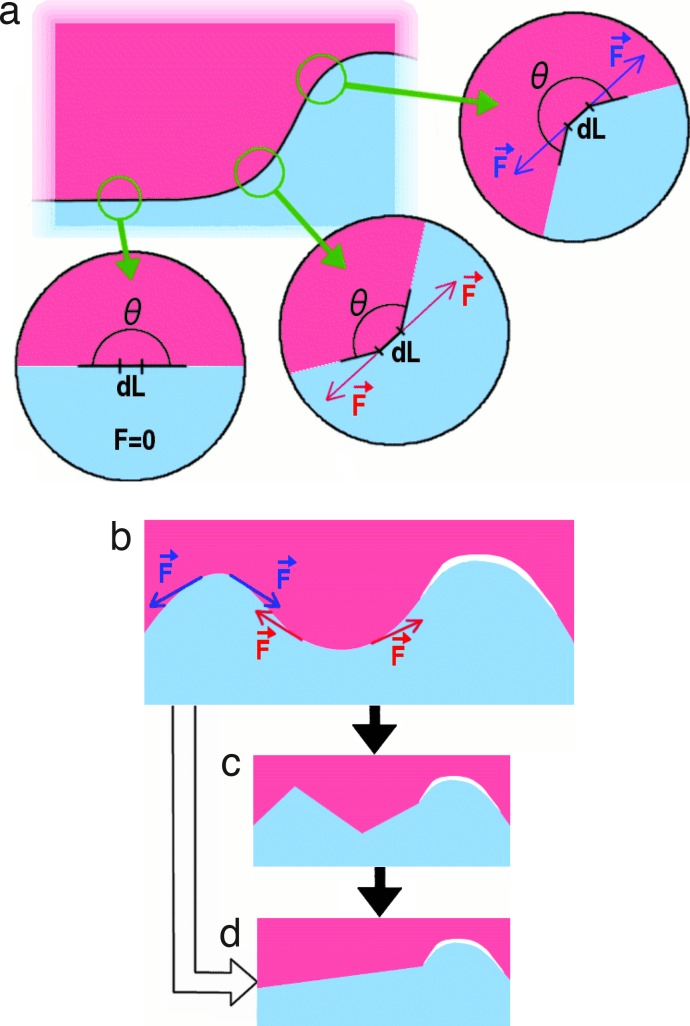
The basic utility function in the Schelling model is the step function shown in Fig. 1. The energy is either a constant ε₀ for θ > 180° or zero for θ ≤ 180°. From Eq. 1 it follows that any convex cluster surface experiences the tangential force F = nε₀, which tends to flatten the surface (Fig. 2). Because the utility function depends only on neighbors and ignores empty spaces (empty space yields ε = 0, hence F⃗ = 0), a boundary layer of empty space stabilizes a cluster by preventing it from having direct contact with other clusters. The outcome of this surface reshaping is clusters with flat surfaces, except for parts adjacent to a boundary layer of empty space.

Fig. 2.

Forces in a continuous version of the Schelling model. The evolution of clusters can be analyzed by considering the forces on the surface of a cluster, where the utility function defines the surface tension force (Eq. 1). (a) Shown are forces on infinitesimally small sections dL of the surface when x = 0.5 in the utility function from Eq. 2. Vector colors correspond to the color of the cluster experiencing these forces. (b–d) A sequence in surface evolution. The forces have a tendency to flatten the surface (b → d), but this process will go through an intermediate phase (solid arrows), where the surface flattens first locally (b → c → d), if agents are allowed to move only to the closest available location. The evolution is faster (hollow arrow) if agents can move any distance because then they can immediately participate in flattening of the whole cluster. Empty space (white regions) can form a boundary layer where the surface can maintain its irregular shape.

The cluster dynamics resulting from Eq. 1 have been extensively explored in theoretical and experimental physics (see Related Physical Phenomena). A detailed quantitative description (cluster size distribution, timescale of cluster growth, etc.) is beyond the scope of this article, although the qualitative description goes as follows.

When clusters start to grow they compete for particles. Initially, small clusters are kinetically favored because they are easy to form. If the system does not reach its energy minimum after this initial clustering then bigger clusters start to grow by taking particles from, or by merging with, smaller clusters. Particles on the cluster surface risk having low utility and thus, are energetically less favored, which means that bigger clusters now become energetically favored because of their smaller surface-to-volume ratio. Eventually, one cluster grows bigger than the others and grows until it collects all available particles. Smaller clusters can only exist if they “freeze” their particles, preventing them from “evaporating” and traveling to the big cluster. Two things can happen with big clusters. Either clusters touch the system boundaries and the whole system becomes segregated into two distinct clusters separated by a flat surface, or a single spherical cluster forms away from the boundaries because particles have the same probability of reaching the cluster's surface from any direction.

Rules Governing Particle Movement

The exact behavior of the system and its clusters depends not only on the choice of the utility function, but also on the rules governing particle movement. These rules dictate the rate of evolution, whereas Eq. 1 dictates the final configuration that the system tends to reach. In particular, the most important rule is that which determines whether a particle moves only when the move decreases its energy or whether it can move even when its energy remains constant. The former rule leads to the formation of a solid material, where the whole system freezes after all particles reach their minimum possible energy or stay stranded at higher energies when there is no available location that would decrease their energy. The latter rule corresponds to a liquid system where all particles move all of the time. In the economic context this rule corresponds to the case where individuals may change locations for reasons exogenous to the model provided the new location is not worse in terms of the simple utility function. In the physics context these rules are equivalent to the particle mobility, where solids and glasses have very little or no particle mobility, whereas liquids have a limited particle mobility.

Another important rule determines how far a particle can move. One rule could allow a particle to move to the closest acceptable location. Another could allow particles to randomly choose between all acceptable locations regardless of their distance. Economically the distinction between the two would correspond to the cost of moving. In the physical context the two rules correspond to slow and fast diffusion rates, respectively. Similarly, if we allow particles to swap places, that is, move even to nonempty locations, then there are two cases. If only short jumps are allowed, then we slow down the evolution of the whole system because particles will move mostly to their first neighbors. If jumps to any distance are allowed the opposite happens, the diffusion rate becomes high, and the whole system will evolve very quickly.

Boundary Conditions

When the system evolves into a few big clusters then its boundary conditions become important. In the case of nonperiodic boundaries the latter are equivalent to empty space and clusters will tend to stay in contact with the system's boundary edges. If the boundaries are periodic, like the surface of a torus, then the system is infinite. A cluster can eventually see only its mirror cluster because of periodicity. If a cluster touches its image it forms an infinite strip. If it does not touch then a cluster has to become spherical.

Here, we show some representative cases of the Schelling model based on the above-mentioned rules. The utility function is described as a step function:

Because the smallest step in the fraction of unlike neighbors on a rectangular grids is 1/8, we show examples with x = 3/8, 1/2 and 5/8. In addition, we look at the role of empty space by changing the number of empty cells.

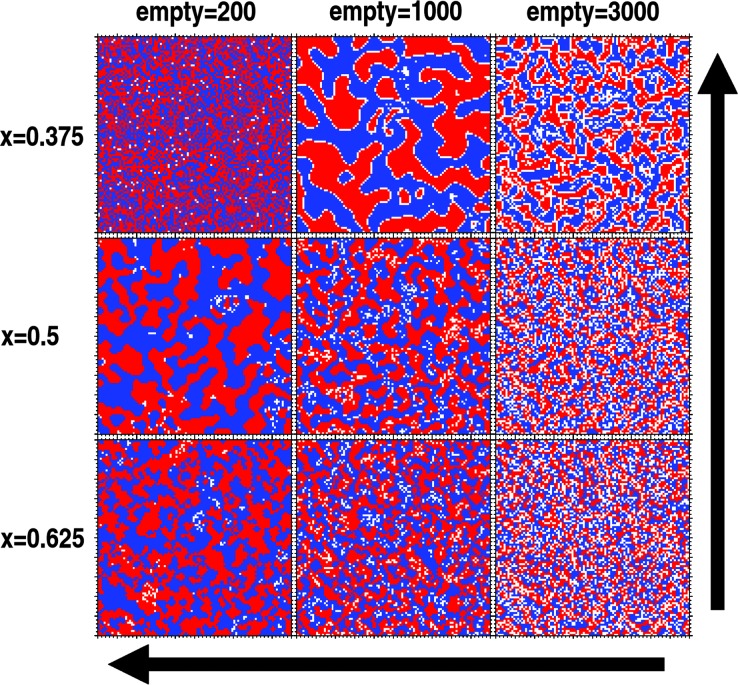
Fig. 3 shows the final results of the Schelling model on a 100 × 100 grid, with the same number of red and blue agents. They are allowed to move only to the nearest empty space that would increase their utility. Notice how the final cluster sizes are bigger for smaller x because a smaller x means also a smaller tolerance of agents to diversity. Also, the cluster size increases if the number of empty spaces is reduced, because empty space provides boundary layers that stabilize clusters.

Fig. 3.

The Schelling model forming a solid structure. This figure is a mosaic of results based on the Schelling model when agents are allowed to move only if their utility strictly increases (that is, energy decreases). This restriction brings the whole system to a halt after all agents reach their maximum utility. In the context of the physical analogue, we can say that the system is frozen into a solid. The utility is given in Eq. 2, and results are shown for three values of x: 0.375 = 3/8, 0.5 = 1/2, and 0.625 = 6/8. The grid size is 100 × 100 and the number of blue and red agents is the same. The number of empty cells is indicated. Arrows show directions of increased clustering. Because a smaller x means a stronger preference for neighbors of the same kind, clustering increases as the value of x decreases. On the other hand, empty space provides boundary layers that can stabilize clusters. Hence, less empty space means larger clusters because of their smaller surface-to-volume ratio. Notice, however, that the model with small x and a small number of empty spaces (x = 0.375, 200 empty cells) does not follow these trends and remains poorly clustered. This exception occurs because many agents are stranded with low utility, but without any empty space to which they could move and increase their utility. Periodic boundaries and distance of movement allowed do not influence the clustering behavior of these models.

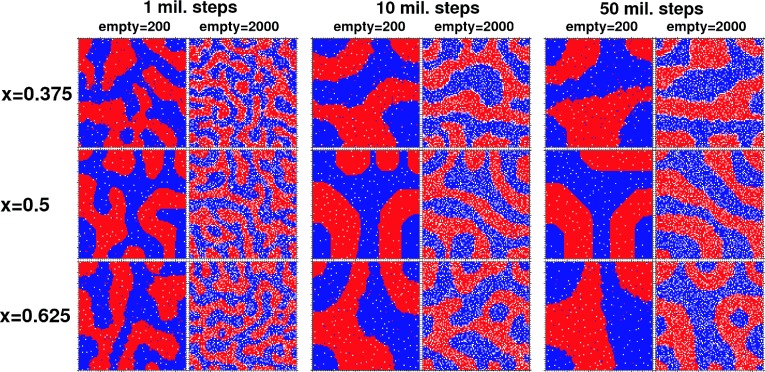
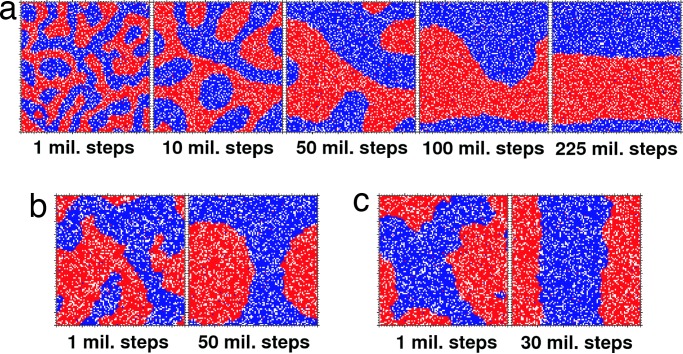
If we let agents move when their utility remains constant then the system behaves like a liquid. Initially the system quickly develops small clusters, but then a slow evolution toward larger clusters follows. Fig. 4 shows this evolution after millions of steps on a nonperiodic grid. As we predicted above, the system evolves toward one big cluster or very few clusters. In the case of x = 1/2 the cluster surface tends to form flat surfaces as predicted by the surface tension forces in Fig. 2. In x ≠ 1/2 cases the surface is bumpy and irregular, with empty space providing a boundary layer when needed. Fig. 5 shows the evolution of x = 1/2 system when the grid is periodic. Now the system evolves either into a sphere or an infinite strip, following the surface dynamics described in Fig. 2. If agents are allowed to swap with other agents the behavior of the system is modified as illustrated in Fig. 6. When only local swaps are permitted the system moves very slowly to large clusters. If agents are allowed to move anywhere, however, the system segregates very rapidly.

Fig. 4.

The Schelling model as a liquid on a nonperiodic grid. The Schelling model on a 100 × 100 grid, with the same number of red and blue agents. Agents move even if their utility remains the same, which makes the model analogous to simulating a liquid. Utility is given by Eq. 2 with the values of x indicated here. Domain boundaries are nonperiodic. We show the evolution of this model for 200 and 2,000 empty cells. An increase in the volume of empty space results in more irregular cluster shapes and slower evolution because empty space behaves like a boundary layer (Fig. 2). In cases with x ≠ 0.5 clusters cannot form a smooth surface, whereas x = 0.5 leads to flat surfaces as predicted in Fig. 2. Supporting information (SI) Movies 1 and 2 show the evolution of clusters with x = 0.5.

Fig. 5.

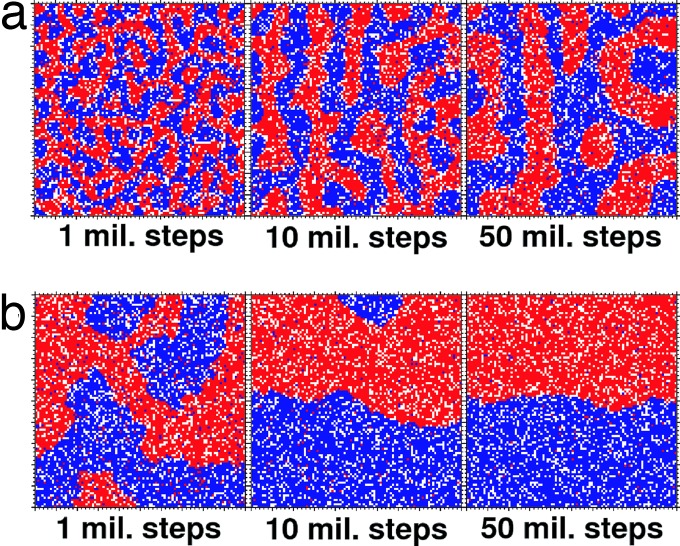
The Schelling model as a liquid on a periodic grid. The same as x = 0.5 in Fig. 4 with 2,000 empty cells, except that the domain boundaries are periodic. Now the system can evolve into only two types of clusters: spherical, when the cluster does not enter into contact with another cluster, or an infinite strip, when the cluster and its mirror cluster merge. (a) Movements are limited to the closest appropriate empty location. The cluster evolution follows closely the prediction from Fig. 2. (b and c) Examples where agents can move any distance to form either a wobbling droplet (b) or a strip (c). SI Movies 3 and 4 show the evolution of these clusters. mil., million.

Fig. 6.

The Schelling model when swapping of agents is allowed. We explore what happens when agents can swap places, that is, when empty space is not required for moving. The grid size is 100 × 100 and nonperiodic. The number of blue and red agents is 4,000, with x = 0.5 for the utility from Eq. 2. We allow any movement that does not incur a loss in utility (a physical model of liquid). (a) A model when only jumps to the nearest acceptable location are allowed. Because swapping is allowed, most movements are now to the first neighboring cells. Hence, agents diffuse very slowly from one part of the domain into another and the evolution of the whole system is very slow. (b) The opposite happens when agents can jump to any location. The diffusion of agents is greatly increased because empty locations are not required for movement any more. Agents have a large number of locations to choose from and, therefore, the whole system evolves very quickly. mil., million.

Related Physical Phenomena

Segregation of particles is a common and widely studied natural phenomenon. The clustering behavior displayed by the Schelling model has analogues in physics. Here, we list only a few illustrative examples, because a detailed review of the vast literature in physics on these subjects is beyond the scope of this work. A typical initial set up for the Schelling model involves randomized positions of particles in the system, which is equivalent to, for example, violently shaking a mixture of oil and water to form an emulsion. After that we let the system evolve and reach its equilibrium condition. Different types of utility functions will have different equivalent physical systems. These will have different underlying interparticle forces. These differences will generate variations in the final cluster shapes attained. These are, in general, either completely irregular (amorphous) or well structured. Glass is an example of the former and crystals or liquid droplets of the latter.

Crystal growth is an example where a big cluster can grow by taking over individual particles from smaller clusters. This phenomenon is known as “Ostwald ripening.” Alternatively, a big cluster can grow by directly incorporating smaller clusters. This phenomenon is called “Smoluchowski ripening.” Reshaping of the surface caused by surface tension is known as “surface (or edge) diffusion.” All of these phenomena are well known in the physics of metal surfaces. There the evolution of fewer but larger nano-structures out of many smaller nano-structures, a phenomenon generally known as “coarsening”, is actively studied (e.g., refs. 7–10). The Schelling model is, therefore, just a discretized model of such physical phenomena. Physical models simulating atom or cluster aggregation closely resemble the Schelling model (11). Extensions of the Schelling model to include more than the first neighbors in the definition of the utility function (12) correspond to medium- or long-range interactions between particles, which can result in gas-like equilibrium lacking segregation patterns. The physics of colloids is another physical analogue, which closely resembles the Schelling model, with theoretical models and direct observations showing cluster formation (13–15). Notice, however, that despite some similarities in clustering, the Schelling model is different from the Ising model (16) because it does not change the color of particles. We are interested in the clustering of particles by their type and not by their internal energy, which is the property of the Ising model.

Conclusion

We propose a simple physical analogy to the Schelling model of segregation. This analogy allows us to show how the various ingredients of the model such as the rules for moving, the utility functions of individuals, and the amount of vacant space can influence the spatial segregation patterns that can occur. The basic model, which is well known in the physics literature, provides a good analytical framework for studying the basic Schelling model and all of its variants. It shows clearly how the energy of individuals who are on the frontier of their own group drives the tendency to cluster, while the rules governing mobility determine the precise form that the segregated clusters will take. The model could be used to study more general situations in which segregation occurs. For example, it would be interesting to analyze cases in which income also plays a part in segregation (17) and to examine empirical regularities such as those found by Möbius and Rosenblat (18) for the evolution of segregation in Chicago.