Order N algorithm for computation of electrostatic interactions in biomolecular systems

Abstract

Poisson–Boltzmann electrostatics is a well established model in biophysics; however, its application to large-scale biomolecular processes such as protein–protein encounter is still limited by the efficiency and memory constraints of existing numerical techniques. In this article, we present an efficient and accurate scheme that incorporates recently developed numerical techniques to enhance our computational ability. In particular, a boundary integral equation approach is applied to discretize the linearized Poisson–Boltzmann equation; the resulting integral formulas are well conditioned and are extended to systems with arbitrary numbers of biomolecules. The solution process is accelerated by Krylov subspace methods and a new version of the fast multipole method. In addition to the electrostatic energy, fast calculations of the forces and torques are made possible by using an interpolation procedure. Numerical experiments show that the implemented algorithm is asymptotically optimal O(N) in both CPU time and required memory, and application to the acetylcholinesterase–fasciculin complex is illustrated.

In recent years, because of the rapid advances in biotechnology, both the temporal and spatial scales of biomolecular studies have been increased significantly: from single molecules to interacting molecular networks in a cell, and from the static molecular structures at different resolutions to the dynamical interactions in biophysical processes. In these studies, the electrostatics modeled by the well established Poisson–Boltzmann (PB) equation has been shown to play an important role under physiological solution conditions. Therefore, its accurate and efficient numerical treatment becomes extremely important, especially in the study of large-scale dynamical processes such as protein–protein association and dissociation in which the PB equation has to be solved repetitively during a simulation.

Traditional numerical schemes for PB electrostatics include the finite difference methods, where difference approximations are used on structured grids, and finite element methods in which arbitrarily shaped biomolecules are discretized by using elements and the associated basis functions. The resulting algebraic systems for both are commonly solved by using multigrid or domain decomposition accelerations for optimal efficiency. However, as the grid number (and thus the storage, number of operations, and condition number of the system) increases proportionally to the volume size, finite difference and finite element methods become less efficient and accurate for systems with large spatial sizes, e.g., as encountered in protein association and dissociation. Alternative methods include the boundary element method (BEM) and the boundary integral equation (BIE) method. In these methods, only the surfaces of the molecules are discretized; hence, the number of unknowns is greatly reduced. Unfortunately, in earlier versions of BEM, the matrix is stored explicitly and the resulting dense linear system is solved by using Gauss elimination, so that O(N²) storage and O(N³) operations are required, where N is the number of nodes defined on the surface to discretize the integrals. Even with the acceleration afforded by Krylov subspace methods, direct evaluation of the N(N − 1)/2 pairs of interactions still requires prohibitive O(N²) operations.

In the last 20 years, novel numerical algorithms have been developed to accelerate the calculation of this N-body problem from the original O(N²) direct method to the O(N log N) hierarchical “tree code”- (1, 2) and fast Fourier transform-based algorithms (3, 4), and later to the asymptotically optimal O(N) fast multipole method (FMM) (5), and eventually to a new version FMM with an optimized prefactor (6). For the PB equation, however, only the original FMM- and fast Fourier transform-based techniques have been introduced into the BEM/BIE formulations. Numerical experiments show that the original FMM (5), although asymptotically optimal, is less efficient for problem sizes of current interest when compared with the tree code- and fast Fourier transform-based O(N log N) techniques, because of the huge prefactor in O(N).

In this article, we present an efficient algorithm to further accelerate the solution of the PB equation. By proper coupling of single and double layer potentials as discussed by Rokhlin (7), we derive an integral equation formulation for systems with an arbitrary number of domains (molecules). Similar formulations have been used for single-domain problems by Juffer et al. (8), Liang and Subramaniam (9), and Boschitsch et al. (10). Compared with “direct” formulations, the condition number of our system does not increase with the number of unknowns, hence the number of iterations in the Krylov subspace-based methods is bounded. For the matrix vector multiplications in each iteration, we use the new version FMM developed for the screened Coulombic interaction by J.H. and his collaborators (11). Compared with the original FMM, the plane wave expansion-based diagonal translation operators dramatically reduce the prefactor in the O(N) new version FMM, especially in three dimensions where a break-even point of ≈600 for 6-digit precision is numerically observed.

Whereas most previous PB electrostatics algorithms have mainly focused on the energy calculations, calculations of the PB forces and torques are also essential in many cases such as in dynamics simulations. In this algorithm, we introduce an O(N) interpolation scheme in the postprocessing stage for calculating the forces and torques. This scheme improves previous O(N²) results based on BEM (12, 13).

Results

Computational Performance.

To assess the accuracy of the algorithm, we first consider a spherical cavity of radius 50 Å with one positive charge located at its center, and compare the numerical solutions with the analytical ones. The surface is discretized at various resolution levels (from 320 to 81,920 elements) by recursively subdividing an icosahedron. Numerical results show that the relative error of the calculated electrostatic potentials decreases with increased number of elements, from ≈8% (320 boundary elements) to <0.3% (81,920 boundary elements).

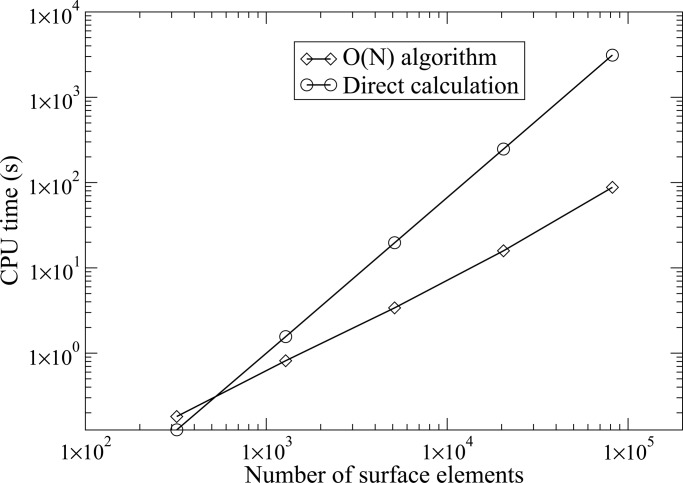
As for the efficiency, we noticed that regardless of the surface resolution, the generalized minimal residual (GMRES) iteration steps never exceed 10, which numerically confirms that the derivative BEM formulation is well conditioned. Furthermore, in each iteration, we compare the new version of FMM with direct method for different resolutions (up to 81,920 boundary elements). Numerical results in Fig. 1 show that the CPU time (on a Dell dual 2.0-GHz P4 desktop with 2 GB of memory) for the new version of FMM scales linearly with the number of boundary elements with correlation coefficient 0.984, and quadratically for the direct integration method with correlation coefficient 0.999. For a system with 81,920 surface elements, the O(N) new version FMM is ≈40 times faster than the direct method.

Fig. 1.

Log–log plot of CPU time vs. the number of elements for the calculation on a sphere case.

The memory requirements of our method are tested on large biomolecular systems. Numerical experiments show that the overall memory requirement scales linearly with the number of surface elements. Compared with existing finite difference and finite element schemes, orders of magnitude reduction in memory usage has been observed in simulations of the nicotinic acetylcholine receptor (30,385 atoms; PDB ID code 2BG9) with 194,428 elements and 97,119 vertices. In our algorithm, we noticed that the majority of computer memory is allocated to store the neighboring list and the corresponding near-field coefficients, the size of which mainly relies on the total number of boundary elements and the level of box subdivision. Depending on a tradeoff between memory and speed, at each iterative step these coefficients can either be saved as in a memory-intensive mode or be discarded as in a memory-saving mode. In a nonadaptive FMM case, the number of neighboring boxes of a box (therefore any vertex located within this box) is 27. If we further assume that the maximum number of elements per box at the finest level is s, then it is easy to see that the number of near-field elements for each vertex can normally be up-bounded by a fixed number 27s. Hence, the size of neighboring list is also up-bounded by 27sN; this and the fact that there are at most 2N/s boxes in the tree structure lead to O(N) overall memory usage.

To further illustrate the performance of our fast BIE technique on protein electrostatic calculations, we computed the electrostatic solvation energies of fasciculinII, a 68-residue protein, and compared the algorithm performance with the multigrid finite difference algorithm, as implemented in the widely used software APBS (14). We want to mention that the two program codes employ very different algorithms and data structures; hence, an exact comparison between them would be difficult. Also, APBS is designed primarily for massively parallel computing, it has an integrated mesh generation routine, and it solves the PB equations twice to obtain the solvation energy. Nevertheless, the preliminary results given below show that present algorithm provides better speed and memory performance than the current version of APBS. For APBS calculations, when using a 161 × 129 × 161 grid with grid spacing of 0.25 Å, the computed electrostatic solvation energy is −525.5 kcal/mol, and the calculation takes 250.8 sec of total CPU time and 742.8 megabytes of memory on our desktop machine. When using a finer grid of 225 × 161 × 225, the total CPU time is increased to 599.9 sec, memory increased to 1,784.6 megabytes, and the total solvation energy is −522.8 kcal/mol. For our calculation to achieve the same level of accuracy, the surface mesh was generated with vertex density of 3 Å⁻², which results in a total of 21,430 triangular elements and 10,717 vertices. In this case, the computed solvation energy is −522.0 kcal/mol, and the calculation takes 129 sec requiring only 90 megabytes of memory if running in a memory-saving mode, whereas the job completes in 44 sec requiring 486 megabytes of memory if running in a memory-intensive mode.

Protein–Protein Interaction of the Acetylcholinesterase (AChE) and FasciculinII (Fas2).

Many experimental and theoretical studies have established that electrostatic interactions dominate the AChE–Fas2 binding process and increase the binding rate by about two orders of magnitude (15, 16). However, in the initial Brownian dynamics (BD) simulations of AChE–Fas2 encounter, the methods for solving electrostatics are not rigorous in the sense that the polarization and electrostatic desolvation effects are neglected to reduce the computational cost. Using these approximate methods, the calculated encounter rates tend to be overestimated especially at high ionic concentration. Elcock and coworkers (16) pointed out this deficiency and used an effective charge approximation to calculate the electrostatic desolvation and observed improved results. In seeking to demonstrate the importance of these desolvation effects, we calculate each electrostatic energy component for a series of structures at different separation distances between AChE and Fas2. These structures are generated by displacing Fas2 away from the binding site, along a preselected direction with possibly the least clashes. For the purpose of demonstration, we also calculate the forces and torques on Fas2 molecule that are essential for running BD simulations.

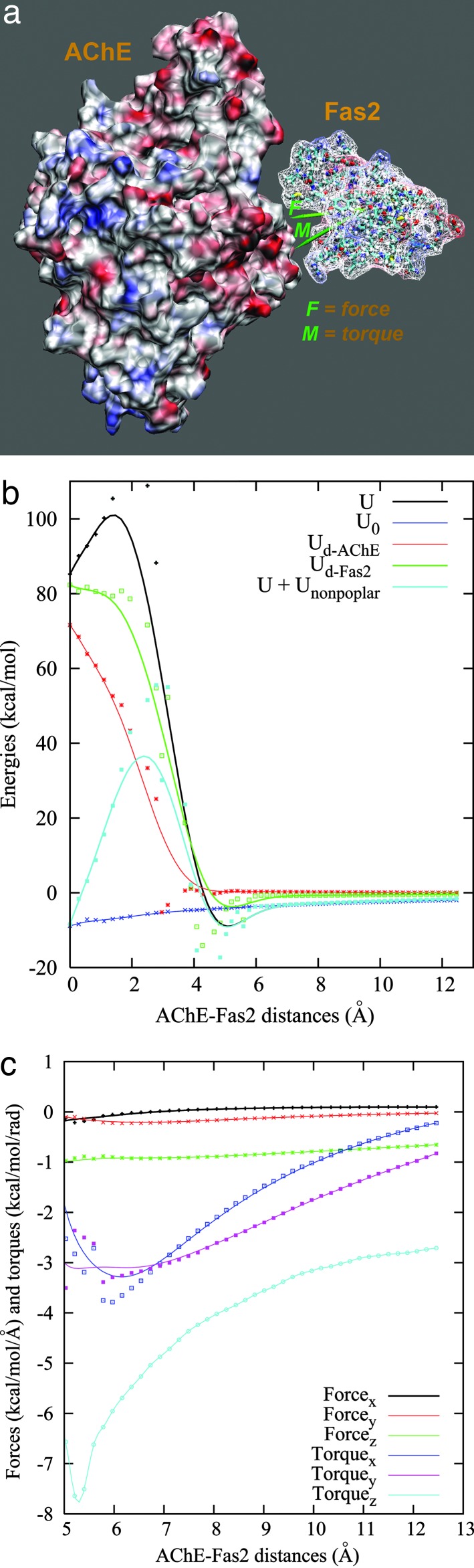
Fig. 2a shows the mutually polarized electrostatic potentials mapped to the molecular surfaces of AChE and Fas2 at a ≈14 Å displacement of Fas2. Not surprisingly, the potential surfaces exhibit qualitative electrostatic complementarity at the binding interface. Fig. 2b shows the electrostatic interaction energy and electrostatic desolvation profiles for the AChE–Fas2 complex as a function of separation distances. Although the data at short range may not be quantitatively accurate because of the atom clashes (which arise from the manually rigid-body unbinding procedure) when AChE and Fas2 are close in (from ≈1.0 Å to 5.0 Å), Fig. 2b shows some interesting results that cannot be expected from previous approximate models. Clearly, the electrostatic interaction energy (black line) is favorable for binding at separations further than 5 Å but becomes increasingly positive at closer separations. The long-range electrostatic attraction is the dominant driving force for the Fas2–AChE binding, which accounts for the observed electrostatic enhancement of the binding rate in experiments. However, given the fact that the AChE–Fas2 complex has a high binding affinity, the unfavorably large positive electrostatic energies at closer distances seem to be surprising. We speculate that this will likely be balanced by the nonpolar interactions. If we take a simple model by adding the surface term U_nonpolar = γΔS, γ = 0.058 kcal·mol⁻¹·Å⁻² (17), to account for the nonpolar contributions, the total binding energy profile (the cyan line in Fig. 2b) will show favorable interactions for the AChE–Fas2 complex.

Fig. 2.

Electrostatics of AChE–Fas2. (a) Surface potential map of AChE and Fas2 at separation of 14 Å. The two green arrows indicated as F and M show the force (0.10, −0.03, −0.69) and torque (−0.35, −1.03, −2.8), respectively, which are scaled for visualization. (b) The interaction energy profiles as functions of separations along a predefined unbinding direction. U, total electrostatic interaction; U₀, electrostatic interaction energy without consideration of the ligand polarization and desolvation effects as the typical treatment in UHBD; U_d-AChE and U_d-Fas2, electrostatic desolvation energies due to AChE and Fas2 cavities, respectively; U_nonpolar, nonpolar contribution from a simple surface term. (c) The x, y, z components of forces, and torques acting on Fas2 as functions of the separation distances along a predefined unbinding direction.

The origin of the large unfavorable electrostatic interaction at closer separations can be attributed to the electrostatic desolvation, an effect due to the unfavorable exclusion of the high dielectric solvent around one protein when the other one approaches (16). The green and red lines in Fig. 2b show the electrostatic desolvation energies of AChE and Fas2, respectively. When AChE and Fas2 stay close, there are large desolvation penalties, but the electrostatic desolvation energies decrease rapidly when two molecules are separated by ≈5 Å or further.

Another interesting observation is that the full electrostatic interaction profile shows a minimum at the distance of ≈5 Å (Fig. 2b). This feature, however, disappears in the calculation without considering the mutual polarization and desolvation contributions (blue line in Fig. 2b). Therefore, it is a result from the competition between the long-range attractive (Coulombic) and short-range repulsive (desolvation) electrostatic interactions.

The present BEM gives the full PB interaction energy that inherently takes into account both the desolvation and polarization contributions from the two proteins. Although the conventional electrostatic calculations as in the UHBD package (18) are capable of including these two contributions, because of the computational cost, these effects are typically approximated or neglected when used for BD simulations. In these simulations, the reaction field of only one molecule (usually protein of larger size) is computed and then acts on the set of atomic charges of the other one. The blue line in Fig. 2b shows the interaction energies obtained with this type of calculation. Whereas it is in good agreement with the full PB energies at large separations (>8 Å), it deviates greatly at short distances, which emphasizes the importance of using more rigorous PB electrostatics in simulating the AChE–Fas2 encounter process.

We show some early results on the force and torque calculations in Fig. 2c. As mentioned above, there exist slight atom clashes between Fas2 and AChE for some structures at short separations. The forces and torques turn out to be more sensitive to these atom clashes than the energy calculation, which exhibit significant fluctuations at short ranges below 5 Å (data not shown). Nevertheless, for electrostatically steered, diffusion-controlled reactions, commitment to reaction typically occurs at surface-to-surface distances on the order of the Debye length (≈10 Å for physiological ionic strength) (16), so that even the current treatment of solvation should yield valuable applications. As shown in Fig. 2c, across the whole separation range, the forces along x and y directions are close to zero, while the z component varies from −1.0 to −0.65 kcal·mol⁻¹·Å⁻¹. Since the direction of the Fas2 displacement is close to the z axis (−0.4, 0.2, 0.89), the force results are consistent with the energy calculations and also suggest that this direction may be close to one of the real association pathways within this spatial range. Fig. 2c also shows torque calculation in all three x, y, and z directions. Those significant values suggest that, if the electrostatics is the dominant interaction at these separations, the present molecular orientations will be adjusted along this association pathway.

Discussion and Conclusions

In this article, an efficient algorithm with optimal computational complexity is presented for the numerical solution of the linearized PB electrostatics. In addition, since coupled with a new version of FMM, the prefactor also has been significantly reduced. The algorithm uses a BIE formulation with unknowns defined only on the surface and is accelerated by the new version of FMM and Krylov subspace methods. The algorithm enables the computational study of relatively large biological systems (approximately hundreds of thousands atoms) on a personal computer and has been applied to the simulation of AChE and Fas2 protein–protein interactions.

In terms of the full PB electrostatic calculation among two or more solute molecules, the BEM-based method has several advantages over some widely used numerical approaches, e.g., using 2D surface mesh instead of 3D volume mesh, using natural (physical) instead of artificial boundary conditions, and convenient force calculations as demonstrated in this article. These features make the present BEM approach a very appealing choice for PB electrostatics calculation in dynamics simulations. Our new algorithm shows several folds speedup relative to some widely used solvers and should have even better performance for larger system or far-separated molecular systems.

Unfortunately, BD and all-atom molecular dynamics simulations with full PB calculation for large systems still exceed the presently available computer capability. For a typical BD trajectory with tens of million steps, the one-step PB solution needs to be completed within no more than a few seconds to meet the total wall-clock time constraint. Based on this estimation, the present BEM solver is still about one order slower. To overcome this hurdle, several techniques are being pursued to further increase the efficiency of the present algorithm for BD simulation, such as using adaptive fast multipole method and curvilinear BEM. For molecular dynamics simulations, still other speedup techniques can be pursued, including (i) parallelization of the present code and (ii) a new multiscale time stepping method that utilizes the efficiency of our algorithm for electrostatics calculations. For i, previous studies show that the BIE method and new version of FMM have excellent scalability for parallel computation; and for ii, as different temporal scales are readily available in the FMM structures, larger time step sizes can be used for the slowly varying far field interactions represented by the local and multipole expansions, and smaller step sizes for the rapid local interactions. Given all these improvements, the BEM-based PB electrostatics will become truly practical for its application to BD and/or molecular dynamics simulations. In addition, the present fast BIE framework can be readily extended to solving other equations, such as the diffusion equations arising from the study of ion permeation and ligand diffusion processes.

Methods

BIE Formulations.

When Green's second identity is applied, traditional BIEs for the linearized PB equations for a single domain (molecule) take the form

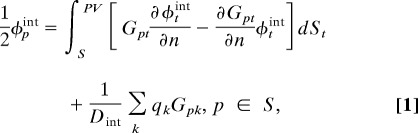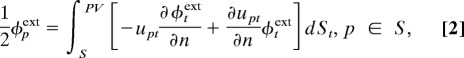where φ_p^int is the interior potential at surface position p of the molecular domain Ω, S = ∂Ω is its boundary, i.e., solvent-accessible surface, φ_p^ext is the exterior potential at position p, D_int is the interior dielectric constant, q_k is the kth source point charge of the molecule, κ is the reciprocal of the Debye–Hückel screening length determined by the ionic strength of the solution, n is the outward normal vector, t is an arbitrary point on the boundary, and PV represents the principal value integral to avoid the singular point when t → p in the integral equations. In the formulas,

and

are the fundamental solutions of the corresponding Poisson and PB equations, respectively. These equations can be easily extended to multidomain systems in which Eq. 1 is enforced for each individual domain and the integration domain in Eq. 2 includes the collection of all boundaries.

To complete the system, the solutions in the interior (Eq. 1) and exterior (Eq. 2) are matched by the boundary conditions φ^int = φ^ext and

where D_ext is the exterior dielectric constant. Using these conditions, we can define f = φ^ext and

as the new unknowns and recover other quantities using boundary integrals of f and h. Unfortunately, theoretical analysis shows that the corresponding equation system for f and h is in general a Fredholm integral equation of the first kind and hence ill conditioned, i.e., when solved iteratively by using Krylov subspace methods, the number of iterations increases with the number of unknowns, and the resulting algorithm becomes inefficient for large systems. Instead of this “direct formulation,” in our method, we adapt a technique introduced by Rokhlin (7) where the single- and double-layer potentials are combined to derive an optimized second kind Fredholm integral equation. Similar techniques have been used by Juffer et al. (8) and others in engineering computations (19–21); however, most of them focus on single-molecule cases. In the following, we present a well conditioned derivative BIE formulation (second kind Fredholm equation) for multiple biomolecule systems, in which j = 1, …, J represents the separated molecules:

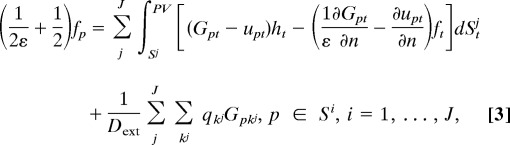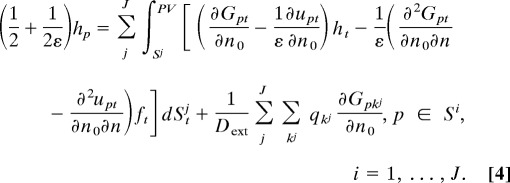As our formulas have the same integrands on different domain surfaces, FMM calculation is convenient and the same as in the single-molecule case. Also, because of the small number of iterations for convergence, the solution of an arbitrary system is directly obtained by solving the PB equations only once, which differs from previous “perturbation” scheme for two-domain systems (12, 22).

New Version Fast Multipole Method.

When Eqs. 3 and 4 are discretized, the resulting linear system is well conditioned and can be solved efficiently by using Krylov subspace methods. As the number of iterations is bounded, the most time-consuming part becomes the convolution type matrix vector multiplication in each iteration. In this section, we discuss how this can be accelerated by the new version FMM.

The fundamental observation in the multipole expansion-based methods is that the numerical rank of the far field interactions is relatively low and hence can be approximated by P terms (depending on the prescribed accuracy) of the so-called “multipole expansion”

where Y_n^m are the spherical harmonics and M_n^m are the multipole coefficients. For arbitrary distribution of particles (meshes), a hierarchical oct-tree (in 3D) is generated so that each particle is associated with different boxes at different levels, and a divide-and-conquer strategy is applied to account for the far-field interactions at each level in the tree structure. In the “tree code” developed by Appel (1) and Barnes and Hut (2), as each particle interacts with 189 boxes in its “interaction list” through P terms of multipole expansions at each level and there are O(log N) levels, the total amount of operations is ≈189 P²N log N. The tree code was later improved by Greengard and Rokhlin (5). In their original FMM, local expansions (under a different coordinate system)

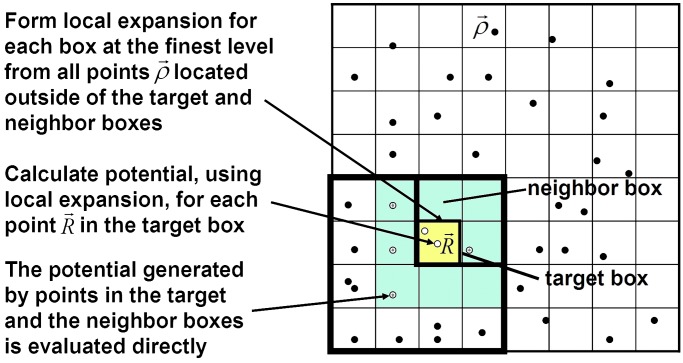
are introduced to accumulate information from the multipole expansions in the interaction list where L_n^m are local expansion coefficients. As the particles only interact with boxes and other particles at the finest level, and information at higher levels is transferred by using a combination of multipole and local expansions as explained in Fig. 3, the original FMM is asymptotically optimal O(N). However, because the multipole to local translation requires prohibitive 189P⁴ operations for each box, the huge prefactor makes the original FMM less competitive with the tree code and other fast Fourier transform-based methods.

Fig. 3.

Schematic showing the source points ρ⇀ and evaluation point R⇀ in the new version FMM. In BEM implementation, the source points are centered at the surface triangular elements.

In 1997, a new version of FMM was introduced by Greengard and Rokhlin (6) for the Laplace equation. Compared with the original FMM, a plane wave expansion-based diagonal translation operator is introduced, and the original 189P⁴ operations were reduced to 40P² + 2P³. In our algorithm, we adapt the new version of FMM for the screened Coulomb interactions (corresponding to the linearized PB kernel) developed by J.H. and his collaborators (11). Preliminary numerical experiments show that the overall break-even point of the new version FMM becomes 600 with 6-digit accuracy, and ≈400 for 3-digit accuracy. However, the new version FMM is more complicated than the original FMM in programming and theory, and we are unaware of any previous implementations for the linearized PB equation.

Krylov Subspace Methods and Mesh Generation.

In our algorithm, a parallel iterative methods package for systems of linear equations PIM23 (23) is used. Several iterative schemes are available in the package including the GMRES method, biconjugate gradients stabilized (BiCGStab) method, and transpose-free quasi-minimal residual (TFQMR) algorithm. Preliminary numerical experiments show that the GMRES method converges faster than other methods, which agrees with existing analyses. Because the memory required by the GMRES method increases linearly with the iteration number k, and the number of multiplications scales like $\frac{1}{2}{k}^{2}N$, for large k, the GMRES procedure becomes very expensive and requires excessive memory storage. For these reasons, instead of a full orthogonalization procedure, GMRES can be restarted every k₀ steps where k₀ < N is some fixed integer parameter. The restarted version is often denoted as GMRES(k₀).

To discretize the BIEs, a triangular mesh is generated by using the package MSMS (24), and zero and extremely small area elements are modified by a mesh-checking procedure in our algorithm. A typical mesh is shown in Fig. 2 (top right).

Force and Torque Calculations.

In addition to energy calculation, an improved procedure is implemented to calculate the force and torque. Compared with previous O(N²) schemes (12, 13), the complexity of the new procedure is O(N). In the calculation, the full stress tensor on the boundary including contributions from conventional Maxwell stress tensor as well as the ionic pressure is given by (25)

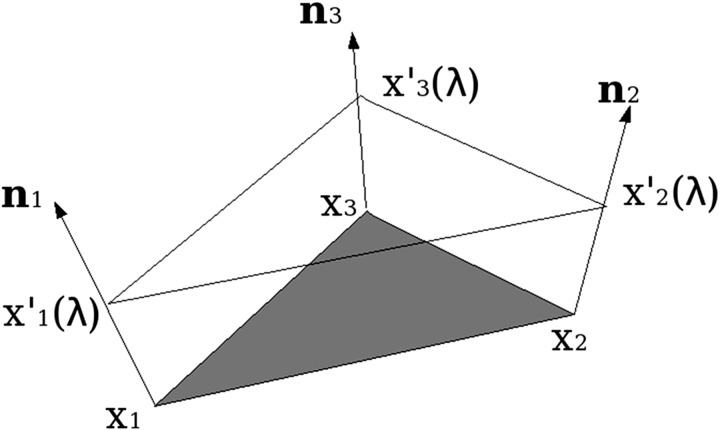
where E is the electrostatic field and δ_ij the Kronecker delta function. For the gradient of the potential, an interpolation scheme is used to construct a trivariate function in the vicinity of the molecular surface. For each triangular element on the surface, we construct a small three-sided prism as shown in Fig. 4. In the prism, the potential is linearly interpolated, and the total PB force F and torque M acting on each molecule are calculated by integrations of F = ∫_ST(x)·dS(x) and M = ∫_Sr_c(x) × [T(x)·dS(x)], where r_c(x) represents a vector from the center of mass of the target molecule to the surface point x, and the dot and cross-vector multiplications are applied to the vector and tensor quantities.

Fig. 4.

The prism constructed on a triangular element. The shadowed triangle is one of the boundary elements, n₁, n₂, and n₃ are three unit normal vectors at the three nodes, and λ is a parameter to describe the third-dimensional position of the prism.

System Set-Up.

For all calculations, the AMBER atomic charges and radii were assigned for protein atoms. A probe radius of 1.5 Å was used to define the dielectric interface. The relative dielectric constants were taken as 2.0 for solute and 80.0 for solvent.

In the protein–protein interaction calculations, the ion concentration was set to 50 mM, which is equivalent to a Debye–Hückel screening length of 13.8 Å. The meshes were generated at a density of 1.0 Å⁻². A single mesh was generated if the two molecular surfaces were separated by <3 Å, whereas for the further separations the system was treated as two separate domains with two sets of meshes.

Abbreviations

AChE

acetylcholinesterase

BD

Brownian dynamics

BEM

boundary element method

BIE

boundary integral equation

FMM

fast multipole method

GMRES

generalized minimal residual

PB

Poisson–Boltzmann.