Sometimes area counts more than number

Abstract

Using an interference paradigm, we show across three experiments that adults' order judgments of numbers, sizes, or combined area of dots in pairs of arrays occur spontaneously and automatically, but at different speeds and levels of accuracy. Experiment 1 used circles whose sizes varied between but not within arrays. Variation in circle size interfered with judgments of which array had more circles. Experiment 2 used displays in which circle size varied within and between arrays. Between-array differences in the amount of “circle stuff” (area occupied by circles) interfered with judgments of number. Experiment 3 examined whether variation in number also interferes with judgments of area. Interference between discrete and continuous stimulus dimensions occurred in both directions, although it was stronger from the continuous to the discrete than vice versa. These results bear on interpretations of studies with infants and preschoolers wherein subjects respond on the basis of continuous quantity rather than discrete quantity. In light of our results with adults, these findings do not license the conclusion that young children cannot represent discrete quantity. Absent data on attentional hierarchies and speed of processing, it is premature to conclude that infant and child quantity processes are fundamentally different from that of adults.

The capacity to represent both discrete and continuous quantity is found in both humans and nonhuman animals (1–3). Discrimination functions in animals and humans yield similar variability signatures for different dimensions of quantification (time, number, distance, and size), suggesting the use of a common representational format across species (4–7) and domains (discrete vs. continuous quantity).

Questions of when in development different quantitative dimensions are represented and how these representations interact have become important issues in research on the development of numerical cognition in humans. On one view, preverbal numerical representations like those found in nonhuman animals are present at a very early age and form the basis for children's later numerical accomplishments, such as counting and the understanding of arithmetic operations (ordination, addition, and subtraction). Consistent with this view are reports that infants discriminate numerically small sets of one to three items (8-10), and larger pairs, like 8 vs. 16 (11). They also respond appropriately to the effects of addition and subtraction (12) and show intermodal numerical matching (13) and intermodal addition (14).

The alternative view is that the ability to represent number (discrete quantity) appears late in development. On this view, infants' behavior in ostensibly numerical experiments is controlled by variation along covarying nonnumerical continuous dimensions of the stimuli (15). Discrete displays span various lengths, and the items cover varying amounts of surface or occupy varying volumes. Studies designed to investigate the idea that infants respond to one or more of these continuous quantities, but not to number, yield conflicting results (12, 15–17).

The shifting results across experiments suggest that we are dealing with an attention hierarchy, one that is altered by experimental conditions that make number more or less salient to the infant. In this regard, it is of interest to know how adults respond to the sort of simple dot displays that have been used in infant experiments. It may be that both infants and adults automatically represent discrete and continuous dimensions of the stimulus and that these representations compete for control of their behavior.

We use an interference paradigm to test for competition between task-relevant and task-irrelevant dimensions of the stimulus display. When, in defiance of task instructions, estimates of the difference along a competing stimulus dimension are involuntarily extracted, they shorten reaction times when the irrelevant difference is congruent with the relevant difference and lengthen them when it is incongruent. The classic numerical Stroop paradigm is one example of an interference task: It asks subjects to compare either the font size or the numerical magnitude of two Arabic numerals, where these are either

When adults are asked to indicate which digit is written in the larger font, they are not able to ignore the numeric value of the digit (refs. 18 and 19, but see ref. 20). They are slower to judge 3 larger than 5 than they are to judge that 5 is larger than 3. The reverse effect also is found: Judgments as to which digit symbolizes the larger number are delayed in the incongruent condition and facilitated in the congruent condition.

The interaction between symbolic representations of number and size or other quanity dimensions have been studied extensively; they are robust in a variety of circumstances (21–23) and even appear in symbol-trained primates (24). However, few human studies pit variation in nonsymbolic discrete quantity (that is, variation in actual numerosity) against variation along continuous dimensions (e.g., size of the stimulus items and total area occupied by them). Studies of this kind are directly relevant to an assessment of the seemingly conflicting results in the infant literature in that an adult attentional preference for discrete over continuous quantities frequently has been asserted but not empirically tested.

We report three experiments on interference effects across quantity dimensions. Experiment 1 used circles whose size varies between but not within arrays. It tested the hypothesis that in a nonverbal numerical comparison task, size estimates interfere with numerical comparisons. Participants were shown pairs of arrays with varying circle sizes (Fig. 1) and asked to make speeded numerosity judgments.

Fig. 1.

All experiments had Congruent, Incongruent, and Neutral displays. In Experiments 1 and 2, the task was to indicate the array with more circles. In Experiment 3, the task was to indicate the array with more combined circle area. The displays in Experiment 2 and 3 were identical except in the Neutral condition.

Experiment 2 investigated whether incongruency in total circle area (number of white pixels) interfered with judgments of which array had numerically more circles. Circles within each array varied in size, so there were both large and small circles in each of the arrays (Fig. 1). To avoid a confound with absolute circle size (i.e., interference from the largest circle), displays were designed such that the largest circle in one array was identical to the largest circle on the other.

Experiment 3 examined whether variations in numerosity interfere with judgments of combined area. Traditional number Stroop experiments show bidirectional interference: Differences in font size interfere with judgments of the numerical magnitudes represented by Arabic numerals, and, conversely, the values represented interfere with judgments of font size (18, 23). Experiment 3 tests whether the continuous/discrete quantity interference effects are similarly bidirectional. Using the same displays as Experiment 2, adults were asked to judge differences in combined circle area, with numerosity as the irrelevant dimension. This design feature allows us to ask whether individuals attend exclusively to continuous extent, a hypothesis that is consistent with Clearfield and Mix's proposals regarding infants (25). The experiment also allows for further exploration on the time course of magnitude judgments and magnitude interference.

Results

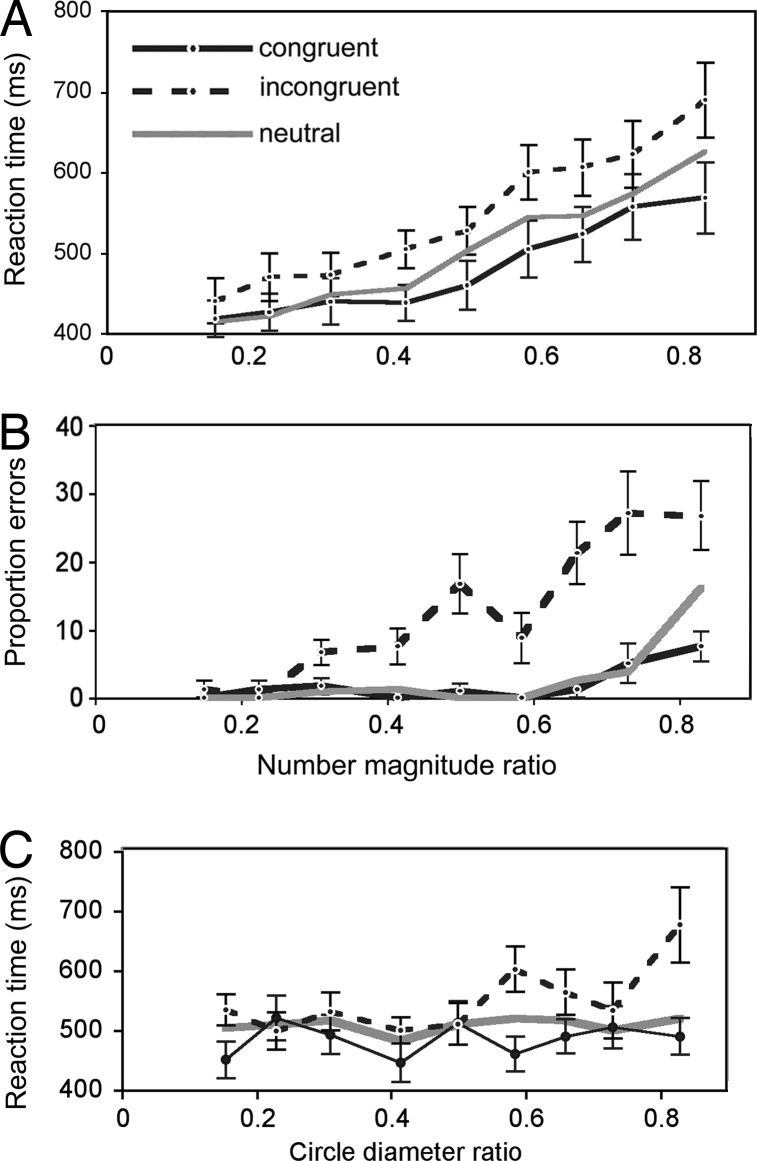
In Experiment 1, congruency/incongruency between the numerical and size dimensions affected both the mean time to correctly judge which array had more circles [F_{(2, 36)} = 16.26, P < 0.001]^§ and the error rate in making this judgment [F_{(2, 36)} = 22.5, P < 0.001] (see Fig. 1). The mean reaction time on correct trials was faster when the more numerous array (the correct response) was on the left [F_{(1, 18)} = 7.00, P < 0.05],^¶ but side-of-correct response did not affect the error rate (F < 1).

The effect of congruency on mean reaction time (RT) and error rate for Experiment 1 was analyzed separately for numerical comparisons in the subitizing range of 1–3 (27). Statistical analysis of the RTs for pairs within this range, [1,2], [1,3], and [2,3], yielded a main effect of congruency [F_{(2, 36)} = 7.5, P < 0.005]. The overall error rate was 4.1%, and the effect of congruency on this measure was significant ([F_{(2, 36)} = 18.7, P < 0.0001]. As illustrated in Fig. 2, the effect of a numerical difference on RT and error rate depended of the ratio of the two numbers: The farther the numerical ratio was from 1, the shorter the time to judge the numerical difference and the lower the error rate. Curiously, a similar dependence on the ratio of circle diameters was not seen.

Fig. 2.

Experiment 1. (A and B) Mean reaction times (A) and mean error rates (B) ± SE as functions of the ratio of the number of circles in the two arrays, in three different conditions: (i) difference in circle size congruent with (in the same direction as) numerical difference, (ii) difference in circle size incongruent with (opposite to) numerical difference, and (iii) no difference in circle size (Neutral). (C) Mean reaction time as function of circle diameter ratio ± SE.

It is of interest that the ratio between pairs of numbers (N) is reliably related to performance, especially given that congruency/incongruency in circle size did not vary systematically with the ratio of the circle sizes. Although we demonstrated an interference effect of circle size on numerical magnitude judgments, the ratio of the diameters does not appear to be the locus of this effect. There are two other possible sources of interference: (i) the sides were categorized as having, on average, “smaller” or “larger” circles, and (ii) the combined area or luminance of each side produced the interference effect.

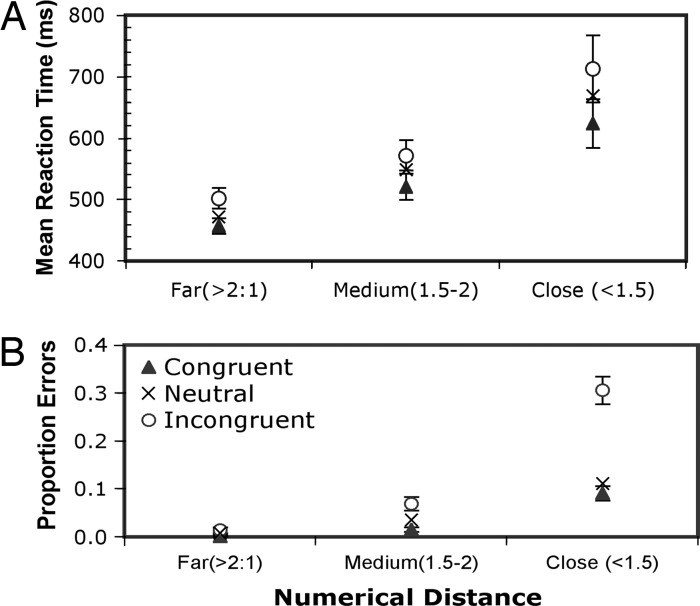
Experiment 2 followed up on Experiment 1 by measuring whether the summated areas for the circles in each display interfered with numerical comparisons, even when the size of the largest circle was controlled. Analysis revealed a strong effect of congruency between combined area and number on mean RT [F_{(2, 56)} = 15.06, P < 0.0001] and on error rate [F_{(2, 56)} = 21.7, P < 0.0001]. As before, responses tended to be faster when the larger number was on the left side.

To examine the effect of numerical distance, ratios were binned into three groups: (i) far (a 2:1 or greater ratio), medium (a ratio between 2:1 and 3:2), or close (a ratio < 3:2). As may be seen in Fig. 3A, the closer the numerical ratio was to one (that is, the closer the two set sizes), the longer was the mean reaction time [F_{(2, 56)} = 16.13, P < 0.001]. Fig. 3B shows the same effect for the error data [F_{(2, 56)} = 91.2, P < 0.0001]. In both the RT data and the error data, the effect of congruency is greater when the numerical distance is small, although this interaction between congruence/incongruence and numerical distance is statistically significant only in the error data [F_{(4, 112)} = 17.62, P < 0.001].

Fig. 3.

Experiment 2. Mean reaction times (A) and mean error rates (B) ± SE as functions of the numerical distance based on the ratio between the numbers of circles in the two arrays, in three different conditions: (i) difference in combined circle areas congruent with (in same direction as) numerical difference, (ii) no difference in combined circle area (Neutral), and (iii) difference in combined circle area incongruent with (opposite to) numerical difference.

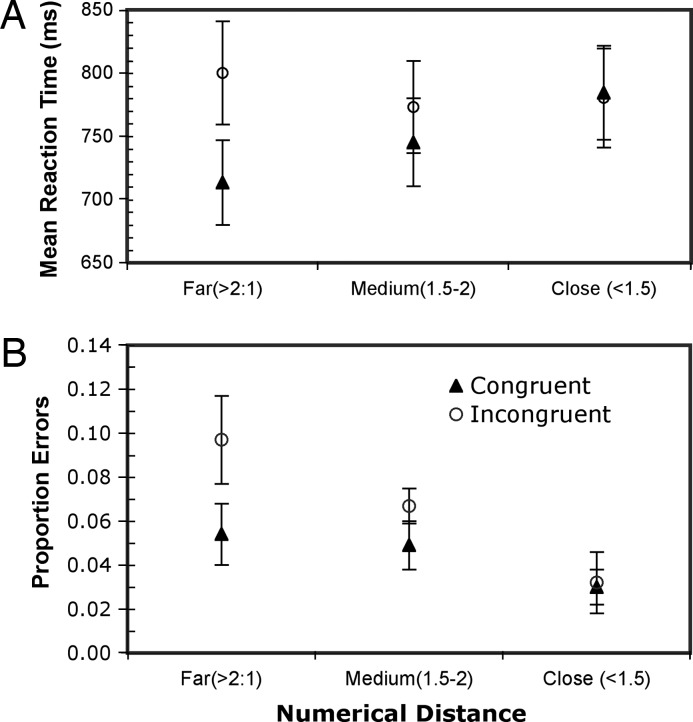
Experiment 3 tested the hypothesis that number acts as an interfering quantity dimension when responding on the basis of summated area (see Fig. 1). Here, congruency was not significant for RT or error rate. Fig. 4 shows that for both mean RT and error rate, the interfering effect of an irrelevant numerical difference on area judgments depends on the numerical distance between arrays. Greater numerical distances were more salient, thereby increasing the tendency for interference to affect the mean RT and error rate [the respective interactions are F_{(2, 58)} = 4.07, P < 0.05 and F_{(2, 60)} = 3.03, P = 0.056].

Fig. 4.

Experiment 3. Mean reaction times (A) and mean error rates (B) ± SE as functions of the numerical distance between the ratios of the number of circles in the two arrays, in two different conditions: (i) difference in numbers of circles congruent with (in same direction as) difference in the combined circle areas, and (ii) difference in numbers of circles incongruent with (opposite to) difference in combined circle area. Neutral RT (768 ± 44 ms) and error rate (3.9 ± 1%) were not included in graph, because numerical distance would consistently have a ratio of 1.

Discussion

Judgments of size, area, and number occur automatically and spontaneously in adult humans. Variation of stimuli along a continuous quantity dimension substantially affects performance on tasks requiring discrete numerical comparisons, and vice versa.

Adults were unable to ignore the relative size of the circles when judging which array had more circles in Experiment 1. This was true even in the “subitizing” numerical range. Some models suggest subitizable numbers are represented by discrete, noise-free symbols, like written digits or sets of hash marks, instead of by noisy mental magnitudes (28). On such models, one might not expect interference with numerical comparisons within the small number range. However, incongruence on the size dimension increased mean reaction time and error rates on the numerical ordering task even when both contained three or fewer circles. The results bolster the finding of Cordes et al. (5) that discrete displays with all tested values of N, including the smallest, are represented by noisy mental magnitudes.

When we controlled for the absolute size of the largest circle in the display, interference effects still occurred. Our participants were sensitive to differences in the combined areas of the circles in the two displays and this sensitivity affected their mean RT when judging differences in the number of circles. This implies that when individuals see an array of circles, they (unconsciously) estimate the combined area of the circles. How they do this remains to be determined. Adults are sensitive to subtle statistical properties of arrays of 2D objects, including, for example, their averages. Chong and Treisman (29) had adults compare arrays of homogenous-sized or heterogeneous-sized circles and report which side had the larger mean circle size. The numbers of circles on the two displays were always the same, so number and area (or average size) never were incongruent. Their subjects excelled at estimating the mean circle size for both homogenous-size and heterogeneous-sized displays and were able to do the task across displays with different distributions of sizes. Apparently adults can extract the average area for a collection of simple shapes in a relatively effortless way.

The interference effect in this experiment may reflect an averaging process. Individuals may have averaged the areas of the circles on each side of the display, in which case the contrasting averaged values may have been the source of interference. Chong and Triesman's results also could reflect the computation of combined area, as their study (by necessity) confounded combined area and average circle size. Neither the present experiment nor the Chong and Treisman experiment can distinguish between these two possibilities (ref. 29, also see ref. 30). Regardless of which account holds in the present case, we can conclude that our participants involuntarily computed a continuous quantity dimension that was irrelevant to the task at hand and that competed for behavioral control with the task-relevant dimension.

We find that adults readily judge which of two arrays of circles has the greater combined area, but while they are making this comparison, they also involuntarily compare the number of circles in the two arrays. The likelihood of the number comparison interfering with the combined-area comparison depends on the numerical distance between the numbers: the greater this distance, the greater the interference. This effect of numerical distance is consistent with many results from nonverbal number experiments in animals and humans, which show faster response times and fewer errors for numerically distant comparisons (5, 31, 32). Thus, the interactions reported for Experiment 3 are as one might expect: When the distance between the values of the irrelevant number dimension is great, the numerical comparison proceeds rapidly enough to interfere with the area comparison. The comparison of numerically close values proceeds too slowly to interfere with a speeded area judgment. This could mean that in those cases, the numerical comparison is incomplete by the time one responds on the basis of area.

The discovery that an irrelevant area dimension affects the ability to respond on the basis of number bears on the interpretation of the conflicting results regarding infants' responses to discrete quantities (number) (15–16). Recall in the incongruent condition of Experiment 2, when the numerical difference was small, the error rate was > 30%. Adults who are fully capable of counting still find it difficult to make numerical estimations while ignoring size/area information. That infants favor continuous quantities over discrete numbers in some experimental paradigms does not indicate an inability to represent discrete quantity any more than a high level of interference from continuous dimensions indicates an inability of 5- to 7-year-old children (33) or our adult subjects to represent numbers per se. Indeed neural evidence suggests facilitation and interference from overlapping tasks may derive in part from the ability to maintain the correct goal (see ref. 34). Given that infants can be presented only with an implicit goal, their susceptibility to interfering dimensions may be substantial. Thus, it is premature to conclude that infant and child quantity processes are fundamentally different from that of adults.

The prominence of one quantity dimension over another may be task- or object-specific and may vary along an attentional hierarchy. Operant studies in animals demonstrate a relationship between continuous and discrete magnitude representations. Timing and numerical magnitude discrimination functions reflect scalar variability (increase in variance of estimate as the magnitude increases) (35). These magnitude values also are frequently correlated in real-life situations. The extent to which various magnitude representations are processed in parallel has been explored in the domain of animal learning. Animals trained to respond on a contingency basis to confounded continuous and numerical cues encode both types of information simultaneously (35–38). However, the experimental paradigm may affect what information is being tracked, with the locus of control depending on the nature of the training (38). When one dimension is uniformly rewarded (e.g., number), animals can learn to ignore confounding factors such as length (39) or duration or timing of light flashes (40).

Cue salience may be highly specific to the situation at hand; the literature suggests there is not one stable preference for volume, number, or size that transcends situational factors (35–41). For example, Boysen et al. (41) tested chimpanzees in an interference task that required them to choose one of two trays of candy. The animals were rewarded with the contents of the nonchosen tray; hence the optimal choice was to choose the tray that contained a smaller number of objects to receive the greatest food reward. When the trays contained candies of the same size, the chimps tended to choose the side that had more candies. That is, the chimps went with a nonoptimal strategy because they were unable to overcome a tendency to indicate the side with more candy. However, when experimenters changed the paradigm to one where candies were of different sizes, the chimps tended to go with the side with larger candies, regardless of which side would produce the larger volume of food or which side has the larger number of candies. So here the size of the items took precedence over volume and number.

Developmental human studies tend to show that children have more trouble overcoming interference from conflicting quantity dimensions than adults. Children may be less able to consciously select among competing quantity dimensions than adults, because children find it difficult to tune out irrelevant information when performing simple tasks. For example, 3-year-old children who can perform a simple card-sorting task are challenged by the same task when an irrelevant stimulus dimension is added (in this case, objects on cards came in two color) (42). This has been explained as “attentional inertia”: Preschoolers have difficulty in disengaging from one way of thinking regarding a stimulus to attend to another dimension (43).

Experiments that examine counting abilities in preschool children often are designed with the expectation that true “counters” can overcome completely the interference from other quantity dimensions (16, 42). Yet, in experiments that systematically vary size, contour, or area as well as number, preschoolers may find it difficult to filter out the irrelevant dimensions necessary to display their competency in counting. Findings that children select area or volume over number do not necessarily reflect a lack numerical competence but rather may reflect limits in inhibitory processing (16, 42–44).

Performance on controlled perceptual versus number tasks possibly would yield improved number awareness if paradigms promoted attention towards number and away from other stimulus dimensions that often converge with number. When tasks are designed with this in mind, results tend to lean toward numerical competency. For example, objects differentiated by movement patterns may sway quantity attention toward discrete number. Several infant habituation/dishabituation studies that employ stimulus movement during the habituation phase find infants have an awareness of discrete number despite controls for overall area (45–46).

Many other factors potentially could influence how much attention is assigned to competing quantity dimensions. For example, it may be that simultaneous versus sequential presentation of stimuli affect this process. Further experiments are required to tease apart the factors that affect how attention is deployed to various magnitude representations. It would be of interest to determine whether young children start out with the same attentional preferences to quantity dimensions as adults or whether the relevance of different quantity dimensions shift as the child develops.

Although we demonstrated that the interference between comparisons along discrete and continuous stimulus dimensions runs both ways, at least in dot displays, the interference runs more strongly from the continuous to the discrete than vice versa. This is surprising given the frequency with which numerical comparisons are called for in ordinary adult life. It implies that the extraction of a representation of this continuous quantity proceeds more rapidly than the extraction of a representation of discrete quantity, even in adults. Future studies are required to more precisely delineate the factors controlling the salience of different quantities dimensions, as array size, the heterogeneity of stimuli, and task demands potentially may exert an influence on this attentional hierarchy.

Methods

Experitment 1.

Participants.

Twenty Rutgers University undergraduates were in this experiment. Their participation partially fulfilled a psychology course requirement. The human subjects review board at Rutgers University approved this research. All participants provided informed consent.

Stimuli and apparatus.

Test displays were shown on a Macintosh G4 (Apple, Cupertino, CA) computer with display set at 1,024 × 768 resolution, a 35 × 23 cm viewable area, and a viewing distance of ≈60 cm resulting in 32 pixels per degree of visual angle. A Matlab program was used with PsychToolbox functions (47). The psychophysics toolbox controlled the selection of displays, the experimental procedure, and the recording of reaction times. At the start of each trial, there was a white cross in the center of a black screen. Subjects were told to fixate on the cross. After 1 second, a short warning beep sounded. One second later, a two-array test stimulus appeared; it stayed on until the subject's button press registered.

The two arrays of white circles appeared inside two side-by-side symmetric gray rectangles drawn on a blue screen. Circle positions were randomly selected for each set on each trial, with the center of each circle placed in the “center” of an imaginary 4 × 3 grid.

The numbers of circles in the two arrays, N_L and N_R were randomly chosen from a list of all combinations from 1 to 7, with the constraint that N_L ≠ N_R. Mirror image displays, [N_L, N_R] and [N_RN_L], were treated as distinct displays. Circle radii were randomly chose from the set of radii of 10, 20, 30, 40, 50, 60, or 70 pixels. (10 pixels ≈ 19-min arc) Thus, both the relevant (circle-number) and irrelevant (circle-size) dimensions had an equal number of possible values. Previous researchers have noted that a more restricted number of values for either the relevant or irrelevant dimension can skew results (20, 48). Also, the ratio of the comparable radii equaled the ratio of the numerical sets (i.e., largest to smallest radius 70:10; largest to smallest numerical set 7:1). The combined area of the circles was congruent with size when size and number were incongruent and with number when sizes were equal.

Images in Fig. 1 show examples of the different display conditions. There were three congruency conditions, Congruent: N_A > N_B, size_A > size_B, area_A > area_B; Incongruent: N_A < N_B, size_A > size_B, area_A > area_B; and Neutral: N_A > N_B, size_A = size_B, area_A > area_B, where N_i is the number of circles in a given array, size_i is the size of every circle in a given array, and area_i is the combined area of all circles in a given array. The trial order was randomized.

Participants were tested individually. Instructions indicated that the display would contain two arrays of circles, one on the left side of the screen and one on the right. Participants indicated the side that had the greater number of circles by pressing the button under the corresponding side as quickly and accurately as possible.

Initially, there was a 20-trial training session, which contained a randomly selected sample of the full list of 42 possible neutral trials. The experimental session consisted of 126 trials, comprising the combination of 42 distinct stimulus combinations and the three conditions. A break occurred halfway through testing.

To remove outliers, the response times were trimmed at 2.5 standard deviations above their mean. RTs < 150 ms were considered accidental button presses and were also removed.

Experiment 2.

Participants.

Thirty Rutgers undergraduates participated.

Stimulus generation.

Display features and design were identical to Experimental 1, except as follows: Set sizes for pairs of arrays were randomly chosen from a list of all combinations of 3 to 9, with ties excluded. In pilot work, we found that individuals tended to focus on the difference between the two largest circles in each display. Therefore, we set the largest circle size per array to be equivalent across array pairs, while still varying summated area. Given that the largest circle size on any given trial had to appear in both arrays, the smallest N we could use was 3; hence, the change in array size values and range. Circle sizes were randomly chosen from values of 10–70 pixels. After the generation of each stimulus set, a randomly chosen circle in one of the arrays (excluding the largest circle) had its size modified so that the difference between the combined total areas of the circles in the two arrays was 5,000 pix² (4.88 deg²), henceforth denoted as A_const. Pilot work revealed that smaller differences in total area were not discriminated reliably.

There were three conditions used in this experiment: Congruent, N_A > N_B, and max (circlesizes_A) = max (circlesizes_B), and area_A = Σarea_B + A_const; Incongruent, N_A < N_B, and max (circlesizes_A) = max (circlesizes_B), and area_A = area_B + A_const; and Neutral, N_A > N_B, and max (circlesizes_A) = max (circlesizes_B), and area_A = Σarea_B, where N_i is the number of circles in array i, max (circlesizes_i) is the largest circle in an array i, and area_i is the combined area of the circles in array i. The sizes of the other circles in an array were not constrained, save by the difference-in-total area requirement. In the Congruent condition, the array containing more circles had a greater combined area than the second array, whereas in the Incongruent condition, the array containing more circles had a smaller combined area. In the Neutral condition, the combined areas were equal. In all, there were 126 randomized test trials, presented with a break halfway. Reaction times on correct trials were trimmed as in Experiment 1.

Experiment 3.

Participants.

Thirty-one Rutgers University undergraduate students participated.

Procedure.

All procedures were identical to those described in Experiment 2, with the following exception: In the Neutral condition N_A = N_B, the size of the largest circle in A equaled the size of the largest circle in B, whereas the difference between the combined areas of the circles on the two sides was equal to A_const. In compiling the training block, the 20 training displays were sampled from the complete list of 42 possible neutral trials by following the guidelines described above. Neutral displays contained an equal number of dots and differed in area (see Fig. 1). Note that the Congruent and Incongruent displays were identical to those used in Experiment 2. Only the task differed; in this experiment, subjects indicated by pressing a button which side of the screen had the greatest combined area.

Abbreviation

RT

reaction time.