Order from disorder: Self-organization in mammalian hair patterning

Abstract

Hairs, feathers, and scales normally exhibit precise orientations with respect to the body axes. In Frizzled6 (Fz6)^−/− mice, the global orientation of hair follicles is disrupted, leading to waves, whorls, and tufts, each comprising many hundreds of hairs. By analyzing the orientation of developing hair follicles, we observed that the nearly parallel arrangement of wild-type (WT) hairs arises from fields of imperfectly aligned follicles, and that the Fz6^−/− hair patterns arise from fields of grossly misoriented or randomly oriented follicles. Despite their large size, both mutant and WT hair follicles display a remarkable and unexpected plasticity, reorienting on a time scale of days in what seems to be a self-organized refinement process. The essential features of this process can be studied with a simple cellular automata model in which a local consensus “rule” acts iteratively to bias each hair's orientation in favor of the average orientation of its neighbors. These experiments define two systems for hair orientation: a global orienting system that acts early in development and is Fz6-dependent, and a local self-organizing system that acts later and is Fz6 independent.

In the animal kingdom, morphologic complexity is ubiquitous but is not well understood at a mechanistic level. One system that controls morphology, the tissue polarity or planar cell polarity (PCP) system, coordinates the spatial orientation of local structures with the principal body axes (1–3). PCP genes were first identified in Drosophila where they control the orientation of hairs and bristles and the chirality of ommatidia. In mammals, PCP genes control the orientation of hair follicles in the skin and sensory hair cells in the inner ear. PCP genes also control neural tube and eyelid closure, processes that rely on oriented cell proliferation and migration.

The present work focuses on the development of hair follicle orientation. Follicles make an acute angle with the skin, giving each hair a particular orientation along the body surface. In general, neighboring follicles exhibit nearly identical orientations. We previously reported that Frizzled6 (Fz6)^−/− mice exhibit a global disorganization of hair orientation, with waves, whorls, and tufts, each comprising many hundreds of hairs, over much of the body surface (4). Interestingly, many of the Fz6^−/− hair patterns are individual-specific, suggesting a stochastic component during pattern formation. In this work, we describe the developmental origin of the Fz6^−/− hair patterns and we explore the broader implications of these findings.

Results and Discussion

Quantitating Hair Follicle Orientation.

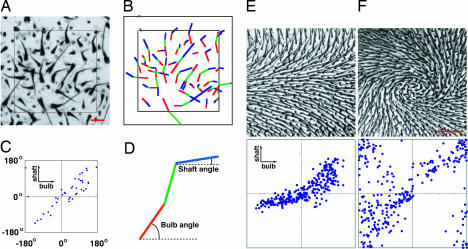
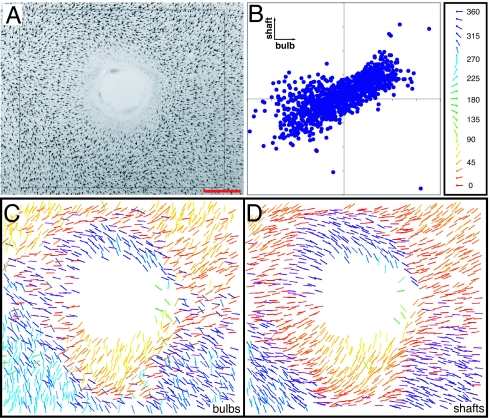
To observe hair follicle orientation, flat mounts of skin were either clarified to visualize melanin along the length of each follicle, or optically sectioned to visualize GFP expressed from a follicle-specific keratin-17 (K17)-GFP transgene (5). The two methods are complementary: melanin accumulates only in more mature follicles [after postnatal day 0 (P0) to P2], whereas K17-GFP can be seen clearly only in flat-mounts if the skin is immature (younger than ≈P3). Follicles are often curved when viewed in a flat mount (Fig. 1A), and therefore we have separately scored the orientation of the follicle bulb (the region furthest from the skin surface) and the follicle shaft (the region closest to the skin surface; Fig. 1 A–D).

Fig. 1.

WT and Fz6^−/− hair follicle patterns and their quantitative analysis. (A) Example of quantification of bulb and shaft angles in a region of P3 back skin. (B) The bulb and shaft orientations are indicated in red and blue, respectively; in some follicles, a straight green line is drawn between the shaft and bulb. Follicles with bulbs residing inside the inner square were scored. (C) Scatterplot of bulb and shaft angles. (D) By convention, an angle of 0° corresponds to the posterior direction when scoring the back and tail, and the distal direction when scoring the paws. (E and F) Dorsal skin on P8 hind paws from WT (E) and Fz6^−/− (F) mice. (Upper) Tissues were clarified in BBBA (2:1 benzyl benzoate:benzyl alcohol) and are oriented with the digits toward the right. (Lower) Scatterplots (as in C) of the orientations of hair bulbs and shafts for each follicle. In the WT sample, bulb angles exhibit greater variability than shaft angles. [Scale bars: 100 μm (A) and 500 μm (E and F).]

Mice are born hairless, but, by the end of the first postnatal week, both WT (Fz6^+/+ and Fz6^+/−) and Fz6^−/− mice are covered with hairs that are locally well oriented, as seen, for example, on the dorsal aspect of the hind paws at P8 (Fig. 1 E and F). As reported by Guo et al. (4), Fz6^−/− mice have a counterclockwise whorl on the left hind paw and a clockwise whorl on the right hind paw; examples of WT and Fz6^−/− left paws are shown in Fig. 1E and F. Careful inspection of Fig. 1 E and F shows that the precise orientation of the hair follicles is largely a property of the shafts; the bulbs are, on average, less well ordered. This visual impression is supported by the corresponding scatter plots of bulb vs. shaft angles, and is observed over the entire body surface in both WT and Fz6^−/− mice [supporting information (SI) Fig. 7].

Each hair follicle arises from an invagination of the surface epithelium. The subsequent elongation of the follicle is driven by the production of new cells within the bulb and their migration into the follicle shaft. Because the bulb is the first part of the follicle to form, its imperfect orientation in mature skin could reflect an imperfect orientation of the follicle earlier in development. For example, the large differences in many bulb and shaft angles on the Fz6^−/− paw could reflect a correspondingly large reorientation of follicles during development.

To test the idea that follicles reorient during development, we examined back, paw, and tail skin at daily intervals in both WT and Fz6^−/− mice. Because each time point is derived from a different animal, this data set does not permit an analysis of the reorientation of any particular follicle. Much of the reorientation described below occurs before P4, the time when the first hairs emerge from the surface of the skin (SI Fig. 8), thus ruling out an effect of grooming on follicle orientation up to this point. We also found that shaving the mice daily beginning at P4 had no effect on the subsequent development of hair patterns, arguing that grooming after hair emergence plays little or no role in patterning (n = 24 mice; data not shown). Loss of Fz6 has no effect on the uniform spacing and average density of hair follicles (SI Fig. 9), and therefore the observed orientation defects occur within the context of a normal follicle lattice.

Dynamic Reorientation of Hair Follicles During Development.

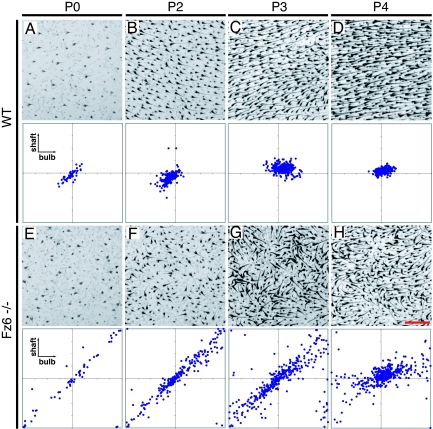
In the WT back, the distribution of shaft angles at P0 encompasses a range of roughly ± 45° relative to the anterior-posterior (A-P) axis, and this distribution narrows progressively between P0 and P4; the distribution of bulb angles shows a smaller narrowing (Fig. 2A–D; n = 24 mice). In the Fz6^−/− back, follicle angles are initially random or nearly random, but as development proceeds they describe progressively larger spatial domains of correlated orientation (Fig. 2 E–H; n = 27 mice). Moreover, as seen in the flat mount and scatter plot at P4 (Fig. 2H), there is a narrowing in the distribution of shaft angles as the shafts increasingly conform to the local consensus angle. The many curved hair follicles at this age strongly suggest that shafts reorient more rapidly than bulbs.

Fig. 2.

Progressive ordering of hair follicles on the back of WT and Fz6^−/− mice between P0 and P4. Posterior is to the right. (A–D) WT follicles at P0 have orientations that range from approximately −45° to +45°. (E–H) Fz6^−/− follicles at P0 have approximately random orientations. Between P2 and P4, the follicles reorient to produce progressively larger spatial domains of local order. Scatterplots are calibrated as in Fig. 1C. In both WT and Fz6^−/− between P2 and P4, the distribution of shaft angles tightens more than the distribution of bulb angles. (Scale bar: 400 μm.)

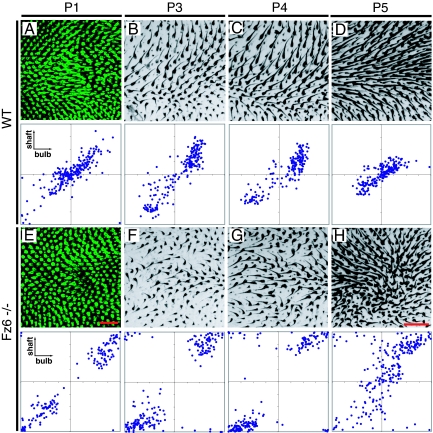
The paws follow a more constrained developmental sequence. In the WT paw, as in the back, there is a progressive narrowing in the distribution of shaft angles and a more modest narrowing of bulb angles during the first postnatal week (Fig. 3A–D; n = 51 paws). In Fz6^−/− mice, the paws have the distinction of being the only regions of the body surface where the same abnormal hair pattern is seen across individuals. Careful inspection of Fig. 3 E–H suggests a simple explanation for this phenomenon. From the earliest time at which their orientations can be scored (≈P1) the follicles in the center of the Fz6^−/− paw are largely reversed relative to the WT; that is, they tend to point proximally rather than distally (compare the scatter plots in Fig. 3 A and E). As development proceeds there is a progressive reorientation of the central follicles into a whorl, thereby maintaining local continuity with the centrifugal orientations of follicles at the sides of the paw and at the base of the digits (Fig. 3H).

Fig. 3.

Development of hair follicle patterns on WT and Fz6^−/− hind paws between P1 and P5. Distal is to the right. (A–D) WT. (E–H) Fz6^−/−. Between P1 and P4, WT follicles in the center of the paw are largely oriented distally whereas Fz6^−/− follicles are largely oriented proximally; in both genotypes, they progressively reorient between P1 and P5. Follicles at P1 were visualized with a K17-GFP transgene. Scatterplots are calibrated as in Fig. 1C. [Scale bars: 100 μm (A and E) and 400 μm (B–D and F–H).]

The WT mouse tail has an almost crystalline arrangement of posteriorly pointing hair follicles (SI Fig. 10 A, B, E, and F; n = 24 tails). Follicles are arranged in triads with a central larger follicle flanked by two smaller ones, and each triad resides at the junction between a pair of brick-like cuticular plates. In neonatal Fz6^−/− mice, the density of hairs and their sites of insertion at the skin surface are unaltered but their orientations are disorganized and over time the regular repeating pattern of cuticular plates is replaced by an irregular series of transverse epidermal ridges (SI Fig. 10 C, D, G, and H; n = 24 tails). The generalized disorganization of the Fz6^−/− tail skin indicates a role for Fz6 in epidermal patterning that extends beyond hair orientation.

In Fz6^−/− mice, the initially random orientation of follicles on the back and the largely reversed orientation of follicles in the center of the paw imply that Fz6 normally functions early in development to set the global orientation of hair follicles with respect to the body axes. The subsequent reorientation is orchestrated by a Fz6-independent system that aligns neighboring follicles. Thus, these data imply the existence of two distinct orienting systems, one that acts early in development and globally, and a second that acts later and locally. We will refer to these two systems hereafter as the global and local orienting systems. Multistage models have also been proposed in the context of PCP signaling in Drosophila (1, 2, 6–10).

Local Interactions: Response to Genetic Chimerism and Injury.

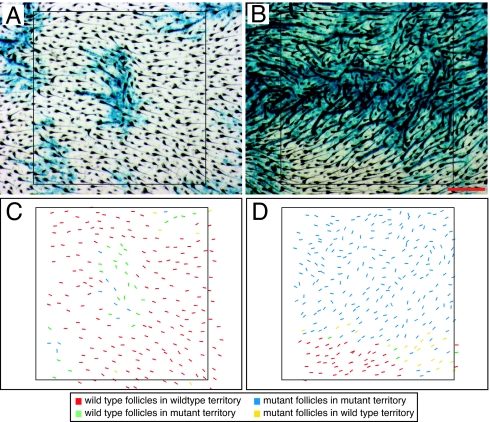
To estimate the spatial scale over which the local orienting system functions, we conducted two experiments to perturb the environment of developing follicles. In the first experiment, interactions between WT and Fz6^−/− follicles were analyzed in Fz6^−/−:WT chimeras. In chimeric skin we identified the Fz6^−/− territory by the presence of nuclear β-galactosidase (expressed from the targeted Fz6 locus) in the epidermis, the tissue layer from which the follicles emerge, and we counted those follicles composed of a mixture of Fz6^−/− and WT cells as part of the Fz6^−/− group. Two images of chimeric back skin at P3 are representative of the patterns observed (Fig. 4). The principal findings from 13 chimeras analyzed at P2 or P3 are as follows: (i) where WT and Fz6^−/− follicles intermingle, a reciprocal interaction occurs such that some WT hairs are aberrantly oriented and some Fz6^−/− hairs are appropriately oriented; and (ii) where contiguous zones of WT and Fz6^−/− follicles meet, the orientations of WT follicles are minimally altered whereas the orientations of Fz6^−/− follicles within two to three inter-follicle diameters of the WT territory are strongly biased toward the WT orientation. In Drosophila, local reorientation of wing hairs is typically observed in crossing a border from mutant to WT tissue in genetic mosaics (1–3).

Fig. 4.

In chimeric Fz6^−/−:WT skin, the orientations of WT and mutant follicles are influenced by short-range interactions. (A) Region of chimeric skin with a small territory of Fz6^−/− epiderimis. (B) Region of chimeric skin with finely interspersed WT and Fz6^−/− epidermis (Top), predominantly Fz6^−/− epidermis (Middle), and a contiguous block of WT epidermis (Bottom). (C and D) Scoring the follicle genotype and the genotype of the surrounding epidermal territory (color coded as indicated in the key below the panels), and the shaft angle (represented by the angle of each bar). Note the generally well oriented follicles (both Fz6^−/− and WT) in the region in and adjacent to the contiguous territory of WT epidermis (Bottom third of B and D). (Scale bar: 400 μm.)

In the second experiment, an ≈1-mm-diameter circle of back skin was removed from WT mice at P0, and the effect on hair orientation was determined between 2 and 10 days later (n = 95; in most of the experiments, the skin was examined at P3). In roughly 50% of the samples there was little or no effect on the orientation of nearby hairs. However, in the remaining samples, many nearby hair follicles turned toward the wound, in some cases exhibiting a nearly 180° bend (Fig. 5, SI Fig. 11, and SI Fig. 12). This phenomenon might have a purely mechanical explanation: for example, a differential retraction of epidermis vs. dermis in response to wounding could reorient the shafts, which are attached to the epidermis, more than the bulbs, which are embedded in the dermis. To test this possibility, we used glass micropipettes to create 8–10 vertical India Ink tracks in the skin immediately surrounding each circular wound (n = 15). When the skin was clarified and flat mounted 3 days later, there was minimal distortion of the microscopic India Ink tracks (data not shown), indicating that differential retraction is minimal. Therefore, the change in hair follicle orientation induced by wounding most likely reflects the local production or destruction of an orienting signal, providing further evidence for a local orienting system that operates on a rapid time scale. A similar response to wounding was observed in Fz6^−/− skin (n = 39; data not shown).

Fig. 5.

Rapid and coordinated reorientation of WT hair follicles in response to wounding. (A) Approximately 1-mm-diameter circular wound was made in the back skin at P0 and visualized at P3. (A) Follicles have reoriented within several hundred micrometers of the wound, including an ≈90° reorientation on either side of the wound. Posterior is to the right. (B) Bulb and shaft orientations for all follicles in the boxed area in A; there is a substantially greater range of orientations relative to unperturbed back skin at this age (Fig. 2C). (C and D) For each follicle in the boxed area, bulb (C) and shaft (D) angles are shown separately, and their orientations are represented by the angle and color of the corresponding bar (key, B Right). (Scale bar: 1 mm.)

Modeling Hair Orientation with Cellular Automata.

As first noted by Lewis and Davies (11) and as demonstrated experimentally in this work, PCP patterning bears a conceptual resemblance to the patterning of electron spins in a ferromagnet (12). As in PCP, there are both local and global effects: local quantum mechanical interactions favor the alignment of adjacent electron spins, and a global signal, in the form of an external magnetic field, biases the alignment probabilities of individual spins. If the ferromagnet is maintained below a critical temperature (the Curie temperature), then the configuration of aligned spins will remain relatively stable because the local interactions create an energy barrier to spin inversion.

Modeling of ferromagnetism and related systems has been an area of active investigation since the introduction of the Ising model in the 1920s (13). In this model, a lattice of points in a Cartesian coordinate system defines the locations of the individual spin vectors, each of which interacts with its immediate neighbors. An analytical solution for a two-dimensional Ising model was obtained by Onsager in 1944, but many recent analyses of Ising-type lattice models have generated empirical solutions by the iterative application of local interaction rules (14, ^‖). With this approach one can readily examine the effect of different starting configurations, boundary conditions, and local interactions on the evolution of the system.

At present there are only two published mathematical models for PCP (15, 16). Both are analytic and attempt to account for cell behavior by quantitative analyses of protein interactions and subcellular localization. These two models have, respectively, eight and ten nonlinear partial differential equations and 15 and 20 empirical constants, most of which have not been experimentally defined. Inspired by the conceptual clarity of Ising-type models, we have designed a simple two-dimensional lattice model that captures the essential features of the follicle alignment system. Like the original Ising model for ferromagnetism, our model is not tied to any particular underlying machinery but simply exhibits macroscopic behavior based on local interactions. In brief, each hair follicle is represented by a unit-length vector placed at one of the vertices of a lattice of equilateral triangles [the optimal close packing lattice for 2D objects and a good approximation to the close packing of follicles in WT and Fz6^−/− mice (SI Fig. 9)]. After the initial vector orientations are set, the lattice develops by repeated application of an updating rule specifying that the orientation of each vector be modified by adding to it the vector sum of its 18 closest neighbors after that sum has been scaled to 2% of its magnitude. Eighteen neighbors corresponds to two concentric circles of surrounding lattice points, and it approximates the spatial range of orientation effects estimated from the chimera and skin wounding experiments.

In this PCP model, the simplest stable states are ones in which all vectors are parallel. States with perfect radial symmetry are also stable, including those in which all vectors point radially, circumferentially, or some symmetric combination of the two (forming a whorl or tuft). In practice, nearly all patterns eventually progress to a completely parallel arrangement because perfect radial symmetry is rarely realized.

We have used the PCP model to address three questions. First, what patterns are observed as a set of randomly oriented vectors develop? Second, if the random orientations are initially modified by a global bias, what is the relationship between bias strength and pattern development? And third, how do uniformly oriented vectors at the edge of a field modify the development of randomly oriented vectors within the remainder of the field?

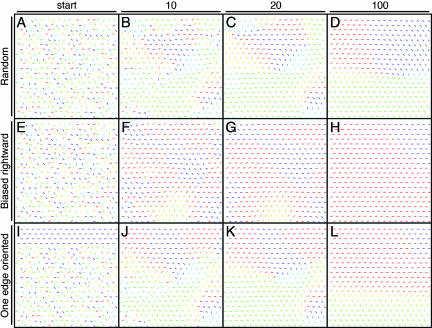
With respect to the first question, if the updating rule is applied iteratively to a lattice of vectors with initially random orientations, a characteristic progression is observed in the spatial scale of organization (Fig. 6A–D and SI Fig. 13). After only 10 iterations, the lattice exhibits numerous foci of correlated orientation (Fig. 6B). With additional iterations, the number of patterns shrinks as lattice points at the edges of “losing” patterns are steadily incorporated into “winning” patterns (Fig. 6 C and D). This temporal-spatial progression bears a close resemblance to the developing follicle patterns in Fz6^−/− mice (e.g., Fig. 2 E–H).

Fig. 6.

Modeling the development of hair follicle orientation with 2D cellular automata obeying a simple short-range consensus rule. (A, E, and I) Starting configurations. (A) A set of randomly oriented vectors. (E) The same randomly oriented set of vectors as in A, but each vector's orientation was biased by the addition of a vector of length 0.5 directed toward the right. (I) The same randomly oriented set of vectors as in A, but the top four rows were uniformly oriented toward the right. The development of each starting lattice is shown after 10, 20, and 100 iterations of the local consensus algorithm. Each vector orientation is represented by the angle and color of the corresponding bar as shown in Fig. 5.

In addressing the second question, each randomly oriented vector was given an initial bias equivalent to 10%, 20%, or 50% of the unit vector length and directed toward the right (examples of 50% bias are shown in Fig. 6 E–H and SI Fig. 14). As expected, with a greater bias the lattice is directed more rapidly to a fully parallel configuration. Somewhat unexpected was the strength of the effect: a 50% initial bias leads to complete or nearly complete convergence in only 30–50 iterations, and even a 10% initial bias leads to predominantly parallel vectors after 100 iterations. This effect may account for the largely posterior orientation of follicles on the back of mature Fz6^−/− mice because at early postnatal times there is a subtle bias toward posterior follicle orientations (Fig. 2 E–H). A similarly efficient convergence of follicle orientations is obtained by precisely orienting 11% or 25% of the vectors in the same direction (SI Fig. 15), an arrangement that models the progressive recruitment of later born follicles into a preexisting hair pattern comprising the earliest follicles (SI Fig. 9). These models imply that the global signal may produce no more than a rough alignment of follicles, which is then refined by application of a local consensus rule.

In addressing the third question, four rows at the edge of the lattice were initially assigned parallel orientations, with the remaining points given random assignments (Fig. 6 I–L and SI Fig. 16). Subsequent lattice development shows an interesting asymmetry: the four initially parallel rows progressively dominate pattern evolution in the rest of the lattice but are themselves minimally perturbed by patterns originating in other regions. This asymmetry reflects both passive buffering against perturbations and active propagation of the orientation from these four rows. Both effects arise when a block of aligned vectors dominates the local calculation that updates the orientations of adjacent lattice points. This phenomenon is likely to play a critical role in generating the stereotyped follicle patterns on both WT and Fz6^−/− paws because follicles at the sides of the paws and the bases of the digits are well aligned earlier than the follicles in the center (Figs. 1 E and F and 3). It also explains why a block of WT follicles dominates the orientation of adjacent Fz6^−/− follicles in Fz6^−/−:WT chimeric skin (Fig. 4B).

Conclusions

The principal findings of this work are as follows: (i) mammalian hair follicles are remarkably mobile despite their large size; (ii) PCP in mammalian skin proceeds via distinct global and local systems, and Fz6 participates in the former but not the latter; (iii) the local system minimizes orientation differences between neighboring hair follicles and this efficiently generates a mature hair pattern starting from an imperfect template of follicle orientations; and (iv) the essential features of follicle orientation can be captured with a simple Ising-type lattice model. At present, the cell biological mechanisms involved in orienting hair follicles are unknown.

Some of the strategies used by hair follicles may apply to other developmental systems where cells or multicellular structures are oriented with respect to the body axes. For example, this system probably orients feathers and scales. In the mouse inner ear, the alignment of stereociliary bundles on sensory hair cells depends on multiple PCP genes, including Fz6 (17–19). In the developing inner ear there is a refinement of sensory hair bundle orientation (20, 21), consistent with the action of a local consensus rule. In insects, neighboring ridges and bristles generally exhibit a parallel alignment. When this alignment is disrupted by surgical manipulations, the ridges and bristles realign to minimize nearest neighbor differences in orientation (22–24), a response that can be explained by local consensus mechanisms of the type studied here. Finally, we note that dermatoglyphs (fingerprints) represent a stochastic individual-specific patterning system analogous to the Fz6^−/− hair patterns on the back and head (25).

A more tenuous connection can be made between hair patterning and some aspects of axonal development. Fz3, a close relative of Fz6, plays an essential role in the growth and guidance of corticothalamic and thalamocortical axons and in the rostral orientation of spinal cord sensory axons (26–28). A connection with PCP comes from the finding that Fz3 and Fz6 function redundantly in the control of inner ear sensory hair bundle orientation and neural tube closure (19), and that targeted disruption of the gene coding for Celsr3, a homologue of the Drosophila PCP protein Flamingo/Starry Night, produces defects nearly identical to those in Fz3^−/− mice (29). In Fz3^−/− and Celsr^−/− mice, thalamic axons fasciculate but fail to enter the cortex, suggesting that, as in Fz6^−/− skin, a global guidance signal is defective but a local interaction signal remains intact. Thus, fasciculation or other forms of inter-axon communication may represent a local consensus mechanism that averages guidance decisions over many individually imperfect elements, in much the way that hair follicles locally communicate to produce a consensus orientation. The well known role for fasciculation in guiding late-born axons along the trajectory of pioneer axons represents a variant of this idea (30) and also has an analogy in the skin where new hair follicles are added over a period of 1–2 weeks to a field of oriented “pioneer” follicles (the guard hairs) as seen in SI Fig. 9.

Finally, we note that local consensus interactions, conceptually similar to those that align hair follicles, influence group behavior in a variety of complex social systems, including locust migration and fish schooling (31, 32). These interactions presumably represent an economical way to propagate global signals across the population and to enhance precision in the context of imprecise individual responses.

Experimental Procedures

Mouse Husbandry and Chimera Production.

Fz6^+/− and Fz6^−/− littermates and Fz6^+/−; K17-GFP/+ and Fz6^−/−; K17-GFP/+ littermates were studied on a mixed C57Bl6 × 129 background. Fz6^−/−:WT embryo chimeras were generated with ICR mice as the WT (4). All experiments were carried out in accordance with the guidelines of the Johns Hopkins Animal Care and Use Committee.

Skin Preparation.

For nonfluorescent postnatal skin, samples were manually dissected, pinned flat to Sylgard 184 plates, fixed in 4% paraformaldehyde at room temperature for 1.5 h, and then sequentially dehydrated in 70% and 100% ethanol, cleared in BBBA (2:1 benzyl benzoate:benzyl alcohol), and mounted in Permount. For K17-GFP skin, samples were pinned and fixed as described above, washed in PBS, and mounted in Fluoromount-G.

Data Analysis.

Skin images were converted to grayscale in Adobe Photoshop (San Jose, CA), and bulb and shaft angles were traced and digitized by using an object macro written in ObjectImage. X-Y measurements were exported to Microsoft Excel (Redmond, WA). Data analysis and modeling were performed with visual basic routines compiled and run as Microsoft Excel macros. To generate the images of bulb and shaft orientations for the wounding experiments and vector orientations for the PCP model, we used a modified version of ImageJ with a rainbow table of 254 levels to represent orientations.

Modeling Dynamic Hair Follicle Reorientation.

Lattices (18 × 22) of equilateral triangles were generated in Microsoft Excel with randomly oriented, unit length vectors located at each vertex. A Visual Basic routine was used to update the orientation of each vector as follows: the vector sum for the closest two concentric circles of neighboring vectors was computed, scaled by a factor of 1/50, and then added to the central vector, which was then rescaled to unit amplitude. We chose a 1/50 scaling factor so that only a small change in orientation would be produced at each cycle.

Abbreviations

PCP

planar cell polarity

K17

keratin-17

Pn

postnatal day n.