Pharmacokinetic/pharmacodynamic modelling of NSAIDs in a model of reversible inflammation in the cat

Abstract

1. Data on the relationships between plasma concentration and analgesic and anti-inflammatory effects of NSAIDs are limited because most inflammation models do not permit pharmacokinetic/pharmacodynamic (PK/PD) modelling to be readily performed.

2. In this study, a kaolin-induced inflammation model in the cat was evaluated for pre-clinical characterization of the pharmacodynamic profiles of NSAIDs (determination of efficacy, potency, sensitivity (that is the slope of the concentration–effect relationship) and duration of drug response), using meloxicam as a probe article.

3. Indirect response PK/PD models described the time course and magnitude of responses produced by 0.3 mg kg⁻¹ meloxicam administered subcutaneously. For endpoints for which spontaneous recovery from inflammation was superimposed on drug response, a PK/PD model with a time-dependent K_in was used to allow for the spontaneous changes of the inflammation with time.

4. The selected endpoints were suitable for studying simultaneously the analgesic, anti-inflammatory and antipyretic effects of meloxicam, allowing comparison of relative potencies for these effects. Mean±s.d. IC₅₀ or EC₅₀ values (ng ml⁻¹) were 777±124 (body temperature), 841±187 (locomotion variable), 883±215 (pain score), 911±189 (lameness score) and 1298±449 (skin temperature difference). Corresponding mean times±s.d. of peak responses (h) were 5.6±1.3, 8.6±3.8, 5.2±5.0, 5.6±3.7 and 4.3±2.4, respectively.

5. As the pharmacokinetic profiles of meloxicam in cats and humans are similar, simulations of several dosage regimens in the cat provided a pre-clinical basis, illustrating the value of the cat model for predicting a clinical dose regimen for evaluation in man. The predicted loading doses (mg kg⁻¹) of meloxicam in the cat producing 70% of the maximum attainable responses were 0.29 (body temperature), 0.32 (lameness score), 0.33 (overall locomotion variable), 0.36 (pain score) and 0.50 (skin temperature difference). The values are similar to or somewhat greater than the clinically recommended doses both in cats (0.3 mg kg⁻¹) and humans (7.5–15 mg, that is, between 0.1 and 0.3 mg kg⁻¹).

6. These findings indicate the potential value of the cat as a laboratory model, and of a PK/PD modelling approach in assisting NSAID development programs in animals and humans.

Introduction

In vivo pharmacokinetic/pharmacodynamic (PK/PD) modelling is increasingly accepted as a powerful approach for determining pharmacodynamic parameters, and thus for selecting effective and safe dosage regimens for clinical use. However, despite a large body of scientific literature on nonsteroidal anti-inflammatory drug (NSAID) pharmacokinetics and pharmacodynamics, relatively few pre-clinical studies have attempted to model blood or plasma concentration–time profiles with the time course of NSAID effects (Toutain et al., 1994; Granados-Soto et al., 1995; Landoni & Lees, 1995; Landoni et al., 1995; Torres-Lopez et al., 1997; Flores-Murrieta et al., 1998; Josa et al., 2001; Toutain et al., 2001; Lees, 2003). PK/PD modelling approaches permit the in vivo determination of numerical values for the three pivotal pharmacodynamic parameters of a drug, namely efficacy, potency and sensitivity (that is the slope of the concentration–effect relationship). These parameters allow prediction of the magnitude and time course of drug effect for any formulation, route of administration or dosage regimen, provided corresponding pharmacokinetic data are available (Toutain et al., 2001; Toutain, 2002). In addition, if drug plasma concentrations required to produce a given degree of pharmacological effect are similar in animals and man (Levy, 1993), PK/PD modelling in a non-human species offers a valuable approach to dosage regimen prediction for human use.

Currently, the application of PK/PD principles to determination of the pre-clinical profile of NSAIDs is limited by the availability of validated animal models and the inability of existing models to provide clinically relevant endpoints of drug response. Most of the inflammation models that have been developed in rodents and dogs (e.g. carrageenan-induced paw oedema, uric acid-induced arthritis) are too short-lasting to permit an accurate determination of the complete drug concentration–effect relationship. This partially accounts for the fact that dose-titration approaches, based on pre-challenge NSAID administration, have been preferred. A further drawback of rodent models is that they do not readily permit measurement of clinically relevant endpoints (e.g. lameness scoring). On the other hand, irritants such as Freund's complete adjuvant result in a sustained and relatively stable inflammatory response in the dog (Botrel et al., 1994; Toutain et al., 1994, 2001), allowing measurement of relevant and sensitive endpoints (e.g. vertical force applied by the hind limb, lameness score, etc.). However, for ethical reasons, the use of this irreversible inflammation model may be questioned. Consequently, an acceptable inflammation model should be neither too severe nor irreversible, but should be sufficiently long lasting to allow an accurate evaluation of the three main responses to NSAIDs, namely their anti-inflammatory, antipyretic and analgesic effects. The model should also be developed in a medium-sized species (e.g. dog, cat) to enable both collection of clinically relevant endpoints and sequential blood sampling for determination of drug concentration in blood/plasma–time profiles.

Recent studies by our group have shown that subcutaneous (s.c.) injection of kaolin in a cat's paw produces a well-defined, reproducible and reversible inflammatory response (Giraudel et al., 2005a). The signs of inflammation induced with 500 mg kaolin were relatively constant between 2 and 4 days after kaolin injection, allowing administration of the NSAID on day 2. This model also incorporated (a) quantitative measurement of objective endpoints relevant to therapeutic efficacy and (b) the possibility of sequential blood sampling. Based on statistical (reproducibility and accuracy of the measurement) and biological significance, it was anticipated that body temperature, gait scoring, times for performance of locomotion tests and possibly paw volume and skin temperature might be suitable for PK/PD studies (Giraudel et al., 2005a). Moreover, the model was found to be suitable for studying simultaneously the analgesic, anti-inflammatory and antipyretic effects of NSAIDs. This is of considerable interest, because it is possible and even likely that concentration–effect relationships will differ for each of these effects. Whereas analgesia seems to occur in a concentration-dependent manner, anti-inflammatory effect is more closely correlated with the time of exposure to a given drug (Walker, 1995). Such differences and the characteristics of the dose–effect relationship (efficacy, potency and slope, for example, ‘all or nothing' response compared with a progressive graded response) can be readily determined using a pre-clinical PK/PD modelling approach.

The aim of the current study was to assess the value of the feline paw inflammation model for pre-clinical characterization of the full pharmacological profile of a NSAID and then to apply it to prediction of dosage regimens for evaluation in other animal species and in man. Meloxicam was selected as a reference NSAID, because it has been used extensively as a therapeutic agent in both animals and humans, and its dosage regimen is now well established both in man and the cat (Engelhardt, 1996; Turck et al., 1996; Busch et al., 1998; Slingsby & Waterman-Pearson, 2000; Lascelles et al., 2001).

Methods

Animals

The study was performed in six healthy European short-haired cats of both sexes (three males, three females), maintained in a temperature-controlled environment (20±2°C) and either loose-housed in a colony (between experiments) or kept in individual stainless steel cages (during experimental phases). Weights and ages ranged from 3.2 to 4.6 kg and 1.4 to 1.6 years, respectively. They were fed each evening after the last measurements with commercial dry food. The housing and experimental facilities at the National Veterinary School of Toulouse were approved by the French Ministry of Agriculture, and animal care and conduct of the study were performed in accordance with the Guide for the Care and Use of Laboratory Animals (Institute of Laboratory Animal Resources, Commission on Life Sciences, National Research Council, 1996).

Drugs and chemicals

Kaolin (hydrated aluminium silicate) was purchased from Sigma-Aldrich (Saint Quentin Fallavier, France). The solution for injection of meloxicam (5 mg ml⁻¹) was obtained from Boehringer Ingelheim Vetmedica GmbH (Ingelheim/Rhein, Germany).

Animal preparation and inflammation induction

Animal anaesthesia and preparation as well as inflammation induction were performed using standardized procedures (Giraudel et al., 2005a). At 4 days prior to inflammation induction, each cat was anaesthetized to insert and secure a central venous catheter in a jugular vein. Both hind paws were shaved from the toes up to the hock joint and marked for skin temperature, withdrawal time and paw volume measurements (for details, see Giraudel et al., 2005a).

On the day of inflammation induction (day 0), each cat was re-anaesthetized to facilitate the s.c. injection of a 1.75 ml sterile suspension of about 500 mg kaolin.

Endpoint measurements

All animals were accustomed to experimental conditions and trained for recording of the endpoints during 4 weeks before the onset of the trial. During the experiment, the endpoints were recorded by the same two trained operators using standardized procedures (Giraudel et al., 2005a). Briefly, the gait was scored with a numerical rating scale (NRS) and the corresponding lameness score ranged from 0 (no lameness) to 5 (avoidance of any contact of the affected paw with the ground). Pain was evaluated as the time required by the cat to withdraw its paw after stimulation with the radiant heat emitted from an analgesia meter (Model 390, IITC Inc./Life Science, Woodland Hills, CA, U.S.A.). The animal was confined for a few min in a Plexiglas chamber adapted to the size of a cat, and placed on top of the glass panel of the device. This method avoids animal manual restraint and delegates to the cat control of the duration of the stimulus. Radiant heat was delivered as a beam of focussed light of fixed intensity (20% of maximal intensity). The stimulation was stopped as soon as the animal started to withdraw its paw. Only a clear withdrawal or lateral translatory movement of the paw was accepted as an accurate cutoff point. The withdrawal time was transformed into a pain score (%) according to the following equation:

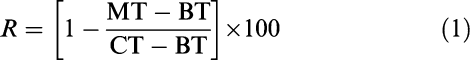where MT (s) is the withdrawal time after meloxicam administration, BT (s) is the withdrawal time shortly before injection of meloxicam and CT (s) is the mean withdrawal time recorded for the same paw before kaolin injection.

Locomotion was quantified as the time required by the cat to perform a series of tests (animal ascending or descending a wooden staircase and animal creeping under a grid). Using an equivalent of equation (1), the three locomotion times were expressed as percentages, thereby taking account of both baseline and control (pretreatment) values. The resulting locomotion variables were then analysed collectively by summing the corresponding percentages to obtain an overall locomotion variable.

Hind paw skin temperature was measured with an infrared thermometer (Raynger® MX4™ Raytek®, Fisher Bioblock Scientific, Illkirch, France); the difference between the temperature of the injected and the control paw was determined. Finally, the volume of the inflamed hind paw was measured with a water displacement technique and body (rectal) temperature was recorded with an electronic thermometer.

Experimental design

The six cats were randomly allocated to two groups of animals. In the first period of the study, the right paw of the cats was injected with kaolin. A jugular catheter was also placed in the cats administered with meloxicam on day 2 (group 1); the other cats (group 2) were sham-prepared (same anaesthesia and bandage as treated cats, but no catheter insertion in control cats) and did not receive meloxicam. After a washout interval of at least 5 weeks, the left paws were injected with kaolin (second period) and the treatments were crossed over. Meloxicam was injected s.c. 47 h after kaolin injection at a dose rate of 0.3 mg kg⁻¹ body weight, which is the manufacturer's recommended dose for cats. Blood samples (1 ml) were taken before and 5, 20, 40, 60 and 90 min and 2, 3, 6, 9, 12, 24, 36, 48, 72 and 96 h after meloxicam administration. Samples were collected in heparinized tubes and centrifuged within 15 min at 4°C, 3000 × g for 10 min. Plasma samples were frozen at −20°C until analysed for meloxicam concentration by high-performance liquid chromatography (HPLC).

Endpoints were measured before (days −3 and −2) and up to 5 days after kaolin injection (days 1–5). On day 2, measurements for the treated cat were performed 1.5 h before and 0.75, 1.5, 3, 5, 8 and 12 h after meloxicam administration. Measurements were also taken 1, 3, 4 and 5 days after kaolin injection and on day 7 for control cats and day 8 for treated cats to assess recovery from the induced inflammation. At the end of the study, no animal exhibited any persisting clinical sequelae and all were re-homed.

Analysis of meloxicam in plasma

Plasma samples were analyzed by a validated HPLC procedure using ultraviolet (UV) detection. Briefly, internal standard (piroxicam) and meloxicam were extracted from plasma by solid-phase extraction. The HPLC apparatus comprised a pump system equipped with an automatic injector and a UV detector (360 nm). Separation was achieved by a reverse-phase column (Hypersil BDS C₁₈, 3 μm, 150 × 2.0 mm), using a guard column (Hypersil BDS C₁₈, 10 × 2.0 mm). The mobile phase was a 40 : 60 mixture of 1% acetic acid : methanol at a flow rate of 0.12 ml min⁻¹. Under these conditions, meloxicam and piroxicam were eluted at retention times of 9.9 and 7.4 min, respectively. The method was linear over the calibration range of 10–1500 ng ml⁻¹, using a weighted linear regression model. Within-day and day-to-day coefficients of variation were less than 9% and the accuracy ranged from 96 to 99%, indicating an appropriate precision and accuracy for the analytical method. The lack of interference from endogenous compounds was verified on blank plasma from untreated cats, establishing the specificity of the method. The validated limit of quantification was 10 ng ml⁻¹.

Data analysis

Pharmacokinetic and PK/PD modelling were performed by least-squares regression analysis using WinNonlin Professional software (WinNonlin®, Version 4.0.1, Pharsight Corporation, Mountain View, CA, U.S.A.).

Meloxicam plasma concentrations were fitted for each cat using an equation corresponding to a two-compartmental model with first-order absorption and a lag time:

where C(t) (ng ml⁻¹) is the meloxicam plasma concentration at time t, Y₁, Y₂ (ng ml⁻¹) are the coefficients of the exponential terms, λ₁, λ₂ (h⁻¹) are the exponents of the exponential terms, ka (h⁻¹) is the first-order rate constant of absorption and lag (h) is the lag time for absorption.

The data were weighted by the inverse of the squared-fitted value and goodness of fit was determined using the Akaike Information Criterion (AIC) (Yamaoka et al., 1978) and by visual inspection of the fittings and the residuals. Individual animal pharmacokinetic parameters of meloxicam were then used as constants in the integrated PK/PD model.

The PK/PD relationships were described using indirect pharmacodynamic response models (Dayneka et al., 1993). In these models, the measured response (R) is assumed to result from factors controlling either the input or the dissipation of the measured response:

where dR/dt is the rate of change of the response over time, K_in represents the zero-order rate constant for production of the response and K_out the first-order rate constant for loss of the response.

For the skin temperature difference (measured as the difference between the temperature of the inflamed paw and the control paw), data were described with the following model:

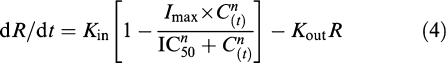where K_in (°C h⁻¹) represents the zero-order rate constant for production of the thermal inflammatory response and K_out (h⁻¹) is the first-order rate constant for dissipation of the thermal component of inflammation. The drug effect was described with a Hill equation in which C_(t) (ng ml⁻¹) is the meloxicam plasma concentration at time t, IC₅₀ (ng ml⁻¹) is the meloxicam plasma concentration producing half the maximum drug effect (i.e., half I_max), I_max is the maximum possible inhibition and n is the exponent expressing the sigmoidicity of the meloxicam concentration–effect relationship.

The control value for the response (R₀, °C) corresponds to the steady skin temperature plateau achieved 2 days after kaolin injection; it is determined by both K_in and K_out from the equation:

The time course of the analgesic effect was best described using the model represented by equation (4). The derived IC₅₀ was therefore the meloxicam plasma concentration, producing half of the maximum inhibition of the factors controlling pain production.

The antipyretic effect was described as the consequence of a stimulation of the factors controlling heat loss (Dayneka et al., 1993; Toutain et al., 2001) by the equation:

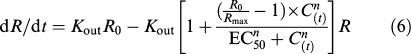where K_out (h⁻¹) represents the first-order rate constant for heat loss, R₀ (°C) is the steady body temperature before meloxicam administration on day 2, R_max (°C) is the maximum response attributed to the drug (i.e., the minimum body temperature predicted after meloxicam administration) and EC₅₀ (ng ml⁻¹) is the meloxicam plasma concentration producing half the maximum stimulation of heat loss. C_(t) and n are as described in equation (4).

For those endpoints for which spontaneous recovery from inflammation (assessed from the data obtained in the absence of meloxicam) was superimposed on drug response (lameness score and locomotion variables), K_in was no longer considered as a parameter, but as a time-dependent variable. A gamma function (Wise, 1985) was used to describe the time course of K_in and equation (3) was therefore transformed into an equation that takes into account the spontaneous time changes in inflammation intensity:

where A (response unit h⁻²), α (no unit) and β (h⁻¹) are the parameters of the gamma function describing the time course and intensity of the inflammation production rate (as assessed by the lameness score and the overall locomotion variable), K_out (h⁻¹) is the first-order rate constant for loss of the response and t is the time after kaolin injection.

Estimates of A, α, β and K_out were obtained by fitting this model to the data obtained during the control period (that is when the cats were injected with kaolin but did not receive meloxicam). These values were then used as initial estimates for fitting the data collected in the period during which meloxicam was administered on day 2 (referred to as the meloxicam period). For these data, a combined model incorporating drug effect was used to account for the meloxicam effect as well as the confounding spontaneous changes in the inflammatory condition. In this model, production of the inflammatory response is governed by the time-dependent gamma function, which is multiplied by an inhibition function after meloxicam administration:

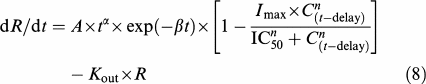where delay is the time between kaolin injection and meloxicam administration, C_(t−delay) is given by equation (2) if t>delay or is equal to 0 if t⩽delay, and other parameters are as indicated in equation (4).

Using mean pharmacokinetic and pharmacodynamic parameters, simulations were performed to predict the time course of meloxicam response for each endpoint for doses ranging from 0.01 to 10 mg kg⁻¹. Because the distribution of individual pharmacokinetic parameters was close to log-normality, the geometric mean was calculated. Data from all individual animals were used to compute mean pharmacokinetic parameters but, only those cats with acceptable pharmacodynamic fittings (five animals for most PD parameters) were taken into account for the calculation of average (arithmetic mean) pharmacodynamic parameters.

For each simulation, a summary parameter, the average drug response, was used to characterize the time course of each endpoint after meloxicam administration. All drug effects were considered to have waned 24 h after meloxicam administration and all calculations were therefore performed by considering the 24-h period following s.c. injection of the drug.

Simulated average drug responses were calculated for all endpoints as follows:

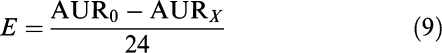where E (°C, % or without unit for the lameness score) is the average drug response over the first 24 h after meloxicam administration, AUR₀ (°C h, % h or h) is the area under the time–response profile for the same time period but without meloxicam administration and AUR_X (°C h, % h or h) is the same area but after administration of X mg kg⁻¹ meloxicam.

The average drug response was then expressed as a percentage of the maximum possible average drug response, that is the response obtainable for a very high s.c. dose of meloxicam (10 mg kg⁻¹) (Figure 1). The 50, 70 and 90% effective doses were also calculated for each endpoint.

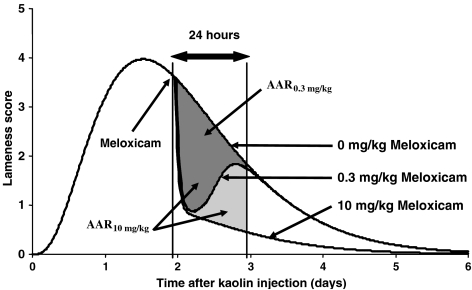
Figure 1.

Method for computation of the drug response as a percentage of the maximum possible drug response. Time course of the simulated mean lameness score (from 0 to 5, with 0 indicating no lameness and 5 maximum lameness) after injection of 500 mg kaolin into the hind paw of six cats under control conditions (0 mg kg⁻¹), after a 0.3 mg kg⁻¹ and a 10 mg kg⁻¹ meloxicam administration. 10 mg kg⁻¹ was the dose assumed to give the maximum possible response. AAR_{0.3 mg kg⁻¹} (h) (dark grey area) and AAR_{10 mg kg⁻¹} (h) (dark and light grey area) are the areas above the time–response profiles during the 24 h following the administration of 0.3 and 10 mg kg⁻¹ meloxicam, respectively. AAR_{0.3 mg kg⁻¹} (h) represents approximately 64% of AAR_{10 mg kg⁻¹} (h); therefore a single s.c. administration of 0.3 mg kg⁻¹ meloxicam is associated with a drug response that corresponds to 64% of the maximum drug response that can be achieved with s.c. administration of meloxicam.

Statistical analysis

Results are presented as mean data and standard deviation (s.d.). For half-lives, the harmonic mean and corresponding 95% confidence interval were calculated.

Results

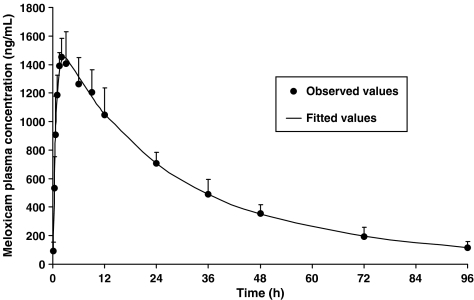
The biexponential decline in meloxicam plasma concentration after s.c. administration of 0.3 mg kg⁻¹ in each of six cats was interpreted as a two-compartment open model with first-order absorption and a short lag phase (Figure 2). The apparent total plasma clearance (Cl F⁻¹, that is clearance scaled by bioavailability) was low (6.00±1.06 ml kg⁻¹ h⁻¹) and the apparent steady-state volume of distribution (Vss F⁻¹, volume of distribution scaled by bioavailability) was relatively small (273±96 ml kg⁻¹). Peak meloxicam plasma concentration (C_max=1482±172 ng ml⁻¹) was achieved relatively rapidly (T_max=2.2±0.7 h) and the lag time for absorption was very small (lag=0.13±0.11 h). The harmonic mean and 95% confidence intervals for the terminal half-life (h) and the apparent half-life of absorption (h) were 37.0 (27.1; 58.3) and 0.42 (0.25; 1.18), respectively.

Figure 2.

Observed (mean±s.d.) and fitted meloxicam plasma concentration (ng ml⁻¹) vs time (h) after s.c. administration at a nominal dose of 0.3 mg kg⁻¹ in six cats.

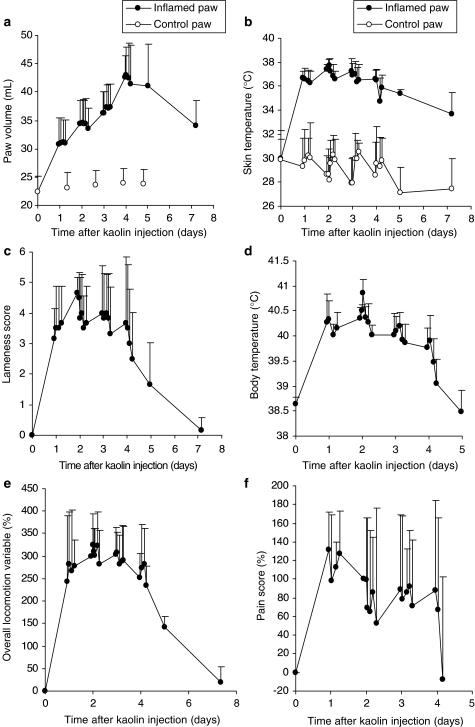
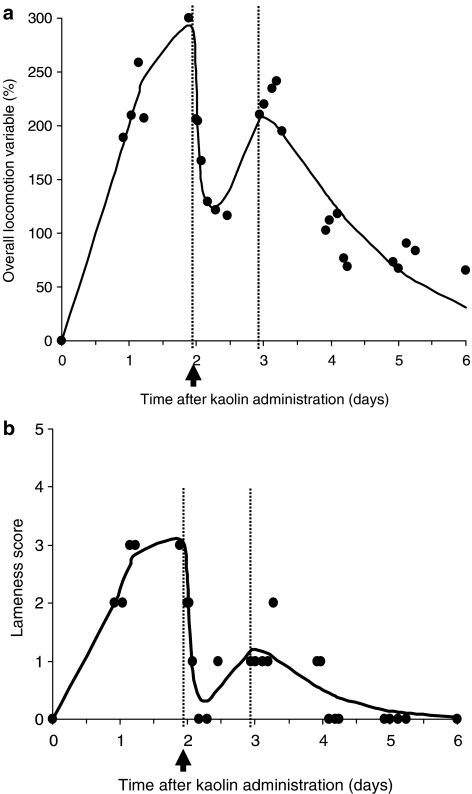
Both magnitude and time course of the inflammatory response were measured as changes in the values of the selected endpoints (Figure 3). Figure 3 demonstrates that the inflammatory response developed rapidly after kaolin injection. Within 1–2 days, values of these endpoints (with the exception of paw volume) reached a maximum, before returning to basal levels (pre-inflammation values) approximately 1 week after kaolin administration. For body temperature, lameness score and the overall locomotion variable, values reached a maximum on the morning of day 2 and an apparent steady-state inflammatory condition was maintained for approximately 2 further days (Figure 3c–e). Skin temperature of the inflamed paw followed the same time course as the lameness score and the overall locomotion variable. Circadian changes in each measurement were observed: for skin temperature this was noted for both paws, but was more pronounced for the control than the inflamed paw (Figure 3b).

Figure 3.

(a–f) Time course of observed values (mean±s.d.) of six endpoints following injection of 500 mg kaolin in the hind paw of six cats. Corresponding values (open circles) for the control (noninflamed) paw are given for paw volume (a) and skin temperature (b). For lameness score (c), a score of 0 indicates no lameness and a score of 5 maximum lameness. For body temperature (d) a return to pre-treatment values was obtained 5 days after meloxicam administration. The overall locomotion variable (e) corresponds to a composite variable obtained from climbing, descending and creeping tests. For pain score (f), values for the contralateral paw are not given because these were influenced by the pain experienced on the inflamed paw.

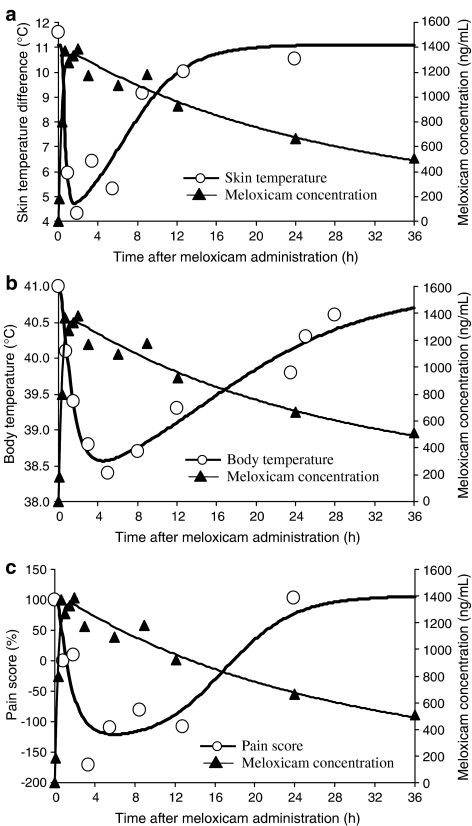
Figure 4 illustrates the effect on the time course of the inflammatory response of a 0.3 mg kg⁻¹ dose of meloxicam administered 2 days after the inflammation induction. Inflamed paw volumes for the control and the meloxicam periods were very similar on days 1–3, with slightly, but not significantly, lower volumes for the treated animals thereafter. For all remaining endpoints, on the other hand, significant inhibitory effects were consistently produced by meloxicam. After meloxicam administration, the mean time of maximum decrease in body temperature occurred at 5.6 h (range 5–8 h) (Figure 4d and Table 1) and the mean time of peak response for the lameness score was also 5.6 h (range 3–12 h) (Figure 4c and Table 2). Skin temperature differences followed the same time course, with a maximum decrease (range 2.4 to 7.3°C) obtained approximately 4.5 h after meloxicam administration.

Figure 4.

(a–f) Time course of observed values (mean±s.d.) for six endpoints (paw volume (a), skin temperature (b), lameness score (c), body temperature (d), overall locomotion variable (e) and pain score (f)) following injection of 500 mg kaolin into the hind paw of six cats and administration of 0.3 mg kg⁻¹ meloxicam on day 2 (arrow). Mean observed values for the control period (open circle) are also presented as a comparative curve. Considering the 24 h following meloxicam administration (grey area), clear-cut effects were observed for all endpoints except paw volume (a).

Table 1.

Observed and fitted pharmacodynamic parameters describing meloxicam anti-inflammatory (skin temperature difference), analgesic (pain score) and antipyretic (body temperature) effects after a single s.c. administration of a nominal dose of 0.3 mg kg⁻¹ meloxicam in five cats

End point	Tmin (h)	Rmin (°C or %)	Kin (°C h−1 or % h−1)	R0 (°C)	Rmax (°C)	Kout (h−1)	Imax (%)	IC50 or EC50 (ng ml−1)	n (no unit)
Skin temperature difference (°C)	4.3±2.4	5.1±2.1	91.1±28.2	NA	NA	8.83±2.67	68.5±24.4	1298±449	6.4±4.2
Pain score (%)	5.2±5.0	228.3±84.5	365.9±440.0	NA	NA	3.72±4.43	247.9±154.6	883±215	10.0±0.0
Body temperature (°C)	5.6±1.3	1.96±0.40	NA	40.5±0.4	38.4±0.4	1.30±0.87	NA	777±124	6.1±2.4

Values are mean±s.d. NA: not applicable in the model. T_min (h) and R_min (same unit as endpoint, i.e., °C or %) are observed values for the time of occurrence of the peak response and the maximum meloxicam response expressed as a decrease in the endpoint value, respectively. Data were fitted using an indirect response model in which meloxicam produces its pharmacodynamic effect by inhibiting the factors controlling K_in. The rate of change of the response over time and the significances of K_in, K_out, IC₅₀, EC₅₀, I_max and n (upper limit fixed at 10) are given by equation (4). For body temperature, another indirect response model was used describing drug effect as stimulating heat loss (see equation (6)).

Table 2.

Observed and fitted pharmacodynamic parameters describing improvement of locomotion after a single administration of a nominal dose of 0.3 mg kg⁻¹ meloxicam in five cats

End point	Tmin (h)	Rmin (no unit or %)	A (h−2 or % h−2)	Alpha (no unit)	β (h−1)	Kout (h−1)	Imax (%)	IC50 (ng ml−1)	n (no unit)
Lameness score (no unit)	5.6±3.7	3.0±0.0	494±396	2.66±1.13	1.80±0.65	24.7±16.1	75.4±18.2	911±189	8.2±2.4
Overall locomotion variable (%)	8.6±3.8	206.2±42.7	46027±49527	1.30±0.61	0.91±0.16	76.7±88.9	64.1±20.9	841±187	10.0±0.0

Values are mean±s.d. T_min (h) and R_min (same unit as endpoint, i.e., no unit (lameness score) or % (overall locomotion variable)) are observed values for the time of occurrence of the peak response and the maximum meloxicam response expressed as a decrease in the endpoint value, respectively. Locomotion times were transformed to percentages (using an equivalent of equation (1)) and added to obtain an overall locomotion variable. Data were fitted with an integrated PK/PD model, taking into account the spontaneous evolution of the inflammation (see equation (8)). The rate of change of the response over time as well as the meaning of the parameters of the gamma function (A, α and β) and K_out, IC₅₀, I_max and n are given by equation (8).

The time course of the pain score correlated well with other surrogate clinical responses, notably skin and body temperature (Figure 4b, d and f), displaying an average decrease of 228% compared to pretreatment values. The maximal decrease in pain score occurred at 5.2 h (range 1–12.5 h) after meloxicam administration (Table 1 and Figure 4f).

Because the onset of the meloxicam response occurred relatively rapidly, the total duration of the response was considered to correspond to the time between drug administration and disappearance of drug response. This ranged from 12 to 32 h, with slightly smaller values for skin temperature differences and an average duration of drug response for all the other endpoints of approximately 24 h.

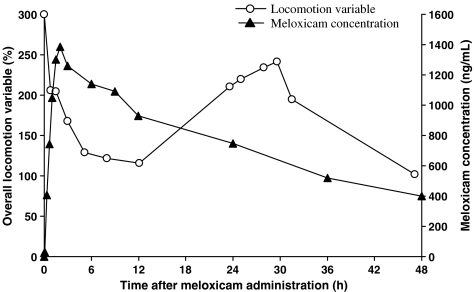
For all endpoints, the response–time profile and the meloxicam concentration–time profile were not in phase. Figure 5 illustrates the delay between the maximum decrease in the overall locomotion variable (occurring approximately 12 h after meloxicam administration) and the maximum meloxicam plasma concentration (at 2 h after drug injection).

Figure 5.

Time courses of observed meloxicam plasma concentration (ng ml⁻¹) and the overall locomotion variable (%) in a representative cat after administration of 0.3 mg kg⁻¹ meloxicam. The locomotion times corresponding to the climbing, descending and creeping tests were transformed into percentages and summed to compute an overall locomotion variable describing the cat's locomotion.

The application of indirect response models together with a sigmoid E_max model for drug effect dealt adequately with this temporal delay between pharmacokinetic and pharmacodynamic data. Figure 6 illustrates for a representative cat the fittings for three endpoints analyzed with the classical indirect response models, and Table 1 gives the corresponding mean pharmacodynamic parameters for skin temperature difference, pain score and body temperature. For the lameness score and the overall locomotion variable, the time course of the response was fitted with a PK/PD model, taking the spontaneous development of the inflammatory response into account (Figure 7a and b). For these endpoints, maximal inhibition (I_max or efficacy) ranged from 64 to 75% (Table 2). On the other hand, for body temperature R_max was similar to normal temperature, indicating that complete suppression of hyperthermia can be achieved with meloxicam. For analgesia, I_max was greater than 100% because pain thresholds for cats treated with meloxicam were consistently higher than those recorded on the same cats before inflammation induction (two-fold increase on average) (Table 1). Meloxicam sensitivity (that is, the slope of the concentration–effect relationship in the Hill equation) was relatively high for all measured endpoints, ranging from 6.1 to 10.0, thus illustrating that there is an almost ‘all or nothing' effect on the input or output processes of the indirect response models. Another feature of the data was the relatively high inter-animal variability for most pharmacodynamic parameters (Tables 1 and 2). However, coefficients of variation for IC₅₀ and EC₅₀ were relatively low, ranging from 16% (body temperature) to 35% (skin temperature difference). Mean values of IC₅₀ and EC₅₀ ranged from 777 (body temperature) to 1298 ng ml⁻¹ (skin temperature difference).

Figure 6.

(a–c) Time courses of observed and fitted meloxicam plasma concentration (ng ml⁻¹) and (a) skin temperature difference (°C), (b) body temperature (°C) and (c) pain score (%) in a representative animal after administration of 0.3 mg kg⁻¹ meloxicam. An indirect response model describing drug effect as inhibiting inflammation production was used to fit the time course of skin temperature difference.

Figure 7.

(a, b) Time courses of observed and fitted (a) overall locomotion variable and (b) lameness score in the same animal as in Figure 6. Meloxicam was administered at day 2 (arrows). An indirect response model describing drug effect as inhibiting inflammation production combined with a model of inflammation progression was used to fit the time course of the locomotion variable.

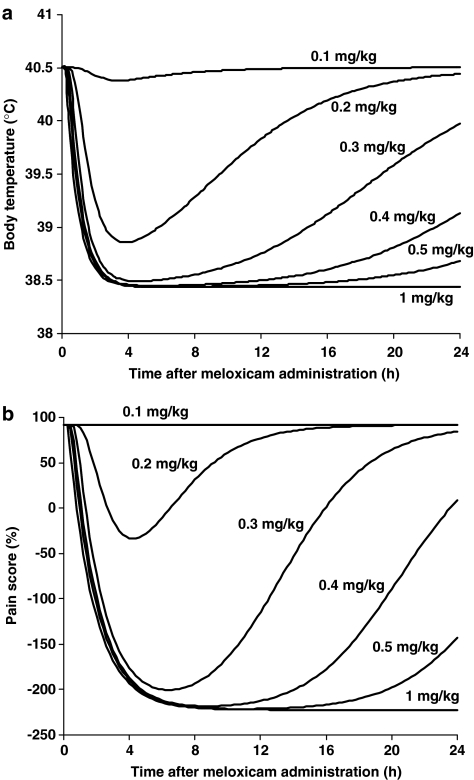
Mean pharmacokinetic and pharmacodynamic parameters were used to simulate dosage regimens ranging from 0.01 to 10 mg kg⁻¹ meloxicam. Simulations for body temperature and pain score are illustrated in Figure 8. As a consequence of the steepness of the concentration–effect relationship, it is predicted that the lowest dose (0.1 mg kg⁻¹) would exert no analgesic effect, 0.2 mg kg⁻¹ would provide only a weak and transient effect, while 0.5 mg kg⁻¹ would provide good efficacy for almost 24 h. Table 3 presents the simulated average drug responses for a range of dosage regimens (single-dose administrations of 0.1–1 mg kg⁻¹ meloxicam) and the doses producing 50, 70 and 90% of the maximum possible average drug response that can be obtained with a single s.c. administration of meloxicam.

Figure 8.

(a, b) Simulated time profiles of (a) body temperature and (b) pain score for single-dose administrations of 0.1, 0.2, 0.3, 0.4, 0.5 and 1 mg kg⁻¹ meloxicam.

Table 3.

Simulated average drug responses (expressed as percentages of the maximum possible average drug response, i.e., the response obtained with 10 mg kg⁻¹ meloxicam) for different end points and doses ranging from 0.1 to 1 mg kg⁻¹

	Average response (from 0 to 100%)						Meloxicam dose (mg kg−1)
End point	E0.1a	E0.2a	E0.3a	E0.4a	E0.5a	E1a	ED50b	ED70b	ED90b
Skin temperature difference	0.05	3.60	23.9	49.8	70.6	98.4	0.40	0.50	0.67
Pain score	0.02	11.30	51.2	81.1	94.9	99.4	0.30	0.36	0.45
Body temperature	1.6	34.90	72.4	90.7	96.5	99.5	0.235	0.29	0.39
Lameness score	0.2	21.9	63.7	87.2	95.9	99.3	0.26	0.32	0.42
Overall locomotion variable	0.03	15.80	59.4	86.1	96.2	99.3	0.275	0.33	0.43

^aE_X (%) represents the predicted average drug response for a single s.c. dose of X mg kg⁻¹ meloxicam.

^bED_Y (mg kg⁻¹) is the meloxicam dose producing Y% of the maximum possible average drug response that can be obtained with a single s.c. administration of meloxicam.

Discussion

The aim of this study was to investigate the value of a new inflammation model for pre-clinical characterization of NSAIDs using a PK/PD modelling approach, with meloxicam as a test drug. Information on the relationship between plasma concentration and analgesic, anti-inflammatory and antipyretic effects are very limited for this class of compound, despite both a mechanistic and a clinical relevance (Landoni & Lees, 1995; Landoni et al., 1995; Brown et al., 1998; Flores-Murrieta et al., 1998). In the present feline model, both of these aspects of PK/PD modelling were successfully documented by using two types of endpoints: (i) those exploring a specific component of the inflammatory response and having a mechanistic interest, such as central and local hyperthermia (body and skin temperature), hyperalgesia (pain score) and oedema (paw volume) and (ii) hybrid endpoints having direct clinical relevance and reflecting both the pain experienced by the cat and functional impairment due to oedema (lameness score and overall locomotion variable).

Ideally, the change in the value of an endpoint produced by a drug should be related solely to its pharmacodynamic properties. However, the time course of the pharmacological response may also be influenced by inflammation induction, progression and then recovery. This confounding factor deserves special attention for drugs such as meloxicam, with a relatively long duration of effect. In the present study, for example, measurements of the overall locomotion variable and lameness score, obtained after the drug response had waned, did not give results similar to those obtained before drug administration. Therefore, a mathematical model describing the inflammatory response to kaolin was used to take progression of the inflammatory process into account. This model showed a good ability to describe the time course of the endpoints during the control period (no meloxicam administration). Moreover, combining this model with the PK/PD model predicted accurately both time course and extent of drug responses, and allowed estimation of individual pharmacodynamic parameters of efficacy, potency and sensitivity.

Body temperature, pain and paw volume are routinely used early in the course of new drug development for mechanistic purposes to characterize the pharmacological profile of NSAIDs (Riendeau et al., 2001). In this study, paw volume was the only endpoint for which the test drug had no evident effect on the experimentally induced inflammation. A similar finding has been observed in other studies in which the NSAID was administered after inflammation induction (Holsapple & Yim, 1984; Engelhardt et al., 1995; Zhang et al., 1997; Giraudel et al., 2005a). Possible explanations are that oedema response involves many other mediators than prostaglandins and that the time required for the clearance of fluid already accumulated in tissues is considerable (Lees, 2003; Giraudel et al., 2005a).

One of the key requirements of an inflammation model is a sustained hyperalgesic response that can be reversed by NSAID administration (Zhang et al., 1997; Dirig et al., 1998). This requirement was met in the present study, a complete reversal of hyperalgesia being achieved approximately 1 h after meloxicam administration. In addition, the threshold for pain sensation at later time points significantly exceeded the levels observed before inflammation induction. This hypoalgesic state, in which the animal withstands longer exposure to a heat stimulus, has recently been described by others (Francischi et al., 2002). The fact that antinociception and analgesia after NSAID administration may involve mechanisms of action other than COX inhibition (Sandrini et al., 2002; Pinardi et al., 2003; Koppert et al., 2004) may provide an explanation for the hypoalgesic state observed in the present study and by Francischi et al. (2002).

As in previous studies (Shirota et al., 1984), skin temperature was shown to be a good marker of inflammation development and suppression. The finding in the present study of a circadian rhythm of skin temperature change that was more pronounced in control paws extends earlier observations obtained in the rat (Kessler et al., 1983). After meloxicam administration, a small decrease in skin temperature of the control paw was observed in some cats, and this was probably related to the decrease in body temperature (Giraudel et al., 2005a). Skin temperature difference, on the other hand, was not confounded by the decrease in body temperature and this derived variable could therefore be conveniently used for PK/PD modelling.

The time courses of all endpoints analysed using PK/PD modelling were well described by the selected indirect response models and permitted evaluation of two important drug pharmacodynamic properties, namely sensitivity and potency. Sensitivity, which gives information on the range of efficacious concentrations, was high in this study, indicating that there is probably a threshold concentration close to the IC₅₀ below which no drug effect occurs. This explains why no drug effect persisted beyond 30 h, despite relatively high meloxicam plasma concentrations (200–700 ng ml⁻¹) up to 72 h after dosing. Classically, potency for analgesic and antipyretic effects of NSAIDs is higher than potency for their anti-inflammatory effect (Toutain et al., 2001; Lees, 2003). In the present study, however, the IC₅₀ computed for the pain score was of a magnitude similar to potencies obtained for other endpoints. This might be explained by the fact that the potency computed for the pain score reflects not only the antihyperalgesic effect of meloxicam (possibly due to inhibition of prostaglandin synthesis) but also its hypoalgesic effect.

As the in vivo determined potencies calculated in the present study are likely to reflect meloxicam effects on prostaglandin synthesis, it is relevant to compare these IC₅₀'s with the potency for COX-2 inhibition obtained for meloxicam in feline whole-blood assays (Giraudel et al., 2005b). These potencies were of the same magnitude (710 ng ml⁻¹ for the in vitro determined potency for COX-2 inhibition and 883 and 911 ng ml⁻¹ for the inhibition of the pain and lameness production, respectively), which is consistent with COX-2 inhibition being the major mechanism of action of meloxicam.

Regarding clinical relevance, the present study showed that endpoints, such as body and skin temperature and pain score, could be also used as surrogate endpoints of NSAID efficacy. These endpoints demonstrated good metrological performances, but, equally important, they displayed a time course similar to the more clinically related endpoints (lameness score and overall locomotion variable), resulting in a duration of meloxicam response that was very consistent for all endpoints. In addition, it was shown that the clinical remission observed on days 4 and 5 was generally greater after meloxicam compared to control. Interestingly, this also occurred when a return to pre-administration values was obtained 24 h after meloxicam administration, suggesting that the subsequent faster clinical remission when animals were treated with meloxicam might be due to some additional effect of the drug. This finding is potentially of considerable clinical significance and deserves further investigation. Another feature of clinical interest was the high inter-animal variability observed for most pharmacodynamic and disease parameters. Similarly, anti-inflammatory therapy in humans is also characterized by a marked individual variation in patient responses (Levy, 1998).

Drug potencies and sensitivities computed with indirect response models are not of direct clinical application, but they are essential when using preclinical data to predict effective dosage regimens. In the present study, these parameters reflect drug effect on a physiopathological mechanism (likely to be prostaglandin synthesis for NSAIDs) and are not genuine parameters describing drug response on the relevant endpoints (e.g. lameness). Therefore, other parameters (ED₅₀, ED₇₀, ED₉₀) were calculated by simulating different dosage regimens and this allowed characterization of the dose–response relationship of meloxicam for each endpoint.

Such simulations may be very helpful in assisting clinicians to select a dosage regimen not only in the species investigated but also in man. This may be especially relevant for meloxicam, because the pharmacokinetic profile in cats closely resembles that obtained in humans (Turck et al., 1996). In the only published pharmacokinetic study in cats (Scientific Discussion on Metacam 5 mg kg⁻¹ Solution for Injection for Dogs and Cats. EMEA CVMP/263/00-Rev.3), it was shown that the bioavailability from the s.c. route of administration was 100%. The clearance determined in this study (Cl F⁻¹, 6.0 ml kg⁻¹ h⁻¹) can therefore be compared to the i.v. clearance determined in man (6.1 ml kg⁻¹ h⁻¹ for a body weight of 70 kg) (Turck et al., 1996). As these values are virtually identical and as drug potencies are commonly similar between species (Levy, 1993; Busch et al., 1998), it is suggested that the present results could also be relevant for predicting a dosage regimen in man. For NSAIDs with different pharmacokinetic profiles in cats and humans, dose prediction must take into account differences in drug clearance. In this study, it can be concluded that a dose of 0.25–0.3 mg kg⁻¹ (i.e., a dose close to the ED₅₀ for all the endpoints) might be an effective loading dose in the cat. This dose is very similar to the clinically recommended dose not only in cats (0.2 or 0.3 mg kg⁻¹) but also in humans (7.5–15 mg, i.e., between 0.1 and 0.3 mg kg⁻¹ for a body weight of 50–70 kg). This comparison demonstrates the potential usefulness of this pre-clinical PK/PD modelling approach for predicting a dosage regimen, not only in the target species but also in humans.

In conclusion, the present investigation provides evidence that a reversible and ethical model of inflammation in a medium-sized species allowed measurement of a range of endpoints characterizing the anti-inflammatory, analgesic and antipyretic effect of a NSAID. For these drug properties, the main pharmacodynamic parameters (efficacy, potency and sensitivity) and time course of drug response were determined. This facilitated establishment of drug concentrations and dosage regimens that may be used to plan dose-ranging studies in human drug development.

Abbreviations

COX

cyclooxygenase

COX-2

cyclooxygenase-2 isoform

HPLC

high-performance liquid chromatography

i.v.

intravenous

NSAID

nonsteroidal anti-inflammatory drug

PK/PD

pharmacokinetic/pharmacodynamic

s.c.

subcutaneous

UV

ultraviolet