Microtubule Stability Studied by Three-Dimensional Molecular Theory of Solvation

Abstract

We study microtubular supramolecular architectures of tubulin dimers self-assembling into linear protofilaments, in turn forming a closed tube, which is an important component of the cytoskeleton. We identify the protofilament arrangements with the lowest free energy using molecular dynamics to optimize tubulin conformations. We then use the three-dimensional molecular theory of solvation to obtain the hydration structure of protofilaments built of optimized tubulins and the solvent-mediated effective potential between them. The latter theoretical method, based on first principles of statistical mechanics, is capable of predicting the structure and thermodynamics of solvation of supramolecular architectures. We obtained a set of profiles of the potential of mean force between protofilaments in a periodic two-dimensional sheet in aqueous solution. The profiles were calculated for a number of amino acid sequences, tubulin conformations, and spatial arrangements of protofilaments. The results indicate that the effective interaction between protofilaments in aqueous solution depends little on the isotypes studied; however, it strongly depends on the M loop conformation of β-tubulin. Based on the analysis of the potential of mean force between adjacent protofilaments, we found the optimal arrangement of protofilaments, which is in good agreement with other studies. We also decomposed the potential of mean force into its energetic and entropic components, and found that both are considerable in the free-energy balance for the stabilized protofilament arrangements.

INTRODUCTION

All living cells utilize a complicated dense jungle of protein polymers known as the cytoskeleton. This is a three-dimensional fine network of three kinds of filament structures (actin filaments, intermediate filaments, and microtubules), thoroughly coordinated and subtly structurally and functionally linked, and performing as “bones and muscles” of the cell. Microtubules, polymers of tubulin dimers, are considered to be involved in various tasks or cellular features, including cell morphology, intracellular transport (e.g., endoplasmic reticulum-Golgi transport), centralization of nucleus, chromosome segregation during cell division, chromosome motility after DNA damage, cell stiffness control, pathogen infections, memory, and consciousness (1–12). Responsible for different complex tasks, microtubules undergo equally complex posttranslational modifications and unique interactions with multiple families of satellite proteins (13–20). They are very dynamical systems, growing and shrinking in a guanosine-triphosphate (GTP)-hydrolysis-dependent manner (21–26).

The dynamic nature of microtubules makes them susceptible to pharmacological agents. Compounds that perturb microtubule dynamics are currently some of the most effective drugs to treat medical conditions (27–29). Tubulin-assembly modulators represent an important class of antitumor drugs, as they have been proven to be an effective tool for cancer chemotherapy (30,31). Numerous tubulin ligands with antimitotic properties and anticancer potential have been discovered recently (28,32,33). Apart from pharmacology, microtubules can be used in bionanotechnology to form nanowires (when plated with metals) and scaffolds for nanofabrication. Another potential nanotechnology application involves the molecular transport machinery of microtubules and kinesin proteins that can be integrated in kinesin-powered microdevices (34–36). This opens up new possibilities for the development of guided nanotransport mechanisms in nanodevices.

Microtubules are composed of dimers of protein tubulin. The heterodimer consists of one α-tubulin and one β-tubulin subunit (each ∼40 Å in diameter), which are homologous. The dimers are aligned head-to-tail in rows called protofilaments. A variable number of protofilaments form a hollow tube, that is, a microtubule. The external and internal diameters of the microtubule are ∼240 and 150 Å; in vitro, the length can reach up to 10–50 μm. Polymerization is a polar process that reflects the polarity of the microtubule. Tubulin polymerizes more quickly from the plus end, which is terminated by the β-subunit. The other end, growing more slowly, is known as the minus end, and is terminated by the α-subunit.

In vivo, microtubule cylinders usually have 13 protofilaments, though the number may be different in particular situations. In vitro, it is possible for purified tubulin to assemble with a fairly wide range of diameters containing 9–18 protofilaments. This variation reveals that there is some flexibility in the bonds between adjacent protofilaments, at least in the direction involved in the curvature of the microtubule wall. In vivo, the occurrence of microtubules with a number of protofilaments other than 13 appears to be determined by isoforms with specific changes in the amino acid sequences of α- and β-tubulin, as, for example, in the case of some specialized 15-protofilament microtubules in neurons of the nematode Caenorhabditis elegans (37,38).

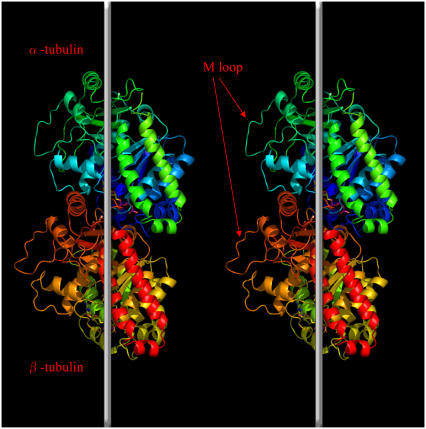
There are three published structures of pure tubulin dimers, i.e., those not complexed with other proteins: Protein Data Bank (pdb) code 1TUB, described by Nogales and Downing (39); pdb code 1JFF, by Lowe et al. (40); and pdb code 1TVK, by Nettles et al. (41). All of these are of relatively poor quality, with the best resolution, 2.9 Å, for the 1TVK structure. Tubulin, an ∼55-kDa protein, has an α/β fold where a core of two β-sheets is surrounded by α-helices. Each monomer is composed of three functional domains, the nucleotide-binding (containing the Rossman fold), drug-binding, and motor-protein-binding domains (Fig. 1).

FIGURE 1.

Ribbon diagram of the conformation of tubulin dimer and the schematic orientation of tubulin dimers in two adjacent protofilaments. Vertical white lines denote the long axis of the microtubule. The position of the M loop is indicated by arrows. The figure was generated with PyMOL (91).

Tubulin exists in different isotypic forms (seven for α-tubulin and eight for β-tubulin in mammals), the biological significance of which is still a matter of debate (14). In our study, we investigated five different human isotypes of β-tubulin (β_I–β_V). There is considerable variability between these isotypes in terms of sequence identity. The value of 78–95% sequence identity between β-tubulins is significantly lower than that found between α-tubulins, 89–97%. There is a possible relevance of isotype composition to the stability and functionality of microtubules in the cell (42).

The tubulin polymerization process involves two types of contacts between tubulin subunits: head-to-tail binding of dimers, resulting in protofilaments that run along the length of the microtubule; and lateral interactions between parallel protofilaments, which complete the microtubule wall. Lateral interaction surfaces are more electrostatic and less hydrophobic than the longitudinal contacts. The longitudinal contacts along protofilaments appear to be much stronger than those between adjacent protofilaments (43). Structural studies have established the critically important role of two tubulin loops, the M loop (S7-H9 loop) and the N loop (H1–S2 loop), in microtubule self-assembly. These loops coordinate lateral interactions between protofilaments to build a microtubule. Studies with docking the tubulin dimer structure into low-resolution images of microtubules have established that M loops interact with N loops of laterally adjacent subunits (44). Moreover, organisms with increased microtubule stability (such as arctic fish) have two amino acid substitutions in the M loop (45). The “stickiness” of the M-loop side of the protofilament appears to be largely responsible for the polymorphic nature of tubulin polymers (46).

Microtubules constitute one of the most intriguing questions of modern biophysics. Although much progress has been made, there are still many unresolved issues concerning their molecular structure, architecture, and dynamic behavior. Due to their interesting and important features, microtubules are attracting increased attention from researchers (42–44,47–52). Various aspects of the structure, dynamics, self-assembly, and stability of microtubules have been studied using theoretical and computational approaches. However, most of these studies included no atomic representation of microtubules (7,8,10,53–67). Limited exceptions include an all-atom study of 90 dimers, extremely CPU-intense (∼700 processors with an aggregate speed of 1 TFlops), where electrostatics was treated by applying the Poisson-Boltzmann equation (68). Another study published by the same group addressed a very small portion of a microtubule (five dimers only) by a combination of the Poisson-Boltzmann electrostatics and the surface-area term (69). The apolar contribution was obtained by assuming that each Ų of buried solvent-accessible area contributed 11 cal/mole to the binding energy. The authors found that the B-lattice is the most favorable configuration of protofilaments and that lateral bonds are significantly weaker than longitudinal bonds along protofilaments.

In this study, we treat sets of protofilaments in the all-atom representation using a method of integral equation theory of molecular liquids and solutions, namely, the three-dimensional reference interaction site model (3D-RISM) (70). In the search for factors determining the microtubule architecture for a sequence of different tubulin isotypes and conformations of the crucial β-tubulin M loop at the protein-protein interface, the 3D-RISM theory yields potentials of mean force between adjacent protofilaments as a function of the relative orientation of protofilaments and of the vertical and horizontal distances between them.

METHODS

The coordinates of the heavy atoms for the bovine tubulin dimer were obtained from the Protein Data Bank, entry 1TVK, as determined by Nettles et al. (41) via electron crystallography. All the cofactors visible in the structure (epothilone, GTP/GDP) were removed for the sake of simplicity. The missing loop (residues 35–60) not visible in the α-tubulin monomer was built using the coordinates from the β-tubulin structure as a guide, with subsequent energy minimization. Hydrogen atoms were added in the AMBER package (71). As the resolution of the experimental structure was relatively low (2.9 Å), the original tubulin dimer was subjected to molecular dynamics for 3 ns using the AMBER force field with the generalized Born model of implicit solvation (72). During molecular dynamics, all hydrogen-containing bonds were constrained using the SHAKE algorithm (73).

The final snapshot from the well equilibrated trajectory of the original bovine dimer was mutated (via in silico substitutions) to generate five different β-tubulin isotypes (β_I–β_V). When building different tubulin isotypes, we decided to keep the α monomer unchanged and vary only the β-monomer sequence, as the variability of sequence is observed mostly in β-tubulin. A guide for mutations was performed by sequence alignment in the Clustal W program accessible on-line (74). Clustal W is a general-purpose, multiple-sequence alignment program for DNA or proteins. It produces biologically meaningful multiple-sequence alignments of divergent sequences. It calculates the best match for the selected sequences, and lines them up so that identities, similarities, and differences can be seen. Each isotype dimer was again equilibrated in 1 ns of molecular dynamics in the AMBER force field with implicit solvent.

As a next step, a series of four different conformers was generated for the M loop in β_V-tubulin, as this loop is regarded as the main player in the interprotofilament interactions. The β_V isotype was chosen as a random example, with no particular reason to give preference to any other isotype. In high-temperature simulation, the M-loop residues were allowed to move while the rest of the protein was frozen. Tubulin was heated in constrained simulated annealing from 0 to 1000 K in 1 ps, and snapshots were then generated every 5 ps in a 40-ps thermal stabilization. Of the resulting eight snapshots, the four most structurally divergent ones were selected by visual inspection (snapshots 1, 3, 6, and 7), cooled down for 50 ps, and then used for further calculations of the potentials of mean force (see below). In the simulated annealing, the following general constraints were used: positional constraints for all C_α atoms in tubulin, except for M-loop residues; and angular constraints for all peptide bonds and all improper dihedrals to retain proper chirality.

Using the periodic boundary conditions of a supercell in the 3D-RISM calculation (see below), we built two-dimensional sheets of protofilaments. The protofilaments were incrementally translated along the long axis to vary the offset of dimers (Fig. 2). We started with the zero-offset, a configuration in which the dimers would form a ring in the microtubule, and slid the protofilaments in 2-Å increments until a second ring conformation was obtained at ∼80 Å offset in direction h. Simultaneously, the distance between the long axes of protofilaments (direction r) was varied in the range 54–63 Å, with a step of 1 Å; the minimal distance between protofilaments with no severe van der Waals collisions between adjacent strands is 54 Å. As a result, we obtained 10 × 40 nodes, giving 400 cases of spatial arrangement (Fig. 2). Counting five different isotypes, with and four conformers for one of them, this totaled 3200 values of the potential of mean force. (We chose to present only the most representative results, i.e., the sections passing through the minima in both the h and r directions).

FIGURE 2.

Schematic representation of spatial arrangements between two adjacent protofilaments, with the r and h directions indicated as discussed in the text (α-tubulins and β-tubulins are represented as white and dark ribbons, respectively). The figure was generated with PyMOL (91).

MOLECULAR THEORY OF SOLVATION FOR EFFECTIVE POTENTIALS BETWEEN PROTOFILAMENTS

To precisely describe the assembly and stability of a microtubule (or an array of 2D sheets of protofilaments, for that matter), one has to include detailed consideration of hydrogen bonding, hydrophobic effect, electrostatic interactions, and solvent effects for a system heavily exceeding typical sizes of solvated biomolecules amenable at present to molecular simulations. Modeling of microtubules even with recent computational chemistry and biology methods, if feasible at all, requires “heroic” (i.e., extremely CPU-time-consuming) molecular simulations. Therefore, theoretical tackling of these complex systems requires a new approach. Such a possibility is provided by the methodology of statistical mechanics: it is molecular theory of solvation, also known as integral equation theory of molecular liquids and solutions (75,76).

To obtain the structure and thermodynamics of hydration of protofilaments, we employed the 3D-RISM integral equation complemented with the Kovalenko-Hirata (KH) closure approximation (70,77). The 3D-RISM-KH integral equation theory of molecular solvation explicitly accounts for the effect of chemical specificities of molecular and ionic species in electrolyte solution on the solvation structure and thermodynamics, in particular, association effects and formation of supramolecules. For instance, the 3D-RISM-KH theory has been proven to be efficient and uniquely capable of treating and predicting self-assembly and conformational stability of such complex organic supramolecular architectures as synthetic organic rosette nanotubes in solution (78). This method provides a detailed microscopic insight into the organization of solvent molecules in the solvation shell and their role in thermodynamic stability and optimal arrangement of the fragments that self-assemble into a supramolecule in solution.

The theory yields the solvation structure in the form of a three-dimensional distribution of normalized probability density, the three-dimensional distribution function 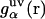of solvent site α, showing site density enhancement (g_α > 1) or depletion (g_α > 1) around the solute macromolecule relative to the average site number density ρ_α in the solution bulk. The 3D-RISM integral equation is written as (70,77,79,80)

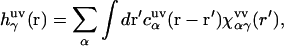(1)

where 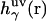is the three-dimensional total correlation function of site γ related to the three-dimensional distribution function as 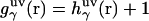, and 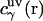is the three-dimensional direct correlation function which has the asymptotics of the solute-solvent site interaction potential: 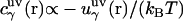; 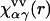is the site-site susceptibility of pure solvent; superscripts u and v denote solute and solvent, respectively; and the site subscript indices α and γ enumerate all sites on all sorts of solvent molecules. The convolution in Eq. 1 is calculated by using the three-dimensional Fast Fourier Transform technique, with special analytical treatment of the electrostatic asymptotics of all the correlation functions (70,82). The other relation between the three-dimensional total and direct correlation functions, complementing the 3D-RISM integral equation (Eq. 1) is the 3D-KH closure approximation (70,82),

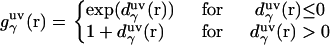(2)

where 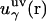is the three-dimensional intermolecular interaction potential between the whole solute and solvent site γ, which is specified by the molecular force field, and k_BT is the Boltzmann constant times the solution temperature. This relation combines, in a nontrivial manner, the advantages of two known closures: the mean spherical approximation (75) is applied to high association peaks and long-range electrostatic tails for 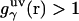and the hypernetted chain approximation (75) is used in the core repulsion and other depletion regions for 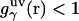, with the switching occurring smoothly, at 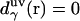, or equally, at .

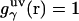The site-site susceptibility of solvent breaks up into the intra- and intermolecular terms,

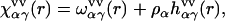(3)

where the intramolecular correlation function, or intramolecular matrix, 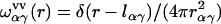represents the geometry of solvent molecules with the site-site separations l_αγ (z-matrix) specified by the molecular force field, and 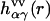is the radial total correlation function between sites α and γ in bulk solvent. In advance of the 3D-RISM-KH calculation, the site-site correlation functions 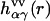of bulk solvent are obtained from the dielectrically consistent RISM theory (81) coupled with the KH closure (DRISM-KH) (70,82). The bulk solvent susceptibility (Eq. 3) is then input into the 3D-RISM integral equation (Eq. 1).

For a given arrangement of the solute supramolecule immersed in multicomponent solvent, the solvation free energy is obtained from the 3D-RISM-KH integral equations (Eqs. 1 and 2) in a closed analytical form in terms of the three-dimensional correlation functions (70,77). The potential of mean force (PMF) between protofilaments can then be obtained as a difference between the solvation free energy of the protofilaments in the supramolecule and those pulled apart (70,82). However, this approach is less practical, as it requires calculation of the three-dimensional correlation functions and the solvation free energy of the supramolecule for a sequence of protofilament arrangements to map the PMF landscape. Instead, in this work we use the definition of the PMF between two molecules in solution in terms of the 6D distribution function,

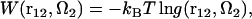(4)

where r₁₂ and Ω₂ are the position and orientation of solute molecule 2 with respect to the coordinate system fixed at solute molecule 1. (The orientation of molecule 1 is thus fixed, too.) The distribution function 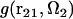between molecules 1 and 2 at a given orientation Ω₂ can be conveniently obtained from the 3D-RISM-HNC integral equation for solute-solute correlations at infinite dilution (70,83). The PMF (Eq. 4) is thus obtained in the form

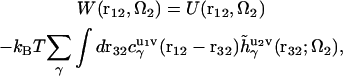(5)

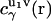where is the direct interaction potential between molecules 1 and 2 as a function of coordinates r₁₂ and Ω₂, and the latter term gives the solvent-mediated part of the PMF. The three-dimensional direct and total correlation functions and 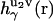of solvent site γ around solute molecules u₁ and u₂ are obtained from the 3D-RISM-KH integral equations (Eqs. 1 and 2). The three-dimensional correlation function 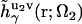at a particular orientation Ω₂ of solute molecule 2 is nothing but 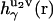rotated by angle Ω₂, and can be obtained by rendering. Equation 5 yields the PMF 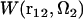between protofilaments 1 and 2 and all their images with the supercell periodicity, specified on a three-dimensional grid of their relative coordinates r₁₂ at a given orientation Ω₂ of protofilament 2. Notice that the 3D-RISM equations operate with a system at constant density, and so the PMF obtained corresponds to the NVT ensemble.

To obtain the PMF for each system, the 3D-RISM-KH equations were solved on a three-dimensional grid in a rectangular supercell of the following sizes set to accommodate the two-dimensional periodic sheet of protofilaments: 1) the current value of separation r between protofilaments in the sheet; 2) ∼128 Å (commensurate with the distance between tubulin dimers in a protofilament) in direction h; and 3) the same value ∼128 Å. The grid resolution of ∼0.5 Å we used was fine enough to obtain the results without significant numerical errors. The SPC/E water model (84) was used, and the water solvent was at ambient thermodynamic conditions of T = 298 K and density ρ = 0.997 g/cm³. The Amber parameter set (amber99) was used for the interaction site charges and Lennard-Jones parameters of proteins (85).

RESULTS AND DISCUSSION

The results of sequence alignment for β-tubulin are shown in Fig. 3. It is very clear that there is almost no variability in the M-loop sequence (residues 279–287), whereas most of the differences among the isotypes are clustered in the C-terminal region. This region plays a major role in regulating microtubule assembly (86). The majority of differences between the known isotypes localize within the last 15 residues of the sequences. The PMF between protofilaments as a function of the offset h is presented in Fig. 4. Only the β_V isotype is presented, as all the isotypes display almost identical plots. It might be surprising that there are no differences in the PMF among isotypes. The main difference between the isotype sequences is within the C-terminus, where the homology is the lowest. These C-termini tails are exposed on the outside surface of the microtubule and are very flexible in molecular dynamics runs. The difference in the C-terminus sequence could possibly affect the dynamical process of microtubule assembly or translate into different spatial arrangements of protofilaments in a microtubular cylinder. However, their conformations do not affect the PMFs between protofilaments arranged in a 2D sheet. It can be seen clearly that there is one sharp global minimum at approximately h = 6 Å. It corresponds very well with the value found by Sept et al. (69) in their CPU-time-consuming approach to a single system. This global minimum corresponds to the so-called B-lattice. It is generally established that a B-lattice is the predominant arrangement of tubulin monomers in the microtubule lattice (87), where lateral contacts are made between homologous subunits, that is, α-α and β-β. Our results confirm that.

FIGURE 3.

Results of the sequence alignment performed in Clustal W for five β-tubulin isotypes. An asterisk (*) means that the residues or nucleotides in the column are identical in all sequences in the alignment; a colon (:) means that conserved substitutions have been observed; and a period (.) means that semiconserved substitutions are observed.

FIGURE 4.

Profile of the potential of mean force (PMF) between adjacent protofilaments of β_V-tubulin, conformer 1, as a function of their offset h at separation r = 54 Å.

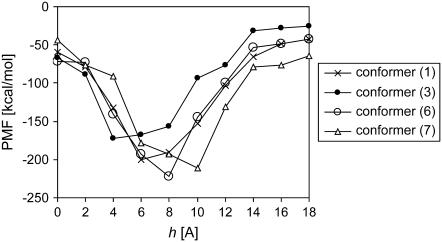
Apart from investigating various sequences, another variable in our simulations was changing the conformation of the M loop of β-tubulin. This loop is particularly important in the so-called lateral (protofilament-protofilament) interactions, possibly having an influence on the PMFs between adjacent protofilaments. Fig. 5 shows a close-up of the global minimum region of the PMF between adjacent protofilaments as a function of the offset h (see Fig. 2), presented for all M-loop conformers of β_V-tubulin. Although it is hard to draw any structural conclusions from these results, it is clear that there are visible differences between different conformers, even though they are still close to the value of h for the B-lattice. Keeping in mind the above-discussed crucial role of the M loop in lateral interactions, it is not surprising that our results indicate that the optimum spatial arrangement between adjacent protofilaments is sensitive to the M-loop conformation. Figs. 6 and 7 show the PMF as a function of distance r between the strands (see Fig. 2). Again, all isotypes showed an almost identical dependence on r, marking a shallow minimum at ∼4 Å of “empty space” separation between the adjacent protofilaments. Similar to the dependence on the offset h, there are visible differences between all the conformers, with conformer 7 being a clear outsider, although the variability among conformers is not as clear as in the case of varying h (compare Fig. 5). It should be noted that as the M loop is involved in lateral interactions, changes in its conformation could possibly influence the dependence of PMF on both the offset h and distance r.

FIGURE 5.

Global minimum region of the potential of mean force (PMF) between adjacent protofilaments as a function of the offset h at separation r = 54 Å. All conformers of β_V-tubulin.

FIGURE 6.

Potential of mean force (PMF) between adjacent protofilaments of β_V-tubulin, conformer 1, as a function of the separation r at a the offset h = 6 Å in the B-lattice.

FIGURE 7.

Global minimum region of the potential of mean force (PMF) between adjacent protofilaments as a function of the separation r at the offset h = 6 Å in the B-lattice. All conformers of β_V-tubulin.

Determination of particular amino acid residues involved in lateral interactions would probably have less meaning, because the difference between the arrangements of protofilaments in zinc sheets and microtubules strongly suggests some local conformational changes in the regions of interaction, particularly concerning loops (43). However, it is of interest to look into the general thermodynamics of these interactions, as lateral contacts between tubulin subunits in neighboring protofilaments have a decisive role for microtubule stability, rigidity, and architecture (49). Therefore, we decomposed the PMF into the energetic and entropic contributions (in the NVT ensemble we are working in), following the work of Pettitt and Rossky (88): 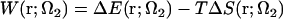. The latter term is calculated from the temperature derivative of the PMF via a central two-point finite difference (for more detail, see, e.g.,Choudhury and Pettitt (89)),

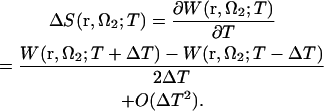(6)

In this calculation, we chose the temperature difference value to be ΔT = 10 K. It should be noted that the intramolecular entropy of tubulin is not included in the decomposition (6) giving the thermodynamics of solvation only.

We performed the decomposition (6) for one selected system built of β_v-tubulin, conformer 1. Fig. 8 shows the PMF decomposition into the energetic and entropic terms ΔE(h) and −TΔS(h) as functions of the offset h between the protofilaments. The entropic contribution clearly forms two minima corresponding to lattices A and B. It is interesting to note that the second minimum is pronounced much more clearly than in the full PMF profile. Investigating the lateral interactions, Sept et al. (69) decomposed the free energy into the electrostatic and apolar contributions. The latter term can be seen as hydrophobic, and was calculated assuming that each Ų of solvent-accessible surface area (SASA) that is buried contributes 11 cal/mol to the binding energy. The hydrophobic effect is generally known to be entropically rather than enthalpically driven, which gives a rationale for comparing this apolar term to our entropic contribution to the PMF. Both the studies localize two distinct minima, and both locate them at approximately the same offset h. However, somewhat contrary to our results, Sept et al. (69) see both minima as equally deep, arguing that because the two tubulin monomers are structurally homologous, the A- and B-lattices have similar amounts of buried surface area. As distinct, our results show that the minimum associated with the B-lattice is the main one, being deeper by 80 kcal/mol than the second one for the A-lattice. It is difficult to speculate about the exact nature of the observed difference, but one obvious explanation might be that we calculate a pure entropic term, whereas Sept at al. (69) deal with an “entropy-like” term within the empiric SASA approach. Another explanation could be that the PMF decomposition from 3D-RISM is simply inaccurate. Some problems with the 1D-RISM-HNC theory for hydrophobic interactions were reported previously (90). In that study, the enthalpy and entropy were found to make comparable contributions to the attraction of nonpolar solutes in water, and that observation disagreed with the conventional description of an entropy-driven hydrophobic interaction (90). However, in our case of the 3D-RISM-KH theory, we actually do not observe comparable contributions of energetic and entropic parts, i.e., the enntropic term is about twice as large in magnitude and opposite in sign. Nevertheless, the changes in these terms at the positions around the second minimum are quite comparable, implying that they are both important in formation of the second minimum. Our results indicate that the entropic contribution around the offset h corresponding to the A-lattice has a well defined minimum that is strongly suppressed in the PMF by the maximum of the energetic term (see Fig. 8). This makes the second minimum much shallower and wider, unlike the arrangement corresponding to the B-lattice, where both of them have a well pronounced minimum.

FIGURE 8.

Decomposition of the potential of mean force (PMF) between protofilaments into the energetic and entropic contributions, W(h) = ΔE(h) − TΔS(h), as functions of the offset h at the separation r = 54 Å. β_v-tubulin, conformer 1.

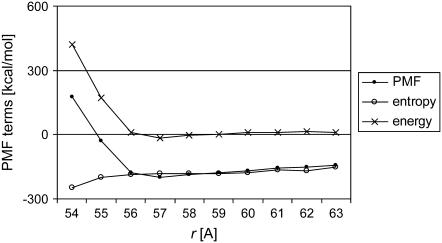
For the lateral interaction of protofilaments as a function of the separation r, Fig. 9 shows the PMF decomposition into the energetic and entropic contributions. It seems that lateral association of protofilaments is a complex process, as both the energetic and entropic components apparently make significant contributions to the lateral interactions up to a protofilament separation of ∼3–4 Å. Beyond that point, the association process seems to be mainly entropy-driven, as the energy values oscillate close to zero in a range of 3–10 Å. In general, we obtained a complex view in which both the energy and entropy contributions are highly involved in the lateral interactions.

FIGURE 9.

Decomposition of the potential of mean force (PMF) between the protofilaments into the energetic and entropic contributions, W(r) = ΔE(r) − TΔS(r), as functions of the separation r at offset h = 6 Å corresponding to the B-lattice. β_v-tubulin, conformer 1.

There are some limitations of our current protocol of building and treating tubulin superstructures. First and most obvious, we investigated 2D sheets of protofilaments rather than microtubules. Second, we neglected GDP/GTP molecules. The implication that the nucleotide influences lateral interactions between protofilaments is surprising at first sight, since the exchangeable site on the β-subunit lies at the longitudinal interface between tubulin dimers along the protofilaments; however, several regions directly involved with nucleotide binding could possibly affect the position of helices or loops involved in lateral interactions (46,49). Last, we used the atomic structure of the dimer obtained from zinc-induced sheets, and its conformation might be different in microtubules existing in vivo. Zinc ions are used in incubation buffer to induce and stabilize sheets, and are not visible in the solved structure. In zinc-induced sheets, dimers make different contacts with the adjacent protofilament, on the surface that corresponds to the outside of the microtubule. This provides an explanation of why kinesin is unable to bind to tubulin in these sheets. The 8-Å resolution microtubule map (44) shows that the M loops are also in a slightly different conformation in a microtubule, compared to a zinc-induced sheet (47). Having proved the usefulness of the 3D-RISM method, at the next step we will consider the fully three-dimensional structures of microtubules carrying nucleotides, built on the model of in vivo systems.

To summarize, the 3D-RISM method proved to be useful and capable of reproducing the thermodynamically preferable self-organizing supramolecular architecture, which has been suggested by experimental results and obtained in computationally intense molecular simulations. With reasonable computational effort much smaller than molecular simulations the 3D-RISM method allows one to predict, from the first principles, the three-dimensional solvation structure and solvation thermodynamics of a supramolecule in molecular solvent. This gives access to the PMFs between protofilaments in solution, yielding predictions for the conformational stability and optimal arrangement of protofilaments in a supramolecule. These characteristics are very difficult, and mostly not feasible, to obtain from molecular simulations. Being cost-effective, the 3D-RISM method allows one to scan a large number of systems.

We can conclude that our results for the potential of mean force between adjacent protofilaments in aqueous solution indicate that the interactions between protofilaments are independent of isotype studied. However, they strongly depend on the M-loop conformation of β-tubulin, suggesting that the microtubular architecture may be more sensitive to the M-loop conformation than to the isotype sequence. These data were obtained for the first time that we know of. Based on the analysis of the potential of mean force between adjacent protofilaments, we also found the optimal arrangement of protofilaments, which is in good agreement with other theoretical studies, as well as experiment.