Phase Resetting Curves and Oscillatory Stability in Interneurons of Rat Somatosensory Cortex

Abstract

Synchronous oscillations in neural activity are found over wide areas of the cortex. Specific populations of interneurons are believed to play a significant role in generating these synchronized oscillations through mutual synaptic and gap-junctional interactions. Little is known, though, about the mechanism of how oscillations are maintained stably by particular types of interneurons and by their local networks. To obtain more insight into this, we measured membrane-potential responses to small current-pulse perturbations during regular firing, to construct phase resetting curves (PRCs) for three types of interneurons: nonpyramidal regular-spiking (NPRS), low-threshold spiking (LTS), and fast-spiking (FS) cells. Within each cell type, both monophasic and biphasic PRCs were observed, but the proportions and sensitivities to perturbation amplitude were clearly correlated to cell type. We then analyzed the experimentally measured PRCs to predict oscillation stability, or firing reliability, of cells for a complex stochastic input, as occurs in vivo. To do this, we used a method from random dynamical system theory to estimate Lyapunov exponents of the simplified phase model on the circle. The results indicated that LTS and NPRS cells have greater oscillatory stability (are more reliably entrained) in small noisy inputs than FS cells, which is consistent with their distinct types of threshold dynamics.

INTRODUCTION

Neural oscillations and rhythmic activity are observed in a variety of brain functions, including central pattern generation (1), locomotion (2,3), breathing (4,5), physiological/Parkinsonian-resting tremor (6,7,8), sleep spindles (9,10), slow sleep rhythms (10,11), and gamma, theta and epileptic rhythms in the cortex and hippocampus (12,13). However, little is understood of the complex mechanism of neural population oscillations, of how and why they initiate and break up—what determines their stability. Although the characteristics of synchrony induced by common input and by various types of coupling are quite different, the coherence of oscillations in neuronal populations must depend on the oscillatory stability of the individual participating cells. As a first step in understanding the dynamics of cortical oscillations, therefore, it is necessary to understand quantitatively how individual cell types preserve firing regularity in the face of intrinsic and synaptic noise.

Independent of the precise mechanism of oscillations, certain mathematical concepts are generally applicable to analyzing the mechanism of synchrony (14,15). Phase resetting is a quantity that can be directly measured experimentally by delivering a perturbing stimulus to an oscillating system and monitoring the resulting change in the phase of its dynamics ((14,16); for review (17)). In a reduced phase model of the oscillator's dynamics, the phase resetting curve (PRC) provides a complete description of the dynamics and can be analyzed to predict the stability of entrainment or synchrony, even in the presence of noisy fluctuations. This strategy of determining the response of biological oscillators to perturbation administered at different timings of the cycle has yielded important insights into oscillators such as Aplysia bursting cells (18), cardiac cells (19–22), pacemaker neurons and their networks (23–26), central nervous systems (27,28), and respiratory rhythm (29–32).

Details of the neuronal microcircuits in the mammalian cortex that underlie oscillatory firing are becoming more apparent (33,34), although the mechanism of stable oscillations in the gamma and beta frequency ranges is still far from clear (35). It is believed that inhibitory interneurons such as fast-spiking (FS) and low-threshold spiking (LTS) cells, two major classes of GABAergic interneurons, play a significant role in promoting stable synchronous oscillations in the local cortical circuit (36). Recent studies also show that adjacent pairs of interneurons of the same class in the layer 4 of somatosensory cortex are often interconnected simultaneously by gap junctions and GABAergic synapses (37,38). Nonpyramidal regular spiking (NPRS) cells are another major class of interneurons, which are excitatory (39).

Here we have examined some of the important components of synchronization in the cortical circuit, by measuring PRCs of these three types of interneuron, in response to small current perturbations. We found that in each cell type, PRCs could be classified as monophasic or biphasic, with FS cells in particular showing a preponderance of biphasic PRCs. To gain insight into the biophysical basis of the PRCs, we compared them with results from conductance-based neural models. Finally, we introduce the concept of a stability index, a measure derived directly from the PRC using the theory of random dynamical systems, which expresses the rate of divergence of the phase during oscillation due to noise. We found that LTS and NPRS cells have a rather higher oscillatory stability than FS cells, and we discuss the potential meaning of these results in terms of the roles of interneurons in cortical networks.

MATERIALS AND METHODS

Slice preparation and recording

Transverse slices were prepared from somatosensory cortex of 18- to 24-day-old Wister rats using standard techniques (40). During slicing, tissue was kept in sodium-free solution that had the following composition (in mM): 254 sucrose, 2.5 KCl, 26 NaHCO_2, 10 glucose, 1.25 NaH₂PO₄, 2 CaCl₂, and 1 MgCl₂. Slices of 300-μm thickness were cut on a vibrating slicer (Microslicer DTK-3000, D.S.K., Kyoto, Japan) and kept in Ringer's solution at room temperature for at least 2 h before recording. The Ringer's solution contained (in mM): 125 NaCl, 2.5 KCl, 25 NaHCO_2, 25 glucose, 1.25 NaH₂PO₄, 2 CaCl₂, and 1 MgCl₂. Both slicing and recording solutions were equilibrated with 95% O₂, 5% CO₂ gas to a final pH of 7.4. Slices were viewed with an upright microscope (Olympus BW50WI, Olympus UK, London, UK) using infrared differential interference contrast optics. All experiments were performed at 34 ± 1°C. Whole-cell patch-clamp recordings were made from the somas of neurons in layers 3 and 4, targeting cells of nonpyramidal morphology with multipolar dendrites. Among these, NPRS, LTS, and FS cells were distinguished on the basis of their action potential shape and firing patterns (41,42). NPRS cells had typical regular-spiking features, and we selected those with only slight firing-frequency adaptation. FS cells were distinguished as described previously (43). LTS cells distinctively exhibited prominent low-threshold action potentials after hyperpolarizing current steps (“anode-break” firing). During recording, the slices were perfused continuously with Ringer's solution in which 10 μM bicuculline or gabazine (Sigma, St. Louis, MO), 10 μM CNQX, and 10 μM AP5 (Tocris Cookson, Bristol, UK) were included to block most intrinsic synaptic conductances. Somatic patch-pipette recordings were made with a Multiclamp 700A amplifier (Axon Instruments, Foster City, CA) in current-clamp mode, correcting for prenulled liquid junction potential. Whole-cell recording pipettes (Clark GC150T-7.5) of 3.9–4.3 MΩ resistance were filled with the standard intracellular solution: 105 mM K gluconate, 30 mM KCl, 10 mM HEPES, 10 mM phosphocreatine Na₂, 4 mM ATP-Mg, and 0.3 mM Na-GTP, balanced to pH 7.3 with NaOH. Series resistance compensation was used. Signals were filtered at 5 kHz and sampled with 12-bit resolution at 20 kHz.

Spike statistics

Spike times were measured as the times of upwards zero crossing of the membrane potential. Instantaneous frequency (reciprocal of each interspike interval) was computed from trains of action potentials evoked by 600-ms duration pulses for the 1st, 2nd, 4th, and last interspike intervals. Steady-state (SS) firing frequency was computed as the average of instantaneous frequency for the last three intervals of a train. Current strength was usually progressively increased or decreased in small (10- or 20-pA) steps. Initial instantaneous frequency and steady-state firing rate were plotted as a function of the injected current strength, to construct frequency-current (f-I) relationships. The maximum firing rate of a neuron was computed from the number of spikes per trial at the highest current strength before depolarization block. The frequency adaptation properties of neurons were characterized by calculating the instantaneous firing rate as a function of time since the beginning of the 600-ms pulse. For each current intensity, the decay of firing rate was fitted to a single exponential function:

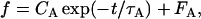(1)

where f and t, respectively, represent the firing rate and time after the stimulus onset and C_A, τ_A, and F_A are positive constant parameters. F_A represents the adapted firing rate. The strength of adaptation (adaptation index, A) was quantified as 100 × (1 − F_A/F₁), where F₁ corresponds to the firing rate of the first interspike interval. Because adaptation depended on the current intensity for any given neuron, we used the highest current level not producing depolarization block of spiking, to allow comparison among cells. For some cells, no adequate exponential fit could be obtained, and in these cases, F_A was calculated as the mean firing rate for the last 50 ms of the 600-ms current pulse and used to calculate the adaptation index. Results are reported as means ± SD. Membrane time constants were obtained by fitting a single exponential function to the initial part of >10 time-averaged voltage responses to small (−20 or −10 pA), 600-ms-long hyperpolarizing current pulses. Input resistance was calculated from Ohm's law by dividing the maximal average voltage deflection by the amplitude of the applied current pulses.

Phase resetting plot

To determine how spike timing during periodic firing is shifted by perturbations, we applied positive or negative 2-ms-width current pulses at 300–400 ms after the onset of regular firing evoked by a 1-s depolarizing current step (Fig. 3 A). The depolarizing current intensity (I_d) ranged from 50 to 800 pA and the additive perturbation step-current intensity (I_p) 5–200 pA (see also Table 2). The state of the neuron was characterized by a single quantity, the phase (φ), which without perturbation increases linearly with time, modulo 2π, with a spike occurring whenever φ = 0. Perturbation can change the phase, and hence the timing of the following spikes (Fig. 3, A and B). The spike-time response plot (STRP) is defined as the time difference between the first control spike and the first perturbed spike after the time of perturbation. Similarly, the phase resetting plot (PRP) is defined as the difference between the phase immediately after the stimulus, and that immediately before: 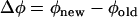. Hence, a PRP is obtained by normalizing a STRP by the average firing period. Positive (negative) values of the PRP correspond to phase advances (delays), with the timing of the next spike advanced compared to the unperturbed case. The spike-time response curve (STRC) or phase resetting curve is obtained by fitting the STSP and PRP with smooth curves, as explained below. The amount of the phase shift (Δφ) of the spike train depends on: i), the exact timing of the perturbation relative to the phase or the state of membrane-voltage oscillation; ii), the polarity of perturbation (positive or negative I_p), and iii), the magnitude of the perturbing current. STRCs or PRCs were constructed from 80 to 120 successive trials of perturbation. Each set of trials was termed a “session”. Before each session, a depolarizing current step was applied at several levels to determine an appropriate current level for producing stable “periodic firing” with only a brief initial adaptation period (<150 ms) (Fig. 1 C). To this end, interspike intervals during the period from 200 to 600 ms before the perturbation were calculated to evaluate the “periodic firing”. If the standard deviation of intervals was <5% of the average, the firing was considered periodic. For the ith trial in a session, similarly, interspike intervals during the period from 200 ms to the time of perturbation and its average (T_i) were calculated. If without perturbation the standard deviation of the average intervals (T_i) for the trials was <5% of the overall average, the firing was considered stationary.

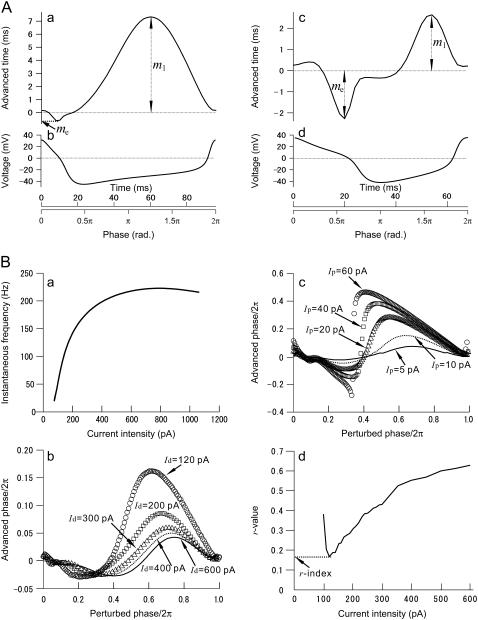
FIGURE 3.

Spike time response plot and phase response curve for an LTS cell. (A) Spikes (top, dotted line) evoked by a 1000-ms duration, 80-pA depolarizing current step (bottom) are perturbed by a 2-ms duration, 30-pA additional current step, indicated by the arrow. Action potentials in the unperturbed control are plotted as a solid line. (B) Phase shift of the postperturbed spikes depending on the perturbed phase. Stimulus 1 (perturbation at a late phase) induced phase advance (response 1), whereas stimulus 2 (at an early phase) produced phase delay (response 2). (C) Spike time response plot. The timing of perturbation is plotted by short bars. (D) A PRC is plotted using the same data shown in C. The average curve was fitted by a 7th-order polynomial curve (see Materials and Methods). The dotted curve shows the phase shift of the 2nd postperturbed spike with respect to the 1st spike after perturbation, and indicates a small 2nd-order effect on the interspike intervals immediately after perturbation.

TABLE 2.

Summary of perturbation conditions for obtaining PRCs

	LTS	NPRS	FS
No. of cells	18	23	28
No. of total sessions	31	36	41
Depolarizing current (Id), pA	169 ± 49	377 ± 277	184 ± 68
Perturbation magnitude (|Ip|), pA	45.0 ± 28.2	77.5 ± 72.0	48.9 ± 37.9
Firing period (Ti), ms	37.1 ± 9.7	24.5 ± 9.9	31.4 ± 9.0
Mean ± SD of Ti, ms	1.58 ± 0.50	1.47 ± 0.43	1.20 ± 0.44

LTS, low threshold spiking; NPRS, nonpyramidal regular spiking; FS, fast spiking.

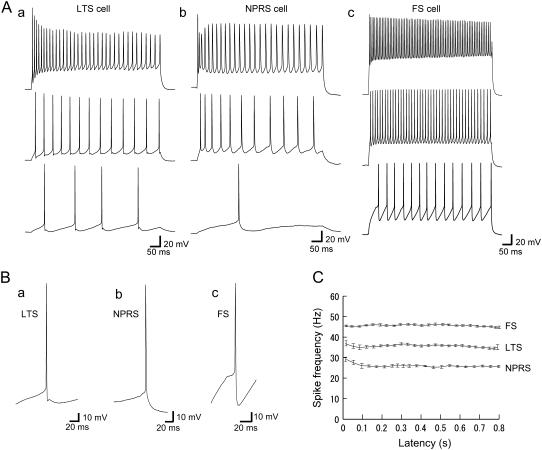
FIGURE 1.

Firing properties of three classes of neurons in layer 3/4 somatosensory cortex. (A) Repetitive firing for three different current steps of increasing amplitude: (a) LTS cell (20–250 pA); (b) NPRS cell (90–450 pA); and (c) FS cell (50–300 pA). (B) Expanded view of single spikes and afterhyperpolarizations for an LTS (a), an NPRS (b), and an FS (c) cell. FS cells had larger AHPs than LTS and NPRS cells. (C) Instantaneous firing frequency (1/interspike interval) versus time after the onset of current pulse for LTS, NPRS, and FS cells. Depolarizing current steps were, respectively, 120 pA, 200 pA, and 160 pA for LTS, NPRS, and FS cells. For each case, firing frequency was stable after 150 ms from the stimulus onset and the adaptation effect was small at these levels of current input.

Curve fitting

To create PRCs, the average values of PRPs were fitted using a polynomial function of phase (28). The polynomial function we used was of the form: 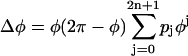, where p_i (i = 0,…,2n + 1) are free parameters. The parameters were determined to minimize the mean square error between data points and the average function. We determined the order (2n + 1) by using the Akaike information criterion (AIC) to maximize the likelihood of the model, assuming that the residual is normally distributed. This usually resulted in a 5th- or 7th-order polynomial. This fitting function ensured that the curve is continuous and had zeroes at its left and right extremes. However, this restriction was occasionally not suitable for describing the distribution of original data points. In this case, following Netoff et al. (28), we used the function 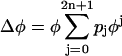, which was not constrained to zero at φ = 2π. Each PRC was classified as monophasic or biphasic. Local extrema in both early and late phases, respectively, denoted by m_e and m_l, were evaluated as shown in Fig. 7, Aa and Ac. If the ratio (r-index) between the absolute values (i.e., | m_e/m_l | for | m_e| ≤ |m_l | or | m_l /m_e | for | m_e| >|m_l |) was <0.175, we regarded its PRC as monophasic; otherwise, it was biphasic. Note that if there is only one extremum in a PRC, it was classified as monophasic (c.f., Fig. 5 C). The value of 0.175 was obtained through a numerical simulation of the fast-spiking cell model proposed by Erisir et al. (44) (see Fig. 7 Bd and Results). The original leak-conductance parameter g_L = 10 (nS) in the model was modified to g_L = 4.1 (nS) to produce an f-I curve resembling our previous results on FS cells (43). Note that using a different value of the r-index would result in a different proportion of mono- and biphasic PRCs.

FIGURE 7.

Oscillatory properties of the Morris-Lecar (ML) and fast-spiking cell models. (A) The ML model. A monophasic phase resetting curve in a type-1 regime (a) and a biphasic PRC in type-2 regime (b), and the corresponding one-cycle membrane voltage traces during periodic oscillation (b and d), respectively. (B) The fast-spiking-cell model proposed by Erisir et al. (44). (a) The frequency versus current intensity curve. The original model was modified to fit the curve to experimentally obtained data in Tateno et al. (43). The bifurcation point is at I = 76.4 pA. (b) Perturbation magnitude dependence of biphasic PRCs. (c) Depolarizing current intensity dependence of PRCs with a perturbation magnitude I_p = 5 pA; (d) r-value versus depolarizing current (I_d) intensity. The curve takes a minimum value (0.175), which is referred to as the r-index, ∼120 pA with a perturbation magnitude I_p = 5 pA.

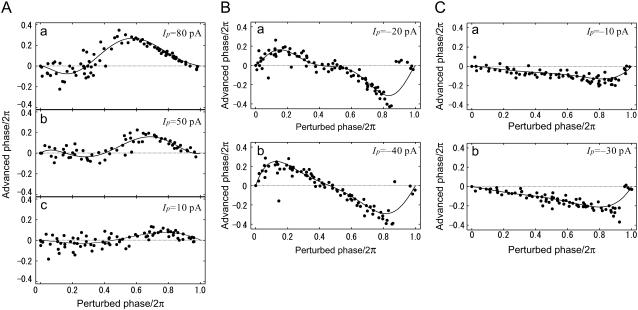
FIGURE 5.

Phase resetting curves for three FS cells. (A) Biphasic-PRC cell; a, b, and c show dependence of PRC on perturbation magnitude. The depolarizing current-step (I_d) was 200 pA and the magnitude of perturbation (I_p) was 80, 50, and 10 pA (top to bottom). (B) For one FS cell, biphasic PRCs are shown for negative perturbations of I_p = −20 pA (a) and I_p = −40 pA (b). (C) For one cell, monophasic PRCs are shown for negative perturbation of I_p = −10 pA (a) and I_p = −30 pA (b).

Stability index

We calculated a stochastic version of a Lyapunov exponent as a quantitative index of the stability of periodic firing under noisy perturbation. The method we used is based on random dynamical system theory (45). To calculate the stability index, we first assume that the periodic firing can be expressed as the simple reduced phase model

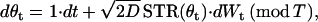(2)

where θ_t is phase on the circle, STR is a spike-time response curve, 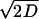is the noise intensity, T is the period of the oscillation, and W_t is the standard Wiener process (46). With an appropriate initial condition, Eq. 2 is an Ito stochastic differential equation and its linearized or variational equation is expressed by

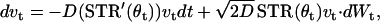(3)

where STR′(θ) = dSTR/dθ and v₀ ≠ 0. Because we can obtain an explicit solution of Eq. 3, the Lyapunov exponent is directly defined as the exponential growth rate

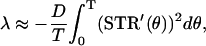(4)

for a small level of the noise. Because, from Eq. 4, the Lyapunov exponent λ is a linear function of D, we define the stability index (SI) as λ/D, that is,

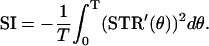(5)

By this definition, SI is always negative, and the more negative the value of SI, the greater the degree of oscillatory stability. Using Eq. 5, once we obtain the STR curve of a system from an experiment, we can directly calculate its SI value, even if we do not know an explicit expression for the underlying dynamics of the system. Thus, despite the simplicity of Eq. 5, it is a very useful relationship for gaining insight into the stability of an oscillator experiencing noisy perturbation (for more details, see Pakdaman and Mestivier (46)). To calculate SI, we used STRCs obtained for the smallest practical perturbation size, which are assumed to be proportional to the infinitesimal STRC, normalized by the magnitude of the perturbing current.

Numerical simulation methods of neural models

All numerical simulation of noiseless neural models was performed by the 4th-order Runge-Kutta method with a fixed time step of 0.1 μs. For noisy neural models, trajectories of state variables were numerically calculated by the forward improved Euler or the Heun method with a fixed time step of 0.1 μs. A more detailed description can be found in Tateno and Pakdaman (47).

RESULTS

Cell types in the layer 3/4 of rat somatosensory cortex

On the basis of responses to injected step currents, nonpyramidal cells with a multipolar dendritic morphology, recorded in layer 3 or 4 of somatosensory cortex, were classified into three groups: low-threshold spiking, nonpyramidal regular-spiking, and fast-spiking cells (36,39,42,48), as shown in Fig. 1 A. This study is based on recordings from 18 LTS, 23 NPRS, and 28 FS neurons. See Table 1 for basic firing statistics of the three types.

TABLE 1.

Summary of basic statistics on LTS, NPRS, and FS cells

	LTS	NPRS	FS
No. of cells	18	23	28
Resting potential, mV	−73.4 ± 5.3	−74.3 ± 3.2	−68.5 ± 5.1
Input resistance, MΩ	558 ± 142	333 ± 120	344 ± 87
Maximum firing rate, spikes/s	49.2 ± 16.4	43.5 ± 7.7	92.5 ± 16.4
Time constant, ms	25.1 ± 10.1	72.1 ± 14.9	41.0 ± 9.5
Adaptation index, %	50.1 ± 11.6	77.2 ± 8.5	46.0 ± 8.5
Adaptation decay time constant, ms	173 ± 63.6	192 ± 102	208 ± 92

LTS, low threshold spiking; NPRS, nonpyramidal regular spiking; FS, fast spiking.

As shown in Fig. 2 A, LTS cells were easily distinguished from the other two cell classes by low-threshold action potentials produced when stimulated from hyperpolarizations (36). LTS cells show strong spike-frequency adaptation at larger levels of injected current, but little adaptation at lower levels (Figs. 1 Aa and 2, Ab and Ba). They also support lower regular firing frequencies than FS cells (Fig. 2, Ab and Bb) and at low frequencies, show a biphasic afterhyperpolarization (AHP), as shown in Fig. 1, Aa, Ba, and Ab.

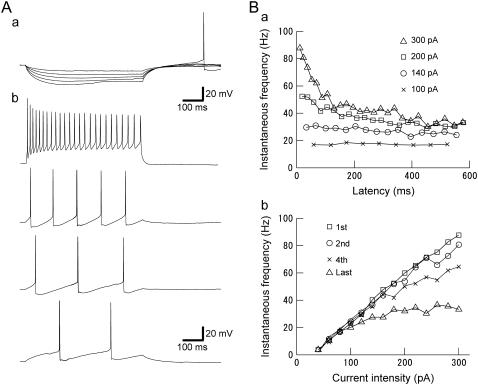
FIGURE 2.

(A) Firing properties of LTS cells. (a) Membrane responses for five increasingly negative current steps (from −10 to −50 pA). Hyperpolarizing current injection (−50 pA) leads to a rebound spike. (b) Repetitive firing for four different current steps of increasing amplitude (20–260 pA). LTS cells support low firing frequency. (B) (a) Instantaneous firing frequency (1/interspike interval) versus time after the onset of current pulse at four selected current strengths (100, 140, 200, and 300 pA). LTS cells show strong adaptation at higher current strength (i.e., 300 pA), but little adaptation at lower current strength (i.e., 100 pA). (b) LTS neuron firing frequency versus injected current (f-I) relationship. Frequencies corresponding to the 1st, 2nd, 4th, and last spike intervals increased monotonically with the current strength, starting from 2 to 4 spikes/s, as low as could be assessed with this stimulus duration. This result indicates that LTS cells effectively have “type 1” threshold dynamics.

As described previously (43), Fig. 1, Ab and Ac, respectively, shows typical action potential waveforms for an NPRS cell and an FS cell at three levels of injected step-current. NPRS cells and FS cells showed monophasic and biphasic AHPs, respectively, as seen in Fig. 1, Bb and Bc. NPRS cells and FS cells differed in their basic electrical parameters, particular in resting potential, maximum firing rate, and adaptation index (see Table 1). We also used several other measures to distinguish NPRS and FS cells, as reported in Ref. (43). At intermediate current intensities, LTS, NPRS, and FS cells show periodic firing after 150 ms from the onset during a current step injection, as shown in Fig. 1 C, although the current intensities required to produce such regular firing differed between cells and cell types (see the next subsection and Table 2).

Phase resetting curves

We next examined how perturbing current inputs affect spike timing and shift the phase of spiking, using short (2-ms-width) current pulses of varying magnitude (I_p) and polarity (see Materials and Methods). Before each test condition, we first checked the periodicity of regular firing during the control application of a depolarizing step current (e.g., see Fig. 1 C). Table 2 summarizes the perturbation test conditions used, and control periodicity, for each cell type.

Fig. 3 A shows superimposed waveforms of action potentials in the control and with a perturbation, in an LTS cell. Compared with the control, the spike time was changed after short and small current-step perturbations, indicated by the arrow, although there was small spike-time jitter (<2 ms) before the perturbation and the final period (>800 ms) of the stimulus (see Table 2). The amount of spike time or phase shift depended on both individual cells and the timing or phase of perturbation during one cycle of firing. As seen in Fig. 3 B, compared with the control condition, a perturbation at a late phase (stimulus 1) advanced the next spike time (response 1), whereas a perturbation at a very early phase (stimulus 2) delayed the next spike time (response 2). By successively changing the perturbation time relative to that of the preperturbed spike, a spike-time response plot is obtained, as shown in Fig. 3 C. Normalizing by the average of the firing intervals (firing period, T) produces a phase resetting plot, as shown in Fig. 3 D. We obtained the corresponding phase resetting curve by polynomial fitting (Fig. 3 D), as described in Materials and Methods. The effect of perturbation on following spikes can be systematically evaluated by calculating the phase of nth-order interspike intervals (modulo T), which are phase-independently distributed around zero, in the absence of a perturbation. For the case of Fig. 3 C, the average perturbation effect on the succeeding (2nd order) interspike intervals is plotted by a dotted curve in Fig. 3 D, showing only a slight phase delay. Thus, the major effect of the perturbation is confined to the spike interval in which it occurs (1st order).

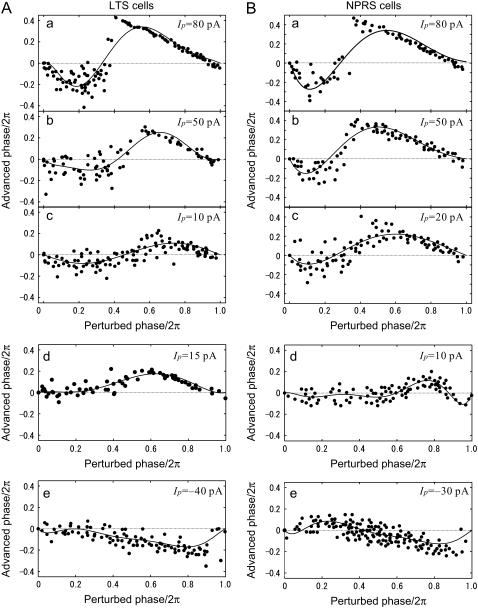
Fig. 4, Aa-c and Ba-c, shows examples of PRCs and the effects of perturbation intensity on the shape of the PRCs, for LTS and NPRS cells, respectively. In these cases, the average PRCs are biphasic; the postperturbed phase is delayed by perturbations early in the period, whereas it was advanced by late perturbations. In addition, with respect to the perturbation amplitude, phase resetting curves were almost linearly scaled for smaller levels of the perturbation (e.g., I_p = 5–50 pA). At large perturbation magnitudes (>50 pA), a clear discontinuity in the PRCs becomes apparent, which is not well fitted by low-order polynomials. Another typical finding was that the zero crossing points in PRCs were shifted leftward as the perturbation magnitude increased. PRCs are also shown for two other LTS cells (Fig. 4, Ad and Ae) and two NPRS cells (Fig. 4, Bd and Be) perturbed by small positive (I_p = 20 pA) or negative (I_p = −20 pA) current steps. Fig. 4, Ad,e and Bd, shows examples of monophasic PRCs, whereas the NPRS cell in Fig. 4 Be had a biphasic PRC. Overall, for smaller perturbing current-steps (|I_p| = 24.2 ± 13.1 pA) in 18 LTS neurons, 72.2% of the cells showed monophasic PRCs and the remaining 27.8% were biphasic, using an r-index of 0.175, which means the ratio between the local extrema at early and late phases (see Materials and Methods). Similarly, for relatively smaller perturbations (|I_p| = 26.9 ± 11.1 pA) in 22 NPRS cells, 54.5% of cells were classified as monophasic and 45.5% as biphasic with the same r-index. For statistics of the points of local extrema and of zero crossing in the PRCs, see Table 3.

FIGURE 4.

Phase resetting curves for three of LTS and NPRS cells. (A) LTS cells. For an LTS cell, dependency of biphasic PRCs on perturbation magnitude is shown in a, b, and c. The depolarizing current-step (I_d) was 200 pA and the magnitude of perturbation (I_p) was 80, 50, and 10 pA (top to bottom). (d and e) For two other LTS cells, monophasic PRCs for positive perturbations (d, I_p = 15 pA) and negative perturbation (e, I_p = −40 pA). (B) NPRS cells, biphasic PRCs at three perturbation magnitudes. The perturbation magnitude I_p was, respectively, 80, 50, and 20 pA in a, b, and c. (d and e) For two other NPRS cells, monophasic and biphasic PRCs are shown, for positive (d, I_p = 10 pA) and negative (e, I_p = −30 pA) perturbations, respectively.

TABLE 3.

Summary of PRCs for small current-step perturbation

	LTS	NPRS	FS
No. of cells	18	22	23
Depolarizing current (Id), pA	148 ± 50	237 ± 105	168 ± 68
Perturbation magnitude (|Ip|), pA	24.2 ± 13.1	26.9 ± 11.1	30.0 ± 12.1
Firing period, ms	38.4 ± 9.7	46.4 ± 9.2	27.1 ± 6.8
Monophasic PRCs, % (cells)	72.2 (13)	54.5 (12)	30.4 (7)
Absolute local extremum, ×2π rad.	0.14 ± 0.11	0.12 ± 0.09	0.16 ± 0.10
Biphasic PRCs, % (cells)	27.8 (5)	45.5 (10)	69.6 (16)
*Maximum advanced phase, ×2π rad.	0.091 ± 0.021	0.17 ± 0.08	0.17 ± 0.11
*Minimum delayed phase, ×2π rad.	−0.048 ± 0.026	−0.084 ± 0.061	−0.098 ± 0.111
*Zero crossing phase, ×2π rad.	0.37 ± 0.08	0.45 ± 0.09	0.35 ± 0.08

LTS, low threshold spiking; NPRS, nonpyramidal regular spiking; FS, fast spiking. The perturbation magnitude I_p was <40 pA in all cases, and the r-index used was 0.175.

^*Indicates that each of the values is calculated only by positive current-pulse perturbations.

Several examples of PRC curves for FS cells are shown in Fig. 5. Fig. 5 A shows the almost linear scaling of PRCs in one cell as the magnitude of a small perturbation is increased (I_p = 5–50 pA), although the zero crossing points shifted leftward slightly. There was a less pronounced discontinuity in the PRCs at high intensities of perturbation (Fig. 5 Aa) than for the other cell types. Two other FS cells showed biphasic and monophasic PRCs in Fig. 5, B and C, respectively, in response to negative current perturbation. Asymmetrical PRCs were obtained for larger levels (I_p > 80 pA) of positive and negative perturbation (cf. Fig. 5, Aa and Ba), although the exact shape of PRCs greatly depended on individual FS cells. In total, for smaller current steps (|I_p| = 30.0 ± 12.1 pA) in 23 NPRS cells, 30.4% of the cells were monophasic and 69.6% were biphasic with the r-index value 0.175. For other statistics of the PRCs, see Table 3.

Firing stability under noisy perturbation

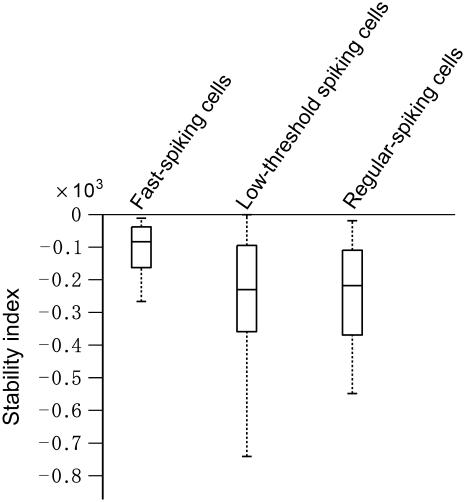
To characterize the oscillatory stability of periodic firing under noisy perturbation, we analyzed the stability index for all the cells of the three cell types (see Materials and Methods). This index uses random dynamical system theory to quantify the stability of stochastic systems, in a way that is analogous to the analysis of stability of a deterministic system. It gives a measure of the duration of the transient period or relaxation to a stochastic equilibrium, under stationary conditions of the stochastic components. The stability index (see Materials and Methods) was calculated from normalized PRCs obtained at low (I_p < 40 pA) perturbation magnitudes (see Table 3). For LTS, RS, and LTS cells, the index values were, respectively, −2.72 ± 2.33, −3.16 ± 3.44, and −1.54 ± 2.19. As also shown in the box plot of Fig. 6, LTS and RS cells have more negative index values on average than FS cells (P < 0.05, see Table 4). This result implies that LTS and RS cell firing can be more easily stabilized under fast noisy inputs than can FS cells. Moreover, if they have stochastic equilibria (see Fig. 8), FS cells would approach them more slowly than LTS and RS cells on average.

FIGURE 6.

Stability index for FS, LTS, and NPRS cells. Box plots are shown for the three cell types, with lines at the lower quartile, median, and upper quartile values. Also, see Table 4.

TABLE 4.

Summary of stability index for LTS, NPRS, and FS cells

	LTS	NPRS	FS
No. of cells	18	22	23
Stability index (×10−4)	−2.72 ± 2.33	−3.16 ± 3.44	−1.54 ± 2.19
P	<0.05	<0.05	–

The significant difference of LTS versus FS or NPRS versus FS cells is indicated in P.

FIGURE 8.

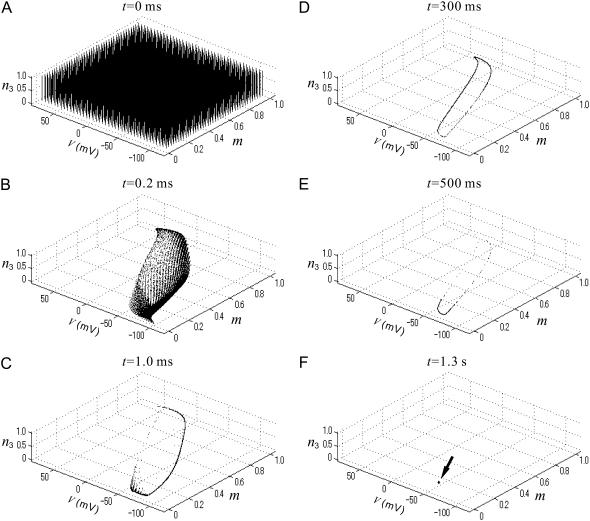
(A) Time evolution of many state points on the V-m-n₃ phase space for an identical noise realization input, in an oscillatory regime of the FS-cell model. In the absence of noise, the model has a stable limit cycle. For D = 2.0 mV, snapshots of the state points are illustrated in the space for a starting grid of 64,000 initial conditions regularly positioned in hexahedral grids at t = 0 ms (A), t = 0.2 ms (B), t = 1.0 ms (C), t = 300 ms (D), t = 500 ms (E), and t = 1.3 s (F).

Numerical simulation of neural models

For some low-dimensional Hodgkin-Huxley type conductance-based neural models, numerical simulations indicate a close link between threshold dynamics and the shape of PRCs: PRCs are mostly positive in a type-1 parameter regime, whereas they become markedly biphasic in a type-2 regime (49). Type-1 neurons show continuous frequency versus steady current intensity (f-I) relationship, whereas type-2 neurons show a discontinuous relationship at lower frequency. For example, typical PRCs of the Morris-Lecar model (50) in type-1 and type-2 regimes are shown in Fig. 7 A; r-values (| m_e/m_l |) were 0.00886 in Fig. 7 Aa and 0.864 in Fig. 7 Ac because | m_e| ≤ |m_l |. However, actual cortical interneurons are likely to have more complexity and variability, requiring more realistic neural models. For instance, Fig. 7 B shows some characteristics of an FS-cell model with Kv3.1-channel-like current proposed by Erisir et al. (44), with a model parameter (leak conductance) modified to fit an experimentally obtained f-I curve (c.f., Fig. 7 Ba and Tateno et al. (43)). As shown in Fig. 7 Ba, the model has type-2 membrane excitability and shows an abrupt onset of regular firing at ∼20 spikes/s beyond a subcritical Hopf bifurcation point in response to steady injected current of 76.4 pA. Fig. 7 Bb shows the dependence of biphasic PRC shape on depolarizing current intensity (I_d). At small perturbation magnitude (I_p = 20 pA) and larger depolarizing current intensity (e.g., I_d = 600 pA), the PRC seems to be monophasic, but is in fact biphasic. Although the theory of phase models and weakly coupled networks (51) considers infinitesimal perturbations, in an experiment, of course, one must use a finite nonzero perturbation magnitude. The shape dependence of PRCs on perturbation magnitude introduces additional variability in the shape of experimentally recorded PRCs, for example, as illustrated in Fig. 7 Bc. However, one may minimize this problem by using small (e.g., 5–30 pA) perturbations because, with respect to the perturbation amplitude, the PRC essentially scales linearly in this range (c.f., Fig. 4, A and B). Therefore, we take the normalized, small-perturbation PRC to represent the infinitesimal PRC, as a characteristic function describing how a particular neuron reacts to small perturbations. We classified the shape of PRCs using the r-value, the ratio of minimum phase delay (advance) to maximum phase advance (delay) (c.f., Fig. 7, Aa and c). For the Erisir et al. model (44), the relationship between r-value and injected current intensity is shown in Fig. 7 Bd. This shows that the r-value of this type-2, biphasic-PRC model reaches a minimum value of 0.175, which we designate as the r-index for discriminating between monophasic (r < 0.175) and biphasic (r ≥ 0.175) PRCs experimentally.

DISCUSSION

Cell types, threshold dynamics, and PRC shape

In a study of the responses of axons isolated from Carcinus maenas to various intensities of rectangular current stimuli, Hodgkin found that some axons could show a continuous transition from zero frequency to arbitrarily low frequencies of firing, whereas others show an abrupt onset of repetitive firing at a nonzero firing frequency (52). These types of threshold excitability are recently referred to as “type 1” and “type 2”, respectively. RS cells in the cortex are well known to have “type 1” excitability, i.e., continuous frequency versus steady current intensity (f-I) relationship, because they support extremely low frequency firing (53,54). In contrast, it has quite recently been reported that FS interneurons in the rat somatosensory cortex demonstrate “type 2” membrane excitability because FS cells begin repetitive firing with an abrupt onset at increasing levels of sustained current step stimuli, i.e., discontinuous f-I relationship (42–44). In addition, in this study, we demonstrate that LTS cells are “type 1” with a continuous f-I relationship (Fig. 1, Cb and Db), which to our knowledge has not been reported previously.

As shown in Fig. 7, for some low-dimensional Hodgkin-Huxley type conductance-based neural models, numerical simulations indicate a close link between threshold dynamics and the shape of PRCs. Experimentally, in contrast, PRCs classified as monophasic or biphasic did not always strictly correspond with type-1 and type-2 excitability, respectively. An interesting aspect of our results is the heterogeneity of PRC type within cell types as defined by action potential shape and firing pattern, which indicates that a cell “type” may in fact encompass cells with a variety of dynamical behaviors and perhaps distinct subtypes. In future experimental studies, there is certainly scope for a more sophisticated classification of PRC shape than we have attempted here, for example, by using the approach of Galán et al. (55).

Cell-type dependent noise-induced stability of neural oscillations

Cortical neurons in vivo must operate in high levels of noise resulting from channel gating fluctuations, noisy synaptic transmission, and background network activity (56–58). “Noise” may also include, or even be dominated by the complex, apparently stochastic input that must be encoded and processed as information by a cortical neuron. It is important, therefore, to begin to quantify and elucidate the stability of oscillations of cortical interneurons under noisy perturbation, and its functional impact. For cortical neurons, significant questions are: i), What is the effect of oscillatory stability on neural coding? ii), How do different cell types differ in their oscillatory stability? iii), What noise level in neural models is appropriate for representing stable and unstable firing in actual cortical circuits?

Our approach to these problems has been to apply the recently developed theory of random dynamical systems (45) to a simple, reduced one-dimensional phase-model mimicking experimentally observed neural oscillations, and to obtain a stability index that is a stochastic version of a Lyapunov exponent, from experimentally observed PRCs. In general, it is always true that adding noise to any oscillator will induce variability of oscillations, and in neural oscillators, a certain degree of randomness in spike timing. However, perhaps unexpectedly, the variability or the randomness is not always sufficient to make the system lose oscillation regularity and to drastically change its asymptotic behavior. Such randomness may not necessarily have a negative functional impact on neural systems and may contribute to creating new order, for example, as in the enhancement of signal detection through stochastic resonance described in sensory systems (59,60) or noise-induced synchronization of neural oscillations proposed in olfactory bulb mitral cells (61).

As some recent studies have described (46,47,62,63), from a random dynamical system viewpoint, the destruction of limit cycles of deterministic conductance-based neural models by weak additive noise is replaced by the concept of stochastic equilibria. That is, in a certain situation, even weak noisy perturbation to a neural model is sufficient to transform its limit cycle into a single stochastic equilibrium point, which is a stochastic process and continues to fluctuate in the future. This means that for almost all initial conditions and under the same noise realization, any sample path of the state point converges to a single (stationary) stochastic process after a transient period. Fig. 8 shows such an example of the noisy FS-cell model in an oscillatory regime. In Fig. 8, under the same noise realization, state points of the identical FS-cell units start from many different initial conditions (Fig. 8 A) and finally converge to a single point (Fig. 8 F), which is a stochastic process, after a transient period (Fig. 8, B–E). Therefore, for the same noisy, complex input or “frozen noise” stimulus, the set of trajectories and, in the sense of neural coding, the spike timing is reliable across an ensemble after the transient period (62,63).

As in neural models, weak noisy inputs to cortical interneurons could create a similar situation, either stabilizing or destabilizing the oscillation, leading to more reliable or unreliable spike timing. The oscillatory stability and the transient period to stochastic equilibrium must depend on the specific cell type, e.g., on the balance among various transmembrane ion channels including Kv1 and Kv3 channels (63). We found that FS cells have a smaller average stability index value than the other two cell types, but less variability in the index values. This indicates that FS cells may have a longer transient period on average to approach their putative stochastic equilibria. One interpretation of this result is that FS cells are driven less easily by noisy input than are the other two cell types, because they have a comparatively strong preferred oscillation frequency or resonance. In other words, FS cells may avoid becoming entrained to a driving noisy input over short periods.

There are rather few reports of stable intracellular recordings in awake animals (56,57,64–67). However, these studies indicate that cortical neurons typically have a depolarized membrane potential ∼−60 mV, with a standard deviation of fluctuations of 2–6 mV. In addition, Tateno and Robinson (63) recently showed that at such noise levels, the leading Lyapunov exponents of an FS-cell model are strictly negative for each realization. This result supports the idea that the analysis described in this study could be quite relevant to the normal function of cortical networks.

Possible roles of interneurons in cortical population activity

Networks of GABAergic interneurons are implicated in synchronizing cortical activity over a wide range of frequencies. For cognitive processes such as perception and attention, fast network oscillations in the cortex are proposed to establish transient temporal correlations between spatially distributed neurons with a temporal resolution of <10 ms (67). Both synchronizing and desynchronizing mechanisms provided by GABAergic interneurons are thought to be important in governing such concerted activity. In the cortex, population oscillations appear to arise as an emergent property of networks of interneurons, mutually connected both through electrical coupling and chemical synaptic connections (37,38,68). It is also known that gap junctions almost exclusively connect GABAergic neurons belonging to the same class (33). That is, the interneuron network connections in the cortex are strictly cell-type dependent and homogeneous within cell types, and network activity is thus influenced by the distinctive dynamics of each cell type. The different phase resetting properties of each cell type corresponds to a type-specific strategy for participating in concerted rhythmic activity.

The PRC as a tool to examine oscillatory stability

We have demonstrated that using random dynamical system theory, PRCs can become a useful practical tool not only for understanding the phase shifts of neural oscillation in response to small perturbations, but also for characterizing and classifying oscillatory behavior for noisy or complex inputs. This approach is quite general for oscillators in the presence of noise, and is also applicable to a variety of other biological oscillators.