Lateral Organization in Lipid-Cholesterol Mixed Bilayers

Abstract

Interactions between lipid and cholesterol molecules in membranes play an important role in the structural and functional properties of cell membranes. Although structural properties of lipid-cholesterol mixtures have been extensively studied, an understanding of the role of cholesterol in the lateral organization of bilayers has been elusive. In this article, we propose a simple yet powerful model, based on self-consistent mean-field theory and molecular dynamics simulations, for lipid bilayers containing cholesterol. Properties predicted by our model are shown to be in excellent agreement with experimental data. Our model predicts that cholesterol induces structural changes in the bilayer through the formation of regions of ordered lipids surrounding each cholesterol molecule. We find that the “smooth” and “rough” sides of cholesterol play crucial roles in formation and distribution of the ordered regions. Our model is predictive in that input parameters are obtained from independent atomistic molecular dynamics simulations. The model and method are general enough to describe other heterogeneous lipid bilayers, including lipid rafts.

INTRODUCTION

Cholesterol (chol) is an essential component of all mammalian cell membranes. It exists in concentrations varying from ∼10% up to 50% (1). Chol is also an essential component of lipid rafts (2), nanoscopic domains that form within membranes. These rafts are rich in sphingolipids as well as chol, and have increased order, thickness, and rigidity compared to the rest of the membrane. Rafts are implicated in a variety of diseases including Alzheimer's disease, diabetes, influenza, and prion diseases (3). Motivated by the numerous biological roles of cholesterol, purely physical studies of the properties of cholesterol in lipid membranes are of interest both in biophysics and in soft condensed matter physics (4). Of particular interest is the lipid-chol “phase diagram,” which describes thermodynamic and structural states of lipid-chol mixtures as functions of temperature and chol concentration. The most commonly used lipid in the determination of lipid-cholesterol interactions is dipalmitoylphosphatidylcholine (DPPC), containing two saturated hydrocarbon chains of 16 carbons each. DPPC undergoes a first-order phase transition in the absence of chol at 41.5°C. This transition is primarily driven by the melting of chains of DPPC from an ordered (gel) phase to a disordered (liquid crystalline) phase within the bilayer. Between the gel and fluid phases, there is an intermediate gel-like “ripple” phase in DPPC, which exists only in pure DPPC, and at very low chol concentrations. Hence, this phase is not considered further in this study. Chol severely affects the nature of phase transitions above concentrations of ∼5%. Published phase diagrams, based on NMR and differential scanning calorimetry (DSC) experiments, map the effect of chol (5–7). Phase diagrams from different sources differ considerably about the exact location of the boundaries of the coexistence regions, although each group examines subtle changes in NMR spectra and/or DSC thermograms to identify boundaries separating thermodynamic phases. The order of the transition between coexisting phases is not established by the current set of experiments.

Three distinct regions in DPPC-chol mixtures are observed in all of the proposed experimental phase diagrams: 1), a gel phase, in which lipid chains are highly ordered and lipid diffusion in two dimensions is very low; 2), a liquid-crystalline phase (L_α), where lipid chains are disordered and lipid diffusion is much higher compared to the gel phase; and 3), an intermediate state usually referred as the “liquid ordered phase” (β), a state in which chains are highly ordered, as in the gel phase, but lipid diffusion is enhanced, similar to the L_α phase. Although experimental data from different sources support the existence of these three phases, the studies differ in their locations of phase boundaries and coexistence regions in the phase diagram.

Lipid-cholesterol phase properties were examined in lipid monolayers by McConnell and co-workers (8–13). They found that by varying temperature and surface pressure, a rich set of phase properties were observed, including critical points. The data are well explained by a thermodynamic model based on the formation and interaction of condensed complexes consisting of stoichiometric mixtures of lipid and cholesterol molecules. In recent work, McConnell and Radhakrishnan developed a theoretical model for the deuterium NMR spectra of lipid-sterol mixtures (14). Based on this model, they concluded that lipid-cholesterol mixtures are monophasic at all temperatures and cholesterol concentrations, rather than having coexisting thermodynamic phases. The changes in deuterium NMR spectra that form the basis for proposed phase diagrams (5–7) are explained by McConnell and Radhakrishnan in terms of the formation of DPPC-chol complexes. There is, consequently, some controversy regarding the nature of the ordering in DPPC-chol mixtures. The goal of this article is to address this issue from a modeling perspective.

Computational and theoretical modeling can help in the interpretation of experimental data, predict new results, and steer future experiments. Molecular dynamics (MD) simulations, based on independently calculated and tested force fields have the potential to predict properties of lipid mixtures in bilayers that result from microscopic intermolecular interactions. Indeed, a number of researchers have published MD simulations of bilayers (see references cited in Scott (15)). Our earlier simulations of the condensing effect of cholesterol on PC lipids (16,17), which accurately replicated corresponding experimental work by the McConnell lab (9,11), suggest that our force fields are capable of meaningful representation of phospholipid-chol interactions. However, MD simulations, although increasing in power, are still limited to timescales of hundreds of nanoseconds to a few microseconds at most, and to sizes of a few hundred to a thousand lipids. Even if the force fields are sufficiently accurate, this is a severe limitation, since large-scale lateral molecular translations require much longer timescales in a mixed lipid bilayer. At best, MD simulations provide insight into the nature of the molecular interactions that lead to the formation of separated phases.

To address the timescale limitation of MD, it is necessary to employ coarse–grain models for lipid mixtures. Recently, Elliot et al. (18) proposed a model based on self-consistent mean-field theory for binary and ternary lipid-chol mixtures. At a qualitative level, the model of Elliot et al. yields a phase diagram that resembles the experimental diagram proposed by Vist and Davis (5). However, the coexisting regions are wider and occur at larger chol concentrations, compared to experimental data. In this article, we present an alternate model of the DPPC-chol mixture, where, instead of tuning model parameters to fit empirical quantities, we derive the model parameters and chain conformations from MD simulations. Our model also provides a temporal view of the organization of the DPPC-chol system, since this approach is based on time-dependent self-consistent mean-field theory (SCMFT). This enables us to extend predictions of atomistic simulations to timescales of tens of microseconds, and to 0.1-μm lengthscales on a desktop computer. On a high-performance computing platform, we see no reason why the method could not be extended to simulate domain formation across an entire vesicle, with parameters derived directly from the atomistic simulations of the neighbor interactions.

MODEL AND METHODS

Basic model

SCMFT modeling has its origin in the Ginzburg-Landau approach to the study of coexisting phases (19). In this approach, one defines a local order parameter (OP), 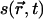, which characterizes the thermodynamic behavior of the system, and a time-dependent free energy functional, 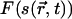. The OPs evolve in time according to the time-dependent Ginzburg-Landau equation (19,20). However, if the order parameter equilibrates rapidly compared to the lateral diffusion rate, equilibrium OPs, 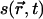, can be obtained from the solution of self-consistent equations after each time step. For a lipid bilayer, we define s as the average chain OP at a position ,

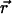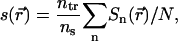where 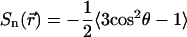is the C-H OP at carbon n for the chain at position 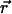, and θ is the angle between the C-H bond vector and the bilayer normal, N is the total number of carbons for which S_n is calculated in the chains of the lipids, n_s is the number of dihedral angles in a chain, and n_tr is the number of dihedrals in trans conformations. The set of elements 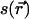defines a field in a two-dimensional plane that represents one leaflet of the bilayer in this model. We model chol molecules as discrete rods, represented by a position vector 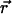and orientation θ. These model chol evolve in the bilayer plane (the field of lipid-chain order) in time according to the following stochastic equations (20):

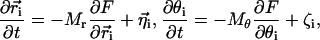(1)

where M_r and M_θ are mobilities related to the experimental diffusion constant D and the rotational diffusion constant D_rot by M_r = D/K_BT and M_θ = D_rot/K_BT, and η_i and ζ_i are thermal fluctuations modeled as random variables satisfying the fluctuation-dissipation theorem (19). The above equations are also known as position Langevin equations, and are obtained in the diffusive limit of the ordinary Langevin equation. This description is effective for dense systems in which the solute's behavior in solution is continuously altered by collision with solvent molecules (21).

We express the continuum field as a lattice field on a square lattice with a lattice constant based on the average area per DPPC chain in MD simulations. We derive our free energy from a simple Hamiltonian, similar to the Hamiltonian proposed by Marčelja (22), and mean-field theory,

(2)

Here, the first term is the lipid-lipid interaction energy, and the coupling constant V_o represents net effect of headgroups and hydration on the thermodynamic behavior of a pure lipid system. The summation in this term runs over all the nearest-neighbor pairs of chains. The second term is the lipid-chol interaction function. The form of this function is based on the azimuthal anisotropy exhibited by lipid-chol interactions that we observe in long MD simulations (23): V_lc(r_α,i, θ_α,i) = 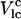(1 − Δsin(θ_α,i)). (In earlier work (24), we used a simple isotropic cholesterol-lipid interaction, but the earlier model was not adequate to describe the lipid-cholesterol interaction. To include the MD-observed preference of cholesterol for saturated chain lipid toward its α-face (23), we postulate this new interaction form.) This particular form of the interaction orders lipid chains that are toward the α-face of cholesterol and disorders chains toward the β-face. Fig. 1 illustrates the definition of the angle θ. This choice is the simplest (first two terms in the Fourier expansion of the function of azimuthal angle) way to model the anisotropic interactions we calculate from MD simulations (23). In the following subsection, we describe the procedure used to determine the values of V_lc and Δ. The summation in the second term runs over all nearest-neighbor chol-chain pairs. It turns out that with the anisotropic lipid–cholesterol interaction, the cooperative effect of cholesterols at high concentration and/or lower temperature provides for the required disordering of lipid chains. Such disordering is also proposed by Greenwood et al. (25). The third term corresponds to chol-chol interactions between all pairs of chols in the system.

FIGURE 1.

An illustration of the angle used on the anisotropy term V_lc(r_α,i, θ_α,i) in the Hamiltonian (Eq. 2). The square grid outlines the underlying lattice for the lipid chain order field. Different shades represent different degrees of order, with black representing the highest order. To include chol orientation we assign a “rough” and a “smooth” side to each chol rod. The sidedness translates and rotates as the rod moves through the order field. The angle θ_α,i is defined between the midpoint of the rough side of the chol rod and the grid point i (a grid point is the center of a lattice cell) under consideration.

We point out that this model consists of a continuous field of chain order (with a discrete square lattice for numerical purposes) onto which are placed the rods representing cholesterol. Thus, after the initial model construction, one should associate order with points in the model field rather than individual chains. Cholesterols are then discrete rods that move continuously over the order field. All partition sums are carried out by evaluating the order at the sites on the grid, which for each site depends on the order at neighboring sites and the presence or absence of cholesterol within the near-neighbor distance from the site.

In mean-field theory, the mean field is the average chain-order field at site i due to neighboring lipids and chols (22), given by

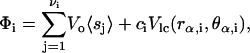(3)

where c_i is the number of neighboring cholesterols at site i, ν_i is the coordination number (ν_i = 4 for the square lattice), and 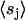denotes the ensemble average of s_j. Under this approximation, we can write the expectation value of order-parameter field at site i as

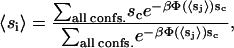(4)

where the summation is over all possible conformations of a single chain. These are self-consistent equations in 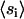. The partition sum in the self-consistent equation was originally performed on a computer-generated library of single-chain rotational isomeric states (22). Instead, we use configurations generated in an MD simulation at 50°C of a large (1600 DPPC) hydrated lipid bilayer for the self-consistent mean-field (SCMF) calculation (24). The reason for this substitution is that MD simulations by several researchers have shown that the simple three-state rotational isomeric model is not a good model for the conformations of lipid chains confined to a bilayer. Due to other attractive contributions to the energy, dihedrals are able to take on values outside the bottoms of the trans and gauche wells. Multiplied down the length of a chain, this can cause a very large difference between chain conformations. Details of the generation of these chain libraries including the order-parameter renormalization procedures are presented in our earlier work (24). In these MD simulations, we observed that even at 50°C many chains have a gauche/trans ratio closer to zero, hence we use the same chain library even at lower temperatures. There were significant numbers of nonzero Boltzman weights at the temperatures below DPPC phase-transition temperature in our simulations with this library.

Parameter determination

To develop this model into a successful multiscale simulation strategy, we determine all the model parameters from atomistic MD simulations. The model parameter V_o was initially estimated by linearly fitting interchain nonbonded interaction energy to the product of corresponding order parameters in MD simulations. For this purpose, the entire chain is used, starting from the first carbon along with the carbonyl oxygen. The linear fit in the procedure has a large uncertainty due to noisy MD data. Still this value of V_o predicts the pure DPPC phase-transition temperature within 15°C of the experimental value. The V_o is further adjusted (V_o = 60 kJ/mol) so that the model, in the absence of chol, reproduces the correct DPPC transition temperature, 41.5°C. In this sense, the model indeed utilizes experimental data to estimate one of its parameters. However, we believe that a much longer and larger simulation may provide a better fit and eliminate the need to tune the parameter V_o. Even without adjustments to V_o the model produces the accurate qualitative behavior, albeit with different phase-transition temperature.

The lipid-cholesterol interaction parameter 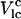(7.5/2π kJ/mol) is determined by linearly fitting the chol-chain interaction energy to the corresponding chain order in MD (24). Since the lipid-chol interaction is short-range, we compute this interaction for the nearest-neighbor pair of chol and chain. The anisotropy factor Δ (1.07 ± 0.05) is obtained using the same method as for V_lc. In this method, we linearly fit chol-chain interaction energy for neighboring chains that are toward the α-face of chol separately from that for chains toward the β-face, where a chain is considered the nearest neighbor to chol if any atom of the chain is within 14 Å of any atom of the chol molecule. We take these values to be approximations for V_lc(1 + Δ) (α-face) and V_lc(1 – Δ) (β-face). The final Δ value is an average of these two Δ values. The fits in these cases are very noisy; however, our trial simulation studies show that the properties of the system are not sensitively dependent on Δ as long as it is of the order of 1. For this calculation, MD simulations of DPPC-chol systems at 323 K are used (17). Pairwise interaction energy between chols in the MD simulation shows a core repulsion and a small attractive part, which is less than k_BT. Hence, V_cc is taken to be a purely repulsive interaction.

Simulation methods

Our lattice-based field of lipid order is constructed as a 100 × 100 lattice of OP values, uniformly randomly initialized, between −1 and 0.5. This corresponds to a bilayer of 5000 lipids or 10,000 chains or a bilayer patch of size ∼3000 nm². Chols are placed uniformly randomly over this field (not necessarily on the lattice points). All the length, time, and energy units of the simulations were expressed in terms of the lattice constant a, 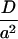, and k_BT, respectively. For a given chol distribution, the order-parameter field is obtained by solving the self-consistent equation (Eq. 4). A simple Jaccobi iteration scheme is used to solve the nonlinear self-consistent equation. The iteration scheme is stable for almost all the temperatures and chol concentrations except at the exact phase-transition temperature in the pure system. The convergence of the method is poor near the transition point in the pure system and in the so-called “coexistence” region in chol mixtures.

After equilibration of the order-parameter field, chol positions and orientations are propagated in time according to Eq. 1. We use the dimensionless time step Δτ ≈ 0.01 typically, and thereby achieve nanosecond real time step sizes for the coarse-grained simulation. For higher chol concentrations, smaller time steps are needed. However, the self-consistent equations converge faster in this case, compensating for the shorter time step. The SCMFT runs were done at multiple temperatures using the same library of chains on a desktop machine. The translational mobility of chol M_r is determined from the chol diffusion constant calculated in our long MD simulations (23), and M_θ, in dimensionless units, is taken to be ∼10–100 times the M_r in dimensionless units. However, we verify that the results of our simulations are insensitive to the value of M_θ.

RESULTS

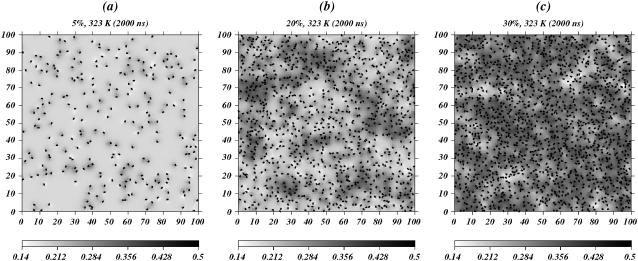
We used the SCMFLD method to simulate DPPC-chol mixtures at chol concentrations of 5%, 10%, 15%, 20%, 25%, 30%, and 35%. Simulations were carried out at temperatures between 293 K and 343 K for each concentration. This range spanned the pure DPPC chain-melting temperature (315 K). Fig. 2 shows snapshots after 2 μs of simulation for two systems. The figures clearly show the localized ordering effect chol has on neighboring lipids. Each chol molecule creates a surrounding region of ordered lipid that is about one near-neighbor shell in size. Similar ordering regions are observed in recent MD simulations by Edholm and Nagle (26). For small chol concentrations, the shells remain randomly distributed across the membrane. As the concentration increases, ordered regions begin to overlap, further increasing the state of lipid order in the system.

FIGURE 2.

Order parameter density snapshots of the DPPC-chol systems at 323 K for (a) 5%, (b) 20%, and (c) 35% concentration of chol. Darker shades of gray locate chains with higher values for the chain order parameter. Small black segments locate the rods that represent chol molecules.

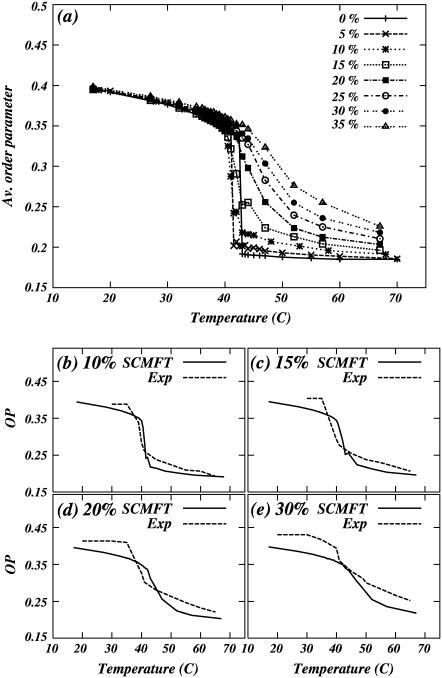
In Fig. 3 a, we plot the average OP as a function of temperature for various chol concentrations. In the absence of chol, the model clearly exhibits a first-order phase transition at 315 K. The OPs at temperatures below and above phase transition are similar to the values expected in gel and liquid crystalline phases of DPPC, respectively. A closer examination of Fig. 3 a reveals that with increasing chol concentration, the phase transition diminishes and completely vanishes for concentrations >15%. At concentrations >25%, the system has uniform order across all the temperatures investigated here, representing the liquid ordered (β) phase. Similar results are reported by the NMR and DSC experiments of Huang et al. (27). Fig. 3, b–e, shows a comparison of average order parameters obtained using our model, and the NMR quadrupolar shift reported by Huang et al. In their study, Huang et al. report the shift for the sixth carbon atoms in DPPC hydrocarbon chains. Since the OP of the sixth atom is on the plateau region of the OP profile, we expect the average OP over the entire chain to be lower than the OP of the sixth atom. As Fig. 3, b–e, shows, this is indeed the case. The model average OPs show remarkable agreement with the NMR data for various temperatures and cholesterol concentrations. Vist and Davis (5) have also used deuterium NMR to study the ordering of DPPC chains as a function of cholesterol concentration. Our data are consistent with this data, presented as a histogram of first moments of the NMR spectra, as well.

FIGURE 3.

(a) Average order parameter as a function of temperature for various chol concentrations. Comparison of the average order parameter in the model with the order parameter of the sixth carbon atom reported by Huang et al. (27) for (b) 10% chol, (c) 15% chol, (d) 20% chol, and (e) 30% chol.

The model is validated further by computing the specific heat as function of temperature. As discussed in our earlier article (24) the order parameter field that defines this model describes a system at fixed pressure, with volume changes implicitly tied to changes in the order field. Hence, the specific heat at constant pressure is calculated by

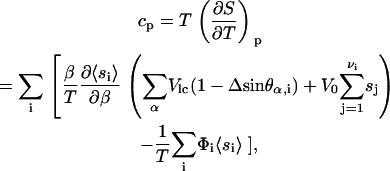where the ∂〈s_i〉/∂β in the expression was obtained by solving the self-consistent equation

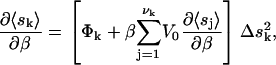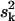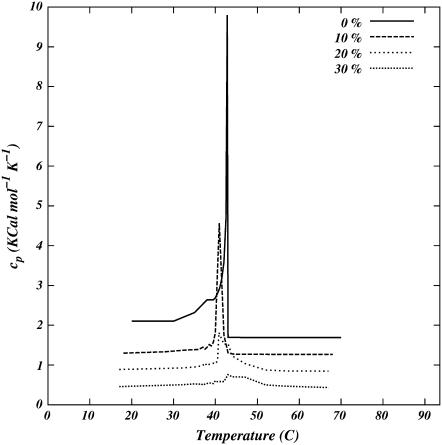
with Δ = 〈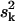〉 − 〈s_k〉², using the generalized minimal residual algorithm (28). Fig. 4 shows specific heat as a function of temperature for systems with 0%, 10%, 20%, and 30% concentration of cholesterol. A comparison with Fig. 5 of Huang et al. (27) shows that the model DSC curves are in good agreement with the experimental DSC curves.

FIGURE 4.

Plots of specific heat as a function of temperature for several cholesterol concentrations.

FIGURE 5.

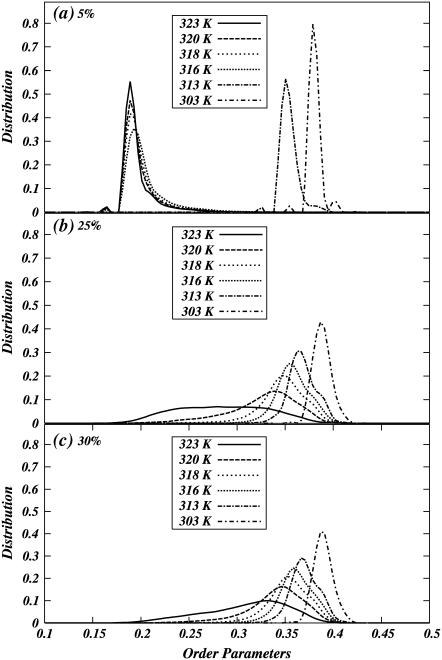
Normalized distribution of the average chain order in the systems for various temperatures and (a) 5%, (b) 25%, and (c) 30% chol concentrations.

The OPs of systems with coexisting regions show a bimodal distribution. We use this property to detect different regions of a “phase diagram” for DPPC-chol mixtures within this model. Fig. 5 shows distributions of OPs at 5%, 25%, and 30% of chol concentration at various temperatures. We note that the distributions show peaks around the OP values corresponding to gel and liquid-crystalline order. For certain values of concentrations and temperatures, these distributions show two peaks indicating coexistence of two “phases,” e.g., at 50 C and 25% chol concentration the system clearly has multiple peaks in OP distribution.

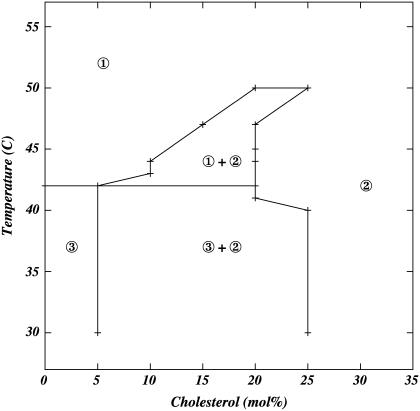
By examining all distributions at various temperatures and chol concentrations, we construct a “phase diagram” (Fig. 6). This figure is in excellent agreement with the phase diagram proposed by Vist and Davis (5). In particular, both model and experiment exhibit two coexisting regions of different chain order at the same cholesterol concentrations and temperatures as the Vist-Davis diagram. Specifically, we observe, at temperatures below 315 K, within the two dimensional field of chain order, separate regions of gel-like order and regions of intermediate order, between gel-like and fluid-like states. This is the same distribution of chain order identified by Vist and Davis as the gel + β region (5). At temperatures >315 K, we see separate regions of intermediate and low levels of fluid-like order, similar to the L_α + β region of Vist and Davis (5). The model could not resolve the three-phase region near the lipid melting temperature and low chol concentration observed by Vist and Davis. The agreement between our model diagram and the Vist-Davis diagram is especially important, since no parameters in the model were set to force it to match the experimental plot. The horizontal line in Fig. 6 separating fluid + intermediate from ordered + intermediate regions is determined from Fig. 3 a, where we notice a perceptible drop in order near the phase-transition temperature for chol concentrations <15%.

FIGURE 6.

Lateral organization of the DPPC-chol bilayer as determined from regions of bimodal distributions of order. Lines are guides to the eye. At a given simulation temperature, data points represent boundaries within which the chain order-parameter distribution is bimodal. Regions are numbered according to the values of the average order at the peak of the respective distribution shown in Fig. 4: , peak ≈ 0.2 (fluid lipid chains); , peak ≈ 0.35 (intermediate, or liquid-ordered chains); , peak ≈ 0.4 (ordered, gel-like chains).

DISCUSSION

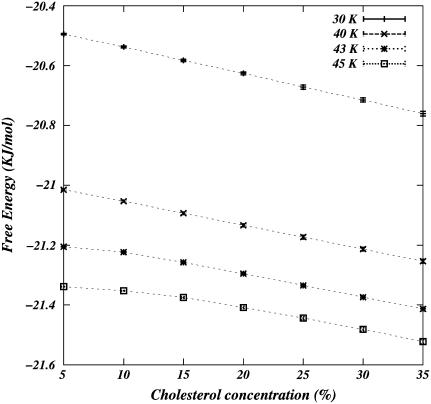
We emphasize that the single peaks in OP distributions are quite broad (Fig. 5 c). That is, even the apparent single-phase regions have mixtures of lipids with a distribution of OP values, and the peak can, in principle, be fitted with many overlapping peaks. Hence, we refrain from using the term “phase” here. A sharp peak in the OP distribution corresponding to a pure phase is seen only in pure DPPC systems. The boundaries in Fig. 6 define regions that are characterized by two nonoverlapping, broad peaks in the OP distributions. Discontinuous phase transitions of first order are identified by discontinuities in the derivative of the relevant free energy. Within the limitations of model and the accuracy of the computations, we do not observe any discontinuity in free energy derivatives (Fig. 7) in concentration. This result is in full accord with the conclusions of McConnell and Radhakrishnan's interpretation of deuterium NMR data for DPPC-chol mixtures (14), namely, that there is no region of two-phase coexistence in the DPPC-chol mixtures at any temperature, i.e., the DPPC-chol mixture is a single thermodynamic phase.

FIGURE 7.

Free energy per chain as a function of chol concentrations for various temperatures.

The results of our calculations can be related to the condensed complex models of McConnell and co-workers (10,11). Condensed complexes consist of sets of p lipid molecules that form a complex with q cholesterol molecules. In the present model, we can interpret regions of ordered lipid that surround cholesterol as a “complex.” At low chol concentration, complexes consist of single chol molecules surrounded by four to six near-neighbor lipid molecules. As the chol concentration increases, the isolated single-chol complexes coalesce into larger complexes, until, at ∼15% chol, the complexes form a percolating network that spans the membrane. In this interpretation, the exact stoichiometry of the complexes varies with the chol concentration.

In comparing our model with the model of Elliot et al. (18), we first note that our model predicts regions of bimodal chain order. The existence of these regions in the temperature-composition plane is consistent with the Vist and Davis diagram. This agreement is not possible without the anisotropic interaction term. Another important difference between our model and that of Elliot et al. (18) is the order of the transitions predicted by the models. The DPPC-chol phase diagram of Elliot et al. (18) consists of boundaries between regions that are separated by first-order phase transitions. In contrast, our model suggests that “changeover” in lipid order as a function of chol concentration is a continuous change, or at most a higher-order phase change. The chol-rich domains in our model do not increase in size as functions of chol concentration. Such an increase would have been consistent with a first-order phase transition. Rather, chol-rich domains increase in number and eventually form a percolating network over the entire system. The regions in the temperature-composition diagram over which a percolating network is observed are regions of bimodal distributions of order, as shown in Figs. 5 and 6. As a function of chol concentration, the system exhibits a smooth change from liquid-crystalline to liquid-ordered phase.

SUMMARY

We have developed an SCMFT based model for lipid-chol mixtures. The model represents lipids as a lattice field of order parameters and chol as hard-core rods with anisotropic interaction with order-parameter field. The coupling constants in the model are derived from atomistic MD simulations of lipid-chol mixtures. The chain conformations in partition sum in the model are taken from atomistic MD simulations.

The predicted average order parameters and the specific heat from the model agree well with the NMR and DSC experiments. Further, based on the bimodality of the order parameters, we identify regions in temperature–composition space that are in good agreement with the coexistence phase regions proposed by Vist and Davis. However, within our model we do not observe any phase transition in lipid order as a function of chol concentration. The ability to replicate thermodynamic quantities with interaction functions derived directly from atomistic simulations suggests that our MD simulations, including force fields, and our mode of inferring the SCMFT parameters from the MD, are essentially correct.

Thus we achieved an enormous effective quantitative increase in compute power. We also achieved a qualitative increase in power in that we could use MD simulations at one temperature to parameterize the SCMFT model at a range of temperatures, with good accuracy. Future applications of this modeling approach include the study of ternary mixtures of raft-like composition, and the use of larger chain libraries in SCMFT calculations. In ongoing work, we have now successfully extended this model to include a composition field for simulation of complex mixtures of “raft” forming lipids. Larger and longer MD simulations on the scale reported by Grossfield et al. (29) have the potential to provide input data to the methods described in this article. This would represent a major step toward simulation of lateral organization of multicomponent membranes of the degree of complexity of biological membranes.