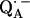Abstract
The geometry of the hydrogen bonds to the two carbonyl oxygens of the semiquinone  in the reaction center (RC) from the photosynthetic purple bacterium Rhodobacter sphaeroides R-26 were determined by fitting a spin Hamiltonian to the data derived from 1H and 2H ENDOR spectroscopies at 35 GHz and 80 K. The experiments were performed on RCs in which the native Fe2+ (high spin) was replaced by diamagnetic Zn2+ to prevent spectral line broadening of the
in the reaction center (RC) from the photosynthetic purple bacterium Rhodobacter sphaeroides R-26 were determined by fitting a spin Hamiltonian to the data derived from 1H and 2H ENDOR spectroscopies at 35 GHz and 80 K. The experiments were performed on RCs in which the native Fe2+ (high spin) was replaced by diamagnetic Zn2+ to prevent spectral line broadening of the  due to magnetic coupling with the iron. The principal components of the hyperfine coupling and nuclear quadrupolar coupling tensors of the hydrogen-bonded protons (deuterons) and their principal directions with respect to the quinone axes were obtained by spectral simulations of ENDOR spectra at different magnetic fields on frozen solutions of deuterated
due to magnetic coupling with the iron. The principal components of the hyperfine coupling and nuclear quadrupolar coupling tensors of the hydrogen-bonded protons (deuterons) and their principal directions with respect to the quinone axes were obtained by spectral simulations of ENDOR spectra at different magnetic fields on frozen solutions of deuterated 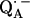 in H2O buffer and protonated
in H2O buffer and protonated 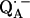 in D2O buffer. Hydrogen-bond lengths were obtained from the nuclear quadrupolar couplings. The two hydrogen bonds were found to be nonequivalent, having different directions and different bond lengths. The H-bond lengths rO⋯H are 1.73 ± 0.03 Å and 1.60 ± 0.04 Å, from the carbonyl oxygens O1 and O4 to the NH group of Ala M260 and the imidazole nitrogen Nδ of His M219, respectively. The asymmetric hydrogen bonds of
in D2O buffer. Hydrogen-bond lengths were obtained from the nuclear quadrupolar couplings. The two hydrogen bonds were found to be nonequivalent, having different directions and different bond lengths. The H-bond lengths rO⋯H are 1.73 ± 0.03 Å and 1.60 ± 0.04 Å, from the carbonyl oxygens O1 and O4 to the NH group of Ala M260 and the imidazole nitrogen Nδ of His M219, respectively. The asymmetric hydrogen bonds of 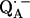 affect the spin density distribution in the quinone radical and its electronic structure. It is proposed that the H-bonds play an important role in defining the physical properties of the primary quinone, which affect the electron transfer processes in the RC.
affect the spin density distribution in the quinone radical and its electronic structure. It is proposed that the H-bonds play an important role in defining the physical properties of the primary quinone, which affect the electron transfer processes in the RC.
INTRODUCTION
Two ubiquinones, QA and QB, are present in the reaction centers (RCs) of photosynthetic purple bacteria and are actively involved in the coupled electron-proton transfer processes that lead to the formation of the proton gradient across the photosynthetic membrane required for ATP synthesis (1). The two quinones have different redox potentials providing the driving force for the vectorial electron transfer (ET) from the primary to the secondary quinone. Since QA and QB are chemically identical molecules, their different properties in the ET chain must result from specific interactions with the protein environment (2–6). One of these interactions is hydrogen bonding between the carbonyl oxygens of the quinones and the RC protein. QA forms two hydrogen bonds to the RC protein (2,3,7). The bonds contribute to the binding and to the unusual chemical properties and function of the quinone. It is, therefore, important to characterize them in detail.
X-ray crystallographic structures of proteins are usually not obtained at high enough resolution to provide direct information on the positions of protons (e.g., the protons hydrogen-bonded to the quinones). Furthermore, specific intermediate states of the reaction cycle (e.g., the semiquinone radical anions 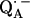 and
and 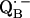 ) are only accessible in exceptional cases by x-ray crystallography (e.g., (3,8)). Consequently, other methods have been used, in particular electron paramagnetic resonance (EPR) and electron nuclear double resonance (ENDOR) spectroscopies, to study semiquinone radicals in bacterial RCs (4–6,9–19). These spectroscopies provide information about the electronic and spatial structure of the transient radicals
) are only accessible in exceptional cases by x-ray crystallography (e.g., (3,8)). Consequently, other methods have been used, in particular electron paramagnetic resonance (EPR) and electron nuclear double resonance (ENDOR) spectroscopies, to study semiquinone radicals in bacterial RCs (4–6,9–19). These spectroscopies provide information about the electronic and spatial structure of the transient radicals 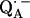 and
and 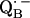 (reviewed in (4–6)).
(reviewed in (4–6)).
In this work we focus on the primary quinone QA, which accepts one electron to form the ubisemiquinone radical anion, 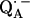 . The experiments were performed on RCs in which the Fe2+ was replaced by Zn2+. However, we expect our results to be valid for native RCs since all spectral and kinetic properties of Zn-RCs are identical to Fe-RCs (20,21). Details on the spin-density distribution of this species have been obtained earlier by EPR and ENDOR spectroscopy (9–18) and showed pronounced shifts of the hyperfine couplings of
. The experiments were performed on RCs in which the Fe2+ was replaced by Zn2+. However, we expect our results to be valid for native RCs since all spectral and kinetic properties of Zn-RCs are identical to Fe-RCs (20,21). Details on the spin-density distribution of this species have been obtained earlier by EPR and ENDOR spectroscopy (9–18) and showed pronounced shifts of the hyperfine couplings of 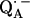 when compared with the free
when compared with the free 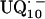 radical anion in organic solvents. This effect has been attributed to asymmetric hydrogen bonding to
radical anion in organic solvents. This effect has been attributed to asymmetric hydrogen bonding to 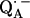 in the RC proteins (9,10). The hydrogen-bonded protons are exchangeable with deuterons (in D2O buffer) and could thus be identified via 1H → 2H exchange experiments in the spectra.
in the RC proteins (9,10). The hydrogen-bonded protons are exchangeable with deuterons (in D2O buffer) and could thus be identified via 1H → 2H exchange experiments in the spectra.
In a previous article (19), the ENDOR lines belonging to the exchangeable protons have been assigned to two protons hydrogen-bonded to the two carbonyl oxygens of 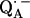 . In this work, we used 1H- and 2H-ENDOR spectroscopies to determine the geometry of the two hydrogen bonds. The ENDOR experiments were performed at 80 K and at a microwave frequency of 35 GHz (Q-band), which provides improved spectral resolution compared to the commonly used frequency of 9 GHz (X-band). This enabled us to select molecules with particular sets of orientations with respect to the magnetic field (22). Since the 1H and 2H ENDOR spectra occur in different, nonoverlapping, frequency regions of the spectrum, we were able to simplify the ENDOR spectra (i.e., focus on the H-bonds) by using deuterated RCs in H2O buffer and protonated RCs in D2O buffer. Furthermore, the different 1H → 2H exchange rates of the two protons enabled us to preferentially deuterate (or protonate) one of the two carbonyl oxygens as described in (19). A standard spin Hamiltonian was fitted to the ENDOR spectra obtained at different magnetic field positions using the EasySpin package developed by Stoll and Schweiger (23). The fit yielded the principal components of the 1H and 2H hyperfine coupling (hfc) and the 2H nuclear quadrupolar coupling (nqc) tensors and their principal directions with respect to the g-tensor axes of
. In this work, we used 1H- and 2H-ENDOR spectroscopies to determine the geometry of the two hydrogen bonds. The ENDOR experiments were performed at 80 K and at a microwave frequency of 35 GHz (Q-band), which provides improved spectral resolution compared to the commonly used frequency of 9 GHz (X-band). This enabled us to select molecules with particular sets of orientations with respect to the magnetic field (22). Since the 1H and 2H ENDOR spectra occur in different, nonoverlapping, frequency regions of the spectrum, we were able to simplify the ENDOR spectra (i.e., focus on the H-bonds) by using deuterated RCs in H2O buffer and protonated RCs in D2O buffer. Furthermore, the different 1H → 2H exchange rates of the two protons enabled us to preferentially deuterate (or protonate) one of the two carbonyl oxygens as described in (19). A standard spin Hamiltonian was fitted to the ENDOR spectra obtained at different magnetic field positions using the EasySpin package developed by Stoll and Schweiger (23). The fit yielded the principal components of the 1H and 2H hyperfine coupling (hfc) and the 2H nuclear quadrupolar coupling (nqc) tensors and their principal directions with respect to the g-tensor axes of 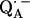 , which are related to the molecular axes of the quinone (13). The hydrogen-bond lengths were obtained from the 2H nuclear quadrupolar couplings using the empirical relations of Soda and Chiba (24) and of Hunt and Mackay (25). By these procedures, the geometries of both hydrogen bonds were completely characterized.
, which are related to the molecular axes of the quinone (13). The hydrogen-bond lengths were obtained from the 2H nuclear quadrupolar couplings using the empirical relations of Soda and Chiba (24) and of Hunt and Mackay (25). By these procedures, the geometries of both hydrogen bonds were completely characterized.
THEORY
Spin Hamiltonian and its relation to the structure
We focus on the interaction between the magnetic moment of the unpaired electron of 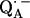 and the magnetic moments of protons or deuterons that form hydrogen bonds to the quinone oxygens O1 and O4 (see Fig. 1). The observed ENDOR spectra were interpreted using a spin Hamiltonian, ℋ, containing the electron and nuclear Zeeman interactions with the applied magnetic field Bo, the hfc, and the nqc terms (e.g., (26)):
and the magnetic moments of protons or deuterons that form hydrogen bonds to the quinone oxygens O1 and O4 (see Fig. 1). The observed ENDOR spectra were interpreted using a spin Hamiltonian, ℋ, containing the electron and nuclear Zeeman interactions with the applied magnetic field Bo, the hfc, and the nqc terms (e.g., (26)):
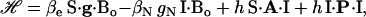 |
(1) |
where S is the electron spin operator, I is the nuclear spin operator of protons or deuterons in H-bonds to the carbonyl oxygens; A and P are the hfc and nqc tensors in frequency units, g is the electronic g-tensor, gN is the g-factor of the corresponding magnetic nucleus (proton or deuteron) and βe and βN are the electron and nuclear magnetons, respectively, and h is Planck's constant. The first term in Eq. 1 represents the electronic Zeeman term that gives rise to the observed EPR spectra. The other three terms represent nuclear interactions, which are small and not resolved in the EPR spectrum but give rise to the ENDOR spectra. The hyperfine tensor component Ai is composed of anisotropic (dipolar) and isotropic contributions that can be written as
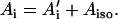 |
(2) |
FIGURE 1.
Structure in the vicinity of QA in the RC of Rb. sphaeroides (Brookhaven data bank entry 1AIG (3)) with the H-bonds (a), or the D-bonds (b) to the two carbonyl oxygens, O1 and O4. The principal axes of the g-tensor are along the molecular axes x, y, z (a). The principal axes of the hfc tensors of the protons in H-bonds are along the axes x′, y′, z′ (for simplicity x′ and y′ are not shown, they lie in the plane perpendicular to z′), and are related to the g-tensor axes by the Euler angles φ and θ (31) (a). The proton in the hydrogen bond is characterized by the bond-length r and the angles θ and φ (a). The principal axes of the nqc tensor are along x″, y″, z″ (for simplicity x″ and y″ are not shown, they lie in the plane perpendicular to z″), and are related to the g-tensor axes by the Euler angles α, β and γ (31) (for simplicity γ is not shown) (b).
For a proton in a typical hydrogen bond, the isotropic part Aiso is small compared to the anisotropic term A′i, which arises from the dipolar interaction between the unpaired electron and the proton. In the simple point-dipole approximation (e.g., (26)) the anisotropic term can be written as
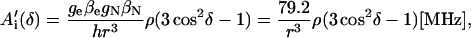 |
(3) |
where ge and gN are the electron and proton g-values, ρ is the unpaired electron spin density at the quinone oxygen, δ is the angle between the applied magnetic field and the direction of the hydrogen bond, and r is the H-bond length in Å (for deuterons the numerical factor 79.2 is replaced by 12.16). The traceless tensor resulting from this approximation is axially symmetric, with principal components A′‖ for δ = 0° (direction along the hydrogen bond) and A′⊥ for δ = 90°, with A′‖ = −2 A′⊥. The point-dipole model for the hyperfine interaction of H-bonds (see Eq. 3) has been shown to be valid in good approximation for quinone model compounds (27,28), in which the H-bonds lie in the quinone plane. In RCs, this is not the case leading to the difficulties discussed in the section on the H-bond lengths.
For nuclei with I ≥ 1, the nuclear quadrupolar interaction is described by a traceless tensor with principal components Pi (i = 1,2,3) with |P1| ≥ |P2| ≥ |P3|. It has been shown (24,29,30) that the largest component P1 is approximately along the direction of the H-bond, P2 is parallel to the normal of the plane of the hydrogen-bond donor molecule, and P3 is perpendicular to the directions of P1 and P2. The principal values Pi can be obtained from single crystal or, as has been done in this work, from orientationally selected ENDOR spectra. It is customary to describe the nqc tensor by the nuclear quadrupole coupling e2qQ/h (in frequency units) and an asymmetry parameter η (e.g., (26)) as
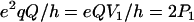 |
(4) |
and
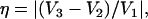 |
(5) |
where Q is the scalar nuclear quadrupole moment (Q2H = +2.74 × 10−27 cm2), e the electronic charge, the Vi values are the principal values of the electric field gradient tensor Vij = ∂2V/(∂xi∂xj), where xi and xj are the nuclear coordinates and V is the electrostatic potential. The parameter η describes the deviation from axial symmetry of the quadrupolar tensor, i.e., of the electric field gradient. The field gradient Vij is related to the distribution of electrical charges around the nucleus and thus to the specific bonding geometry. Its value can, therefore, be used to obtain information on the hydrogen bonds (24,25,27–30).
Molecular structure and axis system
Since the hfc and nqc tensor axes are not collinear with the g-tensor axes of the semiquinone (27,28), we describe these tensors by their principal components and the Euler angles (31) relating their principal axes to the g-tensor axes (see Fig. 1). Furthermore, the hfc tensor of the H-bond is expected to have nearly axial symmetry (27,28). Therefore, its axes with respect to the g-tensor axes can be determined by only the two Euler angles defining the axial direction, which corresponds to the largest component of the hfc tensor (see Eq. 3).
In this work, we used samples frozen at 80 K containing randomly oriented molecules. ENDOR spectra were obtained at different magnetic fields within the EPR spectrum, along which molecules with a particular set of directions were selected (22,31–33). The orientation selection is produced by the anisotropy of the electronic g-tensor. The global analysis by computer simulations of the ENDOR spectra (e.g., (32,33)), using the spin Hamiltonian of Eq. 1, yielded both the principal components of the hyperfine and quadrupolar coupling tensors, and their orientation (i.e., Euler angles) with respect to the principal axes x, y, z of the g-tensor of  , whose orientation with respect to the molecular axes is known from EPR experiments performed in single crystals of RCs (13) (see Fig. 1).
, whose orientation with respect to the molecular axes is known from EPR experiments performed in single crystals of RCs (13) (see Fig. 1).
The 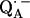 molecule with two H- or D-bonds from the carbonyl oxygens to the imidazole nitrogen of His (M219) (Nδ−H…O4) and to the NH group of Ala (M260) (N−H…O1) are shown in Fig. 1, a and b, respectively. The principal axes of the g-tensor are parallel to the molecular axes x, y, z, with the z-axis perpendicular to the π-plane (13). The principal axes of the hfc tensor of the hydrogen bonds H or D are denoted by x′, y′, z′ (for simplicity x′ and y′ are omitted in Fig. 1 a) and those of the nqc tensor by x″, y″, z″ (for simplicity x″ and y″ are omitted in Fig. 1 b), with z′ and z″ (axes defined by the two first Euler rotations) corresponding to the largest components of the hfc and nqc tensors, respectively. Fig. 1, a and b, also show the Euler angles (φ, θ) and (α, β) relating the x′, y′, z′ and x″, y″, z″ axes to the g-tensor axes (31) (for simplicity γ is omitted). Note that for the hfc tensor, only two Euler angles are needed. Our goal is to determine the geometry of the H-bonds (i.e., r, θ, and φ) from the values of the principal components of the hfc and nqc tensors and their respective Euler angles.
molecule with two H- or D-bonds from the carbonyl oxygens to the imidazole nitrogen of His (M219) (Nδ−H…O4) and to the NH group of Ala (M260) (N−H…O1) are shown in Fig. 1, a and b, respectively. The principal axes of the g-tensor are parallel to the molecular axes x, y, z, with the z-axis perpendicular to the π-plane (13). The principal axes of the hfc tensor of the hydrogen bonds H or D are denoted by x′, y′, z′ (for simplicity x′ and y′ are omitted in Fig. 1 a) and those of the nqc tensor by x″, y″, z″ (for simplicity x″ and y″ are omitted in Fig. 1 b), with z′ and z″ (axes defined by the two first Euler rotations) corresponding to the largest components of the hfc and nqc tensors, respectively. Fig. 1, a and b, also show the Euler angles (φ, θ) and (α, β) relating the x′, y′, z′ and x″, y″, z″ axes to the g-tensor axes (31) (for simplicity γ is omitted). Note that for the hfc tensor, only two Euler angles are needed. Our goal is to determine the geometry of the H-bonds (i.e., r, θ, and φ) from the values of the principal components of the hfc and nqc tensors and their respective Euler angles.
MATERIALS AND METHODS
Sample preparation and nomenclature
The preparation and deuteration of the reaction centers, the proton-deuterium exchange, and the generation of the semiquinone radical anion have been described in a previous article (19). The paramagnetic nonheme Fe2+ was chemically removed and replaced with diamagnetic Zn2+ to reduce the EPR line width of the semiquinone, following the procedure of Utschig et al. (21). The ratio of Zn/RC was determined by atomic absorption spectroscopy and Q-band EPR spectroscopy to be ≥0.90. Since we used several combinations of protonated and deuterated RCs and buffer, we define the following notation: p for
for 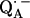 in fully protonated RCs, d
in fully protonated RCs, d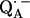 for
for 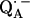 in fully deuterated RCs, and H2O for fully protonated and D2O for fully deuterated buffer.
in fully deuterated RCs, and H2O for fully protonated and D2O for fully deuterated buffer.
EPR and ENDOR instrumentation
EPR and ENDOR measurements were performed at 35 GHz (Q-band) and 80 K. The Q-band spectrometer has been previously described (19). ENDOR experiments were performed with the EPR spectra 50% saturated. ENDOR spectra were recorded for different settings of the magnetic field within the EPR spectrum (12 positions for protons and 11 positions for deuterons), using frequency modulation (FM) of ±140 kHz for protons and ±30 kHz for deuterons. The output of the RF amplifier (ENI 3100L) feeding the ENDOR coils was 50 W for protons and 25 W for deuterons. To improve the signal-to-noise ratio many ENDOR traces were averaged.
RESULTS AND DISCUSSION
EPR experiments
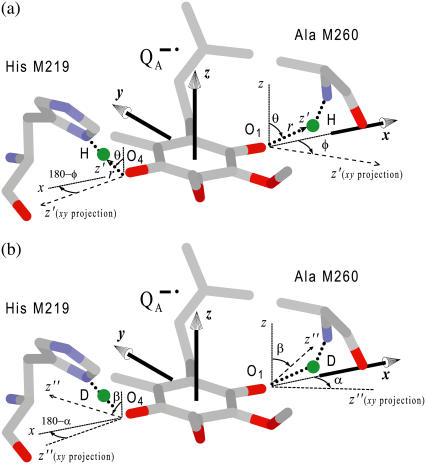
The Q-band EPR spectrum of 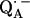 at T = 80 K in deuterated RCs and protonated buffer (
at T = 80 K in deuterated RCs and protonated buffer (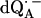 in H2O) is shown as a solid line in Fig. 2 a and the spectrum in protonated RCs and deuterated buffer (
in H2O) is shown as a solid line in Fig. 2 a and the spectrum in protonated RCs and deuterated buffer (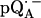 in D2O) in Fig. 2 b. For
in D2O) in Fig. 2 b. For 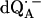 in H2O (Fig. 2 a), the broadening of the spectrum is mainly due to hyperfine interactions of protons in solution (exchangeable protons), including the H-bonds to the carbonyl oxygens. For
in H2O (Fig. 2 a), the broadening of the spectrum is mainly due to hyperfine interactions of protons in solution (exchangeable protons), including the H-bonds to the carbonyl oxygens. For 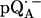 in D2O (Fig. 2 b), the broadening is mainly due to the hyperfine interactions of quinone protons (methyl, methoxy, and methylene protons) and those associated with the protein in the vicinity of the binding site. To obtain molecular orientation selection, ENDOR spectra were recorded at the magnetic field positions indicated by arrows in Fig. 2, a and b (magnetic field positions corresponding to the principal directions of the g-tensor are also given in Fig. 2 a).
in D2O (Fig. 2 b), the broadening is mainly due to the hyperfine interactions of quinone protons (methyl, methoxy, and methylene protons) and those associated with the protein in the vicinity of the binding site. To obtain molecular orientation selection, ENDOR spectra were recorded at the magnetic field positions indicated by arrows in Fig. 2, a and b (magnetic field positions corresponding to the principal directions of the g-tensor are also given in Fig. 2 a).
FIGURE 2.
EPR powder spectra of 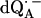 in H2O (solid lines) (a) and
in H2O (solid lines) (a) and 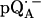 in D2O (solid lines) (b). ENDOR spectra were taken at the field positions indicated by arrows. The inset shows the principal axes of the g-tensor of the ubisemiquinone. The simulated spectra are shown by dashed lines. The line-width values of ΔBx, ΔBy, and ΔBz obtained from the simulation are 0.45 mT, 0.34 mT, and 0.16 mT, respectively, for
in D2O (solid lines) (b). ENDOR spectra were taken at the field positions indicated by arrows. The inset shows the principal axes of the g-tensor of the ubisemiquinone. The simulated spectra are shown by dashed lines. The line-width values of ΔBx, ΔBy, and ΔBz obtained from the simulation are 0.45 mT, 0.34 mT, and 0.16 mT, respectively, for 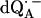 in H2O (a) and 0.47 mT, 0.64 mT, and 0.47 mT, respectively, for
in H2O (a) and 0.47 mT, 0.64 mT, and 0.47 mT, respectively, for 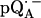 in D2O (b). Experimental conditions: T = 80 K, microwave (MW) frequency = 35.03 GHz, MW power = 1 × 10−7 W (a) and 3 × 10−7 W (b); field modulation = 0.15 mT peak-to-peak at 270 Hz, average of nine scans (a) and of four scans (b), 20 s per scan.
in D2O (b). Experimental conditions: T = 80 K, microwave (MW) frequency = 35.03 GHz, MW power = 1 × 10−7 W (a) and 3 × 10−7 W (b); field modulation = 0.15 mT peak-to-peak at 270 Hz, average of nine scans (a) and of four scans (b), 20 s per scan.
ENDOR experiments
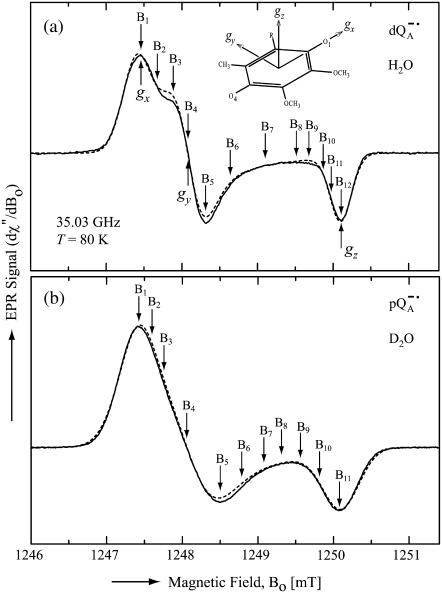
Fig. 3 shows the experimental Q-band 1H ENDOR spectra (solid lines) of 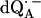 in H2O, arising from the two 1H-bonds (at frequencies <51.5 MHz and >55.0 MHz) and from exchangeable protons belonging to other residues in the neighborhood of
in H2O, arising from the two 1H-bonds (at frequencies <51.5 MHz and >55.0 MHz) and from exchangeable protons belonging to other residues in the neighborhood of 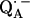 (in the frequency region between 51.5 MHz and 55.0 MHz). At the magnetic field positions from B1 (gx) to B6 (Fig. 3) the spectra correspond to a two-dimensional powder-type spectrum with weighted contributions mainly from molecules that have the magnetic field pointing in the plane of the quinone (referred to as in-plane directions). Therefore, a powder spectrum with two sharp features, corresponding approximately to the Ax′ and Ay′ components of the hfc tensor is observed for each H-bond. The lines associated with the H-bonds are labeled L1, L2, and L3 in Fig. 3, B4 (gy). The splittings observed at gy are similar to those previously observed at X-band (6). These ENDOR lines were recently identified by selectively deuterating one of the H-bonds to the quinone (19). It was shown that the peaks L1 and L2 are associated with two different protons and that the peak L3 is an overlap of two lines, one being a partner of L1 and the other of L2.
(in the frequency region between 51.5 MHz and 55.0 MHz). At the magnetic field positions from B1 (gx) to B6 (Fig. 3) the spectra correspond to a two-dimensional powder-type spectrum with weighted contributions mainly from molecules that have the magnetic field pointing in the plane of the quinone (referred to as in-plane directions). Therefore, a powder spectrum with two sharp features, corresponding approximately to the Ax′ and Ay′ components of the hfc tensor is observed for each H-bond. The lines associated with the H-bonds are labeled L1, L2, and L3 in Fig. 3, B4 (gy). The splittings observed at gy are similar to those previously observed at X-band (6). These ENDOR lines were recently identified by selectively deuterating one of the H-bonds to the quinone (19). It was shown that the peaks L1 and L2 are associated with two different protons and that the peak L3 is an overlap of two lines, one being a partner of L1 and the other of L2.
FIGURE 3.
Experimental (solid lines) and simulated (dotted lines) 1H ENDOR spectra of 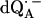 in H2O, at 35 GHz, at 12 different magnetic field positions of the EPR spectrum (see arrows in Fig. 2 a). In the fitting of the spin Hamiltonian to the data the frequency range between 51.5 MHz and 55.0 MHz was excluded. The H-bond ENDOR lines L1, L2, L3 are labeled in (B4). The hfc splitting Az is shown by an arrow in (B12). Experimental conditions: T = 80 K, MW power = 3 × 10−6 W, and frequency modulation (FM) = ±140 kHz at a rate of 947 Hz. Number of scans per position: 600. Scan time: 4 s.
in H2O, at 35 GHz, at 12 different magnetic field positions of the EPR spectrum (see arrows in Fig. 2 a). In the fitting of the spin Hamiltonian to the data the frequency range between 51.5 MHz and 55.0 MHz was excluded. The H-bond ENDOR lines L1, L2, L3 are labeled in (B4). The hfc splitting Az is shown by an arrow in (B12). Experimental conditions: T = 80 K, MW power = 3 × 10−6 W, and frequency modulation (FM) = ±140 kHz at a rate of 947 Hz. Number of scans per position: 600. Scan time: 4 s.
At higher magnetic field positions (Fig. 3, B7–B12), the ENDOR spectra arise mainly from the weighted contributions from molecules that have the magnetic field pointing out of the plane of the quinone (referred to as out-plane directions), and contain one sharp feature for each H-bond tensor. The lines corresponding to the 1H-bonds are centered around the 1H Larmor frequency (53.3 MHz at B12) and are split by their respective Az values (Fig. 3, B12). At B12 (gz) (Fig. 3) the lines corresponding to the two H-bonds overlap.
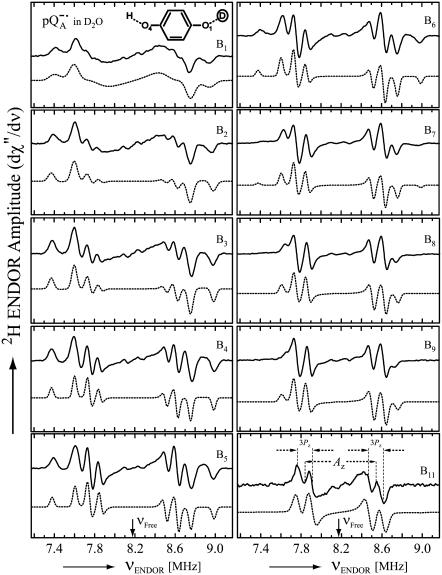
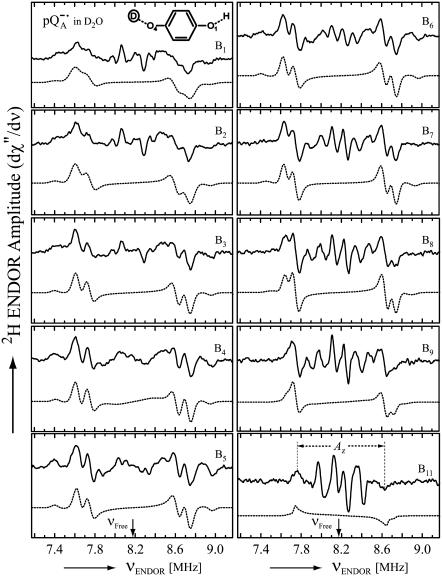
Fig. 4 shows the 2H ENDOR spectra (solid lines) of 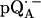 observed after preparing the RCs in H2O and incubating them for 50 min in D2O. Under these conditions, the hydrogen bond to O1 (see Fig. 1) is preferentially deuterated, as described in Flores et al. (19). Thus, the observed lines arise from the D-bond to O1 (see inset in Fig. 4) and from other exchangeable deuterons (see also Fig. 5). At the magnetic field positions from B1 to B9 (see arrows in Fig. 2 b), a two-dimensional powder-type spectrum, analogous to Fig. 3, is obtained. At B11 a single-crystal like spectrum with two doublets centered around the 2H Larmor frequency (8.18 MHz) is observed. The splitting of the doublets is given approximately by the quadrupolar interaction 3Pz; the splitting between the centers of the doublets is ∼Az.
observed after preparing the RCs in H2O and incubating them for 50 min in D2O. Under these conditions, the hydrogen bond to O1 (see Fig. 1) is preferentially deuterated, as described in Flores et al. (19). Thus, the observed lines arise from the D-bond to O1 (see inset in Fig. 4) and from other exchangeable deuterons (see also Fig. 5). At the magnetic field positions from B1 to B9 (see arrows in Fig. 2 b), a two-dimensional powder-type spectrum, analogous to Fig. 3, is obtained. At B11 a single-crystal like spectrum with two doublets centered around the 2H Larmor frequency (8.18 MHz) is observed. The splitting of the doublets is given approximately by the quadrupolar interaction 3Pz; the splitting between the centers of the doublets is ∼Az.
FIGURE 4.
Experimental (solid lines) and simulated (dotted lines) 2H ENDOR spectra of 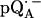 at 35 GHz in RCs prepared in H2O and incubated for 50 min in D2O (see (19)), at 10 different magnetic field positions of the EPR spectrum (see arrows in Fig. 2 b). Inset shows the preferential deuteration of the bond to O1. The quadrupolar splittings 3Pz and hyperfine splitting Az are shown by arrows in the single-crystal-type spectrum at position B11. Experimental conditions: T = 80 K, MW power = ∼5 × 10−6 W, and FM = ±30 kHz at a rate of 985 Hz. Number of scans per position: 45,000. Scan time: 4 s.
at 35 GHz in RCs prepared in H2O and incubated for 50 min in D2O (see (19)), at 10 different magnetic field positions of the EPR spectrum (see arrows in Fig. 2 b). Inset shows the preferential deuteration of the bond to O1. The quadrupolar splittings 3Pz and hyperfine splitting Az are shown by arrows in the single-crystal-type spectrum at position B11. Experimental conditions: T = 80 K, MW power = ∼5 × 10−6 W, and FM = ±30 kHz at a rate of 985 Hz. Number of scans per position: 45,000. Scan time: 4 s.
FIGURE 5.
Experimental (solid lines) and simulated (dotted lines) 2H ENDOR spectra of 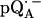 at 35 GHz in RCs prepared in D2O and incubated for 190 min in H2O (see (19)), at 10 different magnetic field positions of the EPR spectrum (see arrows in Fig. 2 b). Inset shows the preferential deuteration of the bond to O4. The hyperfine splitting Az is shown by an arrow in the single-crystal-type spectrum at position B11. Experimental conditions: T = 80 K, MW power = ∼5 × 10−6 W, FM = ±30 kHz at a rate of 985 Hz. Number of scans per position: 70,000. Scan time: 4 s.
at 35 GHz in RCs prepared in D2O and incubated for 190 min in H2O (see (19)), at 10 different magnetic field positions of the EPR spectrum (see arrows in Fig. 2 b). Inset shows the preferential deuteration of the bond to O4. The hyperfine splitting Az is shown by an arrow in the single-crystal-type spectrum at position B11. Experimental conditions: T = 80 K, MW power = ∼5 × 10−6 W, FM = ±30 kHz at a rate of 985 Hz. Number of scans per position: 70,000. Scan time: 4 s.
Fig. 5 shows the 2H ENDOR spectra (solid lines) of 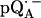 observed after preparing the RCs in D2O and incubating them for 190 min in H2O. Under these conditions, the hydrogen bond to O4 (see Fig. 1) is preferentially deuterated (19) (see inset in Fig. 5). 2H ENDOR lines observed at frequencies <7.8 MHz and >8.5 MHz correspond to the D-bond to O4. 2H ENDOR lines observed in the region between 7.8 MHz and 8.5 MHz correspond to exchangeable deuterons from residues in the neighborhood of
observed after preparing the RCs in D2O and incubating them for 190 min in H2O. Under these conditions, the hydrogen bond to O4 (see Fig. 1) is preferentially deuterated (19) (see inset in Fig. 5). 2H ENDOR lines observed at frequencies <7.8 MHz and >8.5 MHz correspond to the D-bond to O4. 2H ENDOR lines observed in the region between 7.8 MHz and 8.5 MHz correspond to exchangeable deuterons from residues in the neighborhood of 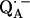 (e.g., Trp M252 and Thr M222). The lines corresponding to the D-bond to O4 show a two-dimensional powder pattern from B1 to B9 (Fig. 5) as in Fig. 4. At B11 (gz) the nqc splitting becomes small and only the hfc splitting is observed.
(e.g., Trp M252 and Thr M222). The lines corresponding to the D-bond to O4 show a two-dimensional powder pattern from B1 to B9 (Fig. 5) as in Fig. 4. At B11 (gz) the nqc splitting becomes small and only the hfc splitting is observed.
Analysis of the data
Numerical fitting procedures
To compare experimental and simulated EPR and ENDOR spectra, we divided the spectra into N intervals, i.e., we treated the spectrum as an N-dimensional vector R. Each component Rj has the amplitude of the signal at a frequency νj, with j varying from 1 to N. The amplitudes of the experimental and simulated spectra were normalized so that the span between the maximum and minimum values of Rj is 1. We compared the calculated amplitudes 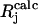 of the signal with the observed values Rj defining a root mean-square deviation σ by
of the signal with the observed values Rj defining a root mean-square deviation σ by
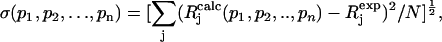 |
(6) |
where the sums are over the N values of j, and p-values are the fitting parameters that produced the calculated spectrum. For the simulation of the EPR spectra N = 1024 and of the ENDOR spectra N = 667.
The EPR spectra were fitted with the program SAFIT, which we had developed earlier for randomly oriented radicals (powder samples) (34). The program is based on the simulated annealing method (35) and uses a Monte Carlo type iteration to minimize the root mean-square deviation, σ (see Eq. 6), between measured and simulated spectra. We searched for the optimum values of the parameters gx, gy, and gz and the line-widths ΔBx, ΔBy, and ΔBz..
For the ENDOR spectra, we defined a global root mean-square deviation σG by
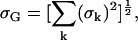 |
(7) |
where σk is the root mean-square deviation (given by Eq. 6) corresponding to the ENDOR spectrum at the magnetic field position Bk. For the 1H ENDOR spectra k = 1,…,12 and for 2H ENDOR spectra k = 1,…,11.
The ENDOR spectra were simulated using EasySpin, a computational package developed by Stoll and Schweiger (23) and based on Matlab (The MathWorks, Natick, MA). EasySpin calculates ENDOR frequencies using the energies of the states of the spin system obtained by direct diagonalization of the spin Hamiltonian (see Eq. 1). Two sets of parameters were used in the simulations. The first set includes the EPR parameters, i.e., the microwave frequency, g-factors (obtained from the fitting of the EPR line) and magnetic field position. These parameters remained fixed in the ENDOR simulations. The second set consists of the following fitting parameters: the principal values and Euler angles of the hyperfine interaction (Ax′, Ay′, Az′, φ, θ) and nuclear quadrupolar (Px″, Py″, −Px″ − Py″, α, β, γ) tensors, the excitation width (Δwk) (i.e., the EPR line-width at the magnetic field position of the ENDOR measurement), and the ENDOR line-width (Δνk). These parameters were varied iteratively, one at a time, to simultaneously optimize the fit of the ENDOR spectra at different positions of the EPR spectrum by minimizing the value of σG (Eq. 7, global fitting). Typical values of σG were between 3% and 8%, with the lowest values corresponding to the 1H ENDOR spectra. The process was terminated when no further changes in the values of the fitting parameters were observed. This required typically between 6 and 10 iterations over the full set of fitting parameters.
1H ENDOR spectra corresponding to each H-bond were not obtained separately, due to the short 1H → 2H exchange time of the H-bond to Ala (M260) in deuterated RCs (see Fig. 4 a in reference 19). Preparing a high concentration sample takes at least 25 min (see (19), Materials and Methods). Therefore, we fitted the 1H ENDOR spectra that contain the lines associated with the two H-bonds (see Fig. 3). Thus, two spectra were calculated simultaneously, one corresponding to N−H…O1 (Ala M260) and the other one corresponding to Nδ−H…O4 (His M219) taking into account the overlap observed at L3. Consequently, σ and σG were calculated for the sum of these two spectra. Because of the interfering 1H ENDOR lines from other exchangeable protons, the region of the spectrum between 51.5 MHz and 55.0 MHz was excluded from the calculation of σ and σG. However, the 2H ENDOR spectra corresponding to each D-bond, i.e., N−D…O1 (Ala M260, see Fig. 4) or Nδ−D…O4 (His M219, see Fig. 5), were obtained separately due to the longer 1H → 2H exchange times observed in protonated RCs (see Fig. 4 b in reference 19). Therefore, the 2H ENDOR spectra of each D-bond were fitted independently. To avoid interfering 2H ENDOR lines from other exchangeable deuterons, the region between 7.8 MHz and 8.5 MHz was excluded from the simulation of the spectra corresponding to Nδ−D…O4 (see Fig. 5).
Spin Hamiltonian parameters obtained from the fit of the spectra
The fit of the EPR spectra is shown by dotted lines in Fig. 2. The values of gx, gy, and gz were obtained from the fitting and are summarized in Table 1. These values are in agreement with those reported previously (13,36). The principal axes of the g-tensor are along the quinone axes xyz (13) (see inset in Fig. 2), providing a convenient reference system for describing the geometry of the hydrogen bonds (see Fig. 1). The values of ΔBx, ΔBy, and ΔBz obtained from the fitting are given in the caption of Fig. 2. However, these values are not used in the simulation of the ENDOR spectra (see previous section).
TABLE 1.
Parameters used in the fittings of ENDOR spectra of 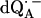 in H2O and
in H2O and 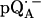 in D2O at 35 GHz and T = 80 K
in D2O at 35 GHz and T = 80 K
| Direction | x | y | z |
|---|---|---|---|
| g-value (±0.0001) | 2.0065 | 2.0053 | 2.0021 |
| Hyperfine components (Ai) | Ax′ [MHz] | Ay′ [MHz] | Az′ [MHz] |
| N−H…O1 (Ala M260) | −4.54 ± 0.02 | −4.93 ± 0.02 | +8.95 ± 0.07 |
| N−D…O1 (Ala M260) | −0.70 ± 0.01 | −0.76 ± 0.01 | +1.37 ± 0.02 |
| Nδ−H…O4 (His M219) | −6.49 ± 0.03 | −6.51 ± 0.02 | +9.15 ± 0.10 |
| Nδ−D…O4 (His M219) | −0.98 ± 0.01 | −1.00 ± 0.01 | +1.36 ± 0.03 |
| Euler angles (between A and g) [deg] | φ | θ | |
| N−H…O1 (Ala M260) | −16 ± 8 | 63 ± 2 | |
| N−D…O1 (Ala M260) | −14 ± 8 | 68 ± 3 | |
| Nδ−H…O4 (His M219) | −167 ± 2 | 50 ± 2 | |
| Nδ−D…O4 (His M219) | −160 ± 6 | 54 ± 2 | |
| Quadrupolar components (2Pi) | 2Px″ [kHz] | 2Py″ [kHz] | 2Pz″ [kHz] |
| N−D…O1 (Ala M260) | −140 ± 10 | −62 ± 6 | +202 ± 6 |
| Nδ−D…O4 (His M219) | −82 ± 6 | −86 ± 8 | +168 ± 10 |
| Euler angles (between P and g) [deg] | α | β | γ |
| N−D…O1 (Ala M260) | −17 ± 10 | 47 ± 3 | 10 ± 10 |
| Nδ−D…O4 (His M219) | −175 ± 8 | 37 ± 3 | −* |
The nqc tensor corresponding to Nδ−D…O4 has axial symmetry, so its axes with respect to the g-tensor are determined by only two Euler angles (α and β).
The principal components of the hfc tensor A and the Euler angles, φ (in-plane angle) and θ (azimuthal angle), associated with rotations of the principal axes x′y′z′ with respect to the g-tensor axes xyz (see Fig. 1 a), were obtained from the global fitting of the 1H ENDOR spectra of 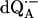 in H2O (see Fig. 3). As explained before, only two Euler angles are relevant as a consequence of the nearly axial symmetry of the hfc tensor (the deviation from axial symmetry is ∼8% for N−H…O1 and ∼0.3% for Nδ−H…O4; see Table 1). They determine the direction of z′ with respect to the xyz axes. The values obtained at the minimum σG are summarized in Table 1. The hfc values are in agreement with earlier, less accurate, 1H ENDOR experiments (6,10). The signs of the 1H hfc values were deduced from theoretical considerations assuming that the largest anisotropic tensor component is positive, which also follows from the dipolar model and is in agreement with molecular orbital calculations (28,37). Since we are working with samples containing randomly oriented molecules, multiple (eight) solutions were obtained for the orientation (φ and θ) of the hfc tensor. Fig. 1 a shows one of the eight possible solutions for each H-bond. The other solutions are those obtained by reflections on the planes xy, yz, and zx. EPR and ENDOR cannot, in principle, distinguish between these solutions. To select the correct solution for the orientations of the hfc and nqc tensors we compared our results with structural data derived from x-ray crystallography on the RC ground state (see below). This approach assumes that the position of the quinone does not change significantly in the relaxed, charge separated state (8). The data provide a crude structural guideline, which is, however, sufficient to select the right solution (see section on the geometry of the H-bonds to QA).
in H2O (see Fig. 3). As explained before, only two Euler angles are relevant as a consequence of the nearly axial symmetry of the hfc tensor (the deviation from axial symmetry is ∼8% for N−H…O1 and ∼0.3% for Nδ−H…O4; see Table 1). They determine the direction of z′ with respect to the xyz axes. The values obtained at the minimum σG are summarized in Table 1. The hfc values are in agreement with earlier, less accurate, 1H ENDOR experiments (6,10). The signs of the 1H hfc values were deduced from theoretical considerations assuming that the largest anisotropic tensor component is positive, which also follows from the dipolar model and is in agreement with molecular orbital calculations (28,37). Since we are working with samples containing randomly oriented molecules, multiple (eight) solutions were obtained for the orientation (φ and θ) of the hfc tensor. Fig. 1 a shows one of the eight possible solutions for each H-bond. The other solutions are those obtained by reflections on the planes xy, yz, and zx. EPR and ENDOR cannot, in principle, distinguish between these solutions. To select the correct solution for the orientations of the hfc and nqc tensors we compared our results with structural data derived from x-ray crystallography on the RC ground state (see below). This approach assumes that the position of the quinone does not change significantly in the relaxed, charge separated state (8). The data provide a crude structural guideline, which is, however, sufficient to select the right solution (see section on the geometry of the H-bonds to QA).
The values of θ indicate that both hydrogen bonds lie out of the quinone plane (see Fig. 1 a). Furthermore, both H-bonds deviate by φ ≈ 15° from the C−O bond direction (projection on the plane of the quinone) (see Fig. 1 a). This situation is different from that observed for the benzosemiquinone radical anion in water (27,28), in which the H-bonds lie in the quinone plane and approximately along the direction of the lone pair orbital of the oxygen (φ ≈ 36°). The uncertainties of the values of the fitting parameters (see Table 1) were estimated from the sensitivities of σG to these parameters (as discussed in (27); see Fig. 6 in that article). The simulated spectra calculated with the optimum values of the parameters are shown in Fig. 3 (dotted lines).
The principal components of the nqc tensor P and the Euler angles, α, β, and γ, associated with rotations of the x″, y″, z″ axes with respect to the g-tensor axes, x, y, z (see Fig. 1 b), were obtained from the fitting of the 2H ENDOR spectra (see Figs. 4 and 5). The principal components of the 2H nqc and 2H hfc tensors, and the values of the Euler angles (α, β, γ) and (φ, θ) are summarized in Table 1. The correct set of values of α, β, and γ was selected by comparison with the x-ray crystallographic structure of the RC, as described above. The signs of the Pi″ components were determined from the following consideration: For the vast majority of hydrogen bonds the largest principal component of the 2H nqc is positive (24,30,38,39), which is also supported by recent DFT calculations (28). A negative sign has only been proposed for extremely short H-bonds (39). Thus, the positive sign chosen for the larger principal component (Table 1) can safely be assumed to be correct for both 2H nqc tensors. The quadrupole coupling constants (see Eq. 4 and Table 1) and in particular the asymmetry parameters (using Eq. 5, a value of η = 0.39 and η = 0.02 is obtained for Ala M260 and His M219, respectively) are quite different for the two hydrogen bonds, indicating different strengths and geometries of the two bonds (see below). The values of θ and φ obtained from the 2H ENDOR spectra are, within experimental error, in agreement with those obtained from the fitting of the 1H ENDOR spectra (see Table 1). The simulated spectra calculated with the optimum values of the parameters are shown in Figs. 4 and 5 (dotted lines); the agreement with the experimental spectra is very satisfying.
Geometry of the H-bonds to QA inferred from the x-ray structure
The occurrence of several (eight) numerical solutions for φ and θ described in the previous section is a general problem that occurs in magnetic resonance experiments on powder samples containing randomly oriented molecules. This problem has not been well discussed in previous ENDOR studies. The occurrence of several solutions is due to the invariance of the simulated ENDOR spectra under reflections of the proton position on the planes xy, yz, zx (see Fig. 1). Thus, the eight solutions are mathematically equivalent (symmetry-related) but differ in geometry. To solve this problem, we estimated values for φ and θ using the x-ray structure of the RC. Although these values are taken from the RC ground (dark) state and are not very precise due to the limited resolution of the crystals, they are sufficiently accurate to select the correct solution for our problem. This assumes that the charge separated and non-charge-separated structures do not differ significantly. This has been shown to be the case for QA and 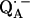 by Abresch et al (8).
by Abresch et al (8).
We inferred the geometry of the H-bonds to QA from the x-ray structure using the following procedure:
The protons in hydrogen bonds were placed in the structure at ideal positions determined geometrically by the theoretical values of the N−H bond length (1.0 Å) and the C−N−H angle (120° for Ala M260 and 126° for His M219), with the protons located in the plane of the C−N−C bond (from the backbone for Ala M260 and from the aromatic ring for His M219).
To model the deviations from the ideal positions, due to interactions with the surroundings (e.g., with the quinone), the positions of the protons were optimized by minimizing their van der Waals energies.
The hydrogen-bond lengths (r) and directions (φ and θ) were calculated using the coordinates of the quinone and the optimized coordinates of the protons; r is the distance between O and H, θ is the angle between the vector along the H-bond and the molecular z axis of the quinone, and φ is the angle between the projection of the H-bond onto the quinone plane and the x axis (see Fig. 1).
The first two steps (1 and 2) were done using the program CNS_Solve (40) and the last step (3) using a routine written in Matlab. This procedure was applied to nine x-ray structures from RCs of Rb. sphaeroides (PDB entries: 1AIG, 1AIJ (3); 1DS8, 1DV3, 1DV6 (41); 1L9B, 1L9J (42); 1OGV (7); and 1PCR (2)). The values of r, φ, and θ obtained from the structures (see Supplementary Material) do not show large deviations, indicating that the x-ray structures used in this work are reliable and represent a statistical collection of similar crystals. Thus, the mean values and standard deviations of the lengths and directions of the H-bonds to QA were calculated and are summarized as follows:
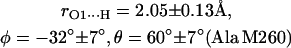 |
(8) |
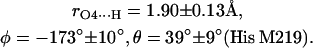 |
(9) |
The geometry of the H-bonds to QA obtained here (Eqs. 8 and 9) was used to select the right solution out of the eight possible ones obtained experimentally for  . Thus, the correct values for φ and θ obtained from the ENDOR analysis are those in Table 1 (see also Fig. 1).
. Thus, the correct values for φ and θ obtained from the ENDOR analysis are those in Table 1 (see also Fig. 1).
The lengths of the H-bonds to  are expected to be shorter than those to QA, since the C−O bond lengths in the semiquinone radical anion are larger than in the quinone and the negative partial charge on the carbonyl oxygens in
are expected to be shorter than those to QA, since the C−O bond lengths in the semiquinone radical anion are larger than in the quinone and the negative partial charge on the carbonyl oxygens in  attracts the proton and leads to a shortening of the H-bond. A different approach to obtain the geometry of the H-bonds to QA is to perform a geometry optimization within the framework of density functional theory. Such an approach is described in Sinnecker et al. (43).
attracts the proton and leads to a shortening of the H-bond. A different approach to obtain the geometry of the H-bonds to QA is to perform a geometry optimization within the framework of density functional theory. Such an approach is described in Sinnecker et al. (43).
Directions of the H-bonds to QA· −
The fitting of the ENDOR spectra (see Figs. 3–5), modeled by the spin Hamiltonian of Eq. 1, yielded the principal components of the hyperfine and quadrupolar coupling tensors corresponding to the two protons or deuterons hydrogen bonded to 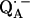 , as well as their orientation with respect to the principal axes xyz of the g-tensor which are equivalent to the molecular axes of the quinone (see Table 1 and Fig. 1). This determines the directions of the hydrogen bonds to the two carbonyl oxygens of
, as well as their orientation with respect to the principal axes xyz of the g-tensor which are equivalent to the molecular axes of the quinone (see Table 1 and Fig. 1). This determines the directions of the hydrogen bonds to the two carbonyl oxygens of  . Two different H-bond directions were obtained. The H-bond to His (M219) is oriented out of the quinone plane by ∼40°, whereas the one to Ala (M260) is ∼27° out of the plane. Both are not oriented along the lone pair direction at the oxygen (judged from the in-plane angle φ, see Fig. 1). Strong hydrogen bonds are in general linear (44), i.e., the N−H…O angle is close to 180° with the proton located in the plane of the C−N−C bond structure (backbone of Ala or ring plane of His). This condition is closely fulfilled for the H-bond to His (M219) (160° ± 9°, obtained from the analysis described in the previous section) but not for the one to the N−H backbone of Ala (M260), where the respective angle is 133° ± 10°. This is clearly evident from Fig. 1. This geometrical situation found for the two hydrogen bonds to
. Two different H-bond directions were obtained. The H-bond to His (M219) is oriented out of the quinone plane by ∼40°, whereas the one to Ala (M260) is ∼27° out of the plane. Both are not oriented along the lone pair direction at the oxygen (judged from the in-plane angle φ, see Fig. 1). Strong hydrogen bonds are in general linear (44), i.e., the N−H…O angle is close to 180° with the proton located in the plane of the C−N−C bond structure (backbone of Ala or ring plane of His). This condition is closely fulfilled for the H-bond to His (M219) (160° ± 9°, obtained from the analysis described in the previous section) but not for the one to the N−H backbone of Ala (M260), where the respective angle is 133° ± 10°. This is clearly evident from Fig. 1. This geometrical situation found for the two hydrogen bonds to 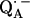 indicates that the one to Ala (M260) is probably weaker than the one to His (M219) (see Table 2 in reference 45). This idea is supported by the fact that the length of the H-bond is shorter to His (M219) than to Ala (M60) (see below).
indicates that the one to Ala (M260) is probably weaker than the one to His (M219) (see Table 2 in reference 45). This idea is supported by the fact that the length of the H-bond is shorter to His (M219) than to Ala (M60) (see below).
TABLE 2.
Dipolar (Ai′) and isotropic (Aiso) hyperfine couplings corresponding to protons and deuterons in hydrogen bonds to 
To fully characterize the H-bond geometry we also need to determine the bond lengths. These values can, in principle, be obtained either from the 1H or 2H dipolar coupling (Eq. 3) or from the 2H nuclear quadrupolar couplings as discussed in the next two sections.
H-bond lengths calculated from the dipolar hyperfine couplings
The point-dipole model (Eq. 3) has been shown to be applicable to quinone model compounds in which the H-bonds lie in the quinone plane (27,28). In this geometrical situation the effective overlap of the hydrogen 1s orbital with the π-orbital at the oxygen is small and the point-dipole approximation is valid for distances ≥2.0 Å (28). However, in RCs the H-bond is up to 40° out of the quinone plane (Table 1). This results in an additional interaction between the proton and the π-orbital of the oxygen. This increased interaction effectively leads to a smaller (and erroneous) bond length when Eq. 3 is used (28). An additional disadvantage of the application of the point-dipole model is that the spin density at the contact position (here the carbonyl oxygens) must be known. For 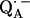 this has been determined by EPR performed on 17O-labeled
this has been determined by EPR performed on 17O-labeled 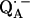 (6,9,10). Using spin densities at the quinone oxygens, of ρ(O1) = 0.21 and ρ(O4) = 0.15 (6,10), Eq. 3 yields bond lengths of rO1⋯H = 1.54 Å and rO4⋯H = 1.32 Å. These lengths are very short compared with typical hydrogen bonds in proteins (44,46) and are considered unrealistic for
(6,9,10). Using spin densities at the quinone oxygens, of ρ(O1) = 0.21 and ρ(O4) = 0.15 (6,10), Eq. 3 yields bond lengths of rO1⋯H = 1.54 Å and rO4⋯H = 1.32 Å. These lengths are very short compared with typical hydrogen bonds in proteins (44,46) and are considered unrealistic for 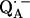 . This indicates that the point-dipole model is inadequate for the case of
. This indicates that the point-dipole model is inadequate for the case of 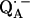 . A more reliable determination of hydrogen-bond lengths is obtained from the 2H nuclear quadrupolar coupling of the deuterated H-bond as discussed in the next section.
. A more reliable determination of hydrogen-bond lengths is obtained from the 2H nuclear quadrupolar coupling of the deuterated H-bond as discussed in the next section.
H-bond lengths obtained from the quadrupole couplings of 2H
To obtain the hydrogen-bond length from the nqc of 2H, empirical linear relationships were proposed by Soda and Chiba (24) and Hunt and Mackay (25). These are based on a large variety of different hydrogen bonds in chemical and biological systems for which the 2H nqc was determined (mostly by nuclear quadrupole resonance). It should be mentioned that these systems are all diamagnetic, but the addition of an unpaired electron is not expected to significantly change the field gradient and the nqc. We therefore assume that these relationships are also valid for the case of hydrogen bonding to quinone radical anions. This has been corroborated by DFT calculations (28), which showed good agreement with the empirical relations proposed in (24,25). It has been shown (24,25) that the nqc follows a 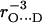 dependence of the form
dependence of the form
 |
(10) |
where P1 is the largest principal component of the nqc tensor, in our case Pz″ (see Table 1), and a, b are empirical parameters. Their values are given to: a = 310 kHz, b = 572 kHz · Å3 (24): a = 328 kHz, b = 643 kHz · Å3 (25). We have used this model to determine the lengths of the D-bonds to benzosemiquinone in water and have shown that the value obtained was in agreement with that obtained by other methods (e.g., DFT) (27,28). Using the average of the two sets of values of a and b (a = 319 kHz, b = 607 kHz · Å3), and the value of Pz″ measured for the two D-bonds to 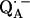 (Table 1), we obtain from Eq. 10 bond lengths of
(Table 1), we obtain from Eq. 10 bond lengths of
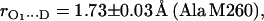 |
(11) |
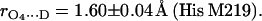 |
(12) |
The errors in Eqs. 11 and 12 were obtained considering only the statistical uncertainties of Pz″ (see Table 1). If the uncertainties of a and b (estimated from the discrepancies obtained in refs. (24) and (25)) are considered the errors increase to 0.05 Å in both cases. The bond length of N−D…O1 (Ala M260) is similar to that observed for the benzosemiquinone radical anion in water (1.76 ± 0.03 Å) (27,28), whereas the bond length of Nδ−D…O4 (His M219) is in the range of short hydrogen bonds for biological systems (44,46).
Comparison of the dipolar hyperfine coupling tensor components of 1H and 2H
We determined the D-bond length from the nqc values (Eqs. 11 and 12). To ascertain whether the H-bond length is the same we need to determine whether there is an isotope effect, i.e., whether the bond length changes when 1H is replaced by 2H. This was accomplished by comparing the magnitudes of the dipolar hfc tensor components of 1H and 2H. To compare 1H and 2H dipolar hfc values, the 2H couplings were multiplied by the ratio of their magnetic moments (γ1H/γ2H = 6.514) (see Table 2). The comparison shows that within experimental error the same dipolar hfc tensor components of 1H and 2H (i.e., equal bond lengths) were obtained for Ala M260 (O1). However, in the case of His M219 (O4), the observed anisotropic hfc of 2H is ∼2% smaller than that of 1H, indicating an isotope effect. This is barely outside the experimental error, but when taken at face-value, would result in a 0.01 Å longer D-bond length as expected for an isotope effect (46). For hydrogen bonds in the solid state with lengths similar to those of the H-bonds to  in RCs, isotope effects have been reported to lie between 0 and ∼0.02 Å (45). Thus, the magnitude and direction of the observed effect is consistent with an isotope effect for the strong hydrogen bond from His (M219) to
in RCs, isotope effects have been reported to lie between 0 and ∼0.02 Å (45). Thus, the magnitude and direction of the observed effect is consistent with an isotope effect for the strong hydrogen bond from His (M219) to  . However, the putative change in bond length of 0.01 Å is considerably smaller than the uncertainty (see Eq. 12), and therefore Eqs. 11 and 12 are also applicable to the H-bond lengths.
. However, the putative change in bond length of 0.01 Å is considerably smaller than the uncertainty (see Eq. 12), and therefore Eqs. 11 and 12 are also applicable to the H-bond lengths.
The significance of the isotropic hyperfine interaction
From the hfc tensor analysis a significantly larger isotropic component has been found for the proton hydrogen-bonded to His (M219) compared to Ala (M260) (Table 2). This indicates a partial covalent character of the hydrogen bond to histidine (45,47). This can be explained by a shorter distance and also a larger out-of-plane angle of this H-bond. Both effects lead to a stronger interaction with the electron spin that is located in the π-system of the quinone radical anion. A large isotropic hfc has also been reported for the donor nitrogen Nδ of His (M219) (12,15). This indicates a flow of spin density via the hydrogen bond to the histidine that is ligated to the metal. This suggests that the hydrogen bonds not only have a structural function in the RC but also play a role in the electron transfer process (15,43).
Effect of the H-bonds on the electronic structure and function of the primary quinone
The full characterization of the geometry of the H-bonds to  clearly shows an asymmetrical H-bond situation with the shorter bond, the larger isotropic hfc, and the larger out-of-plane angle corresponding to His (M219). This indicates that the stronger hydrogen bond is to His (M219), which is in agreement with previous interpretations (6,11,14,48–50). The asymmetry of the H-bonds has a profound effect on the spin density distribution of the quinone radical anion that can be rationalized in a simple valence bond model (see, e.g., (6,51)). The consequences are seen in the 13C (11,14,48), 17O (10), and even the 1H hfc values (6,10) of
clearly shows an asymmetrical H-bond situation with the shorter bond, the larger isotropic hfc, and the larger out-of-plane angle corresponding to His (M219). This indicates that the stronger hydrogen bond is to His (M219), which is in agreement with previous interpretations (6,11,14,48–50). The asymmetry of the H-bonds has a profound effect on the spin density distribution of the quinone radical anion that can be rationalized in a simple valence bond model (see, e.g., (6,51)). The consequences are seen in the 13C (11,14,48), 17O (10), and even the 1H hfc values (6,10) of 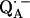 that are shifted when compared with the same ubiquinone radical anion outside the protein—e.g., in organic solvents (4,6,10,17,51,52). The asymmetric H-bonds and the change of the electronic structure of
that are shifted when compared with the same ubiquinone radical anion outside the protein—e.g., in organic solvents (4,6,10,17,51,52). The asymmetric H-bonds and the change of the electronic structure of 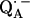 might have several implications for the function of this quinone in the RC. First, it can be expected that the redox potential is changed; in particular, the second reduction of the quinone is more difficult. This is in agreement with the fact that QA in the RC only accepts one electron, i.e., it functions as a one-electron-gate, whereas QB, which has more symmetrical H-bonds (6), can be doubly reduced and protonated and forms the hydroquinone. Secondly, it has been shown in this work that the formation of
might have several implications for the function of this quinone in the RC. First, it can be expected that the redox potential is changed; in particular, the second reduction of the quinone is more difficult. This is in agreement with the fact that QA in the RC only accepts one electron, i.e., it functions as a one-electron-gate, whereas QB, which has more symmetrical H-bonds (6), can be doubly reduced and protonated and forms the hydroquinone. Secondly, it has been shown in this work that the formation of 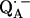 leads to significantly shorter H-bonds as compared to QA (see Eqs. 8, 9, 11, and 12), which stabilizes the radical anion. A shorter H-bond is found to the histidine that is liganded to the divalent metal. From the measured isotropic hfc values of the hydrogen-bonded proton and the histidine nitrogen Nδ, a flow of spin density of the transferred electron is evident. It is suggestive that this experimental finding is related to the electron transfer process from
leads to significantly shorter H-bonds as compared to QA (see Eqs. 8, 9, 11, and 12), which stabilizes the radical anion. A shorter H-bond is found to the histidine that is liganded to the divalent metal. From the measured isotropic hfc values of the hydrogen-bonded proton and the histidine nitrogen Nδ, a flow of spin density of the transferred electron is evident. It is suggestive that this experimental finding is related to the electron transfer process from 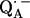 to
to 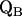 and also from
and also from 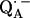 to
to 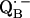 via the histidine(s). A possible involvement of the divalent metal is still under discussion (53). In this respect it is worth mentioning that for the biradical state
via the histidine(s). A possible involvement of the divalent metal is still under discussion (53). In this respect it is worth mentioning that for the biradical state 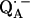
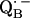 an exchange coupling (Jo/h = −82 MHz) has been determined (34,54) that can be related to the electron transfer between the two quinones. A possible pathway for the ET is via the histidine residues. It has been experimentally determined that these histidines carry a small portion of spin density in the respective
an exchange coupling (Jo/h = −82 MHz) has been determined (34,54) that can be related to the electron transfer between the two quinones. A possible pathway for the ET is via the histidine residues. It has been experimentally determined that these histidines carry a small portion of spin density in the respective 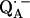 and
and 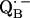 states (12,15,16).
states (12,15,16).
SUMMARY AND CONCLUSION
From a fitting of a model spin Hamiltonian to the ENDOR spectra of 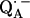 we were able to characterize the hydrogen bonds to the two carbonyl oxygens of
we were able to characterize the hydrogen bonds to the two carbonyl oxygens of 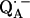 in bacterial reaction centers of Rb. sphaeroides. The directions of the hydrogen bonds were obtained from the hyperfine coupling tensors and the bond lengths from the magnitude of the nuclear quadrupolar couplings. An asymmetrical H-bond situation was obtained for
in bacterial reaction centers of Rb. sphaeroides. The directions of the hydrogen bonds were obtained from the hyperfine coupling tensors and the bond lengths from the magnitude of the nuclear quadrupolar couplings. An asymmetrical H-bond situation was obtained for 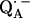 with the shorter H-bond to His (M219) (Nδ−H…O4) and the longer one to Ala (M260) (N−H…O1). The H-bond to the histidine is shorter, better aligned to the N−H…O axis and more out-of-plane with respect to the quinone π-system. This leads to an effective flow of spin density via this H-bond onto the histidine. This aspect may be important for the electron transfer process from
with the shorter H-bond to His (M219) (Nδ−H…O4) and the longer one to Ala (M260) (N−H…O1). The H-bond to the histidine is shorter, better aligned to the N−H…O axis and more out-of-plane with respect to the quinone π-system. This leads to an effective flow of spin density via this H-bond onto the histidine. This aspect may be important for the electron transfer process from 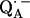 to QB (or from
to QB (or from 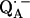 to
to 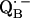 ). It is suggestive that nature might use the H-bonds to fine-tune the geometrical and electronic structure and thereby optimize the ET in the RC.
). It is suggestive that nature might use the H-bonds to fine-tune the geometrical and electronic structure and thereby optimize the ET in the RC.
It is known from studies of the primary donor in RCs that H-bonding can drastically affect the redox potential of a cofactor (55–59). The asymmetric H-bond situation to 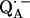 is known to have a profound effect on the spin density distribution and the electronic structure of the ubiquinone radical anion
is known to have a profound effect on the spin density distribution and the electronic structure of the ubiquinone radical anion 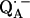 . This may also affect the redox potential of the primary quinone and contribute to the fact that QA has the correct potential for the activationless electron transfer from the bacteriopheophytin
. This may also affect the redox potential of the primary quinone and contribute to the fact that QA has the correct potential for the activationless electron transfer from the bacteriopheophytin 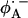 to QA and functions as a one-electron gate in the ET to QB.
to QA and functions as a one-electron gate in the ET to QB.
The approach described in this work should be applicable to 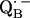 in bacterial RCs, and to the quinones in PSI and PSII of oxygen-evolving organisms. Quinones also play an important role in many other energy-conserving systems, e.g., in the proteins of the respiratory chain (60). In many of these systems stable semiquinone radical intermediates have been detected (e.g., (61)). We believe that the principles described here also apply to these systems.
in bacterial RCs, and to the quinones in PSI and PSII of oxygen-evolving organisms. Quinones also play an important role in many other energy-conserving systems, e.g., in the proteins of the respiratory chain (60). In many of these systems stable semiquinone radical intermediates have been detected (e.g., (61)). We believe that the principles described here also apply to these systems.
SUPPLEMENTARY MATERIAL
An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.
Acknowledgments
We thank H. Axelrod (Stanford Synchrotron Radiation Laboratory) for assistance in the use of the program CNS_Solve and for helpful discussions.
This work was supported by National Science Foundation grant No. MCB 99/82186 and National Institutes of Health grant No. GM13191 and by the Max-Planck Society, and Fonds der Chemischen Industrie (to W.L.).
References
- 1.Cramer, W. A., and D. B. Knaff. 1990. In Energy Transduction in Biological Membranes. Chapter 5. Springer-Verlag, New York.
- 2.Ermler, U., G. Fritzsch, S. K. Buchanan, and H. Michel. 1994. Structure of the photosynthetic reaction centre from Rhodobacter sphaeroides at 2.65 Å resolution: cofactors and protein-cofactor interactions. Structure. 2:925–936. [DOI] [PubMed] [Google Scholar]
- 3.Stowell, M. H. B., T. M. McPhillips, D. C. Rees, S. M. Soltis, E. Abresch, and G. Feher. 1997. Light-induced structural changes in photosynthetic reaction center: implications for mechanism of electron-proton transfer. Science. 276:812–816. [DOI] [PubMed] [Google Scholar]
- 4.Feher, G. 1998. The primary and secondary electron acceptors in bacterial photosynthesis: I. A chronological account of their identification by EPR. Appl. Magn. Reson. 15:23–38. [Google Scholar]
- 5.Feher, G., and M. Y. Okamura. 1999. The primary and secondary acceptors in bacterial photosynthesis: II. The structure of the Fe2+-Q· − complex. Appl. Magn. Reson. 16:63–100. [Google Scholar]
-
6.Lubitz, W., and G. Feher. 1999. The primary and secondary acceptors in bacterial photosynthesis: III. Characterization of the quinone radicals
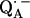 and
and 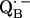 by EPR and ENDOR. Appl. Magn. Reson. 17:1–48. [Google Scholar]
by EPR and ENDOR. Appl. Magn. Reson. 17:1–48. [Google Scholar] - 7.Katona, G., U. Andreasson, E. M. Landau, L. E. Andreasson, and R. Neutze. 2003. Lipidic cubic phase crystal structure of the photosynthetic reaction centre from Rhodobacter sphaeroides at 2.35 Å resolution. J. Mol. Biol. 331:681–692. [DOI] [PubMed] [Google Scholar]
-
8.Abresch, E. C., A. P. Yeh, S. M. Soltis, D. C. Rees, H. L. Axelrod, M. Y. Okamura, and G. Feher. 1999. Crystal structure of the charge-separated state,
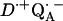 , in photosynthetic reaction centers from Rb. sphaeroides. Biophys. J. 76:A141. (Abstr.). [Google Scholar]
, in photosynthetic reaction centers from Rb. sphaeroides. Biophys. J. 76:A141. (Abstr.). [Google Scholar] - 9.Lubitz, W., E. C. Abresch, R. J. Debus, R. A. Isaacson, M. Y. Okamura, and G. Feher. 1985. Electron nuclear double resonance of semiquinones in reaction centers of Rhodopseudomonas sphaeroides. Biochim. Biophys. Acta. 808:464–469. [DOI] [PubMed] [Google Scholar]
- 10.Feher, G., R. A. Isaacson, M. Y. Okamura, and W. Lubitz. 1985. ENDOR of semiquinones in RCs from Rhodopseudomonas sphaeroides. In Antennas and Reaction Centers of Photosynthetic Bacteria—Structure, Interactions and Dynamics. M. E. Michel-Beyerle, editor. Springer-Verlag, Berlin.
- 11.van den Brink, J. S., A. P. Spoyalov, P. Gast, W. B. S. van Liemt, J. Raap, J. Lugtenburg, and A. J. Hoff. 1994. Asymmetric binding of the primary acceptor quinone in reaction centers of the photosynthetic bacterium Rhodobacter sphaeroides R26, probed with Q-band (35 GHz) EPR spectroscopy. FEBS Lett. 353:273–276. [DOI] [PubMed] [Google Scholar]
-
12.Bosch, M. K., P. Gast, A. J. Hoff, A. P. Spoyalov, and Y. D. Tsvetkov. 1995. The primary acceptor quinone QA in reaction centers of Rhodobacter sphaeroides R26 is hydrogen-bonded to the Nδ(1)−H of His M219. An electron spin echo study of
 . Chem. Phys. Lett. 239:306–312. [Google Scholar]
. Chem. Phys. Lett. 239:306–312. [Google Scholar] -
13.Isaacson, R. A., F. Lendzian, E. C. Abresch, W. Lubitz, and G. Feher. 1995. Electronic structure of
 in reaction centers from Rhodobacter sphaeroides. I. Electron paramagnetic resonance in single crystals. Biophys. J. 69:311–322. [DOI] [PMC free article] [PubMed] [Google Scholar]
in reaction centers from Rhodobacter sphaeroides. I. Electron paramagnetic resonance in single crystals. Biophys. J. 69:311–322. [DOI] [PMC free article] [PubMed] [Google Scholar] -
14.Isaacson, R. A., E. C. Abresch, F. Lendzian, C. Boullais, M. L. Paddock, C. Mioskowski, W. Lubitz, and G. Feher. 1996. Asymmetry of the binding sites of
 and
and  in reaction centers of Rb. sphaeroides probed by Q-band EPR with 13C-labeled quinones. In The Reaction Center of Photosynthetic Bacteria: Structure and Dynamics. M. B. Michel-Beyerle, editor. Springer-Verlag, Berlin.
in reaction centers of Rb. sphaeroides probed by Q-band EPR with 13C-labeled quinones. In The Reaction Center of Photosynthetic Bacteria: Structure and Dynamics. M. B. Michel-Beyerle, editor. Springer-Verlag, Berlin.
- 15.Lendzian, F., J. Rautter, H. Kass, A. Gardiner, and W. Lubitz. 1996. ENDOR and pulsed EPR studies of photosynthetic reaction centers: protein-cofactor interactions. Ber. Bunsen. Phys. Chem. 100:2036–2040. [Google Scholar]
-
16.Spoyalov, A. P., R. J. Hulsebosch, S. Shochat, P. Gast, and A. J. Hoff. 1996. Evidence that Ala M260 is hydrogen-bonded to the reduced primary acceptor quinone
 in reaction centers of Rb. sphaeroides. Chem. Phys. Lett. 263:715–720. [Google Scholar]
in reaction centers of Rb. sphaeroides. Chem. Phys. Lett. 263:715–720. [Google Scholar] -
17.Rohrer, M., F. MacMillan, T. F. Prisner, A. T. Gardiner, K. Mobius, and W. Lubitz. 1998. Pulsed ENDOR at 95 GHz on the primary acceptor ubisemiquinone
 in photosynthetic bacterial reaction centers and related model systems. J. Phys. Chem. B. 102:4648–4657. [Google Scholar]
in photosynthetic bacterial reaction centers and related model systems. J. Phys. Chem. B. 102:4648–4657. [Google Scholar] -
18.Paddock, M. L., E. C. Abresch, R. A. Isaacson, W. Lubitz, M. Y. Okamura, and G. Feher. 1999. Identification of hydrogen bonds to
 in RCs of Rb. sphaeroides by ENDOR spectroscopy. Biophys. J. 76:A141. (Abstr.). [Google Scholar]
in RCs of Rb. sphaeroides by ENDOR spectroscopy. Biophys. J. 76:A141. (Abstr.). [Google Scholar] -
19.Flores, M., R. Isaacson, E. Abresch, R. Calvo, W. Lubitz, and G. Feher. 2006. Protein-cofactor interactions in bacterial reaction centers from Rhodobacter sphaeroides R-26: I. Identification of the ENDOR lines associated with the hydrogen bonds to the primary quinone
 . Biophys. J. 90:3356–3362. [DOI] [PMC free article] [PubMed] [Google Scholar]
. Biophys. J. 90:3356–3362. [DOI] [PMC free article] [PubMed] [Google Scholar] - 20.Debus, R. J., G. Feher, and M. Y. Okamura. 1986. Iron-depleted reaction centers from Rhodopseudomonas sphaeroides R-26.1: characterization and reconstitution with Fe2+, Mn2+, Co2+, Ni2+, Cu2+, and Zn2+. Biochemistry. 25:2276–2287. [DOI] [PubMed] [Google Scholar]
- 21.Utschig, L. M., S. R. Greenfield, J. Tang, P. D. Laible, and M. C. Thurnauer. 1997. Influence of iron-removal procedures on sequential electron transfer in photosynthetic bacterial reaction centers studied by transient EPR spectroscopy. Biochemistry. 36:8548–8558. [DOI] [PubMed] [Google Scholar]
- 22.Rist, G. H., and J. S. Hyde. 1968. Ligand ENDOR of Cu-8-hydroxyquinolinate substituted into a single crystal and a powder of phthalimide. J. Chem. Phys. 49:2449–2451. [Google Scholar]
- 23.Stoll, S., and A. Schweiger. 2006. EasySpin, a comprehensive software package for spectral simulation and analysis in EPR. J. Magn. Reson. 178:42–55. [DOI] [PubMed] [Google Scholar]
- 24.Soda, G., and T. Chiba. 1969. Deuteron magnetic resonance study of cupric sulfate pentahydrate. J. Chem. Phys. 50:439–455. [Google Scholar]
- 25.Hunt, M. J., and A. L. Mackay. 1974. Deuterium and nitrogen pure quadrupole resonance in deuterated amino acids. J. Magn. Reson. 15:402–414. [Google Scholar]
- 26.Weil, J. A., J. R. Bolton, and J. E. Wertz. 1994. Electron Paramagnetic Resonance. Elementary Theory and Practical Applications. Wiley, New York.
- 27.Flores, M., R. A. Isaacson, R. Calvo, G. Feher, and W. Lubitz. 2003. Probing hydrogen bonding to quinone anion radicals by 1H and 2H ENDOR spectroscopy at 35 GHz. Chem. Phys. 294:401–413. [Google Scholar]
- 28.Sinnecker, S., E. Reijerse, F. Neese, and W. Lubitz. 2004. Hydrogen bond geometries from electron paramagnetic resonance and electron-nuclear double resonance parameters: density functional study of quinone radical anion-solvent interactions. J. Am. Chem. Soc. 126:3280–3290. [DOI] [PubMed] [Google Scholar]
- 29.Blinc, R. 1976. Magnetic resonance studies of hydrogen bonding in solids. In The Hydrogen Bond; Recent Developments in Theory and Experiments. II. Structure and Spectroscopy. P. Schuster, G. Zundel, and C. Sandorfy, editors. North-Holland, Amsterdam.
- 30.Soda, G., and T. Chiba. 1969. Deuteron magnetic resonance study of cupric formate tetrahydrate Cu(DCOO)2.4D2O. J. Phys. Soc. Jpn. 26:249–261. [Google Scholar]
- 31.Schweiger, A., and G. Jeschke. 2001. Principles of Pulse Electron Paramagnetic Resonance. Oxford University Press, Oxford.
- 32.Hoffman, B. M., V. J. DeRose, P. E. Doan, R. J. Gurbiel, A. L. P. Houseman, and J. Telser. 1993. Metalloenzyme active-site structure and function through multifrequency CW and pulsed ENDOR. In Biological Magnetic Resonance, Vol. 13. Chapter 5. L. Berliner and J. Reuben, editors. Plenum Press, New York.
- 33.Hüttermann, J. 1993. ENDOR of randomly oriented mononuclear metalloproteins: toward structural determinations of the prosthetic group. In Biological Magnetic Resonance, Vol. 13. Chapter 5. L. Berliner and J. Reuben, editors. Plenum Press, New York.
-
34.Calvo, R., E. C. Abresch, R. Bittl, G. Feher, W. Hofbauer, R. A. Isaacson, W. Lubitz, M. Y. Okamura, and M. L. Paddock. 2000. EPR study of the molecular and electronic structure of the semiquinone biradical
 in photosynthetic reaction centers from Rhodobacter sphaeroides. J. Am. Chem. Soc. 122:7327–7341. [Google Scholar]
in photosynthetic reaction centers from Rhodobacter sphaeroides. J. Am. Chem. Soc. 122:7327–7341. [Google Scholar] - 35.Kirkpatrick, S., C. D. Gelatt, and M. P. Vecchi. 1983. Optimization by thermal annealing. Science. 220:671–680. [DOI] [PubMed] [Google Scholar]
-
36.Burghaus, O., M. Plato, M. Rohrer, K. Mobius, F. MacMillan, and W. Lubitz. 1993. Three-mm high-field EPR on semiquinone radical anions Q· − related to photosynthesis and on the primary donor P·+ and acceptor
 in reaction centers of Rhodobacter sphaeroides R-26. J. Phys. Chem. B. 97:7639–7647. [Google Scholar]
in reaction centers of Rhodobacter sphaeroides R-26. J. Phys. Chem. B. 97:7639–7647. [Google Scholar] - 37.O'Malley, P. J. 2001. Electronic structure studies of quinone and semiquinones: accurate calculation of spin densities and electron paramagnetic resonance parameters. Antioxid. Redox. Sign. 3:825–838. [DOI] [PubMed] [Google Scholar]
- 38.Lucken, E. A. C. 1969. Nuclear Quadrupole Couplings Constants. Academic Press, London, New York.
- 39.Mayas, L., M. Plato, C. J. Winscom, and K. Mobius. 1978. Deuterium quadrupole coupling constants in hydrogen bonded dicarboxylic acids. A distant ENDOR study. Mol. Phys. 36:753–764. [Google Scholar]
- 40.Brunger, A. T., P. D. Adams, G. M. Clore, W. L. DeLano, P. Gros, R. W. Grosse-Kunstleve, J. Jiang, J. Kuszewski, M. Nilges, N. S. Pannu, R. J. Read, L. M. Rice, T. Simonson, and G. L. Warren. 1998. Crystallography and NMR system: a new software suite for macromolecular structure determination. Acta Crystallogr. D. 54:905–921. [DOI] [PubMed] [Google Scholar]
- 41.Axelrod, H. L., E. C. Abresch, M. L. Paddock, M. Y. Okamura, and G. Feher. 2000. Determination of the binding sites of the proton transfer inhibitors Cd2+ and Zn2+ in bacterial reaction centers. Proc. Natl. Acad. Sci. USA. 97:1542–1547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Axelrod, H. L., E. C. Abresch, M. Y. Okamura, A. P. Yeh, D. C. Rees, and G. Feher. 2002. X-ray structure determination of the cytochrome c2: reaction center electron transfer complex from Rhodobacter sphaeroides. J. Mol. Biol. 319:501–515. [DOI] [PubMed] [Google Scholar]
- 43.Sinnecker, S., M. Flores, and W. Lubitz. 2006. Protein-cofactor interactions in bacterial reaction centers from Rhodobacter sphaeroides R-26: effect of hydrogen bonding on the electronic and geometric structure of the primary quinone. A density functional theory study. Phys. Chem. Chem. Phys. 8:5659–5670. [DOI] [PubMed] [Google Scholar]
- 44.Jeffrey, G. A. 1997. An Introduction to Hydrogen Bonding. Oxford University Press, Oxford.
- 45.Steiner, T. 2002. The hydrogen bond in the solid state. Angew. Chem. Int. Ed. Engl. 41:48–76. [DOI] [PubMed] [Google Scholar]
- 46.Jeffrey, G. A., and W. Saenger. 1991. Hydrogen Bonding in Biological Structures. Springer-Verlag, Berlin.
- 47.Gilli, P., V. Bertolasi, V. Ferretti, and G. Gilli. 1994. Covalent nature of the strong homonuclear hydrogen bond. Study of the O−H−O system by crystal structure correlation methods. J. Am. Chem. Soc. 116:909–915. [Google Scholar]
- 48.Hoff, A. J., T. N. Kropacheva, R. I. Samoilova, N. P. Gritzan, J. Raap, J. S. van den Brink, P. Gast, and J. Lugtenburg. 1996. Site-directed isotope labelling as a tool in spectroscopy of photosynthetic preparations. Investigations on quinone binding in bacterial reaction centers. In The Reaction Center of Photosynthetic Bacteria: Structure and Dynamics. M. B. Michel-Beyerle, editor. Springer-Verlag, Berlin.
- 49.Breton, J., C. Boullais, J. R. Burie, E. Nabedryk, and C. Mioskowski. 1994. Binding sites of quinones in photosynthetic bacterial reaction centers investigated by light-induced FTIR difference spectroscopy: assignment of the interactions of each carbonyl of QA in Rhodobacter sphaeroides using site-specific 13C-labeled ubiquinone. Biochemistry. 33:14378–14386. [DOI] [PubMed] [Google Scholar]
- 50.Brudler, R., H. J. M. de Groot, W. B. S. van Liemt, W. F. Steggerda, R. Esmeijer, P. Gast, A. J. Hoff, J. Lugtenburg, and K. Gerwert. 1994. Asymmetric binding of the 1- and 4-C=O groups of QA in Rhodobacter sphaeroides R26 reaction centres monitored by Fourier transform infra-red spectroscopy using site-specific isotopically labelled ubiquinone-10. EMBO J. 13:5523–5530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.MacMillan, F., F. Lendzian, and W. Lubitz. 1995. EPR and ENDOR characterization of semiquinone anion radicals related to photosynthesis. Magn. Reson. Chem. 33:S81–S93. [Google Scholar]
- 52.Das, M. R., H. D. Conner, D. S. Leniart, and J. H. Freed. 1970. An electron nuclear double resonance and electron spin resonance study of semiquinones related to vitamins K and E. J. Am. Chem. Soc. 92:2258–2268. [DOI] [PubMed] [Google Scholar]
- 53.Remy, A., and K. Gerwert. 2003. Coupling of light-induced electron transfer to proton uptake in photosynthesis. Nat. Struct. Biol. 10:637–644. [DOI] [PubMed] [Google Scholar]
-
54.Calvo, R., R. A. Isaacson, M. L. Paddock, E. C. Abresch, M. Y. Okamura, A. L. Maniero, L. C. Brunel, and G. Feher. 2001. EPR study of the semiquinone biradical
 in photosynthetic reaction centers of Rhodobacter sphaeroides at 326 GHz: determination of the exchange interaction Jo. J. Phys. Chem. B. 105:4053–4057. [Google Scholar]
in photosynthetic reaction centers of Rhodobacter sphaeroides at 326 GHz: determination of the exchange interaction Jo. J. Phys. Chem. B. 105:4053–4057. [Google Scholar] - 55.Allen, J. P., and J. C. Williams. 1995. Relationship between the oxidation potential of the bacteriochlorophyll dimer and electron transfer in photosynthetic reaction centers. J. Bioenerg. Biomembr. 27:275–283. [DOI] [PubMed] [Google Scholar]
- 56.Rautter, J., F. Lendzian, C. Schulz, A. Fetsch, M. Kuhn, X. Lin, J. C. Williams, J. P. Allen, and W. Lubitz. 1995. ENDOR studies of the primary donor cation radical in mutant reaction centers of Rhodobacter sphaeroides with altered hydrogen-bond interactions. Biochemistry. 34:8130–8143. [DOI] [PubMed] [Google Scholar]
- 57.Muh, F., F. Lendzian, M. Roy, J. C. Williams, J. P. Allen, and W. Lubitz. 2002. Pigment-protein interactions in bacterial reaction centers and their influence on oxidation potential and spin density distribution of the primary donor. J. Phys. Chem. B. 106:3226–3236. [Google Scholar]
- 58.Lubitz, W., F. Lendzian, and R. Bittl. 2002. Radicals, radical pairs and triplet states in photosynthesis. Acc. Chem. Res. 35:313–320. [DOI] [PubMed] [Google Scholar]
- 59.Kalman, L., R. LoBrutto, J. P. Allen, and J. C. Williams. 1999. Modified reaction centres oxidize tyrosine in reactions that mirror photosystem II. Nature. 402:696–699. [Google Scholar]
- 60.Berg, J. M., J. L. Tymoczko, and L. Stryer. 2002. Biochemistry. W. H. Freeman, New York.
-
61.Grimaldi, S., F. MacMillan, T. Ostermann, B. Ludwig, H. Michel, and T. Prisner. 2001.
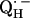 ubisemiquinone radical in the bo3-type ubiquinol oxidase studied by pulsed electron paramagnetic resonance and hyperfine sublevel correlation spectroscopy. Biochemistry. 40:1037–1043. [DOI] [PubMed] [Google Scholar]
ubisemiquinone radical in the bo3-type ubiquinol oxidase studied by pulsed electron paramagnetic resonance and hyperfine sublevel correlation spectroscopy. Biochemistry. 40:1037–1043. [DOI] [PubMed] [Google Scholar]