The Origin of Long-Range Attraction between Hydrophobes in Water

Abstract

When water-coated hydrophobic surfaces meet, direct contacts form between the surfaces, driving water out. However, long-range attractive forces first bring those surfaces close. This analysis reveals the source and strength of the long-range attraction between water-coated hydrophobic surfaces. The origin is in the polarization field produced by the strong correlation and coupling of the dipoles of the water molecules at the surfaces. We show that this polarization field gives rise to dipoles on the surface of the hydrophobic solutes that generate long-range hydrophobic attractions. Thus, hydrophobic aggregation begins with a step in which water-coated nonpolar solutes approach one another due to long-range electrostatic forces. This precursor regime occurs before the entropy increase of releasing the water layers and the short-range van der Waals attraction provide the driving force to “dry out” the contact surface. The effective force of attraction is derived from basic molecular principles, without assumptions of the structure of the hydrophobe-water interaction. The strength of this force can be measured directly from atomic force microscopy images of a hydrophobic molecule tethered to a surface but extending into water, and another hydrophobe attached to an atomic force probe. The phenomenon can be observed in the transverse relaxation rates in water proton magnetic resonance as well. The results shed light on the way water mediates chemical and biological self-assembly, a long outstanding problem.

INTRODUCTION

A large hydrophobic surface, i.e, larger than a surface area required for placing a hydrogen bond (say, A₁), reduces the number of possibilities for the hydrogen (H) bond exchange of an interface water molecule (1). This H-bond depletion leads also to extended lag times for reorientation of a water molecule's dipole moment. This delay enhances the probability that one water dipole joins the slowly fluctuating dipole of a neighbor and creates a relatively long-lived dipole pair. These dipole pairs (and presumably larger assemblies as well) give rise to a structured water shell around the hydrophobic unit. Recently (2), we analyzed the consequences of the dipole-dipole correlation of water molecules under hydrophobic confinement and formulated a statistical self-consistent approach describing the response behavior of such semiconfined water. That approach provides the background for our interpretation and quantification here of the physical effects that underlie the attraction between hydrophobes in water. The molecular mechanism of the long-range hydrophobe-hydrophobe attraction is our main focus in this discussion.

The origin of the hydrophobic force is a long-standing problem (3). Chandler and co-workers suggested that the free energy of solvation scales with volume for small hydrophobes and with surface area for large hydrophobes (4–6). Strong hydrophobic forces are expected to occur on a molecular length scale at the crossover between these two types of behaviors and are associated with the formation of a drying interface between the large hydrophobe and water (4). This drying interface concept was used also by Berne in a model for the dewetting-induced collapse of two close hydrophobe molecules (7–10). The dewetting is attributed to the unfavorable interactions between water and hydrophobic solute and it was inferred that the process is initiated by short range repulsive forces acting at this interface. Under such circumstances, an interaction between well-separated hydrophobic surfaces may potentially arise from the growth and bridging of submicroscopic bubbles between the surfaces (11,12).

Distinct from this drying-induced interaction for adjacent hydrophobic surfaces, we show how two hydrophobes may attract each other at longer distances, via dipole-dipole and induction-dispersion effects generated by the polarization fields of the water structured at the interface (Fig. 1). Specifically, this analysis reveals that the mechanism of the hydrophobic aggregation may involve an initial step in which nonpolar solutes approach one another via long-range electrostatic forces. This precursor regime occurs before the entropy of releasing the water layers (4–10) and attractive, short-range van der Waals forces may provide enough driving force to “dry out” the contacting surfaces.

FIGURE 1.

Schematic representation of the long-range attraction between hydrophobes initiated by the domains of polarized water (a) and by induced dipoles on the surface of the hydrophobic solutes (b).

Evidence of a water organization at a hydrophobic interface has been seen in molecular dynamics (MD) simulation (13–16), as originally supposed six decades ago (17). The lack of hydrogen bonding interactions with the surface represents the source of orientational ordering of these water molecules, as indicated by a recent MD study (16). Direct measurements also revealed long-range attractive forces between hydrophobic surfaces in water (18–20), yet attempts to identify a relevant parameter that can relate water's structural effects to the strength of the hydrophobic interactions have heretofore been unsuccessful. Here we show how we can understand the physical origin of this long-range hydrophobic attraction from basic molecular principles, and also that one can define a determining parameter of the interaction in a convenient way. Thus, we explain how water molecules with depleted availability of H-bonds and consequent slow reorientation of their intrinsic molecular dipoles organize themselves around hydrophobic units and give rise to polarization fields that can generate effective long-range attractions between these hydrophobic units. The strength of interaction depends on the degree of depletion of H-bonds of water molecules at interface; this degree of depletion is the parameter of interest. Thus, our approach offers a practical way to quantify these hydrophobic interactions. Understanding the molecular mechanism of hydrophobic forces is likely to contribute to understanding many biological self-organizing processes, such as protein folding and assembly of membrane structures, as well as to improve our knowledge about the driving force in ligand binding to hydrophobic patches on target proteins (21–24). Deciphering the hydrophobic interactions can also have profound implications for drug design and delivery to specific target proteins in a cell (25). In addition, the hydrophobic force is crucial to phenomena such as mineral flotation, wetting, coagulation, and many processes that involve surfactant aggregation, e.g., detergency.

THE POLARIZATION FIELD OF WATER STRUCTURED AT A HYDROPHOBIC INTERFACE

The dynamics of water molecules at a hydrophobic interface is different from that in bulk (13–16). Apparently, the absence of hydrogen bonding interactions with the surface makes water molecules move slower than in bulk (2), and facilitates an orientational ordering of these water molecules (17). Some immediate consequences of the depletion of water-water HBs, such as a “red shift” of the relaxation frequency of water and a decrease of the dielectric susceptibility, were reported in our previous article (2). Recently (26–28), several other aspects of the depletion of the HBs of water under hydrophobic confinement came into discussion. Recent experiments on the orientational dynamics of water molecules under an amphiphilic confinement (29) provided further support for the theoretical predictions in Despa et al. (2). Thus, these measurements demonstrated that, in contrast with bulk water, the anisotropy of the orientational dynamics of confined water molecules displays a second frequency relaxation component, which is “red shifted”. Similar behavior was observed in the dynamics of water confined at the surface of monellin, which is a mostly hydrophobic protein (30). It has been measured that the main component of the frequency relaxation of the hydration water is also “red shifted”. The estimated value is in excellent agreement with the theoretical prediction (2).

The inhibition of H-bond exchange between water molecules at a hydrophobic interface hinders the reorientation of the water molecular dipole and facilitates the occurrence of persistent dipole pairs (2). The spacing 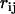between the molecular dipoles in a pair depends on an entropic penalty, which measures the depletion of water H-bonding. For instance, if m is the average number of H-bond exchange possibilities for a bulk water molecule and f is a parameter measuring the degree of depletion of these H-bonds at the hydrophobic interface, the entropic penalty of the interface water molecules will be (2). Consequently, the variable 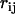can take any value in the range given by the typical distance between bulk water molecules a₀ (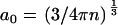) and 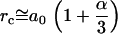, , 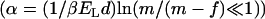the critical distance between two dipoles in a pair. The distance 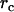is derived from equilibrium energy considerations (2). Here, 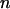is the number density of bulk water, d is the magnitude of the dipole moment of a single water molecule (for convenience, we assign 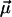to have a magnitude of unity), and 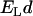is the Lorentz energy of a dipole pair, ; 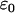represents the dielectric constant of the vacuum. This pair correlation depends also on temperature T ().

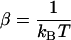Because 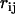is random within its range (), the vector dipole field at each site in the correlated region is also a random variable, and so is the thermodynamic average 〈…〉 of the water molecular dipole moment 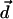, 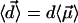. Therefore the mean value of the water molecular dipole in a fixed internal field 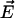of all the other water molecular dipoles in the correlated region is obtained by averaging 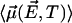over the probability distribution of all fields. This is . 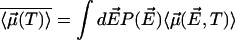The probability distribution of the random internal field acting on each water molecule in the correlated region is given by the self-consistent integral equation (2)

(1)

with 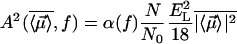and 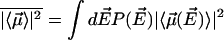. Here is the number of sites in the correlated region, N of which are occupied by molecular dipoles. In principle, N₀ is a measure of the water-accessible surface area ASA of the hydrophobic unit, i.e., 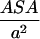, where a is the radial dimension of a water molecule.

By using Eq. 1 we readily obtain the average polarization in the correlated region as a function of T from the equation

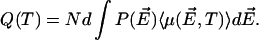(2)

For simplicity, we assume in the following that 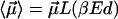, where 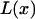is the Langevin function . Fig. 2 shows as a function of . The curves reflect water behavior under various hydrophobic depletions f = 1, 2, and 3. We also note that f can be related to the shape of the hydrophobic unit and that, due to obvious geometrical considerations, the situation f = 3 corresponds to water molecules rotationally immobilized by hydrophobic interfaces (caged water); f = 2 is appropriate for describing water molecules at planar interfaces. Small hydrophobic species lead to and a subsequent decrease of ordering. Therefore f→1, in this case, which yields small values for 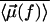; see Fig. 2. A fraction of 10–15% of correlated water molecules persists above room temperature (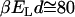). This vanishes rapidly with increasing T, 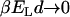, and approaches 1 asymptotically at low temperatures, 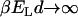, (not shown).

FIGURE 2.

The effective polarization as a function of the temperature-normalized field for 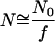. The curves reflect the behavior of water molecules under various degrees of hydrophobic confinement f = 1, 2, and 3.

THE PRECURSOR STAGE OF THE HYDROPHOBIC AGGREGATION: THE LONG-RANGE POTENTIAL OF HYDROPHOBIC ATTRACTION

Basic electrostatic principles insure that the domains of polarized water will establish long-range dipole-dipole interactions with each other. These interactions depend on the magnitude of the effective polarization fields 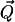(see Fig. 1 a). Therefore, if the hydrophobes are free to reorient and move in water, the shells of polarized water will drag these solutes together (18,31); this also explains how like-charged species can show attraction (31). This is because the dipole-dipole attraction is lower in energy than the dipole-dipole repulsion.

Moreover, if the hydrophobic units are polarizable (32), the polarizing field of outer correlated water dipoles induces a dipole , , along the axis () of highest polarizability of the molecule (see Fig. 1 b). Here, γ is the polarizability of the molecule and l is its characteristic length. They depend on the geometry of the hydrophobic molecule. The overall average interaction energy between two identical (nonrigid) hydrophobic units results in an attractive energy term varying as of the form

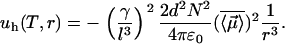(3)

Here r can be regarded as the instantaneous distance between two neighboring hydrophobic units. If we write , where 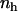is the density of hydrophobic units (the number of hydrophobic units in the volume V), then Eq. 3 can be expressed in the form

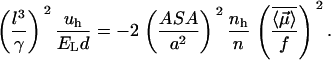(4)

By looking at the above equation, we can see that, to strengthen the interaction, water molecules must leave the thin layer separating two hydrophobes when the system comes to equilibrium (7–10). This shows that, within the Berne model (7–10) of dry hydrophobic surfaces in contact at equilibrium, the forces that bind hydrophobes together can perfectly well be all the van der Waals contacts between them. But those forces have short range, and they cannot account for why the hydrophobes ever want to come together. The interaction mechanism described by Eq. 3 gives the long-range potential that induces them to approach one another. Then, when they are very close, the entropy of releasing the water layers (4–10) and of course the van der Waals attractions may well provide enough driving force to “dry out” the contact surface.

DISCUSSION

Equation 4 allows one to compare the strength of the hydrophobic interaction 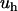with the Lorentz energy 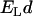of a dipole pair. We can see that the hydrophobic interaction depends directly on the hydrophobic exposure to water (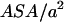) and on the relative volume partition of the two phases (). For small hydrophobic species we have 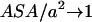, which also means a low ordering () because small hydrophobic solutes cannot deplete many H-bonds. This, in turn, yields small values for , which may eventually increase by increasing 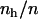. The attractive energy 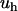depends explicitly on the shape of the hydrophobic molecule through γ and l and, implicitly, through the depletion parameter f, as discussed above. Because 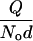decreases at high temperatures as shown in Fig. 2, thermal agitation can be sufficient to overcome hydrophobic attraction ( 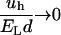for ). Thus the attraction between the two hydrophobes is typically low in comparison with usual electrostatic forces () and depends on the amount of correlated water at the interface. However, in the range of temperatures of biological interest (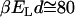), the hydrophobic attraction can be sufficiently strong to keep nonpolar molecules together. For example, under the assumptions that the relative volume partition of the water and hydrophobic species is , the hydrophobic molecules are nonrigid, and 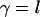, the energy of the attraction per surface area 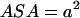(where a² represents the surface area required to place a H-bond), at 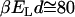, is 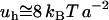. This is the order of the magnitude of the energy of H-binding of water molecules at a protein-water interface at physiological temperature, 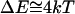per bond () (33). We readily estimate that 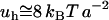is also in the range of the measured value for the surface tension of oil-water interface (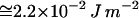) (34).

Another interesting observation is that the induced dipole 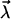may align water dipole pairs along the axis of high polarizability of the molecule. This second-order perturbation field is purely the result of induction and has a self-consistent character. This is the field acting on the water molecular dipoles 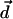due to the electric dipole 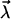induced by their polarization field 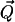in the hydrophobe. This interaction is always attractive and reveals that oil and water molecules actually attract each other (35). Being a second-order effect, this attraction is weaker than the attraction of water molecules for each other (21).

Several interesting experimental observations need to be mentioned at this point. More than a decade ago (19), atomic force microscopy (AFM) measurements showed that the energy of attraction between two hydrophobic monolayers deposited on mica, at 3 – nm separation distance and at 25°C, is about 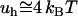per A°², which is in the range of predictions of this theory. The origin of the attraction between such surfactant-coated surfaces is subject to a long controversy (see Meyer et al. (20) for a chronological review). Recently (20), AFM images of such surfaces showed that, after immersing them in water, the hydrophobic monolayer transforms in patchy bilayers. Thus, the positive charges on the surfactant bilayer and the negative charges on mica naturally align themselves to generate a long-range electrostatic attraction between these surfaces. In this context, only the initial step of forming patchy bilayers after immersing the surfactant in water would be a hydrophobic effect. An interesting question is “What triggers this spontaneous transformation?” Only the weak van der Waals interaction of water with the hydrophobic monolayer might be not enough to detach the surfactant coat and make it roll on the mica substrate. Our approach suggests that the polarization of water at the interface with the hydrophobic monolayer might play an important role in initiating this transformation. Moreover, the long-range interaction between the surfactant-coated surfaces reported by Mayer et al. (20) is likely to be augmented by the polarizability of the hydrophobic monolayer itself, in the manner we discussed above.

It is also worthy mentioning that the above estimate of the hydrophobic attraction (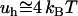 per A°²) is also in the force range measured in spontaneous resealing of hydrated lipid pores in a plasma membrane (36). To reseal spontaneously, these pores cannot exceed a radial dimension of ∼1 nm or less (37). In addition, sealing larger pores in a plasma membrane is mediated by amphiphilic polymers, and the efficiency of sealing seems to depend critically on the presence of the hydrophobic core in the polymer structure (38). Thus, this approach can be valuable in optimizing the structure of surfactants for sealing disrupted membranes after injuries.

LONG-RANGE ATTRACTION BETWEEN HYDROPHOBES IN WATER CAN CHANGE THE MAGNETIC SIGNAL OF SURROUNDING WATER

Because the dipole correlation makes water molecules move more slowly at the biological interface (2), we can predict that the transverse magnetic relaxation time of these water molecules decreases in comparison with that of bulk water (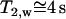). By quantifying the delay time in the relaxation process induced by different fractions 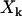of interface water protons, magnetic relaxation measurements not only can detect this slow moving water in solutions containing biomolecules, but can also provide details about the incipient stage of the hydrophobic aggregation described above, as follows. Suppose that one measures the transverse magnetic relaxation time T₂ of water protons in a solution containing hydrophobic molecules and η percent water. At the time 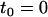, when hydrophobes are well dispersed, the measured T₂ represents the effective relaxation of a system with two phases (k = 2): water protons surrounding a single hydrophobic molecule 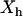, which, according to the scaled particle theory (39), can be expressed by 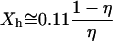, and the remaining bulk-like water 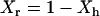. At , the long-range interaction between hydrophobic molecules would lead to the formation of large hydrophobic assemblies caging water molecules inside. This introduces a new water phase 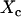, which is a function of the average packing density of a hydrophobic assembly ρ. The observed transverse relaxation time would change to a new value 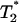(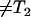). This new value can be predicted based on the Zimmerman-Brittin model (ZB) (40). The ZB model assumes that the single relaxation rate 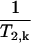of water molecules is different in each water phase (). This depends on the Larmor frequency of the MR scanner (ω) and values of the time (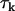) for thermal randomization of each spin population , which can be computed or measured experimentally. In Fig. 3 we present 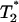as a function of η for various (imposed) values of the parameter ρ. We can infer from this result that the occurrence of hydrophobic assemblies (ρ > 0) is likely to change the MR signal of surrounding water. Therefore, measurements of magnetic relaxation of water in solution containing hydrophobic solutes can prove the existence of the precursor, long-range interaction regime of the hydrophobic aggregation. In addition, a kinetic T₂-MR imaging measurement of hydrophobic solution based on the above scheme would allow us to derive actual 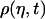maps. These maps can be used to extract dynamical information about hydrophobic interactions.

FIGURE 3.

Predicted trends for the value of the transverse magnetic relaxation time of water protons in solutions containing hydrophobic molecules that interact via long-range attraction forces. For calculations we used the Zimmerman-Brittin model discussed in the text and assume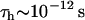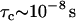d , , , , and .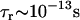

FINAL REMARKS

By employing basic molecular principles, we have shown how water molecules with depleted H-bonds and slow reorientation of their intrinsic molecular dipoles organize themselves around hydrophobic units and give rise to polarization fields that can set effective long-range attractions between these hydrophobic units. The analysis reveals that the mechanism of the hydrophobic interaction may involve an initial step stage in which nonpolar solutes approach one another via a long-range electrostatic potential. This precursor regime occurs before the entropy of releasing the water layers may well provide enough driving force to “dry out” the contact surface. This theory offers a practical way to quantify these hydrophobic interactions and to correlate the solvent effects to the effective interactions between biomolecules. We believe that this is the first approach that shows that an effective force of attraction between hydrophobes in water can be derived without detailed assumptions of the structure of the hydrophobe-water interaction. The strength of this force can be measured directly from AFM images of a hydrophobic molecule tethered to a surface but extending into water, and another hydrophobe attached to an atomic force probe.

This theory predicts the consequences of confining water in nanoscale hydrophobic environments and offers a reliable way to describe them in a quantitative manner. The approach can be valuable in questions related to various engineering applications as, for example, controlling the formation of nanoparticles, improving the quality of surface catalysts, as well as designing synthetic molecular chaperones. Also, understanding essential features of the hydrophobic hydration opens new ways for using MR imaging to infer structural changes at the molecular level in cells and living tissues (e.g., deciphering MR images of biological tissues containing denatured proteins), an initiative with immediate clinical applications.