Magnetic Optimization in a Multicellular Magnetotactic Organism

Abstract

Unicellular magnetotactic prokaryotes, which typically carry a natural remanent magnetic moment equal to the saturation magnetic moment, are the prime example of magnetically optimized organisms. We here report magnetic measurements on a multicellular magnetotactic prokaryote (MMP) consisting of 17 undifferentiated cells (mean from 148 MMPs) with chains of ferrimagnetic particles in each cell. To test if the chain polarities of each cell contribute coherently to the total magnetic moment of the MMP, we used a highly sensitive magnetization measurement technique (1 fAm²) that enabled us to determine the degree of magnetic optimization (DMO) of individual MMPs in vivo. We obtained DMO values consistently above 80%. Numerical modeling shows that the probability of reaching a DMO > 80% would be as low as 0.017 for 17 randomly oriented magnetic dipoles. We simulated different scenarios to test whether high DMOs are attainable by aggregation or self-organization of individual magnetic cells. None of the scenarios investigated is likely to yield consistently high DMOs in each generation of MMPs. The observed high DMO values require strong Darwinian selection and a sophisticated reproduction mechanism. We suggest a multicellular life cycle as the most plausible scenario for transmitting the high DMO from one generation to the next.

INTRODUCTION

Magnetotactic bacteria (MTBs) are motile aquatic prokaryotes (microorganisms without nucleus) that have the ability to propel along geomagnetic field lines (magnetotaxis) (1). MTBs synthesize intracellular ferrimagnetic crystals, called magnetosomes, which are typically arranged in the form of one or several chains and impart a permanent magnetic dipole moment to the bacterium (2). From the viewpoints of structural complexity, magnetism, and self-organization, the most intriguing magnetotactic organisms reported thus far comprise the group of multicellular magnetotactic prokaryotes (MMPs), also referred to as magnetotactic multicellular aggregates, and more recently, as magnetotactic multicellular organisms (3–7). For a detailed review of the MMP group, see Keim et al. (8). Depending on the variety (location) and maturity level, an MMP consists of between a dozen and not more than 45 Gram-negative, flagellated cells, and measures between 4 and 9.5 μm in diameter (7) (Fig. 1 A). The cells have an approximately pyramidal shape and are distributed radially about an acellular compartment in such a way that each cell has contact to both the external environment and the acellular center (7). Each cell contains up to 50 magnetosomes, usually made of the ferrimagnetic thiospinel greigite Fe₃S₄ (4) and arranged in planar arrays of two to five chains, located at the periphery of the cell (Fig. 1, B and C). The flagellar movement of the cells is highly coordinated and allows the MMP to swim not only along magnetic-field lines, but also sideways when it reaches the edge of the water film. Escape motility against the magnetic-field direction, also referred to as rapid “ping-pong” excursions (5,9), demonstrate overall coordination of motion in the MMP in such a way that a number of cells simultaneously start to activate their flagella bundles in case the MMP needs to accelerate, for example, when escaping from unfavorable redox conditions.

FIGURE 1.

Electron micrographs of the MMP. (A) Scanning electron micrograph picture showing the spherical arrangement of cells in the MMP. (B) Part of an MMP in whole mount. The TEM picture shows the arrangement of the magnetic crystals in the form of double or multiple chains. The MMP has partly disintegrated due to desiccation. Bars 1 μm. (C) Thin section of an MMP, showing the natural radial arrangement of cells. The magnetosomes (dark) are found mainly near the periphery of the organism.

The symmetric structure of the MMP and the morphological equivalence among its cells a priori excludes any type of cellular differentiation, a diagnostic criteria commonly used to distinguish true multicellular organisms from other multicellular architectures, such as colonies or aggregates (10). However, up to this day no viable unicellular stages have been observed during the MMP life cycle. Each of its constituent cells is incapable of individual development, an observation that is in stark contrast to classic colony-forming multicellular prokaryotes, such as cyanobacteria, myxobacteria, or actinomycetes. This has led to the suggestion that the MMP may in fact represent a true multicellular organism. Recently, a multicellular life cycle has been postulated for the MMP (11), partly based on putative reproduction episodes observed under the light microscope (Fig. 2). Due to its slow in vitro reproduction rates, the probability of capturing a complete reproduction sequence is rather low and alternative ways of testing that postulate have to be explored.

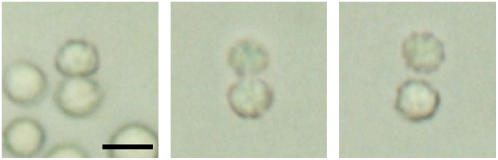
FIGURE 2.

Terminal stage of reproduction sequence under the LM. (Left) The MMP in its eight-shaped stage. (Middle) This stage was observed for 2 h, during which the MMP always moved as a unit. (Right) Eventually it splits up into two equal organisms. Bar = 10 μm. From our light microscopic studies we can rule out that the eight-shaped form represents two different MMPs adhered to each other. Collisions among MMPs are frequent events, but none of the collisions we observed resulted in a physical connection, let alone an indentation.

We will show here that indirect, yet strong evidence for the multicellular life cycle can be obtained from magnetic measurements on a population of MMPs. For complex body architectures such as that of the MMP, the efficiency of the magnetotactic response greatly depends on the coordinated movement of each cell's flagellae and the total magnetic dipole moment, which in turn depends on the relative orientation of the magnetosome chains to each other and their polarity distribution. Each cell i carries a remanent magnetic moment 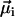, the direction of which is given by the orientation of the magnetosome-chain axis and its magnetic polarity. The total remanent magnetic moment of the MMP, 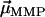, is thus given by the vector sum over all its N dipole moments 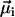, i = 1…N. A quantity commonly used in magnetism to characterize the domain state of a particle is the ratio of magnetic remanence to the saturation magnetization, here

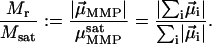(1)

If each cell were to align its magnetosome chain parallel to the other ones, with the same polarity, Eq. 1 would yield M_r/M_sat = 1 and the magnetic material would be used in the most efficient way. Given the complicated structure of the MMP, however, it is not likely that the chain axes all have the same orientation in space. Consequently, the natural (remanent) magnetic moment of the MMP will be lower than the saturation magnetic moment. Thus, the quantity M_r/M_sat is not the most appropriate measure of the degree of magnetic optimization in the MMP. M/M_sat still reflects the degree of control of the cell ensemble over the relative orientation of magnetosome chains, which is a function of the body structure, the mineralization process, the attachment of magnetosomes to the cell structural scaffold, the cell division mechanism, and the magnetostatic interactions between the chains.

It therefore makes more sense to ask for the maximum magnetic moment under the constraint that the chain axes are fixed in the cells and the cells are fixed in the whole MMP structure. We define the degree of magnetic optimization (DMO) as the magnitude of the natural remanent magnetic moment in relation to the maximum remanent magnetic moment under the given boundary conditions, i.e.,

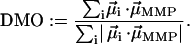(2)

The numerator in Eq. 2 measures the actual contributions of each dipole 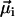to the resulting remanent moment 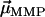. The normalizer measures the maximum possible contribution of each dipole under the constraint that the chain axis is fixed in space. The contribution of each 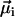is maximum (minimum) when 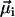has the same (opposite) polarity as 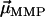, that is, when the 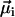points in the same (opposite) hemisphere as 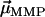. The effect of a brief, but strong magnetic pulse applied in the direction of 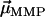is to reverse the polarity of those dipole moments that point in the opposite hemisphere. Therefore, the DMO according to Eq. 2 can be determined experimentally as

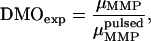(3)

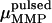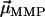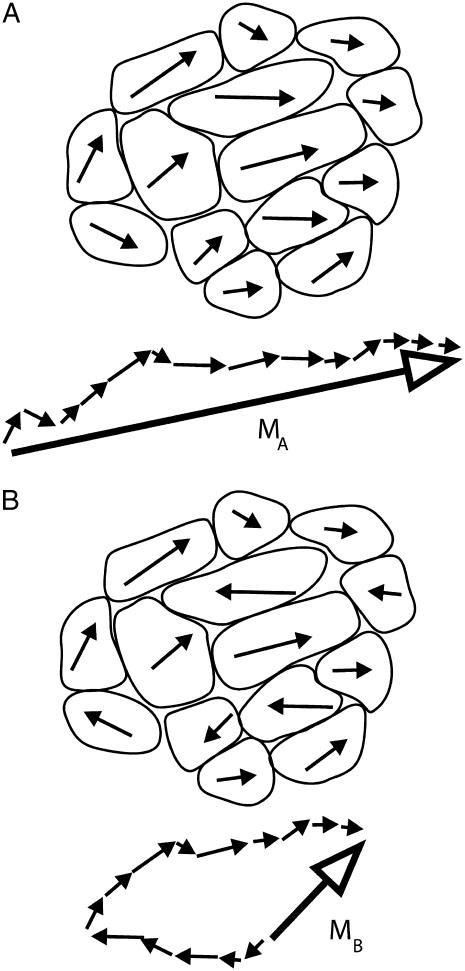
where is the magnetic remanence measured after the application of a brief but strong magnetic pulse in the direction of the natural remanence. A DMO of 100% is achieved when all the magnetic crystals in the MMP have the same polarity as (here South-seeking); in other words, when all 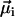-values point in the same hemisphere (see Fig. 3 A). If the magnetosome chains of adjacent cells on the other hand have alternating polarities (see Fig. 3 B), their magnetic moments would partially or fully cancel, yielding a largely reduced DMO, which makes magnetotaxis less efficient.

FIGURE 3.

Sketches to illustrate the degree of magnetic optimization (DMO). The (in-plane) projection of the magnetic dipole moment vector of each cell is represented by an arrow. In panel A, all the arrows point in the same hemisphere and so contribute coherently to the net magnetic moment vector M_A (resultant after vector summation, solid arrow). The resulting DMO is 100%, that is, a pulse applied in the direction of M_A will not increase M_A any more. In panel B, 6 out of 14 cells have reversed polarity (compared to polarity distribution in A), the length of the resultant, M_B ≈ 0.14 M_A. A strong magnetic pulse in the direction of M_B will flip the polarities of the six cells with reversed polarity, yielding the same configuration as in panel A. Thus, configuration A is the optimum of B, and the DMO in B is M_B/M_A ≈ 14% (Eqs. 2 and 3).

MATERIALS AND METHODS

Samples

Surface-sediment samples were collected from the hypersaline Araruama lagoon near Iguaba Grande (salinity ∼6%) in Rio de Janeiro state, Brazil. The geographic coordinates of the site are 22°51′S, 317°48′E, the local geomagnetic field inclination is –35°, and the intensity is 0.23 Oe (23 μT in SI). The MMPs found here on average consisted of 17.4 ± 3.6 cells (n = 148) per organism. The experimental determination of the DMO was done in the Munich lab. For each experiment, a few milliliters of sediment were placed on a coverslip and diluted with a drop of lagoon water. The MMPs observed were South-seeking, that is, their magnetic polarity is such that they swim antiparallel to an applied field, which in the natural environment makes them swim down into the sediment (12). Magnetotactic organisms other than the MMP were not observed in the sediment.

In vivo DMO measurements

For our magnetic studies, we focused on the central part of the fluid drop since the swimming behavior of the MMPs near the edge of the fluid film differs radically from the free motion displayed in the inner parts of the fluid. To measure the magnetic moment of individual MMPs in vivo, we used the rotating-field technique, based on the swimming behavior of magnetotactic organisms in a magnetic field that rotates in the optical plane of the microscope (13–15). The observations were carried out in the “bacteriodrome,” a light microscope (Leitz Laborlux D, Leitz, Wetzlar, Germany) equipped with two independent rectangular coils to realize various field situations and a smaller pair of coils to generate a magnetic pulse. In a rotating magnetic field, a magnetotactic organism is forced to swim on a circular trajectory, such that the magnetic torque is counterbalanced by a viscous torque, that is,

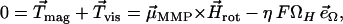(4)

where 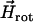is the magnetic field rotating with angular velocity Ω in the focal plane, η is the viscosity of the medium, F is the viscous resistance factor, and 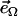the unit vector pointing along the axis of rotation. For a spherical organism such as the MMP, 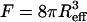, where R_eff is the hydrodynamic effective radius. Above a critical frequency Ω_crit, the viscous torque becomes too large for the organism to follow the rotating field and it escapes the circular trajectory, from which its magnetic moment is obtained as

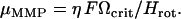(5)

Alternatively, one could use the u-turn method (16–18), by which the magnetic moment can be determined from the width of the u-turn executed by a bacterium after an instantaneous polarity reversal of a direct field 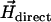applied in the optical plane. That method turned out to be less robust than the rotating-field method since the MMPs would perform a u-turn not necessarily in the optical plane, from which only the apparent width of the u-turn can be determined. Similar to magnetotactic cocci, the axis of the net magnetic moment of the MMP does not coincide with the flagellar propulsion axis, which gives rise to a helical trajectory about the axis of 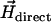(19) and often results in a u-turn plane that is inclined with respect to the optical plane. This also makes it difficult to pinpoint the onset and end of the u-turn motion. Another advantage of the rotating-field method over the u-turn method is that the former is insensitive to variations in swimming speed since the magnetic moment depends only on the escape frequency (as long as we can rule out small-scale fluctuations in fluid viscosity). Besides, variations in swimming speed can easily be monitored by the diameter of the circle the swimming microorganism describes in the rotating field.

To obtain the DMO, we devised two different protocols—one to study individual organisms, the other one on an ensemble of MMPs to improve the statistics. The first protocol consisted of measuring the backfield remanence curve of individual organisms, which allows one to determine the optimum magnetic moment (and hence the DMO of individuals), as well as the field strength required to turn the South-seeking organisms into North-seeking ones (i.e., the switching field). Starting from the natural state, we applied a sequence of pulsed magnetic fields of increasing strength from 50 to 1000 Oe (applied in opposite direction to a weak alignment field), and determined Ω_crit after each pulse with the rotating-field method. The duration of the pulse (≈2 ms) was brief enough to avoid letting magnetomechanical torques become effective, which would rotate the chains out of their fixed position. This way, we can manipulate selectively the magnetic state of each MMP without affecting their internal structure. The pulse field was always oriented antiparallel with respect to a direct alignment field (∼10 Oe) to make sure that all pulses of the series were applied consistently in the direction of the total magnetic dipole moment of the MMP. Note that while the experimentally determined values of the magnetic moment depend crucially on R_eff (see Eq. 5), the DMO according to Eq. 3 is independent of R_eff.

The second protocol consisted of determining the frequency distribution n(Ω_crit) in several groups of between 10 and 20 individual MMPs. Here, the statistical DMO is defined as

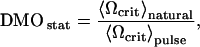(6)

where 〈Ω_crit〉_natural is the ensemble average of Ω_crit in the natural state and 〈Ω_crit〉_pulse is the ensemble average of Ω_crit after application of a magnetic pulse of 1000 Oe. After pulsing and measuring one subgroup, a fresh sample was placed under the microscope to observe a new subgroup that had not been pulsed yet. We observed occasionally how the microorganisms quivered briefly under the applied pulse, but without slowing down. We attribute this transient behavior to the peculiar helical trajectories of the MMP. The magnetic moment of the MMP performs a helical movement about the main propagation direction and therefore is not strictly co-linear with the pulse field either. Thus, for the brief duration of the pulse, the equilibrium motion along the helix is perturbed, which manifests itself as short tremor, before the stable helical trajectory redevelops.

RESULTS

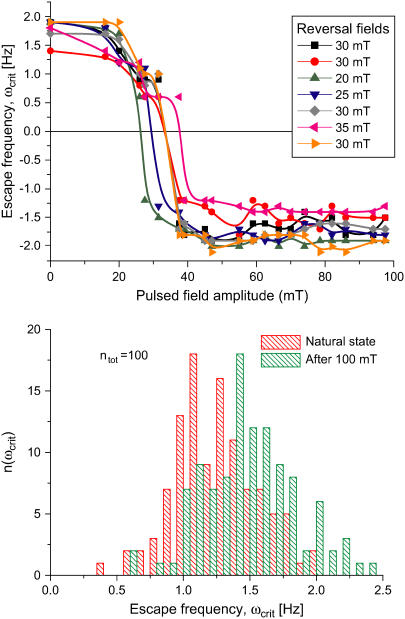
In Fig. 4, the individual and ensemble measurements are juxtaposed. The backfield remanence curves measured on individual MMPs are roughly similar (Fig. 4, top). The interpolated switching fields are located between 250 and 400 Oe and saturation is reached at ∼500 Oe. These values are on average 100 Oe higher than those Penninga et al. (20) obtained for their many-celled magnetotactic prokaryote (200 Oe, five organisms). Importantly, the obtained switching fields are at least one order-of-magnitude higher than the intensity of the rotating field used. Therefore, the comparatively weak magnetic fields used for the determination of the escape frequency do not affect the polarity distribution in the MMP. From Fig. 4 (top) one can also see that some curves have a small shoulder at approximately half the initial remanence value before the switching sets in. This bimodal distribution of coercivities can be explained by the following end-member cases: 1), uniform chain coercivities with a bimodal distribution of angles that the chains make up with the pulse field; and 2), a bimodal distribution of chain coercivities, where all chains have the same orientation, which in this case would be parallel to the external field. From the curves, it is not possible to distinguish which end-member case is the one most likely represented. Because of the distribution of chain coercivities, it is likely that the organisms can be demagnetized only if one happens to set the correct pulse-field strength (which is not known in advance, however). This requires a closer spacing of pulse-field strengths and hence more time, which is itself limited by the reduced lifetime of MMPs in the artificial environment (∼10 min, on average).

FIGURE 4.

Pulsed-field remanence measurements on MMPs. (Top) Remanence magnetization curves of individual organisms resulting from a sequence of remanent moment measurements and pulses applied opposite to a weak alignment field. The remanent magnetic dipole moment is expressed in terms of the escape frequency ω_crit (see Eq. 5). Note that the initial values of ω_crit (MMPs in the natural state) are close to the final values in each curve (after treatment with a pulse of 1000 Oe). The DMO is obtained from the ratio between the initial and the final ω_crit values, as 90%. (Bottom) Distribution of ω_crit from ensemble measurements. The frequency distribution n(ω_crit) in the natural state is centered at 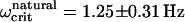and increases only slightly after pulsing (100 mT), with a new mean of 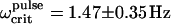(n = 109). The ensemble DMO amounts to 85% (Eq. 6).

Importantly, the initial values of Ω_crit (MMPs in the natural state) and with it the relative magnetic moments are close to the final values in each curve (after treatment with a pulse of 1000 Oe). According to Eq. 3, we obtain the DMO as ≈90%. While the escape frequency can in principle be determined with a nominal accuracy of 0.1 Hz, the wiggly shape of the remanence curves indicate that the uncertainty of this method is closer to 0.2 Hz. A possible source of this uncertainty are slight variations in the hydrodynamic effective radius R_eff caused by different modes of coordinated flagellar action (14,19).

The high DMOs determined on individual MMPs were confirmed by ensemble measurements (Fig. 4, bottom). The frequency distribution in the natural state is centered at 〈Ω_crit〉_natural = 1.25 ± 0.31 Hz (±1σ) and increases only slightly after pulsing, with a new mean of 〈Ω_crit〉_pulse = 1.47 ± 0.35 Hz (n_tot = 109 organisms). Possible reasons for the slight increase in remanence are: 1), the presence of a few magnetosome chains with opposite polarity, which reduce the total magnetic moment in the natural state, but become remagnetized after the pulse treatment, thus contributing to the total magnetic moment; and 2), more likely, the cluttered arrangement of the magnetosomes, as seen in Fig. 1 A. In the natural state, this disordered array of magnetosomes results in a distribution of individual magnetic moments around a preferential direction, which is reduced after the pulse treatment, thus increasing the total magnetic moment. From Eq. 6 we obtain an ensemble DMO of 85%.

The absolute values of μ_MMP according to Eq. 5 are difficult to determine because the hydrodynamically effective radius R_eff of the MMP is not known with certainty. R_eff is somewhat larger than the optically determined radius R_opt because of the additional hydrodynamic resistance of the flagella. Nevertheless, R_opt can be used as a minimum estimate of R_eff. Accordingly, we obtain lower estimates of μ_MMP in the range 3…12 · 10⁻¹² Gcm³ (10⁻¹² Gcm³ = 1 fAm²), or, 75…200 k_BT/Oe, where kT is the thermal energy. This is in good agreement with the values obtained with the u-turn method ((17), organisms 5 and 7 therein), which are minimum estimates as well. For greigite-bearing magnetotactic multicellular aggregates collected in New England, Rodgers et al. (5) reported values ranging from 0.5…1 · 10⁻¹² Gcm³, which is still sufficient to explain the magnetotactic response, but one order-of-magnitude smaller than the values obtained on the Brazilian MMPs. We can explain these higher dipole moments to some extent by the on-average higher number of cells or higher number of magnetic crystals in the Brazilian MMP, probably required to compensate the lower geomagnetic field intensity in Rio de Janeiro, which is half as much as in New England.

It is interesting to compare μ_MMP with the cellular dipole moment μ_cell, which can be conveniently estimated from the TEM pictures (Fig. 1 C). Each cell contains roughly 30 crystals composed of greigite. Despite much work on greigite, its saturation magnetization remains poorly characterized, with values ranging from 80 to 123 G (see compilation in (21)). We use the in-between value of 100 G (22) in the following. With average crystal dimensions of 50-nm width and 75-nm length (7,23), the typical cellular dipole moment amounts to 5 · 10⁻¹³ Gcm³ or μ_cell = 12 k_BT/Oe. Thus, μ_MMP/N ≈ 0.3…0.5μ_cell, which suggests that the chain moments are not aligned strictly parallel to each other (in which case their absolute moments would add up linearly), but deviate more or less from the direction of the total magnetic moment vector (as shown in Fig. 3 A).

THEORY

In the following, we will suggest a series of possible scenarios leading to the formation of an MMP, assuming that each generation is formed through agglomeration processes, in other words, that the MMP does not have a fully multicellular life cycle in the first place. The scenarios we discuss can be divided into two main categories: One with precursory magnetic cells agglomerating into an aggregate (MMPs Formed from Precursory Magnetic Cells), the other one with precursory nonmagnetic cells that develop their magnetosomes after aggregation (Cluster of Initially Nonmagnetic Cells). For each major scenario, we present a theoretical analysis of the probability of the resulting MMP to achieve a DMO value of 80–90%, as obtained in the in vivo experiments.

MMPs formed from precursory magnetic cells

Here we start by calculating the DMO of a cluster of identical cells with randomly oriented noninteracting magnetic dipoles (DMO of a Randomly Formed Cluster). We then consider the case of a hypothetical proto-MMP in which the magnetic cells are still free to rotate, before they become glued together and locked in their final orientation (Self-Organization of Magnetically Interacting Cells—Proto-MMPs with Magnetic Cells Free to Rotate). Finally, we numerically simulate the dynamics of the agglomeration of individual magnetic cells (Self-Organization of Magnetically Interacting Cells—Aggregation of Individual Cells into Proto-MMPs).

DMO of a randomly formed cluster

Random agglomeration of magnetic cells into an MMP forms a convenient null hypothesis since it can be tested directly on our experimental data. More specifically, random agglomeration denotes aggregation of magnetic cells into a cluster without magnetic forces playing a role during the agglomeration process.

The probability distribution of the DMO can be expressed analytically for an Ising-type (24) spin system s_1…N, in which each spin can take only two orientations, up or down (one-dimensional spins), that is, s_i = ±1. For k down-spins and N – k up-spins, there are ^NC_k = ^NP_k/k! different combinations that all yield the total magnetization (N – 2k) s, where ^NP_k = N!/(N – k)! are the number of permutations. For a configuration consisting of k down-spins and N – k up-spins, the DMO is the same as for N – k down-spins and k up-spins, and the probability distribution writes to

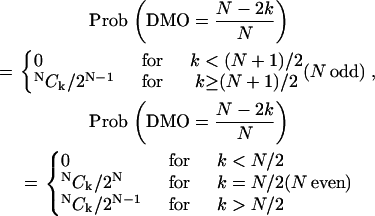(7)

The probability distribution of M/M_sat is the same as Prob(DMO). However, if the spins s_i are not of the same magnitude, but allowed to assume any value from the interval [– 1, 1], then Prob(M/M_sat) becomes a (right-sided) Gaussian and half as narrow compared to the pure s = ±1 case, while the distribution of the DMO can still be described by Eq. 7 to a good approximation.

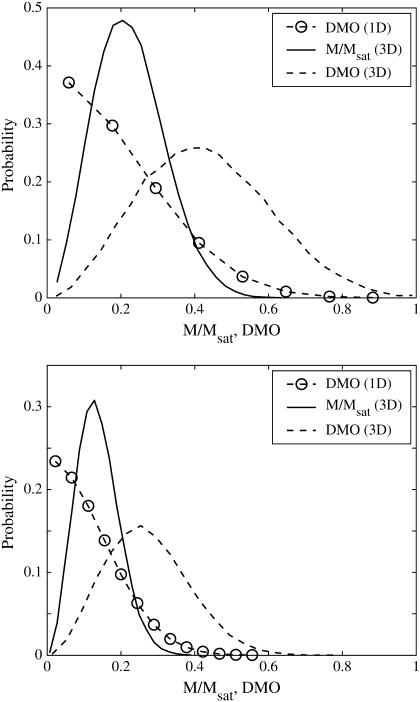
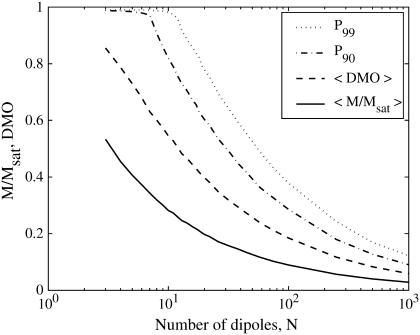
For dipoles oriented at random in three-dimensional space, we numerically approximated the probability distributions of the DMO and of M/M_sat. For a series of N, we produced some 5 · 10³ different configurations with N identical dipoles whose axes are oriented at random with random initial polarity. Two examples are shown in Fig. 5 for N = 17 and N = 45, which represent typical and maximum cell numbers observed in the MMP. Compared to the one-dimensional case, the probability distributions are now shifted to the right, that is, the probability of achieving a high DMO state in three dimensions is higher than in one dimension. The results for N = 3…1000 are summarized in Fig. 6. Table 1 shows the statistical results for some selected values of N. From Fig. 6 it can be seen that the expectation value of the DMO is roughly twice that of the (normalized) spontaneous magnetic moment. Significantly, the probability of obtaining a configuration with a spontaneous magnetic moment and reasonably high DMO decreases rapidly with N. For the case of N = 17, for example, only 1.7% of randomly assembled dipole configurations would have a DMO above 0.8. This is in stark contrast to our experimental results yielding DMO values of 85–90% for the majority of the studied organisms.

FIGURE 5.

Probability density of the DMO and spontaneous (normalized) magnetization for N = 17 (top) and N = 45 (bottom) randomly oriented dipoles (see DMO of a Randomly Formed Cluster). The DMO distribution for one-dimensional dipoles (spin-up or spin-down) is shown for comparison, which on average leads to smaller DMO values than can be achieved with dipoles oriented at random in space. In one dimension, the DMO distribution is identical to the magnetization distribution.

FIGURE 6.

The 99th and 90th percentiles of DMO, expectation value of DMO, and spontaneous (normalized) magnetization as a function of N. The probability of obtaining a high DMO value decreases rapidly with the number of dipoles per configuration.

TABLE 1.

Summarized results from the numerically determined probability distributions for randomly oriented dipoles

N	〈M/Msat〉	〈DMO〉	P90	P99	p > 0.8
5	0.41	0.73	0.98	0.99	0.454
8	0.32	0.60	0.91	0.99	0.204
12	0.26	0.50	0.76	0.96	0.068
14	0.24	0.47	0.71	0.89	0.044
17	0.22	0.43	0.66	0.84	0.017
22	0.19	0.38	0.58	0.75	0.005
32	0.16	0.32	0.49	0.64	0.000
45	0.13	0.27	0.42	0.55	0.000

Columns: N, number of dipoles per configuration; 〈M/M_sat〉, expectation value of spontaneous magnetization normalized by saturation magnetization; 〈DMO〉, expectation value of DMO; P₉₀, 90th percentile of DMO, that is, Prob(DMO < P₉₀) = 0.9; and P₉₉, 99th percentile of DMO. Five-thousand configurations were computed for each N to obtain a good estimate of the probability distribution. (p > 0.8: Prob(DMO > 0.8).)

Assuming a random agglomeration of magnetic cells, we can offer the following scenario: From the above, it can be argued that, in the case of MMPs formed through random agglomeration of magnetic cells, if the external magnetic field exerts no influence on the magnetic cells during the process of agglomerating and if dipolar forces between the cells can be neglected, then the whole range of DMO values from 0% to 100% would be observed in natural MMPs, which is not the case. Under this scenario, the observed MMPs with DMO ∼80% would represent the result of Darwinian evolution selecting those clusters with high DMO and a sophisticated reproduction mechanism is required to maintain the high DMO over generations (see Discussion).

Self-organization of magnetically interacting cells—proto-MMPs with magnetic cells free to rotate

One possibility to obtain the high DMO values observed in natural MMPs would be through self-organization of the magnetic cells within the cluster after the random agglomeration process, resulting in magnetization configurations which are energetically stable and yet magnetically optimized. Such a mechanism of course requires that the cells be free to rotate or that the magnetosome chains be free to rotate within each cell. Without rotational freedom, the realignment of a chain is restrained by its shape anisotropy. From Fig. 4 (top) the minimum chain coercivity can be obtained as 200 Oe. Since this is three orders-of-magnitude stronger than the geomagnetic field, there is no way of naturally altering the magnetic state of an aggregate with fixed cells and chains. In particular, the DMO distribution of an ensemble of aggregates would remain unaffected.

Because of the close spacing of cells in an MMP, the cells will interact magnetically and depending on the relative orientation of the dipole moments of adjacent cells, the interactions have stabilizing (magnetizing) and destabilizing (demagnetizing) effects. The relative influence of dipolar interactions can be estimated from the micrographs. Fig. 1 shows the spacing between adjacent cells to be ∼1 μm, which together with μ_cell = 0.5 · 10^{− 12} Gcm³ leads to a characteristic interaction strength of H_dip ∼ 0.5 Oe, that is, twice the local geomagnetic field strength. Importantly, the chains of adjacent cells appear to be oriented in the energetically unfavorable side-by-side position (demagnetizing) rather than in the more stable head-to-tail position (Fig. 1 B), although they may have some inclination to reduce the high energy associated with the side-by-side orientation. Given the negative interactions, the high-remanence state inferred from the measurements, albeit biologically reasonable, seems difficult to reconcile with magnetostatic principles. It is clear that the diameter of the organism and with it the spacing between the chains needs to be large enough so that the dipolar interactions (promote low remanence states) are outweighed by the external magnetic field (promotes high remanence states). We have determined the critical optical radius of the MMP, 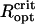, as 3.2 μm and 4.25 μm for N = 22 and N = 45 cells, respectively (see Supplementary Material for details of the modeling). Magnetization states with DMO = 1 are stable only for organisms with radius >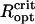, while they will relax into an equilibrium configuration with DMO <1 for 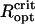. It is interesting to compare the critical sizes with typical MMP sizes. From the two histograms of organism size and number of cells per organisms (Fig. 1 in (11)), we infer that N = 22 and N = 45 cells per organism correspond to MMP diameters of ≤ 6.5 μm and ≥ 9 μm, respectively. Curiously, this in excellent agreement with the 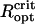values as determined with the unconstrained energy minimization (6.4 μm and 9 μm for N = 22 and N = 45). From 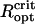, we obtain the critical volume per cell,

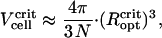as 6.2 μm³ (N = 22) and 7.1 μm³ (N = 45). Again, these values are in good agreement with the cell dimensions as determined by confocal laser scanning microscopy (11). The numerical coincidence may be fortuitous and cannot be used to conclude that the natural MMPs have DMOs near unity. The crucial question to be answered first is whether or not cell rotations are possible in an agglomerate during the early stage of formation. Chain rotations are unlikely to occur because magnetosome chains in most magnetic bacteria are attached to cytoskeleton filaments (25,26) to transfer the magnetic torque effectively to the cell body.

Self-organization of magnetically interacting cells—aggregation of individual cells into proto-MMPs

So far we have made no assumptions on the specific processes that might lead to the formation of an MMP-like aggregate from separated cells. The best-known example of aggregation of bacterial cells to form a multicellular body is the formation of fruiting bodies by myxobacteria. These are gliding microorganisms found in soil that collectively prey on other bacteria. When the concentration of some nutrients decreases and the cells are in a high density, these bacteria secrete chemical signals that lead to aggregation and development of a complex fruiting body. During development, part of the cells die to form a stalk, and part of the cells differentiate into spores for dispersion (27).

One way into aggregation may be through band formation, as reported for dense cell suspensions (28–30). The formation of cell bands is a consequence of hydrodynamic coupling between swimming cells. This coupling is characterized by lateral attraction and longitudinal repulsion (31), leading to the formation of broad, thin bands of cells that translate with the broad side perpendicular to the common swimming direction. The magnetic interaction between adjacent cells has exactly the opposite effect to the hydrodynamic interaction and leads to lateral repulsion and longitudinal attraction. However, as shown by Guell et al. (31), magnetic interactions do not come into effect until the cells practically touch and so are negligible for the observed cell separation distances of five body diameters within a band. Interestingly, when the cells were subject to physiological stress such as high sulfide concentrations, the bands would collapse into aggregates of linear chains of cells (28), but not into spherical aggregates like the MMP.

From the considerations on band formation it becomes obvious why we can restrict ourselves to passive cells when simulating possible aggregation scenarios. We now assume that cells are subject to motion and rotation forced by magnetic interactions with the other cells (see Supplementary Material for computational details). Our parameters were as follows: geomagnetic field strength: 0.25 Oe; cellular dipole moment: 0.5 · 10⁻¹² Gcm³; diameter of each cell 2.4 μm, corresponding to a cell volume of 7.2 μm³, which is a little greater than the critical volume obtained in Self-Organization of Magnetically Interacting Cells—Proto-MMPs with Magnetic Cells Free to Rotate. Several configurations of loosely spaced cells with varying degree of order were chosen as the initial value of the problem, each configuration consisting of N = 13 cells. The initial arrangement of cells turned out to be less critical for the evolution of the system than was the initial configuration of dipoles. When the dipole of each cell was initially aligned with the external field, the cells would self-organize into linear chains or bent-chains with high DMO, but not into compact arrangements similar to the MMP, not even when starting from a configuration in which the central cell was in 12-fold coordination with its nearest-neighbors (see online movie in Supplementary Material). When, on the other hand, the initial magnetization configuration was chosen at random, we still observed chain formation as dominating agglomeration mode. The tendency to form chains was also observed for superparamagnetic clusters (32). In a few runs the cells agglomerated into cluster-like structures, but with DMO values close to zero. From this we can conclude that agglomeration into three-dimensional, close-packed aggregates with high DMO is not among the likely scenarios.

Clusters of initially nonmagnetic cells

The last scenario to be discussed is a cluster of nonmagnetic cells that start synthesizing magnetosomes once the aggregate is formed, that is, the cells already have the genetic machinery to synthesize magnetosome chains, but this does not happen until they form an aggregate. The magnetic polarity of a magnetotactic microorganism is generally epigenetic and the question now rises as to whether the weak geomagnetic field can control the polarity of growing magnetosome chains. It is clear that as long as magnetosome chains are not yet fully developed, their magnetic moment is small and magnetic interactions between the cells can be neglected. However, as we shall argue in the following, a growing crystal will not necessarily adopt the polarity of the external field, unless that crystal is free to rotate. Once a ferrimagnetic crystal has nucleated and starts growing, it inevitably goes through the superparamagnetic (SP) stage before reaching the stable single-domain (SSD) stage. SP particles cannot retain a stable magnetic remanence because the magnetization fluctuates in the crystallographic frame of the particle. (Concerning the interactions between two SP particles: The situation of two SP particles with dipole moments fluctuating in direction is analogous to two interacting rotating polar molecules. Here, the mean potential energy decays much faster with distance (d⁻⁶ law) than the interaction energy of two static dipoles.) As the crystal grows further and eventually arrives at the SSD stage, its magnetization will be blocked in stably. According to the theory of remanence acquisition by Néel (33), the ratio of crystals blocked with magnetization parallel to the external field direction to the ones blocked in the antiparallel state is

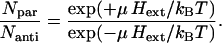(8)

For a population of greigite crystals with edge-length 50 nm (μ = 0.3 k_BT/G) we obtain a ratio of 1.17 at H_ext = 0.25 G. The fraction of crystals with same polarity as the external field in this case is only 17% larger than the fraction of crystals with opposite polarity. Once the first particle of a nascent chain has been magnetically blocked, its dipolar field will influence its local neighborhood much more than the external magnetic field and impose its polarity on adjacent particles in the chain. Therefore, Eq. 8, by controlling the polarity of the first particle of a magnetosome chain, also determines the overall distribution of chain polarities in a hypothetical MMP that starts out as nonmagnetic agglomerate. The chances of obtaining a high DMO when starting from a nonmagnetic MMP are not significantly better than for the random assembly of magnetotactic cells.

Note that this consideration also holds for the case of an MMP with all its chains composed of a nonmagnetic precursory mineral. In the MMP, Mackinawite (tetragonal FeS) was identified as a crystalline nonmagnetic precursory phase to ferrimagnetic greigite, with the conversion (probably topotactic) taking place within a few days (34). Again, the conversion will involve an SP to SSD transition. In case a precursory phase already fills the magnetosome vesicles, it is very unlikely that the converted ferrimagnetic crystal (SSD) is still free to rotate and so to align its magnetization vector with the local effective field (vector sum of external magnetic field and stray fields due to magnetic moments of adjacent cells).

DISCUSSION

In the case of MTB, evolution and natural selection in the Earth's magnetic field has maximized the efficiency of their magnetic orientation mechanism: bacterial magnetosomes are stable magnetic single domains (SD), characterized by a stable and uniform magnetization, such that the magnetic moment of the particle assumes the maximum value attainable. Meta-stable SD magnetosomes, which are SD when arranged in chains and multidomain when not, were reported as the only exception (35). The arrangement of magnetosomes in chains results in a net magnetic moment directed along the chain axis and equal to the sum of each magnetosome's magnetic moment. All these properties confer the MTB with a DMO that lies close to the maximum value that can be possibly achieved from physical principles, indicating a strict control of the organism over the mineralization process.

In the case of the MMP, our results demonstrate that it too is magnetically optimized to a large degree. This observation is otherwise expected, since the magnetotactic response of the MMPs is obvious under the light microscope. However, the interpretation of these results is far from straightforward if we consider the architecture of the MMP and invoke physical principles. Based on our theoretical analysis, we can rule out the following possible scenarios for the formation of the MMP when searching for a direct explanation of the high DMO values observed in the experiments:

1. Random agglomeration of individual magnetic cells (DMO of a Randomly Formed Cluster).

2. Magnetically driven agglomeration of individual magnetotactic cells (Self-Organization of Magnetically Interacting Cells—Aggregation of Individual Cells into Proto-MMPs).

3. Growth of magnetosomes after aggregation of nonmagnetic cells (Clusters of Initially Nonmagnetic Cells).

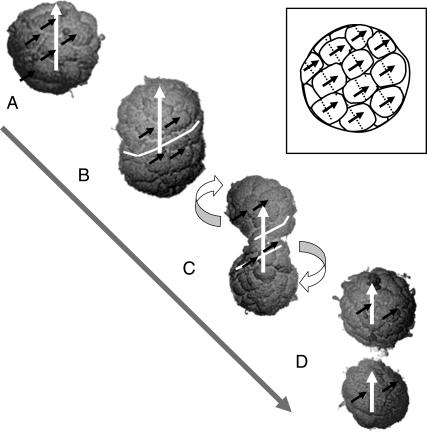
Any of these mechanisms result in a broad DMO distribution in the first generation of MMPs, with only a small percentage of aggregates reaching DMO values of 80% or more. Hence, our analysis shows that each generation of MMPs cannot be formed through agglomeration of individual cells, and still show a high DMO at the population level. We suggest that a continuously multicellular life cycle is required to transfer the high DMO over successive generations. Such a lifestyle was proposed by Keim et al. (11) and elaborated in Keim et al. (8), and is thought to happen in such a way that a mature organism, consisting of say 40 cells, splits up into only two organisms with 20 cells each (Fig. 7). This mechanism is in excellent agreement with the histograms (Fig. 1 in (11)), showing that the number of cells per organism varies between ∼20 and 45.

FIGURE 7.

Postulated reproduction mechanism to transfer the high DMO to the offspring in a continuously multicellular life cycle. The scanning electron micrographs of selected individual MMPs are assumed to represent four different stages in the life cycle: Mature organism, in which the cells are about to divide (A); differential movement of cells after cell division, entailing elongation (B); constriction (C); and fission at the organism level (D), which results in two equal organisms with the same general cell arrangement and direction of total magnetic moment (white arrows) as the parental one. Note that the cells in the MMP are arranged along a right-handed spherical spiral (see also Fig. 1 A). The magnetosome chains are always near the external surface (Fig. 1 B). Provided that the chains are oriented and polarized in the way depicted (solid arrows) and that the cell division planes (stippled lines) are perpendicular to the laps of the spiral (see sketch in inset), the chain polarity of each cell is transmitted coherently to its daughter cells. Cell movement can occur most easily along the spiral laps and, with it, about the polar axis. By moving along the spiral laps the cells can preserve the polar component of their magnetic moment vectors of the cells (note that the tangential components cancel each other because of the helical magnetization structure). Cells in the upper hemisphere move up along the spiral, cells in the lower hemisphere move down along the spiral (see curved arrows). The organism is being twisted due to the opposite sense of rotation, which conserves the total angular momentum. The white line, representing an equatorial segment of the spiral in panel B, starts coiling with proceeding cell motion (C). The shape changes in the reproducing organism can mathematically be described by varying the shape parameter of a Cassini oval of revolution, into which a spherical spiral is inscribed (8).

The possibility that magnetotactic cells after aggregation self-organize into a high DMO structure (Self-Organization of Magnetically Interacting Cells—Proto-MMPs with Magnetic Cells Free to Rotate) cannot be ruled out, but relies heavily on the unlikely assumption that the cells are still free to rotate once they have agglomerated. The usage of the term magnetotactic multicellular aggregate should therefore be avoided because it suggests without evidence that the organisms form by aggregation.

An altogether different possibility is the formation of a whole MMP from a single cell through cell division in radial planes, maintaining the magnetic polarity of the magnetosomes of the initial cell in the resulting adult organism. If all cells were equivalent, a strict control of both magnetosome biomineralization and cell division events could result in an adult MMP with a high DMO. Now we first consider a life cycle, in which the organism disaggregates into individual daughter cells that in turn divide successively according to the above scheme. The problem with this type of proliferation mechanism is that the daughter cells would all have different magnetic polarities with respect to their flagella axis. Thus, only a few would generate organisms with the correct magnetic polarity. Natural selection would eliminate the organisms with wrong magnetic polarity, rendering this type of proliferation highly inefficient. It follows that only the multicellular life style can sustain high DMOs. Note that the same argument applies to the evolutionary scenario, in which nonmagnetic cells agglomerated sometime in the past and then developed the trait of magnetotaxis, for example, by lateral transfer of magnetosome genes from other magnetotactic bacteria into each constituent cell of the aggregate. Once magnetotaxis has been perfected through time, a DMO of 80–90% would result. Since magnetotaxis here only appears at the organism level, and not at the individual level, a continuously multicellular life style is necessary for the MMP to preserve its magnetically optimized state during reproduction, and to retain its capability to swim along magnetic field lines.

To conclude, the results presented here indicate that the optimization of the magnetotactic response, and the need to transfer efficiently the magnetic polarity from the parental organism to the two daughter organisms, may be a major selective force toward multicellularity among magnetotactic prokaryotes. The MMP does represent a novel category of multicellular life form, adding more complexity to existing theories on the origins of multicellular life.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ online at http://www.biophysj.org.