Guest exchange in an encapsulation complex: A supramolecular substitution reaction

Abstract

Encapsulation complexes are reversibly formed assemblies in which small molecule guests are completely surrounded by large molecule hosts. The assemblies are held together by weak intermolecular forces and are dynamic: they form and dissipate on time scales ranging from milliseconds to days—long enough for many interactions, even reactions, to take place within them. Little information is available on the exchange process, how guests get in and out of these complexes. Here we report that these events can be slow enough for conventional kinetic studies, and reactive intermediates can be detected. Guest exchange has much in common with familiar chemical substitution reactions, but differs in some respects: no covalent bonds are made or broken, the substrate is an assembly rather than a single molecule, and at least four molecules are involved in multiple rate-determining steps.

Molecule-within-molecule complexes can be regarded as a phase of matter wherein guest molecules are kept inside host structures held together by strong covalent bonds. The earliest systems were prepared a decade ago by Cram and co-workers (1) and Collet and co-workers (2) and were kinetically stable. In these systems—carceplexes and cryptophanes—the hosts can stabilize reactive intermediates (3), produce new forms of stereoisomerism (4), and distinguish between guests and their mirror images (5). Encapsulation complexes are related recently synthesized structures in which hosts are held together by weaker forces, such as hydrogen bonds (6) and metal–ligand interactions (7, 8). The systems self-assemble reversibly from subunits and are dynamic (9). They can feature large cavities in which more than one guest can be accommodated (10), behave as nanometric chambers for bimolecular reactions, and offer promise in catalysis (11). We have now examined one such system, the conceptual “softball” (12) and address here a fundamental step of assembly and encapsulation—how guests enter and depart.

MATERIALS AND METHODS

The solvent p-xylene-d₁₀ was obtained from Cambridge Isotope Laboratories and was used as received for all guest exchange experiments. All the guests employed for the study were obtained from Aldrich. Adamantane (A) and ferrocene (F) were further purified by sublimation under reduced pressure. Standard solutions of the capsule 1⋅1 (2 mM) and the guests (10–50 mM) were prepared for the kinetic experiments. The guest exchange was monitored by ¹H NMR (600 MHz) with the probe maintained at constant temperature. For the study represented in Fig. 4 each data point was obtained under pseudo-first-order kinetic conditions. The components for all of the samples were mixed at 293 K, and data acquisition was automatically performed at 289 K every 3.5 min. For the experiment represented in Fig. 3 the data points were taken every 5 min.

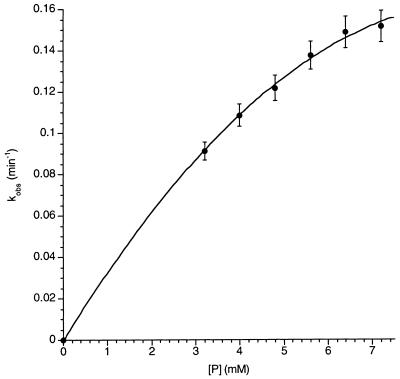
Figure 4.

Observed first-order rate constants for the guest exchange and kinetic parameters at large excess of the incoming guest P. For the reaction

under the steady-state approximation,

The rate constants were obtained at 289 K and 0.4 mM concentration of the fully loaded complex 1⋅A⋅1, and [A] = 3.2 mM. Error bars are estimated at 5%.

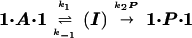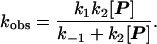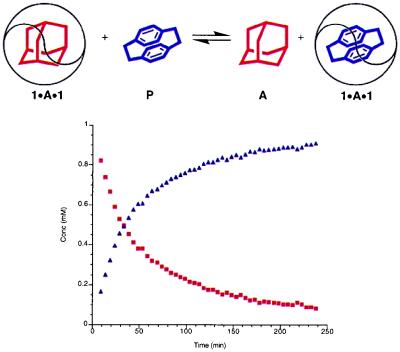
Figure 3.

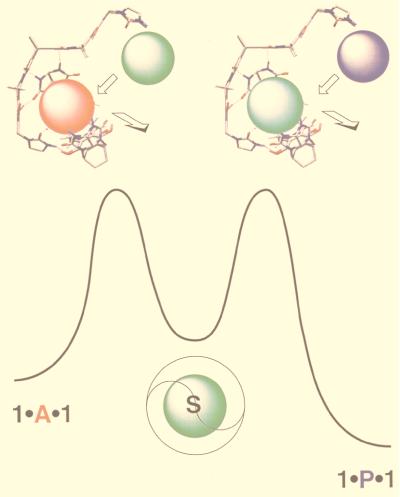
Replacement of adamantane (A; red) inside the softball by [2.2]paracyclophane (P; purple). The data were obtained at 295 K and 1 mM concentrations of the components in p-xylene-d₁₀.

RESULTS AND DISCUSSION

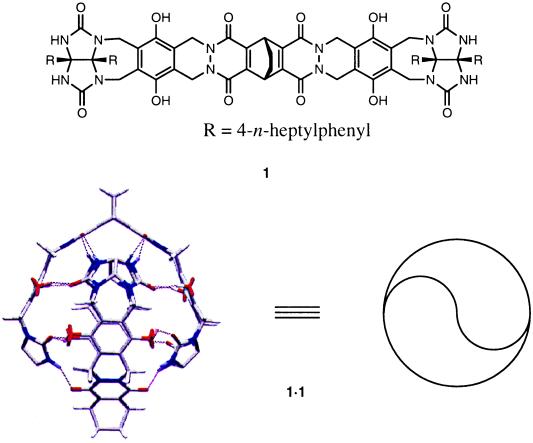
The softball consists of two self-complementary subunits held together by a seam of 16 hydrogen bonds in a roughly spherical assembly (Fig. 1). In solvents such as p-xylene-d₁₀ the NMR spectrum indicates a well defined structure, and addition of guests such as adamantane (A) or [2.2]paracyclophane (P) gives the respective encapsulated species within seconds. The sharp and widely separated signals for free and encapsulated guests are characteristic of an exchange rate that is slow on the NMR time scale: accordingly, sizable energetic barriers separate free and encapsulated states. Equilibrium binding studies show that A is a rather reluctant guest (K_a = 1.7 × 10³ M⁻¹) (11); some 8 equivalents of A are required before the solvent-filled softball is no longer visible in the NMR spectrum at ambient temperature. The larger P is a willing guest. In terms of the binding constant in p-xylene-d₁₀, a factor of more than two orders of magnitude favors P over A, and this feature allows the practically irreversible conversion of 1⋅A⋅1 to 1⋅P⋅1.

Figure 1.

Energy-minimized (13) depiction of the softball 1⋅1 and the structure of the monomer 1. The substituents (R) on the glycoluril units have been omitted for viewing clarity.

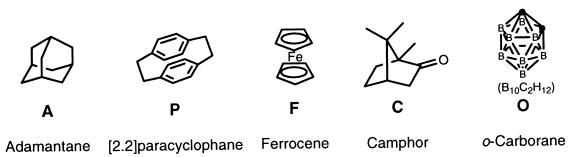
The substitution of A in the softball by P at millimolar concentrations is slow on the human time scale, and the reaction is followed conveniently by NMR. Similar behavior is observed in the displacement of ferrocene (F), camphor (C), or o-carborane (O) (Fig. 2) from the interior of the capsule by P, but the substitution of A was examined in detail.

Figure 2.

Structures of guests involved in the exchange study.

Fig. 3 shows the changes in concentration of 1⋅A⋅1 and 1⋅P⋅1 with time for the process at room temperature and the concentrations specified.

Lowering the concentration of 1⋅A⋅1 causes a decrease in the rate of substitution. To study the substitution under pseudo-first-order conditions (i.e., with a large excess of the incoming P), we lowered the temperature to 289 K. (At room temperature, the reaction is too fast to follow accurately by NMR at these concentrations). The reaction rate as a function of [P] is plotted in Fig. 4. At low concentrations the rate is proportional to [P], but at higher concentrations the rate approaches a maximum value of 0.16 min⁻¹. By further lowering the temperature (287 K), the plateau was obtained at lower concentration of incoming guest: the rate remained constant for [P] from 3.2 to 8 mM.

The data in Fig. 4 implicate a change in the rate-determining step of a two-step substitution process. With two steps, there must be an intermediate. Steady-state kinetic treatment of the intermediate (I) follows equations described by Huisgen (14) in certain Diels–Alder reactions of cyclooctatetraene in which its valence tautomer is intercepted by various dienophiles (15). The equation is shown in the legend of Fig. 4. At low concentrations of the incoming guest P, return of the intermediate to the starting capsule 1⋅A⋅1 is faster than its conversion to product 1⋅P⋅1, whereas at high concentrations the opposite is the case. The curvature of Fig. 4 indicates that the two processes, k₋₁ and k₂[P] have comparable rates in this concentration range.

What is the intermediate? Two plausible candidates involve the opening of “flaps” on the softball (16). Ring inversion of the six-membered heterocyclic ring fused to the hydroquinone ruptures 6 hydrogen bonds and opens one flap. A similar motion of an adjacent flap (a flap of the other monomeric subunit) breaks another 4 hydrogen bonds and leaves the resident guest exposed on two sides. Displacement of the resident guest by solvent or incoming guest can occur in a continuous manner. A related mechanism involves opening a second flap on the opposite side of the softball, breaking a total of 12 hydrogen bonds. In p-xylene-d₁₀ the energetic cost per hydrogen bond is likely to be about 2 kcal/mol, and the inversion of the rings should involve only small energetic costs, so the rate of formation of these structures is reasonably consistent with the value of k₁ obtained from the plateau in Fig. 4.

A second possible mechanism involves predissociation of 1⋅A⋅1 to give free A and the solvated softball. In this case the overall rate of return of the intermediate to 1⋅A⋅1 depends on [A], and we observe that increasing [A] by a factor of 4 (from 4.25 mM to 17 mM) lowers the overall rate of substitution by roughly a factor of 3 (from 0.079 to 0.026 min⁻¹) when [P] is held fixed at 0.62 mM. The presence of some direct displacement cannot be ruled out, but its contribution to the overall rate equation does not appear to be significant at these concentrations. A simple analysis of the change in rate shows that k₂ is comparable in magnitude to k₋₁, which is consistent with the results shown in Fig. 4. Furthermore, k₋₁ and k₂ can be deduced from the known association constant of 1⋅A⋅1 in p-xylene-d₁₀ (12), and we find that the encapsulation of guest at millimolar concentrations occurs in tens of seconds, providing an indirect measure of a rate that is too fast to measure directly.

The process by which A and P exchange with solvent in the softball is less clear. The mechanism could involve the direct S_N2-like displacement from the opened solvated softball, or it might require that the softball completely dissociate and reform around the guest. Intuitively, it would seem that the supramolecular S_N2-like displacement would be favored because it retains the stability of an additional 4–6 hydrogen bonds relative to dissociation, despite the added entropic cost. The opening of two of the flaps in the capsule creates an effective sluice through which the resident guest is carried into the solvent (Fig. 5). This mechanism is supported by comparison with the “tennis ball,” a smaller but similar structure with 8 hydrogen bonds, the complete dissociation of which takes place on the time scale of seconds (16). The additional 8 hydrogen bonds in the softball are expected to slow the rate several more orders of magnitude, placing it well beyond the time scale for substitution observed in this study.

Figure 5.

Proposed mechanism and transition state structures for guest substitution. Guest exchange does not proceed directly; rather, many individual solvent molecules (green) may enter and leave the interior of the softball between dissociation of adamantane (red) and incorporation of [2,2]paracyclophane (purple). In the structures, the substituents of the glycoluril units and some hydrogens have been omitted for viewing clarity.

Dissociation may be somewhat more facile than expected, however. An upper limit of the time scale and energetics of the dissociation rate of 1⋅P⋅1 can be obtained from heterodimerization experiments using two different softballs. To a solution of 1⋅P⋅1 was added another softball (lacking phenolic hydroxyl groups) (17). The appearance of the new heterodimer containing P requires the dissociation of 1⋅P⋅1 and takes place over the course of days. The time scale for dissociation from 1⋅A⋅1 should be 2–3 orders of magnitude faster if the dissociation kinetics fully reflect the decreased stability of 1⋅A⋅1 relative to 1⋅P⋅1, placing it potentially in line with the few minutes observed in this study for the predissociation.

Hemicarceplexes provided the first examples of supramolecular substitution reactions (18). Guest exchange in these systems was characterized as a unimolecular process in which dissociation of the outgoing guest creates an empty cavity before the incoming guest is permitted to enter. The exchange of guests in the hemicarceplexes involves high activation barriers because vacuums are created and bond distortions are required to provide openings large enough to allow the exit and entry of guest species (19). For the case at hand, the weak intermolecular forces that hold the systems together allow the substitution processes to take place rapidly under ambient conditions, and complete dissociation of the assemblies may not be required (20).

In conclusion, conventional kinetics can be used to detect reactive intermediates in an unconventional substitution process. We have demonstrated that the displacement of adamantane from the softball by [2.2]paracyclophane proceeds through predissociation of the guest from the softball in p-xylene solvent. Our current research efforts are focused on the mechanism of supramolecular substitution in capsules of other shapes and sizes (21).