Local Osmosis and Isotonic Transport

Abstract

Osmotically driven water flow, u (cm/s), between two solutions of identical osmolarity, co (300 mM in mammals), has a theoretical isotonic maximum given by u = j/co, where j (moles/cm²/s) is the rate of salt transport. In many experimental studies, transport was found to be indistinguishable from isotonic. The purpose of this work is to investigate the conditions for u to approach isotonic. A necessary condition is that the membrane salt/ water permeability ratio, ε, must be small: typical physiological values are ε = 10⁻³ to 10⁻⁵, so ε is generally small but this is not sufficient to guarantee near-isotonic transport. If we consider the simplest model of two series membranes, which secrete a tear or drop of sweat (i.e., there are no externally-imposed boundary conditions on the secretion), diffusion is negligible and the predicted osmolarities are: basal = c_o, intracellular ≈ (1 + ε)c_o, secretion ≈ (1 + 2ε)c_o, and u ≈ (1 – 2ε)j/c_o. Note that this model is also appropriate when the transported solution is experimentally collected. Thus, in the absence of external boundary conditions, transport is experimentally indistinguishable from isotonic. However, if external boundary conditions set salt concentrations to c_o on both sides of the epithelium, then fluid transport depends on distributed osmotic gradients in lateral spaces. If lateral spaces are too short and wide, diffusion dominates convection, reduces osmotic gradients and fluid flow is significantly less than isotonic. Moreover, because apical and basolateral membrane water fluxes are linked by the intracellular osmolarity, water flow is maximum when the total water permeability of basolateral membranes equals that of apical membranes. In the context of the renal proximal tubule, data suggest it is transporting at near optimal conditions. Nevertheless, typical physiological values suggest the newly filtered fluid is reabsorbed at a rate u ≈ 0.86 j/c_o, so a hypertonic solution is being reabsorbed. The osmolarity of the filtrate c_F (M) will therefore diminish with distance from the site of filtration (the glomerulus) until the solution being transported is isotonic with the filtrate, u = j/c_F.With this steady- state condition, the distributed model becomes approximately equivalent to two membranes in series. The osmolarities are now: c_F ≈ (1 – 2ε)j/c_o, intracellular ≈ (1 – ε)c_o, lateral spaces ≈ c_o, and u ≈(1 + 2ε)j/c_o. The change in c_F is predicted to occur with a length constant of about 0.3 cm. Thus, membrane transport tends to adjust transmembrane osmotic gradients toward εc_o, which induces water flow that is isotonic to within order ε. These findings provide a plausible hypothesis on how the proximal tubule or other epithelia appear to transport an isotonic solution.

Introduction

The most widely accepted model of epithelial transport is that salt is transported across the epithelium by a series of active and passive mechanisms, and water follows by osmosis (Whittembury & Reuss, 1992; Schultz, 2001). However, osmosis is not the only theory of how tissues transport water. Some recent reports have suggested the existence of transmembrane water pumps (Meinild et al., 1998; Zeuthen et al., 2001; reviewed in Loo et al., 2002). Electro-osmosis is another mechanism that probably has some role in fluid movement (McLaughlin & Mathias, 1985). Recently, Sanchez et al. (2002) and Fischbarg and Diecke (2005) suggested fluid transport by the corneal endothelium is driven by electroosmosis. Lastly, hydrostatic pressure is an essential part of water flow and its presence will alter osmotic gradients (Mathias, 1985). A comprehensive model that includes all of these factors would be complex and unlikely to provide much insight on the role of any particular factor. We therefore focus on osmosis, since it always plays an important role in transport, regardless of the presence of water pumps, electroosmosis or hydrostatic pressure. The goal is to understand the subtleties of osmosis through investigation of a series of simple models with different geometries and boundary conditions. Since most experimental data suggest epithelia are capable of near-isotonic transport, special attention will be given to understanding how local osmosis might lead to isotonic transport.

There has been a plethora of models of local osmosis and fluid transport by epithelia, starting with the three-compartment model of Curran and Macintosh (1962). In general, these calculations have all concluded that the transported fluid would be measurably hypertonic, unless some ad hoc assumptions were added to the model. For example, to make the transport nearer to isotonic, Diamond and Bossert (1967) located the site of solute transport at the apical end of the channel. Sackin and Boulpaep (1975) showed that if the basement membrane had an appreciable salt reflection coefficient, transport would be nearer to isotonic. With regard to isotonic transport, Ussing and Eskesen (1989) state: ‘‘None of the hypotheses advanced in the past seemed to explain the phenomenon convincingly.’’ They suggested that solute would have to be recirculated. This led Larsen et al. (2000) to derive a solute recirculation model. However, a perspective by Spring (2002) points out limitations of the recirculation model. Fischbarg and Diecke (2005) simply discarded local osmosis and modeled transport driven entirely by electro-osmosis. Thus, despite many years and many models, some important concept seems to be missing. The trend has been to make more complex models to explain the experimental observation of isotonic transport, whereas we have chosen to make simpler models to insure we truly understand local osmosis.

The relevant features of the osmotic hypothesis are illustrated in Fig. 1. Water and salt are thought to cross the membrane via independent pathways. Salt transport relies ultimately on the Na/K ATPase as the source of energy, but it also involves secondary active transport processes and electro diffusion of ions through membrane channel proteins. These processes depend on intracellular ATP, transmembrane voltage and Nernst potentials, hence they are not significantly affected by the small concentration gradients that drive water flow. In what follows, we will assume the transmembrane flux of salt j (moles/cm²/s) is established by factors outside of the scope of our analysis, so it enters the model as a constant, which is uniform along the apical or basolateral membranes, but constrained such that apical and basolateral membrane salt fluxes always balance. The transport of salt creates a transmembrane osmotic gradient Δc (M), which causes water to follow by osmosis. Water traverses the membrane primarily via the aquaporins, which are a class of integral membrane proteins that form channels permeable to water but not salt (reviewed in Verkman, 1989; van Os et al., 2000; King, Kozono & Agre 2004;). The presence of aquaporins confers a relatively high membrane water permeability P (cm/ s/M), which carries a water flow u (cm/s), where u = P Δc. Moreover, whereas Δc is established by j, it depends on u, since water flow convects solute away and reduces Δc. For example, if P is doubled, u will increase but it will not double. Indeed, as P → ∞, u will approach a limiting maximum value as Δc → 0. This limit can be deduced by considering the flux of salt to and from the membrane. As Δc →0, diffusion becomes negligible and j is carried by convection only, hence j → uc_o. The maximum limiting water flow is therefore:

Fig. 1.

The main components of transmembrane osmosis. Bulk solution is assumed to have osmolarity c_o, with possible local gradients of order Δc. Salt is actively transported across the membrane at a rate j nd water follows by osmosis at a rate u through an independent pathway, primarily via aquaporins. The presence of aquaporins confers a specific membrane osmotic permeability P, so the rate of fluid transport is determined by u = PΔc.

$$u=j/c_{\text{o}}\mathrm{\hspace{0.17em} }\text{isotonic\hspace{0.28em}limit}\text{.}$$ (1)

Since this is the theoretical maximum rate of flow, as argued by Ussing and Eskesen (1989), it cannot be attained; however, it is possible that fluid transport could be experimentally indistinguishable from this limit. First, we need to define P → ∞, which has no real meaning without some reference. Since u = PΔc ≤ j/c_o, we can deduce that:

$$\frac{\mathrm{\Delta }c}{c_{\text{o}}}\le \frac{j/c_{\text{o}}}{P{c}_{\text{o}}}$$

Define:

$$\epsilon =\frac{j/c_{\text{o}}}{P{c}_{\text{o}}}$$ (2)

The fundamental requirement is that P be sufficiently large so that ε is small, then the concentration gradient will be small. For a typical fluid transporting epithelium, a moderate value of P would be 3.3 × 10⁻⁴ cm/s/M, and a fairly large value of j would be 3 × 10⁻¹¹ moles/cm²/s, suggesting that ε < 10⁻³ (Whittembury & Reuss, 1992). These values of P and j refer to a unit area of membrane. Because of extensive membrane folding, the water permeability and solute flux per unit area of epithelium will be 20– to 50–fold greater, but ε depends on the ratio, so its value is not affected by folding. At the outset we can therefore deduce that all solutions will be nearly isotonic, but a much more detailed analysis is required to determine how closely u approaches its isotonic limit.

In what follows, the smallness of ε will be used to generate approximate analytic solutions of the transport equations. These perturbation solutions are in the form of a series of terms of increasing powers in ε. The first, or order-zero term, is independent of ε, while the next order-one term is proportional to ε. In general, the first two terms of such series are adequate to accurately describe the concentration gradients and fluid flow. This is verified by comparison of the analytic expressions with more exact computer-generated solutions for each model. Segel, 1970, first used this particular perturbation expansion to analyze the ‘‘standing gradient model’’ of Diamond and Bossert (1967). He derived analytic expressions to describe local osmosis when salt transport is localized to one end of a membrane tube. The work presented here is an extension of the original model of Diamond and Bossert and of the analysis by Segel.

Results

As indicated in the Introduction, the models will focus on local osmosis and not consider the effects of hydrostatic pressure, electro osmosis, voltage gradients in the lateral spaces or any sort of additional complications due to recirculation of salt across basal membranes, as suggested by Nedergaard, etal., 1999. We will simply evaluate the conditions in which local osmosis will lead to near isotonic transport. For simplicity, the analysis will consider only transcellular transport, so the apical junctions are assumed to be impermeable to salt and water.

A Simple Two-Membrane Model

The model shown in Fig. 2 (first proposed by Curran, 1960; Curran & Mclntosh, 1962) treats an epithelium as three compartments (basal, intracellular, and apical), separated by two membranes (basolateral and apical). Although this model may seem too simple, we will subsequently show that more complex and realistic models will often reduce to an equivalent of this simple model. Moreover, it illustrates the extreme sensitivity of local osmosis to the boundary conditions. Lastly, it illustrates the degree of spatial uniformity of the intracellular concentration of solute, c_i (moles/cm³). In subsequent calculations, c_i is assumed to be uniform, as suggested by the results presented here.

Fig. 2.

A simple two-membrane model of epithelial transport. (A) Secretion of fluid without boundary conditions on the secretion. The basolateral membranes are washed with a well-stirred solution of osmolarity c_o; the intracellular osmolarity C_i(X) is allowed to vary across the epithelium, but the calculations suggest it is essentially constant because difiusion is very effective over short distances; the secreted solution has osmolarity c_s, which is determined by the membrane water permeability and the rate of salt transport, j. Since the flux of salt in the secretion is carried entirely by convection, it is given by j = uc_s. Hence the boundary condition on the osmolarity of the secretion is c_s = j/u for model A. (B) The same simple model of an epithelium, but now each side is washed with a well-stirred solution whose osmolarity is c_o. Thus the difference in the two models is the boundary condition on the secretion, which is c_s = c_o for model B.

Figure 2A represents an epithelium secreting fluid when the secretion is not subjected to external boundary conditions (e.g., a tear or drop of sweat). At the apical surface, previously secreted solution is pushed away by newly secreted solution, so all of the secreted solution has the same solute concentration, c_s (moles/cm³). Since there are no diffusion gradients in the secretion, the flux of salt j (moles/cm²/s) is carried away from the apical surface entirely by convection (i.e., j = uc_s), hence the concentration of solute at the apical surface is c_s = j/u. Note that this boundary condition also applies to experimental situations where the transported solution (secretion or absorption) is collected and its tonicity measured (e.g., Diamond, 1964 Barfus & Schafer, 1984;). As will be seen in these calculations, when transport determines the osmolarity of the transported solution, transport is dramatically different from when the osmolarity is maintained the same on both sides of the epithelium (Fig. 2B). In Fig. 2B, both sides of the epithelium are assumed to be washed with a well stirred solution whose solute concentration is c_o, hence the boundary condition on the apical secretion is c_s = c_o. Except for this difference in the apical boundary condition, the transport equations describing Fig. 2A or B are the same. In this simple model, the flux of salt j and fluid u are both constants. We assume the value of j is known, so it is the independent variable whereas u is the dependent variable to be determined. Within the cell layer, j is carried by a combination of diffusion and convection:

$$\begin{array}{l}j(\text{diffusion)}=-D_{\text{i}}\frac{\text{d}{c}_{\text{i}}(x)}{\text{d}x}\\ j(\text{convection)}=u{c}_{\text{i}}(x)\\ j=u{c}_{\text{i}}(x)-D_{\text{i}}\frac{\text{d}{c}_{\text{i}}(x)}{\text{d}x}\end{array}$$ (3)

Fluid follows the solute flux j due to osmotic gradients that are generated across apical and basolateral membranes. Since the fluid entering the cells basolaterally must exit the cells apically, there are two expressions for fluid flow:

$$\begin{array}{l}u=P_{\text{BL}}(c_{\text{i}}(0)-c_{\text{o}})\\ u=P_{\text{A}}(c_{\text{s}}-c_{\text{i}}(h))\end{array}$$ (4)

The difference between the models in Fig. 2A vs B is the value of c_s

$$c_{\text{s}}\stackrel{A}{‗}\hspace{0.17em}j/u\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{c}_{\text{s}}\stackrel{B}{‗}\hspace{0.17em}{c}_{\text{o}}$$ (5)

For these models, isotonic transport is the limiting situation where:

IsonaticTransport

$$\begin{array}{l}u=j/c_{\text{o}}\\ c_{\text{i}}(x)=c_{\text{o}}\\ c_{\text{s}}=c_{\text{o}}\\ j_{\text{i}}(\text{diffusion})=0\end{array}$$

To calculate how closely these models approach their isotonic limit, it is useful to normalize the transport variables with respect to their isotonic values. The normalized parameters are:

$$\begin{array}{l}y=x/h\\ C_{\text{i}}(y)=c_{\text{i}}(y)/c_{\text{o}}\\ C_{\text{s}}=c_{\text{s}}/c_{\text{o}}\\ U=u/(j/c_{\text{o}})\end{array}$$ (6)

The normalized transport equation is given by:

$$\begin{array}{l}1=U{C}_{\text{i}}(y)-\frac{1}{\epsilon k_{\text{i}}}\frac{\text{d}{C}_{\text{i}}(y)}{\text{dy}}\\ \epsilon =\frac{j/c_{\text{o}}}{P_{\text{BL}}{c}_{\text{o}}}\\ k_{\text{i}}=\frac{P_{\text{BL}}{c}_{\text{o}}}{D_{\text{i}}/h}\end{array}$$ (7)

The normalized boundary conditions are:

$$\begin{array}{l}\epsilon U=C_{\text{i}}(0)-1\\ \alpha \epsilon U=C_{\text{s}}-C_{\text{i}}(1)\\ \alpha =P_{\text{BL}}/P_{\text{A}}\end{array}$$ (8)

And the difference between the models in Fig. 2A vs B is:

$$\begin{array}{cc}A& B\\ C_{\text{s}}=1/U& C_{\text{s}}=1\end{array}$$ (9)

When these equations are solved, the nearness to isotonic transport is determined by how closely U and C_i approach unity. For this particular problem, one can solve the equations exactly to obtain a nonlinear, implicit relationship between U and C_i. These solutions can be expanded in a Taylor series in powers of ε to obtain explicit expressions. Equivalently, one can start with a perturbation expansion of U and C_i in powers of ε, which leads to a series of problems that define the terms of the expansions. The perturbation approach is illustrated by example in the Appendix. Either approach leads to the approximate solutions given in Eq. 10 The left-hand results labeled A refer to Fig. 2A, whereas the right-hand results labeled B refer to Fig. 2B

$$\begin{array}{cc}A& B\\ C_{\text{i}}\approx 1+\epsilon & C_{\text{i}}\approx 1+\epsilon \frac{k_{\text{i}}}{\text{1}+\alpha +k_{\text{i}}}[1-(1+\alpha )y]\\ C_{\text{s}}\approx 1+\epsilon \text{ (1}+\alpha \text{)}& C_{\text{s}}=1\\ U\approx 1-\epsilon \text{\hspace{0.17em}(1}+\alpha )& U\approx \frac{k_{\text{i}}}{1+\alpha +k_{\text{i}}}\end{array}$$ (10)

These results are shown graphically in Fig. 2, using the parameter values in Table 1. The parameter values were chosen as being typical of results reported in a number of studies reviewed in Whittembury and Reuss, 1992. These parameters refer to a unit area of epithelium rather than a unit area of membrane, hence P and j are increased by 36-fold over their per unit area of membrane values to account for lateral membrane area and apical membrane microvillae.

Table 1.

Parameter values for Figure 2

co	300×10−6 moles/cm3
Di	10)5 cm2/s
H	10×10−4 cm
J	1.0×10−9 moles/cm2/s*
P	12 (cm/s) /(moles/cm3)*
α	1
ε	10−3
ki	0.36

^*Based on per unit area of epithelial surface.

The analysis of Fig. 2A suggests the natural steady-state condition for a transporting epithelium is to generate a concentration gradient of εc_o across each membrane, in which case, the flux of salt (j) is carried by convection to within order (ε), hence salt concentrations are uniform to within order (ε). In Fig. 2A, we have modeled the epithelium as 2 membranes in series, hence the overall concentration gradient is 2εc_o, assuming PA = PBL (i.e., α = 1). In general, the two sides may have different membrane areas or specific water permeabilities, but there can be only one mathematical ε, hence the appearance of α (Eq. 8). Physically, ε is the ratio of salt to water permeability, which for basolateral membranes is ε but for apical membranes is α ε. Thus the concentration gradient across basolateral membranes is εc_o and across apical membranes is α εc_o, giving the overall concentration difference of (1 + α )εc_o (Eq. 10). The implication is that fluids will always be within order ε of isotonic, and for fluid transporting epithelia, ε is a very small number (about 10⁻³a for cells of proximal tubule or 10⁻⁵ for fiber cells of the lens).

The original experiments of Diamond, 1964, were to collect the fluid transported by the gall bladder and measure its osmolarity. To within experimental error, the fluid appeared to be isotonic, but that result can be entirely explained by the model in Fig. 2A. The fact that the fluids on the two sides of the epithelium appeared to have the same osmolarity prompted Diamond and Bossest, 1967, and others who followed their lead, to generate a model that was more equivalent to Fig. 2B. Although the model in Fig. 2B is obviously too simple, it illustrates the extreme sensitivity of the system to the boundary conditions. In model A, the apical solution is within order ε of c_o. This is physically indistinguishable from c_o; however, if we mathematically impose the condition that the apical solution is precisely c_o, there is a dramatic reduction in water flow: the flow in A is 99.8% isotonic whereas in B it is 15% isotonic.

For the model in Fig. 2B, the membrane concentration gradients that generate osmotic flow are diffusional gradients within the cell. These diffusional gradients are small for two reasons: 1) cellular dimensions are small (h ≈ 10 μm) and diffusion is very effective at maintaining even concentrations over short distances; 2) the surface to volume ratio of a cell is relatively small. For the lateral intercellular space, distances can be significantly larger. Meanderings of the lateral spaces of a single layered epithelium increase membrane area by an order of magnitude (Whittembury & Reuss, 1992), hence the distance is increased by about 3-fold (l ≈ 30 μm) while the surface to volume ratio of the lateral spaces is hundreds of times greater than that of the cell. Thus, one must include the effects of lateral spaces to properly analyze the situation pictured in Fig. 2B. But is this situation relevant? While it is probably not a relevant model for any experiment that has been done, it is physiologically relevant. In the proximal region of the renal proximal tubule, the newly filtered luminal (apical) solution has composition c_o while the peritubular capillaries maintain the external (basal) solution at c_o. Thus, it is of physiological relevance to assess the effects of long, narrow intercellular spaces on the osmolarity of transported solution.

A Membrane Tube

The model pictured in Fig. 3 is very similar to that which generated the original computer simulations of Diamond and Bossert, 1967, and the perturbation analysis by Segel, 1970. The only difference is that, in Fig. 3, solute transport is assumed to be uniform along the lateral membranes, whereas Diamond and Bossert, 1967, localized the solute transport to the apical end of the tube. In the perturbation analysis by Segel, 1970, the fraction of the tube that transported solute was allowed to be a variable, and if that fraction is set to one, then the analysis presented here is identical to that in Segel. So this is not really new, but it is an important step in dissecting the various factors that are involved in local osmosis.

Fig. 3.

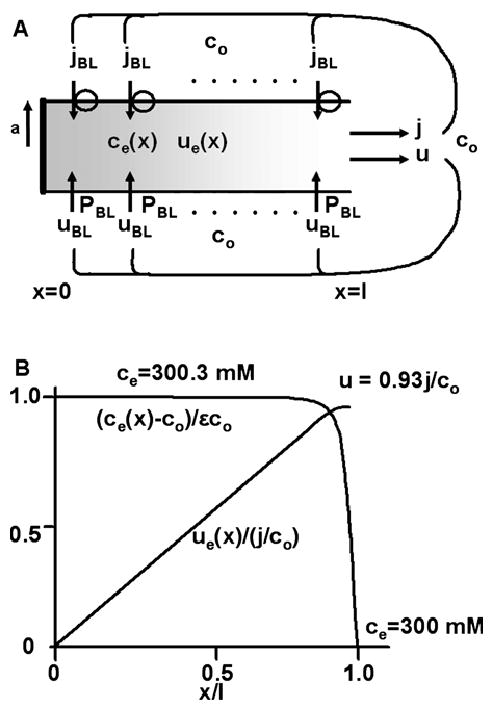
A tube of transporting membrane immersed in a solution of osmolarity c_o. This model has been used to represent the lateral intercellular spaces of a transporting epithelium (Diamond & Bossert, 1967). (A) The geometric and transport properties of the tube. The transmembrane salt flux, j_BL, is assumed to be uniform along the lateral membrane. This leads to a longitudinal flux j_e(x) (moles/cm²/s) that increases linearly with distance from the apical junction (x = 0), which is assumed to be impermeable to solute or fluid. Local osmotic gradients c_e(x) (moles/cm³) generate transmembrane water flow u_BL(x) (cm/s) and cumulative longitudinal water flow u_e(x) (cm/s). The emerging solution has osmolarity j/u, where u = u_e(l) and j = 2πal j_BL. At the end of the tube, c_e(l)= c_o The transport equations are derived in the text, where approximate solutions are presented. (B) Graphical representations of the solutions to the transport equations. The normalized concentration gradient and water flow are graphed. The calculated values of the concentration of solute along the majority of the tube and just at the end of the tube are indicated on the graph.

The subscript e is used to emphasize that this analysis is of extracellular fluxes along the lateral spaces. Once again, the solute flux is carried by convection plus diffusion.

$$j_{\text{e}}(x)=u_{\text{e}}(x)c_{\text{e}}(x)-D_{\text{e}}\frac{\text{d}{c}_{\text{e}}(x)}{dx}$$ (11)

Basolateral membrane solute transport, j_BL (moles/ cm²/s), is assumed to be uniform, and the apical junctions are assumed to be closed to solute or water transport, viz

$$\begin{array}{l}\frac{\text{d}{j}_{\text{e}}(x)}{\text{d}x}=\frac{2}{a}{j}_{\text{BL}}\\ j_{\text{e}}(0)=0\end{array}$$ (12)

One can integrate Eq. 12 to obtain another expression for j_e(x).

$$j_{\text{e}}(x)=\frac{2l}{a}{j}_{\text{BL}}\frac{x}{l}$$ (13)

These results lead to the following equations and boundary conditions.

$$\begin{array}{l}\frac{2l}{a}{j}_{\text{BL}}\frac{x}{l}=u_{\text{e}}(x)c_{\text{e}}(x)-D_{\text{e}}\frac{\text{d}{c}_{\text{e}}(x)}{\text{d}x}\\ \frac{\text{d}{u}_{\text{e}}(x)}{\text{d}x}=P_{\text{BL}}(c_{\text{e}}(x)-c_{\text{o}})\\ c_{\text{e}}(l)=c_{\text{o}};\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }{u}_{\text{e}}(0)=0\end{array}$$ (14)

In the isotonic limit, the results would be:

$$\begin{array}{l}{c}_{\text{e}}(x)=c_{\text{o}}\\ u_{\text{e}}(x)=\frac{j}{c_{\text{o}}}\frac{x}{l}\end{array}$$ (15)

Where

$$\begin{array}{l}j=\frac{2l}{a}{j}_{\text{BL}}\\ u=\frac{j}{c_{\text{o}}}\end{array}$$

Again, the variables are normalized with respect to their isotonic limit

$$\begin{array}{l}y=x/l\\ C_{\text{e}}(y)=c_{\text{e}}(y)/c_{\text{o}}\\ U_{\text{e}}(y)=u_{\text{e}}(y)/(j/c_{\text{o}})\end{array}$$ (16)

The resulting, normalized equations are

$$\begin{array}{l}y=U_{\text{e}}(y)C_{\text{e}}(y)-\frac{1}{\epsilon k_{\text{e}}}\frac{\text{d}{C}_{\text{e}}(y)}{\text{d}y}\\ \epsilon \frac{\text{d}{U}_{\text{e}}(y)}{\text{d}y}=C_{\text{e}}(y)-1\\ C_{\text{e}}(1)=1;\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }{U}_{\text{e}}(0)=0\end{array}$$ (17)

Where

$$\begin{array}{l}\epsilon =\frac{j_{\text{BL}}/c_{\text{o}}}{P_{\text{BL}}{c}_{\text{o}}}\\ k_{\text{e}}=\frac{2l}{a}\frac{P_{\text{BL}}{c}_{\text{o}}}{D_{\text{e}}/l}\end{array}$$

The approximate solutions below were obtained using a perturbation expansion in ε. In this model, the order-zero solution for fluid flow deviates significantly from isotonic (see below), hence we have not bothered to include the order-one term, which does not affect the conclusions discussed below.

$$\begin{array}{l}{C}_{\text{e}}(y)\approx 1+\epsilon \left(1-\frac{cosh\sqrt{k_{\text{e}}y}}{cosh\sqrt{k_{\text{e}}y}}\right)\\ U_{\text{e}}(y)\approx y-\frac{1}{\sqrt{k_{\text{e}}}}\frac{sinh\hspace{0.17em}\sqrt{k_{\text{e}}y}}{\text{cosh}\sqrt{k_{\text{e}}}}\end{array}$$ (18)

The normalized fluid flow exiting the tube is given by

$$U=1-\frac{1}{\sqrt{k_{\text{e}}}}tanh\sqrt{k_{\text{e}}}$$ (19)

Using the parameter values in Table 2, $\sqrt{k_{\text{e}}}=13.3$ and tanh $\sqrt{k_{\text{e}}}=1.0$, hence U ≈ 0.92. Assuming c_o = 300 mM, the osmolarity of the transported solution, j/u = 326 mM. Although this is only 8.7% above c_o, the 26 mM difference would be easily detected if one could design an appropriate experiment to measure j/u. Note that in either the previous ‘‘twomembrane model’’ or in this ‘‘simple membrane tube’’ model, the parameter k must be large for transport to approach isotonic. In both models, k_i,e depends on the ratio of the membrane water permeability, c_oP (cm/s), to the solute permeability of the appropriate length of fluid, D_i/h or D_e/l (cm/s). The tube model can produce much more nearly isotonic transport because ke also depends on the surface to volume ratio times the length of tube, 2 l/a = 6000.

Table 2.

Parameter values for Figures 3 and 4

a	100 × 10−8cm
co	300 × 1 0−6 moles/cm3
De	10−5cm2/s
jA = jBL	3 × 10−11moles/cm2/s
L	30 × 10−4cm
PA = PBL	0.33 (cm/s) /(moles/cm3)
∝	1
ε	10−3
ke	178

The parameter values in Table 2 were chosen for a typical single-layered epithelium like the proximal tubule. There are also double-layered epithelia like the ciliary epithelium, and multilayered epithelia like the corneal endothelium or the lens. Although the tube diameter 2a is typical of the width of the intercellular spaces in all of these tissues, the layering of cells can greatly increase l. In this particular model, for values for l ≥ 300 μm, transport will be greater than 99% isotonic. To understand this effect of length, consider c_e in Fig. 3. Along most of the length of the tube, the luminal concentration c_e(x) is approximately (1 +ε)c_o and transmembrane water flow is nearly isotonic, but near the basal opening diffusion becomes important and the boundary condition that c_e(l) = c_o causes a deviation from the linear (isotonic) flow. Although the deviation at the mouth of the tube will always be present, as l becomes large, this deviation becomes a smaller fraction of the total transmembrane flow, leading to the conclusion that long clefts produce near isotonic transport. Surprisingly, this simple conclusion does not hold up when one generates a more realistic model that includes a cytoplasmic compartment in which the osmolarity is determined such that apical and basolateral water flows are equal.

A Cellular Model

The model in Fig. 4 assumes that most of the basolateral membrane area is within the cleft, hence basal flow is neglected. The dimension r (cm) can be chosen such that the ratio of apical to basolateral membrane areas is appropriate for the tissue of interest. In the proximal tubule, this ratio is near unity, so the value of r is determined from πr² = 2πal Using parameter values in Table 2, the value of r for the proximal tubule would be about 0.8μm. This rather small radius is because we are treating clefts of width 2a as if they were a tube of radius a, and a tube has much less membrane area than a cleft. The major new factor is the intracellular concentration c_i, which is determined from the transport equations such that apical and basolateral water flows are equal, as they obviously must be in a transporting epithelium at steady state. Based on the analysis of Fig. 2, we assume c_i is uniform, but not necessarily the same as c_o, as it was in the situation analyzed in Fig. 3. Although the geometry is contrived to simplify analysis, it should be congruent with the geometry of a real epithelium and provide intuition on the physics of physiological fluid transport.

Fig. 4.

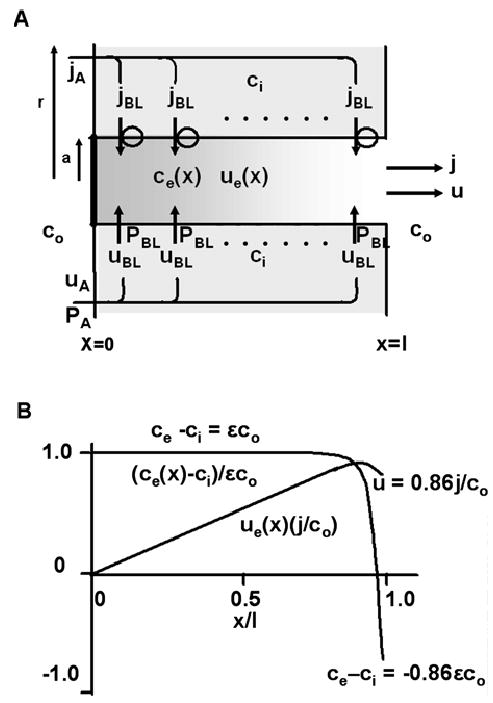
A cellular model of epithelial transport. (A) The geometric and transport properties of the cellular transport model. The properties of the lateral intercellular spaces are the same as described in Fig.3. The cellular dimension r (cm) is chosen so that the area of apical membrane relative to basolateral membrane is appropriate for the tissue of interest (see text). The new feature of this model is the osmolarity of the intracellular compartment, c_i (moles/cm³), which is determined such that apical and basolateral membrane water fluxes are the same. In addition, apical and basolateral membrane solute fluxes are constrained to be the same, implying πr²j_A = 2πal j_BL. The transport equations are derived in the text, where approximate solutions are presented. (B) Graphical representations of the solutions to the transport equations. The normalized concentration gradient and water flow are graphed. The calculated values of the concentration of solute along the majority of the tube and just at the end of the tube are indicated on the graph.

Since the transmembrane solute flux, j_BL, is assumed to be uniform along the lateral membranes, Eqs. 11–13 are valid for Fig. 4 as well as Fig. 3. However, the fluid flow equations will differ. Viz

$$\begin{array}{l}\frac{2l}{a}{j}_{\text{BL}}\frac{x}{l}=u_{\text{e}}(x)c_{\text{e}}(x)-D_{\text{e}}\frac{\text{d}{c}_{\text{e}}(x)}{\text{d}x}\\ \frac{\text{d}{u}_{\text{e}}(x)}{\text{d}x}=P_{\text{BL}}(c_{\text{e}}(x)-c_{\text{o}})\\ c_{\text{e}}(l)=c_{\text{o}};\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }{u}_{\text{e}}(0)=0\\ u_{\text{A}}=P_{\text{A}}(c_{\text{i}}-c_{\text{o}})\end{array}$$ (20a)

And balance between apical and basolateral flows requires

$$\begin{array}{l}u=\frac{r^2}{a^2}{u}_{\text{A}}=u_{\text{e}}(l)\\ j=\frac{r^2}{a^2}{j}_{\text{A}}=\frac{2l}{a}{j}_{\text{BL}}\end{array}$$ (20b)

The normalization with respect to isotonic transport is the same as in Eq. 16 with the addition that U_A = U_A/(j_A/c_o). The definitions of k_e and εare the same as in Eq. 17. However, because of the cellular compartment of normalized osmolarity C_i = c_i/c_o, the transport equations are now given by:

$$\begin{array}{l}y=U_{\text{e}}(y)C_{\text{e}}(y)-\frac{1}{\epsilon k_{\text{e}}}\frac{\text{d}{C}_{\text{e}}(y)}{\text{d}y}\\ \epsilon \frac{\text{d}{U}_{\text{e}}(y)}{\text{d}y}=C_{\text{e}}(y)-C_{\text{i}}\\ \alpha \epsilon U_{\text{a}}=C_{\text{i}}-1\\ C_{\text{e}}(1)=1;\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }{U}_{\text{e}}(0)=0\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }{U}_{\text{e}}(1)=Ua\end{array}$$ (21)

where

$$\alpha =\frac{2al{P}_{\text{BL}}}{r^2{P}_{\text{A}}}$$

The parameter αonce again represents the ratio of total basolateral membrane water permeability to total apical membrane water permeability, so it depends on both the specific water permeability of each membrane and the length of cleft relative to the area of apical membrane. The solutions to these equations are in some ways similar to those for a membrane tube, but there are significant differences that were missed in the analyses of Diamond and Bossert, 1967, or Segel, 1970. The perturbation solutions to Eq. 21 predict the emerging flow velocity, U = U_e(1) = U_a, is given by:

$$U\approx \frac{1-\frac{1}{\sqrt{k_{\text{e}}}}tanh\sqrt{k_{\text{e}}}}{1+\frac{\alpha }{\sqrt{k_{\text{e}}}}tanh\sqrt{k_{\text{e}}}}$$ (22)

The concentrations are given by:

$$\begin{array}{l}{C}_{\text{e}}(y)\approx 1+\epsilon \text{(1}-U)\frac{cosh\sqrt{k_{\text{e}}}-cosh\sqrt{k_{\text{e}}y}}{sinh\hspace{0.17em}\sqrt{k_{\text{e}}}}\\ C_i\approx 1+\epsilon \alpha U\end{array}$$ (23)

And the flow along the tube is:

$$U_{\text{e}}(y)\approx y-(1-U)\frac{sinh\sqrt{k_{\text{e}}y}}{sinh\sqrt{k_{\text{e}}}}$$ (24)

Based on parameter values in Table 2, the emerging flow is 86% isotonic, which is somewhat less than for a simple tube. The reason for the reduction is that c_i, has to be higher than c_o in order to pull water across apical membranes, but c_e →c_o at the end of the tube, hence the transmembrane osmotic gradient actually reverses direction and some fluid moves back into the cell. Given the approximate nature of this analysis, the difference between 86% and 93% isotonic is not significant; however, the physical reason for the difference has interesting implications.

Consider water flow (Eq. 22) when the basolateral membrane water permeability increases: the result is completely counter-intuitive. Indeed, in the limit that P_BL →∞, one can see from Eq. 22 that u → 0, which implies that increasing water permeability can decrease water flow. To understand this apparent anomaly, consider the limit P_A → ∞. In this case the only change is that α → 0, and inspection of Eq. 22 indicates that flow slightly increases to that predicted by the model of a membrane tube (Eq. 19). This is easily understood: as the apical membrane water permeability becomes large, the concentration of water across apical membranes approaches equilibrium and the concentration of solute in the cell approaches c_o, which is the physical situation analyzed for a membrane tube. Water flow is then generated entirely by standing osmotic gradients within the tube. In the situation that P_BL → ∞, the concentration of water within the cell and the tube approach equilibrium, standing osmotic gradients in the tube approach zero, so the concentration of solute goes to c_o in both compartments, but this also eliminates osmotic gradients across the apical membranes and water flow goes to zero. The behaviors of u and c_i are shown in Fig. 5, in which P_A is fixed at its value in Table 2 while P_BL is normalized to P_A, then the normalized value is varied and the values of u and c_i are calculated. The water flow is maximum when apical and basolateral water permeabilities are equal (Fig. 5A), which is the condition where c_i – c_o is also maximum (Fig. 5B). When the basolateral membrane water permeability decreases relative to the apical membrane water permeability, basolateral water flow becomes rate limiting and total flow decreases. Whereas when the basolateral permeability increases relative to apical, apical water flow becomes rate limiting and total flow also decreases. Interestingly, based on parameter values from the proximal tubule (Whittembury & Reuss, 1992), that epithelium is working near the optimum where total apical and basolateral membrane water permeabilities are equal.

Fig. 5.

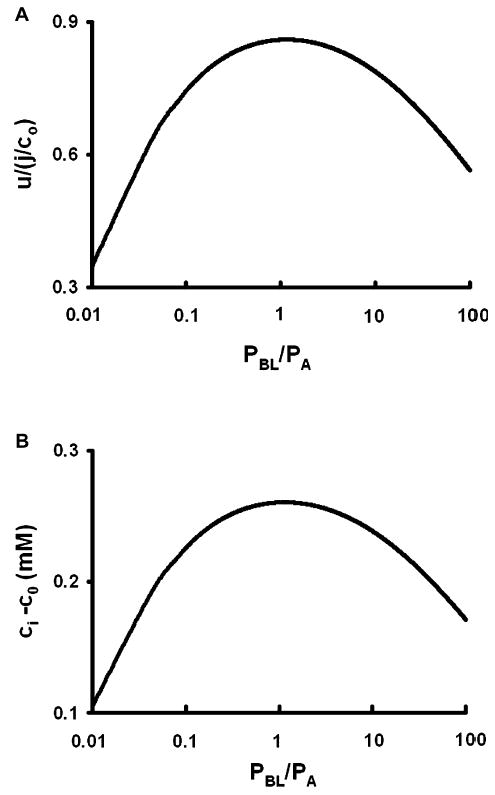
The effect of increasing basolateral membrane water permeability (P_BL), with all else constant. The calculations are based on the cellular model shown in Fig. 4. (A) The rate of fluid transport as a function of P_BL. Fluid transport is maximum when total apical and basolateral water permeabilities are equal: πr²P_A = 2πal P_BL. (B) The osmotic gradient across apical membranes as a function of P_BL. As P_BL decreases, basolateral water flow becomes rate limiting and the concentration of solute in the cell decreases to reduce apical flow and maintain balance. As P_BL increases, the concentration of solute in the lateral spaces and the cell approach c_o, causing the apical transmembrane osmotic gradient to decrease and apical flow becomes rate limiting.

Another way for the total basolateral membrane water permeability to increase is for the length of the lateral spaces, l, to increase as in layered epithelia. For the cellular model, total salt transport across basolateral and apical membranes has to be the same, so as l increases, either j_BL must decrease or j_A must increase. For the calculations in Fig. 6A, we chose to keep j_A constant and decrease j_BL in proportion to 1/l. As previously described for a simple membrane tube, as l → ∞ the end of the tube effects become negligible and transport becomes isotonic. However, for the more realistic cellular model, there are two competing effects: 1) the end of tube effects become negligible causing flow to increase; 2) the total water permeability of the basolateral membranes increases relative to apical, causing flow to be rate-limited by the apical membrane. The net effect is for flow to increase, but it does not reach its isotonic limit, rather it reaches a maximum of 92% isotonic. This behavior is illustrated in Fig. 6A. Figure 6A shows that the normalized flow velocity has essentially reached its limiting value for values of l ≥ 300 μm.

Fig. 6.

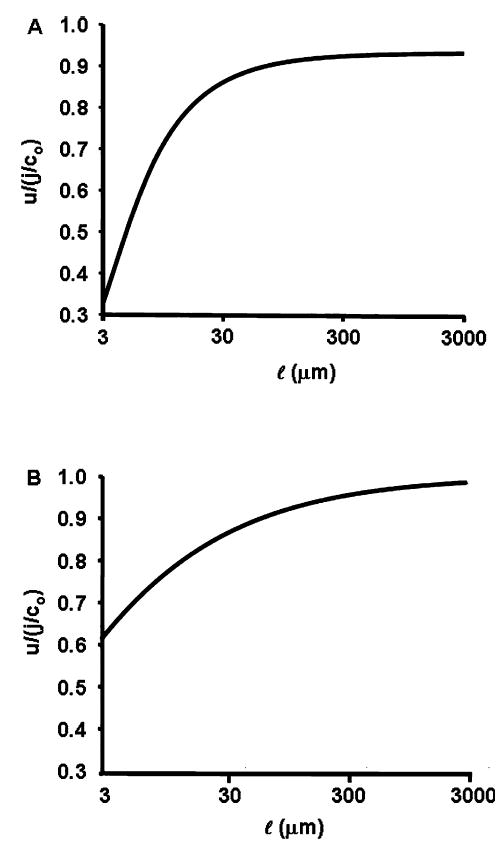
The effect of increasing the length of lateral spaces as in layered epithelia or the lens. To maintain equality of salt transport, we set πr²j_A = 2πal j_BL by reducing j_BL in proportion to 1/l, with j_A constant. (A) Fluid transport as a function of l when apical and basolateral membrane water permeabilities are maintained constant. Because the boundary condition effect at the mouth of the tube reduces net transport (see text describing Fig. 4A), the longer the cleft the less important this effect and transport increases. However, because increasing cleft length also has the effect of increasing total basolateral membrane water permeability relative to apical, eventually apical water transport becomes rate limiting and water transport never exceeds 92% isotonic. (B) Fluid transport as a function of l when apical and basolateral membrane water permeabilities are maintained equal by reducing P_BL as 1/l. In this situation, the mouth of the tube effect becomes negligible at long l, but apical flow does not become rate limiting, hence water transport approaches its isotonic limit.

The discussion above suggests that if P_BL decreases as l increases, such that balance between apical and basolateral membrane water permeabilities is maintained, then long clefts would indeed lead to isotonic transport. To demonstrate this, Fig. 6B graphs the behavior of Eq. 22 when l increases but P_BL decreases as 1/l. In this situation, for values of l ‡ 300 μm, transport is more than 95% isotonic, which is greater than the maximum of 92% isotonic in Fig. 6A, so decreasing P_BL leads to increased water flow. For l ≥ 300 μm, flow is more than 99% isotonic, so long clefts do lead to isotonic transport, but the effect depends on the square root of l, so the isotonic limit requires very long clefts. In the lens where cleft lengths are quite long, anywhere from 0.1 cm in a small mouse lens to 1 cm in a cow lens, the water permeability of the membranes lining the clefts (fiber cell membranes) is indeed much smaller than in most epithelia. Varadaraj et al., 1999, reported values in the rabbit lens range from 0.058 (cm/s)/(mole/cm³) for peripheral fibers to 0.015 (cm/ s)/(mole/cm³) for interior fibers, whereas surface epithelial cells of the lens have a water permeability of about 0.25 (cm/s)/(mole/cm³). Thus, contrary to intuition, these relatively low values of fiber cell membrane water permeability should actually generate more water flow, which should be near to isotonic.

The Renal Proximal Tubule

The newly-filtered solution exiting the glomerulus will have the osmolarity of plasma, c_o, and the basal solution will be maintained at c_o by the peritubular capillaries. Thus the above analysis suggests that the proximal region of the proximal tubule will be reabsorbing solution that is 86% isotonic, hence the concentration of the reabsorbed solution is about 1.16c_o, which means the concentration of the filtrate, c_f, is decreasing with distance along the tubule. As c_f decreases, the rate of reabsorbing fluid will also change until the concentration of the reabsorbed fluid is the same as c_f. Thereafter all concentrations will remain constant. The first step in analyzing this situation is to consider an epithelium with diffierent concentrations on the apical vs basal sides. Assume the peritubular capillaries maintain the basal concentration at c_o, whereas the concentration of the filtrate, c_f, on the apical side is arbitrary.

$$\begin{array}{l}y=U_{\text{e}}(y)C_{\text{e}}(y)-\frac{1}{\epsilon k_{\text{e}}}\frac{\text{d}{C}_{\text{e}}(y)}{\text{d}y}\\ \epsilon \frac{\text{d}{U}_{\text{e}}(y)}{\text{d}y}=C_{\text{e}}(y)-C_{\text{i}}\\ \alpha \epsilon U_{\text{a}}=C_{\text{i}}-C_{\text{f}}\\ C_{\text{e}}(1)=1;\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }{U}_{\text{e}}(0)=0\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }{U}_{\text{e}}(1)=U_{\text{a}}\end{array}$$ (25)

where

$$\alpha =\frac{2al{P}_{\text{BL}}}{r^{\text{2}}{P}_{\text{A}}}$$

For a perturbation approach to work, we have to assume that C_f = C_f/c_o can be expanded in a series

$$C_{\text{f}}=C_{\text{f}}^{(0)}+\epsilon C_{\text{f}}^{(1)}+{\epsilon }^2{C}_{\text{f}}^{(2)}+\dots$$

When this series is substituded into Eq.25, $C_{\text{f}}^{(0)}=1$ and the solutions to Eq. 25 can be written in terms of the unspecified value of $C_{\text{f}}^{(1)}.$The concentrations are given by

$$\begin{array}{l}{C}_{\text{f}}\approx 1+\epsilon C_{\text{f}}^{(1)}\\ C_{\text{f}}\approx 1+\epsilon \frac{C_{\text{f}}^{(1)}+\alpha -\frac{\alpha }{\sqrt{k_{\text{e}}}}tanh\sqrt{k_{\text{e}}}}{\text{1}+\frac{\alpha }{\sqrt{k_{\text{e}}}}tanh\sqrt{k_{\text{e}}}}\\ C_{\text{e}}(y)\approx 1+\epsilon \frac{C_{\text{f}}^{(1)}+1+\alpha }{1+\frac{\alpha }{\sqrt{k_{\text{e}}}}tanh\sqrt{k_{\text{e}}}}\left[1-\frac{cosh\sqrt{k_{\text{e}}y}}{cosh\sqrt{k_{\text{e}}}}\right]\end{array}$$ (26)

And the fluid flow is

$$\begin{array}{l}{U}_e(y)\approx y-\frac{C_{\text{f}}^{(1)}+1+\alpha }{1+\frac{\alpha }{\sqrt{k_{\text{e}}}}tanh\hspace{0.17em}\sqrt{k_{\text{e}}}}\frac{sinh\sqrt{k_{\text{e}}y}}{\sqrt{k_{\text{e}}}cosh\sqrt{k_{\text{e}}}}\\ U\approx 1-\frac{C_{\text{f}}^{(1)}+1+\alpha }{1+\frac{\alpha }{\sqrt{k_{\text{e}}}}tanh\hspace{0.17em}\sqrt{k_{\text{e}}}}\frac{1}{\sqrt{k_{\text{e}}}}tanh\sqrt{k_{\text{e}}}\end{array}$$ (27)

There are two ways to specify $C_{\text{f}}^{(1)}$. First, consider steady state. The concentration of the filtrate, c_f, will stop changing when the concentration of the reabsorbed solution equals the concentration of the filtrate. Thus the steady-state condition is c_f = j_A/ u_A, or in normalized parameters

$$U_{\text{A}}{C}_{\text{f}}=1$$ (28)

When the constraint in Eq. 28 is added to Eq. 25, the solutions are:

$$\begin{array}{l}{C}_{\text{f}}\approx 1-\epsilon (1+\alpha )\\ C_{\text{i}}\approx 1-\epsilon \\ C_{\text{e}}\approx 1\\ U_{\text{e}}(y)\approx y+\epsilon (1+\alpha )\frac{sinh\hspace{0.17em}\sqrt{k_{\text{e}}y}}{\text{sinh\hspace{0.17em}}\sqrt{k_{\text{e}}}}\\ U\approx 1+\epsilon (1+\alpha )\end{array}$$ (29)

The solutions in Equation 29 neglect terms of O(ε²) and higher. Remarkably, these solutions are equivalent to the solutions for simple secretion given in Eq. 10A, except fluid flow is in the opposite direction, hence the transmembrane gradients are reversed. Since the reabsorbed solution is isotonic with c_f, the value of c_f is now constant. The remaining question is: What is the distance from the glomerulus at which transport attains this steady state? To answer this question, the transport equations for flow along the lumen of the proximal tubule need to be derived and solved, which is the second way to specify $C_{\text{f}}^{(1)}$, now as a function of distance from the glomerulus.

We assume that within the lumen of the tubule solute is carried by the water flow u_f (cm/s) and that z (cm) is the distance along the tubule from the glomerulus. Further, we assume apical salt transport, j_A (moles/cm²/s), is constant along the tubule, then the solute flow equation within the lumen is given by

$$\begin{array}{l}\frac{\text{d}{u}_{\text{f}}(z)c_{\text{f}}(z)}{\text{d}z}=-\frac{S_{\text{A}}}{V_{\text{T}}}{j}_{\text{A}}\\ u_{\text{f}}(z)c_{\text{f}}(z)-u_0{c}_{\text{o}}=-\frac{S_{\text{A}}}{V_{\text{T}}}{j}_{\text{A}}z\end{array}$$ (30)

Where S_A/V_T (cm⁻¹) is the surface area of apical membrane per unit volume of the tubule lumen and u₀ (cm/s) is the rate of filtration by the glomerulus at z = 0 (see Table 3 and Fig. 7A). Equation 30 is only valid until u_f → 0, but as shown later, this is a large distance, on the order of 20 cm. The rate of decrease in u_f is the rate of fluid reabsorbtion.

Table 3.

Parameter values for Figure 7 and related text

SA/VT	4.8 × 104cm−1
T	0.075
u0	0.1 cm/s
uf →0	z→20 cm

Fig. 7.

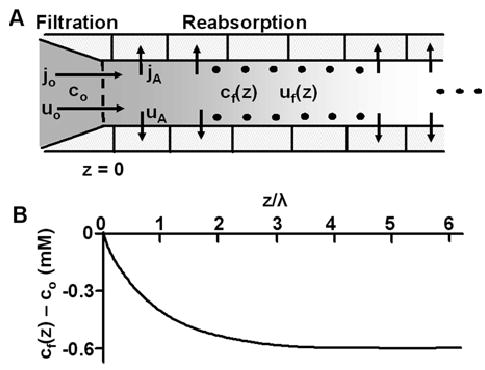
Fluid and salt reabsorption in the renal proximal tubule. (A) The geometric and transport properties of the proximal tubule. The new filtrate c_f= c_o (moles/cm³) is generated by the glomerulus at z = 0. As the filtrate flows along the lumen of the tubule, salt is transported out of the tubule across apical membranes at a rate j_A (moles/cm²/s) and water follows at a rate u_A (cm/s). The osmolarity of the transported solution, j_A/u_A (moles/cm³), is initially c_o/0.86 (Eq. 22 and related text), implying c_f is decreasing with increasing distance from the glomerulus. The transport equations are derived in the text, where approximate solutions are presented. (B) A graphical representation of the solution for c_f as a function of distance from the glomerulus. Based on parameter values in Table 2, ε = 10⁻³ and the total water permeabilities of apical and basolateral membranes are the same, hence α = 1. Initially c_f = c_o = 300 mM, but it exponentially declines to its steady-state value of (1−(1+α)ε)c_o = 399.4 mM with a length constant λ = 0.3 cm. At steady state, the osmolarities of the transported solution and the filtrate are the same: c_f = j_A/u_A.

$$-\frac{\text{d}{u}_{\text{f}}(z)}{\text{d}z}=\frac{S_{\text{A}}}{V_{\text{T}}}{P}_{\text{A}}(c_{\text{i}}(z)-c_{\text{f}}(z))$$ (31)

If u_f is normalized to its initial value such that U_f = u_f/u₀ and other parameters are normalized as before, the dimensionless equations are:

$$\begin{array}{l}{U}_{\text{f}}(Z)C_{\text{f}}(Z)=1-\alpha \epsilon Z\\ \frac{\text{d}{U}_{\text{f}}(Z)}{\text{d}Z}=C_{\text{f}}(Z)-C_{\text{i}}(Z)\\ C_{\text{f}}(0)=1,\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }{U}_{\text{f}}(0)=1\end{array}$$ (32)

where

$$Z=\frac{c_0\frac{S_{\text{A}}}{V_{\text{T}}}{P}_{\text{A}}}{u_{\text{0}}}z$$

If the expression for C_i and C_f from Eq. 26 are substituted into Eq. 32, we can solve for the unspecified $C_{\text{f}}^{(1)}$. The results are:

$$\begin{array}{l}\text{Define T}=\frac{1}{\sqrt{{\text{k}}_{\text{e}}}}tanh\sqrt{{\text{k}}_{\text{e}}}\\ \text{then}\\ C_{\text{f}}(Z)\approx 1-\epsilon (1+\alpha )(1-e^{-\alpha \text{TZ}/\text{(1}+\alpha \text{T)}})\\ U_{\text{f}}(Z)\approx 1-\epsilon [(1+\alpha )(1-e^{-\alpha \text{TZ}/\text{(1}+\alpha \text{T)}})-\alpha Z]\end{array}$$ (33)

Thus C_f(Z) exponentially approaches its steady-state value of 1-ε(1 + α) with a length constant, λ (cm), where

$$\lambda =\frac{(1+\alpha T)u_0}{\alpha T}/\left(c_{\text{o}}\frac{S_{\text{A}}}{V_{\text{T}}}{P}_{\text{A}}\right)$$ (34)

Tables 2 and 3 give the parameter values used to calculate λ = 0.3 cm. As shown in Fig. 7B, flow will attain steady state at about 3 length constants from the glomerulus, or at about 0.9 cm, where Eq. 29 becomes valid. Because we have assumed salt transport is constant along the tubule, once steady state is reached, the longitudinal flow velocity declines linearly with distance. Based on Eq. 33 it will eventually become negative, but that is obviously physically impossible, so Eq. 33 can only be applied up to the distance where all the filtered fluid has been reabsorbed and flow goes to zero. This occurs at Z ≈ 1/αε, which implies z ≈20 cm, given the parameter values in Tables 2 and 3. This is much longer than the length of the proximal tubule, so the analysis is not physically unreasonable as a description of the initial salt and water transport in the proximal tubule.

Experimental Measurements Of Isotonic Transport

In the previous section we derived the remarkable result that, when the filtrate (apical solution) was at its natural steady-state concentration, the distributed model of standing gradients in the lateral intercellular spaces collapsed back to a simple lumped (three-compartment) model similar to that first proposed by Curran and Maclntosh (1962). In all experimental determinations of isotonic transport, the transported solution has been collected (e.g., Diamond, 1964; Barfus & Schafer, 1984), hence it will have its natural steady-state composition. The obvious implication is that experimental protocols may create a situation in which a simple lumped model is appropriate and transport is within order ε of isotonic. To test this hypothesis, we reevaluate the ‘‘Cellular Model’’ given by Eq. 21 with a change in boundary conditions such that the basal solution has the composition of the absorbate. The new boundary condition is c_e(l) = j/u, which when normalized gives the condition

$$U_{\text{e}}(1)C_{\text{e}}(1)=1$$ (35)

Thus we no longer impose the condition that C_e(1) = 1, but use Eq. 35 instead. Imposition of this boundary condition does indeed cause the distributed model to collapse to a lumped three-compartment model. In fact, imposing the boundary condition in Eq. 35 implies that C_e(y) is a constant given by $C_{\text{e}}=(1+\sqrt{1+4\epsilon (1+\alpha )})/2,$ and U_e(y) = y/C_e, C_i = 1+εα/C_e. The ε-expansions of the exact solutions are:

$$\begin{array}{l}{C}_{\text{e}}(y)\approx 1+\epsilon (1+\alpha )\\ C_{\text{i}}\approx 1+\epsilon \alpha \\ U_{\text{e}}(y)\approx y(1-\epsilon \alpha )\\ U\approx 1-\epsilon \alpha \end{array}$$

If we assume α = 1, then apical and basolateral membranes each have seen a transmembrane osmotic gradient of εc_o, and the absorbate is isotonic to within order ε. The absorbate is therefore isotonic to within about one part in one thousand, and experimenters would consider this to be isotonic. The most remarkable feature is the change in the physics of fluid transport. The lateral intercellular spaces are no longer needed to generate the osmotic gradients that drive fluid transport; instead, the differential equations for distributed transport could be replaced with a simple three-compartment system in which apical transmembrane fluid flow is given by P_Aεc_o, basolateral transmembrane fluid flow is P_BLεc_o, and the osmolarities c_o, (1 + ε)c_o and (1 + 2ε)c_o in the apical, intracellular and basolateral compartments respectively. This is the absorption equivalent of the secretion model in Fig. 2A.

Discussion

The central theme of this analysis is that fluid-transporting epithelia have a natural steady state where each membrane has an osmotic gradient of εc_o, water flow is within order ε of isotonic, and osmotic gradients are spatially uniform to within order ε. If the transported fluid is significantly different from isotonic, then the effect of transport will be to adjust gradients until the above condition holds. When this state is reached, standing osmotic gradients in the lateral spaces are negligible.

In the experiments that have suggested isotonic transport, the transported solution has been collected and its osmolarity measured (e.g., Diamond, 1964; Barfus & Schafer, 1984), hence the epithelia were in this natural steady state. The actual osmolarity was probably order ε hypertonic, but since ε is generally less than 10₋₃, the deviation from isotonic could not be detected. Based on these experiments, models of transporting epithelia have assumed the solution on each side of the epithelium had a salt concentration of exactly c_o (Diamond & Bossert, 1967; Segel, 1970), Because the membrane water permeability is relatively large, the models are exquisitely sensitive to the assumed boundary concentrations and the effect of the difference between c_o and (1+2ε)c_o is rather dramatic, as demonstrated in Fig. 2.

Another problem with the early models (Diamond & Bossert, 1967; Segel, 1970) was that they focused on standing gradients in lateral spaces and did not consider the cellular compartment. Later models (Sackin & Boulpaep, 1975; Weinstein & Stephenson, 1981) did include the cellular compartment, but these were complicated numerical models, which do not provide as much insight as an approximate analytic solution (Segel, 1970). The cellular osmolarity links apical and basolateral water flows and significantly affects conclusions on the effects of basolateral membrane water permeability as well as cleft length. The models presented here predict that fluid flow is maximum when total water permeabilities of apical and basolateral membranes are matched. In the proximal tubule, where apical and basolateral membrane areas are similar and both membranes have similar water permeabilities, fluid transport appears to be maximized. Whereas in the lens, where the cleft lengths are exceptionally long, hence the area of lateral membrane is much larger than that of surface cell membrane (reviewed in Mathias et al., 1997), the lateral membrane water permeability is much less than that of surface cells (Varadaraj et al., 1999), once again generating near maximum fluid flow.

Our model calculations on the renal proximal tubule suggest the filtrate will reach an equilibrium concentration that is slightly hypotonic (about 0.6 mM using parameter values in Tables 1–3) relative to the basal solution, which is maintained at the same concentration as the solution in the peritubular capillaries. Green and Giebisch (1984) found that when they perfused the tubules and peritubular capillaries with the same solution, the tubular solution did indeed reach an equilibrium concentration that was slightly hypotonic to that of the capillaries. They estimated they could reliably detect differences of about 1 mM and the differences they found were 1.7 mM or 3.9 mM, depending on the rate of perfusion. In our model, the difference in osmolarity is given by 2εc_o. Based on a range of experimental values, we estimated ε ≈ 10⁻³. For our model to explain their data, the value of ε would have to be 2.9 × 10⁻³ for the 1.7 mM difference or 6.7 × 10⁻³ for the 3.9 mM difference. Since ε depends on the ratio of j/P, given the range of values for j and P reviewed in Whittembury and Reuss (1992), their experiments are in very good agreement with the predictions of our modeling.

Limitations of Models

At the outset, we stated that we would focus on local osmosis and not include voltage gradients, hydrostatic pressure or electro-osmosis, all of which must be present based on simple thermodynamics. Although the analysis of hydrostatic pressure is not presented here, we have looked to see if its inclusion would affect any of the above conclusions. We found that hydrostatic pressure slightly reduced the maximum flow in the models presented in either Fig. 3 or 4, but it did not alter any of the above conclusions. McLaughlin and Mathias, 1985, examined the role of electro-osmosis and concluded that it could substitute for hydrostatic pressure in driving longitudinal fluid flow along the clefts, thus altering the pressure gradient, but not affecting the conclusions on local osmosis. Although these are issues for future analysis, at this stage, we do not think that they alter any of the general conclusions on the role of local osmosis.

Models of epithelial fluid transport are exquisitely sensitive to the assumed boundary conditions. This sensitivity does indeed represent a significant limitation to analyses of fluid transport. There are unstirred layers just adjacent to membranes, and these depend on unknown factors such as the structure of the membrane surface and the degree of stirring. Small deviations in osmolarity in these layers can alter boundary conditions and may significantly affect fluid transport. Thus, it is difficult to derive a quantitatively accurate model of a real epithelium. Our goal in deriving and approximately solving the models presented here was to obtain insight into the physics of fluid transport, particularly with regard to the role of local osmosis and isotonic transport.

Others have suggested the existence of water pumps (Meinild et al., 1998; Zeuthen et al., 2001), and while these may exist, they are not necessary to explain data on isotonic transport. Similarly, models that invoke more complex patterns of flow such as recirculation (Nedergaard et al., 1999) or circulating currents driving fluid transport through electroosmosis (Sanchez et al., 2002; Fischbarg & Diecke, 2005) may be correct, but they are not necessary to explain the data on isotonic transport. Simple physics tells us local osmosis will always be present, regardless of whatever other mechanism is postulated, and based on the calculations here, we conclude that local osmosis is sufficient to generate near isotonic transport.

Appendix

In the text, we have presented results from perturbation expansions of the equations describing Fig. 2, 3, 4 and 7. For each of these models, the perturbation approach is quite similar, so in this Appendix we will go through the expansion for Fig. 2A to demonstrate the approach.

The concentrations and fluid flow in Equations 7–9 are expanded in a series in ε.

$$\begin{array}{l}{C}_{\text{i}}=C_{\text{i}}^{(0)}+\epsilon C_{\text{i}}^{(1)}+\dots \\ C_{\text{s}}=C_{\text{s}}^{(0)}+\epsilon C_{\text{s}}^{(1)}+\dots \\ U=U^{(0)}+\epsilon U^{(1)}+\dots \end{array}$$ (A1)

Equation A1 is inserted into Eqs. 7–9 and terms of like powers in ε are collected to define a series of problems to be solved. For the order (0) problem, we obtain

$$\begin{array}{l}\frac{\text{d}{C}_{\text{i}}^{(0)}(y)}{\text{d}y}=0\\ 1-C_{\text{i}}^{(0)}(0)=0\\ C_{\text{s}}^{(0)}-C_{\text{i}}^{(0)}=1\\ U^{(0)}{C}_{\text{s}}^{(0)}=1\\ \end{array}$$ (A2)

The solutions to Eq. A2 are:

$$\begin{array}{l}{C}_{\text{i}}^{(0)}=1\\ C_{\text{s}}^{(0)}=1\\ U^{(0)}{C}_{\text{s}}^{(0)}=1\end{array}$$ (A3)

The order (1) problems are:

$$\begin{array}{l}\frac{\text{d}{C}_{\text{i}}^{(0)}(y)}{\text{d}y}=k_{\text{i}}(U^{(0)}{C}_{\text{i}}^{(0)}-1)\\ C_{\text{i}}^{(1)}(0)=U^{(0)}\\ C_{\text{s}}^{(1)}-C_{\text{i}}^{(1)}(0)=\alpha U^{(0)}\\ U^{(0)}{C}_{\text{s}}^{(1)}+U^{(1)}{C}_{\text{s}}^{(1)}=0\end{array}$$ (A4)

If the order (0) solutions in Eq. A3 are inserted into Eq. A4, the results are:

$$\begin{array}{l}{C}_{\text{i}}^{(1)}=1\\ C_{\text{s}}^{(1)}=1+\alpha \\ U^{(1)}=-(1+\alpha )\end{array}$$ (A5)

Thus to within order (ε²) the solutions are given by:

$$\begin{array}{l}{C}_{\text{i}}=1+\epsilon +O({\epsilon }^2)\\ C_{\text{s}}=1+\epsilon (1+\alpha )+O({\epsilon }^2)\\ U=1-\epsilon (1+\alpha )+O({\epsilon }^2)\end{array}$$ (A6)

In this simple model, the concentrations and flows are constant to within order (ε²). In the more complicated models of extracellular clefts, the values of $C_{\text{e}}^{(1)}(y)$ and $U_{\text{e}}^{(0)}(y)$ depend on y. Nevertheless, the more complicated models are analyzed in the same manner, so the expansions will not be presented.