Level dependence of auditory filters in nonsimultaneous masking as a function of frequency

Abstract

Auditory filter bandwidths were measured using nonsimultaneous masking, as a function of signal level between 10 and 35 dB SL for signal frequencies of 1, 2, 4, and 6 kHz. The brief sinusoidal signal was presented in a temporal gap within a spectrally notched noise. Two groups of normal-hearing subjects were tested, one using a fixed masker level and adaptively varying signal level, the other using a fixed signal level and adaptively varying masker level. In both cases, auditory filters were derived by assuming a constant filter shape for a given signal level. The filter parameters derived from the two paradigms were not significantly different. At 1 kHz, the equivalent rectangular bandwidth (ERB) decreased as the signal level increased from 10 to 20 dB SL, after which it remained roughly constant. In contrast, at 6 kHz, the ERB increased consistently with signal levels from 10 to 35 dB SL. The results at 2 and 4 kHz were intermediate, showing no consistent change in ERB with signal level. Overall, the results suggest changes in the level dependence of the auditory filters at frequencies above 1 kHz that are not currently incorporated in models of human auditory filter tuning.

I. INTRODUCTION

Frequency selectivity, or the ability to distinguish simultaneous sounds of different frequencies, is a fundamental property of the auditory system. From the earliest days of psychoacoustic research, it has generally been assumed that frequency selectivity measured behaviorally reflects the tuning properties of the cochlea. This assumption is supported by various lines of indirect evidence, such as marked changes in frequency selectivity in the presence of hearing losses diagnosed to be of cochlear origin (e.g., Moore and Glasberg, 1986), many qualitative similarities between human behavioral frequency selectivity and physiological studies of auditory-nerve tuning in other mammals (e.g., Moore, 1978), and animal studies showing similar estimates of filter bandwidth using behavioral and neural measures (e.g., Evans, 2001).

Recently, Shera et al. 2002 provided more direct evidence of a correspondence between cochlear tuning and behavioral frequency selectivity in humans. They used a measure based on stimulus-frequency otoacoustic emissions (SFOAEs) to predict cochlear tuning, and measured psychophysical frequency selectivity using a forward masker and a low-level probe. They found a good correspondence between the SFOAE predictions and the psychophysical measures. Although this general finding was in line with earlier studies in animals (Evans, 2001), two aspects of the data were surprising. First, both measures suggested that cochlear tuning in humans was considerably sharper than that found in two mammals (cat and guinea pig) that are often used in auditory experiments. Second, the estimated tuning was sharper and had a different dependence on characteristic frequency (CF) than many earlier psychophysical estimates of tuning: instead of the relative bandwidth staying roughly constant above 1 kHz (e.g., Glasberg and Moore, 1990), tuning was found to sharpen considerably, such that the 8-kHz filter had a Q_ERB (CF divided by the equivalent rectangular bandwidth or ERB) nearly twice that of the 1-kHz filter. This sharpening of tuning with increasing CF is also observed in the auditory-nerve tuning curves of other mammals. Shera et al. 2002 ascribed the differences between their results and those of previous psychophysical studies to their use of nonsimultaneous masking, which reduced possible suppression effects (Delgutte, 1990a,b), and—perhaps more importantly—to their use of a low-level (10 dB SL) probe tone (see Oxenham and Shera, 2003).

The use of a low-level probe tone provided estimates of tuning that were readily comparable to a large body of neural tuning curve data in animals, and they resulted in the conclusion that human cochlear tuning may be sharper than that of other mammals, such as cat and guinea pig. However, the use of a low-level probe tone does not provide a full description of frequency selectivity because of the inherent nonlinearities present in the cochlea, including increases in filter bandwidth with level that are often observed in physiological studies of tuning (Ruggero et al., 1997). Increases in bandwidth with increasing level have been observed in many psychophysical studies of frequency selectivity using simultaneous masking (e.g., Weber, 1977; Rosen and Stock, 1992; Rosen et al., 1998; Hicks and Bacon, 1999; Glasberg and Moore, 2000). In one of the more recent studies, Glasberg and Moore (2000) found that the dependence of the auditory filters on level was similar at all frequencies above about 1 kHz. However, as they used simultaneous masking, it is not clear to what extent their results are due to the effects of suppression, rather than to changes in the underlying co-chlear tuning, such as would be measured by neural tuning curves (Delgutte, 1990a; Moore and Vickers, 1997; Oxenham and Plack, 1998).

Fewer studies have examined changes in frequency selectivity with level using nonsimultaneous masking, where suppression is not thought to play a role. Studies that did use nonsimultaneous masking have employed either psychophysical tuning curves (Moore et al., 1984; Nelson and Freyman, 1984; Nelson et al., 1990; Nelson, 1991) or the notched-noise technique (Glasberg and Moore, 1982). The studies using psychophysical tuning curves have concluded that the masker level at the tip of the tuning curve (i.e., when the masker and signal frequencies are very similar) determines the bandwidth and shape of the filter, and that other variables, such as the gap between the masker and signal, and the signal level, have no effect once the effects of masker level have been accounted for (e.g., Nelson and Freyman, 1984). Furthermore, these studies indicate that the filter shape remains roughly constant for masker levels (at the tip of the tuning curve) up to about 60 dB SPL (Nelson et al., 1990), above which it broadens. Consistent with this, Glasberg and Moore (1982), using a notched-noise masker, found that over the three fixed masker levels (30, 40, and 50 dB SPL spectrum level) and three fixed signal levels (roughly 10, 15, and 20 dB SL), there was no change in filter bandwidth with level. Interestingly, all the studies mentioned used a signal frequency of 1 kHz. To our knowledge, there are no published studies that have used the notched-noise technique to investigate frequency selectivity in nonsimultaneous masking as a function of level for frequencies other than 1 kHz.

The lack of data on the level dependence of frequency selectivity as a function of signal frequency in nonsimultaneous masking is an important omission, particularly given the large changes in tuning with frequency that can occur at low levels (Shera et al., 2002; Oxenham and Shera, 2003). Information on how human cochlear filter shapes change as a function of frequency and level will be crucial in developing and refining computational models of the human auditory periphery. Interestingly, there is also a dearth of systematic data from physiological studies on this topic. Basilar-membrane tuning data are limited mainly to the basal turn of the cochlea, and thus to relatively high CFs (e.g., Ruggero et al., 1997). Although some data from lower CFs in the apical turn exist (Cooper and Rhode, 1995; Rhode and Cooper, 1996), it is not yet clear to what extent the cochlea was damaged in those preparations. There are limited data on the effect of level on neural tuning curves as a function of CF. One problem is that most auditory-nerve fibers have relatively small dynamic ranges, making a study of level effects difficult, because of saturation effects. One study to show some sample neural tuning curves at CFs of around 200, 500, 1500, and 5000 Hz with different rate criteria found little systematic effect of level on bandwidth over the range of criteria tested (Liberman and Mulroy, 1982). Another approach, which is less susceptible to saturation effects, is to use the reverse-correlation (revcor) technique to derive the tuning characteristics of individual neurons (Moller, 1977; Harrison and Evans, 1982; Carney and Yin, 1988). However, this technique is limited to relatively low CFs, at which phase locking to the stimulus fine structure is still strong. Thus, basilar-membrane data are generally limited to high CFs, whereas auditory-nerve data are often limited to low CFs, making it difficult to provide a general survey of level effects in tuning across a wide range of CFs.

Here, we investigate the dependence of auditory filter bandwidths on level at signal frequencies ranging from 1 to 6 kHz using nonsimultaneous masking. We used the notched-noise technique, which has been shown to provide estimates that are in good agreement with estimates of human cochlear tuning using otoacoustic emissions (Shera et al., 2002). Measuring filter shapes at a fixed signal level is closer to the technique used in derived neural and basilar-membrane tuning curves, and has also been shown to provide more consistent estimates of tuning as a function of level than estimates based on a fixed masker spectrum level (e.g., Rosen et al., 1998). However, even if the derived filters are based on a fixed signal level, the data can be collected either with a fixed signal or fixed masker level (Rosen et al., 1998). Both paradigms have some advantages. Collecting data using a fixed signal level and an adaptively varying masker level provides a direct estimate of filter tuning that requires no further transformations, whereas collecting data using a fixed masker level and adaptively varying signal level may require a transformation of the data before tuning estimates for a filter at a given level can be made. In a study of auditory filter shapes in forward masking at 1 kHz, Glasberg and Moore (1982) tested both methods for about a 10-dB range of signal levels and found no significant difference between the two methods. On the other hand, it is possible that for higher signal levels and wide notch widths, a fixed signal level paradigm might lead to somewhat uncomfortable masker levels, which in turn might bias listeners toward responding wrongly, because they realize (consciously or unconsciously) that wrong answers lead to lower and perhaps less objectionable levels. This could be the case, even though listeners are made aware during the process of informed consent that the level cannot exceed safe limits, and that if anything makes them feel uncomfortable they should inform the experimenter immediately.

In this study, we estimated filter shapes using both methods. In the first study, a fixed masker level paradigm was used over a wide range of masker notch widths and masker levels using signal frequencies of 1 and 6 kHz. In the second study, a fixed signal level paradigm was used to test a more limited range of notch widths at more signal frequencies (1, 2, 4, and 6 kHz). The studies were undertaken at different times and with different subjects. In agreement with the data of Glasberg and Moore (1982) no significant differences in estimated filter bandwidths emerged at the two frequencies for which both methods were used (1 and 6 kHz). Overall, we were able to estimate auditory filter bandwidths in non-simultaneous masking at signal frequencies of 1, 2, 4, and 6 kHz for signal levels ranging from 10 to 35 dB SL. Both experiments were consistent in showing a markedly different dependence of filter tuning on level at the different signal frequencies, in contrast to expectations based on the results from simultaneous-masking studies in the same frequency range (Glasberg and Moore, 2000).

II. EXPERIMENT

A. Stimuli

The signal was a tone burst of 20-ms total duration, gated on and off with 10-ms raised-cosine ramps (no steady state). The signal was immediately preceded and followed by noise maskers with total durations of 200 ms, each gated with 5-ms raised-cosine ramps. The beginning and end of the signal temporally abutted the offset and onset of the forward and backward masker, respectively. In this way, the paradigm was similar to simultaneous masking with a brief probe, with the difference that the masker was interrupted for the duration of the signal. Each masker consisted of two bands of Gaussian noise centered below and above the signal frequency ( f_s), each with a bandwidth of 0.25f_s. Each noise burst was generated independently in the spectral domain and was bandlimited by setting all spectral components outside the desired passband to zero. In this way, the slope of the filtering was limited only by the spectral spread caused by the 5-ms onset and offset ramps of the masker. The spectral notch width was defined as the deviation (Δf) of the closer edge of each noise from the signal frequency, divided by the signal frequency, i.e., Δf / f_s. The exact signal and masker levels, as well as the notch widths used, depended on whether the masker or signal level was adaptively varied. These differences are described in the following two subsections.

All stimuli were generated digitally at a sampling rate of 32 kHz and were played out via a LynxStudio LynxOne soundcard at 24-bit resolution. The maskers and signal were passed through different programmable attenuators (TDT PA4) before being mixed (TDT SM3) and passed through a headphone buffer (TDT HB6). The stimuli were presented monaurally in a double-walled sound-attenuating booth via Etymotic Research ER2 insert earphones, which are designed to provide a flat frequency response at the eardrum up to about 14 kHz.

1. Fixed masker level

In each run, the masker spectrum level and notch width were fixed, and the signal level was adaptively varied to track threshold. The signal frequency was either 1 or 6 kHz. There were seven conditions in which the notch was placed symmetrically about the signal frequency; values of Δf / f_s were 0 (no spectral notch), 0.05, 0.1, 0.15, 0.2, 0.3, and 0.4. Four asymmetric conditions were also tested, where the upper and lower normalized deviations were 0.1 and 0.3, or 0.2 and 0.4, and vice versa. This provided a total of 11 different notch widths. Masker levels were chosen at each notch width in order to cover as wide a range of signal levels as possible, between 10 and 40 dB SL for each subject individually. This enabled us to reconstruct filter functions for any given signal level between about 10 and 40 dB SL, as described in the Sec. II D. In general, at least four masker spectrum levels were tested for each notch width, usually in steps of 10 dB, with levels ranging from −10 to 50 dB SPL spectrum level. This corresponded to maximum overall masker levels of about 77 and 85 dB SPL at 1 and 6 kHz, respectively.

2. Fixed signal level

In each run, the signal level was fixed at 10, 15, 20, 25, or 30 dB above absolute threshold, as measured individually for each subject, and the masker spectrum level was varied adaptively. Pilot runs showed that notched noises with normalized deviations greater than 0.2 often resulted in the signal being detectable even at the highest allowable masker levels. Because of this, only symmetrically placed notches were tested with normalized deviations of 0, 0.05, 0.1, 0.15, and 0.2. This allowed us to estimate the bandwidth of the filter tip, but limited our ability to derive the entire shape of the filter. However, because of the reduced number of notch widths, we were able to test more signal frequencies. Frequencies tested were 1, 2, 4, and 6 kHz. The maximum allowable masker level in any run was 60 dB SPL spectrum level, corresponding to a maximum overall level ranging from 87 dB SPL at 1 kHz to 95 dB SPL at 6 kHz.

B. Procedure

All thresholds were measured using a three-interval, three-alternative forced-choice method with a two-down, one-up (fixed masker level) or two-up, one-down (fixed signal level) adaptive procedure that tracks the 70.7%-correct point on the psychometric function (Levitt, 1971). Intervals were marked on a virtual response box on a flat-panel monitor located in the booth. Responses were made via the computer keyboard or mouse, and feedback was provided after each trial. The initial step size was 8 dB, which was reduced to 4 dB after the first two reversals in the direction of the tracking procedure. The final step size of 2 dB was reached after a further four reversals, and threshold was defined as the mean signal level at the remaining six reversals. Runs in which the standard deviation across the last six reversals exceeded 4 dB were discarded and were repeated at a later time. Each reported threshold represents the mean of at least two valid runs. If the standard error of the mean was 2 dB or more, up to four additional runs were included, until the standard error was less than 2 dB. For values based on six runs, an outlier was excluded if threshold was more than 4 standard deviations from the mean of the other five runs. This procedure eliminated less than 1% of all runs.

Initially, thresholds in quiet were measured for the 20-ms signal at 1, 2, 4, and 6 kHz. Following this, thresholds in the presence of the notched noise were measured. The conditions were presented using a randomized block design, with all conditions being run once before any were repeated. Thresholds for all masker levels (or signal levels in the fixed signal level paradigm) of a given notch width were run together in random order, and all notch widths for a given signal frequency were measured before proceeding to the next signal frequency. The presentation orders of levels, signal frequencies, and notch widths were randomized independently for each subject and each repetition.

C. Subjects

Four normal-hearing listeners (two males, two females), aged between 19 and 24 years, served as subjects in the fixed masker level experiment, and five normal-hearing subjects (two males, three females, including author AS), aged between 20 and 39 participated in the fixed signal level experiment. They all had audiometric thresholds of 15 dB HL or less at frequencies of 250, 500, 1000, 2000, 4000, 6000, and 8000 Hz. They received at least 2 h of training before the data were collected. The total number of 2-h sessions ranged from 8 to 12. Initially, five subjects were used in both paradigms, but one subject who participated in the fixed masker level experiment, despite having a normal audiometric threshold at 6 kHz (measured using long-duration tones with TDH39 headphones), had an absolute threshold for the 20-ms signal at 6 kHz that was 10 dB or more higher than that of the other subjects. Because of this, his data were not analyzed further. The absolute thresholds of the nine remaining subjects for the 20-ms signals are shown in Table I.

TABLE I.

Absolute thresholds in dB SPL for the 20-ms signals used in the experiments. Subjects 1–4 were tested only at 1 and 6 kHz.

		Signal frequency (kHz)
Subject	Ear tested	1	2	4	6
S1	R	27	…	…	26
S2	R	22	…	…	23
S3	R	24	…	…	21
S4	R	22	…	…	25
S5	R	21	25	20	22
S6	L	28	26	24	28
S7	R	22	22	14	17
S8	L	24	27	29	20
S9	R	22	22	19	23

D. Results

1. Fixed masker level

The mean data using the fixed masker levels are shown in Fig. 1, with results using a 1- and 6-kHz signal shown in the left and right panels, respectively. Signal level at threshold is plotted as a function of masker spectrum level, with notch width as a parameter. For clarity, only six of the 11 notch widths are shown, as described in the legend. Only points that include data from all four subjects are included in the figure. As expected, signal thresholds increase with masker level and with decreasing masker notch width. Some differences between 1 and 6 kHz are apparent in these raw data. At 1 kHz, once the signal level exceeds about 30 dB SPL, the masking curves are roughly parallel to one another, with the possible exception of the two asymmetric conditions, which diverge somewhat, indicating slightly greater filter asymmetry at higher levels. At 6 kHz, differences in the slopes of the different curves are more marked, suggesting greater changes in tuning as a function of level. The pattern of data from individual subjects was very similar to the average data shown in Fig. 1.

FIG. 1.

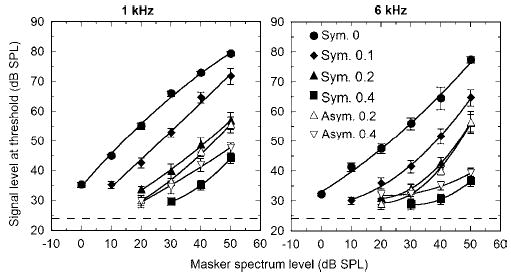
Mean signal thresholds of four subjects as a function of masker spectrum level, from the fixed masker level experiment. The left and right panels show data from a signal frequency of 1 and 6 kHz, respectively. The different symbols represent data from different masker spectral notch widths. Filled symbols represent symmetric notches and open symbols represent asymmetric notches. Up-pointing arrows represent conditions where the center of the masker’s spectral notch was higher than the signal frequency; down-pointing arrows represent conditions where the center of the spectral notch was lower than the signal frequency. Data points falling within 5 dB of absolute threshold have been omitted. The numbers in the legend denote the normalized frequency deviation between the lower edge of the spectral notch and the signal. Error bars denote ±1 standard error between subjects. The curves show second-order polynomial fits to the data. The dashed horizontal lines represent the mean absolute threshold (23.8 dB SPL at both frequencies).

As an initial step in deriving the underlying auditory filter shapes, iso-signal-level curves were calculated from both the individual data and the data pooled across individuals. This was achieved by fitting a second-order polynomial to each of the notch-width data sets, relating signal level at threshold to masker spectrum level. Conditions that resulted in signal thresholds within 5 dB of absolute threshold were excluded from the analysis to reduce the effects of approaching absolute threshold on the masking function. For each subject and signal level, the polynomials were solved to find the masker levels at each notch width corresponding to a given signal level from 10 to 40 dB above the absolute threshold (dB SL) of each subject in 5-dB steps.¹ The procedure can be visualized by imagining a horizontal line on the graph in Fig. 1, and picking all the x values (masker levels) at which the horizontal line intersects with the different masking functions. Finally, all the masker levels corresponding to a given signal level were collected across notch widths to provide a curve that plots masker spectrum level as a function of notch width. These transformations were performed on individual data sets and on the data pooled across all four subjects. In the pooled case, the polynomials were fitted to the individual mean data points, rather than to the raw data from each repetition, so that the data from all subjects would carry equal weight in the fitting procedure. The dB SL values were based on the absolute threshold values averaged across the four subjects. The threshold values derived from the polynomial fits to the pooled data are plotted in Fig. 2 for signal levels of 10, 20, and 30 dB SL. The left panels show data at 1 kHz, and the right panels show data at 6 kHz. These transformed data were then used to derive auditory filter shapes. Note that only relatively narrow notch widths (normalized deviations of 0.2 or less) include masker levels below the maximum measured spectrum level of 50 dB SPL for signal levels of 20 dB SL or more. Thus, in examining the effects of level on auditory filter bandwidth, we are limited to relatively narrow notch widths.

FIG. 2.

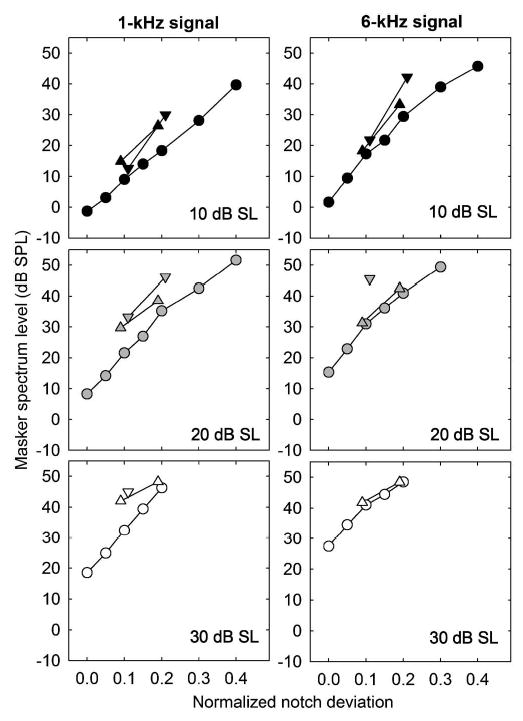
Transformed data from the fixed masker level experiment, pooled across subjects, showing masker spectrum level at threshold as a function of masker notch width. The abscissa shows the frequency difference between the signal and the nearest spectral edge of the notched noise, divided by the signal frequency. Left and right panels show data from 1 and 6 kHz, respectively. The three rows show results from three different signal levels, as shown in the panels. Data from symmetric spectral notches are shown as circles. Data from the asymmetric notches are shown as triangles: upward-pointing triangles denote points where the spectral edge of the lower-frequency noise band was closer to signal frequency, and downward-pointing triangles denote conditions where the spectral edge of the higher-frequency noise band was closer to the signal frequency.

2. Fixed signal level

The results from the fixed signal level paradigm needed no transformation before being used to derive auditory filter shapes at each signal level. The mean data are plotted in Fig. 3, with the results from each signal frequency in a separate panel. For clarity, only the results using signal levels of 10, 20, and 30 dB SL are shown. As expected, the masker level required to mask the signal increases with increasing masker notch width and with increasing signal level. At the higher signal frequencies of 4 and 6 kHz there is a trend for the function relating masker level to masker notch width to be shallower at higher than at lower signal levels, with the three curves at each frequency converging somewhat at the wider notch widths. In contrast, the functions at 1 kHz appear, if anything, to diverge somewhat with increasing notch width. These effects are quantified in the following sections by deriving auditory filters from the data.

FIG. 3.

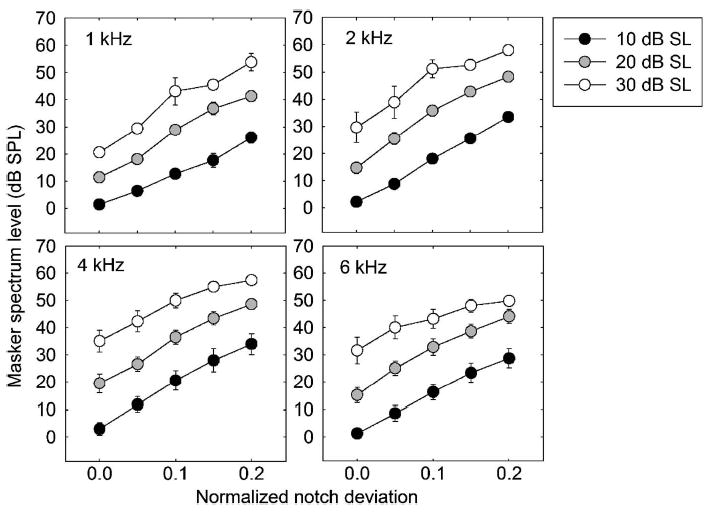
Mean thresholds of five subjects from the fixed signal level experiment. The different panels show the results using different signal frequencies. Black, gray, and white symbols represent signal levels of 10, 20, and 30 dB SL, respectively. Error bars represent ±1 standard error of the mean.

III. DERIVING AUDITORY FILTERS

A. Model implementation and fitting procedures

Before being processed by simulated auditory filters, the stimuli were passed through a middle-ear function described by Moore et al. 1997. As the insert earphones used in this study (Etymotic Research ER2) are designed to produce a flat transfer function at the eardrum for frequencies up to about 14 kHz, no outer-ear transfer function was incorporated into the simulations. The filter shapes were derived using the basic rounded exponential (roex) shape (Patterson and Nimmo-Smith, 1980), with methods similar to those described in many previous studies (e.g., Glasberg and Moore, 1990; 2000). Both the roex(p) (Patterson et al., 1982) and a variant of the roex(p,w,t) (Glasberg et al., 1984; Rosen et al., 1998; Glasberg and Moore, 2000; Oxenham and Shera, 2003) were tested. The equation for each side of the roex(p) filter is

$$W(g)=(1+pg)exp(-pg),$$ (1)

where W is the filter weighting function, g is the normalized deviation from the center frequency (|Δf| / f_c), and p is the parameter determining the slope of the filter. The value for p can either be the same on both sides of the filter to produce a symmetric filter, or can be allowed to differ on either side of the filter (p_u for the upper side and p_l for the lower side). We used the symmetric roex(p) in cases with limited numbers of notch widths (normalized deviations of 0.2 or less), where the tails of the filter and the filter asymmetry were poorly (or not at all) defined. In cases with a wider range of symmetric and asymmetric notch-width data, we continued to use the roex(p) function to describe the upper side of the filter, but used the roex(p,w,t) filter to describe the lower side

$$\begin{array}{l}W(g)=(1-w)(1+p_{l}g)exp(-p_{l}g)\\ +w(1+p_{l}g/t)exp(-p_{l}g/t).\end{array}$$ (2)

In line with Oxenham and Shera (2003), we refer to this hybrid as the roex(p,w,t,p) model. The difference between Eqs. (1) and (2) [and the difference between the upper and lower sides of the roex(p,w,t,p) filter] is that Eq. (2) has two slopes instead of one. This can be important in describing accurately how thresholds change at wider notch widths, but it comes at the expense of an additional two parameters. The parameter t determines the factor by which the second (tail) slope is shallower than the first (tip) slope; the parameter w determines the relative weights of the first and second slopes, or the point on the filter function at which the second slope begins to dominate. The roex(p,w,t,p) filter has been used in a number of recent studies and is favored because it more closely resembles the shape of auditory neural tuning curves (Rosen et al., 1998; Glasberg and Moore, 2000; Oxenham and Shera, 2003). Also, Rosen et al. 1998 found that this shape was the most efficient in terms of giving a low rms error, while maintaining a small number of free parameters.

The data from all notch widths at a single signal level were used to derive a filter shape. A multidimensional nonlinear minimization routine [Nelder-Mead, as implemented in MATLAB (Mathworks, Natick, MA)] was used to find the best-fitting parameters of the filters in the least-squares sense. It was assumed that the signal was detected using the output of the filter with the best signal-to-noise ratio (SNR). In most situations this was also the filter centered at the signal frequency. However, in some cases the filter that had the best SNR was centered somewhat away from the signal frequency, although its CF was always within 10% of the signal frequency. The “efficiency” of the detector, K, is the threshold SNR at the output of the detection filter averaged across all conditions at a given signal level. The minimization routine was driven by the sum of squared deviations of the actual thresholds from the predicted thresholds, based on a constant K value, which was set so that the mean of all the predicted thresholds was equal to the mean of the obtained thresholds. To guard against the minimization routine finding local spurious minima, we often reran the fits using different starting parameter values. This was done for all the fits to the pooled data.

By fitting the data from each signal level with a separate filter function, we assume that the filter shapes at each signal level are independent of each other, and that the signal-to-noise ratio at threshold (K) can vary as a function of signal level. In contrast, Rosen and colleagues (Rosen and Baker, 1994; Rosen et al., 1998) have argued that it is preferable to fit all the data across all signal levels within a single model that allows the filter parameters to vary systematically with level according to a polynomial equation. They found that allowing K to vary with signal level did not improve the model predictions, and were thus able to treat it as a constant across all signal levels. Their approach has the advantage that it reduces the number of free parameters, thereby increasing the stability of the fits. The assumption of a constant K across all signal levels is also well justified for the simultaneous-masking paradigm used by Rosen and colleagues. However, it is not possible to assume a constant K with nonsimultaneous masking, unless some further modeling is introduced to take account of the nonlinear growth of forward and backward masking (e.g., Jesteadt et al., 1982; Oxenham and Moore, 1995; Plack and Oxenham, 1998). Also, because forward masking can involve rather abrupt transitions in masking growth as a function of level (e.g., Plack and Oxenham, 1998), it was decided to allow the filter parameters to vary independently at different signal levels.

B. Auditory filter shapes at low signal levels

Our fixed masker level data for the lowest two signal levels (10 and 15 dB SL) were the only data sets that incorporated the full complement of notch widths, extending out to normalized deviations of 0.4. This allowed us to fit the roex(p,w,t,p) to the data, and to compare the resulting filter bandwidths to those in an earlier study, using just forward masking with a fixed signal level (Oxenham and Shera, 2003). The parameters and ERBs for the filters derived from the pooled data are shown in Table II, along with the mean ERBs taken from fitting filter shapes to the individual data.

TABLE II.

Parameters for the filters fitted to the data from the fixed masker level experiment, pooled across subjects. The parameters are from Eqs. (1) and (2) to describe the upper and lower slopes of the filter, respectively. The error term (rms) is an indication of the goodness of fit. The right-most two columns show the mean and standard deviation of the ERBs derived from filter fits to the individual data.

		Pooled filter parameters
Frequency level (dB SL)		pl	pu	t	10 log(w)	10 log(K)	ERB (Hz)	rms (dB)	Mean of individual filters ERB (Hz) s.d.
1 kHz	10	40.2	29.7	2.01	−13.7	14.4	119	1.6	121	24.0
	15	40.1	42.1	2.30	−18.1	15.2	98	1.6	102	20.3
6 kHz	10	44.0	43.4	2.80	−25.6	4.54	550	1.5	531	155
	15	41.4	63.0	3.94	−30.73	2.47	481	0.7	478	85.4

The ERB values for a signal level of 10 dB SL are generally larger (implying poorer tuning) than the mean ERBs of Oxenham and Shera (2003), which were 98 and 360 Hz at 1 and 6 kHz, respectively. However, a statistical comparison of the present ERBs and those of Oxenham and Shera (2003) revealed that these differences were not significant (two-tailed t-tests; p>0.05 at both frequencies). When equating the masker levels for the on-frequency masking condition (no notch) (Nelson et al., 1990)—Oxenham and Shera’s (2003) data are more comparable to our data with a signal level of 15 rather than 10 dB SL. The filter parameters with a 15-dB SL signal are shown in the second row of Table II. The ERBs tend to be somewhat smaller (narrower) and the standard deviation across listeners is somewhat lower. For the 15-dB SL condition, the ERB at 1 kHz was similar to that found by Oxenham and Shera (2003), while the ERB at 6 kHz was somewhat broader. Again using two-tailed t-tests, differences between the two studies in ERB estimates failed to reach statistical significance at the 0.05 level. The 10- and 15-dB SL signal conditions in the fixed-masker-level paradigm were the only ones to be analyzed with a roex(p,w,t,p) model, as these were the two signal levels where almost all the masker levels fell below 50 dB SPL spectrum level.²

C. Auditory filter bandwidths as a function of level

For signal levels above 15 dB SL in the fixed masker level conditions, and for all signal levels in the fixed signal level condition, only notches with spectral gaps between the masker edge and the signal of 0.2f_s or less were used to derive auditory filters. Because of the reduced number of notch widths (5), and the lack of asymmetric notches, the simple symmetric roex(p) model, with one parameter to describe the filter shape, was used to fit the data [i.e., Eq. (1) for both sides of the filter]. While this method does not provide for very detailed filter shapes, it provides a more robust fit and avoids the danger of “overfitting” the data with too many free parameters.

Each individual data set from the fixed masker level and fixed signal level paradigms was fitted using roex(p) filters, as described above. The resulting ERBs are shown in Fig. 4. Dotted lines show individual fits from the fixed signal level paradigm and dashed lines show individual fits from the fixed masker level paradigm. The heavy solid lines represent the mean ERBs, averaged across listeners (and groups at 1 and 6 kHz) for the level range over which data were collected in both groups (10 to 30 dB SL).

FIG. 4.

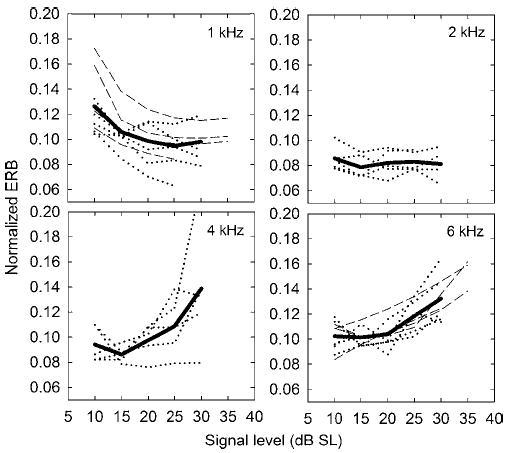
Equivalent rectangular bandwidths (ERBs), derived by fitting the roex(p) filter model to symmetric notch widths between 0 and 0.2 to signal levels between 10 and 35 dB SL. Dashed lines represent individual fits using a fixed masker level paradigm; dotted lines represent individual fits using a fixed signal level paradigm. The heavy solid lines represent the mean ERB values, averaged across both sets of subjects where applicable.

When considering only notch widths of 0.2 or less, the ERB values are somewhat higher than when all notch widths are considered. For instance, the pooled ERB for the 1-kHz, 15-dB SL signal in the fixed masker level paradigm was 96 Hz with all points included using the roex(p,w,t,p) filter, whereas the ERB from the same data using only notch widths of 0.2 or less was 113 Hz using the roex(p) filter. This is primarily a consequence of the simpler filter model, in which one filter slope must account for the whole filter, commonly leading to an underestimate of the slope near the tip and an overestimate near the tail. Thus, the values shown in Fig. 4 should not be taken as accurate estimates of absolute cochlear tuning. Similarly, it is not appropriate to compare absolute ERB values from this analysis with those from previous studies. Nevertheless, the simple model provides a quantitative way of estimating changes in filter bandwidth over a wider range of levels than is possible with the more complex model.

1. Comparing fixed masker level and fixed signal level paradigms

The common conditions (1 and 6 kHz) allowed us to test for any significant differences between the two groups and methods (fixed masker level vs fixed signal level). No difference was expected, given that Glasberg and Moore (1982) had found none when comparing ERBs derived from notched-noise forward masking for signal levels between 8 and about 23 dB SL. However, according to our initial hypothesis, a difference might emerge at high masker levels, where subjects might start responding incorrectly to lower the level of the masker in the fixed signal level conditions. A repeated-measures analysis of variance (ANOVA) was carried out on the normalized ERB values (ERB divided by the signal frequency) with signal level (10 through 30 dB SL) and frequency (1 or 6 kHz) as within-subject factors and masking paradigm as a between-subjects factor. Masker paradigm did not have a significant main effect, nor were the interactions between paradigm and frequency or signal level significant (p>0.2 in all cases). Thus, consistent with Glasberg and Moore {1982), the ERBs derived from fixing the signal level or fixing the masker level in the experimental paradigm were the same, so long as the data were analyzed in terms of signal level.

2. Effects of signal frequency on ERB level dependence

Despite some intersubject variability, some general trends are apparent in the data shown in Fig. 4. For both experimental paradigms at 1 kHz, there is an apparent decrease in ERB, particularly as the signal level is increased from 10 to 15 dB SL, and continuing slightly up to 25 dB SL. This trend was confirmed by subjecting the data using the 1-kHz signal between 10 and 30 dB SL to a one-way repeated-measures ANOVA with signal level as the within-subjects factor and group as the between-subjects factor. The effect of level was highly significant overall [F(3.5,24.6) =13.4, p<0.001],³ and there were both significant linear and quadratic trends, reflecting the general decrease in ERBs with increasing level. This finding was unexpected, given that Glasberg and Moore (1982) had found no significant effect of level on ERBs at 1 kHz in forward masking. However, the trend we observed seemed robust and was apparent in both experimental paradigms. The effect can also be observed in the raw and transformed data of the fixed signal level and fixed masker level paradigms, respectively. In Fig. 2, considering only notch widths up to 0.2, it can be seen that the slope of the function for the 1-kHz signal (left panel) is shallower for the 10-dB SL signal level than for the 20- or 30-dB SL signal levels. Similarly, in Fig. 3, the slopes for the 1-kHz signal (upper-left panel) seem shallower at 10 dB SL than at the higher two levels. We currently have no good explanation for this effect.

At 2 kHz, ERBs remained roughly constant over the level range tested. This was confirmed by a repeated-measures ANOVA, showing no significant effect of level on the ERB [F(4,16) =0.77, p>0.5]. At 4 kHz, the data were rather variable, with one subject showing no change in ERB as function of level and another showing a very dramatic increase in ERB. Overall, the effect of level on the ERB at 4 kHz failed to reach significance [F(2.0,8.2) =3.1, p<0.1). In contrast, at 6 kHz, all nine subjects showed a consistent increase in ERB with increasing level, and the effect of level was significant for the pooled data (F<2.7,19.2) =12.9, p< 0.001], as were linear and quadratic trends (p<0.01). Overall, the mean ERB increased by more than 30% between 10 and 30 dB SL and increased further for the three subjects for whom an ERB could be estimated at a signal level of 35 dB SL.

The results suggest that the dependence of ERB on level varies as a function of signal frequency between 1 and 6 kHz, with the broadening of the ERB as a function of level becoming increasingly pronounced with increasing signal frequency.

3. Changes in filter shape as a function of level

One important question is how the shape (and not just the ERB) of the filter changes with level. In the simple roex(p) model, increases in bandwidth are associated with decreases in the slopes of the filter. Another way a filter’s ERB can increase is for the tuning of the filter tip to remain constant, while its gain decreases relative to the gain of the filter tail (e.g., Rosen et al., 1998; Glasberg and Moore, 2000; Gorga et al., 2003), which can be implemented in the roex(p,w,t) model by an increase in value of the weighting parameter, w. Our data with only 5 data points per signal level above 15 dB SL are generally too limited to permit a serious evaluation of a model with three free filter parameters. However, we carried out an analysis involving two free filter parameters using the roex(p,r) model, the equation for which is

$$W(g)=(1-r)(1+pg)exp(-pg)+r,$$ (3)

where r represents a limit to the filter’s dynamic range. This allowed us to determine whether the changes in ERB found with the roex(p) model could be attributed more to the tip or tail of the filter. This analysis was carried out at the 1-and 6-kHz signal frequencies, which were the frequencies that were tested for both groups of subjects, and which showed significant effects of level on the ERB. At the 1-kHz signal frequency, using the roex(p,r) filter shape, the effect of level on p values was found to be significant [F(2.0,16.4) =3.87, p=0.041], but there was no significant effect of level on the r values [F(2.4,19.2) =0.015, p>0.5]. In contrast, at the 6-kHz signal frequency, there was no significant effect of level on the p values [F(3.7,29.7) =0.48, p>0.5], but a significant effect on the r values [F(1.7,13.8) =6.86, p=0.01]. This suggests that at 6 kHz the increase in ERB found in the original analysis may be ascribed to the decrease in filter tip gain, relative to the tail, as proposed in other psychophysical studies using simultaneous masking (Glasberg and Moore, 2000) and physiological studies using otoacoustic emissions (Gorga et al., 2003).

IV. DISCUSSION

Earlier studies using simultaneous masking have also found changes in level dependence as a function of frequency (e.g., Moore and Glasberg, 1987; Hicks and Bacon, 1999; Glasberg and Moore, 2000). In one of the more recent such studies, Glasberg and Moore (2000) concluded that level dependence (or, in their model, maximum filter gain) increased up to about 1 kHz and remained constant thereafter. On the other hand, an analysis by Baker et al. 1998 suggested that level dependence continued to increase with signal frequency up to 6 kHz. Both these studies used simultaneous masking. The pattern of our results is more in line with those found in Baker et al.’s study (1998). However, both earlier studies showed increasing ERB with increasing level at all signal frequencies tested. Here, a marked and significant increase (at least for signal levels up to 35 dB SL) was only observed at the highest signal frequency of 6 kHz. A possible reason for this apparent discrepancy is that the results were based on simultaneous masking, while ours were based on nonsimultaneous masking. However, a more detailed study is required to confirm this conjecture. In any case, to the extent that nonsimultaneous masking better reflects cochlear tuning, as measured physiologically, it seems that pronounced differences occur between 1 and 6 kHz, which are not captured by current phenomenological models of human auditory filtering (e.g., Glasberg and Moore, 2000; Meddis et al., 2001). One study measured psychophysical tuning curves as a function of level at both 1 and 3 kHz (Green et al., 1981). They found level independence over a 20-dB range of signal levels at both frequencies. However, some aspects of their experiment, such as the abrupt gating of their 10-ms signal (with no onset or offset ramps), the limited number of conditions tested at 3 kHz, and their use of a tonal masker, which can produce so-called “confusion” effects in some cases (e.g., Neff, 1986), make their results somewhat difficult to interpret.

An earlier study, which examined human cochlear tuning only at very low levels, found that filter tuning sharpened considerably as the signal frequency was increased from 1 to 8 kHz (Shera et al., 2002; see also Oxenham and Shera, 2003). Our data suggest that the improvement in tuning with increasing frequency may be a purely low-level phenomenon, and even that the reverse may be true at higher levels. For instance, in the earlier data, the normalized ERB decreased by a factor of about 1.6 as the signal frequency increased from 1 to 6 kHz. Although somewhat variable, our data at 10 dB SL go in the same direction with a decrease in normalized ERB by a factor of about 1.4 for both the full (Table I) and limited (Fig. 4) sets of notch widths. In contrast, at 30 dB SL the present data show that the normalized ERB increases by a factor of about 1.3 between signal frequencies of 1 and 6 kHz, and by about 1.5 at 35 dB SL for those subjects for whom data could be collected that level. These data thus confirm the conjecture of Shera et al. 2002 and Oxenham and Shera (2003), that their revised estimates of human cochlear tuning are only valid at very low stimulus levels.

What accounts for these changes in filter properties at different signal frequencies? One possibility is that the properties of the “cochlear amplifier,” and its role in determining tuning, vary as a function of place along the cochlear partition. It has long been thought that cochlear gain and nonlinearity decrease in the apex of the cochlea, corresponding to low CFs. More recent psychophysical studies suggest that cochlear compression remains relatively constant across a wide range of CFs, at least in humans (Lopez-Poveda et al., 2003; Plack and Drga, 2003; Plack and O’Hanlon, 2003; Oxenham and Dau, 2004). However, all these studies agree that cochlear compression is less frequency specific at low CFs. This suggests that while the cochlear amplifier may provide substantial gain at low CFs, it may not play such an important role in determining tuning at low CFs. The conjecture that different mechanisms determine tuning at low and high CFs is consistent with the observation that the shapes of neural tuning curves differ between low and high CFs. In particular, high-CF tuning curves exhibit clearly defined “tip” and “tail” portions, which have been hypothesized to derive from (at least) two separate modes of IHC excitation (e.g., Mountain and Cody, 1999; Lin and Guinan, 2000), whereas low-CF (including 1000 Hz) tuning curves show a more uniform shape, with no clearly discernible tail portion (e.g., Liberman, 1978). Other evidence for differences between apical and basal cochlear mechanics can be found in data from auditory-nerve-fiber group delays (Pfeiffer and Molnar, 1970) and from otoacoustic emissions (Shera and Guinan, 2003). Finally, it should not be concluded that there is no increase in filter bandwidth with level at frequencies of 1 and 2 kHz. Studies using psychophysical tuning curves have been able to measure tuning at levels higher than we attained in the present study, and have found increases in filter bandwidth once the masker level exceeds about 60 dB SPL (Nelson and Freyman, 1984; Nelson et al., 1990; Nelson, 1991). To our knowledge, no similar studies have been done at higher signal frequencies.

In summary, our nonsimultaneous-masking data reveal a striking difference between the level dependence of the ERB as the signal frequency increases from 1 to 6 kHz: filter bandwidths decreased somewhat with increasing level at 1 kHz, remained constant at 2 kHz, showed a tendency to increase at 4 kHz, and increased consistently at 6 kHz. A similar level dependence has not been reported in earlier studies using simultaneous masking, where changes in tuning with level appear not to vary as much with frequency for signal frequencies of 1 kHz and above (Glasberg and Moore, 2000). The difference between our and previous results may be due to our use of nonsimultaneous masking, which may better reflect cochlear tuning as measured physiologically (e.g., Shera et al., 2002).