Abstract
Accurate quantification of the MRSI-observed regional distribution of metabolites involves relatively long processing times. This is particularly true in dealing with large amount of data that is typically acquired in multi-center clinical studies. To significantly shorten the processing time, an artificial neural network (ANN) based approach was explored for quantifying the phase corrected (as opposed to magnitude) spectra. Specifically, in these studies radial basis function neural network (RBFNN) was used. This method was tested on simulated and normal human brain data acquired at 3T. The N-acetyl aspartate (NAA)/ creatine (Cr), choline (Cho)/Cr, Glutamate + Glutamine (Glx)/Cr, and Myo-inositol (mI)/Cr ratios in normal subjects were compared with the line fitting (LF) technique and jMRUI-AMARES analysis, and published values. The average NAA/Cr, Cho/Cr, Glx/Cr and mI/Cr ratios in normal controls were found to be 1.58 ± 0.13, 0.9 ± 0.08, 0.7 ± 0.17 and 0.42 ± 0.07 respectively. The corresponding ratios using the LF and jMRUI-AMARES methods were 1.6 ± 0.11, 0.95 ± 0.08, 0.78 ± 0.18, 0.49 ± 0.1 and 1.61 ± 0.15, 0.78 ± 0.07, 0.61 ± 0.18, 0.42 ± 0.13 respectively. These results agree with those published in literature. Bland-Altman analysis indicated an excellent agreement and minimal bias between the results obtained with RBFNN and other methods. The computational time for the current method was 15 seconds compared to approximately 10 minutes for the LF-based analysis.
Keywords: Magnetic Resonance Spectroscopic Imaging, Artificial Neural Networks, Radial Basis Function Neural Network, Parametric Spectral Analysis
INTRODUCTION
Proton magnetic resonance spectroscopic imaging (MRSI) or multi-voxel magnetic resonance spectroscopy (MRS) can noninvasively provide tissue biochemical information and has the potential for improving pathologic specificity [1]. Usually, the MRSI quantification procedures involve manual intervention and extensive computational time. Currently, the most commonly used quantification methods are based on line fitting (LF) using a non linear least square optimization, such as Levenberg - Marquardt algorithm [2-5]. All these procedures involve relatively long computational times. This problem becomes even more acute for 3D MRSI data and multi center clinical trials where a large amount of data needs to be processed. For MRSI to become a routine clinical tool there is a need to completely automate the quantification procedures and reduce the processing times close to real-time. Such a goal could possibly be realized using methods based on artificial neural networks (ANN). The ability of ANN for classification of spectra for various pathologies has been demonstrated [6-14]. However, relatively little attention has been paid to metabolite quantification using ANN [15-16]. Recently, ANN has been used to develop automated methods to quantify MRS data [15-16]. These studies demonstrated a high correlation between the areas of metabolite peaks computed with ANN and LF methods. However, these techniques were limited to either single voxel MRS or magnitude spectral data acquired at long echo times (or TE). There is an increasing interest in short echo time MRSI for visualizing short T2 metabolites for improved tissue pathology [17]. In addition, analysis of phased spectra provides more accurate quantification of metabolites. However, short echo time MRSI suffers from relatively ill defined baseline and is more difficult to analyze. The above studies also employed Lorentzian lineshapes in their analyses. It is well known that the Voigt lineshape provides a better approximation of the observed lineshapes compared to Lorentzian or Gaussian alone [18].
In the current studies, we have explored the use of radial basis function neural network (RBFNN) to overcome many of the limitations of the previously published studies. This technique was applied for automatic quantification of short echo time, multi-voxel, phased spectral data. In the present study, the RBFNN was trained with simulated Voigt line shapes to achieve quantitative values. The baseline and first order phase corrections were included in the preprocessing steps. The inclusion of magnetic field inhomogeneity correction in the present approach further improved the quality of analysis. Both single and overlapping (two and three) peaks were included in training the network to make the technique more general. Since the network is trained in a generic manner, inclusion of additional resonances for quantification does not require retraining the network. The robustness of RBFNN in the presence of noise and phase distortion was demonstrated using simulated data. Bland-Altman analysis [19] was performed for comparing the metabolite ratios, NAA/Cr, Cho/Cr, Glx/Cr and mI/Cr computed on 7 normal controls using the RBFNN and the LF methods. All the area ratios were computed relative to the Cr peak at 3.03 ppm.
MATERIALS AND METHODS
Spectroscopic Data Acquisition
Two-dimensional MRSI was acquired on a 3 T Philips Intera scanner using the PRESS localization and 24 × 24 phase encoding steps. The sequence parameters were: TR = 1500 ms, TE = 39 ms, field of view = 240 mm × 240 mm × 12 mm, spectral width = 2000 Hz, and number of points = 1024. Spectroscopic volume was contained within the centrum semiovale region of the brain with minimal CSF contamination. Unsuppressed water spectra with identical sequence parameters, except for 12×12 phase encoding steps, were acquired for automatic phase correction and inter-voxel spectral alignment [2]. Data were acquired on 7 normal controls (NC).
Data Processing
The flowchart depicting various steps involved in the RBFNN-based metabolite quantification is shown in Fig. 1. Implementation of each individual step is described below.
FIG. 1.
Flow chart summarizing various steps involved in the spectral quantification using RBFNN.
Preprocessing
All the FIDs were DC shifted by taking the average of the last one-eighth complex points of the FID. Hanning filter was used for apodization along the spatial dimensions. Zero-order phase correction was performed by multiplying the complex points of the suppressed data set by the complex conjugate of the unsuppressed data normalized to its magnitude data [20, 21]. Residual water peak was suppressed by low frequency filtering for improved baseline flatness as described elsewhere [2]. Spectral resolution in each voxel was enhanced by zero filling the FID to 4096 points. The intervoxel spectral alignment was performed, on a voxel-by-voxel basis, using the unsuppressed water signal. An automatic first order phase correction was performed as described elsewhere [2].
Baseline Correction
Spectra acquired at short echo times contain broad unresolved peaks from macromolecules which have short T2 and distort the baseline that affects spectral quantification. In the LF-based approaches for quantitative MRS analysis, the baseline is usually modeled by polynomials or B-splines [5]. In the present study, spectra were corrected for baseline using the wavelet shrinkage approach [22]. This approach involved two steps: 1) baseline recognition and 2) baseline characterization. In the baseline recognition step, all the known metabolite peaks (NAA, Cr, Cho, Glx and mI) were automatically identified based on their position information (known a priori) and the sign of the first derivative of the amplitude with respect to frequency (computed using finite differences). For better estimation of the baseline, any remaining narrow metabolite peaks were separated from the baseline in the baseline recognition step. This was achieved by utilizing the signal power criterion [23]. This involved computation ofσsig, which is the mean of the variances of the signal in the NAA, Cr and Cho peaks. To determine whether a point in the spectrum belongs to a peak or baseline, a rectangular window was placed around that point and the variance,σw, of the spectral points within the window was computed. This spectral point was considered to be part of the baseline if
| [1] |
or else it was considered to be a part of a metabolite peak. Applying the above procedure on a large number of data with different values of the weighting factor, W, we observed that the narrow peaks and baseline were well distinguished for the value of W = 0.5. Once all the narrow peaks in the spectrum were identified then each peak was replaced by a straight line connecting the end points of the base of the peak.
The procedure for baseline characterization was similar to that suggested in Ref. [22]. The spectra were subjected to a discrete wavelet transformation (DWT). To ensure the broadness criterion for the baseline, all the wavelet coefficients at a scale smaller than the peaks of interest were zeroed. The biorthogonal spline wavelets were used for the decomposition. The spectrum was subjected to DWT up to 6 levels and all the coefficients at level 5 and smaller were zeroed. The remaining coefficients were thresholded, based on denoising criterion [24]. The baseline estimate was obtained by performing an inverse wavelet transform on the remaining coefficients. The estimated baseline was subtracted from the phased spectrum.
B0 Field Inhomogeneity Correction by Water Reference Deconvolution
The magnetic field (B0) is generally nonuniform across the spectroscopy slab. The field inhomogeneity distorts the lineshapes and this distortion varies from voxel-to-voxel. This can lead to poor resolution and significant overlap between adjacent peaks like Cr and Cho, making accurate quantification difficult. In the present study we have employed water reference deconvolution for correcting the B0 field inhomogeneity as suggested elsewhere [20, 21, 25, 26] and implemented for MRSI by Maudsley et al. [3]. We used as target lineshape for reference deconvolution a Lorentzian with width equal to that of the sharpest unsuppressed water peak measured, i.e. the water peak from the voxel with the most uniform magnetic field. Unlike most of the existing approaches that use a fixed value for the target linewidth, our procedure makes the target linewidth adaptive to each MRSI acquisition. It is important to point out that Lorentzian lineshape is assumed only for implementing the water reference deconvolution, and not for spectral quantification, for mathematical simplicity. The distortion function gn(t) was estimated for each voxel as described by Metz et al. [27]. Direct division of the FID (xn(t)) by the distortion function (gn(t)) in the time domain (deconvolution in the frequency domain) leads to ringing in the corrected spectrum. To avoid this ringing we have applied the Wiener filtering approach. Mathematically this can be written as [28]
| [2] |
where, the subscript n stands for the voxel number, xn(t), , and gn(t) are the input and corrected FIDs and the distortion function for a particular voxel. The value Kn(t),contains information about the noise present in the signal. Ideally, for very noisy data, Kn(t) should be high and for low noise data Kn(t) should be close to zero. We have developed an approach, where the value of Kn(t) was varied, based on the signal strength at each point in the FID. The value of Kn(t) for each point of the FID was computed as follows,
| [3] |
where xn(t) is a complex point of the FID and is its conjugate. The noise power Sn for a particular voxel was computed using the vector xn corresponding to the last 1/8th points of the FID, as shown below.
| [4] |
where xn* is the complex conjugate of xn and N is the number of points in the FID. Thus the inverse filtering problem was fully automated taking into consideration both the degree of noise present in the signal and the distortion function. The efficiency of Wiener filtering approach compared to the inverse filtering with fixed threshold was demonstrated with simulated and human brain data. The simulations were performed in the time domain, using Eq. [5].
| [5] |
where ν and εj represent the position of the peak and additive noise respectively. α , a are related to the half width at half maximum (HWHM) and height of the peaks (in frequency domain) as shown below [29],
| [6] |
The spectral data with peaks, NAA, Cr and Cho were simulated using Eqs. [5] and [6]. These simulations were only meant to compare the Wiener filtering approach with inverse filtering with a fixed threshold. The HWHM and amplitudes of the peaks were varied randomly. Gaussian noise was added to each of the three peaks for a realistic simulation. A sample distortion function g(t) , which was obtained from experimental data [27] was applied to the simulated spectrum for generating the distorted spectrum. The Wiener filter and inverse filter with fixed threshold were then applied to the distorted data to obtain the corrected spectrum. The normalized energy of the difference between the estimated and actual spectrum, referred to as the L2error, defined as
| [7] |
was computed. In the above equation, zj and represent the real parts of the original and corrected spectra respectively.
Quantification with RBFNN
RBFNN has the property of modeling any nonlinear function in a single layer [30], thus avoiding the design decision about the number of hidden layers to be used in the network. Also RBFNN has faster training speeds compared to the multilayer perceptron (MLP) [30]. Thus RBFNN was used for spectral quantification in the current studies. The strategy we used was to design a generic network to quantify any peak which is given as its input. This eliminates the peak position as a variable. The peak only needs to be identified from the spectrum and given to the network as input. Fig.2 shows the schematic representation of a 2 layer RBFNN for quantification of a single peak in the MRSI data. The input vector is d-dimensional, [a1, a2, … ad]. This is basically the entire peak that needs to be quantified. The peak is automatically identified from the spectrum based on its position information (known a priori) and the sign of the first derivative of the amplitude with respect to frequency. There is only a single hidden layer which computes the nonlinear function ϕc (basis function), based on the distance of the input vector from the center of the particular unitμc. The functionϕc is a nonlinear function such as Gaussian, thin-plate spline, multiquadratic etc. The Gaussian function is most commonly used as it is localized and has a number of useful analytical properties [30]. For these reasons, we have used the Gaussian function for the hidden layer.
| [8] |
where, a: d-dimensional input vector, μc : d-dimensional vector determining the center of the basis function, σc : variance or width of the basis function.
FIG. 2.
Schematic representation of 2 layer RBFNN. The input spectrum is a d-dimensional vector. The basis functions are shown in the hidden layer. Outputs of the network are amplitude HWHM and fraction of the Lorentzian component of the peak.
Here the basis functions are assumed to be spherical, i.e. all the variances are equal and the covariances are 0. The second layer or output layer is purely linear and it computes a weighted combination of the outputs of the hidden layer. For the kth output, this is mathematically expressed as
| [9] |
where, wck is the weight of the basis functions in the final output, yk, of the network and M is the number of basis functions in the network. These weights were computed during training as described below. For the present application there are three outputs as shown in Fig. 2: amplitude, line width, and the proportion of the Lorentzian component in the peak. These three parameters provide a parametric representation of the peak that can be used for computing its area.
Training the Network
The RBFNN was trained in two stages. In the first stage, the centers (positions), widths, and number of basis functions were fixed. This stage of training is unsupervised. In the second stage the weights were computed. The error, E(w), that is minimized during the second stage is a function of the weights and is given by:
| [10] |
where tkj is the targeted output for the input vector aj, P is the number of input vectors in the training set and M is the number of basis functions in the network This training stage was supervised and involves a simple matrix operation given by,
| [11] |
where W, Φ and T are the corresponding matrices for the training set. This was solved using the singular value decomposition.
Simulated peaks, based on the approximation to the Voigt line shape (Eq. [12]), were used to train the RBFNN.
| [12] |
where the Lorentzian peak is defined as,
| [13] |
and the Gaussian peak is defined as,
| [14] |
In the above equations, b is the amplitude, h is the HWHM, v0 is the central frequency, μ is the proportion of Lorentzian (varies from1 for pure Lorentzian to 0 for pure Gaussian). For training the net Gaussian noise was added as shown in Eq. [15]:
| [15] |
where εn is the additive Gaussian noise. In the simulations the amplitude, HWHM (Hz), and μ were varied in the ranges of 0-1.5, 0.975 - 6.84, and 0-1, respectively. These ranges are typically encountered in the experimental data. Gaussian noise of 3% of the maximum amplitude of the peak was added to the input peaks during training, to make the networks more robust. Since the peaks were identified locally in each spectrum, the dimension of the input vector could be variable. To take care of this problem, multiple RBFNN's with wide range of input vector lengths were trained. The RBFNN with the input vector length closest to the identified peak was automatically chosen for quantification.
Positions and Widths of Basis Functions
The simulated peaks with the range of parameters indicated above were used to select the basis functions. A Gaussian mixture model (GMM), with parameters optimized using expectation maximization algorithm [30-32], was generated using the set of peaks. The centers of the GMM were then used as the basis functions for the network. The width of each function was set to the maximum squared distance between the centers.
Computation of Weights
The weights in the second layer were computed based on the input-output pairs as specified in Eq [11]. The input was the set of simulated spectral peaks along with noise and the output was the corresponding amplitude, half width and fraction of Lorentzian for that peak.
Number of Centers / Basis functions
The early stoppage criterion was used to select the optimal number of centers for the RBFNN. The number of centers was varied from 40 through 140 with a step size of 20, and multiple RBFNN's were trained. Errors were computed for two types of input data sets: 1) with no noise and 2) with 5% noise. The point at which the input set with 5% noise had minimum error was chosen as the number of centers for the final network. The errors with no noise data were used to observe the asymptotic decrease in the error.
Overlapping Peaks
The methodology explained above was based on identifying and quantifying a single peak at a time. This single peak strategy works well for resonances such as NAA (2.02 ppm), which are well resolved, but is prone to failure in the case of overlapping peaks. In order to account for such overlap, two separate RBFNN's, which simultaneously estimate 2 and 3 overlapping peaks, were trained. These networks were trained using simulated data and the same criterion as stated earlier. The number of centers in these 2 and 3 overlapping peaks networks was 344 and 500 respectively. In the current studies, the 2.25 − 2.5 ppm spectral region that has three resonances [33-36] from glutamate and glutamine (collectively referred to as Glx) was quantified using three overlapping peaks. The myo-inositol (3.52 ppm and 3.61 ppm) peaks [33, 36] were quantified by the network based on 2 overlapping peaks. When the magnetic field homogeneity is suboptimal, the Cr (3.19 ppm) and Cho (3.03 ppm) peaks also exhibit some overlap. Therefore, this region was quantified using both single and two overlapping peaks. The result which had minimum L2 error (Eq. [7]) between the input and estimated peaks was automatically selected for the final quantification.
In addition to the above resonances, the Glx (3.75 ppm) and Cr (3.91 ppm) resonances were estimated by the single peak estimation strategy, since they are well resolved. All the peak assignments were based on Ref. [33 - 36].
Computation of Areas
Following the estimation of the amplitude b, HWHM, and proportion of Lorentzian μ for each peak, the area, which is proportional to the metabolite concentration, was computed using the analytical expressions given below. The areas of the Lorentzian and Gaussian peaks can be expressed as [29]
| [16] |
| [17] |
The final area of the peak is computed as
| [18] |
Simulations
Simulations were performed in the frequency domain to test the performance of the trained networks using the following equations:
| [19] |
| [20] |
| [21] |
where, b is the amplitude, h is the HWHM, ϕp is the Phase angle and vp is the position of the peak. The amplitude, HWHM and the fraction of Lorentzian were randomly varied in the range indicated earlier. Noise and phase were also incorporated to generate more realistic simulations. Noise was varied between 0 and 10 % of the maximum amplitude and the phase was varied from 0-450. A total of 600 spectra were simulated for each value of noise and phase. The performance of the network was assessed in terms of two metrics: 1) correlation coefficient between true value of the area and the value estimated by the network and 2) the L2 error defined in Eq. [7].
Bland-Altman analysis [19] was used for objectively evaluating the agreement between the ANN and LF results. Bland-Altman method is a commonly used statistical technique for assessing the agreement between two imperfect measures of the same variable. In this method the difference between the two measurements of the same variable (also referred to as bias) is plotted against the estimate of the true value (mean of the two measurements). In the present analysis, difference was computed by subtracting the RBFNN-derived metabolic ratios for each voxel in each subject from the corresponding values obtained with the LF method. Generally the mean and mean ± 2 sd values of the differences are shown on these plots to provide a visual estimation of both random and systematic differences between the two measurements.
All the computations were performed on a 2.39 GHz. Pentium 4 PC. Network was trained using the Netlab software [37] on the Matlab platform (Mathworks, Natick, MA).
RESULTS
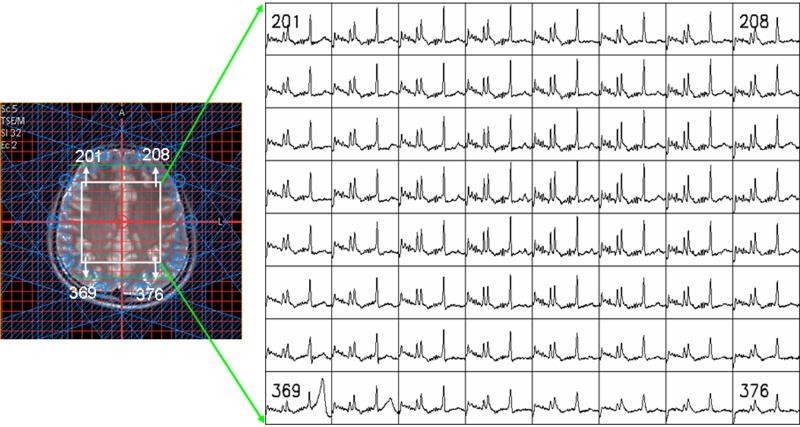
As an example, Fig. 3 shows the spectroscopic VOI along with the eight outer volume suppression bands, superimposed on a T2-weighted image from a volunteer. In this figure, only spectra from inside the VOI are included. The numbers shown in the spectra correspond to the voxel number shown in the image.
FIG. 3.
Spectroscopic VOI (rectangular box) superimposed on the T2-weighted image in a normal volunteer. The eight outer volume suppression bands are also shown in this figure. The spectra along with the voxel numbers are shown on the right.
Baseline Correction
Figure 4 shows an example of the baseline correction procedure. The dotted line in Fig. 4a shows the estimated baseline overlaid on the original spectrum. Fig 4b shows the corrected spectrum obtained after subtracting the estimated baseline from original spectrum. The flat baseline in the corrected spectrum is evident from this figure.
FIG. 4.
Baseline Correction. (a) Original phased spectrum (solid line) overlaid with estimated baseline (dotted line) and (b) Baseline corrected spectrum.
B0 Inhomogeneity Correction
Figure 5 shows a plot of the normalized error between the original and spectra corrected (Eq. [7]) using the Wiener filtering and inverse filtering with fixed threshold for the simulated datasets. The Wiener filter produced errors that were consistently lower than the inverse filter with a fixed threshold, indicating the robustness of the Wiener filter based approach. Figure 6 shows a human brain spectrum prior to (6a) and following the B0 correction using the inverse filter with fixed threshold (6b) and Wiener filter (6c). The effect of B0 correction is apparent from these figures. The peaks which are broader and with considerable overlap (Fig. 6a) have become narrower and better resolved in Figs. 6b and 6c after B0 correction. However, it can be seen that the inverse filter with fixed threshold has introduced ringing in the spectrum (6b), which is absent in the Wiener corrected spectrum (6c). Our studies on both simulated and human brain data show the Wiener filter to be more effective than the inverse filter with fixed threshold in improving data quality without introducing ringing artifacts in the data.
FIG. 5.
Comparison of the Wiener filter and inverse filtering with fixed threshold for B0 inhomogeneity correction using the simulated data.
FIG. 6.
Effect of B0 inhomogeneity correction on the phased spectrum. (a) Original spectrum, (b) deconvolution using inverse filter with fixed threshold. (c) Wiener filter approach.
Quantification with RBFNN
Number of centers
Figure 7 shows the plots of number of centers against the error computed with two types of input data sets. Fig. 7a shows the error in the input set with no noise and Fig. 7b shows the error in the input set with 5% noise. The error in the input set without noise shows a monotonic decrease with the number of centers and reaches an asymptotic value. In contrast, in the presence of 5 % noise, the error initially decreased with the number of centers, followed by an increase. This increase can be attributed to over fitting of the data. The number of centers was set to the point where the error in the input set with 5% noise reached a minimum.
FIG. 7.

Error as a function of the number of centers used in RBFNN: (a) error for input data with no noise, (b) error for 5% noise added in the input. The position where the error in (b) reaches a minimum (marked with the line) is selected as the optimal number of centers/basis functions.
Overlapping Peaks
Figure 8 shows the simulation results for the overlapping peak estimation strategy. The solid line in Fig. 8a was produced using simulations such that the two peaks have significant overlap. They were then quantified separately using the RBFNNs and the sum was plotted as the dotted line in Fig. 8a. The significant overestimation of the actual peaks can easily be seen. The dotted line in Fig. 8b was obtained from the neural network which considered the overlap between the two peaks. The improvement in the estimation of the peaks over that shown in Fig. 8a can easily be appreciated. Fig. 8c shows the results of the RBFNN which estimates 3 peaks simultaneously. The solid line represents simulated peaks with a high degree of overlap. The thin dotted lines represent the 3 individual peaks estimated by the RBFNN. The bold dotted line is the sum of the 3 individual peaks and it is very close to the original input. It is clear that inspite of a high degree of overlap between the peaks the RBFNN has accurately estimated all the 3 peaks.
FIG. 8.
Simulation results for RBFNN estimation for two (a and b) and three (c) overlapping peaks.(a) Simulated peaks with overlap (solid), and summation of the two peaks estimated based on single peak strategy (dotted line); (b) simulated peaks with overlap (solid) and estimation by simultaneously taking both peaks as input and quantifying them after taking the overlap into consideration (dotted line); (c) RBFNN for three overlapping peaks. simulated peaks (solid), individual peak estimates given by RBFNN (dotted –thin) and sum of the 3 estimated peaks (dotted –thick).
Simulations
Figures 9 and 10 shows results of the simulation studies. Fig. 9 shows the L2 error and Fig. 10 shows the correlation coefficient between areas of the true and estimated peaks. The true peak is the one which is free of noise and phase distortion. The estimated peak was generated from the parameter values estimated by the network, when the input data was noisy and phase distorted. As can be seen from Fig. 9 the error was nearly 0 at no noise and no phase conditions. The error increased from this point as the phase and noise increased. The maximum error was about 7% at 10% noise and 450 phase distortion in the input peaks. It can be seen from Fig. 10 that the correlation coefficient for zero phase and zero noise was very close to 1. As the noise increased from 0 to 10% and phase increased from 0 to 450, the correlation coefficient dropped to 0.85. The simulation studies suggest that the RBFNN quantification approach is robust against noise and phase distortions in the input peak.
FIG. 9.

Estimation of L2 errors using RBFNN quantification on simulated data as a function of percentage noise and phase distortions.
FIG. 10.

Correlation using RBFNN quantification on simulated data as a function of percentage noise and phase distortions.
Human Brain Data
Figure 11a shows the phased spectrum from a normal volunteer (solid), overlaid with the estimated baseline (dotted). The flat baseline in the corrected spectrum can be seen in Fig 11b. The NAA (2.02 ppm), Cr (3.03 ppm and 3.91 ppm), Cho (3.19 ppm), Glx (2.25 to 2.5 ppm and 3.75 ppm) and mI (3.52 and 3.61 ppm) peaks were quantified with the RBFNN approach and the result (thick line) is shown along with the original spectrum (thin line) in Fig 11c. The accuracy of the spectral estimation produced by the RBFNN can be appreciated from the difference between the original and estimated spectra shown in Fig. 11d. The magnified Glx peaks (after baseline subtraction) from 2.25 to 2.5 ppm along with the estimated peaks are shown for clarity in Fig. 11e. The excellent quality of the spectral estimation in the presence of the overlapping peaks can be appreciated.
FIG. 11.
RBFNN quantification of phased spectrum acquired on a normal volunteer: (a) phased spectrum (solid) overlaid with estimated baseline (dotted); (b) following baseline subtraction; (c) spectrum estimated with RBFNN approach (thick) overlaid on the original spectrum (thin); (d) difference between the estimate and true spectrum; (e) zoomed version of the Glx region from 2.25 to 2.5 ppm after baseline subtraction (thin) overlaid with the estimated peaks (thick).
The quantitative results obtained with the RBFNN approach were also compared with quantification based on the LF approach [38]. Fig. 12 shows the results of the Bland-Altman analysis comparing the NAA/Cr (12a), Cho/Cr (12b), Glx/Cr (12c) and mI/Cr (12d) ratios derived with the RBFNN and LF methods. The differences in the values are within 2 standard deviations indicating good agreement between these two methods. As judged by the distribution of these points around the zero bias line, the RBFNN method did not introduce bias in the estimation of the ratios of the area. The average area ratios for NAA, Cho, Glx and mI relative to Cr (3.03 ppm), obtained by the RBFNN and LF methods are shown in Table 1. The values in Table 1 represent the mean ratios averaged over all the voxels in all the subjects. The differences in the ratios between the RBFNN and LF methods were not found to be statistically significant. The data was also quantified using the AMARES algorithm [39] using the jMRUI package (Version 3.0), a commonly used spectral analysis software tool [40]. The Gaussian lineshape was used in AMARES for the data quantification. The area ratios obtained by this method are also shown in Table 1. The differences between the NAA/Cr, Glx/Cr and mI/Cr ratios using our method were not statistically significant with those obtained with the jMRUI analysis. However, the Cho/Cr values showed difference with a p value of 0.03. The ratios computed with the RBFNN also compared favorably with those reported in literature [41 - 45]. The slight variations in the area ratios between published and our (RBFNN and LF) values are expected, since our values are averaged over all voxels covering different brain tissue types within the VOI whereas the published values are based on single voxel measurements.
FIG. 12.
The Bland-Altman plot comparing the NAA/Cr (a), Cho/Cr (b), Glx/Cr (c) and mI/Cr (d) ratios estimated with RBFNN and LF methods. The x-axis represents the mean of the two methods and the y-axis represents the difference between the two methods (bias). Each point in this plot represents one voxel in the multivoxel data for all subjects.
Table 1.
Average metabolite area ratios for normal controls (N = 7) computed with RBFNN, LF, and jMRUI-AMARES methods and published values. Values are reported as mean (std).
| Metabolite Area Ratios | NAA/Cr | Cho/Cr | Glx/Cr | mI/Cr |
|---|---|---|---|---|
| RBFNN | 1.58 (0.13)*# | 0.90 (0.08)* | 0.70 (0.17)*# | 0.42 (0.07)*# |
| LF (Rao et al. [38]) | 1.60 (0.11) | 0.95 (0.08) | 0.78 (0.18) | 0.49 (0.1) |
| jMRUI-AMARES [39, 40] | 1.61 (0.15) | 0.78 (0.07) | 0.61 (0.18) | 0.42 (0.13) |
| Narayana et al. 2004 [41] | 1.65 (0.1) | 0.85 (0.12) | ||
| Webb et al. 1994 [42] | 1.51 (0.1) | 0.87 (0.1) | 0.66 (0.07) | |
| Naegele et al. 2000 [43] | 0.6 | 0.85 | 0.6 | |
| Choe et al. 1996 [44] | 1.37 | 0.84 | 0.54 | 0.8 |
| Baik et al. 2003 [45] | 1.38 | 0.87 |
The mI/Cr ratio obtained by the current analysis (RBFNN and LF) is slightly lower than that reported in literature [42 - 44]. This could be because the mI peak at 3.52 ppm is close to the water peak and the water suppression has a great effect on the quantitative values. It is interesting to note that the mI/Cr area ratio of 0.42, obtained by the RBFNN method is comparable to 0.38, which is the value reported by Hattori el al. [36].
The computational time for the LF analysis, including baseline correction, was approximately 10 minutes for each subject while the corresponding time for the neural network analysis was about 15 seconds per subject. This did not include the preprocessing time (2-3 minutes) which was common to both LF and ANN methods.
DISCUSSION
In these studies we have applied RBFNN for automatic quantification of proton MRSI data. This method has been evaluated using both simulations and in vivo human brain data. The simulations demonstrate our approach to be accurate and robust to noise and phase distortions in the input peaks. The area ratios obtained on normal subjects compared favorably with the LF method and published values. The differences in the NAA/Cr, Glx/Cr, and mI/Cr ratios obtained with RBFNN and jMRUI were not statistically significant. However, statistically significant difference was observed in the Cho/Cr values. This could be possibly due different lineshapes used in these two methods. The jMRUI package restricts the lineshapes to either Gaussian or Lorentzian. In the RBFNN method we employed Voigt lineshape. As indicated earlier, Voigt lineshape is a better approximation than Lorentzian or Gaussian alone [18]. It is also worth pointing out that Kanowski et al. [46] have also observed lower Cho values with AMARES compared with the LCModel. The concept of using ANN for the analysis of MRSI is not new. Recently ANN based approaches for automated quantification of MRSI data have been reported [15, 16]. As pointed out earlier these methods suffer from a number of limitations. In the current studies, we have overcome many of these limitations.
We have applied ANN for analyzing short echo time, phased MRSI data. An advantage of long echo times is that the baseline is relatively flat, making the analysis easier. However, at long echo times, information from short T2 species such as lipids and glutamate, and glutamine is lost. Thus it is desirable to develop methods that quantify phased spectral data at short echo times. A problem with the short TE spectrum is the baseline distortions. In the current studies we have used a wavelet shrinkage based method, similar to the one suggested in Ref. [22]. In our studies the sharp spectral peaks were identified and separated from baseline using signal processing method [23] as opposed to the simulated basis spectrum. In our procedure even unknown sharp peaks present in the spectrum would not be included in the baseline. Once the baseline is identified, the characterization step is similar to the wavelet shrinkage procedure.
Most of the published ANN techniques have analyzed the magnitude data. Unless the full echo is acquired, the magnitude data broadens the spectral peaks, particularly around the baseline, and introduces significant errors in the spectral quantification. Thus it is desirable to analyze the phased spectrum. In these studies, we have included the automatic first order phase correction procedure suggested in Ref. [2] into the preprocessing step. This allowed us to train the network for analyzing the phased spectra, rather than the magnitude data for improved spectral quantification.
Generally, the magnetic field varies across the spectroscopic slab and introduces spectral distortion that varies from voxel-to-voxel and significantly affects spectral quantification. To overcome this problem a water peak deconvolution approach [3] was adapted. However, application of inverse filter without accounting for the voxel based noise results in artifactual ringing. Failure to recognize and eliminate this artifact would affect the spectral quantification. In the current studies, this problem was minimized by adapting the method based on Wiener filter approach. The robustness of this automatic method has been demonstrated both on simulations and spectral data acquired on human brain.
In the present study we have introduced the quantification of a generic peak rather than the entire spectrum. This approach facilitates the quantification of any metabolite peak with the same neural network. This also significantly reduces the dimension of the input vector and consequently reduces the computational complexity and time. In order to reduce the number of variables, the ANN-based approaches assume a Lorentzian line shape and that all the lines have the same width. These assumptions are not valid. It is generally agreed that the Voigt lineshape is closer to the observed lineshapes compared to Lorentzian or Gaussian alone [18]. In these studies, we trained the network using the Voigt lineshape. In addition, our method does not assume equal line widths.
In proton MRSI, it is not uncommon to observe overlapping peaks. This overlap affects accurate spectral quantification. We have addressed this problem by using separate networks to quantify two and three overlapping peaks. The effectiveness of this approach has been demonstrated by quantifying the overlapping peaks that include Cr, Cho, mI and Glx regions. The same approach could be extended further to quantify more than 3 overlapping peaks if the need arises. However, this requires additional training.
It is relatively straightforward to extend the proposed method to determine the absolute concentrations. A simple way to estimate the absolute concentrations is based on the tissue water concentration [47]. We have discovered that on our new scanner, the water peak in the unsuppressed spectrum and the metabolites in the suppressed spectrum are scaled differently. The scaling factor appears to vary from scan-to-scan and subject-to-subjects. As soon as this problem is resolved, we plan to extend this technique for absolute concentration determination.
A number of excellent software packages, such as LC model [5], are available for spectral quantification. Many of these packages involve minimal human intervention and are capable of providing absolute concentrations, but involve long processing times. However, the main advantage of the proposed technique, compared to many of these established methods, is its speed. Time efficient methods for analyzing large amount of spectral data represent an important advance to overcome the hurdle for routine clinical applications of MRSI.
As indicated earlier the total processing time with the current approach is around 15 seconds under the Matlab environment. Matlab is inherently inefficient in the presence of large number of looping structures. Therefore it is possible to reduce the processing time even further by porting the code to a C/C++ platform.
It is important to point out that these studies must be viewed as a preliminary step towards the real time quantification of MRSI data. This approach needs to be validated using data on a larger cohort acquired on different scanners with different protocols. The effect of the wavelet based baseline correction algorithm on quantitative values needs to be critically evaluated. Even with many limitations, we believe that this approach helps overcome a number of problems that are inherent in many of the published ANN-based methods for MRS quantification. The inherently parallel nature of these computations makes this technique amenable to implementation under parallel computing environment that could result in pseudo real time analysis.
CONCLUSIONS
A RBFNN based method for fast quantification of phased, as opposed to magnitude, MRSI data is presented. Simulations show this method to be robust in the presence of noise and phase distortions. The metabolite area ratios for normal subjects determined using RBFNN compare favorably with the published values. The spectral quantification time on a typical PC was around 15 seconds, compared to 10 minutes, for line fitting methods. This method could be useful for pseudo real time analysis of MRSI data under parallel computing environment.
ACKNOWLEDGEMENTS
This work was supported by NIH grant number EB02095. Authors would like to thank Vips Patel for his technical help in acquiring the MRSI data on normal subjects. The MRUI software package was kindly provided by the participants of the EU Network programmes: Human Capital and Mobility, CHRX-CT94-0432 and Training and Mobility of Researchers, ERB-FMRX-CT970160.
REFERENCES
- [1].Bonavita S, Di Salle F, Tedeschi G. Proton MRS in neurological disorders. Eur J Radiol. 1999;30(2):125–131. doi: 10.1016/s0720-048x(99)00051-0. [DOI] [PubMed] [Google Scholar]
- [2].Doyle TJ, Pathak R, Wolinsky JS, Narayana PA. Automated proton spectroscopic image processing. J Magn Reson B. 1995;106(1):58–63. doi: 10.1006/jmrb.1995.1008. [DOI] [PubMed] [Google Scholar]
- [3].Maudsley AA, Wu Z, Meyerhoff DJ, Weiner MW. Automated processing for proton spectroscopic imaging using water reference deconvolution. Magn Reson Med. 1994;31(6):589–595. doi: 10.1002/mrm.1910310603. [DOI] [PubMed] [Google Scholar]
- [4].Mierisova S, Ala-Korpela M. MR spectroscopy quantification: a review of frequency domain methods. NMR Biomed. 2001;14(4):247–259. doi: 10.1002/nbm.697. [DOI] [PubMed] [Google Scholar]
- [5].Provencher SW. Estimation of metabolite concentrations from localized in vivo proton MR spectra. Magn Reson Med. 1993 Dec;30(6):672–9. doi: 10.1002/mrm.1910300604. [DOI] [PubMed] [Google Scholar]
- [6].Hagberg G. From magnetic resonance spectroscopy to classification of tumors. A review of pattern recognition methods. NMR Biomed. 1998;11(45):148–156. doi: 10.1002/(sici)1099-1492(199806/08)11:4/5<148::aid-nbm511>3.0.co;2-4. [DOI] [PubMed] [Google Scholar]
- [7].Wl-Deredy W. Pattern recognition approaches in biomedical and clinical magnetic resonance spectroscopy: a review. NMR Biomed. 1997;10(3):99–124. doi: 10.1002/(sici)1099-1492(199705)10:3<99::aid-nbm461>3.0.co;2-#. [DOI] [PubMed] [Google Scholar]
- [8].Poptani H, Kaartinen J, Gupta RK, Niemitz M, Hiltunen Y, Kauppinen RA. Diagnostic assessment of brain tumours and non-neoplastic brain disorders in vivo using proton nuclear magnetic resonance spectroscopy and artificial neural networks. J Cancer Res Clin Oncol. 1999;125(6):343–349. doi: 10.1007/s004320050284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Howells SL, Maxwell RJ, Peet AC, Griffiths JR. An investigation of tumor 1H nuclear magnetic resonance spectra by the application of chemometric techniques. Magn Reson Med. 1992;28(2):214–236. doi: 10.1002/mrm.1910280205. [DOI] [PubMed] [Google Scholar]
- [10].Branston NM, Howells SL. Generalization performance using backpropagation algorithms applied to patterns derived from tumour MR spectra. J Microcomp Appl. 1993;16:113–123. RJM. [Google Scholar]
- [11].Usenius JP, Tuohimetsa S, Vainio P, Ala-Korpela M, Hiltunen Y, Kauppinen RA. Automated classification of human brain tumours by neural network analysis using in vivo 1H magnetic resonance spectroscopic metabolite phenotypes. Neuroreport. 1996;7(10):1597–1600. doi: 10.1097/00001756-199607080-00013. [DOI] [PubMed] [Google Scholar]
- [12].Somorjai RL, Dolenko B, Nikulin AK, Pizzi N, Scarth G, Zhilkin P, Halliday W, Fewer D, Hill N, Ross I, West M, Smith IC, Donnelly SM, Kuesel AC, Briere KM. Classification of 1H MR spectra of human brain neoplasms: the influence of preprocessing and computerized consensus diagnosis on classification accuracy. J Magn Reson Imaging. 1996;6(3):437–444. doi: 10.1002/jmri.1880060305. [DOI] [PubMed] [Google Scholar]
- [13].Axelson D, Bakken IJ, Susann Gribbestad I, Ehrnholm B, Nilsen G, Aasly J. Applications of neural network analyses to in vivo 1H magnetic resonance spectroscopy of Parkinson disease patients. J Magn Reson Imaging. 2002;16(1):13–20. doi: 10.1002/jmri.10125. [DOI] [PubMed] [Google Scholar]
- [14].Bakken IJ, Axelson D, Kvistad KA, Brodtkorb E, Muller B, Aasly J, Gribbestad IS. Applications of neural network analyses to in vivo 1H magnetic resonance spectroscopy of epilepsy patients. Epilepsy Res. 1999;35(3):245–252. doi: 10.1016/s0920-1211(99)00019-4. [DOI] [PubMed] [Google Scholar]
- [15].Kaartinen J, Mierisova S, Oja JM, Usenius JP, Kauppinen RA, Hiltunen Y. Automated quantification of human brain metabolites by artificial neural network analysis from in vivo single-voxel 1H NMR spectra. J Magn Reson. 1998;134(1):176–179. doi: 10.1006/jmre.1998.1477. [DOI] [PubMed] [Google Scholar]
- [16].Hiltunen Y, Kaartinen J, Pulkkinen J, Hakkinen AM, Lundbom N, Kauppinen RA. Quantification of human brain metabolites from in vivo 1H NMR magnitude spectra using automated artificial neural network analysis. J Magn Reson. 2002;154(1):1–5. doi: 10.1006/jmre.2001.2457. [DOI] [PubMed] [Google Scholar]
- [17].Narayana PA. Magnetic Resonance Spectroscopy in the Monitoring of Multiple Sclerosis. J Neuroimaging. 2005;15(4):46S–57S. doi: 10.1177/1051228405284200. suppl. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Marshall I, Higinbotham J, Bruce S, Freise A. Use of Voigt lineshape for quantification of in vivo 1H spectra. Magn Reson Med. 1997;37(5):651–657. doi: 10.1002/mrm.1910370504. [DOI] [PubMed] [Google Scholar]
- [19].Bland JM, Altman DG. Comparing methods of measurement: why plotting difference against standard method is misleading. Lancet. 1995;346:1085–1087. doi: 10.1016/s0140-6736(95)91748-9. [DOI] [PubMed] [Google Scholar]
- [20].Roebuck JR, Hearshen DO, O'Donnell M, Raidy T. Correction of phase effects produced by eddy currents in solvent suppressed 1H-CSI. Magn Reson Med. 1993;30(3):277–282. doi: 10.1002/mrm.1910300302. [DOI] [PubMed] [Google Scholar]
- [21].Ordidge RJ. The correction of transient B0 field shifts following the application of pulsed gradients by phase correction in the time domain. J of Magn Reson. 1986;69(1):151–155. CID. [Google Scholar]
- [22].Young K, Soher BJ, Maudsley AA. Automated spectral analysis II: application of wavelet shrinkage for characterization of non-parameterized signals. Magn Reson Med. 1998;40(6):816–821. doi: 10.1002/mrm.1910400606. [DOI] [PubMed] [Google Scholar]
- [23].Golotvin S, Williams A. Improved baseline recognition and modeling of FT NMR spectra. J Magn Reson. 2000;146(1):122–125. doi: 10.1006/jmre.2000.2121. [DOI] [PubMed] [Google Scholar]
- [24].Donoho D, Johnstone I. Adapting to Unknown Smoothness via Wavelet Shrinkage. J American Statistical Assoc. 1995;90:1200–1224. [Google Scholar]
- [25].Morris GA. Compensation of Instrumental Imperfections by Deconvolution Using an internal Reference Signal. J Magn Reson. 1988;80:547–552. [Google Scholar]
- [26].Gibbs A, Morris GA. Reference Deconvolution. Elimination of Distortions arising from Reference Line truncation. J Magn Reson. 1991;91:77–83. [Google Scholar]
- [27].Metz KR, Lam MM, Webb AG. Reference Deconvolution: A Simple and Effective Method for Resolution Enhancement in Nuclear Magnetic Resonance Spectroscopy. Concepts in Magnetic Resonance. 2000;12:21–42. [Google Scholar]
- [28].Gonzalez RC, Woods RE. Digital image processing. Prentice Hall; Upper Saddle River, N.J.: 2002. [Google Scholar]
- [29].Van den Boogaart A. Quantitative Data Analysis of in Vivo MRS Data Sets. Magn Reson Chem. 1997;35:146–152. [Google Scholar]
- [30].Bishop CM. Neural networks for pattern recognition. Oxford University Press; Oxford; New York: 1995. [Google Scholar]
- [31].Redner RA, Walker HF. Mixture densities, maximum likelihood and the EM algorithm. SIAM Review. 1984;26(2):195–239. [Google Scholar]
- [32].Dempster AP, Laird NM, Rubin DB. Maximum Likelihood from incomplete data via the EM algorithm. J Royal Statistical Soc. 1977;39(1):1–38. [Google Scholar]
- [33].Govindaraju V, Young K, Maudsley AA. Proton NMR chemical shifts and coupling constants for brain metabolites. NMR Biomed. 2000 May;13(3):129–53. doi: 10.1002/1099-1492(200005)13:3<129::aid-nbm619>3.0.co;2-v. [DOI] [PubMed] [Google Scholar]
- [34].Drost DJ, Riddle WR, Clarke GD. AAPM MR Task Group #9. Proton magnetic resonance spectroscopy in the brain: report of AAPM MR Task Group #9. Med Phys. 2002 Sep;29(9):2177–97. doi: 10.1118/1.1501822. [DOI] [PubMed] [Google Scholar]
- [35].Lehnhardt FG, Bock C, Rohn G, Ernestus RI, Hoehn M. Metabolic differences between primary and recurrent human brain tumors: a 1H NMR spectroscopic investigation. NMR Biomed. 2005 Oct;18(6):371–82. doi: 10.1002/nbm.968. [DOI] [PubMed] [Google Scholar]
- [36].Hattori N, Abe K, Sakoda S, Sawada T. Proton MR spectroscopic study at 3 Tesla on glutamate/glutamine in Alzheimer's disease. Neuroreport. 2002 Jan 21;13(1):183–6. doi: 10.1097/00001756-200201210-00041. [DOI] [PubMed] [Google Scholar]
- [37].Nabney I. NETLAB : algorithms for pattern recognition. Springer; London ; New York: 2002. [Google Scholar]
- [38].Rao SB, He R, Mehta M, Narayana PA. Automated Quantification of Proton Magnetic Resonance Spectroscopic Imaging; Proc 25th Annual Inter Conf IEEE EMBS; 2003.pp. 17–12. [Google Scholar]
- [39].Vanhamme L, van den Boogaart A, Van Huffel S. Improved method for accurate and efficient quantification of MRS data with use of prior knowledge. J Magn Reson. 1997 Nov;129(1):35–43. doi: 10.1006/jmre.1997.1244. [DOI] [PubMed] [Google Scholar]
- [40].Naressi A, Couturier C, Devos JM, Janssen M, Mangeat C, de Beer R, Graveron-Demilly D. Java-based graphical user interface for the MRUI quantitation package. MAGMA. 2001 May;12(23):141–52. doi: 10.1007/BF02668096. [DOI] [PubMed] [Google Scholar]
- [41].Narayana PA, Wolinsky JS, Rao SB, He R, Mehta M. Multicentre proton magnetic resonance spectroscopy imaging of primary progressive multiple sclerosis. Mult Scler. 2004;10(Suppl 1):S73–78. doi: 10.1191/1352458504ms1035oa. [DOI] [PubMed] [Google Scholar]
- [42].Webb PG, Sailasuta N, Kohler SJ, Raidy T, Moats RA, Hurd RE. Automated single-voxel proton MRS: technical development and multisite verification. Magn Reson Med. 1994;31(4):365–373. doi: 10.1002/mrm.1910310404. [DOI] [PubMed] [Google Scholar]
- [43].Naegele T, Wolfgang G, Viebahn R, Seeger U, Klose U, Seitz S, Kaiser S, Mader I, Mayer J, Lauchart W, Gregor M, Voigt K. MR Imaging and 1H Spectroscopy of Brain Metabolites in Hepatic Encephalopathy: Time Course of Renormalization after Liver Transplantation. Radiology. 2000;216:683–691. doi: 10.1148/radiology.216.3.r00se27683. [DOI] [PubMed] [Google Scholar]
- [44].Choe BY, Suh TS, Shinn KS, Lee CW, Lee C, Paik IH. Observation of metabolic changes in chronic schizophrenia after neuroleptic treatment by in vivo hydrogen magnetic resonance spectroscopy. Invest Radiol. 1996 Jun;31(6):345–52. doi: 10.1097/00004424-199606000-00006. [DOI] [PubMed] [Google Scholar]
- [45].Baik HM, Choe BY, Son BC, Jeun SS, Kim MC, Lee KS, Kim BS, Lee JM, Lee HK, Suh TS. Proton MR spectroscopic changes in Parkinson's diseases after thalamotomy. Eur J Radiol. 2003 Sep;47(3):179–87. doi: 10.1016/s0720-048x(02)00211-5. [DOI] [PubMed] [Google Scholar]
- [46].Kanowski M, Kaufmann J, Braun J, Bernarding J, Tempelmann C. Quantitation of simulated short echo time 1H human brain spectra by LCModel and AMARES. Magn Reson Med. 2004 May;51(5):904–12. doi: 10.1002/mrm.20063. [DOI] [PubMed] [Google Scholar]
- [47].Sharma R, Narayana PA, Wolinsky JS. Grey matter abnormalities in multiple sclerosis: proton magnetic resonance spectroscopic imaging. Mult Scler. 2001 Aug;7(4):221–6. doi: 10.1177/135245850100700402. [DOI] [PubMed] [Google Scholar]