Abstract
The present study tested whether subjects respond to unanticipated short perturbations in voice loudness feedback with compensatory responses in voice amplitude. The role of stimulus magnitude (±1,3 vs 6 dB SPL), stimulus direction (up vs down), and the ongoing voice amplitude level (normal vs soft) were compared across compensations. Subjects responded to perturbations in voice loudness feedback with a compensatory change in voice amplitude 76% of the time. Mean latency of amplitude compensation was 157 ms. Mean response magnitudes were smallest for 1-dB stimulus perturbations (0.75 dB) and greatest for 6-dB conditions (0.98 dB). However, expressed as gain, responses for 1-dB perturbations were largest and almost approached 1.0. Response magnitudes were larger for the soft voice amplitude condition compared to the normal voice amplitude condition. A mathematical model of the audio-vocal system captured the main features of the compensations. Previous research has demonstrated that subjects can respond to an unanticipated perturbation in voice pitch feedback with an automatic compensatory response in voice fundamental frequency. Data from the present study suggest that voice loudness feedback can be used in a similar manner to monitor and stabilize voice amplitude around a desired loudness level.
I. INTRODUCTION
The control of voice amplitude is an essential component of speech and singing and serves several functions. People modulate voice amplitude to attract or diminish attention to themselves, such as in role taking during dialogue, or to overcome environmental noise or distance. Amplitude, along with fundamental frequency (F0) and duration, is used as an indicator of prosody. In this sense, amplitude is used to segment a message and place emphasis on certain words or syllables. Amplitude is also used to disambiguate confusing words or phrases during speech (Titze, 1994).
Understanding amplitude control is important for preventing and treating disorders characterized by abnormal voice. For example, people suffering from Parkinson’s disease have difficulty communicating because the amplitude of their voice tends to be too low and monotonous (Ramig, 1994). Several types of neurological disorders (e.g., Parkinson’s disease, spastic pseudobulbar palsy, dystonia) or mass lesions in the brain also present with instability in voice amplitude as well as voice F0 (Ford and Connor, 2000; Ramig, 1994). Speech of schizophrenics is also seen as lacking emotional prosody and can be flat in affect (Alpert et al., 2000; Leentjens et al., 1998; Murphy and Cutting, 1990).
The peripheral mechanisms of amplitude control are well understood. Voice amplitude depends on complex interactions between the respiratory, laryngeal, and articulatory systems. Generally speaking, increases in lung pressure or F0 lead to increases in voice amplitude. Adjustment, or tuning, of the supraglottal vocal tract, as done by well-trained singers, can also significantly affect voice loudness (Titze, 1994). However, given our detailed understanding of the peripheral mechanisms of amplitude control, there is a paucity of information related to neural control mechanisms of voice amplitude modulation.
Lombard, one of the first to investigate the topic of loudness control, showed the critical importance of voice loudness feedback on amplitude regulation in 1911 (as cited in Lane and Tranel, 1971). Lombard demonstrated that increased noise loudness feedback automatically raises voice amplitude to a level that can overcome environmental noise and thus enable a speaker to make him/herself heard. Adams has since proposed using the Lombard effect to elevate the voice loudness of patients with Parkinson’s disease (Adams and Lang, 1992). A related phenomenon is that of side-tone amplification, where a speaker produces an increase in voice amplitude when they perceive (usually by the use of headphones) that their voice loudness feedback is too quiet for a given communication goal (Lane and Tranel, 1971). Conversely, when voice loudness is perceived as excessive, a speaker will reduce voice amplitude. Thus, speakers modulate their voice amplitude to compensate for changes in the loudness of voice auditory feedback. (We use the term amplitude in reference to voice output and loudness in reference to the voice feedback signal.)
However, one problem in interpreting these data on voice amplitude control relates to the methodology. In the studies of the Lombard phenomenon, a constant noise was added to the feedback signal, and in the side-tone studies, the voice feedback loudness was adjusted and remained at a constant level throughout the testing session (Lane and Tranel, 1971; Siegel and Pick, Jr., 1974; Siegel and Kennard, 1984). Given the ongoing presence of the feedback signals (noise or modulated voice), it is unknown whether the subjects were making voluntary adjustments to the signal or whether the responses were generated as an automatic response to the feedback. This methodology also precluded any temporal response measures (i.e., latency) of the vocal responses.
In a series of recent studies, it has been found that speakers compensate for unanticipated, brief duration perturbations in voice pitch feedback by modulating their voice F0 (Burnett et al., 1998; Burnett and Larson, 2002; Hain et al., 2000, 2001; Jones and Munhall, 2000, 2002; Kawahara and Williams, 1996; Larson et al., 2001, 2000; Natke et al., 2003; Natke and Kalveram, 2001). These studies demonstrated that such compensatory responses have latencies of approximately 130 ms and do not seem to be volitionally controlled. The terms pitch-shift reflex, or response (PSR), has been used to refer to this process. The PSR has been studied during neutral vowel sounds, during pitch glissandos, and as subjects produce nonsense syllables, prolonged vowels during speech and during normal speech. Results from these studies suggest that the PSR helps to stabilize voice F0 around an actual or intended target F0.
More recently, Heinks-Maldonado and Houde (2005) described results of presenting brief perturbations in voice loudness to vocalizing subjects. In this study, the perturbations, ±10 dB, 400-ms duration, resulted in compensatory changes in voice amplitude with latencies of approximately 170 ms. The timing and compensatory nature of these responses were very similar to the results of the pitch-shift studies described above, and suggest similar vocal control mechanisms between F0 and amplitude. However, since only perturbations of 10 dB were presented in the Heinks-Maldonado and Houde (2005) study, it is not clear whether the results generalize to less intense stimuli, such as those more typically encountered during natural speech. Also, the subjects in this task were asked to sustain voice amplitude at a single amplitude level. Thus, it is not known if the same results would be obtained at a lower amplitude level.
Given the wide range of vocal activities in which the PSR has been observed and the similarity of the compensatory nature of the PSR with that of the side-tone amplification studies mentioned above, we hypothesized that subjects would also respond to brief, unanticipated perturbations in voice loudness feedback with compensatory response in voice amplitude. Considering the results of the Heinks-Maldonado and Houde (2005) study mentioned above in which 10-dB stimuli were presented to the subjects, we chose magnitudes of 1, 3, and 6 dB to determine if the results would scale to less intense perturbations which are more typical of those observed in natural speech.
As mentioned previously, it was suggested that the PSR functions to help stabilize voice F0. Recent data indicate that the PSR may also function in a task-dependent manner where the latency of the vocal response is modulated according to the intended speech goals (Bauer, 2004; Xu et al., 2004). If the neural mechanisms responsive to perturbations in loudness feedback help to stabilize voice amplitude, they may also do so in a task-dependent manner. Specifically, subjects may be more sensitive to loudness perturbations during difficult vocal tasks compared to easier vocal tasks. One such difficult task may be vocalization near phonation threshold pressure. In such a situation, if the voice amplitude drops below phonation threshold pressure, vocalization will cease altogether. Controlling vocalization at soft vocal amplitude may require closer monitoring of auditory feedback to insure that vocal amplitude remains above phonation threshold pressure. If subjects monitor auditory feedback more closely at soft vocal amplitude, their responses to perturbations in voice loudness feedback may be greater in magnitude than those seen at normal vocal amplitude. Therefore, an additional hypothesis was tested in this study to assess whether response magnitudes to loudness-shifted voice feedback would be larger as subjects maintain a relatively soft voice compared to normal voice amplitude.
II. METHODS
A. Subjects
Twenty normal young adults (10 male, 10 female; ages 18–22) volunteered as subjects. No subjects reported a history of neurological, speech, or hearing disorders, and all subjects passed a hearing screening at 40-dB HL bilaterally at 500, 1000, and 2000 Hz. Subjects signed informed consent approved by the Northwestern University IRB and were paid for their participation.
B. Apparatus
Subjects were comfortably seated in a sound-attenuated chamber (IAC model 1201) and wore AKG headphones with attached boom-set condenser microphone (AKG HSC 200) at a 1-in. microphone-to-mouth distance during the experiment. The vocal signal was preamplified with a Mackie mixer, modulated for loudness feedback perturbations (loudness-shifted) with a Roland VS 880 EX effects processor coupled to an Ebtech line level shifter (model LLS-2), amplified with a Crown D75 amplifier and routed back to the AKG headphones after attenuation with HP decibel attenuators (model 350D). Masking pink noise (60 dB SPL) was presented to the subjects throughout the experiments using a Goldline audio noise source (model PN2; spectral frequencies 1 to 5000 Hz). Subjects viewed a Dorrough loudness monitor (model 40 A) 0.5 m in front of them throughout the experiment in order to maintain target vocal amplitude and reduce vocal amplitude drift. Marks on the meter indicated calibrated voice amplitude levels of 75 and 60 dB SPL. The loudness monitor provided visual feedback related to the amplitude of the sustained vowel. Subjects were instructed to maintain constant voice amplitude near targeted levels throughout the entire utterance with minimal fluctuations (±3 dB). The Roland effects processor was controlled by MIDI software (MAX/MSP v4.5 by Cycling ’74) from a laboratory computer. The voice, auditory feedback, and control signals (MIDI synchronization pulses and TTL pulses) were digitized on line with a PowerLab A/D converter by AD Instruments (10 kHz, 12-bit sampling, 5-kHz digital low-pass filter).
It was recognized that observation of the loudness monitor might be a confounding factor, because subjects could potentially respond to the visual changes in the monitor. However, the loudness perturbation was not displayed on the monitor, only the subject’s voice output. Moreover, the monitor displays blinking lights that rapidly move left and right, and it was considered highly unlikely that subjects could adjust the amplitude of their voice rapidly enough and in synchrony with the lights so as to respond to individual fluctuations. It was considered more advantageous for the purpose of this study to help the subjects to maintain a relatively constant amplitude level over the course of their vocalizations rather than allow for vocal amplitude drift. As Heinks-Maldonado and Houde (2005) observed, natural speech has a tendency to decrease in amplitude as breath support is diminished throughout an utterance, and we wished to reduce this tendency as much as possible by providing a visual feedback guide of “general” vocal amplitude.
C. Procedures
Subjects were instructed to repeatedly sustain the vowel /u/ for approximately 5-s durations at either a normal (≈75 dB SPL) or soft amplitude level (≈60 dB SPL). Production of ten consecutive vocalizations constituted an experimental block. For each vocalization within a block, the voice loudness feedback was increased or decreased four times in succession, resulting in 20 increasing and 20 decreasing perturbations within each block. The duration of each perturbation was 200 ms and the magnitude was held constant at 1, 3, or 6 dB SPL within each block. In order to reduce potential predictability effects, the initial loudness perturbation occurred between 300 and 600 ms after vocal onset, while successive stimuli were presented with an inter-stimulus interval ranging from 900 to 1200 ms. Likewise, within each block, subjects were instructed to consistently maintain their voice amplitude at either the normal or soft phonation amplitude level. Overall, there were 12 experimental conditions collected across six blocks of vocalizations (2 voice amplitude levels ×2 stimulus directions ×3 stimulus magnitudes). The order of completion of the six experimental blocks was randomized across subjects to prevent potential order-related effects.
Digitized signals were analyzed off-line on a laboratory computer by converting the voice signal to a root-mean-square (rms) voltage signal using IGOR PRO software (v. 4.0 by Wavemetrics). Voice rms was calculated using the formula
| (1) |
where x= the value of each data point, and N= total number of data points. Voice rms voltage measures were then converted to dB SPL using the following formula:
| (2) |
where x= the voltage level corresponding to each data point and c=0.323, which is the rms voltage corresponding to a vocal level of 75 dB SPL that was obtained through calibration procedures (see below). The vocal rms waveform of all 40 trials per block for each subject was then time aligned to the onset of the loudness-shift trigger stimulus, sorted based on stimulus direction, and averaged to produce one event-related averaged response per experimental condition per subject. From each average signal a prestimulus period of 200 ms was used to calculate a mean prestimulus baseline voice rms level. A valid average vocal response was operationally defined as a change in voice rms amplitude of at least two standard deviations (2 SD) from this mean baseline within a poststimulus response window of 900 ms for a duration of at least 50 ms and with a latency greater than 50 ms. Response latency was measured at the point where the rms average wave first crossed the 2-SD threshold after 50 ms. Response magnitude was measured as the greatest point of rms divergence following the response latency. A nonresponse was identified as not meeting the response criteria outlined above. This procedure for determining a valid vocal amplitude response is similar to that used previously to calculate a voice F0 response (Bauer and Larson, 2003; Burnett et al., 1998; Sivasankar et al., 2005). To verify that subjects produced a louder voice for the normal compared to the soft condition, the mean of the prestimulus voice amplitudes under the two voice conditions were submitted to a one-way ANOVA.
Measures of magnitude, gain, and latency were each submitted to statistical analysis using separate three-way factorial ANOVAs with Bonferroni posthoc tests. Square root transformations of response magnitude, gain, and latency measures were done to achieve normal distributions as confirmed by normal probability plots, linear regression analyses (an R2 value of 0.95 was considered acceptable), and coefficients of skewness and kurtosis in DATA DESK software (v6.2 for Mac OSX by Data Descriptions, Inc., Ithaca, NY). An a priori alpha level of 0.05 was used to determine statistical significance. Although these data lend themselves to repeated-measured ANOVAs, a three-way factorial ANOVA without repeated measures was used to identify statistical significance to account for missing data and unequal cell size.
The microphone and headphones were both calibrated with a B&K sound-level meter (model 2203; weighting A), a B&K type 4131 1-in. microphone, and a B&K type 4152 artificial ear. The AKG boom microphone was calibrated within an IAC booth by presenting a triangle waveform (1 kHz from a function generator) through a free-field speaker. The microphone and sound-level meter were placed next to the speaker at the same distance. The function generator was adjusted to produce a 75-dB SPL amplitude signal as measured by the sound-level meter. The output of the microphone amplifier was recorded on the computer and converted to an rms pressure value (in volts). The rms voltage for a 75-dB SPL sound source was 0.323.
To calibrate the output of the headphones, the function generator was adjusted to produce an rms voltage of 0.323 at the output of the headphone amplifier and dB attenuator. This voltage source was presented directly to the input of the headphones (bypassing the microphone), which were placed on the artificial ear connected to the sound-level meter. The dB attenuators were then adjusted to achieve a 10-dB gain from the input of the microphone to the output of the headphones. This adjustment meant that a vocal level at the input to the microphone of 75 dB SPL was heard at the output of the headphones as 85 dB SPL.
III. RESULTS
Figure 1(a) displays a concatenated rms pressure waveform in dB consisting of ten consecutive 5-s vocalizations that comprised one of the average traces shown in Fig. 2. As can be seen in Fig. 1(a), there is considerable variability in the 50-s trace as voice amplitude occasionally drifts downward or upward. However, no consistent pattern appears to be present across vocalizations. Figure 1(b) displays the voice amplitude traces for each analysis window that was used to generate the average waveforms seen in Fig. 2. The traces for each trial (200-ms prestimulus baseline and 900-ms poststimulus response window) are essentially flat (except for the vocal compensation), with no discernible overall upward or downward drift across trials. These data are typical of all the subjects in the study. All subjects produced a lower amplitude voice for the soft condition (mean =70.2, ±1.5 dB) compared to normal (mean=76.1, ±2.3 dB; F=502.3, df=1,227, p<0.0001). However, subjective impressions of voice quality did not change as a result of the phonation amplitude.
FIG. 1.
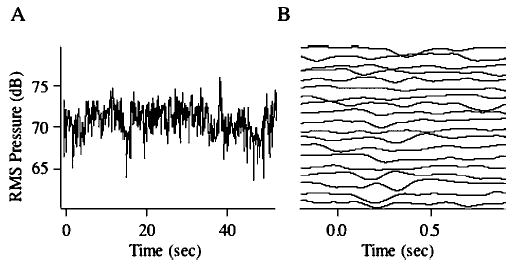
(A) illustrates the voice rms pressure wave in dB across an entire recording session of ten vocalizations for one subject in one condition. (B) illustrates individual trials for upward loudness shifts for portions of the data in (A). The generally horizontal lines indicate there was little tendency for the subject to gradually reduce vocal loudness during the trials.
FIG. 2.
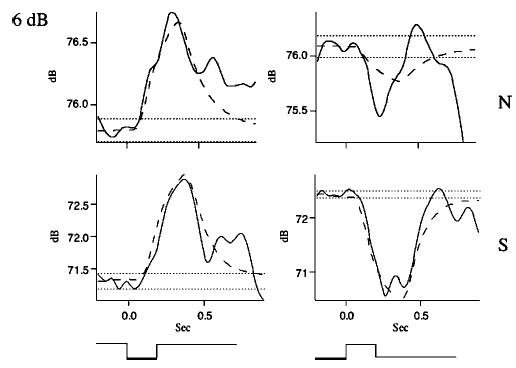
Averaged responses for a representative subject for the 6-dB stimulus magnitude condition, upward and downward stimuli, and voice amplitude conditions. Description of panels: top row shows responses in the normal (N) voice condition, and bottom row shows responses in the soft (S) voice condition. Left column shows responses for downward stimuli, and right column shows responses for upward stimuli. Stimulus timing and direction are illustrated by square trace at bottom of panels. Solid curved line is averaged response. Dashed curved line is simulated response. Horizontal dotted lines indicates ±2 SDs of prestimulus mean. Vertical dashed lines indicate response latency.
All subjects responded to a loudness-shift stimulus, although not with equal frequency. Of the 240 total possible number of averaged responses (20 Ss × 2 voice amplitude levels × 2 stimulus directions × 3 stimulus magnitudes), 183 averaged responses (76%) compensated for the stimulus (response was in the opposite direction of the stimulus), 5 responses (2%) followed the stimulus (response in the same direction as the stimulus), and 52 responses (22%) did not meet the criteria for valid responses. Tables I–III show counts of compensatory, “following,” and nonresponses as a function of voice amplitude, stimulus magnitude, and stimulus direction, respectively. While in most cases response types were evenly distributed across conditions, there were a disproportionate number of nonresponses for the 1-dB stimulus condition compared with the 3-dB and 6-dB stimulus magnitudes as seen in Table II (chi square=23.61, df=4, p < 0.0001).
TABLE I.
Counts of compensatory (Comp.), following (Fol.), and nonresponses (NR) by voice amplitude condition.
| Normal | Soft | Total | |
|---|---|---|---|
| Comp. | 89 | 94 | 183 |
| Fol. | 2 | 3 | 5 |
| NR | 29 | 23 | 52 |
| Total | 120 | 120 | 240 |
TABLE III.
Counts of compensatory (Comp.), following (Fol.), and nonresponses (NR) by stimulus direction.
| Down | Up | Total | |
|---|---|---|---|
| Comp. | 88 | 95 | 183 |
| Fol. | 4 | 1 | 5 |
| NR | 28 | 24 | 52 |
| Total | 120 | 120 | 240 |
TABLE II.
Counts of compensatory (Comp.), following (Fol.), and nonresponses (NR) by stimulus loudness.
| 1 dB | 3 dB | 6 dB | Total | |
|---|---|---|---|---|
| Comp. | 48 | 74 | 61 | 183 |
| Fol. | 3 | 0 | 2 | 5 |
| NR | 29 | 6 | 17 | 52 |
| Total | 80 | 80 | 80 | 240 |
Figure 2 illustrates representative responses for the 6-dB stimulus condition for the normal (top) and soft (bottom) voice amplitude conditions and for upward (right) and downward (left) loudness-shift stimuli. In all four cases, response latencies were close to 100 ms and compensated for the stimulus directions. The responses for the soft voice condition exceeded 1 dB, while those for the normal voice condition were less than 1 dB in magnitude. Similar trends may be seen for the 3-dB (Fig. 3) and 1-dB stimulus conditions (Fig. 4). However in Fig. 4, for the 1-dB normal voice condition, the changes in voice amplitude following the stimulus were quite variable and did not meet our criteria for valid responses. The curved dashed lines in Figs. 2–4 are simulations generated from the model shown in Fig. 7 (see below).
FIG. 3.
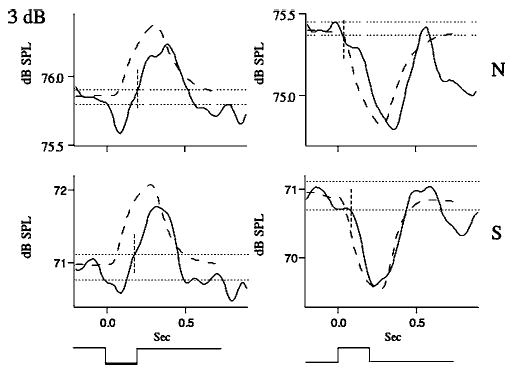
Averaged responses and simulations for the same subject as in Fig. 1 for the 3-dB stimulus condition.
FIG. 4.
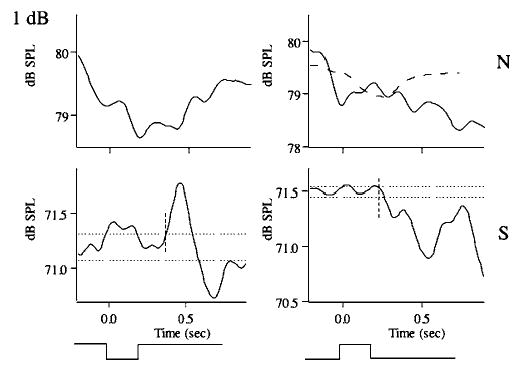
Averaged responses and simulation for the same subject as in Figs. 1 and 2 for the 1-dB stimulus condition. Dotted lines representing the pre-stimulus mean loudness are not shown in the upper traces because these data did not meet the criteria of acceptable responses.
FIG. 7.
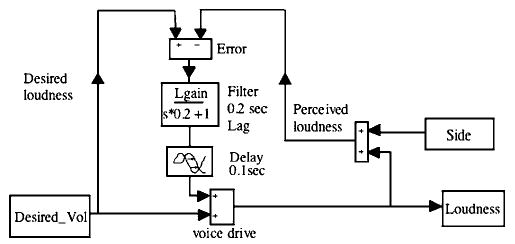
Model of audio-vocal system producing the simulated traces depicted in Figs. 2–4. The variable representing desired loudness, Desired_Vol, is converted through a “black box” representing the entire central vocal production system (here just a summing junction labeled voice drive) into loudness. Loudness can be perturbed by adding a side input, creating perceived loudness. Error is computed by the difference between desired loudness and perceived loudness. Error is low-pass filtered in the element filter by scaling by Lgain and applying a lag with a time constant of 0.2 s. The filtered error signal is then passed through a delay of 0.1 s (to reproduce observed response latency), and added into the voice drive signal.
Statistical analysis using a 2 × 2 × 3 ANOVA of the above magnitude-related trends across subjects revealed significant main effects for the voice amplitude, stimulus direction, and stimulus magnitude conditions. The voice amplitude condition resulted in significantly larger mean response magnitudes for the soft (0.99±0.50 dB SPL) compared with the normal (0.81±0.53 dB SPL) voice loudness condition (F=9.6, df 1,178, p<0.03). There was also a significant effect for stimulus direction with upward stimuli leading to larger mean response magnitudes (1.05±0.57 dB SPL) compared with downward stimuli (0.75±0.42 dB SPL; F=19.6, df=1,178, p<0.0001). There was also an overall significant effect of stimulus magnitude on response magnitude (F =14.1, df=2,178, p<0.0001). Bonferroni posthoc testing showed the 6-dB (0.98±0.27 dB SPL; p<0.0001) and 3-dB (0.96±0.26 dB SPL; p<0.0001) conditions produced significantly larger mean responses than the 1-dB condition (0.75±0.22 dB SPL). There were no significant interactions. Figure 5 (top row) illustrates the increase in response magnitude with stimulus magnitude as box plots for the normal (left) and soft (right) vocal conditions. However, when the same data are plotted as gain (response magnitude / stimulus magnitude) as shown in Fig. 5 (bottom row), an opposite effect is seen. In the gain plots, responses with the 1-dB stimuli approach unity (gain=1), whereas responses for the 3- and 6-dB stimulus magnitudes are less than 0.5.
FIG. 5.
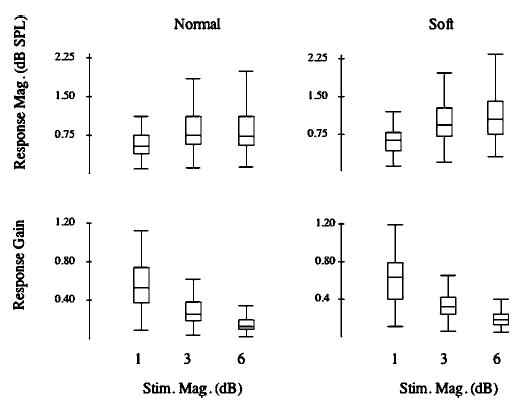
Box plots illustrating response magnitude (dB SPL) (top row) and gain (bottom row) as a function of stimulus magnitude. Normal voice condition is on the left and soft voice condition is on the right. Box definitions: middle line is median, top and bottom of boxes are 75th and 25th percentiles, whiskers extend to limits of main body of data defined as high hinge +1.5 (high hinge—low hinge), and low hinge −1.5 (high hinge—low hinge). Points depicted by a circle extend beyond these limits, unless they exceed high hinge +3.0 (high hinge—low hinge) or low hinge −3.0 (high hinge—low hinge), in which case they are shown by an asterisk (DATA DESK; DATA DESCRIPTION).
Statistical testing of response gain using a 2×2×3 ANOVA also produced significant main effects for the voice amplitude, stimulus direction, and stimulus magnitude conditions. The voice amplitude condition produced a significantly larger gain for the soft (0.39±0.30) than for the loud (0.32±0.25) voice condition (F=10.59, df 1,173, p<0.002). An upward stimulus direction revealed a greater gain (0.41±0.31) than downward stimuli (0.30±0.23; F=16.1, df 1, 173, p<0.0001). Finally, stimulus magnitude produced the largest gain for the 1-dB condition (0.62±0.34) compared with the 3-dB (0.33±0.19) and 6-dB (0.17±0.09) conditions (F=81.8, df 2,173, p<0.0001). Bonferroni posthoc comparisons demonstrated that the gain for the 1-dB condition were significantly larger than that for the 3-dB (p<0.0001) or 6-dB (p<0.0001) conditions, and the gain for the 3-dB condition was also significantly larger than that for the 6-dB condition (p<0.0001).
Response latencies were not affected by the experimental conditions. Although the latencies for 3-dB (mean =144 ms) stimulus magnitude were shorter than for the 1-dB (mean=185 ms) or 6-dB (mean=191) magnitude conditions (F=4.42, df=2,185, p<0.014), Bonferroni posthoc comparisons failed to yield significant comparisons. The overall mean latency was 157±44 ms. Figure 6 illustrates latencies plotted against stimulus magnitude for the normal (left) and soft (right) voice conditions.
FIG. 6.
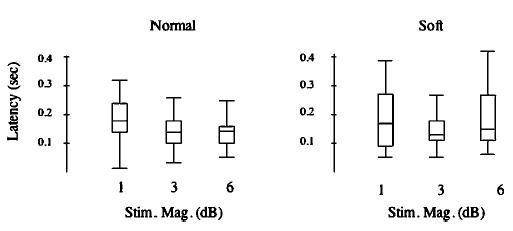
Box plots illustrating response latencies (seconds) as a function of stimulus magnitude (dB). Data for normal voice condition are on the left and soft condition on the right.
We simulated these responses using a simple negative feedback model shown in Fig. 7. This model is similar to that previously reported for stabilization of F0 (Hain et al., 2000). Desired loudness was compared to perceived loudness and computed as potential error. The error was filtered, delayed, and then used to adjust voice drive. For five randomly chosen subjects the scaling and delay parameters were fit using the optimization toolbox of MATLAB (version 14, Natick, MA). The time constant of the low-pass filter was set to 0.2 s based on the median of a preliminary fit where it was also allowed to vary. The variance accounted for (vaf) was used as an index of model performance. A perfect fit corresponded to a vaf of 1.0, and no correlation between the fit and data corresponded to a vaf of 0.
Eleven of 60 trials (12 conditions × 5 subjects) could not be fit with vaf’s greater than 0.1. Six of these were for the lowest (1-dB) perturbation magnitude. As seen in Fig. 4, we were unable to fit the simulations for both “soft” conditions, and the “normal,” down stimulus condition. Table IV shows the mean results of the fit in the remaining 49 trials for the five subjects.
TABLE IV.
Mean values of best fits for simulated variance (vaf), loudness scaling (Lgain), side-tone gain (Sgain), and delay across stimulus direction (up and down) for five representative subjects. n=number of conditions out of 12 for computation of the mean.
| 1 dB Soft | 1 dB Norm | 3 dB Soft | 3 dB Norm | 6 dB Soft | 6 dB Norm | Mean | |
|---|---|---|---|---|---|---|---|
| n | 6 | 8 | 8 | 10 | 9 | 8 | |
| vaf | 0.49 | 0.76 | 0.81 | 0.86 | 0.79 | 0.85 | 0.76 |
| Lgain | 0.97 | 0.33 | 0.56 | 0.42 | 0.30 | 0.23 | 0.47 |
| Sgain | 0.49 | 0.25 | 0.36 | 0.30 | 0.23 | 0.19 | 0.32 |
| Delay (ms) | 74 | 110 | 80 | 80 | 100 | 80 | 90 |
There was a generally good fit of the model to the data and close correspondence between model parameters and experimentally measured values. Across the five modeled subjects, average Lgain (loudness scaling values from the model) ranged from 0.33 to 0.63. Across stimulus magnitude, Lgain decreased with increasing loudness (see Table IV). In this model, overall gain (change in loudness feedback)/(change in side tone) was a function both of Lgain and complex frequency (s). When Lgain was 0, or s was high, overall gain was 0. This can be seen from inspection of the filter element in the model (Fig. 7). When s goes to 0 (dc), neglecting the delays, overall gain was [−Lgain/ (Lgain+1)]. The values shown in Table IV were for s=0.
The delay parameter, the model equivalent to experimental “latency” value, was substantially less (mean =90 ms) than the experimentally measured value (mean =157 ms). Average simulated delay across subjects ranged from 70 to 100 ms. Note that delay in the model was not an exact equivalent to experimental latency, as the delayed signals also passed through a lag, which contributed to the simulated latency. Mean Lgain was slightly larger for the upward stimulus direction (0.52) versus the downward direction (0.48), as well as much larger for the soft voice condition (0.61) versus the normal voice condition (0.32).
IV. DISCUSSION
The present study shows that brief perturbations in voice loudness feedback lead to compensatory responses in voice amplitude. The compensatory nature of these responses is similar to previous observations of side-tone amplification (Lane and Tranel, 1971; Siegel and Pick, Jr., 1974) and to perturbations in speech amplitude (Heinks-Maldonado and Houde, 2005). Furthermore, these data also suggest a mechanism of correcting for errors in amplitude production. Specifically, if voice amplitude, or more properly the perception of voice loudness, does not agree with the intended voice amplitude, the system makes automatic corrective responses in about 150 ms. Stimulus direction (up or down perturbations) or magnitude (1, 3, or 6 dB SPL) did not alter the response latency. Similarly, vocal task (soft or normal voice amplitude) did not change the response latency. However, the mechanism described in this study is not capable of complete compensation for errors. Complete compensation would imply a response magnitude equal to that of the perturbation (unity gain). The compensation responses described here rarely exceeded 1 dB SPL despite perturbations as great as 6 dB. An approximation of unity gain was only observed for the 1-dB SPL magnitude condition.
Responses to the 1-dB stimuli also differed from those to other stimuli by their greater numbers of measured nonresponses, which may indicate the 1-dB stimulus loudness is close to the threshold of the audio-vocal system for voice amplitude regulation. Although responses to 3- and 6-dB stimuli occur with much greater frequency than those to 1-dB stimuli (indicating these larger magnitude stimuli are well above the threshold), the audio-vocal system is not capable of fully compensating for feedback errors of these magnitudes. In a previous study of presenting loudness perturbations to vocalizing subjects, the magnitude of the stimuli were ±10 dB, and in that case there was almost a 100% response rate (Heinks-Maldonado and Houde, 2005). Thus, across the range of stimulus amplitudes from 1 to 10 dB, there is a relatively low response rate at 1 dB, and close to 100% at 10 dB, with 3 and 6 dB showing intermediate response rates. Therefore, the system seems less capable of recognizing small-magnitude stimuli compared to large magnitudes. Even though there was nearly a 100% response rate in the Heinks-Maldonado and Houde (2005) study, their response amplitudes also did not equal the stimulus magnitude. In their results, the mean response amplitude ranged from 0.61 to 1.32 dB, which is similar to results of the present study. It may be concluded then that even with very loud or soft stimuli, the system does not fully compensate for perturbations in voice loudness feedback. Similar results have been found also in studies of the pitch-shift response, where full compensation was observed for relatively small stimuli of 25 cents magnitude but not for larger magnitude stimuli of 100 or 200 cents (Burnett et al., 1998; Larson et al., 2000).
The fact that response amplitudes to both loudness and pitch-shifted feedback are limited in magnitude does not reduce their usefulness in stabilizing the voice. The vocal responses can begin within 150 ms of the onset of a loudness or frequency perturbation in voice pitch or loudness, and if the perturbation is small in magnitude (1 dB or 25 cents), the audio-vocal system could compensate for it and thus help to stabilize the voice. If the response does not completely nullify the perturbation, further automatic corrective responses could be triggered, or else voluntary mechanisms could intervene to compensate for the undesired perturbation. It is doubtful that systems as complex as the audio-vocal could rely on a single control mechanism to regulate output; rather, both voluntary and involuntary processes interact to stabilize the voice.
There are no unequivocal explanations for the failure of response magnitudes to equal the stimulus intensities; however, it was also previously noted that neither the Lombard response nor side-tone amplification effects had a gain of 1 (Lane and Tranel, 1971). In most cases the gain of the Lombard and side-tone amplification equaled about 0.5 across a much broader range of stimulus intensities than was used in the present study. One explanation for the response gain in the present study to be generally lower than 0.5 may be that subjects sustained nonspeech /u/ vowel sounds, whereas the studies of the Lombard effect and side-tone amplification were done on speech. The greater salience of the communication goal in speech compared to a sustained vowel without a specific communication goal may help explain why smaller response magnitudes were observed in the present study compared to the results of Lane and Tranel (1971). Future studies incorporating the techniques of the present study in a speech task may clarify this discrepancy.
A second explanation of the somewhat small response gain in the present study is that it may be reflexive, whereas observations of the Lombard and side-tone amplification were probably more of a voluntary response. The primary argument suggesting the responses may be reflexive relies on their latency. Responses that occur with a “short” latency are often described as being “reflexive,” whereas responses with longer latencies are usually thought to be voluntary. Of critical importance is how one defines short. Typical short latency voluntary responses to a sound or visual stimulus by well-trained subjects in a reaction-time paradigm are on the order of 100–120 ms (Luschei et al., 1967). However, these latencies only hold for “simple” reaction times of trained subjects. Reaction times involving a decision, “choice reaction time,” are closer to 300 ms or more (Falkenstein et al., 1993). In the present study, both brief upward and downward stimuli were presented, and untrained subjects generally produced compensatory responses, i.e., as if it were a choice reaction-time task with latencies around 150 ms. Therefore, on the basis of response latency, it is argued that the responses are reflexive in nature. Another argument bearing upon the reflexive nature of the responses is that subjects were indeed aware of some sort of feedback perturbation, but they did not know when or what type (upward or downward) of perturbation would be introduced into their auditory feedback. Given the randomized nature of perturbation onset, the brief perturbation duration of 200 ms, and randomization of perturbation type, subjects could not predict the onset time or type of stimulus and therefore could not adjust their vocalizations consciously in response to the perturbation. Nevertheless, the argument as to whether a response is voluntary or reflexive is not easily resolved, as most responses that a lay-person would describe as being reflexive can be voluntarily modulated (Prochazka et al., 2000). Our use of this term is meant to convey the idea that people respond to unexpected perturbations in voice loudness feedback without a conscious effort to do so, in other words automatically. It is possible that reflexive responses, of the type we are suggesting, have a lower gain than voluntary reactions.
If the reflexive responses described here are not capable of fully compensating for perturbations in voice loudness feedback, a reasonable question is what are their functions? Since the response magnitudes are rather small, it is suggested that this mechanism is largely responsible for stabilizing voice amplitude within a restricted range of 1 dB or less. Such a narrow range is one that would reduce the magnitudes of small fluctuations in vocal amplitude. It is also argued, as has been done for the pitch-shift reflex, that if the auditory-vocal system were capable of generating reflexive responses as large as those of the stimuli themselves, then environmental sounds, such as other voices, might cause large, unintended fluctuations in a person’s vocal amplitude. Thus, a person would be unable to hold vocal amplitude steady in the presence of other sounds (Larson, 1998; Sivasankar et al., 2005). Given these considerations, the system presumably relies on slower, consciously controlled voluntary mechanisms to meet the challenges of large drifts in the loudness of vocal feedback and relies on the automatic compensatory mechanisms for small perturbations.
In this study, we also observed that response magnitudes were larger for upward-shifted loudness feedback compared to downward shifts. We have no definitive explanation for this finding, but we suggest some possibilities. First, an increase in voice loudness may have greater salience (i.e., it may be more noticeable) than a decrease, and this may generate a larger response than a reduction in voice loudness. A second explanation may have to do with the reflexive nature of the response. If indeed the response is reflexive, the mechanisms for perception of voice loudness feedback change and/or generating the response may be more sensitive to an increase in voice amplitude than a decrease, which may lead to a stronger reaction. We have no explanation for such an asymmetry, but it could be related to a greater need to control for excessive voice loudness than reduced loudness. There may be no end to possible reasons for this, but it could be related to evolutionary pressures to guard against the possibility of attracting attention to oneself by being excessively loud. As a final note, it is interesting that control of voice loudness is a problem in people suffering from Parkinson’s disease, and the reflexive mechanisms discussed here may not be adequately controlled in this disorder (Kiran and Larson, 2001).
In this study, we tested the hypothesis that control of voice amplitude requires greater reliance on auditory feedback for a soft voice compared to normal voice amplitude. The results supported this hypothesis by showing that response magnitudes were significantly greater under the soft voice production condition compared to the normal voice condition. Thus, it may be suggested that vocalizing, or speaking, with a relatively soft voice requires closer monitoring of auditory feedback than normal voice amplitude.
Our feedback model of loudness control generally reproduced the data well, showing that it is a feasible representation of internal circuitry that produces these responses. We modeled five subjects rather than the full dataset because these subjects are representative of the others. The purpose of the model was only to demonstrate a feasible and simple circuit that could account for the experimental results—a working hypothesis. The delay parameter was stable within subjects, ranging from 70 to 100 ms. Model delay was shorter than experimentally measured latency because of the model’s low-pass filtering, which adds a time lag. This points out a pitfall—neglecting internal dynamics—that could have arisen had we assumed that latencies were derived from a simple internal delay process. As was found in the experimental data analysis, simulated side-tone gain decreased by a factor of about 2 with perturbation loudness and also was increased for the soft versus normal voice conditions. This considerable variability indicates that, at least for the moment, side-tone gain should not be considered “hard-wired.”
V. CONCLUSION
In the present study, subjects were asked to sustain vowel sounds while hearing short perturbations (200 ms) in voice loudness feedback over headphones. Subjects responded to loudness perturbations with compensatory corrections in voice amplitude approximately 76% of the time, but full compensation was generally not achieved. Data analysis included only these compensatory responses. The remaining averages either “followed” the direction of amplitude perturbation (2%), or were classified as nonresponses (24%). Compensatory response magnitudes were further calculated as gain (response magnitude/stimulus magnitude) indicating responses to 1-dB stimuli approximated unity, while those to 3- or 6-dB stimuli were less than 0.5. These findings suggest that the system responsible for compensation is nearly optimal for correcting for small perturbations in voice amplitude, and hence may function to stabilize voice amplitude. However, full compensation was generally not achieved for larger magnitude stimuli. Response magnitudes were also compared across vocal task, indicating that the audio-vocal system relied on auditory feedback to a greater extent during a more difficult vocal task such as low voice intensity production compared to a less-challenging task such as conversational voice intensity production. Furthermore, the overall mean response latency across conditions was 157 ms, suggesting the responses were generated automatically. A relatively simple feedback model of the voice amplitude control system generated response simulations that captured the main features of the compensations, suggesting the model was a feasible representation of the actual internal mechanisms. Overall, the results suggested that auditory feedback was used to correct for small variations in voice loudness feedback and thereby helped stabilize voice amplitude.
Acknowledgments
We would like to thank the reviewers for their insightful comments and helpful suggestions for improvement of the manuscript. This study was supported by NIH Grant No. DC006243-01A1.
References
- Adams SG, Lang AE. “Can the Lombard effect be used to improve low voice intensity in Parkinson’s disease? Eur J Disord Commun. 1992;27(2):121–127. doi: 10.3109/13682829209012034. [DOI] [PubMed] [Google Scholar]
- Alpert M, Rosenberg SD, Pouget ER, Shaw RJ. “Prosody and lexical accuracy in flat affect schizophrenia,”. Psychiatry Res. 2000;97(2–3):107–118. doi: 10.1016/s0165-1781(00)00231-6. [DOI] [PubMed] [Google Scholar]
- Bauer JJ. Ph.D. dissertation, Northwestern University. 2004. “Task dependent modulation of voice F0 responses elicited by perturbations in pitch of auditory feedback during English speech and sustained vowels,”. [Google Scholar]
- Bauer JJ, Larson CR. Audio-vocal responses to repetitive pitch-shift stimulation during a sustained vocalization: Improvements in methodology for the pitch-shifting technique. J Acoust Soc Am. 2003;114(2):1048–1054. doi: 10.1121/1.1592161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burnett TA, Larson CR. Early pitch shift response is active in both steady and dynamic voice pitch control. J Acoust Soc Am. 2002;112(3):1058–1063. doi: 10.1121/1.1487844. [DOI] [PubMed] [Google Scholar]
- Burnett TA, Freedland MB, Larson CR, Hain TC. Voice f0 responses to manipulations in pitch feedback. J Acoust Soc Am. 1998;103(6):3153–3161. doi: 10.1121/1.423073. [DOI] [PubMed] [Google Scholar]
- Falkenstein M, Hohnsbein J, Hoormann J. Late visual and auditory ERP components and choice reaction time. Biol Psychol. 1993;35:201–224. doi: 10.1016/0301-0511(93)90002-p. [DOI] [PubMed] [Google Scholar]
- Ford CN, Connor NP. “Phonatory effects of mass lesions,”. In: Kent RD, Ball MJ, editors. Voice Quality Measurement. Singular; San Diego: 2000. pp. 377–384. [Google Scholar]
- Hain TC, Burnett TA, Larson CR, Kiran S. Effects of delayed auditory feedback (DAF) on the pitch-shift reflex. J Acoust Soc Am. 2001;109(5):2146–2152. doi: 10.1121/1.1366319. [DOI] [PubMed] [Google Scholar]
- Hain TC, Burnett TA, Kiran S, Larson CR, Singh S, Kenney MK. Instructing subjects to make a voluntary response reveals the presence of two components to the audio-vocal reflex. Exp Brain Res. 2000;130:133–141. doi: 10.1007/s002219900237. [DOI] [PubMed] [Google Scholar]
- Heinks-Maldonado TH, Houde JF. “Compensatory responses to brief perturbations of speech amplitude,”. ARLO. 2005;6(3):131–137. [Google Scholar]
- Jones JA, Munhall KG. Perceptual calibration of f0 production: Evidence from feedback perturbation. J Acoust Soc Am. 2000;108(3):1246–1251. doi: 10.1121/1.1288414. [DOI] [PubMed] [Google Scholar]
- Jones JA, Munhall KG. The role of auditory feedback during phonation: Studies of Mandarin tone production. J Phonetics. 2002;30:303–320. [Google Scholar]
- Kawahara H, Williams JC. “Effects of auditory feedback on voice pitch trajectories: Characteristic responses to pitch perturbations,”. In: Davis PJ, Fletcher NH, editors. Vocal Fold Physiology: Controlling Complexity and Chaos. Singular; Sydney: 1996. pp. 263–278. [Google Scholar]
- Kiran S, Larson CR. Effect of duration of pitch-shifted feedback on vocal responses in Parkinson’s disease patients and normal controls. J Speech Lang Hear Res. 2001;44:975–987. doi: 10.1044/1092-4388(2001/076). [DOI] [PubMed] [Google Scholar]
- Lane H, Tranel B. The Lombard sign and the role of hearing in speech. J Speech Hear Res. 1971;14:677–709. [Google Scholar]
- Larson CR. Cross-modality influences in speech motor control: The use of pitch shifting for the study of f0 control. J Commun Disord. 1998;31:489–503. doi: 10.1016/s0021-9924(98)00021-5. [DOI] [PubMed] [Google Scholar]
- Larson CR, Burnett TA, Kiran S, Hain TC. Effects of pitch-shift onset velocity on voice f0 responses. J Acoust Soc Am. 2000;107(1):559–564. doi: 10.1121/1.428323. [DOI] [PubMed] [Google Scholar]
- Larson CR, Burnett TA, Bauer JJ, Kiran S, Hain TC. Comparisons of voice f0 responses to pitch-shift onset and offset conditions. J Acoust Soc Am. 2001;110(6):2845–2848. doi: 10.1121/1.1417527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leentjens AF, Wielaert SM, van Harskamp F, Wilmink FW. Disturbances of affective prosody in patients with schizophrenia; A cross sectional study. J Neurol Neurosurg Psychiatry. 1998;64(3):375–378. doi: 10.1136/jnnp.64.3.375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luschei E, Saslow C, Glickstein M. Muscle potentials in reaction time. Exp Neurol. 1967;18:429–442. doi: 10.1016/0014-4886(67)90060-x. [DOI] [PubMed] [Google Scholar]
- Murphy D, Cutting J. Prosodic comprehension and expression in schizophrenia. J Neurol Neurosurg Psychiatry. 1990;53(9):727–730. doi: 10.1136/jnnp.53.9.727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Natke U, Kalveram KT. Effects of frequency-shifted auditory feedback on fundamental frequency of long stressed and unstressed syllables. J Speech Lang Hear Res. 2001;44:577–584. doi: 10.1044/1092-4388(2001/045). [DOI] [PubMed] [Google Scholar]
- Natke U, Donath TM, Kalveram KT. Control of voice fundamental frequency in speaking versus singing. J Acoust Soc Am. 2003;113:1587–1593. doi: 10.1121/1.1543928. [DOI] [PubMed] [Google Scholar]
- Prochazka A, Clarac F, Loeb GE, Rothwell JC, Wolpaw JR. What do reflex and voluntary mean? Modern views on an ancient debate. Exp Brain Res. 2000;130(4):417–432. doi: 10.1007/s002219900250. [DOI] [PubMed] [Google Scholar]
- Ramig LO. “Voice disorders,”. In: Minifie FD, editor. Introduction to Communication Sciences and Disorders. Singular; San Diego: 1994. pp. 481–519. [Google Scholar]
- Siegel G, Pick HL., Jr Auditory feedback in the regulation of voice. J Acoust Soc Am. 1974;56(5):1618–1624. doi: 10.1121/1.1903486. [DOI] [PubMed] [Google Scholar]
- Siegel GM, Kennard KL. Lombard and sidetone amplification effects in normal and misarticulating children. J Speech Hear Res. 1984;27(1):56–62. doi: 10.1044/jshr.2701.56. [DOI] [PubMed] [Google Scholar]
- Sivasankar M, Bauer JJ, Babu T, Larson CR. Voice responses to changes in pitch of voice or tone auditory feedback. J Acoust Soc Am. 2005;117(2):850–857. doi: 10.1121/1.1849933. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Titze IR. Principles of Voice Production. Prentice-Hall; Englewood Cliffs, NJ: 1994. [Google Scholar]
- Xu Y, Larson C, Bauer J, Hain T. Compensation for pitch-shifted auditory feedback during the production of Mandarin tone sequences. J Acoust Soc Am. 2004;116(2):1168–1178. doi: 10.1121/1.1763952. [DOI] [PMC free article] [PubMed] [Google Scholar]


