Abstract
We have developed a dynamic self-consistent mean field model, based on Molecular Dynamics simulations, to study lipid-cholesterol bilayers. In this model the lipid bilayer is represented as a two-dimensional lattice field in the lipid chain order parameters, while cholesterol molecules are represented by hard rods. The motion of rods in the system is continuous and is not confined to lattice cells. The statistical mechanics of chain ordering is described by a mean field derived from an extension of a model due to Marčelja. The time-evolution of the system is governed by stochastic equations. The ensemble of chain configurations required in partition sums, and the energies of interaction, are taken from atomistic level Molecular Dynamics simulations of a lipid bilayers. The model allows us to simulate systems 500 nm in lateral size for 20 microsecond timescales, or greater. We have applied the model to dipalmitoyl-phosphatidylcholine (DPPC) - cholesterol (Chol) bilayers at 50° C for Chol concentrations between 2 % and 33 %. At low concentrations of Chol (2 – 4 %), the model predicts the formation of isolated clusters of Chol surrounded by relatively ordered lipid chains, randomly dispersed in the disordered bilayer. With increasing Chol composition, regions of Chol-induced order begin to overlap. Starting from about 11 % Chol this ordering effect becomes system-wide and regions unaffected by Chol are no longer detectable. From the analysis of properties of the model we conclude that the change in lipid chain order with increasing Chol concentration is continuous over the 20 μs scale of the simulations. We also conclude, that, at 50° C no large scale Chol-rich and Chol-depleted coexisting phase separated regions form at any concentration. At no point in any of the simulations do we observe a higher degree of lateral organization, such as Chol-based superlattice structures.
Introduction
Binary mixtures of cholesterol and phospholipids have been studied extensively for the past four decades1. The effect of cholesterol on the thermodynamic properties of phospholipid bilayers has been interpreted in terms of a “condensing effect” of cholesterol, the formation of specific cholesterol-lipid complexes2,3, phase separation into co-existing liquid phases4, or the formation of superlattices5. There have been number of studies of phase equilibria in two and three component cholesterol (Chol)/phospholipid (PC) systems which have proposed partial PC-Chol phase diagrams4,6–9. These data suggest several distinct phases in Chol-PC mixtures - a high temperature low Chol liquid-crystalline disordered phase (Lα), a low temperature low Chol gel (Lc) phase, and a “liquid ordered” Chol-rich phase (L0). In the L0 phase, PC hydrocarbon chains are ordered as in a gel phase, but PC molecules are about as mobile as in a fluid phase1. McMullen et al further argue for the existence of two distinct L0 regions, a liquid-crystalline-like (Loα) and a gel-like (L0β) region4, based on experimental observations which suggest that the L0 phase is not homogeneous with respect to temperature7,10,11. An additional conclusion reached by McMullen et al is that, even at low Chol concentrations (2 % – 12 %), above the main lipid phase transition temperature, Chol-rich L0 and very low- Chol Lα phases co-exist.
At a molecular level, the detailed, localized behavior of lipid-cholesterol bilayers is still unclear. Using conventional molecular dynamics (MD) simulations, lipid-cholesterol inter-actions at an atomic level have been examined extensively by a number of workers (for example see references3,12–15). However, available computing power has restricted such simulations to relatively small systems and short timescales, which cannot provide information on structural or dynamical properties over time and length scales of biological interest. In order to better understand phase-separation and/or co-existence in lipid-cholesterol bilayer systems, it is desirable to develop a different type of dynamical modeling which could offer insight into processes that take place over much greater length and time scales in model lipid membranes, than are currently available in atomistic simulations.
The field of coarse-grained simulations of membrane systems is new, however there have been several interesting approaches already. Marrink et al16 have introduced a coarse-grained model in which small group of atoms were represented by single interaction sites, reducing the number of degrees of freedom in the system. Lennard-Jones, harmonic, and electrostatic interaction parameters were adjusted to match independent data from model compounds. Cut-offs of 1.2 nm were used for Lennard-Jones and electrostatic potentials. Compared to full-scale atomistic MD simulations, Marrink et al achieved a gain in computational time of 3–4 orders of magnitude. Shelley et al17 used a similar type of coarse-graining, however their choice of force-field parameters for the coarse-grained particles is somewhat different from that of Marrink et al. The 3 or 4 order-of-magnitude increase in computational scale gained by using coarse-grained model extends the range of simulations to tens of thousands of molecules, and microseconds in time. However for even greater scales of system size and simulation time, other statistical mechanical modeling methods are required. In addition to new methodologies, an overall reduction or even elimination of phenomenological parameters in models is desirable in order that testable predictions can be derived. One way to reduce the level of phenomenology is to utilize information from atomistic simulations to define interactions in coarser grained statistical mechanical models.
Sengupta et al18 carried out off-lattice Monte Carlo simulation of a two- component lipid-cholesterol system. In this model lipids interact with each other and with the cholesterols via a hard-core repulsive potential, whereas the cholesterol molecules, in addition to the hard-core repulsion, experience a longer-range repulsive interaction. Using these interaction potentials, which were not directly derived from experimental or simulation data, the model favored the formation of superlattice structures. However there is no basis, from experiment or atomistic simulation, for the types of potentials chosen.
Recently Vattulainen et al19 proposed a coarse-grained model for DPPC-Chol mixtures based on atomistic level MD simulations of DPPC-Chol bilayers. In this two-dimensional model individual lipid and sterol molecules were represented by point particles. Using an Inverse Monte Carlo (IMC) technique 20,21, the effective intermolecular interactions between different molecules were constructed from radial distribution functions (RDF) obtained from atomistic MD simulations. Then lattice-MC simulations were run using the effective interactions. Vattulainen and co-workers found that their model predicts the formation of Chol-rich and Chol-poor domains at intermediate Chol concentrations. The main limitations of this model are that it does not study dynamical properties of the system and, that chain ordering is not explicitly included. Additionally, the reconstruction of pair potentials from RDF is not a well defined procedure in that very different pair potentials can yield a very similar RDF.
Another promising tool for studying lipid bilayer systems is a self-consistent mean field theory (SCMFT), first introduced for lipid bilayers by Marčelja in 197422 as a generalization of the Maier-Saupe theory for liquid crystals23. Within Marčelja’s framework the lipid tails are treated according to the rotational isomeric states (RIS) model of Flory22,24 which permits only three distinct states for each dihedral: trans, gauche + and gauche−. In general, self-consistent mean field theories are excellent models for the statistical mechanical behavior of complex systems, including phase transitions of all types, provided that one is not close to a critical point, where the range of correlations may diverge25,26. There have been various implementations of SCMFT for lipid bilayer systems. In a recent paper, Elliot et al27, applied self-consistent mean field theory to bilayer systems consisting of fully saturated and mono unsaturated lipids. Constraining the density within the hydrophobic core of the bilayer and introducing phenomenological interaction potential between adjacent chain segments which captures the aligning tendency of the inter-chain packing, Elliot et al calculated phase diagrams for mixtures of saturated and mono unsaturated lipids.
In this paper we present a dynamical statistical mechanical model for lipid-cholesterol mixtures which, like the model of Vattulainen et al, projects lipid chains into a lattice field, but, unlike the model of Vattulainen et al, is based on both MD simulations and SCMFT. Our aim is to model lipid-cholesterol interactions in terms of the self-consistent, dynamical evolution of localized lipid molecular order parameters. We use a temperature 8° C above the main lipid chain melting phase transition so that SCMFT should provide an excellent approximation. Instead of a computer generated library of single-chain RIS states, we utilize a library of chain states which are generated by atomistic MD simulations of a lipid bilayer. This approach enhances the sampling of the thermodynamically important states of flexible hydrocarbon tails. By using an MD-based conformation library we exclude a very large part of the conformation space that would be explored by a single free chain22, but which has a low statistical probability of occurrence in a bilayer environment. Cholesterol molecules are introduced as small hard rods which interact with neighboring lipid chains to locally increase lipid chain order. The motion of the rods is driven by Langevin stochastic equations for center-of-mass and orientation of each cholesterol molecule. The trajectories of the rods are not confined to lattice sites. The effects of the lipid headgroup and of hydration are included indirectly through the coupling constants in the model. The Free Energy functional is calculated using SCMFT. We utilize data from MD simulations to reduce the number of phenomenological parameters in the model. Two parameters which cannot be extracted from MD simulations are determined from experimental data for a cholesterol-free DPPC bilayer. The model is then predictive in its calculation of the distribution and the evolution of molecular order and lateral organization of cholesterol molecules in the lipid membrane. In the following sections we describe the model, and show how data from MD simulations are used as input. After describing the model, we present results of 20 μs simulations for different concentrations of Chol in DPPC.
Theoretical Model
We treat a lipid bilayer as two weakly interacting leaflets, allowing us to focus only on one leaflet. Because of the low level of interdigitation in lipid-Chol bilayers28, this is a valid approximation. Within the single leaflet we consider a system of Nlip saturated hydrocarbon chains on a two-dimensional square lattice. The lattice spacing, l, represents a typical distance between neighboring hydrocarbon chains. From MD simulations of pure DPPC bilayer we found an average separation between carbonyl carbons on neighboring DPPC chains to be 0.65 nm. Thus, we set the lattice spacing to 0.65 nm. The model we develop in this paper should be thought of as a lattice field in the order parameter (defined below) derived by mapping the DPPC chains onto an underlying grid. That is, the model is a lattice-based field theory in the lipid chain order parameters with a graininess defined by the size of a lipid chain.
As we add Chol to the model local changes are induced in the order parameter field. In this manner the well known condensation effect of Chol on a lipid bilayer is represented in the present model by localized increases in the order parameter field around each Chol. In reality lipid chains reduce their area per molecule as they increase their order. Within the order parameter field representation, this can be accomplished by appropriately scaling the underlying lattice grid, but within Mean Field Theory the properties of the model do not depend on the lattice constant as long as the model energies are independent of the lattice spacing. We make this assumption by confining all interactions to nearest neighbor pairs at all Chol concentrations. Then no re-scaling is necessary and the model predicts changes in area through changes in the order parameter field. We also point out for clarification that the rods used to model Chol have no specific volume in this model. In experiments and simulations, the Chol molecules order neighboring chains through the rigid excluded volume within the bilayer. In the present model, this effect is represented by changes in the order parameter field as discussed above.
The thermodynamic properties of the model are also independent of the symmetry of the underlying lattice. The change in the number of near neighbors as one goes from, for example, a square to a hexagonal lattice can be duplicated by a rescaling of the coupling constant in the model energy function. Since this parameter is the one quantity that is set phenomenologically (as described below) to match the pure DPPC phase diagram, and since simulated radial distribution functions for DPPC-Chol14 indicate that each Chol has between four and five nearest neighbor chains, a square lattice geometry was used. We have verified that the results obtained using a hexagonal lattice can be, after scaling the coupling constant, matched to those of a square lattice.
Each point on the underlying lattice represents a chain of N = ns + 2 carbon atoms where ns is the number of internal methylene carbon atoms. We denote by θm,i the angle between the normal to the interface and the plane spanned by the mth carbon on the ith chain and its associated H atoms. The order parameter for the ith chain is defined as the product of the fraction of trans bonds in the ith chain and the average segmental order parameter of the ith chain22
| (1) |
Here ntr is the number of trans bonds in the ith chain and represents the fraction of trans bonds in the ith chain. SCH(m) is the segmental C-H bond order parameter.
To model DPPC-Chol mixtures, Chol molecules are randomly inserted onto the field of chain order. Each Chol molecule is represented by a rod with a position vector of center-of-mass and angle φk it forms with the positive x axis on the lattice. The length of a rod represents roughly the width the ring plane of a Chol molecule. The hard rods interact with each other and with the order parameter field as we describe below. Figure 1 shows an enlarged view of a fragment of the 20 % Chol concentration system in the initial configuration. Chol molecules are shown as black rods, and the grayscale is a measure of the initial level of ordering of the underlying field, with lighter shades indicative of greater order.
Figure 1.

Enlarged view of a fragment of the 20 % Chol concentration system in the initial configuration. Chol molecules are shown as black rods. The grayscale is a measure of the initial order in the lipid field, with lighter shades indicative of greater order.
Following arguments due to Marčelja22, we write the Hamiltonian of the system as
| (2) |
The first sum extends over nearest neighbor pairs of lipid chains. This term represents an extension, due to Marčelja22, of the dispersion energy relation in nematic liquid crystals23 to include flexible hydrocarbon chains. The coupling constant, V0, which describes the strength of the interaction, contains implicitly all information about lipid headgroups, and hydration.
The second term in Eq. (2) describes the order parameter dependent lipid-chol interactions. The lipid-cholesterol coupling constant, Vlc, depends in general on the relative distance rij between lipid chain and cholesterol. In order to estimate the value of Vlc, we analyzed trajectories from MD simulations of DPPC-Chol bilayers14. From the MD trajectories we calculated intermolecular Lennard-Jones and Coulomb interactions between different Chol-lipid chain pairs (the carbonyl group C=O was explicitly included in each hydrocarbon tail). Since the interaction between uncharged lipid chains and Chol is short ranged, we extend chain-Chol interactions to nearest neighbors (nn) only. We calculated the coupling constant Vlc by linear regression analysis of the energies of nn chain-Chol pairs (identified by peaks in MD radial distribution functions), and the corresponding chain order parameter. We indeed found that the interaction is very small beyond nn pairs. Hence, we stipulate that Vlc is nonzero only for nn lipid chain-cholesterol pairs on the square lattice. In this case the coupling constant Vlc is set from the linear regression analysis to 7 KJ/M46.
The third term in Eq. (2) represents pair-wise Chol-Chol interactions and is modeled as the product of distance-dependent and angular contributions, φij = φi — φj describes the relative orientation of neighboring Chol molecules. In order to find a functional expression for , we analyzed Chol-Chol and Chol-lipid pair energies and radial distribution function (RDF) profiles between different atoms on lipid and Chol molecules in trajectories from MD simulations of DPPC-Chol bilayers14. For the energy analysis, from the MD trajectories we calculated average intermolecular van der Waals and Coulomb interactions between different pairs of Chol molecules and between pairs of Chol and lipid molecules. We found that the interaction between pairs of Chol molecules is energetically less favorable than the interaction between Chol and lipid molecules. Energetic plots showed the minima for the Chol-lipid interaction potential to be approximately twice as deep as the minima for the Chol-Chol interaction. Comparison of the locations of those minima indicated that preferred separation between Chol molecules is larger than that of Chol-lipid pairs. Further, analysis of RDF profiles between oxygen atoms on different Chol molecules revealed that even for 50% Chol concentration the first peak, occurring at around ~ 0.5 nm, is very broad, whereas the same peak in RDFs between Chol oxygen and DPPC phosphate oxygen and between Chol oxygen and DPPC carbonyl oxygen is much sharper14.
In order to input the above data from MD simulations to the mean field theory, we model the distance-dependent part of Chol-Chol interaction energy, . as a simple hard core repulsive wall which prevents two Chol molecules from coming any closer than 0.5 nm. This Chol-Chol interaction potential is quite different from one utilized by Sengupta et al18 in their model. Analysis of MD data did not provide any rationale for implementing a long-range repulsive term in Chol-Chol energy used by Sengupta et al.
For the angular part of the Chol-Chol interaction, , we employ a simple short-range repulsive interaction29:
| (3) |
Here γ is an interaction strength and L is the length of a single rod. prevents neighboring Chol molecules from overlapping. We have set γ = 13 × kBT, which represents the minima in the Chol-Chol interaction energy as obtained from the analysis of MD trajectories as described above. is the only term in the Hamiltonian which carries a rod length dependence in the model. L represents the width of a Chol molecule, and we estimated it from DPPC-Chol simulations14 to be about 1.1 times the typical lipid chain separation.
The free energy of the system is given by
| (4) |
where Ztot is the total partition function of the system, kB is the Boltzmann constant, T-temperature, and the summation on the right hand side is over all the possible configurations of all the lipid chains. We calculate the free energy within self-consistent mean field theory (SCMFT). In SCMFT the mean field at site i is the average field due to neighboring lipids and cholesterols22,30
| (5) |
where ci is the number of neighboring cholesterols at site i, v is the coordination number (v = 4 for the square lattice), and 〈sj〉 denotes the ensemble average of sj
For a given value of the order parameter sj for the ith chain, the energy in the mean field approximation is given as22,30
| (6) |
For Vlc > 0 Eq. (6) guarantees that Chol molecules will tend to increase the order of neighboring chains.
By summing over all possible conformations of a single chain one gets the mean field partition function for the ith chain
| (7) |
where β = 1/kBT.
From (1) and (5)–(7) we obtain the self-consistent system of equations for 〈sj〉:
| (8) |
Since Φi depends on the values of 〈sj〉 at the neighboring sites, Equation (8) is a system of Nlip coupled non-linear equations, which can be solved numerically by iteration. The free energy of the system is, for a fixed distribution of Chol molecules on the lattice,
| (9) |
where sum over j extends over the nearest neighbors of the ith site.
For the calculations of configuration sums in Eqs.(7)–(9) we utilize a library of chain states which are generated by a 4 ns (after equilibration) atomistic MD simulation of a bilayer of 1600 DPPC molecules in 51696 water molecules. The MD runs were performed at 50° C under NPT boundary conditions with Parrinello-Rahman pressure coupling31,32. Temperature was maintained by extended ensemble Nosé-Hoover scheme33,34. The Particle-Mesh Ewald method was used for long-range electrostatic interactions, and an 18 Å cutoff was implemented for van der Waals interactions. Structural properties of this bilayer, including area per molecule and order parameter profiles, are in agreement with experimental data for pure DPPC35. The purpose of including only chain states generated by MD simulations, rather than generating chain states, for example, based on the rotational isomeric states (RIS) model, is to improve the sampling efficiency. By doing so, we exclude a very large part of the conformation space that would be explored by a single free chain22, but which has a low statistical weight in a bilayer setting. This procedure also adds many chain states for which dihedrals lie outside the RIS 3-state values. One of the important insights from MD simulations is that these states are common in lipid bilayers.
One consequence of using the MD chain library is that the ratio ntr/(ns − 1) in Eq (1) is nearly constant with an average of 0.7 ± 0.1 for all conformations. This prefactor was introduced by Marčelja to obtain the correct degree of order in the low temperature phase of the original model.22 In the MD library there are a sufficient numbers of gel-like chains that this prefactor is actually not needed. It is explicitly included to maintain the original model structure as much a possible, but is basically an overall scale factor in the intermolecular interaction function.
In order to illustrate the difference between the chain states generated by MD simulations and those generated by the RIS model, in Figure 2 we plot a histogram of lipid chain order parameters from two libraries: one obtained from MD simulations (at 50° C) and the other from the RIS model. The plot reveals that the most preferred chain configurations in RIS library are the ones with s = 0. Further, the order parameter distribution for RIS library is symmetrical around s = 0. The chain states generated from the MD library differ from the RIS library states in several aspects: the order parameter distribution is no longer perfectly symmetrical about s = 0. The mean value of s in the MD library is 0.128; the maximum of the distribution is at s ~ 0.17, not at s = 0 and the MD library distribution is broader than that of the RIS library.
Figure 2.
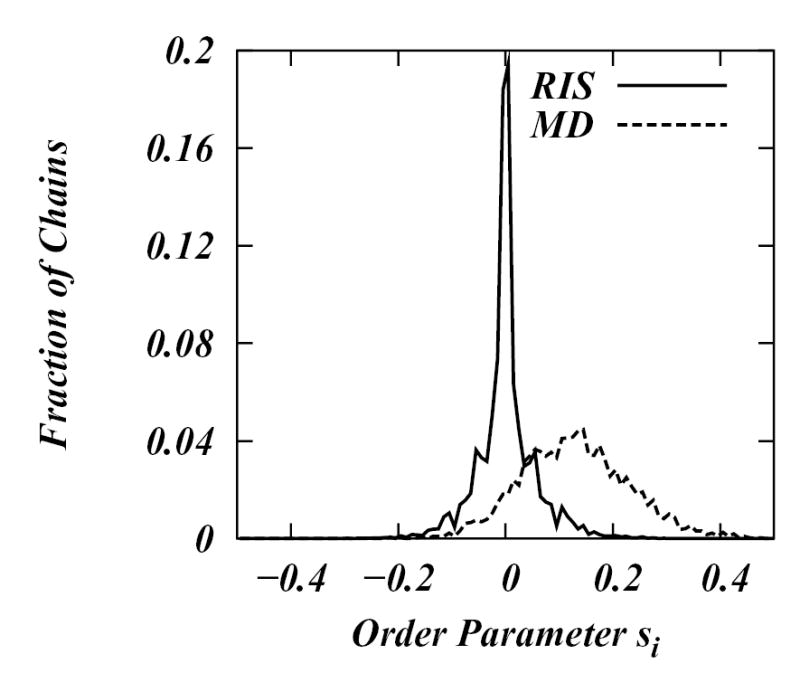
Histogram of lipid chain order parameters, s, in the libraries generated by MD simulation and RIS model.
The differences arise because the lipid chain states generated by the RIS model are independent. These are states that are explored by a single free chain. By contrast, the lipid chain states in the MD library are correlated due to non-bonded interactions between atoms on different lipid molecules as a result of dynamical evolution of the system, and to the confinement to a bilayer geometry by hydrophilic interactions in the polar region. As a consequence, the torsion angles along the lipid chains deviate from simple three state, trans, ± gauche model. Since the bilayer geometry restricts single chain conformations in MD simulations, an effective ordering field exists in the bilayer environment. The original model of Marcelja22 and more recently the model of Elliot et al27 add an explicit area-dependent surface energy to the model free energy and through this term the confinement effect is modeled. This surface pressure-area term allows for the explicit inclusion of the area per molecule, and the free energy in both models exhibits double minima below the phase transition temperature (see Figure 1 of ref. 27, for example). In the present model there is no explicit area term. This effect is implicit in the set of chain states utilized to calculate the partition sums. However, within the structure of the Hamiltonian in Eq.(2), without an explicit surface pressure-area term, the presence of the ordering field precludes the existence of a temperature-driven order-disorder phase transition in the chains. For example, comparison may be made to the Ising model, which exhibits a phase transition as a function of temperature only in zero external field25,36.
In order to utilize the model based on Eq.(2) with the chain states generated by the MD library, it is necessary to offset this effective external field. For mean field and Landau theories one can always scale the order parameter by an additive constant to make the linear term in a Landau expansion of the free energy vanish36. To this end we introduce an effective order parameter field variable, s0 We then redefine the si order parameters which are used in the model Hamiltonian in Eq.(2) as si = si (MD) — s0. In order to determine the value of s0, after performing the above re-normalization, we expanded the free energy given by Eq.(9) for the Chol-free system in the power series of the order parameter. We found that the coefficient of the linear term in the expansion is given by 4V0(save — s0), where save is the average value of the order parameter in the library of chain configurations. From Figure 2 save = 0.128. Thus, to nullify the linear term, one must offset the order parameter values in MD library by sq = 0.128.
In order to reproduce the experimentally observed first order phase transition in pure DPPC bilayers, we adjust the coupling constant V0 to 4.3 KJ/M, a value similar to that used by Marčelja and others22,37–39. For V0 = 4.3 KJ/M, the chain melting phase transition for the pure DPPC model occurs at 42° C temperature. Figure 3 shows the temperature profiles for the order parameter field (which within SCMFT is constant over the system for pure DPPC), free energy, and entropy for the model for this value of V0.
Figure 3.
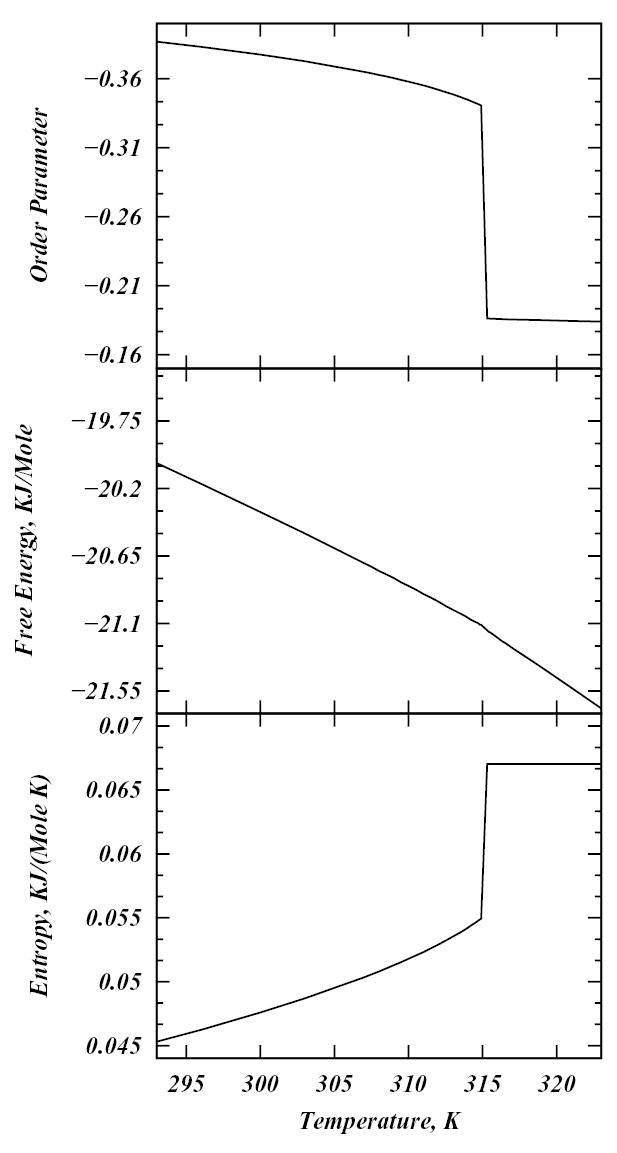
Entropy (per chain), free energy (per chain) and chain-averaged C-H bond order parameter SCH profiles as a function of temperature for pure DPPC model system.
The calculated heat capacity, as measured in a differential scanning calorimetry experiment4, is shown in Figure 4, and is qualitatively similar to published DSC data for DPPC4. The change in enthalpy at the pure DPPC phase transition is obtained to be 2 kcal/M, or approximately a factor of four smaller than the experimental value of 8 kcal/M. The reason for this is clear. The chain state library is obtained from MD simulations of 1600 × 2 chains performed at one temperature, 50° C. In order to obtain better agreement with experiment, and to directly determine V0 from simulations one should carry out MD runs at different temperatures and then combine in one library all the chain states generated by both fluid phase and gel phase simulations. This would increase the size and conformational diversity of the MD-based chain library which would increase the entropy change at the main phase transition. For this reason we confine the current application of this methodology to temperatures above the DPPC phase transition temperature.
Figure 4.
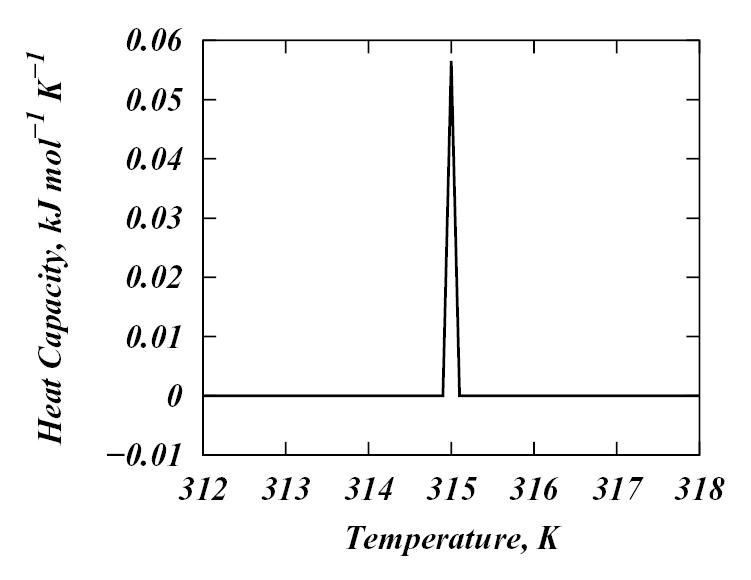
Calculated heat capacity of the pure DPPC field as a function of temperature.
Application to DPPC-Chol mixtures - Dynamical Mean Field Theory
The goal of this paper is to develop a dynamical mean field model capable of predicting phase behavior in DPPC-Chol mixtures above the DPPC chain melting phase transition. To this end, we have applied the model to several systems at different Chol compositions all at 50° C. Table I lists the systems simulated. In the following we outline the theoretical aspects of the model. Then, we present the results for all simulated systems and discuss the model predictions in the light of experimental data.
TABLE I.
Composition of the model systems studied
| Chol% | Number of Chol | Number of Lipids |
|---|---|---|
| 2 | 100 | 5000 |
| 4 | 200 | 5000 |
| 6 | 319 | 5000 |
| 7 | 400 | 5000 |
| 10 | 556 | 5000 |
| 11 | 625 | 5000 |
| 12 | 682 | 5000 |
| 15 | 900 | 5000 |
| 18 | 1098 | 5000 |
| 20 | 1250 | 5000 |
| 25 | 1667 | 5000 |
| 30 | 2143 | 5000 |
| 33 | 2500 | 5000 |
We generate an initial configuration of the system by placing the desired number of hard-rod Chol molecules randomly in the system and solving the set of self-consistent equations (8). We assume that the time evolution of all Chol molecules may be described by Langevin equations29:
| (10) |
| (11) |
Here F is the Free Energy functional for the system and the noise sources and λk(t) are independent random variables satisfying fluctuation-dissipation relations26. Mr and Mφ are translational and rotational mobility constants, respectively, Mr being related to the Chol lateral diffusion coefficient D through Mr = D/kBT. The magnitude of the mobility constant determines the relative strength of the systematic force with respect to the random forces. Equations (10) and (11), known as “position Langevin equations”40,41, are obtained in the diffusive limit of the ordinary Langevin equation40,41. This description is effective for dense systems in which the solute’s behavior in solution is continuously altered by collision with solvent molecules40. We estimate the Chol mobility constant Mr from the experimental value for the diffusion constant of Chol 42, 5 × 10−12 m2/sec. We then set Mφ/Mr = 10, Although the choice of the value for Mφ is not fixed by MD simulations, we have verified that the results were not affected when we used a ratio different by an order of magnitude. The small values for Mr and Mφ enables us to work in the Brownian regime, and to utilize the Langevin equations (10) and (11).
Introducing reduced units, equations (10) and (11) are discretized (the discretization procedure is contained in the Appendix) and numerically integrated on a 100 by 100 square lattice (corresponding to 10000 chains, or 5000 lipid molecules), with periodic boundary conditions. The dimensionless simulation timestep, Δt′, is related to the real-time step Δt, lattice spacing l, and the diffusion coefficient D through
The real-time step Δt for low concentrations (2% – 7%) was 0.5 ns. For higher concentrations (10% – 33%), in order to avoid overlaps between Chol molecules, a 100 ps timestep was used. At each stochastic time-step we solved the self-consistent system of equations for all lipid chains, re-equilibrating the order parameter field. It is possible to introduce dynamics for the order parameter field as well through stochastic equations in which local order is driven by local gradients in free energy (for example see reference29). We have verified that, while re-equilibrating, the self-consistent equations converge to the same values with or without implementing stochastic formalism for order parameter field. Therefore the latter is unnecessary and for computational purposes is not implemented.
Results and Discussion
Figure 5a shows density plots of the C-H bond order parameter fields (−SCH) for 4%, 11%, 18%, 25% and 33% Chol concentrations all at 50° C, at 0 μs and after 20 μs simulations. Chol molecules are represented as linear rods. The rods are too small to be directly observed in this figure, although their locations can be deduced from the locations of the highest local values of the lipid order parameter field. The calculated order parameter values are consistent with experimental data for DPPC-Chol mixtures43. In all cases, final snapshots show, around each Chol rod, localized regions of increased order.
Figure 5a.
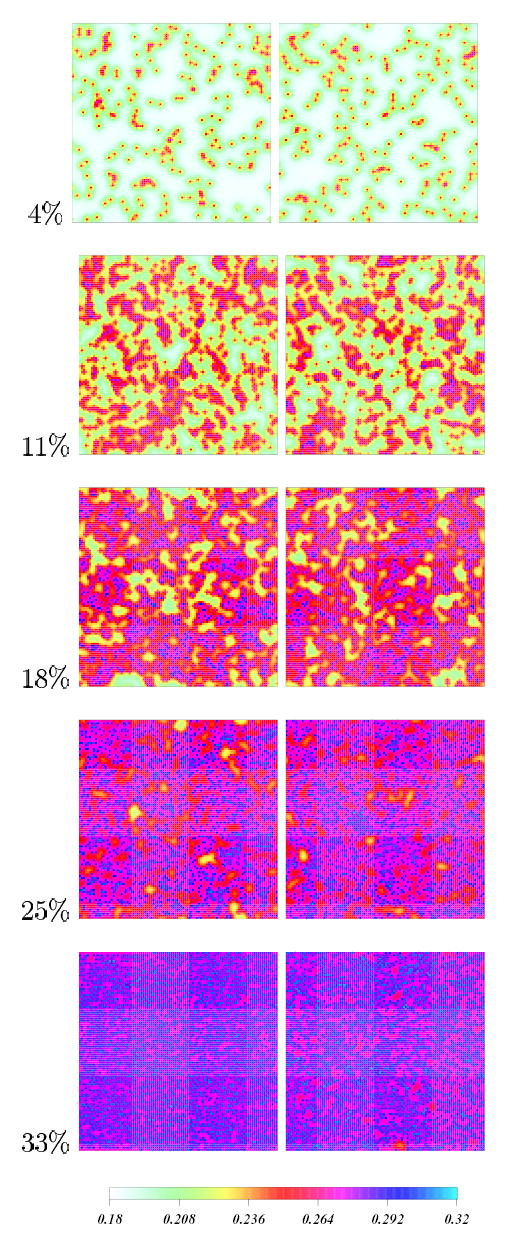
Chain-averaged C-H bond order parameter density plots for 4%, 11%, 18%, 25% and 33 % Chol concentrations at initial (left column) and final configurations (right column). Color code indicates the magnitude of local order parameters on the lattice. Chol molecules are shown as black rods. The time reached by the systems is 20 μs.
At 4 % concentration the motion of Chol molecules is driven mainly by the stochastic forces in Langevin equations (10) and (11). Thus, islands of Chol surrounded by ordered lipids are randomly dispersed in the Chol-free region of lower order. As the cholesterol concentration increases, regions of Chol-induced order overlap, giving rise to larger clusters of Chol surrounded by ordered lipids. At 11 % concentration there is a system-wide competition between lipid chain disorder and Chol-induced order, and connected regions of ordered lipids percolate across the entire simulation area. The bilayer plane order parameter plots resemble spinodal decomposition plots seen in multi-phase co-existence regions in simple fluids29. The order in the entire system is strongly effected by the presence of Chol (green, yellow, red and blue regions), however, regions of lower order also persist (white regions).
Upon further increasing Chol concentration, the order in the system gradually increases. At 18 % – 33 % Chol compositions the motion of individual cholesterol molecule is significantly effected by the surrounding cholesterols. At 33 % Chol, the alignment of cholesterols in the final snapshot shows a nematic ordering seen in simple liquid crystals29 (Figure 5b). This spatial rearrangement creates Chol-free regions in the system, which are characterized by relatively lower order (red regions in 33 % figure), however the overall order in the system remains high.
Figure 5b.
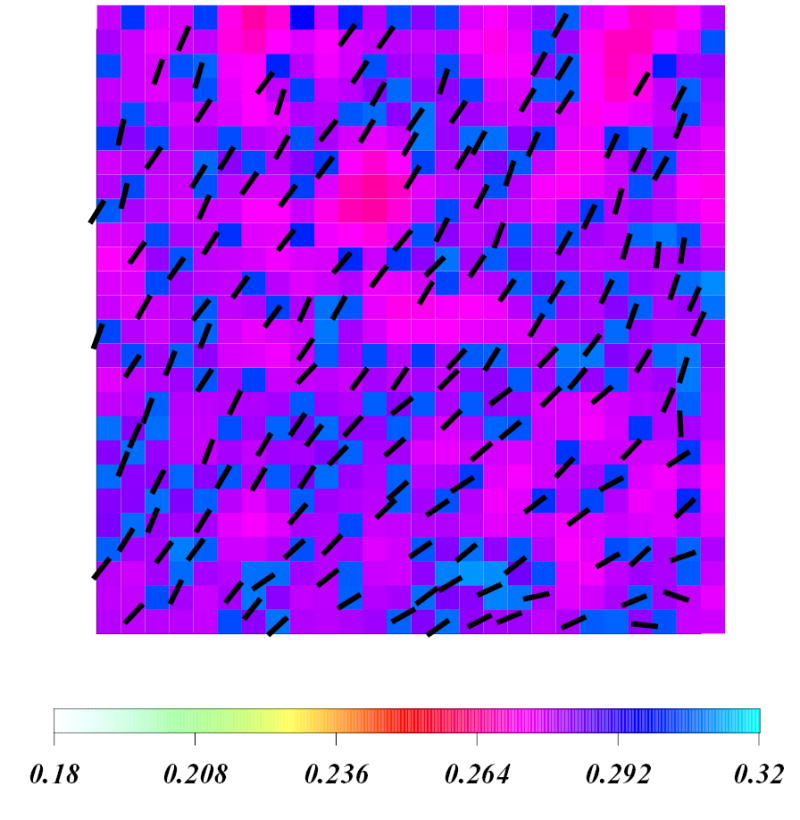
Enlarged view of a fragment of the 33 % Chol concentration system in the final configuration (after 20 μs). Color code is identical to that used in Figure 5a. Chol molecules are shown as black rods.
To better describe the dynamical evolution in all the systems, we calculated the average -SCH order parameter as a function of time (Figure 6) and also analyzed the lateral organization of the Chol molecules for all the simulations. For the latter, because cholesterols were initially distributed randomly on the lattice, we computed the deviation of the distribution of Chol molecules from a uniformly random distribution in each system as a function of time by performing chi-squared tests on sequences of snapshots of the evolving systems. The 100 by 100 square lattice was divided into one hundred 10 by 10 square bins. If Ni denotes the number of Chol molecules in ith bin, then
Figure 6.
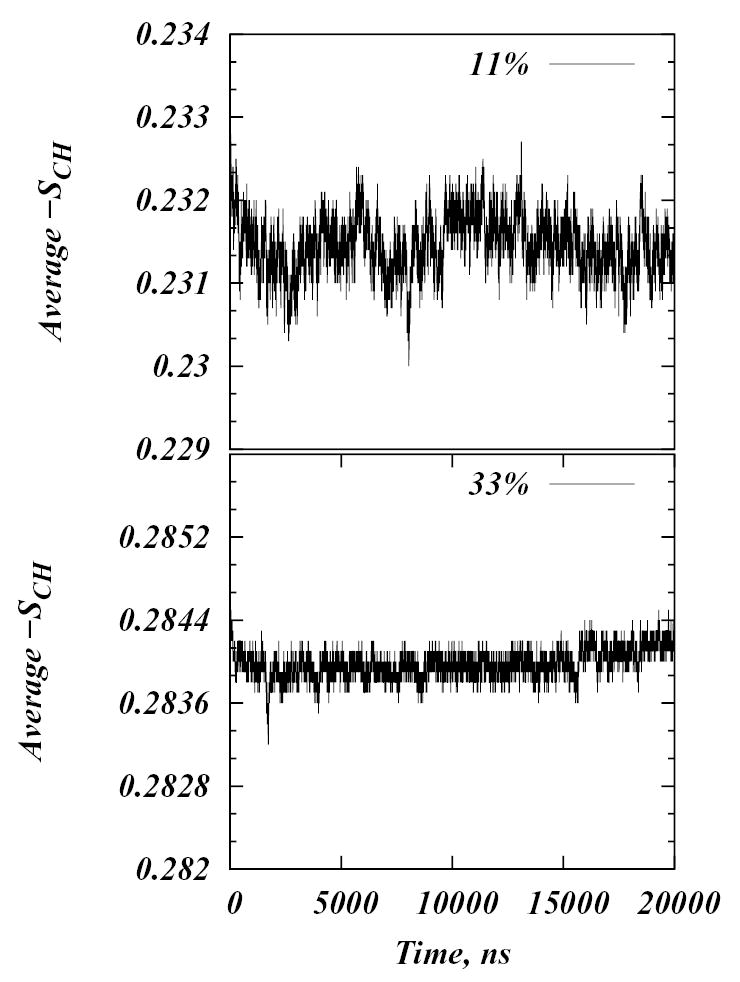
Time evolution of the average C-H bond order parameter, —SCH, for 11% and 33% Chol concentration systems.
| (12) |
where summations are over all the bins and ni is the number of Chol in the ith bin when Chol distribution is uniformly random, ni is the same for all the bins and is given by the ratio of area of the single bin over the area of the simulation cell. Due to the finite size of the simulated systems, χ2 will not be identically zero for a uniformly random distribution of cholesterols. In order to determine a practical lower limit for χ2 for different Chol concentrations, the desired number of Chols were placed randomly on a 100 by 100 square lattice and the distribution of Chol molecules in 10 by 10 size bins was examined. The experiment was repeated 104 times for each concentration and χ2 was calculated from the standard deviation of the distributions. Figure 7 shows χ2 from Eq.(12) as a function of time and the calculated lower limits for χ2, depicted in the figure as dashed lines. Both Figures 6 and 7 show results for 11% and 33% Chol concentrations. For other Chol percentages the data are qualitatively similar and, are not shown.
Figure 7.
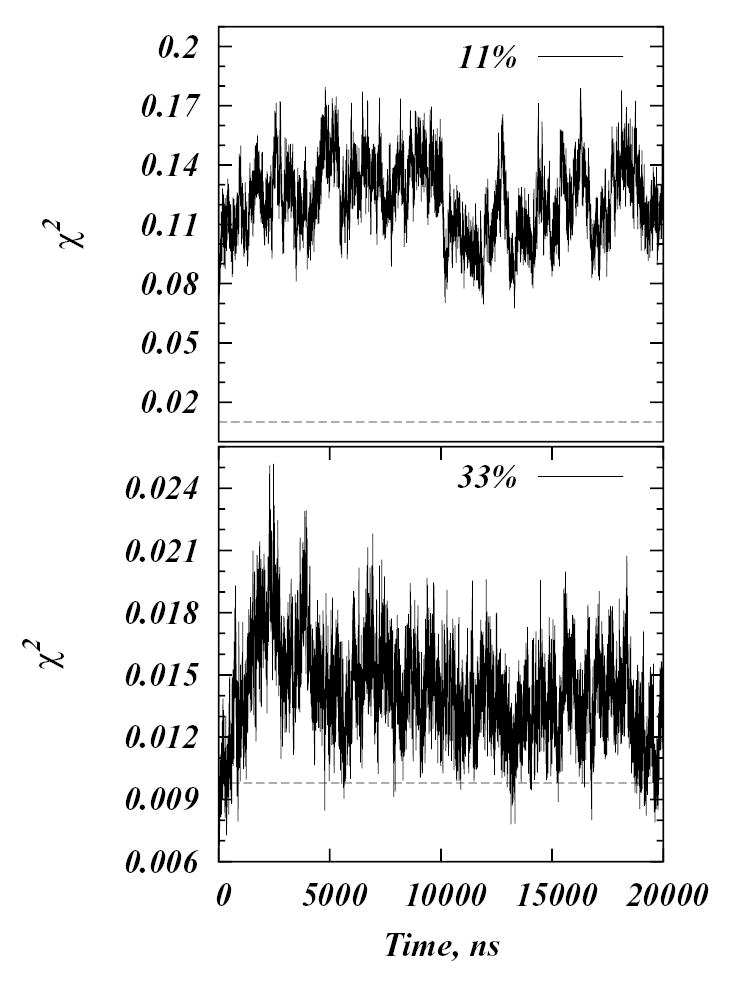
Plot of χ2 as a function of time for 11% and 33% Chol simulations. Dashed lines represent the calculated lower limits of χ2 for these systems from a simple random sampling procedure described in the text.
The order parameter plots in Figure 6 reveal that the average order in the simulated systems does not vary appreciably over the 20 μs of the runs. At 33% Chol, for example, the order in the system decreased slightly during the first 300 ns, but between 300 ns and 15 μs it remained practically unchanged, and finally, during the last 5 μs it increased to return to the initial value. The mixtures with the largest fluctuations in the order parameter are the 10–12% models, for which system-wide percolation of chain order is observed. The χ2 snapshots show that there is no observable trends of Chol clustering in any of the systems, that is, distribution of cholesterol molecules remains close to uniformly random throughout the simulations.
The reason Chol molecules remain relatively randomly distributed in the simulated systems is based on the nature of different forces experienced by cholesterols. Apart from stochastic forces, the motion of Chol molecules is driven by short-ranged repulsive direct Chol-Chol interactions, and by free energy gradients due to the order parameter field. The latter represent indirect interactions between lipid and chol molecules (sometimes interpreted as lipid-mediated interactions30 between cholesterols). We calculated the strength of the lipid-mediated interactions between cholesterols30 and found it to be of the order of the thermal energy at 50° C. We conclude that, the lipid-mediated Chol - Chol attractive interaction does not lead to aggregation of Chol molecules at 50° C. To test this hypothesis we have run simulations starting from a uniformly spaced distribution of Chol, and from a system in which all of the Chol were placed together on one “domain” in the center of the field. In both cases the systems evolved to states in which Chol were randomly dispersed throughout the lattice field. Figure 8 shows initial and 8 μ s states for a system of 18% Chol which was started with all Chol in a central domain. After 8 μs the domain has largely disappeared.
Figure 8.
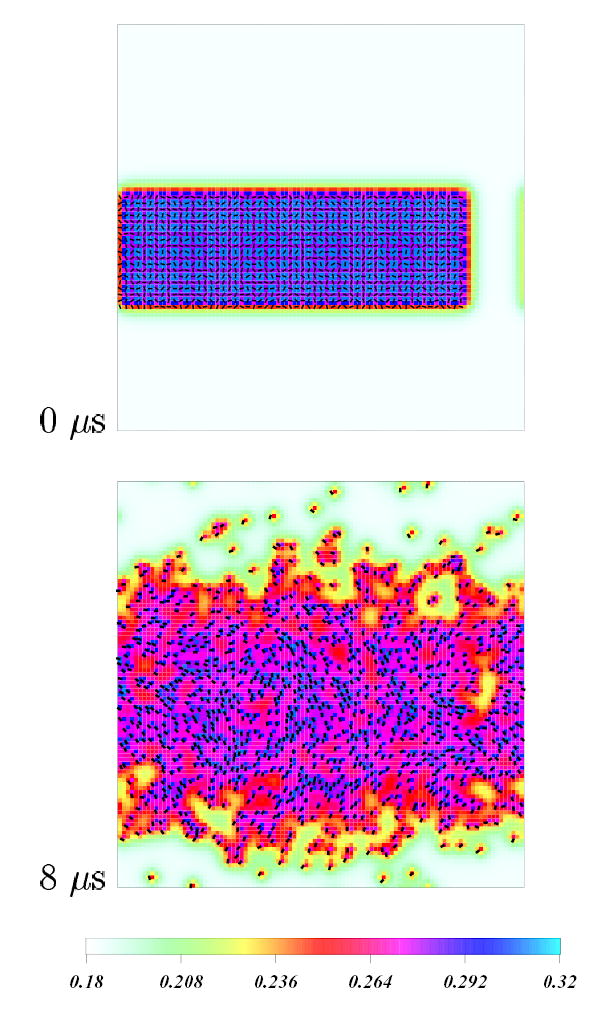
Chain-averaged C-H bond order parameter density plots for 18%, Chol concentrations starting from an initial arrangement of Chol in a close-packed “domain” (top) and final configuration (bottom). Color code as in Figure 5. Chol molecules are shown as black rods. The time reached by the system is 8 μs.
The lipid chain order in the simulated systems depends strongly on the lateral organization of cholesterols. The solution of self-consistent system of equations (8) for lipid chain order parameters at each time step equilibrates the order parameter field around each Chol molecule. Thus, the local order around a single cholesterol “follows” the cholesterol as it moves within the system, ordering neighboring lipids along its trajectory. This ordering effect takes place on the timescales much smaller (picoseconds) than the timestep of the simulations (10−1 ns) and in this model is realized by solving the self-consistent system of equations (8) at each time step. The solution of (8) yields the new equilibrated values of lipid chain order parameters around new positions of Chol molecules. Hence, as long as the Chol distribution remains random, the average order in the bilayer does not change appreciably (see Figure 6) over 20 μs.
Figure 9 shows the free energy of the simulated DPPC-Chol bilayers as a function of Chol concentration. The free energy was calculated from Eq.(9). For each system we first found the free energy as a function of time and then averaged the data over the last microsecond. The plot in Figure 9 reveals that the free energy monotonically increases with the cholesterol concentration.
Figure 9.
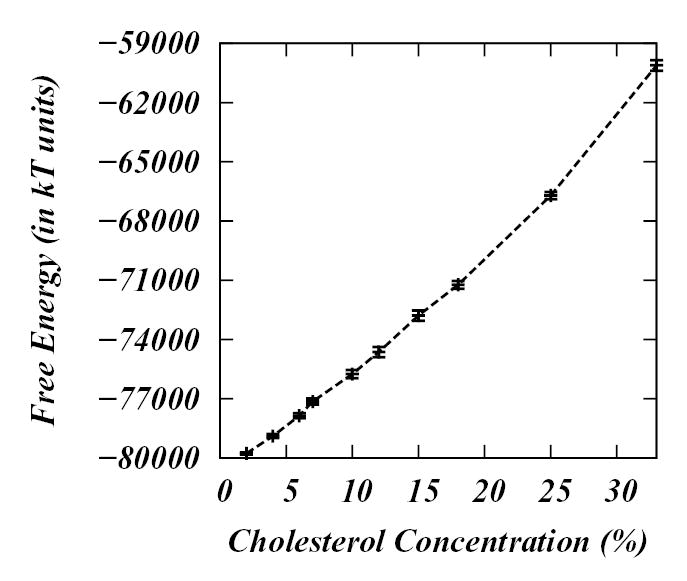
Free energy (in kBT units) of DPPC-Chol bilayers as a function of Chol concentration.
From the slope of the free energy profile it is possible to determine the chemical potential and chemical activity of cholesterol. The chemical potential of cholesterol, μ, is defined as the change in the free energy, ∂F, when number of cholesterols in the system change by ∂Nc at constant volume and temperature: The chemical activity (or fugacity) of cholesterol, ζ, is given by ζ = exp(μc/kBT). From the slope of Figure 9, we find that the chemical activity of cholesterol for the simulated systems is almost constant for 2%–25% Chol concentrations and increases somewhat for the higher Chol compositions (25%–33%). This result is in qualitative agreement with experimental data of Radhakrishnan et al44, where the authors measured the rate constants for Chol release from the Chol/phospholipid monolayers at the air-water interface and found that the rate constant, which is closely related to the chemical activity of cholesterol, is constant for low Chol concentrations and then exhibits sudden increase at around 30–33% Chol concentration. Although the systems studied by Radhakrishnan et al and the conditions under which experiments were performed are somewhat different from our model systems, the similarity of the results provides support for the predictions of the model.
Because the free energy profile precludes the coexistence of distinct phases in the simulated systems, we calculated the susceptibility of the order parameter, κ, defined as the response of the order parameter field to the external field due to cholesterols:
| (13) |
Here Nlip is the number of lipid chains in the system, si and Φi are the order parameter and molecular field respectively at site i, and β = 1/kBT.
The order parameter susceptibility can be expressed in terms of the standard deviation of lipid chain order parameter. To establish the relationship, we use the self-consistent equation (8) for 〈si〉 in (13):
| (14) |
κ describes the fluctuations in the order parameter field as the cholesterol concentration varies. Large fluctuations in the order parameter (large κ) indicate the existence of regions in the system of lipid chains with different level of organization. Smaller values of κ correspond to the states of the system with relatively homogeneous order parameter distribution. Any discontinuity, or divergence in susceptibility signals the abrupt phase transition in the system with respect to the cholesterol concentration.
In Figure 10 we plot the order parameter susceptibility as a function of cholesterol concentration. As we see from the figure, the susceptibility changes gradually when we span the entire range of Chol composition. There is a very broad region of Chol concentration (6–15 %) where susceptibility rises to an anomalously higher value, indicative of a broad and gradual transition from a lower order low Chol state to a higher order high Chol state. The plot shows that the range of Chol compositions were fluctuations in lipid chain order parameters is the largest is around 10%–12%. This is the region of Chol concentrations where there is a system-wide competition between lipid chain disorder and Chol-induced order. By further increasing Chol composition the fluctuations in order parameter field decrease. To ensure that such behavior is not an artifact of finite system size, we ran a set of similar simulations on smaller, 50 by 50 square lattice size systems by appropriately reducing the number of Chol molecules as well. The analysis of the fluctuations for these smaller size systems produced results similar to Figure 10, which indicates that finite size effects in our simulations are small.
Figure 10.

Order parameter susceptibility of DPPC-Chol bilayers as a function of Chol concentration.
In order to further investigate the phase behavior of simulated DPPC-Chol mixtures we analyzed the lateral organization of the Chol molecules in all the systems calculating the radial distribution functions (RDF) between center of masses of different Chol molecules in all the simulated systems. The two-dimensional RDF is defined as
where N(r) is the number of Chol molecules in a shell between r and r + Δr around central Chol molecule; and ρ is the number density of Chol molecules, taken as the total number of Chols per area of the simulation cell. Averaging was performed over every Chol in the system and over the sequence of snapshots of the evolving systems. Figure 11 shows RDF profiles for 6%, 12% and 33% Chol concentrations averaged over the last microsecond of these runs (for other concentrations RDF are qualitatively the same). From the Figure 11 we see that the RDFs have no regular structure for any of the simulated systems. In fact, the peak at 1 nm at 33 % Chol concentration has decreased in magnitude compared to the same peak in the initial configuration of the 33% system (data not shown). This RDF profile reflects cholesterol distribution in the first neighbor shell around each cholesterol, and shows no longer range correlation at any Chol concentrations.
Figure 11.
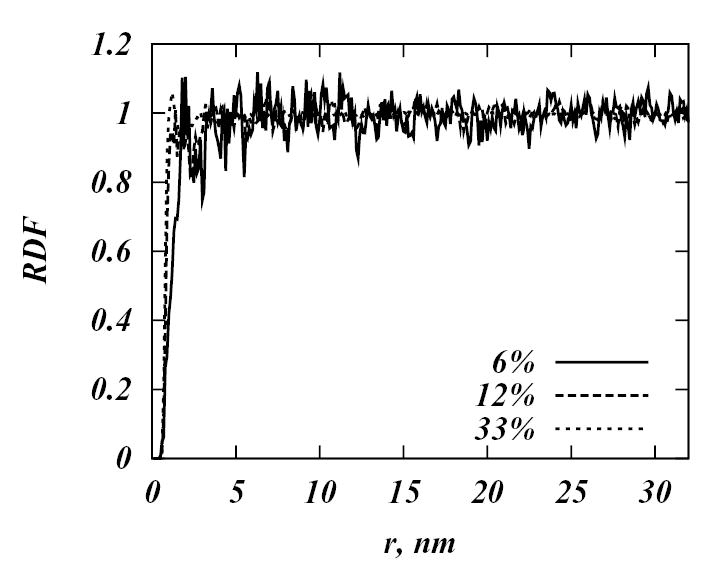
Radial distribution functions between center of masses of different Chol molecules for 6%, 12% and 33 % systems.
All the analysis carried out above points to the conclusion that, on the timescale of the simulations, it is impossible in this model to identify stable phase-separated regions rich in Chol that coexist with Chol-depleted regions in the simulated DPPC-Chol systems. Rather, the change in chain order with cholesterol concentration is continuous over the 20 μs time scale of the present simulations. We cannot rule out aggregation or phase separation, driven by weak lipid-mediated attractive interactions, on longer timescales. This is a subject for further investigation.
If the model predictions hold up over large timescales, a re-interpretation of experimental data is suggested, at least at 50° C. For example, two-phase coexisting regions on the temperature/composition diagram of DPPC-Chol bilayers in DSC experiments are obtained assuming that one can decompose the single complex endotherm of the main phase transition of DPPC-Chol bilayers into separate sharp and broad Gaussian curves. The sharp component is associated with chain-melting phase transition of low Chol low order fluid phase (Lα), and the broad component is related to melting of high Chol high order “liquid ordered” L0 phase4,6. Then, by monitoring the melting temperatures of each component at different Chol concentrations, the transition points and the two-phase coexisting regions on the temperature/composition diagram are determined4,6. Although association of a single endotherm with two Gaussian curves is a reasonable approximation, it is not the only possibility for decomposition of main transition endotherm.
Describing a single endotherm by two Gaussian curves is somewhat similar to putting a cut-off on lipid chain order parameters and assuming that lipid chains with order parameters below the cut-off belong to one phase, whereas the lipid chains with order parameters greater than the cut-off value belong to the other phase. For instance, when analyzing the coexistence of “liquid ordered” L0 and fluid Lα phases in DSC, the assumption is that the Lα phase consists of lipid chains whose order parameters are similar to that of pure PC fluid phase. All other chains belong to “liquid ordered” phase and they are described by relatively higher order parameters. When discussing the coexistence of L0α and L0β phases the similar procedure would apply. This time the lipid chains in L0α would be characterized by values lower than certain cut-off, and L0β phase would consist of chains with higher order.
Obviously, this procedure depends dramatically on the cut-off value. In order to demonstrate how different the results might vary depending on the cut-off value used, we have performed the following analysis on our simulated DPPC-Chol systems: we used seven different order parameter cut-offs, 0.19, 0.21, 0.23, 0.25, 0.27, 0.29 and 0.31 to span the whole spectrum of order parameter values (0.19 is approximately the highest value of the average order parameter field for a pure DPPC bilayer in the fluid phase Lα phase and 0.31 is the lowest value of the average order parameter field for pure DPPC bilayer in gel phase (see Figure 3)). For each cut-off we consider the chains with order parameters greater than the cut-off value as ordered and the regions with such chains is associated with “ordered” regions. All other regions are considered as “disordered”. To identify connected regions having similar local order parameters we utilized a recursive flood-fill algorithm45. For all the simulated systems we then calculated the fraction of chains in the largest “ordered” domain as a function of Chol concentration. The resulting plots are shown in Figures 12a and 12b. By examining these graphs we can identify the percolation threshold for each cut-off, i.e., for each cut-off value find the concentration of Chol when the entire system becomes “ordered”. From Figure 12a we see that as the cut-off value increases so does the percolation threshold. For 0.19 cut-off the threshold appears around 10 % Chol concentration. However, for 0.21 cut-off the critical concentration is around 20 %, for 0.23 cut-off value the percolation occurs at 30 % Chol. By further increasing the cut-off value defining the L0 phase (Figure 12b) no critical concentration can be found. The conclusion is that mapping the order parameter field in DPPC-Chol bilayers onto simpler binary model leads to arbitrary interpretations of phase coexistence depending on the definition of “ordered” and “disordered” regions4,6.
Figure 12a.
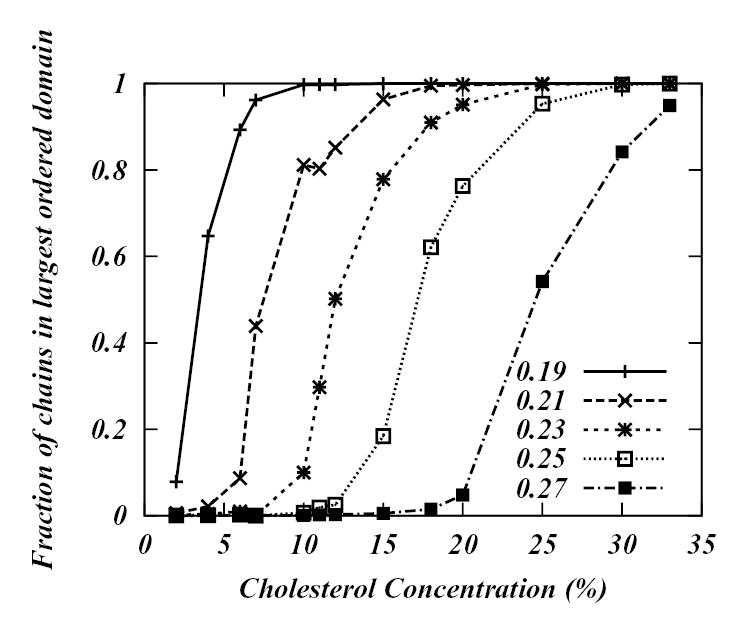
Fraction of chains in the largest “ordered” domain as function of Chol concentration for 0.19, 0.21, 0.23, 0.25 and 0.27 cut-off values.
Figure 12b.
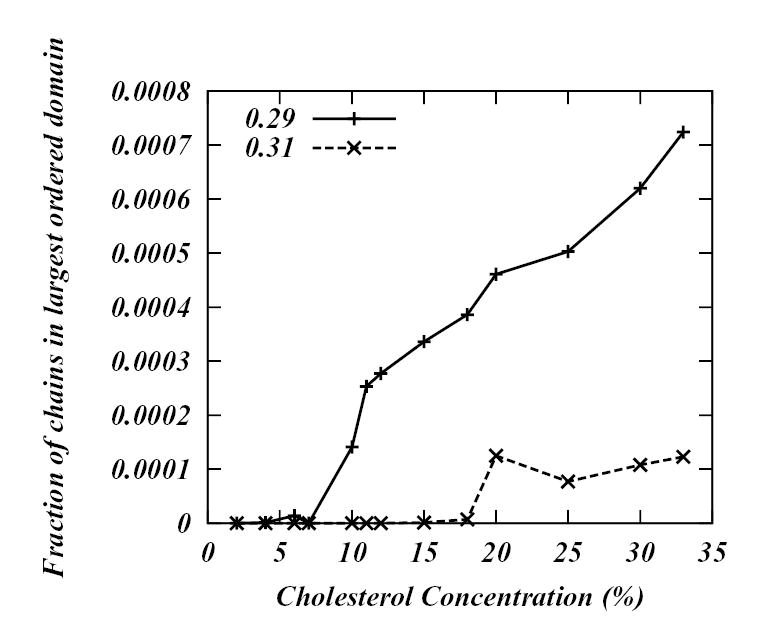
Fraction of chains in the largest “ordered” domain as function of Chol concentration for 0.29 and 0.31 cut-off values.
In conclusion, we have presented a coarse-grained dynamical self-consistent mean field model to study DPPC-Chol bilayer mixtures. Based on input from atomistic level MD simulations and extended by SCMFT to near-biological domains, the model is predictive in the nature of the lateral organization of ordered lipid domains and cholesterol molecules in DPPC-Chol bilayers, and thus has implications for the analysis of phase behavior in these systems. Based on the predictions of our model, we conclude that on a 20 μs time scale the ordering effect from single cholesterol molecule on lipid chains spreads as far as ~2.5 nm. At low Chol concentrations (2 % – 4%) islands of Chol surrounded by ordered lipids are randomly dispersed in Chol-free regions of lower order. As cholesterol concentration increases, regions of Chol-induced order overlap, giving rise to larger clusters of Chol surrounded by ordered lipids. At around 10–11% Chol concentration the order in the entire bilayer if effected by the presence of cholesterol molecules. Further increase in Chol composition leads to clusters of highly ordered lipid surrounding individual Chol molecules. Outside the clusters, regions of lower order are found. The linear size of the regions of lower order ranges from ~ 4 nm (at 33 %) to ~ 17 nm (at 11 %). Comprehensive analysis of the data indicates that this transition from a fluid-like Lα to an ordered L0 phase at 50α C is gradual. The free energy profile of the model showed a monotonic increase with increasing cholesterol concentration. The order parameter susceptibility revealed the existence of a broad region of relatively high values, which, again, is indicative of a gradual transition between Lα and L0 phases in our simulated systems.
Analysis of the lateral organization of Chol molecules via chi-squared tests and the plots of the radial distribution function profiles did not show any aggregation of Chol molecules in the simulated systems. The only attractive force between cholesterol molecules is the lipid-mediated interaction30 between cholesterols, which arises from the free energy gradients due to the order parameter field. At any given stage of the simulations (and at any Chol concentration) Chol molecules are surrounded by relatively ordered lipids. When two cholesterols are far apart, the order parameter distribution around each Chol is isotropic and thus there are only very small free energy gradients due to the order parameter field. As cholesterols move closer, the regions of Chol-induced order overlap. This creates larger gradients in the free energy and attractive interaction between two cholesterols. However, the largest value in magnitude of this interaction potential (corresponding to the situation when two cholesterols are one lattice site apart) is just of the order of thermal energy at 50° C, which is not sufficient to drive any Chol aggregation at least over 20 μs. We do not rule out a much slower rate of aggregation, especially at lower temperatures.
Because cholesterols remain relatively randomly distributed during the simulations, there is no appreciable change in average order parameter in the simulated systems. At no point in any of the simulations do we observe a higher degree of lateral organization, such as large, segregated domains or Chol-based superlattice structures5.
The theoretical model presented in this work promises to be a useful tool for studying lateral organization of cholesterol and ordered lipid domains in lipid/cholesterol bilayer systems. At this time, the application of the model is limited to the DPPC/Chol binary mixtures at temperatures above the main chain-melting phase transition temperature of pure DPPC bilayer. As a next step, we will extend the model to millisecond times, and to a range of temperatures. This way the predictions of the model may aid in filling the gap between theory and experiment for heterogeneous model biological membrane systems.
Acknowledgments
Research is supported by National Institutes of Health Grant RO1-GM 54651.
Appendix: Discretization of Stochastic Equations
This appendix describes the procedure for discretization of equations (10) and (11). First, the equation (10) is rewritten in two separate equations for x and y components of Chol center-of-mass radius-vector, . Using the lattice spacing/and the cholesterol diffusion constant D, we then construct the dimensionless timestep and coordinates:
| (15) |
With (15), stochastic equations (10) and (11) are discretized in the following manner:
| (16) |
| (17) |
| (18) |
where we defined two more dimensionless quantities:
Mr and Mφ are the cholesterol translational and rotational mobilities respectively, in (16)–(18) are Gaussian random variables with zero mean and unit variance.
References
- 1.L. Finegold Cholesterol in Membrane Models (CRC Press, Inc., Boca Raton, 1993).
- 2.Radhakrishnan A, McConnell H. Biophys J. 1999;77:1507. doi: 10.1016/S0006-3495(99)76998-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Pandit SA, Bostick D, Berkowitz ML. Biophys J. 2004;86:1345. doi: 10.1016/S0006-3495(04)74206-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.McMullen TPW, McElhaney RN. Biochim Biophys Acta. 1995;1234:90. doi: 10.1016/0005-2736(94)00266-r. [DOI] [PubMed] [Google Scholar]
- 5.Chong PLG. Proc Natl Acad Sci USA. 1994;91:10069. doi: 10.1073/pnas.91.21.10069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Vist MR, Davis JH. Biochemistry. 1990;29:451. doi: 10.1021/bi00454a021. [DOI] [PubMed] [Google Scholar]
- 7.Huang TH, Lee CWB, DasGupta SK, Blume A, Griffin RG. Biochemistry. 1993;32:13277. doi: 10.1021/bi00211a041. [DOI] [PubMed] [Google Scholar]
- 8.Mouritsen OG, Bloom M. Biohys J. 1984;46:141. doi: 10.1016/S0006-3495(84)84007-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Shimshick EJ, McConnell HM. Biochem Biophys Res Commun. 1973;53:446. doi: 10.1016/0006-291x(73)90682-7. [DOI] [PubMed] [Google Scholar]
- 10.McMullen TPW, Lewis RNAH, McElhaney RN. Biochemistry. 1993;32:516. doi: 10.1021/bi00053a016. [DOI] [PubMed] [Google Scholar]
- 11.Reinl H, Brumm T, Bayerl TM. Biophys J. 1992;61:1025. doi: 10.1016/S0006-3495(92)81910-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Scott HL. Current Opinion in Structural Biology. 2002;12:495. doi: 10.1016/s0959-440x(02)00353-6. [DOI] [PubMed] [Google Scholar]
- 13.Hofsäß C, Lindahl E, Edholm O. Biophys J. 2003;84:2192. doi: 10.1016/S0006-3495(03)75025-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Chiu SW, Jakobsson E, Mashl RJ, Scott HL. Biophys J. 2002;83:1842. doi: 10.1016/S0006-3495(02)73949-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Rog T, Pasenkiewicz-Gierula M. Biophys J. 2003;84:1818. doi: 10.1016/S0006-3495(03)74989-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Marrink SJ, de Vries AH, Mark AE. J Phys Chem B. 2004;108:750. [Google Scholar]
- 17.Shelley JC, Shelley MY, Reeder RC, Bandyopadhyay S, Klein ML. J Phys Chem B. 2001;105:4464. [Google Scholar]
- 18.Sengupta P, Singh RRP, Cox DL, Slepoy A. Phys Rev E. 2004;70:021902. doi: 10.1103/PhysRevE.70.021902. [DOI] [PubMed] [Google Scholar]
- 19.Murtola T, Falck E, Patra M, Karttunen M, Vattulainen I. J Chem Phys. 2004;121:9156. doi: 10.1063/1.1803537. [DOI] [PubMed] [Google Scholar]
- 20.Lyubatsev AP, Laaksonen A. Phys Rev E. 1995;52:3730. doi: 10.1103/physreve.52.3730. [DOI] [PubMed] [Google Scholar]
- 21.Lyubatsev AP, Karttunen M, Vattulainen I, Laaksonen A. Soft Materials. 2003;1:121. [Google Scholar]
- 22.Marčelja S. Biochim Biophys Acta. 1974;367:165. doi: 10.1016/0005-2736(74)90040-6. [DOI] [PubMed] [Google Scholar]
- 23.W. Maier and A. Saupe, Z. Naturforsch., Teil A, 13, 564 (1958)
- 24.P. J. Flory, Statistical Mechanics of Chain Molecules (Wiley-Interscience, New York, 1969).
- 25.K. Huang Statistical Mechanics (John Wiley and Sons, Inc., 1987).
- 26.P. M. Chaikin and T. C. Lubensky Principles of condensed matter physics (Cambridge University Press, Cambridge, 1995).
- 27.Elliot R, Katsov K, Schick M, Szleifer I. J Chem Phys. 2005;122:044904. doi: 10.1063/1.1836753. [DOI] [PubMed] [Google Scholar]
- 28.George A Khelashvili, Larry Scott H. J Chem Phys. 2004;120:9841. doi: 10.1063/1.1724814. [DOI] [PubMed] [Google Scholar]
- 29.Peng G, Qiu F, Ginzburg VV, Jasnow D, Balazs AC. Science. 2000;288:1802. doi: 10.1126/science.288.5472.1802. [DOI] [PubMed] [Google Scholar]
- 30.Marčelja S. Biochim Biophys Acta. 1976;455:1. doi: 10.1016/0005-2736(76)90149-8. [DOI] [PubMed] [Google Scholar]
- 31.Parrinello M, Rahman A. J Appl Phys. 1981;52:7182. [Google Scholar]
- 32.Nosé S, Klein ML. Mol Phys. 1983;50:1055. [Google Scholar]
- 33.Nosé S. Mol Phys. 1984;52:255. [Google Scholar]
- 34.Hoover WG. Phys Rev A. 1985;31:1697. doi: 10.1103/physreva.31.1695. [DOI] [PubMed] [Google Scholar]
- 35.Nagle JF, Tristam-Nagle S. Biochim Biophys Acta. 2000;1469:159. doi: 10.1016/s0304-4157(00)00016-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.M. Plischke and B. Bergerson, Equilibrium Statistical Physics 2nd Ed. World Scientific, Singapore, 1994.pp 86–89.
- 37.Schindler H, Seelig J. Biochemistry. 1975;14:2283. doi: 10.1021/bi00682a001. [DOI] [PubMed] [Google Scholar]
- 38.Gruen DWR. Biochim Biophys Acta. 1980;595:161. doi: 10.1016/0005-2736(80)90081-4. [DOI] [PubMed] [Google Scholar]
- 39.Scoville-Simonds M, Schick M. Phys Rev E. 2003;67:011911. doi: 10.1103/PhysRevE.67.011911. [DOI] [PubMed] [Google Scholar]
- 40.T. Schlick Molecular Modeling and Simulation (Springer, New-York, 2002).
- 41.M. P. Allen, and D. J. Tildesley Computer Simulation of Liquids (Oxford, New-York, 1987).
- 42.Gliss C, Randell O, Casalta H, Sackmann E, Zorn R, Bayerl T. Biophys J. 1999;77:331. doi: 10.1016/S0006-3495(99)76893-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Guo W, Kurze V, Huber T, Afdhal NH, Beyer K, Hamilton JA. Biophys J. 2002;83:1465. doi: 10.1016/S0006-3495(02)73917-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Radhakrishnan A, McConnell HM. Biochemistry. 2000;39:8119. doi: 10.1021/bi0005097. [DOI] [PubMed] [Google Scholar]
- 45.R. A. Plastock, and G. Kalley Schaum’s Outline of Theory and Problems of Computer Graphics (McGraw-Hill, 1986).
- 46.We also carried out a similar calculation in which the interaction between cholesterols and lipid headgroups was also taken into consideration (distributing this interaction evenly between the two hydrocarbon chains within a single lipid). Linear regression analysis did not produce an appreciably different result within error bars for Vlc compared to the calculations in which cholesterol-lipid headgroup interactions were neglected


