Molecular sieving in periodic free-energy landscapes created by patterned nanofilter arrays

Abstract

We present an experimental study of Ogston-like sieving process of rod-like DNA in patterned periodic nanofluidic filter arrays. The electrophoretic motion of DNA through the array is described as a biased Brownian motion overcoming periodically modulated free energy landscape. A kinetic model, constructed based on the equilibrium partitioning theory and the Kramers’ theory, explains the field-dependent mobility well. We further show experimental evidence of the crossover from Ogston-like sieving to entropic trapping, depending on the ratio between nanofilter constriction size and DNA size.

Perhaps the most important application of electromigration of polyelectrolytes in confining environments is the size fractionation of biomolecules with gel electrophoresis. Based on the ratio of the radius of gyration R_g of the molecule to the characteristic pore size a of the gel, three different separation regimes have been identified as Ogston sieving (R_g/a<1), entropic trapping (R_g/a~1), and biased reptation (R_g/a>1) [1]. In Ogston sieving, molecular sieving occurs because of steric hindrance of the molecules within the nanopore. Since R_g/a<1, the molecules move freely through the gel matrix, assuming their unperturbed coiled conformation. The standard model for interpreting mobility μ in the Ogston sieving regime is the so-called “extended Ogston model” [2], where the relative mobility μ^*, the ratio between the mobility μ in gel and the free solution mobility μ₀, of a molecule of given size is assumed to equal the partition coefficient K of the molecule in the gel (K revolves around excluded volume in general configuration space). Even though the assumption of μ^*=μ/μ₀=K has never been properly tested experimentally, largely because the mobility μ and the partition coefficient K of the molecule cannot be measured independently for a gel system, the extended Ogston model has been applied as the theoretical basis for the widely accepted empirical method proposed by Ferguson for determining the molecular weights of biomolecules [3]. As a near-equilibrium theory, the extended Ogston model is also known for failing to explain field-dependent mobility shifts that occur in a medium-to-high field gel electrophoresis [1, 3].

The theoretical study of sieving mechanisms in gel electrophoresis has been limited by the lack of well-controlled experimental platforms for correlating the size and shape of the sieving pores to the observed molecular dynamic behavior. Recently, various microfabricated structures have been proposed as an alternative to the gels [4]. These regular sieving structures have also proven ideal for theoretical study of molecular dynamics and stochastic motion in confining spaces [5]. More recently, patterned periodic nanofluidic filter (nanofilter) arrays were shown to provide fast separation of biomolecules such as proteins [6]. In this Letter, by using a theoretical model based on the equilibrium partitioning theory, we quantitatively characterized the sieving process of rigid, rod-like DNA (New England Biolabs, 50- to 1600-base pairs (bp)) in different microfabricated periodic nanofilter arrays. The nanofilter, which serves as the model pore-constriction system, consists of a deep region and a confining shallow region [Fig. 1]. The depth of the shallow region (d_s) is of the same order of magnitude as the size of probing DNA molecules. Details of the nanofilter array structure and fabrication are described in Ref. [6]. The nanofilter array was filled with Tris-Borate-EDTA 5× buffer to diminish the effect of electroosmotic flow [7]. For fluorescence detection, DNA were labeled with YOYO-1 dye (Molecular Probes) with a dye-to-bp ratio of 1:20; at this ratio, dye intercalation extends DNA length by about 6% [8].

FIG. 1.

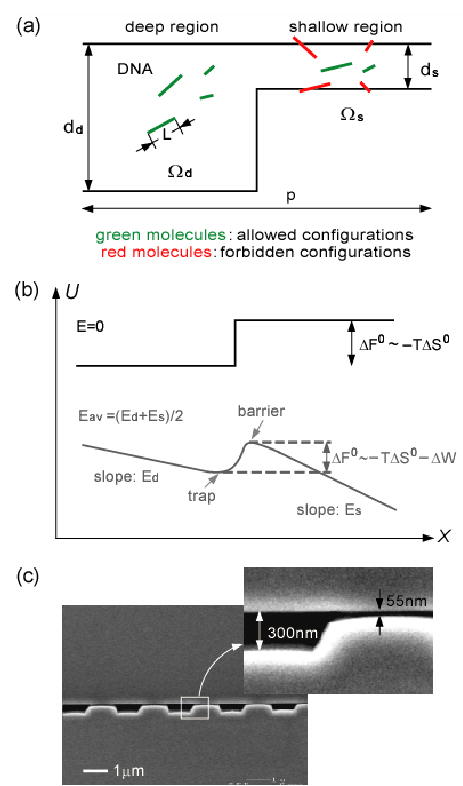
(a) Partitioning of rigid, rod-like DNA across a nanofilter that consists of a deep region (d_d) and a shallow region (d_s) of equal length. The period and width of one nanofilter is p and w, respectively. (b) Free energy landscapes experienced by DNA while crossing a nanofilter (black curve: E=0, grey curve: E_av>0). E_s, E_d: electric fields in shallow and deep regions, respectively. E_av: average electric field over the nanofilter. DNA preserve the free draining property in the shallow and deep region, resulting in the slopes for both regions proportional solely to the local electric field. (c) SEM images of alternating deep (300 nm) and shallow (55 nm) regions. p=2 μm.

The electrophoretic drift of DNA through the nanofilter is essentially an electric-field-driven partitioning process [1]. Compared with the high-entropy deep region, the limited DNA configurational space inside the shallow region creates a configurational entropic barrier for DNA passage at the abrupt interface between the deep and shallow regions [9]. This configurational entropic barrier originates from the steric constraints that prevent a partial overlap of DNA with the wall, and is different from the conformational entropic barrier associated with deformation and entropic elasticity [10]. The configurational entropic barrier is −TΔS⁰~−k_BTln(Ω_s/Ω_d) (T: absolute temperature, S⁰: configurational entropy, k_B: Boltzmann’s constant, Ω_s/Ω_d: ratio of accessible microscopic configuration state integrals within shallow and deep regions) [9]. By definition, Ω_s/Ω_d is equal to K (K=K_s/K_d), the ratio of the partition coefficients in the shallow and deep regions. The partitioning of rigid molecules in various nanopore geometries has been studied both analytically and numerically with geometrical and statistical arguments [9]. In the dilute solution limit, the partition coefficients K_i (i=s, d) of thin rod-like DNA of length L in both shallow and deep regions are calculated as

$$\begin{array}{ll}{K}_i=1-\frac{1+p_i}{2p_i}{\beta }_i+\frac{2{\beta }_i^2}{3\pi p_i}& (\beta \le 1)\\ K_i=\frac{1}{2{\beta }_i}-\frac{{\beta }_i}{2p_i}+\frac{2{\beta }_i^2}{3\pi p_i}+\frac{{\beta }_i}{\pi p_i}arccos\frac{1}{{\beta }_i}-\frac{1}{3\pi p_i}{({\beta }_i^2-1)}^{{}^1/_2}(2{\beta }_i+\frac{1}{{\beta }_i})& (1\le \beta \le p)\end{array}$$ (1)

where β_i=L / d_i (scaled molecular length) and p_i =w / d_i (scaled nanofilter width). For the DNA lengths tested (with contour length l and persistence length l_p), L can be safely treated as equal to the DNA’s mean end-to-end distance <R²>^½ calculated from the Kratky-Porod model [11]

$$L={\langle R^2\rangle }^{1/2}={\left\{2l{l}_p[1-\frac{l_p}{l}\{1-exp(-\frac{l}{l_p})\}]\right\}}^{1/2}$$ (2)

The motion of DNA through the nanofilter array can be described as a biased thermally activated process overcoming periodically modulated free energy barriers ΔF⁰ [Fig. 1(b)]. The free energy landscape U tilted by the electric field E_av contains local maxima (barriers) and minima (traps), similar to a double well potential [12]. We define τ_travel as the DNA drift time between two consecutive trapping events, so τ_travel=L/μ_maxE_av, where μ_max =4d_sd_sμ₀/(d_s+ d_s)² is the maximum sieving free mobility inside the nanofilter. μ_max is obtained by linearly extrapolating the mobility data μ to zero DNA length under various E_av. μ_max shows little variance and is practically independent of E_av. After DNA reaches a trap, it is trapped for a certain lifetime τ_trap before it enters the nanofilter constriction. The relative mobility μ* therefore can be written as μ*=μ/μ_max=τ_travel/(τ_travel+τ_trap).

Two energy terms are included in the barrier ΔF⁰ expression (ΔF⁰ =−TΔS⁰−ΔW) [Fig. 1(b)]. The positive −TΔS⁰ term accounts for the entropic energy increase for DNA entering a confining nanofilter constriction. The ΔW term accounts for the electrical potential energy drop in the translation of DNA over the nanofilter barrier along the field direction. Approximately, ΔW=NqE_avd_d (N: DNA bp number, q: effective charge per bp derived from μ₀) [13]. E_av effectively lowers the energy barrier in the field direction. When E_av→0, |TΔS⁰/ΔW|»1, the entropic energy dominates. This regime provides the greatest size selectivity, but the separation speed and thus efficiency are severely reduced. When |TΔS⁰/ΔW|«1, the trapping effect becomes negligible and no separation should be expected [6]. The optimized separation performance is expected when |TΔS⁰/ΔW|~1. Since ΔF⁰ in this regime is comparable to or larger than k_BT, k_esc, the escape transition rate for DNA to surmount the barrier, as well as the mean trapping time τ_trap, can be obtained from a simplified version of the Kramers’ theory for the overdamped regime [14]

$$k_{esc}^{-1}\sim {\tau }_{trap}\sim \gamma {\int }_{barrier}{e}^{U/k_{B}T}dx{\int }_{trap}{e}^{-U/k_{B}T}dx$$ (3)

where γ is the DNA friction constant and γ ~N. Based on the energy landscape U depicted in Fig. 1(b), τ_trap can be calculated as

$${\tau }_{trap}=\frac{\alpha N}{E_{av}^{2}K}exp(-\varepsilon )$$ (4)

where α is a constant with a unit of sec·V/(bp·m²) and ɛ is the reduced electric field (ɛ =ΔW/k_BT) [1]. The trapping time in Ref. [14] showed a similar dependence on $E_{av}^2.$

Mobility μ was determined by measuring an ensemble-averaged band migration time T_travel over thousands of nanofilters under various E_av. Figure 2(a) shows separation of 100-bp DNA ladder in an 80 nm nanofilter array. The experimental data of μ^* and τ_trap for 100-bp DNA ladder [Fig. 2(b)] and low molecular weight DNA ladder [Fig. 2(c–d)] agree well with the theoretical curves calculated from Eq. (4), especially in the regime of low field (E_av<30V/cm) and short DNA [15]. The best fitting constant α was found fairly constant for all the E_av. The near-equilibrium state of DNA crossing a nanofilter can be estimated with the reduced electric field ɛ [1]. When E_av<30V/cm, ɛ is less than 0.1 for DNA of one persistence length. The small ɛ values associated with low fields validate our near-equilibrium kinetic model, and further suggest the trivial role of the exponential term exp(−ɛ ) in Eq. (4) for fitting the experimental data in the low field regime. The $N/(E_{av}^{2}K)$ factor is explicitly derived from both the equilibrium partitioning (K) and the double well potential $(N/E_{av}^2)$, and clearly serves as the determinant for the fitting. The exp(−ɛ ) term only plays a role as E_av increases and thus ΔW becomes more comparable to the entropic barrier. From our kinetic model, the intrinsic size selectivity of the nanofilter array dμ*/dN(N→0) is calculated as dμ*/dN(N→0)~−(LE_av)⁻¹. Therefore reduced L decreases τ_travel and reduced E_av maximizes the entropic barriers, all accentuating the size-differentiating barrier surmounting process and leading to greater size selectivity [6]. Our kinetic model also implicitly defines a critical field ɛ_c above which the electric force overcomes the entropic force (ΔW>−TΔS⁰). By combining Eq. (1) and the expression of ΔW, we calculated ɛ_c in the short DNA limit to be independent of N and ${\varepsilon }_c\sim d_s^{-1}$, where d_s accounts for the nanofilter sieving property.

FIG. 2.

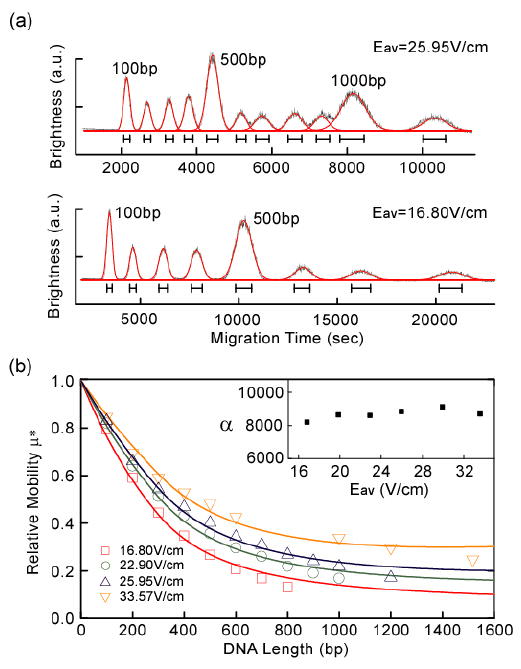
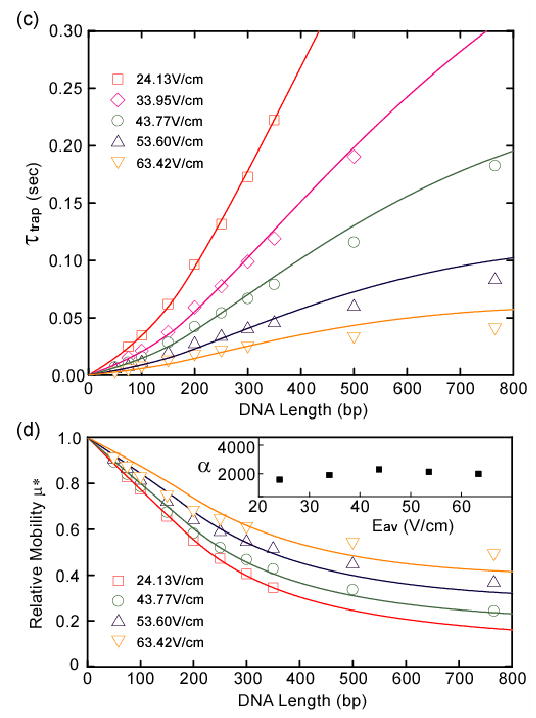
(a) 100-bp DNA ladder separated in a nanofilter array (d_s=80 nm, d_d=580 nm, and p=4 μm). Electropherograms (grey) were taken 1 cm from the injection point. Gaussian functions (red) were used for fitting and the black bars label the peak widths (±s.d.). (b) Relative mobility μ^* of 100-bp DNA ladder with solid fitting curves. The ±s.d. of μ* derived from the half peak width are all less than 4%, so statistical error bars for μ* are not plotted. The inset shows the best fitting constant α for different field strengths. α has a mean about 8684 and a ±s.d. about 3%. (c–d) Mean trapping time τ_trap (c) and relative mobility μ^* (d) with the best fitting curves. τ_trap and μ^* were measured for low molecular weight DNA ladder in a nanofilter array with d_s=55 nm, d_d=300 nm, and p=1 μm. Separation length was 5 mm and τ_trap=T_travel/5000−τ_travel. The ± s.d. of μ* are all less than 6%, so statistical error bars for μ* are not plotted. The inset shows α with a mean about 1990 and a ±s.d. about 13%. All the fitting curves in (b–d) are calculated with q=2.49 × 10⁻²¹ J/V·bp, l_p=53 nm, and l=0.36·N nm.

The experimental data in Fig. 2 deviated slightly from the theoretical curves as the DNA length increases to several persistence lengths. This is expected since for long DNA, other degrees of entropic freedom, such as internal conformation, become non-negligible in the kinetics of crossing the nanofilter barriers. The (conformational) entropic trapping mechanism was used to explain separation of long DNA (>5 kilobase pairs (kbp)) in similar intervening entropic barriers where longer DNA were found to advance faster than shorter ones because of their greater hernia nucleation possibility [16]. We demonstrate the crossover from Ogston sieving to entropic trapping by measuring mobility of DNA of a size ranging from 0.5–8 kbp in a 73 nm nanofilter array. The radius of gyration R_g of these DNA, estimated from the Kratky–Porod model, span a range of 40–220 nm, covering the region around R_g/d_s~1. Figure 3 clearly shows two distinct sieving regimes as evidenced by the valleys existing on the mobility curves. The left side of the valley is Ogston sieving, and μ decreases as DNA length increases. The right side shows evidence of entropic trapping, and μ increases with DNA length. The transition points under different E_av are all at about DNA of 1.5 kbp, where R_g(1.5 kbp)~80 nm, comparable to d_s=73 nm. This observation supports that the transition regime between Ogston sieving and entropic trapping is around R_g/d_s~1. E_av shows different effects on the trapping in the two regimes: in Ogston sieving, the higher barrier height associated with lower E_av leads to greater size selectivity (as seen with the steeper curves); as in entropic trapping, nanofilter shows little size selectivity at low E_av, but mobility curves become steeper as E_av increases. All the mobility curves reach a plateau as DNA length becomes larger than about 5 kbp. The complex field effect pattern near the transition regime cannot be explained by the simple kinetic model proposed in Ref. [16], and further more detailed characterization needs to be conducted.

Fig. 3.

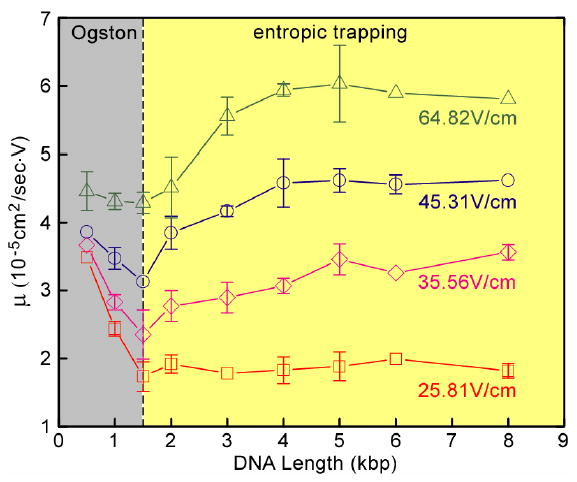
Mobility μ as a function of DNA length. DNA fragments were extracted after agarose gel separation. The nanofilter array has d_s=73 nm, d_d=325 nm, p=1 μm. The relative large statistical error bars (drawn if larger than the symbol) is likely due to the low DNA concentrations. The grey and yellow areas indicate Ogston sieving and entropic trapping, respectively. The transition points are marked with the vertical dashed line drawn for DNA length=1.5-kbp.

We acknowledge support from NSF (CTS-0347348), NIH (EB005743), and Singapore-MIT Alliance (SMA-II, CE program). J. Yoo was supported by the Caltech Summer Undergraduate Research Program. We thank P. Mao for helping take the SEM images.