Abstract
Lipid-coated perfluorocarbon nanodroplets are submicrometer-diameter liquid-filled droplets with proposed applications in molecularly targeted therapeutics and ultrasound (US) imaging. Ultrasonic molecular imaging is unique in that the optimal application of these agents depends not only on the surface chemistry, but also on the applied US field, which can increase receptor–ligand binding and membrane fusion. Theory and experiments are combined to demonstrate the displacement of perfluorocarbon nanoparticles in the direction of US propagation, where a traveling US wave with a peak pressure on the order of megapascals and frequency in the megahertz range produces a particle translational velocity that is proportional to acoustic intensity and increases with increasing center frequency. Within a vessel with a diameter on the order of hundreds of micrometers or larger, particle velocity on the order of hundreds of micrometers per second is produced and the dominant mechanism for droplet displacement is shown to be bulk fluid streaming. A model for radiation force displacement of particles is developed and demonstrates that effective particle displacement should be feasible in the microvasculature. In a flowing system, acoustic manipulation of targeted droplets increases droplet retention. Additionally, we demonstrate the feasibility of US-enhanced particle internalization and therapeutic delivery.
Keywords: Targeted imaging, targeted drug delivery, ultrasound, nanoparticles, nanodroplets, radiation force, acoustic streaming
Introduction
Perfluorocarbon emulsion nanoparticles are under investigation as ultrasound (US) contrast agents and ultrasonically enhanced drug delivery vehicles. With a mean diameter on the order of hundreds of nanometers, approximately 10-fold smaller than commercially available microbubble contrast agents, targeting of, and extravasation through tumor endothelium may be superior to microbubbles [1,2]. The speed of sound of the perfluorocarbon liquid contained within the particle is ~500 m/sec, significantly different from that of the surrounding plasma (~1500 m/sec). This liquid core distinguishes liquid-filled nanoparticles from solid nanoparticles, which are also considered as imaging and therapeutic agents [3,4]. When oil is incorporated into the core, hydrophobic chemotherapeutics can be solubilized in these droplets. Compared with microbubbles, liquid-filled nanodroplets are more stable under pressure and mechanical stress and are capable of carrying a larger drug payload, although they are also less echogenic. Both microbubbles and liquid-filled nanoparticles can be encapsulated by a molecularly targeted lipid shell.
Adhesion of targeted US agents has been demonstrated for angiogenic, ischemic, and thrombolytic tissues [5,6]. Lanza and coworkers have described the use of perfluorocarbon emulsion nanoparticles as US contrast agents [7–9] and have developed theoretical models for estimating acoustic reflectivity of different perfluorocarbon nanoparticle formulations [10–14]. Nanoparticles have low acoustic reflectivity in solution; however, their echogenicity increases when they are deposited in a layer, resulting in a targeted contrast agent that is detectable only when adherent at the target site [9]. Perfluorocarbon nanoparticles can also serve as magnetic resonance imaging (MRI) contrast agents when gadolinium is incorporated into their lipid shell, so they may be useful for multimodality imaging studies [15–21]. In addition to their application as US contrast agents, perfluorocarbon nanoparticles have also been used as therapeutic delivery vehicles for doxorubicin, paclitaxel, and other therapeutic agents [8,22,23]. Crowder et al. [24] have shown that US enhances transmembrane delivery of fluorescent dye from nanoparticles to C32 melanoma cells.
Ultrasonic molecular imaging is unique in that the optimal application of these agents depends not only on the surface chemistry, but also on the applied US field, which can increase receptor–ligand binding and membrane fusion [25–27]. Dayton et al. [26] and Rychak et al.[25] have previously demonstrated that acoustic radiation force produced by US can enhance the efficiency of targeted imaging with microbubble-based agents by deflecting targeted particles to the endothelium and facilitating bond formation. Lum et al. [28] and Shortencarier et al. [29] have demonstrated that physically localizing drug delivery vehicles with acoustic radiation force can enhance localized drug delivery. Recently, Crowder et al. [24] have observed acoustically enhanced dye delivery from perfluorocarbon nanoparticles and postulated that acoustic radiation force is partially responsible for this effect. However, to date, previous studies of radiation forces on imaging and drug delivery vehicles have examined only gas-core type agents rather than liquid perfluorocarbon agents. Although radiation forces can deflect gas-filled particles with low time-averaged acoustic intensity, a greater intensity is required to deflect liquid and solid particles. At these greater intensities, the effect of radiation force directly on the bulk fluid produces fluid movement known as acoustic streaming. Acoustic streaming and the radiation force on the particle each produce particle translation in the acoustic field and their effects can be combined. Nightingale et al. have shown that a clinical US system can produce streaming of bulk fluid in breast cysts with a diameter on the order of millimeters [30]. Measurements by Shi et al. [31,32] indicate that the translational velocity produced by acoustic streaming in millimeter vessels decreases with decreasing vessel diameter. In this article, we focus on the characterization and optimization of the US field in localizing the particles on the cell surface. This complex process is nearly independent of the surface chemistry and requires a fundamental and separate evaluation.
We evaluate the feasibility of using US to enhance the concentration of perfluorocarbon nanoparticles through several studies. First, the velocity of translating nanoparticles in an acoustic field is quantified as a function of acoustic parameters, and this dependence is compared with a theory describing radiation force on droplets and bulk fluid. Analytical methods are used to extend our experimental results to predict translation in smaller vessels in which radiation force is assumed to dominate. Second, we demonstrate the increased adhesion of targeted nanoparticles in a flowing system in response to application of US. Third, we demonstrate spatial localization of nanoparticles on a cell monolayer with US, and subsequent delivery of a fluorescent dye or drug from the nanoparticles to the cells. Lastly, we demonstrate the cytotoxic effect produced when US and drug-carrying nanodroplets are combined, and the absence of toxicity in the presence of US alone.
Theory
Sound propagating through a medium produces a force upon the medium itself, resulting in translation of the fluid, called acoustic streaming, and also on particles suspended in the medium, called radiation force. Acoustic radiation force has been studied in detail since the 19th century, and new applications for this force have arisen with the recent application of bubbles and droplets being considered as US contrast agents and drug delivery vehicles. The radiation force produced on small spheres in an acoustic field has been discussed in detail by Shi et al. [31,32], Alekseev [33], Bjerknes [34], Doinikov [35–38], King [39], Nyborg [40], Yosioka and Kawasima [41], Wu and Du [42,43], among others. A recent review by Doinikov [44] summarizes much of the development and current state of theory regarding acoustic radiation forces. Here, models for radiation force and streaming are examined to evaluate the contributions of these forces to the velocity of liquid-filled droplets when insonified.
The goal for ultrasonic displacement of nanoparticles is to induce a cross-vessel displacement (as shown in Figure 1A) increasing the adhesion of targeted particles to the vessel wall (Figure 1B). The US beam has a finite width, on the order of millimeters to centimeters, and therefore this displacement must be accomplished in the time interval over which a particle crosses the beam. Ideally, a cross-vessel velocity on the order of micrometers per second (or greater) would allow a particle to cross a capillary as it crosses the beam.
Figure 1.
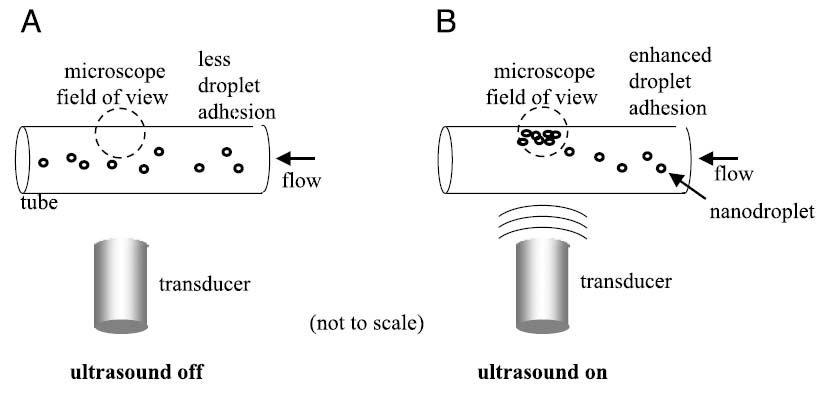
Illustration of the effect of radiation force and streaming force on targeted agents with US. (A) Without acoustic force, the majority of the contrast agents fail to contact the target site and therefore do not bind. (B) Ultrasound pushes flowing targeted agents into contact with cells along a vessel wall where they bind to target receptors.
For a droplet such as those studied in this article, the radiation force due to a traveling wave can be written as:
| (1) |
The resulting translational velocity produced by radiation force on a droplet is considered in the Appendix and approximated as Equation 2.
| (2) |
Based on Equations 1 and 2, radiation force and the resultant particle velocity vary linearly with frequency and intensity, have a nonlinear dependence on particle size, are dependent on particle impedance, and are independent of the vessel geometry. Numerical evaluation of Equation 2 can be used to estimate the translation of a droplet due to radiation force for any set of parameters (Figure 2). For a perfluorohexane droplet insonified at 10 MHz and an Ispta of 480 mW/cm2, Kong et al. [2] predict that a particle diameter of 500 nm or greater would be required for translation on the order of 10 μm/sec due to radiation force. To achieve the same translational velocity, a droplet of 200 nm diameter must be insonified with an Ispta of 3500 mW/cm2.
Figure 2.
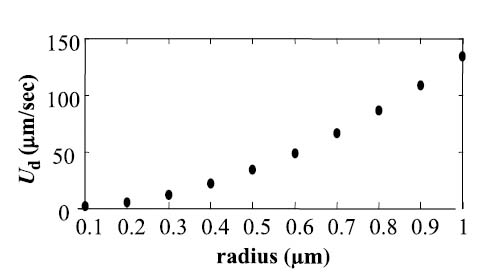
Simulations of translational velocity of perfluorohexane nanodroplets from radiation force component only at 10 MHz and 480 mW/cm2 for varying R0.
The bulk fluid surrounding the droplet is also affected by the acoustic field. For a plane wave propagating in an infinite medium, Nightingale and Trahey provide the expression for the acoustic streaming force [30].
| (3) |
The acoustic streaming force is proportional to temporal average acoustic intensity at the interrogation point and is a function of the acoustic frequency due to the frequency-dependent absorption coefficient α. For a spatial region where there is minimal variation in the intensity, such as the small optical field of view in experiments described in this article, I is approximately equivalent to the spatial peak intensity. The velocity of the fluid resultant from this force can thus be expressed as Equation 4 [31], assuming the streaming occurs in water where the absorption coefficient can be written as α0f2 [45] and that the vessel cross sectional area is large (assuming normal incidence) [31].
| (4) |
Experimental results are highly dependent on the geometric factor G, which describes the beam and media in which the streaming occurs. Expressions for streaming-induced cross-vessel velocity have not yet been derived for a vessel with a diameter on the order of the microcirculation; however streaming velocity was shown to be decreased for smaller diameter tubes [31]. Shi et al. demonstrated that the effect of the boundary conditions can substantially affect the streaming velocity in a constrained volume. The acoustic streaming produced in water (Equation 4) is predicted to vary as a function of the square of the center frequency, to be linearly dependent on transmitted intensity, is independent of particle size and properties, and is dependent on the vessel geometry.
Our experiments will evaluate the relative magnitude of the translational velocity due to radiation force and streaming within vessels on the order of hundreds of micrometers to millimeters in diameter.
Materials and Methods
Nanoparticles
In this study, we consider perfluorocarbon nanoparticles designed for therapeutic delivery and produced by ImaRx Therapeutics (Tuczon, AZ), which are 270 ± 90 nm in diameter. The nanoparticles contain a core of at least 50% liquid perfluorocarbons and a mixture of triacetin and soybean oils. The oils serve as a carrier medium for hydrophobic drugs such as the chemotherapeutic paclitaxel. Droplets were stabilized by a lipid membrane containing dipalmitoylphosphatidylcholine (DPPC), dipalmitoylphosphatidyl-ethanolamine polyethylene glycol MW 5000 (DPPE PEG5000), and dipalmitoylphosphatidic acid (DPPA), 82:10:8, m/m/m (the total lipid concentration was 0.5 or 1 mg/mL). The perfluorocarbon mixture in the droplet core consisted of 90% perfluorohexane and 10% perfluoropentane or 100% perfluorohexane, which had nearly identical size distributions. The physical properties of these materials are detailed in Table 1. The properties of the perfluorocarbon liquids are similar, with a lower speed of sound than water or blood and higher than gas.
Table 1.
| Material* | Density (kg/m3) | Compressibility (m2/N) | Viscosity (kg/msec [cP/1000]) | Sound Speed (m/sec) | Boiling Point (°C) | Impedance (kg/m2 sec [× 10−6]) |
|---|---|---|---|---|---|---|
| Air | 1.2 | 7.0 × 10−6 | 0.000018 | 340 | −195 | 0.0004 |
| Perfluoropentane (C5F12) | 1660 | † | 0.00065 | 471 | 29 | † |
| Perfluorohexane (C6F14) | 1700 | 2.5 × 10−9 | 0.00067 | 520 | 56 | 0.88 |
| Water | 1000 | 4.6 × 10−10 | 0.001 | 1480 | 100 | 1.48 |
Values listed at 20–25°C and 1 atm.
Indicates properties not available.
For measurements of the translational velocity and concentration of nanoparticles, a carbocyanine dye solution (Vybrant DiI V-22885, Molecular Probes, Eugene, OR) was added to the droplet composition at 1 wt% to allow enhanced tracking of the particles.
Dynamic targeting experiments were conducted with droplets incorporating 5 wt% biotin in the lipid shell, and experiments were conducted within an avidin-coated cellulose tube as described below. For comparison to solid particles, 0.5-μm-diameter polystyrene beads were substituted for nanodroplets (Polybead, Polysciences, Warrington, PA).
For confocal microscopy, targeted nanodroplets were formulated with triacetin in which the fluorescent drug Oregon Green paclitaxel had been solubilized at a concentration of 17 μM. Cell viability studies were performed with these paclitaxel-carrying droplets.
Ultrasound
For all studies, US was produced with either a 10, 5, 2.25, or 1 MHz ¾-in. single-element transducer spherically focused at 2-in. (IL1006HP, IL0506HP, IL0206HP, IL0106HP; Valpey Fisher, Hopkinton, MA). All transducer −6 dB bandwidths were on the order of 15–20%. The −6 dB beam width at the transducer focus, where samples were placed, was approximately 0.4, 0.8, 1.8, or 4 mm, at 10, 5, 2.25, and 1 MHz, respectively. Ten-cycle rectangularly windowed waveforms were utilized in all experiments, produced by an arbitrary waveform generator (AWG2021, Tektronix, Irvine, CA). Signals were amplified for transducer excitation with an RF amplifier (3200L, ENI, Rochester, NY). Acoustic pressure measurements and simultaneous optical and acoustical alignment were performed with a calibrated needle hydrophone (PZT-0400, Onda Corp, Sunnyvale, CA).
Ultra-high-speed Photography
The use of ultra-high-speed photography is well documented as a method to analyze the effect of acoustic energy on US contrast agents [51–53]. The radius–time oscillation and translation of an individual microbubble contrast agent can be observed at high frame rates. The same techniques applied previously to microbubble contrast agents were applied to nanoparticles in this study to assess nanoparticle response to US. An Imacon 468 (DRS Hadland, Cupertino, CA) high-speed camera system coupled to an Olympus IX-70 (Melville, NY) microscope was used to optically record the nanoparticle behavior. Magnification was provided by a water-immersion Achroplan 100× with a numerical aperture of 1.0 (Carl Zeiss, New York, NY). A 10-MHz spherically focused transducer was positioned such that the beam focus overlapped the optical focus; thus, objects in the optical focus were exposed to peak pressures from the transducer. Nanoparticles were manually microinjected into a 200-μm cellulose tube that constrained the droplets and allowed them to be positioned in the optical focus. The cellulose tube (Spectrum Laboratories, Rancho Dominguez, CA), with a wall thickness on the order of 10 μm, was nearly optically transparent and relatively non-echogenic. Nanoparticle dilution in water provided on the order of 10–20 nanoparticles per optical field of view. Larger droplets, with diameters on the order of 500–1000 nm were chosen for high-speed photography studies because smaller droplets were below the resolution of the optical system. Optical streak images showing the diameter of a droplet over time were recorded during the incidence of the acoustic pulse on the droplets.
Particle Tracking for Velocity Measurements
Measurements of translational velocity of nanoparticles in an acoustic field were made using a similar microscopy system described for ultra-high-speed imaging. A 0.7-mm-diameter polyester tube (Advanced Polymers, Salem, NH) that was nearly optically transparent and weakly echogenic was placed into the mutual acoustical–optical focus. Nanoparticles were injected into the tube with a manual microinjector (Narishige International, East Meadow, NY), and the flow through the tube was stopped. A 600-frame/sec camera (Motion-corder Analyzer, Redlake, Tucson, AZ) recorded the movement of the droplets during repeated insonation. The tube position was adjusted so that the region of observation was at the center of the tube and the droplet direction was perpendicular to the transducer face. Particle velocity was measured by off-line analysis of recorded video frames.
Measurements were conducted for four center frequencies (10, 5, 2.25, and 1 MHz) and three acoustic intensity levels (480, 240, and 120 mW/cm2) within a 0.7-mm tube in order to explore the effect of center frequency and intensity on nanodroplet translation. Within each experiment of constant intensity, the pulse repetition frequency (PRF) was varied to examine the effect of acoustic pressure. At 480 mW/cm2, the PRF values included 4, 8, 16, and 32 kHz. For 240 and 120 mW/cm2, the PRF values were reduced by an additional factor of 2 or 4, respectively. Data sets consisted of velocities averaged over 5 to 10 droplets.
For studies of the effect of center frequency, acoustic intensity was held constant while varying the frequency. Because the pulse length was fixed at 10 cycles, reducing the center frequency required decreasing the acoustic pressure to maintain constant intensity.
For studies of the effect of acoustic intensity, acoustic pressure was maintained constant, and pulse repetition frequency was varied. These experiments also provided information as to the effect of acoustic pressure, which was varied inversely to PRF in order to maintain constant intensity.
Acoustically Mediated Adhesion of Targeted Nanoparticles
To evaluate the ability of US to concentrate targeted nanoparticles in a flowing system, we examined the accumulation of fluorescent biotin-targeted nanoparticles on a 200-μm avidin-coated cellulose microtube, similar to studies described in Ref. [27]. A 10-MHz transducer and the microscope objective were mutually focused on the sample volume. The sample volume containing flowing nanoparticles was observed for 30 sec without US, 30 sec with US, and 30 sec after the US had been removed. Flow in the tube was maintained at a mean velocity of approximately 9 mm/sec. Acoustic intensity applied was approximately 1300 mW/cm2. Images of the tube were acquired by using an inverted fluorescence microscope (IX71, Olympus) and a cooled CCD camera system (CCD-300, Dage-MTI, Michigan City, IN) with fixed gain and black level settings. The mean fluorescence intensity of the tube wall over time was measured off-line using MATLAB (Mathworks, Natick, MA). Data were averaged over 12 experiments. Figure 1A and B illustrate the experimental system for measuring adhesion of flowing nanoparticles with and without US.
Acoustically Enhanced Delivery of a Fluorescent Dye to Cell Monolayers
To quantify the relative transfer of a fluorescent dye to cell membranes using the combination of US and perfluorocarbon nanoparticles, a set of in vitro dye-transfer experiments were conducted. These experiments utilized custom chambers consisting of a steel frame that holds approximately 1 mL of liquid between two 25-mm coverslips made of Thermanox (Nalge Nunc, Rochester, NY). Human prostate carcinoma cells (PC3) were deposited on one of the Thermanox coverslips and grown to confluence in an incubator (MCO-17AIC, Sanyo, Bensenville, IL) prior to the experiment. Targeted nanoparticles were loaded with the fluorescent dye DiI that fluoresces weakly in water, is well retained in cell membranes, and demonstrates very little cell-to-cell transfer [54]. Nanoparticles were diluted 25 μL to 1 mL in phosphate-buffered saline (PBS) before addition to the chamber. For each experiment, a 1-mL solution of diluted perfluorocarbon nanoparticle solution was injected into a static chamber. The static chamber was mounted in a polycarbonate tank containing an ultrasonic transducer such that the acoustic focus was at the center of the cell monolayer. The tank was filled with distilled water and maintained at 37°C. A 0.5 cm-thick block of acoustically absorbent rubber (Aptflex F28, Precision Acoustics Ltd, Dorchester, UK) was placed in the tank behind the chamber in the rear of the box in order to minimize multiple reflections. Acoustic energy was applied at 10, 5, 2.25, or 1 MHz, at 2.4 W/cm2, for 2 min. After insonation, the chamber was removed from the tank and disassembled, and the coverslips were thoroughly rinsed with PBS to remove the majority of free droplets. The coverslips were then examined by fluorescence microscopy. Fluorescence images were acquired with a Cascade 512b CCD camera mounted on a Mikron IV600L microscope. Regions of interest (ROIs) were chosen based on the beam width of 10-MHz insonation, and this ROI was used across all frequencies to normalize for the effect of beam width. The exposure, magnification, and camera gain were kept constant across all samples. Mean pixel intensity was calculated off-line using MATLAB. Fluorescence intensity in the ROI was assumed to correlate with density of the fluorescent nanoparticles. Two cell plates were analyzed for each parameter set.
Studies of Droplet Internalization
Confocal microscopy was utilized to determine the localization of the drug carried within the nanoparticles after insonation. Sample preparation was identical to that described above, except that the nanodroplets contained Oregon Green paclitaxel, and studies were limited to 5-MHz insonation. After US exposure, the cells were returned to the incubator for 30 min, after which they were removed and observed with a Zeiss LSM-5 confocal microscope. Stacks of 20 images with a 1.0-μm step size were recorded using a 60× oil-immersion objective (NA = 1.3) to allow assessment of localization for the Oregon Green paclitaxel.
Cell Viability after Ultrasound Exposure
Cell viability 5 min after US exposure was determined by trypan blue exclusion. Coverslips containing PC3 monolayers were stained with 30 μL of trypan blue and were then examined with low-magnification (5×) color video microscopy. The quantity of trypan blue stained (nonviable) cells for each case was quantified using image processing software (ImagePro, Media Cybernetics). Studies were performed in cases where the cells were treated with US only, US plus paclitaxel-carrying droplets, and paclitaxel-carrying droplets only.
Statistics
Statistical differences in the data were determined by the two-sided Student’s t test for unequal variances. Statistical significance was determined by p < .05.
Results
High-speed Photography
Ultra-high-speed photography (10 ns time resolution) of near-micrometer-sized nanoparticles demonstrated that perfluorocarbon nanoparticles oscillated very little at the acoustic pressures used in this study (Figure 3). The ~900-nm-diameter nanoparticle (Figure 3B), insonified with a 10-cycle, 10-MHz acoustic pulse at 3 MPa, oscillates with a maximum expansion that is barely detectable beyond its resting diameter (less than 5%). In comparison, a 4-μm-diameter microbubble (Figure 3A) insonified with a 20-cycle, 2.25-MHz acoustic pulse at 180 kPa oscillates with a maximum expansion 100% greater than its resting diameter. The displacement of the microbubble due to acoustic radiation force during the acoustic pulse is on the order of 3 μm, whereas the displacement of the nanoparticle during the acoustic pulse is negligible. The US parameters used in these examples were selected to maximize the effect on each type of particle. Oscillation and displacement of the microbubble have been previously shown to be larger at lower frequencies [51].
Figure 3.
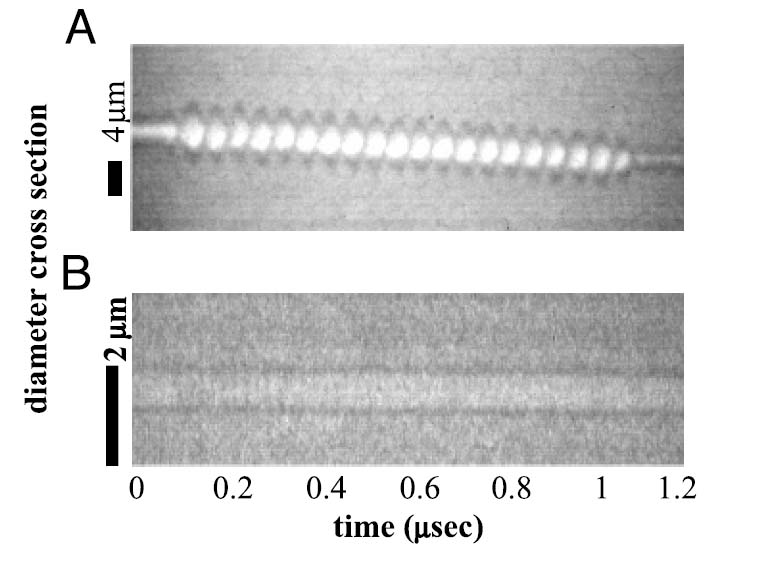
(A) Radius – time oscillation of a 2-μm-radius microbubble in response to a 180-kPa acoustic pulse at 2.25 MHz. (B) Radius – time oscillation of a 450-nm-radius nanoparticle in response to a 3-MPa acoustic pulse at 10 MHz.
Ultrasound-induced Nanoparticle Translation
Increasing center frequency while maintaining constant Ispta increased translation velocity in all cases (p < .05) (Figures 4 and 5). In general, droplet velocity was proportional to the transmitted frequency squared, although for matched intensities, a small increase in translational velocity was observed as the acoustic pressure increased (see Figure 4). For a transmitted intensity of 480 mW/cm2, linear fits to the logarithmic data indicate that the droplet translation velocity increased as a function of center frequency to the nth power, where n was measured to be 2.1, 2.2, 2.2, and 2.3 for 32, 16, 8, and 4 kHz studies (R2 values were 0.97, 0.97, 0.94, and 0.94), respectively.
Figure 4.
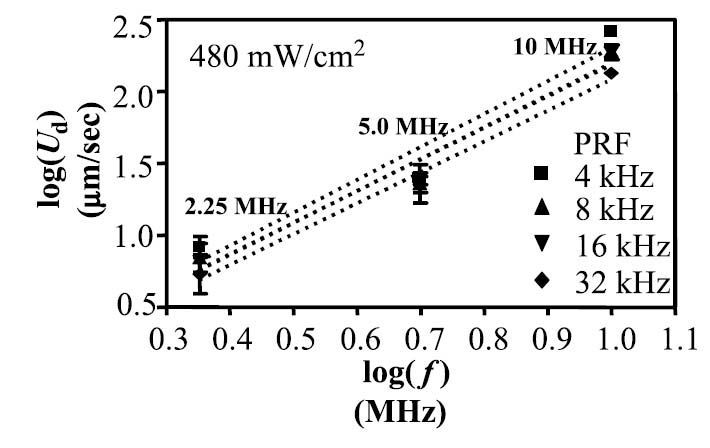
Translational velocity in micrometers per second of insonified nanodroplets for 10, 5, and 2.25 MHz. Data are illustrated for four cases of varying PRF. In each case of increasing PRF, acoustic pressure was decreased accordingly to maintain a constant acoustic intensity of 480 mW/cm2.
Figure 5.
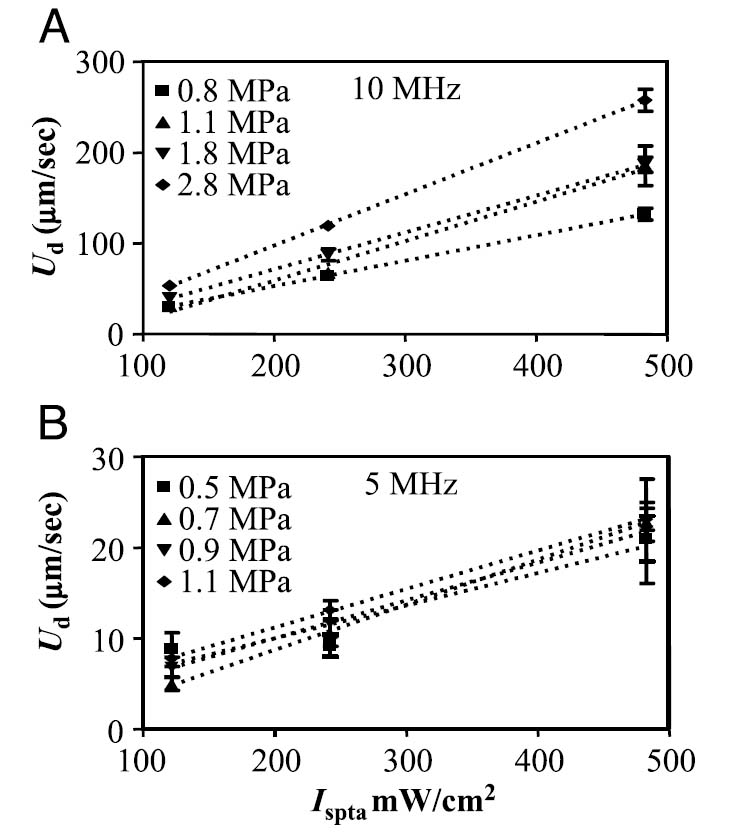
Translational velocity in micrometers per second of insonified nanodroplets for 10 (A) and 5 MHz (B), as a function of acoustic intensity. For each increasing intensity, PRF was increased accordingly to maintain constant pressure. Data are shown for four different values of pressure.
Translational velocity varied linearly as a function of transmitted intensity for matched acoustic pressures and fixed center frequencies, obtained by varying PRF (see Figure 5). Increasing the transmitted intensity significantly increased the translational velocity as compared with lower intensities in all cases (p < .05). Data for a 10-MHz center frequency are shown in Figure 5A, and for 5 MHz in Figure 5B. Linear fitting of the data resulted in R2 values of 1.0, 0.99, 0.99, and 0.99 for 10-MHz transmission at 0.8, 1.1, 1.8, and 2.8 MPa, respectively, and for the 5-MHz center frequency, 0.91, 0.99, 0.99, and 0.99 for intensities of 0.5, 0.7, 0.9, and 1.1 MPa, respectively. Translational velocities were below measurable resolution at 2.25 MHz for intensities less than 480 mW/cm2, so the data are not shown.
Nearly all nanodroplets suspended in the solution were observed to translate at approximately the same velocity. Rarely, larger “micro” droplets, with a diameter on the order of 1 μm, were observed. These microdroplets were displaced to the wall of the vessel at a velocity substantially greater than the majority population of droplets in the 300-nm-diameter range. During this experiment, it was observed that once localized along the vessel wall, nanoparticles often aggregated but did not fuse, similar to the aggregation of bubbles observed due to secondary radiation force.
Concentration of Targeted Nanoparticles Using Ultrasound in a Flowing System
Ultrasound was shown to significantly increase the brightness intensity of a 200-μm phantom vessel by displacement of fluorescent targeted nanodroplets from the 9-mm/sec flow stream to the vessel wall. Sections of the tube were observed with fluorescence microscopy for 30-sec periods with, without, and after insonation at 10 MHz and 2.4 W/cm2 (Figures 6A–C). Without US, the fluorescence intensity did not increase above baseline. During insonation, the fluorescence intensity on the tube wall opposite the US source increased over 100-fold as fluorescent nanoparticles accumulated on the wall surface. After US was removed, some of the nanoparticles were washed off by the fluid flow, and mean fluorescence intensity decreased by a factor of 2 over 30 sec. The average fluorescence intensity of 12 tube sections was significantly higher immediately and after 30 sec after US application (Figure 7) (p < .05).
Figure 6.

(A – C) Fluorescence microscopy images illustrating the buildup of fluorescent material from targeted nanodroplets along the wall of a 200-μm vessel due to US.
Figure 7.
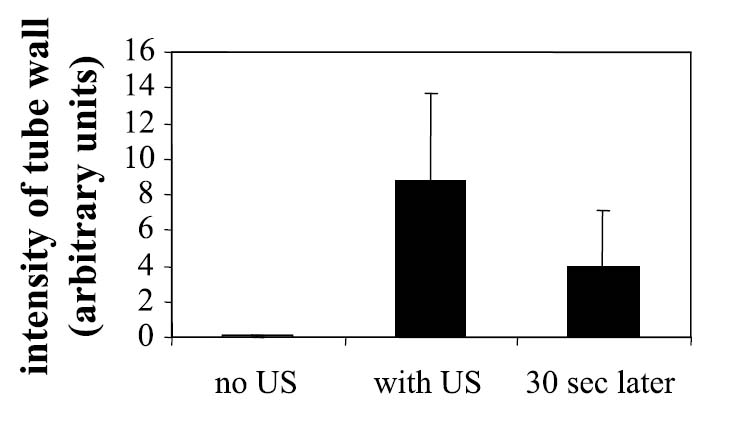
Relative brightness of a phantom vessel through which fluorescent nanoparticles are flowing over 30-sec intervals without the application of US, with US, and after US has been removed.
Application of Ultrasound to Spatially Concentrate Nanoparticles on a Cell Monolayer
Ultrasound substantially increased the localization of fluorescent targeted nanoparticles on a monolayer of PC-3 cells. Images of the cell monolayer obtained after a 2-min exposure to US with a 5-MHz center frequency and Ispta of 2.4 W/cm2 (Figure 8A) were compared to images obtained from monolayers prepared identically, except without US exposure (Figure 8B). Following US exposure and washing, cells at the acoustic focus were covered with adherent nanoparticles, in contrast to cells not exposed to US, which retained few or no nanoparticles (camera gain settings were optimized for imaging higher concentrations of nanoparticles after US, hence residual concentrations of nanoparticles that may have been present without US were not obvious). Additionally, after insonation, cells in the acoustic sample volume incorporated the membrane dye carried by the nanoparticles, in contrast to cells outside of the acoustic volume that remained unstained. Without insonation, incubation with nanoparticles over the same 2-min period (followed by washing) did not result in an increase in fluorescence intensity above baseline.
Figure 8.
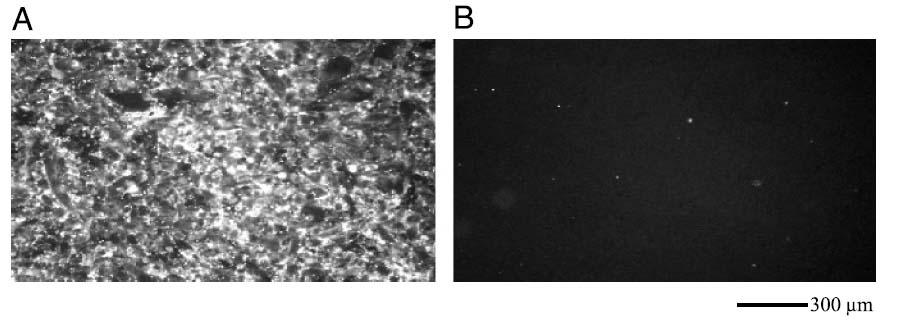
Fluorescence microscopy of PC3 monolayers exposed to targeted nanodroplets containing DiI and (A) US treatment at 5 MHz and 2.4 W/cm2 for 2 min and (B) no US.
The efficacy of US to concentrate nanodroplets on a cell monolayer was demonstrated across the range of frequencies tested (10, 5, 2.25, and 1 MHz) with an intensity of 2.4 W/cm2 (Figure 9), although the magnitude of concentration was most substantial at the 5-MHz center frequency (p < .05).
Figure 9.
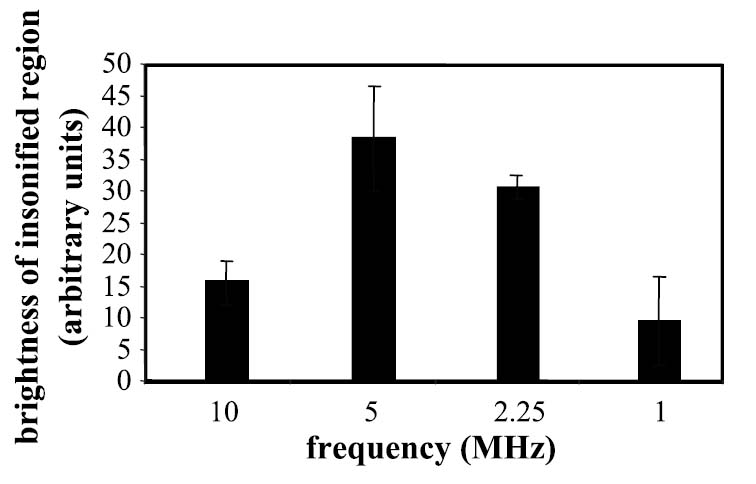
Brightness of PC3 cells exposed to fluorescent targeted nanodroplets and US at 10 kHz and 2.4 W/cm2, with center frequencies varying from 10, 5, 2.25, to 1 MHz.
Intracellular Delivery of Fluorescent Paclitaxel
Confocal microscopy of cells within the insonified region indicated that nanoparticles were not only concentrated on the cell surface, but also that the nanoparticle contents were internalized within the cell (Figure 10) after insonation. One-micrometer optical slices acquired through the cell center revealed the presence of the Oregon Green paclitaxel within the cell cytoplasm.
Figure 10.
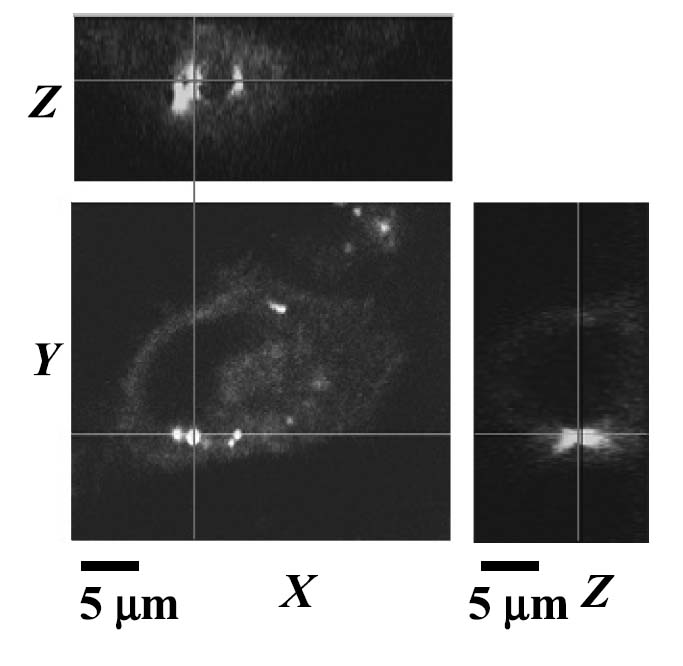
Confocal microscopy of PC3 cell after combined treatment with Oregon Green paclitaxel-loaded nanodroplets and US at 2.4 W/cm2, illustrating internalization of droplet contents.
Cell Viability after Ultrasound Exposure
Cell viability after exposure to US, droplets, or both, was determined by trypan blue exclusion. Treatment by US at 5 MHz and 2.4 W/cm2 without the presence of nanodroplets did not produce significant toxicity (Figure 11A). Treatment of the monolayer with paclitaxel-carrying droplets without US also did not produce significant toxicity. However, treatment by the combination of US and the paclitaxel-carrying nanoparticles produced a region of cell death centered around the acoustic focus (Figure 11B). Addition of 0.2%, 0.6%, and 2.5% of the nanodroplet solution to the cell plate before treatment resulted in a 2-, 7-, or 9-fold increase in cytotoxicity, respectively (Figure 12). Data in Figure 12 are normalized to exposure of the cells with 2.5% nanodroplet solution without US treatment, which resulted in no significant cytotoxicity (less than 1% of the cell population stained blue).
Figure 11.
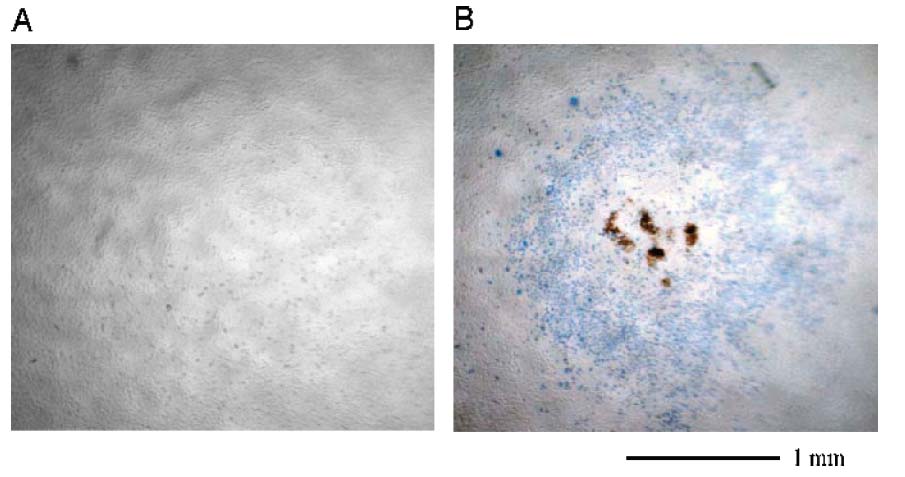
Trypan blue cell viability studies. Cells in (A) are exposed to US at 2.4 W/cm2 for 2 min without droplets, and remain viable after treatment. Cells in (B) are exposed to both US at 2.4 W/cm2 for 2 min and a solution of paclitaxel-loaded nanodroplets. Cells in and surrounding the region of the acoustic focus are not viable after treatment.
Figure 12.
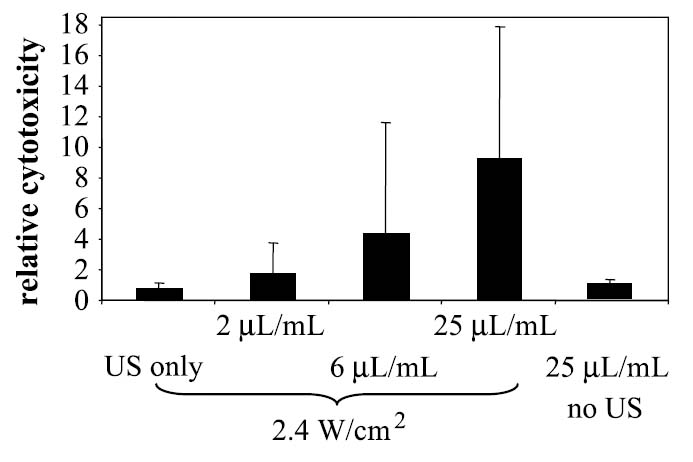
Relative cell toxicity in response to US only, US plus paclitaxel-loaded nanodroplet solution at increasing concentration, and nanodroplets only without US at the highest concentration.
Discussion
Streaming and Radiation Force
In this study, we have demonstrated that with sufficient acoustic intensity perfluorocarbon nanoparticles will translate away from the US source and concentrate along a vessel wall. As predicted in Equations 2 and 4, for low acoustic pressures, translational velocity is approximately linear as a function of acoustic intensity. Also based on Equations 2 and 4, it was expected that for radiation-force-induced displacement, particle velocity would be proportional to transmitted center frequency, whereas for fluid streaming, particle velocity is proportional to frequency squared. The empirically determined relationship between translation velocity and center frequency was approximately a function of frequency squared for data at the lowest pressure studied (a curve fit indicated a power of 2.1, with R2 value of 0.97). At the highest pressures studied, curve fitting indicated a power value of 2.3, with an R2 value of 0.94. Due to practical constraints, our experiments were conducted within tubes with a diameter between 200 and 700 μm, using water as a coupling medium. In the vessels used within the experimental study, fluid streaming was the dominant mechanism for displacement, with a magnitude of hundreds of micrometers per second for the parameters employed. The translational velocity induced by streaming decreases with vessel size and the velocity imparted by radiation force is expected to be dominant in capillaries.
The magnitude of the velocity component due to radiation force, Urad, increases approximately as a function of R2 0, and thus for a droplet with a radius of 1 μm, in fluid with the same streaming velocity (UL ~ 200 μm/sec), the contributions of the radiation and the drag forces can be of the same order, and the velocity of the droplet can considerably exceed the velocity of the acoustic streaming. In our experiments, although the motion of the droplets could be detected, it was not possible to accurately estimate the diameter of the majority of the droplets due to the limited optical resolution of our system, which we estimate to be on the order of 0.5 μm. Based on the data, we hypothesize that the majority of the droplets were in the size regime where the dominant contribution to the force upon the droplet was due to streaming of the fluid. Occasionally, droplets on the order of 1 μm were observed, and these droplets translated to the vessel wall much faster than the majority of nanometer-sized droplets, consistent with theory for radiation force.
Additional observations indicated that radiation force on the particles themselves was present in our studies. A weak secondary radiation force was observed that produced aggregation as described in Refs. [55–57]. This attraction was not observed in a dilute solution, but occurred once the nanoparticles were localized against a vessel wall during high-intensity insonation. In addition, although not shown, nanoparticles were observed to translate more efficiently than red blood cells in response to US pressure, and therefore the properties of the particle alter the velocity. For parameters used in the described experiments (Ispta = 480 mW/cm2, f = 10 MHz, and R0 = 0.2 μm), one can estimate the velocity of the particles due to radiation force effects to be on the order of Urad ≈ 5 μm/sec [2]. In capillaries with a typical diameter of 5 μm, the streaming velocity of the fluid may be very small, and the displacement of these particles would be largely due to radiation force. Given that tumor permeability varies greatly with particle diameter, minimizing particle diameter is important; however, the trade-off between extravasation potential and the magnitude of radiation force must be considered.
Monopole Oscillation of Droplets
Nanoparticles photographed during insonation did not exhibit the large radial oscillations observed with microbubble contrast agents, even at acoustic pressures up to 3 MPa at 10 MHz. These data are in agreement with [9], which demonstrated that perfluorocarbon nanoparticles in solution are not readily detectable with clinical frequency US. It is important to note that Equation A8 neglects nonlinear effects resulting from the radial oscillation of the droplet by neglecting the time dependence of the radius. Although with the droplets studied, the time variance of the radius is observed to be very small, it is important to note that for an oscillating particle, additional nonzero mean terms can emerge from the added mass and drag forces. Their contribution to translation can be correctly estimated only by numerical simulations using equations that describe coupled instantaneous radial and translational motions of a liquid droplet, similar to those used in the case of a gas bubble in a strong field. Derivation of such equations is not available in the literature at present; however, other studies have demonstrated that oscillations of highly compressible particles in an acoustic field can result in substantially increased radiation force as the particles undergo larger expansion and contraction near resonance [52].
Increasing Spatial Localization of Nanoparticles with US
The application of US was effective in increasing the adhesion of targeted nanoparticles in a flowing model system. In the flowing system, targeted droplet adhesion without insonation was virtually nonexistent. Without US, few of the droplets approach the proximity required for ligand–receptor interaction with the vessel wall.
The ability to bring nanoparticles into contact with the monolayer was shown to be necessary for efficient transfer of a fluorescent dye (DiI) to the cell monolayer. Without US, a small number of nanoparticles adhered to the cells on the monolayer; with application of US, both the concentration of the nanoparticles on the cell surface and the corresponding transfer of the fluorescent nanoparticle contents to the cells increased substantially. This observation of fluorescent dye transfer from nanoparticle to cell membrane has also been observed by Crowder et al. [24], who postulate lipid mixing across the membranes as a possible mechanism.
In addition to droplet-to-cell membrane dye transfer, US was also observed to mediate the internalization of fluorescent nanoparticle contents (Oregon Green paclitaxel) into the cells within the acoustic focus. Although further understanding of this internalization effect is beyond the scope of this article, this preliminary observation is promising for US-enhanced therapeutic nanoparticle delivery.
In a static environment, our studies indicate that the application of an US field can result in nanoparticle concentration on a monolayer, where the nanoparticles are not readily removed by subsequent washing. Thus, in a static environment, the application of US could alter the specificity that might otherwise result from a targeted nanoparticle. In vivo studies are required to further investigate these observations.
Safety
US effectively increased the local concentration of targeted nanoparticles, both in static solution and in flow up to 9 mm/sec in a 200-μm vessel; however, the acoustic intensities used were over the Ispta limit of 720 mW/cm2 for ultrasonic imaging. Trypan blue exclusion studies demonstrated that insonation of a cell monolayer at 2.4 W/cm2 and 5 MHz without the presence of nanodroplets did not affect cell viability. The safety of this technique must be further validated in vivo to further assess the safety of moderate-intensity US with specific drugs.
Combining paclitaxel-carrying droplets with insonation at 2.4 W/cm2 and 5 MHz resulted in a significant increase in cell death in the area of acoustic focus (p < .05 for 2.5% droplet solution combined with US vs. US alone or droplets alone), the degree of which increased with increasing nanodroplet concentration. These initial results hold promise for the ability of US to spatially localize the therapeutic effect from drug-carrying nanodroplets and will be studied in more detail in future experiments.
Perfluorocarbon nanoparticles were intact following the application of acoustic pressure that would destroy microbubbles. Although microbubbles fragment at relatively low acoustic pressures (Chomas et al. [51] predict acoustic pressures of 300 kPa at 2.25 MHz will destroy most bubbles less than 3 μm in diameter), the droplets described in this article, made with 90% or greater perfluorohexane, can be insonified with acoustic pressures on the order of several megapascals without a detectable change in properties; hence we do not anticipate the occurrence of cavitation-based bioeffects as observed with microbubbles.
Limitations of These Studies
Several limitations of the theory in this manuscript should be noted. With the diameters and frequencies tested, the nanodroplets do not fully meet the criteria for weak dissipation required for Equation 2 of R0 〉〉 δv or because in our case these terms are closer to the same order of magnitude. A new theoretical development for insonation of nanometer droplets will be required to more accurately characterize the effect of acoustic radiation forces on these particles. As such, we do not directly compare magnitude estimates from the theory to experimental data.
Another factor confounding comparison of theory to experiment is the presence of significant nonlinear wave propagation for the acoustic pressures and frequencies studied that is not accounted for with Equation 6, which will substantially increase the streaming velocity of a fluid [42,58,59].
Although we observed internalization of nanodroplet contents and cytotoxicity with combined US and paclitaxel-loaded droplets at the acoustic focus, further studies will be required to understand the mechanism for these observations.
Conclusion
Through optical observation of the translation of targeted perfluorocarbon nanoparticles, we conclude that these particles can be manipulated and concentrated with US. We have demonstrated that application of US with high duty-cycle pulses can “deflect” perfluorocarbon nanoparticles in the acoustic field. Theory and experiments demonstrated the displacement of perfluorocarbon nanoparticles in the direction of US propagation, where a traveling US wave with a peak pressure on the order of megapascals and frequency in the megahertz range produces a translational velocity that is proportional to acoustic intensity and increases with increasing center frequency. For a vessel diameter on the order of hundreds of micrometers or larger, particle velocity on the order of hundreds of micrometers was produced and the dominant mechanism for droplet displacement appears to be bulk fluid streaming. A model for radiation force displacement of particles was developed and demonstrates that effective particle displacement should be feasible in the microvasculature. The application of US greatly increased the adhesion of targeted nanoparticles flowing in a mimetic vessel and the localization of nanoparticles on a cell monolayer at the acoustic focus. Transfer of a fluorescent dye from the particles to the cells was increased in the presence of US. Insonation alone did not produce significant cytotoxicity in a monolayer of PC3 cells, but resulted in significant cell death when used in combination with nanodroplets carrying a cytotoxic drug. Future experiments will investigate optimization of the surface architecture used for targeting in conjunction with US, as well as the particle stability and maximum drug loading. Our analyses indicate that increasing the percentage of a drug reaching a region of interest using US and targeted nanoparticles is feasible.
Acknowledgments
The authors thank the funding sources NASA/NCI N01 CO 37118 and NIH R01 CA 103828. The contributions of Jennifer McCallan for cell culture and Roger Adamson for confocal microscopy are gratefully acknowledged. Additionally, we appreciate the helpful discussions with Dustin Kruse and Doug Stephens regarding intensity and acoustic absorption.
Appendix
The radiation force exerted on a liquid droplet by a traveling wave is described in its simplest form in Equation A1. (A list of symbols is provided in Table 2.)
Table 2.
List of Symbols
| A | Complex amplitude of the velocity potential of the imposed sound field |
| α | Absorption coefficient |
| c | Speed of sound in the fluid |
| δt | Thermal penetration depth in the host fluid |
| δν | Viscous penetration depths in the host fluid |
| f | Center frequency of transmitted US |
| Frad | Radiation force |
| Fdrag | Drag force on a liquid droplet moving in a immiscible liquid |
| Radiation force on a liquid droplet | |
| Fs | Acoustic streaming force |
| G | Geometric factor |
| γ | Ratio of specific heats in the fluid |
| Ispta | Spatial-peak temporal-average intensity |
| k = ω/c | Wave number in the fluid |
| λα | Ratio of volume thermal expansion coefficient of the host fluid to sphere material |
| λκ | Ratio of thermal conductivity of the host fluid to sphere material |
| λn | Ratio of dynamic viscosity of the host fluid to sphere material |
| λp | Ratio of density of the host fluid to sphere material |
| md | Mass of the droplet |
| η | Dynamic viscosity of the host fluid |
| ρ0 | Fluid density at rest |
| Pa | Pressure amplitude |
| P(t) | Time-varying pressure wave |
| R0 | Equilibrium radius of the particle involved |
| TPRF | Period of pulse repetition frequency (PRF) |
| TP | Period of pulse wave |
| Ud | Observed velocity of the droplet due to all forces |
| UL | Velocity of the ambient liquid due to acoustic streaming and other nonlinear effects that may develop in the insonified volume |
| Urad | Velocity of the droplet due to radiation force on the droplet |
| Va | Amplitude of the velocity of the incident plane traveling wave |
| ν | Kinematic viscosity of the fluid |
| ω | Angular driving frequency |
Tilde over variable denotes quantities that concern the medium inside the drop rather than the host medium.
| (A1) |
This relation is based on the assumption that the host fluid is ideal, that is, nonviscous and non-heat-conducting. In the limiting case Equation A1 simplifies to the expression for radiation force on a solid particle [39,44]. With this assumption of an ideal fluid medium, these equations describe the force on the particle due to the sound wave, but ignore forces that are due to acoustic streaming that develops around the particle and forces on the particle due to the acoustic streaming that would develop in the bulk fluid even if the particle was absent. For nanometer-sized droplets, such as those studied in this article, viscous effects should be considered because the viscous force on the particle due to acoustic streaming can be as much as 25–75% of the total force in a limited set of conditions [43]. Doinikov [44] further developed the theory for droplets to incorporate effects of a viscous heat-conducting fluid. Because the resulting general formula is intricate, it is analyzed for the limiting cases of weak or strong dissipation. The case for weak dissipation is presented here as Equation A2 [44],
| (A2) |
where
| (A2a) |
and
| (A2b) |
Intensity of US waves is frequently summarized by the spatial-peak temporal-average intensity (Ispta), which is the best measure of the amount of heat delivered to a tissue by US. Ispta for a pulsed wave in general is defined as:
| (A3) |
with TPRF ≫ Tp. Based on Equation A3, changing the pulse repetition frequency (PRF) changes the intensity linearly, and changing the pulse amplitude (the acoustic pressure) changes the intensity nonlinearly. Note that the amplitude of the velocity potential can be written as and thus Equation A2 can also be written in a form that illustrates the dependence on acoustic intensity for our experimental conditions.
| (A4) |
At small Reynolds numbers, the drag force on a liquid droplet moving in a different immiscible liquid can be written as Equation A5 [60].
| (A5) |
Note that for , which corresponds to a solid sphere, Equation A5 turns into the Stokes formula. It is easy to check that in the experiments described, the Reynolds numbers are much smaller than unity for both the acoustical velocity, Va, and the observed values of the translational velocity of the droplets, Ud. For example, for Ispta = 480 mW/cm2, f = 10 MHz, R0=200 nm, and Ud = 200 μm/sec:
| (A6a) |
| (A6b) |
Therefore Equation A5 is reasonable approximation. Using this equation, the equation describing the time-averaged translation of the droplet can be written as:
| (A7) |
The second term on the left is the added mass force, and Frad is the radiation force that can be estimated by, for example, Equation A4. Assuming that UL is constant (over distances traveled by the droplets during measurements) and that Ud = 0 at t = 0,
| (A8) |
where
| (A8a) |
and
| (A8b) |
Evaluation of ln 2/β indicates time constants on the order of 0.4 μsec for droplets on the order of 1 μm, and less than 5 nsec for droplets on the order of 0.1 μm for parameters considered here, so droplet velocity approaches streaming velocity within microseconds. The steady-state value of Ud tends to the sum UL + Urad.
The contribution to Equation A8 of the radiation force-induced particle velocity, Urad can be determined by using Equation A4 and the relationship δv ≈ R0 and the expression for particle velocity induced by radiation force given by Equations A9 and 2.
| (A9) |
Thus, for the experimental conditions Ispta = 480 mW/cm2, f =10 MHz, and R0 = 200 nm, Urad ≈ 5 μm/sec.
References
- 1.Kong G, Braun RD, Dewhirst MW. Characterization of the effect of hyperthermia on nanoparticle extravasation from tumor vasculature. Cancer Res. 2001;61:3027–3032. [PubMed] [Google Scholar]
- 2.Kong G, Braun RD, Dewhirst MW. Hyperthermia enables tumor-specific nanoparticle delivery: Effect of particle size. Cancer Res. 2000;60:4440–4445. [PubMed] [Google Scholar]
- 3.Fontana G, Maniscalco L, Schillaci D, Cavallaro G, Giammona G. Solid lipid nanoparticles containing tamoxifen characterization and in vitro antitumoral activity. Drug Deliv. 2005;12:385–392. doi: 10.1080/10717540590968855. [DOI] [PubMed] [Google Scholar]
- 4.Zharov VP, Mercer KE, Galitovskaya EN, Smeltzer MS. Photothermal nanotherapeutics and nanodiagnostics for selective killing of bacteria targeted with gold nanoparticles. Biophys J. 2005;90:619–627. doi: 10.1529/biophysj.105.061895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Lindner JR. Evolving applications for contrast ultrasound. Am J Cardiol. 2002;90:72J–80J. doi: 10.1016/s0002-9149(02)02951-x. [DOI] [PubMed] [Google Scholar]
- 6.Bloch SH, Dayton PA, Ferrara KW. Targeted imaging using ultrasound contrast agents. Progress and opportunities for clinical and research applications. IEEE Eng Med Biol Mag. 2004;23:18–29. doi: 10.1109/memb.2004.1360405. [DOI] [PubMed] [Google Scholar]
- 7.Lanza GM, Abendschein DR, Yu X, Winter PM, Karukstis KK, Scott MJ, Fuhrhop RW, Scherrer DE, Wickline SA. Molecular imaging and targeted drug delivery with a novel, ligand-directed paramagnetic nanoparticle technology. Acad Radiol. 2002;9:S330–S331. doi: 10.1016/s1076-6332(03)80220-9. [DOI] [PubMed] [Google Scholar]
- 8.Wickline SA, Lanza GM. Nanotechnology for molecular imaging and targeted therapy. Circulation. 2003;107:1092–1095. doi: 10.1161/01.cir.0000059651.17045.77. [DOI] [PubMed] [Google Scholar]
- 9.Lanza GM, Wickline SA. Targeted ultrasonic contrast agents for molecular imaging and therapy. Curr Probl Cardiol. 2003;28:625–653. doi: 10.1016/j.cpcardiol.2003.11.001. [DOI] [PubMed] [Google Scholar]
- 10.Marsh JN, Hughes MS, Hall CS, Lewis SH, Trousil RL, Brandenburger GH, Levene H, Miller JG. Frequency and concentration dependence of the backscatter coefficient of the ultrasound contrast agent Albunex (R) J Acoust Soc Am. 1998;104:1654–1666. [Google Scholar]
- 11.Marsh JN, Hall CS, Scott MJ, Fuhrhop RW, Gaffney PJ, Wickline SA, Lanza GM. Improvements in the ultrasonic contrast of targeted perfluorocarbon nanoparticles using an acoustic transmission line model. IEEE Trans Ultrason Ferroelectr Freq Control. 2002;49:29–38. doi: 10.1109/58.981381. [DOI] [PubMed] [Google Scholar]
- 12.Marsh JN, Hall CS, Wickline SA, Lanza GM. Temperature dependence of acoustic impedance for specific fluorocarbon liquids. J Acoust Soc Am. 2002;112:2858–2862. doi: 10.1121/1.1517251. [DOI] [PubMed] [Google Scholar]
- 13.Hall CS, Marsh JN, Scott MJ, Gaffney PJ, Wickline SA, Lanza GM. Temperature dependence of ultrasonic enhancement with a site-targeted contrast agent. J Acoust Soc Am. 2001;110:1677–1684. doi: 10.1121/1.1395584. [DOI] [PubMed] [Google Scholar]
- 14.Hall CS, Marsh JN, Scott MJ, Gaffney PJ, Wickline SA, Lanza GM. Time evolution of enhanced ultrasonic reflection using a fibrin-targeted nanoparticulate contrast agent. J Acoust Soc Am. 2000;108:3049–3057. doi: 10.1121/1.1322566. [DOI] [PubMed] [Google Scholar]
- 15.Lanza GM, Winter PM, Caruthers SD, Morawski AM, Schmieder AH, Crowder KC, Wickline SA. Magnetic resonance molecular imaging with nanoparticles. J Nucl Cardiol. 2004;11:733–743. doi: 10.1016/j.nuclcard.2004.09.002. [DOI] [PubMed] [Google Scholar]
- 16.Morawski AM, Winter PM, Crowder KC, Caruthers SD, Fuhrhop RW, Scott MJ, Robertson JD, Abendschein DR, Lanza GM, Wickline SA. Targeted nanoparticles for quantitative imaging of sparse molecular epitopes with MRI. Magn Reson Med. 2004;51:480–486. doi: 10.1002/mrm.20010. [DOI] [PubMed] [Google Scholar]
- 17.Schmieder AH, Winter PM, Caruthers SD, Harris TD, Williams TA, Allen JS, Lacy EK, Zhang H, Scott MJ, Hu G, Robertson JD, Wickline SA, Lanza GM. Molecular MR imaging of melanoma angiogenesis with alphanubeta3-targeted paramagnetic nanoparticles. Magn Reson Med. 2005;53:621–627. doi: 10.1002/mrm.20391. [DOI] [PubMed] [Google Scholar]
- 18.Anderson SA, Rader RK, Westlin WF, Null C, Jackson D, Lanza GM, Wickline SA, Kotyk JJ. Magnetic resonance contrast enhancement of neovasculature with alpha(v)beta(3)-targeted nanoparticles. Magn Reson Med. 2000;44:433–439. doi: 10.1002/1522-2594(200009)44:3<433::aid-mrm14>3.0.co;2-9. [DOI] [PubMed] [Google Scholar]
- 19.Winter PM, Caruthers SD, Kassner A, Harris TD, Chinen LK, Allen JS, Lacy EK, Zhang H, Robertson JD, Wickline SA, Lanza GM. Molecular imaging of angiogenesis in nascent Vx-2 rabbit tumors using a novel alpha(nu)beta3-targeted nanoparticle and 1.5 tesla magnetic resonance imaging. Cancer Res. 2003;63:5838–5843. [PubMed] [Google Scholar]
- 20.Winter PM, Morawski AM, Caruthers SD, Fuhrhop RW, Zhang H, Williams TA, Allen JS, Lacy EK, Robertson JD, Lanza GM, Wickline SA. Molecular imaging of angiogenesis in early-stage atherosclerosis with alpha(v)beta3-integrin-targeted nanoparticles. Circulation. 2003;108:2270–2274. doi: 10.1161/01.CIR.0000093185.16083.95. [DOI] [PubMed] [Google Scholar]
- 21.Cyrus T, Winter PM, Caruthers SD, Wickline SA, Lanza GM. Magnetic resonance nanoparticles for cardiovascular molecular imaging and therapy. Expert Rev Cardiovasc Ther. 2005;3:705–715. doi: 10.1586/14779072.3.4.705. [DOI] [PubMed] [Google Scholar]
- 22.Lanza GM, Wickline SA. Targeted ultrasonic contrast agents for molecular imaging and therapy. Prog Cardiovasc Dis. 2001;44:13–31. doi: 10.1053/pcad.2001.26440. [DOI] [PubMed] [Google Scholar]
- 23.Larina IV, Evers BM, Ashitkov TV, Bartels C, Larin KV, Esenaliev RO. Enhancement of drug delivery in tumors by using interaction of nanoparticles with ultrasound radiation. Technol Cancer Res Treat. 2005;4:217–226. doi: 10.1177/153303460500400211. [DOI] [PubMed] [Google Scholar]
- 24.Crowder KC, Hughes MS, Marsh JN, Barbieri AM, Fuhrhop RW, Lanza GM, Wickline SA. Sonic activation of molecularly-targeted nanoparticles accelerates transmembrane lipid delivery to cancer cells through contact-mediated mechanisms: Implications for enhanced local drug delivery. Ultrasound Med Biol. 2005;31:1693–1700. doi: 10.1016/j.ultrasmedbio.2005.07.022. [DOI] [PubMed] [Google Scholar]
- 25.Rychak JJ, Klibanov AL, Hossack JA. Acoustic radiation force enhances targeted delivery of ultrasound contrast microbubbles: In vitro verification. IEEE Trans Ultrason Ferroelectr Freq Control. 2005;52:421–433. doi: 10.1109/tuffc.2005.1417264. [DOI] [PubMed] [Google Scholar]
- 26.Dayton P, Klibanov A, Brandenburger G, Ferrara K. Acoustic radiation force in vivo: A mechanism to assist targeting of microbubbles. Ultrasound Med Biol. 1999;25:1195–1201. doi: 10.1016/s0301-5629(99)00062-9. [DOI] [PubMed] [Google Scholar]
- 27.Zhao S, Borden M, Bloch SH, Kruse D, Ferrara KW, Dayton PA. Radiation-force assisted targeting facilitates ultrasonic molecular imaging. Mol Imaging. 2004;3:135–148. doi: 10.1162/1535350042380317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lum AF, Borden MA, Dayton PA, Kruse DE, Simon SI, Ferrara KW. Ultrasound radiation force enables targeted deposition of model drug carriers loaded on microbubbles. J Control Release. 2006;111:128–134. doi: 10.1016/j.jconrel.2005.11.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Shortencarier MJ, Dayton PA, Bloch SH, Schumann PA, Matsunaga TO, Ferrara KW. A method for radiation-force localized drug delivery using gas-filled lipospheres. IEEE Trans Ultrason Ferroelectr Freq Control. 2004;51:822–831. doi: 10.1109/tuffc.2004.1320741. [DOI] [PubMed] [Google Scholar]
- 30.Nightingale KR, Trahey GE. A finite element model for simulating acoustic streaming in cystic breast lesions with experimental validation. IEEE T Ultrason Ferroelectr Freq Control. 2000;47:201–215. doi: 10.1109/58.818763. [DOI] [PubMed] [Google Scholar]
- 31.Shi X, Martin RW, Vaezy S, Crum LA. Quantitative investigation of acoustic streaming in blood. J Acoust Soc Am. 2002;111:1110–1121. doi: 10.1121/1.1428544. [DOI] [PubMed] [Google Scholar]
- 32.Shi XG, Martin RW, Vaezy S, Kaczkowski P, Crum LA. Color Doppler detection of acoustic streaming in a hematoma model. Ultrasound Med Biol. 2001;27:1255–1264. doi: 10.1016/s0301-5629(01)00428-8. [DOI] [PubMed] [Google Scholar]
- 33.Alekseev VN. Force produced by the acoustic radiation pressure on a sphere. Sov Phys Acoust. 1983;29:77–81. [Google Scholar]
- 34.Bjerknes VFK. Fields of force. New York: Columbia University Press; 1906. [Google Scholar]
- 35.Doinikov AA. Acoustic radiation pressure on a rigid sphere in a viscous-fluid. Proc R Soc Lond A Math Phys Sci. 1994;447:447–466. [Google Scholar]
- 36.Doinikov AA. Radiation force due to a spherical sound field on a rigid sphere in a viscous-fluid. J Acoust Soc Am. 1994;96:3100–3105. [Google Scholar]
- 37.Doinikov AA. Acoustic radiation force on a spherical particle in a viscous heat-conducting fluid 1. General formula. J Acoust Soc Am. 1997;101:713–721. [Google Scholar]
- 38.Doinikov AA. Acoustic radiation force on a bubble: Viscous and thermal effects. J Acoust Soc Am. 1998;103:143–147. [Google Scholar]
- 39.King LV. On the acoustic radiation pressure on spheres. Proc R Soc Lond A Math Phys Sci. 1934;147:212–240. [Google Scholar]
- 40.Nyborg W. Radiation pressure on a small rigid sphere. J Acoust Soc Am. 1967;42:1762. [Google Scholar]
- 41.Yosioka K, Kawasima Y. Acoustic radiation pressure on a compressible sphere. Acustica. 1955;5:167–173. [Google Scholar]
- 42.Wu JR, Du GH. Acoustic streaming generated by a focused gaussian-beam and finite-amplitude tonebursts. Ultrasound Med Biol. 1993;19:167–176. doi: 10.1016/0301-5629(93)90008-c. [DOI] [PubMed] [Google Scholar]
- 43.Wu JR, Du GH. Acoustic radiation force on a small compressible sphere in a focused beam. J Acoust Soc Am. 1990;87:997–1003. [Google Scholar]
- 44.Doinikov AA. Acoustic radiation forces: Classical theory and recent advances. Recent Res Devel Acoustics. 2003;1:39–67. [Google Scholar]
- 45.Daft CM, Briggs GA, O’Brien WD., Jr Frequency dependence of tissue attenuation measured by acoustic microscopy. J Acoust Soc Am. 1989;85:2194–2201. doi: 10.1121/1.397868. [DOI] [PubMed] [Google Scholar]
- 46.Vacek V, Hallewell G, Lindsay S. Velocity of sound measurements in gaseous per-fluorocarbons and their mixtures. Fluid Phase Equilib. 2001;185:305–314. [Google Scholar]
- 47.Shung K, Smith MB, Tsui B. Principles of medical imaging. San Diego: Academic Press; 1992. [Google Scholar]
- 48.Rose J, Goldberg BB. Basic physics in diagnostic ultrasound. New York: Wiley; 1978. [Google Scholar]
- 49.Repacholi M, Garandolfo M, Rindi A. Ultrasound: Medical applications, biological effects and hazard potential. New York: Plenum Press; 1987. [Google Scholar]
- 50.Kripfgans OD, Fabiilli ML, Carson PL, Fowlkes JB. On the acoustic vaporization of micrometer-sized droplets. J Acoust Soc Am. 2004;116:272–281. doi: 10.1121/1.1755236. [DOI] [PubMed] [Google Scholar]
- 51.Chomas JE, Dayton P, May D, Ferrara K. Threshold of fragmentation for ultrasonic contrast agents. J Biomed Opt. 2001;6:141–150. doi: 10.1117/1.1352752. [DOI] [PubMed] [Google Scholar]
- 52.Dayton PA, Allen JS, Ferrara KW. The magnitude of radiation force on ultrasound contrast agents. J Acoust Soc Am. 2002;112:2183–2192. doi: 10.1121/1.1509428. [DOI] [PubMed] [Google Scholar]
- 53.Bouakaz A, Versluis M, de Jong N. High-speed optical observations of contrast agent destruction. Ultrasound Med Biol. 2005;31:391–399. doi: 10.1016/j.ultrasmedbio.2004.12.004. [DOI] [PubMed] [Google Scholar]
- 54.Gant VA, Shakoor Z, Hamblin AS. A new method for measuring clustering in suspension between accessory cells and T lymphocytes. J Immunol Methods. 1992;156:179–189. doi: 10.1016/0022-1759(92)90024-n. [DOI] [PubMed] [Google Scholar]
- 55.Zheng XY, Apfel RE. Acoustic interaction forces between 2 fluid spheres in an acoustic field. J Acoust Soc Am. 1995;97:2218–2226. [Google Scholar]
- 56.Doinikov AA. Bjerknes forces between two bubbles in a viscous fluid. J Acoust Soc Am. 1999;106:3305–3312. [Google Scholar]
- 57.Dayton PA, Morgan KE, Klibanov ALS, Brandenburger G, Nightingale KR, Ferrara KW. A preliminary evaluation of the effects of primary and secondary radiation forces on acoustic contrast agents. IEEE Trans Ultrason Ferroelectr Freq Control. 1997;44:1264–1277. [Google Scholar]
- 58.Starritt HC, Duck FA, Humphrey VF. An experimental investigation of streaming in pulsed diagnostic ultrasound beams. Ultrasound Med Biol. 1989;15:363–373. doi: 10.1016/0301-5629(89)90048-3. [DOI] [PubMed] [Google Scholar]
- 59.Nightingale KR, Palmeri ML, Nightingale RW, Trahey GE. On the feasibility of remote palpation using acoustic radiation force. J Acoust Soc Am. 2001;110:625–634. doi: 10.1121/1.1378344. [DOI] [PubMed] [Google Scholar]
- 60.Landau LD, Lifshitz EM. Fluid mechanics. Oxford: Pergamon; 1987. [Google Scholar]


