Population size and relatedness affect fitness of a self-incompatible invasive plant

Abstract

One of the lingering paradoxes in invasion biology is how founder populations of an introduced species are able to overcome the limitations of small size and, in a “reversal of fortune,” proliferate in a new habitat. The transition from colonist to invader is especially enigmatic for self-incompatible species, which must find a mate to reproduce. In small populations, the inability to find a mate can result in the Allee effect, a positive relationship between individual fitness and population size or density. Theoretically, the Allee effect should be common in founder populations of self-incompatible colonizing species and may account for the high rate of failed introductions, but little supporting evidence exists. We created a field experiment to test whether the Allee effect affects the maternal fitness of a self-incompatible invasive species, wild radish (Raphanus sativus). We created populations of varying size and relatedness. We measured maternal fitness in terms of both fruit set per flower and seed number per fruit. We found that both population size and the level of genetic relatedness among individuals influence maternal reproductive success. Our results explicitly define an ecological genetic obstacle faced by populations of an exotic species on its way to becoming invasive. Such a mechanistic understanding of the invasions of species that require a mate can and should be exploited for both controlling current outbreaks and reducing their frequency in the future.

Exotic, invasive species are a modern biological paradox. Founder populations are characteristically small in number of individuals and/or low density. Low density and small population size not only increase the risk of stochastic extinction (1) but also limit opportunities for individuals to mate effectively (2). The latter may result in an Allee effect, a positive relationship between population size and individual fitness (3). Finding compatible mates in a small population presents a problem for plants, which are sessile during the reproductive stage, and is especially challenging for obligately outcrossing species, such as those that are self-incompatible or dioecious. For example, self-incompatibility systems both prohibit self-pollination and significantly reduce successful cross-pollination of individuals with shared S-alleles, (e.g., close relatives) (4). “Baker's law” predicts that a self-compatible species will have a much greater chance of establishing in a new location after a long-distance dispersal event than a self-incompatible species because the former can create a sexually reproducing population with a single individual (5, 6). Nonetheless, self-incompatibility is not rare for invasive plants. Founder populations of self-incompatible species that become invasive must experience a “reversal of fortune.” That is, individuals within these small populations overcome the limitations of small population size to reproduce and spread successfully.

Theoretical models and a handful of empirical studies suggest that the Allee effect is most important in very small or sparse populations (7–10), wherein declines in individual fitness can lead to population contraction. Mechanisms responsible for the Allee effect do not always depend directly on mating system. For example, in animals they may also include reduced efficiency of antipredator vigilance behavior in small populations (11, 12).

A paucity of empirical data has encouraged us to examine whether the Allee effect is present in a self-incompatible, invasive plant. Our study organism, Raphanus sativus (commonly known as California wild radish), is an annual, sporophytically self-incompatible plant (13, 14) pollinated largely by honey bees and syrphid flies (15, 16). California wild radish is of hybrid origin (5, 17); it is descended from hybrids between R. sativus (cultivated radish) and Raphanus raphanistrum (an agricultural weed known as jointed charlock). Since introduction of these species >100 years ago and their subsequent hybridization, California wild radish has spread throughout the state of California, south into Baja California and north through Oregon, invading such diverse habitats as inland roadsides and coastal dunes (5, 17, 18). California wild radish seeds disperse via spongy, indehiscent fruits containing three or more seeds (5, 19). Like fruits of the cultivated radish progenitor parent, California wild radish fruits generally do not break into single-seeded segments upon maturity.

We created experimental stands of wild radish in the field to measure the impact of the Allee effect in this invasive species (Fig. 1). We predicted that maternal fitness (fruit and seed production) would increase with population size (i.e., that we would observe an Allee effect). We also expected maternal fitness to decline as genetic relatedness increased. Because R. sativus exhibits sporophytic self-incompatibility, we predicted that fitness would be lowest in the smallest populations of full-siblings, because they carry, on average, the fewest incompatibility genotypes.

Fig. 1.

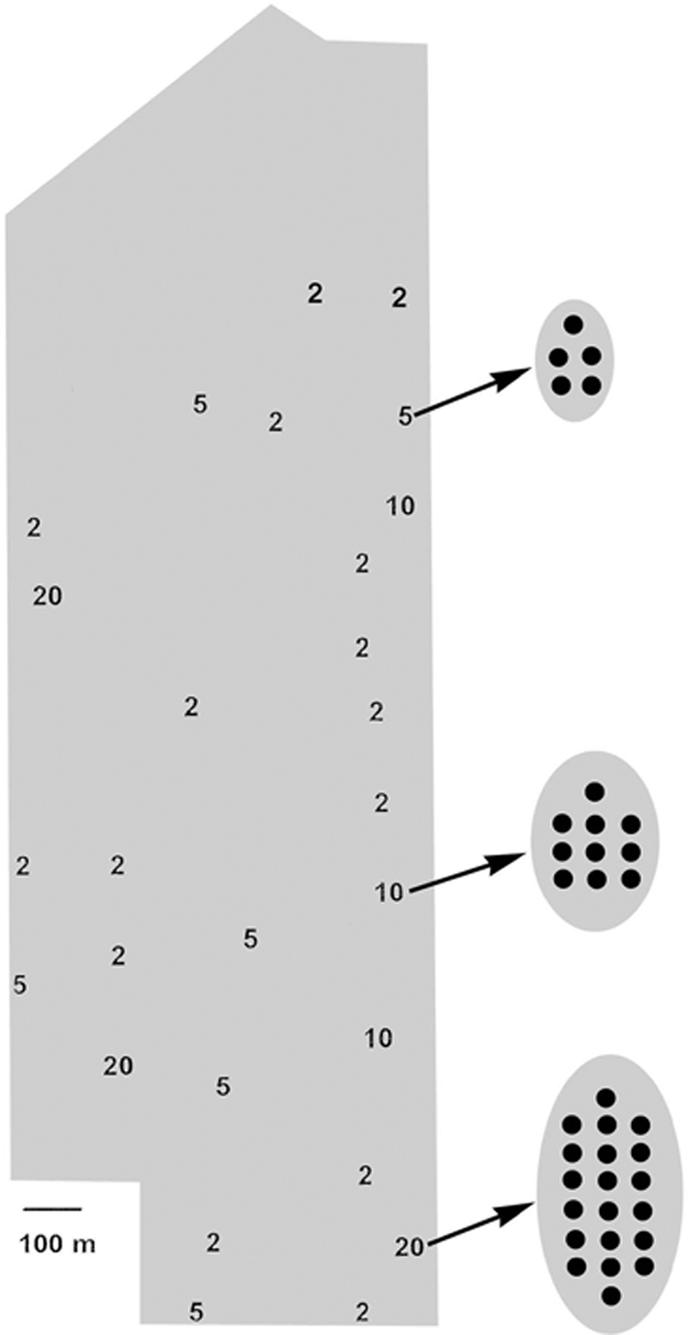
Map of our field site with the locations of the experimental populations (sizes indicated by numbers) during a sample temporal replicate (time) of the experiment. Magnified areas indicate how plants were arranged spatially within populations of 5, 10, and 20. The shaded area shows the area occupied by a surrounding citrus grove.

Results

To test the effect of population size and genetic relatedness on maternal reproductive success in California wild radish, we constructed artificial, replicated populations of 2, 5, 10, and 20 plants in three relatedness classes (full-sibling, half-sibling, and unrelated) in a factorial design. We counted the number of flowers produced by each plant. At the end of flowering we harvested all of the fruits produced by each plant. Subsequently, the number of seeds from a random sample of five fruits from each plant was counted.

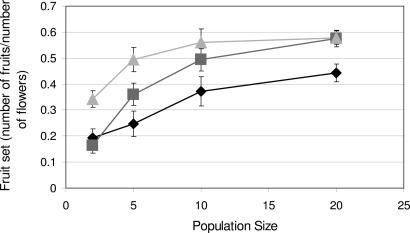
As predicted, individual fruit set (number of fruits/number of flowers) increased significantly with population size, with average fruit set 2.5-fold greater in populations of size 20 than those of size 2 averaged over all relatedness classes (Fig. 2 and Table 1). Furthermore, we found evidence for a threshold effect of population size; fruit set increased with population size up to five individuals (Fig. 2 and Table 2). Increasing relatedness among individuals reduced fruit set (Fig. 2 and Table 1). Mean contrasts indicated little difference between full-sibling and half-sibling populations in fruit set, but both produced significantly fewer fruits than unrelated populations (Table 2). Contrary to our expectations, there was no significant interaction between population size and relatedness (Table 1).

Fig. 2.

The effects of population size and genetic relatedness on fruit set (number of fruits/number of flowers) (see also Tables 1 and 2). Symbols (diamonds, full-siblings; squares, half-siblings; triangles, unrelated individuals) represent means across populations ± SEM.

Table 1.

ANOVA results showing the fixed effects of population size and genetic relatedness on two measures of individual maternal fitness, arcsine square root (fruit set) and square root (mean number of seeds per fruit)

Source	Numerator degrees of freedom	Fruit set (n = 437)		Mean no. of seeds per fruit (n = 401)
		Denominator degrees of freedom	F value	Denominator degrees of freedom	F value
Population size	3	359	11.40***	331	6.18**
Population relatedness	2	359	7.12**	331	7.44**
Size × relatedness	6	359	1.04	331	1.27

***, P < 0.0001;

**, P < 0.001.

Table 2.

Mean contrasts for ANOVA of arcsine square root (fruit set) and square root (mean number seeds per fruit)

Contrast	Fruit set, F value	Mean no. of seeds per fruit, F value
Population size
Size 2 vs. 5, 10, and 20	29.02***	11.91**
Size 2 and 5 vs. 10 and 20	22.68***	11.25**
Size 5 vs. 10	2.87	0.53
Size 10 vs. 20	1.19	2.39
Population relatedness
Full-sibling vs. half-sibling	3.25	4.03*
Full- and half-sibling vs. unrelated	11.08**	11.19**
Half-sibling vs. unrelated	3.95*	3.48

For fruit set, n = 437, numerator degrees of freedom = 1, and denominator degrees of freedom = 359. For mean no. of seeds per fruit, n = 401, numerator degrees of freedom = 1, and denominator degrees of freedom = 331.

***, P < 0.0001;

**, P ≤ 0.001;

*, P ≤ 0.05.

Mean seed production per fruit increased with population size an average of nearly 1.5-fold from populations of size 2 to populations of size 10 over all relatedness classes (Fig. 3 and Table 1). Mean contrasts revealed a threshold effect of size similar to that for fruit set; mean number of seeds per fruit increased with population size up to populations of five plants, above which we detected no significant increase in seed production. Increasing relatedness negatively affected mean seed production per fruit. Specifically, individual mean seed production per fruit increased with decreasing relatedness from full-sibling to half-sibling, but not from half-sibling to unrelated populations (Table 2).

Fig. 3.

The effects of population size and genetic relatedness on the mean number of seeds per fruit (see also Tables 1 and 2). Symbols are as in Fig. 2 and represent means across populations ± SEM.

Discussion

We have demonstrated that the Allee effect has a significant impact on maternal fitness in a self-incompatible, invasive plant. That is, we observed that, as population size increases, so does individual maternal fitness in experimental populations of California wild radish. Overall, mean seed production per flower increased with population size an average of ≈4-fold from populations of size 2 to populations of size 20 over all relatedness classes. Furthermore, we observed that the relatedness of individuals within populations can also significantly impact fitness. Interestingly, population size did not interact synergistically with relatedness to reduce maternal fitness more in small populations of closely related individuals than in small populations of unrelated individuals.

Finding a mate has been receiving increased attention as a problem in plant conservation (e.g., ref. 20). However, studies of the Allee effect's role in limiting the success of invasive or weedy plants remain few. The extant relevant studies of the Allee effect in other exotic, invasive species have produced mixed results. An invasive population of the largely self-incompatible smooth cordgrass Spartina alternifora was the object of a pollen supplementation and exclusion experiment (21). At the low-density leading edge of the invasion, pollen availability appears to limit seed production to an 8-fold disadvantage relative to the maximum observed, indicating a strong Allee effect. In another study artificial patches of 81 individuals of the self-compatible, invasive vine Vincetoxicum rossicum produced significantly more seeds per individual (approximately three times more) than patches of one or nine individuals (22). Interestingly, the author of the study states that “unlike most other examples of Allee effects in plants, the effect in V. rossicum was not due to differences in pollinator visitation rates,” but she does not address possible differences in pollen load size or pollen quality due to the availability of more mates. In contrast, natural stands of the invasive shrub Senna didymobotrya in South Africa display no relationship between plant density and seed production (23). Furthermore, pollen supplementation did not result in increased seed or fruit set. The absence of an Allee effect in the self-compatible S. didymobotrya is surprising, given that some individuals experience considerable isolation and that high-frequency vibrations of visiting pollinators are required for successful reproduction. In our study of California wild radish, the Allee effect in our smallest experimental populations resulted in seed production per flower averaging ≈25% of that in the largest populations.

An Allee effect can pose a demographic challenge to any population, invasive or not. With regard to invasiveness, an Allee effect may reduce the likelihood of establishment. In terms of establishment success, the total number of seeds created by the population is more relevant than individual plant fitness. If the total number of seeds created by a population correlates closely with establishment success, then relative colonization success should be calculated by comparison of total seed production. In our study of California wild radish the relative establishment success of the populations of size 20 compared with that of populations of size 2 should be the 4-fold Allee advantage times 20 individuals divided by the two individuals in the small populations, that is, a 40-fold relative advantage to the large populations!

For those populations that do establish with a small number of individuals, an Allee effect is expected to increase the lag time before the appearance of invasiveness, a period during which populations remain small and stationary. When range expansion occurs, an Allee effect should retard it (24). The Allee effect adds to the paradox of exotic, invasive species, which must overcome a suite of ecological, evolutionary, and genetic obstacles to establish and spread upon their introduction. Mechanisms by which successful invaders overcome demographic consequences of the Allee effect include large introductions, multiple introductions, the ability to clone or self-fertilize, the evolution of self-compatibility, and the hybridization of introduced species with related species and subspecies (2, 25, 26). Most of these mechanisms would increase the number of available mates with which an individual can reproduce.

Our results demonstrate that maternal success is determined by population size and relatedness in California wild radish. How then have California wild radish populations become successful invaders despite the challenge of an Allee effect? California wild radish seeds are dispersed in multiseeded, spongy lomenta (5). These fruits usually hold three to five seeds (19). Furthermore, paternity analysis has demonstrated the seeds held by a single fruit are half-siblings, sired by more than one father (27). Therefore, if the seeds in a single fruit germinate and grow up in isolation from conspecifics, they are likely to suffer reduced fitness. Our results indicate the Allee effect is strongest with founder population size <10. Thus, if the seeds from as few as three or four fruits set by different plants found a population, we would expect the Allee effect to be minimal. Wild radish's multiseeded fruits are an apparent adaptation to overcome the challenge of an Allee effect.

Our results have broad and important implications for invasive species in general. It is not uncommon for invasive species to be dioecious (especially many animals) or self-incompatible (especially many plants). Individuals of such species will require a mate and are likely to suffer an Allee effect in small populations as we observed in our experiments. In the case of self-incompatible plants, this result is exacerbated when the individuals are related to one another.

Our results highlight two easily studied ecological attributes of potentially invasive organisms, mating system and dispersal mode, that offer powerful insights into management strategies. When zero-tolerance eradication or containment is impossible, but the founding colonies of species that must outcross can be reduced to numbers that are so low that the Allee effect severely impacts reproduction's role in establishment, those efforts will still be worthwhile. Furthermore, rules of thumb could be developed for those industries that import exotic plants and animals. For example, if vegetatively propagated, obligately outcrossing ornamentals are restricted to a single genotype, they are much less likely to spread by seed. Essentially, the Allee effect can be used as a weapon against invasive species that require a mate to reproduce.

Materials and Methods

Experimental Design.

The California wild radish seeds used were progeny of hand-crosses. The plants were germinated and grown to flowering in the greenhouse. Flowering plants in 2-gallon pots were used to create synthetic populations of size 2, 5, 10, and 20 at the University of California, Riverside, Agricultural Experiment Station. Populations of each size comprised full-siblings, half-siblings, or unrelated plants in a factorial design. Numbers of populations within each size-relatedness combination are summarized in Table 3. Populations of full-siblings are expected to have higher levels of cross-incompatibility than those of half-siblings or unrelated individuals. Populations of half-siblings are expected to have, on average, intermediate levels of cross-incompatibility (14). Neighboring populations were separated by at least 100 m, a distance that had been previously found to substantially reduce gene flow among small populations of R. sativus (28).

Table 3.

Experimental design

Population relatedness	Population size
	2	5	10	20
Full-siblings	5	2	1	1
Half-siblings	5	2	1	1
Unrelated	5	2	1	1

Data shown represent the number of populations for each population size (with a total of 27 populations and 150 individuals). The design was repeated three times for a total of 81 populations and 450 individuals.

Most of the surrounding landscape was citrus orchards, avocado orchards, and fallow fields. Normally, local wild radish populations would have been flowering at the time of the experiment. However, the winter of the experiment, 1993–1994, was during one of California's periodic droughts. Sufficient rainfall for natural germination did not occur until the end of our experiment. The few flowering resident R. sativus plants within 1 km of our experimental plants resided within the boundaries of the Experiment Station property. Thus, they were easily identified and eradicated to minimize external gene flow.

The entire experimental design was repeated three times for a total of 81 populations and 450 plants. Plants within populations were placed 0.75 m from nearest neighbors. Populations were left in the field for 16 days to allow natural insect pollination. Only flowers open during the 16 days of the experiment were considered in the analysis. After 16 days, the plants were returned to the greenhouse, and the fruits were allowed to mature. For each plant, we counted the total number of flowers open during the experiment and the total number of fruits produced from experimental flowers. Fruit set was calculated as the number of fruits produced divided by the total number of experimental flowers. The number of seeds produced in a random sample of five fruits from each plant was determined for individuals in each of the three experimental repeats.

Statistical Analyses.

Separate analyses were conducted for the two measures of individual maternal fitness, fruit set and mean number of seeds per fruit, because the data sets differed slightly. Plants producing no fruits were excluded from the seeds per fruit analysis. For this reason, multivariate tests that consider both variables simultaneously were not possible.

Fruit set data were arcsine square root transformed and seed production data were square root transformed to meet the assumptions of the analyses. For both transformed versions of fruit set and mean seed production per fruit, a mixed-model ANOVA was conducted by using the PROC MIXED in SAS 9.1 (29). The main effects of population size and population relatedness and their interaction were considered fixed. Experimental repeat and population replicate were random factors. We used the variance components covariance structure and restricted maximum-likelihood estimation technique. Planned mean contrasts were calculated to test for specific differences between size and relatedness classes.