Chaotic flow: The physics of species coexistence

Abstract

Hydrodynamical phenomena play a keystone role in the population dynamics of passively advected species such as phytoplankton and replicating macromolecules. Recent developments in the field of chaotic advection in hydrodynamical flows encourage us to revisit the population dynamics of species competing for the same resource in an open aquatic system. If this aquatic environment is homogeneous and well-mixed then classical studies predict competitive exclusion of all but the most perfectly adapted species. In fact, this homogeneity is very rare, and the species of the community (at least on an ecological observation time scale) are in nonequilibrium coexistence. We argue that a peculiar small-scale, spatial heterogeneity generated by chaotic advection can lead to coexistence. In open flows this imperfect mixing lets the populations accumulate along fractal filaments, where competition is governed by an “advantage of rarity” principle. The possibility of this generic coexistence sheds light on the enrichment of phytoplankton and the information integration in early macromolecule evolution.

In most natural habitats numerous competing species are able to coexist, while generally only few resources limit these communities. This contradicts classical studies predicting competitive exclusion of all but the most perfectly adapted species for each limiting factor in homogeneous environments. A typical example of ecosystems where competitive exclusion (1, 2) contradicts observations are phytoplankton communities (3). Numerous investigations have suggested resolutions for this paradox by showing that there are several different mechanisms, environmental heterogeneity, predation, disturbance, coevolution that maintain the diversity (4, 5). In this paper we provide a hydrodynamical explanation for the spatial and temporal heterogeneity of resources and populations in the presence of imperfect chaotic mixing (6–8).

One can meet a surprisingly similar problem in early evolution of genetic replication. Most probably, at the dawn of life there was a phase of evolution when the only evolutionary units were certain self-replicating nucleic acids (9). They were competing for a few limiting resources and making copies of themselves without any specific enzyme. Consequently, the copying accuracy could not be very high. Estimating the selective superiority of the best replicator and the copying accuracy per nucleotide, one can conclude that the maximum length of these molecules is about 100 nucleotides (10). In a well-mixed homogeneous environment, as the prebiotic ocean is often assumed to have been, there are only a few winners of the selection, the most-fit macromolecule surrounded by its closest mutants (10, 11). But how can we surmount the gap between these primitive replicators with 100 nucleotides and the most simple RNA viruses with 4,000–5,000 nucleotides? Specific replicase enzymes are needed to increase the copying fidelity, and thus the length of the replicator, but these replicators are too short to code specific enzymes. This is the “Catch 22” of the prebiotic evolution (12). This catch can be resolved if a mechanism maintains the coexistence of several different replicator molecules and therefore the information necessary for more accurate multiplication can be coded by the union of smaller information carriers. Current theories point out coexistence of replicators moving on a surface in a constrained manner (13, 14), preferring thus the concept of “prebiotic pizza” against the concept of “prebiotic soup” (15). We show that chaotic advection also can provide an alternative explanation for information integration in early evolutionary systems.

In aquatic systems of large extension, on the time scales characteristic to the life cycle of microorganisms and replicators, the hydrodynamical flows are locally open, i.e. there is a net current flowing through the typical observation region transporting both competitors and nutrients. It is even more obvious that the flow is open in the wake of islands surrounded by strong ocean currents (16) and around the deep sea hot springs where the cradle of life probably swung (17).

It became clear in the past decade that the motion of passive tracers advected by open hydrodynamical flows is typically chaotic (18–22) even for simple, time-dependent flows, which are not turbulent. These flows, characterized by strong imperfect mixing, lead to a fractal spatial distribution of advected particles, also observed in laboratory experiments (20). Recent studies of chemical reactions superimposed on such flows (23) revealed that chemical activity is concentrated along fractal filaments, and that the reaction typically reaches a steady state. More importantly, due to the small scale inhomogeneities, the kinetic equation derived for the macroscopic distribution of the chemical components strongly deviate from that valid in well-stirred containers. A kinetic differential equation was derived (23) for an autocatalytic reaction in two-dimensional (i.e. practically depth-independent) time periodic flows that describe the accumulation of the product on the surface of fractal filaments (of the so-called outflow curves). In each horizontal layer of the flow these filaments move periodically in time but have a fractal dimension D, (1 < D < 2), which is time-independent. The kinetic equation gives the rate of change of the number B(t) of the autocatalytic reagent B in time t as

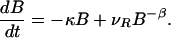1

The first term on the right describes the exponential decay of the species with a decay rate κ, which is due to the outflow from the fixed region of observation. The next term is the production term, which contains the velocity ν_R of the reaction front within one fluid layer, while β = (D − 1)/(2 − D) > 0 depends uniquely on the fractal dimension D of the filaments. This nontrivial, singular scaling with the negative exponent −β is due to the enhancement of the perimeter with decreasing area, a characteristics of filamental fractals. The reactions are speeded up by the presence of the dynamical fractal catalyst. This leads to an advantage of rarity, because the loss due to outflow is reduced if the amount of reagents is small (first term), while the reactions are strongly enhanced (second term). These properties reflect an enhancement of chemical activity catalyzed by the spatial fractal structures. Therefore, one expects similar characteristics of the biological interaction of advected species along the fractal filaments. Note that Eq. 1 describes a dissipative area-dynamics with a (nonzero) stable steady state B* = (ν_R/κ)^1/(β+1). The role of the quantity ν_R as the velocity of the reaction front is especially clear in nonchaotic flows, when the dimension of the outflow curve is D = 1 and hence β = 0. In the steady state the broadening by ν_R is exactly compensated by the escaping product of amount κB*.

We are mainly interested in the dynamics of competing advected species in relatively slow, time-dependent but not turbulent flows, such as in the wake of rocks, islands, or peninsulas. For our analysis we consider the flow around a cylinder. For moderate inflow velocities there is a periodic detachment of vortices in the wake with period T, which forms the von Kármán vortex street (18–20). The flow in the wake is time-dependent but still spatially regular. The numerical simulations were performed with a two-dimensional analytic model of this flow (19, 21). It is a specific model in the broad class of spatially extended systems (24, 25), but here the motion of individuals is determined by well-known physical (hydrodynamical) laws. Technically, we do not study a partial differential equation or cellular automaton governing the dynamics of populations as in most available approaches (24, 25) but follow the interaction of individuals whose motion is driven by the advection of the hydrodynamical flow (26).

We consider a simple kinetic model (23, 26) of replication and competition with passively advected point like individuals of type B and C, multiplying themselves instantaneously after certain replication times. This kinetic model is similar in spirit to the one used in ref. 27 for modeling chemical reactions in closed flows. In our open flow, there is a constant inflow of the resource material A into the system, which the different species B and C compete for. In addition, there is a spontaneous mortality of individuals. Therefore two autocatalytic processes A + B _→^γB 2B, B _→^δB A and A + C _→^γC 2C, C _→^δC A represent the replication and competition process in our model in an imperfectly mixed environment. The kinetic coefficient γ(δ) gives the birth (mortality) rate, i.e., number of individuals being born (dying) in unit time in a homogeneous environment. An important feature of the advection dynamics is its deterministic nature. Concerning the population dynamics this implies that we work in the limit of weak diffusion and assume that the mutual diffusion coefficient between any pair of the constituents is small. The resource A is the only common limiting factor for both species B and C, thus by the traditional theory (1, 2) species with lower γ/δ ratio would be outcompeted in a homogeneous, well-mixed environment.

The competitive dynamics starts with the full surface occupied by the background material A. Initially, we place two droplets of individuals from species B and C into the flow in front of the cylinder with C being the weaker competitor. The fixed region of observation is a rectangle containing the cylinder and the wake. We monitor the number of individuals present in this region during the competition process. After an initial rapid increase the number of B and C cells becomes synchronized with the flow (see Inset of Fig. 1a). We emphasize that species B and C coexist in spite of their very different γ/δ ratio. The filamental structure shown in Fig. 1 is reminiscent of the patterns found in mesoscale plankton models (28–30), which do not study competition, and in remote sensing images of chlorophyll concentration in the wake of islands (16). Field observation in the same region (31) indicate increase of biomass belonging to Cyanobacteria and Phytoflagellates taxa in monthly averages.

Figure 1.

(a) Spatial distribution of species B (green) and C (red) are shown on a snapshot taken after 24 periods T of the flow. They both cover a fractal curve and are present at all times in the wake of the cylinder. The initial position of species B and C is a rectangle of linear size 0.07 × 0.76 centered around x = −1.36, x = −1.10, and y = 0, respectively. (The length is measured in units of cylinder radius R.) (Inset) The percentage n_B (n_C) of species B (C) present in the wake is shown by green (red) line as a function of time, measured in units of T. Note the steady time-periodic behavior reached after about 40 time units. The simulation was performed on a rectangular grid of size ɛ = 2 × 10⁻³ times the cylinder radius. Species B and C are passively advected during time lags τ_B = 0.6T, and τ_C = 0.8T, respectively, then they reproduce instantaneously, with new individuals being “born” within a distance σ_B = σ_C = 1/500 of the “parent” if there is resource A available there [γ_B ∼ σ_B/τ_B = 1/(300T), γ_C ∼ σ_C/τ_C = 1/(400T)]. Additionally, at each time lag τ_B (τ_C) B (C) individuals die with a probability τ_Bδ_B (τ_Cδ_C) [δ_B = δ_C = 1/(10T)]. In our model σ_B (σ_C) also plays the role of a diffusive length scale. There is efficient diffusive mixing within this distance, and there is thus no need to introduce an additional stochastic noise to mimick diffusion (33). (b) A high-resolution image of the small rectangular region from a indicates self-similarity. The grid size is ɛ = 8 × 10⁻⁴. The total area covered by B and C in the wake follows a fractal scaling with dimension D ≈ 1.6, the same as in the autocatalytic chemical model (23). Note that the increase of the resolution does not alter the coexistence, only reveals more details of the fractal structure.

The explanation of the coexistence of species is based on concepts of the theory of chaotic advection. To have an intuitive understanding of the complexity of the advection dynamics, let us first imagine how a droplet of dye behaves in a simple uniform flow when it is advected past an obstacle of small spatial extent like a fixed needle. The dye particles that touch the needle remain attached, but the bulk of the droplet moves further downstream. As the droplet flows past the needle, its shape starts to change, developing tongues on both sides of the needle. These tongues are becoming ever longer and narrower and asymptotically the droplet traces out a line extending downstream to infinity. We call it the outflow curve. Geometrical points of the fluid surface from where dye particles can reach the needle form another straight line, the inflow curve extending upstream. If the needle is oscillating perpendicularly to the direction of the flow, both the inflow and outflow curves become bent and take on a wavy shape. Having infinitely many needles, all moving in a complicated manner in a finite region of the flow, the inflow and outflow curves of all these needles form a complicatedly interwoven striation of the fluid.

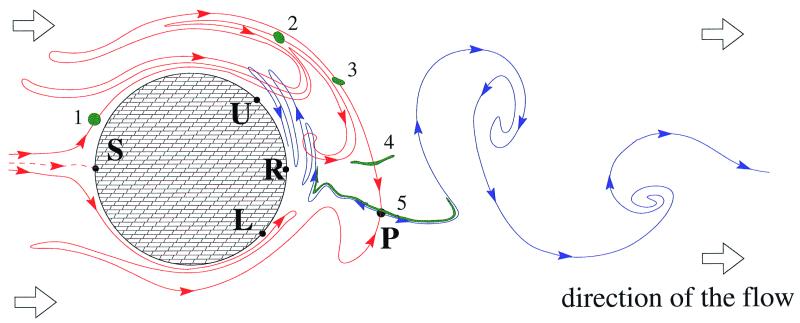
If a circular cylinder is placed in a moderately fast uniform flow, there is a periodic detachment of vortices from the upper and the lower segments, UR and RL, respectively (Fig. 2). A close analysis shows (19) that the periodic vortex shedding generates never escaping periodic paths in the wake, i.e., particle motions that return to their original positions after the full period of the flow, or an integer multiple of it. Naturally, these paths are unstable. Each such periodic orbit plays the role of a moving needle: they can be reached along some inflow curves (red lines in Fig. 2), particles can remain hung up on them, and droplets flow away from them along their outflow curves (blue lines in Fig. 2). A close analysis shows that there is an infinity of different periodic paths, all unstable arranged in a fractal set in the wake. Therefore their inflow and outflow curves are complicatedly winding in the wake and can even intersect each other at a given time, as indicated schematically in Fig. 2. Because the particle motion around the infinitely many periodic orbits is irregular, chaotic, the union of all the periodic orbits is called the chaotic set of the advection dynamics. The bundle of inflow and the outflow curves (called stable and unstable manifolds in the jargon of dynamical system theory) provides a fractal foliation of the fluid surface.

Figure 2.

The topology of inflow and outflow curves and their relation to a passively advected droplet. Schematic drawing of the inflow and outflow curves of a period-one orbit P at a given instant of time. They are very similar to the inflow and outflow curves of the full chaotic set. The outflow curve (blue line marked by outgoing arrows) is a complicated winding fractal curve extending downstream to infinity. The inflow curve of this orbit (red line entering P) foliates regions around the cylinder and upstream to it. The time evolution of a green droplet overlapping initially with the inflow curve of P is also indicated. Its shape is shown after integer multiples of the flow's period. Note the convergence toward the outflow curve.

The physical relevance and observability of the outflow curve is due to the fact that a droplet of particles initially overlapping with the inflow curve traces out the outflow curve as it is advected past the cylinder (19, 20; shown in green in Fig. 2). This implies that if the tracers are chemically or biologically active, the active process mainly takes place along the outflow curve because it is there where the particles spend a long time in the wake (Fig. 1). The fractal filaments on which reactions accumulate are in fact filaments of the outflow curve.

If the initial droplets of both species overlap with the inflow curve of the chaotic set, they are trapped in the wake, and accumulate along the filaments of the fractal outflow curve (Fig. 1). This leads to an enhancement of their activity, because the continuous stretching and folding action of the underlying flow provides them with increased access to the background A for which they compete. Consequently, in the steady state, filaments of B and C along the outflow curve are separated efficiently by narrow bands of material A (see Fig. 1b).

In analogy with chemical reactions, we find that species with low concentration replicate with an increased efficiency. Thus the rare species has an advantage over the common one. Spatial separation and increased replication activity of the rare species results in the coexistence of the competing species for a wide range of the parameter values.

The boundary layer surrounding the cylinder's surface also plays an important role. The species populating the boundary layer is in a favorable position, because it acts as a stable source for generating offsprings into the wake without being subject to mixing and competition. To underline this argument we placed a droplet C upstream close to the cylinder followed by a droplet B further upstream. We find that in spite of B being the stronger competitor, it is unable to outcompete C from the boundary layer. On the other hand, if the B droplet is placed closer to the cylinder than C, B populates the boundary layer acting as a strong B source in the wake. In spite of this favorable position, the weaker species C still survives in the wake, provided the initial droplet also intersects the inflow curve of the chaotic set (Fig. 1). The initial conditions thus determine which organisms occupy the boundary layer after a long time, but they do not change the fact that both organisms can survive. Different species can occupy different niches simply by appearing at different places in the flow. Niches of both species are narrow bands along the unstable curve. This underlines again that in open chaotic flow the traditional picture of well-mixed systems is broken: the weaker competitor can even become dominant over the stronger one due to the advection dynamics.

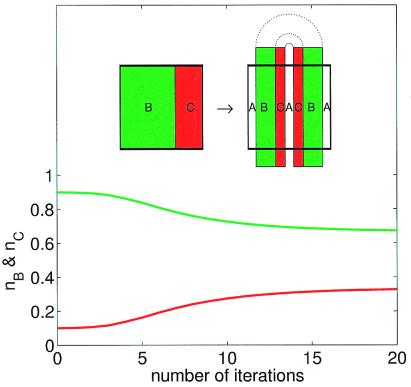
To check the generic nature of these results, similar numerical experiments were performed with three different competitors, competing for the same unique limiting resource A. We found that in a wide range of the reproduction abilities of the competitors the coexistence was robust, even if randomly mixed species were starting from the same initial droplet in front of the cylinder. It was also checked whether coexistence is possible without the effect of the boundary layer by carrying out further simulations with the so-called “baker map.” The baker map is the paradigm of mixing exemplified by its successive stretching and folding actions (6, 32; see the Inset of Fig. 3). If green (B) and red (C) regions are covered by nonreproducing individuals, by successive actions of the baker map the density of species decays in the unit square with equal rates, and the individuals staying forever in the unit square cover a fractal set (like in the wake). If, however, the reproducing B and C species are allowed to occupy neighboring regions covered by A within certain different distances, then they compete for this only limiting resource. The time evolution of the percentage of species B and C is shown for such a case in Fig. 3. These simulations were repeated for various parameter regimes and initial conditions and showed a robust coexistence of the competitors. The boundary layer is thus not necessary for coexistence, but its presence certainly enhances the effect.

Figure 3.

Time evolution of the competitor densities in a baker map mixing model. The percentage n_B (green line) and n_C (red line) of B and C, respectively vs. the number of iterations of the baker map on the unit square. Species B and C occupy neighboring regions of A within a distance σ_B = 2σ_C = 1/500, and have mortality rates of δ_B = δ_C = 1/5. In spite of C being outnumbered 9:1 at the beginning of the simulation, C can coexist with B in the long time limit. (Inset) The stretching and folding action of one step of the baker map is illustrated. First, the unit square (shown in bold lines) is compressed by a factor a (=0.4) in horizontal direction and stretched by 1/a in the vertical direction while keeping the area constant. Next this stretched rectangle is folded in two over the unit square. This process is then iterated several times. Note that the “flow” described by the baker map is open because at each iteration of the map a portion (1 − 2a) of particles leaves the unit square and is being replaced by regions of the background material A.

The inclusion of a molecular (or small-scale turbulent) diffusion does not modify the qualitative picture. Due to the presence of a background flow and a fixed region of observation, diffusion does not lead to an unlimited broadening because it is balanced by the shrinking of the filaments due to the escape from this region. As a result diffusion leads only to a renormalization of the reaction front velocity v_r (33).

We claim that the coexistence of competing species is a generic feature expected to be found in open flows exhibiting chaotic advection. We emphasize that the qualitative features of the fractal patterns (and of the boundary layer), which are essential for our study, are robust and can be found in any open time-dependent flow. The shape of the obstacle and the time periodicity of the flow are considered only for convenience and the ease of presentation.

Although stratification of aquatic systems often ensures the planar nature of the flow, we briefly comment on possible effects of the third dimension. It has been shown that in the advection by stationary three-dimensional flows the third dimension might play an analogous role to that of the time in time-dependent two-dimensional flows (34). The concept of inflow and outflow curves therefore should be replaced by that of inflow and outflow surfaces. In flows with chaotic advection these are a bundle of highly convoluted, nested sheets. A periodic time dependence of the three-dimensional flows makes these sheets to oscillate. The coexistence of competing advected species is expected along these outflow surfaces. Any planar intersection of them exhibits the same filamental structure as in the two-dimensional models discussed in this paper.

Typical fluid motions are rarely time-periodic. In a broad class of flows, however, when the flow field is chaotic in time but exhibits a kind of structural stability (like in the example of randomly driven or chaotically moving vortices; refs. 35 and 36) the topology of the advection patterns remains unchanged. This means that although the inflow and outflow surfaces move in a nonperiodic, chaotic fashion, their fractal dimension and the escape rate of the open flow remains well defined (35).

Although we restricted our discussion to two-dimensional time-periodic flows, based on these observations we expect to see coexistence in similar competitive models in three-dimensional open chaotic flows and possibly in two-dimensional turbulence (28) as well.

Finally, we remark that in the absence of enzymes, replicating macromolecules at high concentrations are bound together effectively with hydrogen bonds (37, 38). This self-inhibition can lead to the so-called parabolic growth, implying that competitive replicators coexist even in a well-stirred environment (39). The concentrations required are, however, unrealistically high. The pure hydrodynamic effect we present in this paper shows that the coexistence is a consequence of the imperfect mixing dynamics of the flow, and the concentrations of replicators accumulated along the outflow curve need not reach irrealistically high values as needed for parabolic growth.

Open chaotic flows have the role of maintaining diversity in competing advected populations (e.g. phytoplankton), and also give a natural solution for the problem of information integration in early evolutionary units. The issues presented in this paper are, however, of larger generality. They show that novel effects and phenomena can arise if a population dynamics is subjected to an underlying chaotic spatial mixing.