Predicting the local dynamics of epizootic rabies among raccoons in the United States

Abstract

Mathematical models have been developed to explore the population dynamics of viral diseases among wildlife. However, assessing the predictions stemming from these models with wildlife databases adequate in size and temporal duration is uncommon. An epizootic of raccoon rabies that began in the mid-Atlantic region of the United States in the late 1970s has developed into one of the largest and most extensive in the history of wildlife rabies. We analyzed the dynamics of local epizootics at the county level by examining a database spanning more than 20 years and including 35,387 rabid raccoons. The size, number, and periodicity of rabies epizootics among raccoons were compared with predictions derived from a susceptible, exposed, infectious, and recovered model of raccoon rabies [Coyne, J., Smith, G. & McAllister, F. E. (1989) Am. J. Vet. Res. 50, 2148–2154]. After our methods for defining epizootics were applied to solutions of the model, the time series revealed recurrent epizootics in some counties, with a median first epizootic period of 48 months. Successive epizootics declined in size and the epizootic period progressively decreased. Our reanalysis of the model predicted the initial-epizootic period of 4–5 years, with a progressive dampening of epizootic size and progressive decrease in epizootic period. The best quantitative agreement between data and model assumed low levels of immunity (1–5%) within raccoon populations, suggesting that raccoons develop little or no rabies immune class. These results encourage the use of data obtained through wildlife surveillance in assessing and refining epidemic models for wildlife diseases.

Simple epidemic models have been applied to infectious diseases of humans (1) and wildlife (2). A particularly useful system for modeling has been the epizootic of rabies among red foxes in Europe that began in Poland in 1939 (3). Epidemic models of the spatial spread and the population dynamics of rabies in red foxes have yielded tools to predict propagation routes and to identify potential measures for preventing the spread of rabies epizootics in this species (3–5).

Although the local dynamics of rabies within a host population is the critical determinant of spatial and temporal patterns, rarely have large databases, collected over years, been available to monitor and assess local trends and local transmission. We are unaware of any detailed studies assessing the temporal dynamics of rabies with the aim of characterizing epizootics within the context of existing epidemic theory.

Epizootic rabies among raccoons (Procyon lotor) in the United States was first identified in Florida in the 1940s (6), and the area affected gradually expanded into other southeastern states. In the late 1970s, a second focus of rabies among raccoons emerged on the West Virginia/Virginia border (Fig. 1a). Epizootiologic and virologic investigations indicated this new focus resulted from the translocation of raccoons incubating rabies from the southeastern United States (7, 8). The epizootic front of the mid-Atlantic outbreak has progressed in a primarily northeasterly direction at a rate of 30–47 km/year (9, 10). The northern extension of this epizootic reached Canada in 1999 (11), whereas to the south, the once separate epizootics of raccoon rabies in the mid-Atlantic and southeastern states converged in North Carolina in 1994 (12).

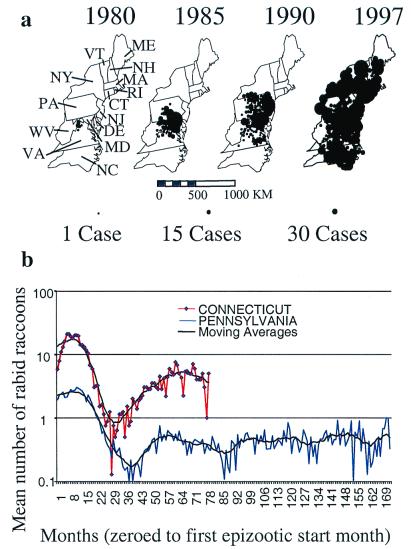
Figure 1.

The spread of epizootic rabies among raccoons in the mid-Atlantic and northeastern United States from a focus on the Virginia/West Virginia border is illustrated for selected years from 1980 and 1997. (a) The size of the dot is proportional to the annual totals for reported rabid raccoons centered by individual counties within a state. Data from the majority of counties shown were used in our analyses. (b) Examples of the time series of mean monthly reports of rabid raccoons from counties within two of the 11 states used in the analyses. Pennsylvania has experienced enzootic rabies since March 1982; Connecticut since April 1991. Black lines represent 11-month moving averages of the monthly counts of rabid raccoons to highlight low-frequency variation in reports.

The epizootic of rabies involving raccoons that developed in the mid-Atlantic region is one of the largest documented outbreaks in the history of wildlife rabies (Fig. 1a). More than 50,000 cases of rabies among raccoons have been reported to the Centers for Disease Control and Prevention since 1980, with most occurring in mid-Atlantic and northeastern states. The size and time span covered by this database make it an unique resource for examining the local dynamics of rabies epizootics. We examined the temporal structure of rabies epizootics occurring within counties of mid-Atlantic and northeastern states since the mid-1970s. We compared our results with the predictions from a model of raccoon rabies that determines changes in the densities of susceptible, exposed, infectious, and recovered (SEIR) individuals (13). We analyze the numerical solutions of the model in the same way as the data, so as to ensure a robust test of the predictions. We then varied a critical and controversial component of the SEIR model, the fraction of raccoons surviving rabies virus challenge to become immune to future exposures, to assess changes in the concordance of our empirical findings with theoretically derived values. The sensitivity of our conclusions with respect to a second less-known parameter—the transmission rate—was assessed through repeated analyses of the model.

Methods

Surveillance Data.

Rabies in domestic and wild animals has been a nationally notifiable disease, reportable to the Centers for Disease Control and Prevention, since 1961. All states, the District of Columbia, and Puerto Rico report data monthly on the number of animal rabies cases, by county of origin and type of animal. Annual rabies figures are compiled at the Centers for Disease Control and Prevention and verified with individual states. Although the criteria for submitting animals suspected as being rabid for testing varies somewhat by state, testing procedures to detect rabies virus antigen use a standard methodology. Surveillance efforts and testing methods have remained largely unchanged in the United States over the period of this study. The data were collected at the unit of the individual county and were not pooled. The analyses used metrics derived separately from each county's time series of rabies reports. These methods would minimize the impact of any variation in surveillance across counties and states.

Identifying Epizootic Structure.

To match predictions from the SEIR model to the empirical structure within the raccoon rabies data, we established epizootic algorithm 1 (EA1) for defining when epizootics occurred and for measuring their duration and the duration of interepizootic intervals. The sum of these two values defined the epizootic period. First, for each county the median number of raccoons reported rabid per month to the Centers for Disease Control and Prevention was determined over the entire time interval rabies was present among raccoons (the duration of enzootic rabies). The duration of enzootic rabies was defined from the month of the first reported case of raccoon rabies in the county through December 31, 1997, or December 31, 1998 (Maryland only). Second, an epizootic was defined as beginning when the monthly number of rabid raccoons reported was greater than the county median for 2 consecutive months and ended when this number was less than or equal to the county median for 2 consecutive months. In addition, an epizootic had to have a minimum duration of 5 months to reduce the effects of short-term fluctuations in reporting.

Successive epizootics within a county were numbered sequentially (n = 1, 2, …). The period of an epizootic was defined as the time interval (months) from the start month of one epizootic (n) to the start month of the next epizootic (n + 1). The time elapsed between the last month of an epizootic and the first month of the next epizootic was defined as the interepizootic interval. When epizootic or interepizootic intervals were right censored, data on those parameters were excluded from analyses. Right censoring occurred when an epizootic or interepizootic interval was ongoing at the termination date of the study. Structural analysis of the data using this algorithm then was compared with the structure predicted from various solutions of the mathematical model proposed by Coyne et al. (13).

A comparison of the trend of the sizes of sequential epizootics was performed by calculating ratios of the cumulative number of rabid raccoons reported in epizootic (n + 1) to the cumulative number of rabid raccoons reported in epizootic (n). Successive paired-ratio values then were compared by individual county (Mann–Whitney u test).

Model Predictions.

The EA1 generates conclusions from data independent of any assumptions of population dynamics. Alternatively, an a priori epizootic model (EM) can be constructed on the basis of population dynamics that can then predict temporal patterns in case occurrence. Coyne et al. (13) constructed such a model and studied the rate of change in susceptible raccoon hosts (X), exposed hosts (i.e., infected but not infectious; H₁), hosts exposed that eventually develop immunity (H₂), rabid hosts (Y), and hosts that are immune (I), using the following set of coupled differential equations:

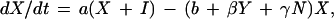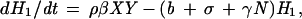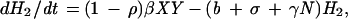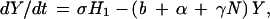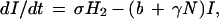where N is the total raccoon population size (X + H₁ + H₂ + Y + I). The SEIR model was first solved by Coyne et al. using the following parameters: birth rate (a = 1.34/year), death rate (b = 0.836/year), density-dependence in mortality (γ = 0.0397 km²/yr), incubation period (1/σ = 0.13 year), rabies-induced mortality (α = 66.36/year), transmission rate (β = 33.25/year), and proportion of raccoons that develop natural immunity ([1 − ρ] = 0.20).

Qualitative predictions of the EM are as follows: (i) the first-epizootic period should be approximately 48 months; (ii) subsequent epizootics should occur with diminishing periods (i.e., with increasing frequency), and (iii) epizootics should occur with diminishing amplitude.

The quantitative predictions of the EM model are, however, sensitive to specific parameter values, most notably the proportion of raccoons surviving rabies virus challenge to enter the immune class (1 − ρ). The rate of decline in frequency of oscillations is a function of (1 − ρ), and as this value increases (i.e., higher levels of immunity) epizootics dampen more rapidly. We therefore varied (1 − ρ) in the EM from 1% to 20% to generate a range of outcomes. These time series subsequently were analyzed by using the same epizootic algorithms as were applied to the county case-report data.

Although (1 − ρ) was the primary model parameter of interest in our analyses based on its theoretical significance in influencing epizootic behavior (13), the transmission rate, β, is poorly known and could potentially influence the temporal structure of epizootics as well. For this reason, the time series generated with varying values of (1 − ρ) were repeated with β set at the original value (13), and at values 25% above (41.38/year) and 25% below (25.12/year) this value. These analyses were performed to highlight how robust our results were to variations in the transmission rate.

The EM was run over the course of five complete epizootics. We chose five epizootics because this was the greatest number of epizootics reported by at least 10 counties. Only six counties experienced six epizootics and only two had seven.

Sensitivity Analysis.

Although no attempt was made at an exhaustive sensitivity analysis of EA1 described above, county data from three states (Maryland, New York, and West Virginia) that contributed >40% of the first epizootics were reanalyzed by using a modified alternative epizootic algorithm (EA2). Under the modified conditions, epizootics began when the monthly number of rabid raccoons reported was greater than the county median for 3 consecutive months and ended when that number was less than or equal to the median for 3 consecutive months. Additionally, the duration of an epizootic had to be ≥7 months. Agreement between patterns generated by EA1 and EA2 was assessed by computing the sensitivity and specificity of EA2's classification of months as epizootic or nonepizootic in each county's time series of rabies reports, as compared with their classification by the EA1 standard. Sensitivity was defined as the number of months classified as epizootic by both EA1 and EA2 divided by the number months classified as epizootic by EA1. Specificity was defined as the number of months classified as nonepizootic by both EA1 and EA2 divided by the number of months classified as nonepizootic by EA1.

In addition, kappa statistics (14), which measure the percent agreement between two outcomes over that expected by chance alone, were determined. Kappa statistic outcomes of <0.4, 0.4–0.75, and >0.75 were considered poor, good, and excellent, respectively (14).

Results

A total of 35,387 rabid raccoons were reported during the study from 390 counties from 11 mid-Atlantic and northeastern states. However, epizootics of raccoon rabies were defined by EA1 for only 251 (64.4%) of these counties that experienced at least one case of raccoon rabies (Table 1). Most counties that had detectable epizootics (55%) had only a single epizootic. This finding was influenced by the moderate rate of spread of rabies (Fig. 1a), so that many counties at the northern and southern extremes of the study area first experienced raccoon rabies in the 1990s. However, counties involved earlier in the epizootic frequently experienced multiple outbreaks. In particular, seven epizootics were identified from two Maryland counties located close to the site of the initial introduction of raccoon rabies.

Table 1.

Characteristics of the counties within each state experiencing epizootics of rabies among raccoons

State	No. counties with ≥1 epizootics (% of total counties in state)	Maximum number of epizootics	Median duration (mo) of enzootic rabies within counties	No. rabid raccoons in first epizootic by county	First epizootic
					Duration (mo)	Period (mo) (N; min-max)*
CT	8 (100)	3	71 (69–80)	244 (170–494)	21 (17–28)	45 (7; 39–58)
DE	3 (100)	2	89 (74–123)	159 (33–202)	22 (10–24)	50 (3; 29–51)
MA	10 (71)	2	70 (66–71)	135 (37–300)	20 (13–25)	22 (3: 16–46)
MD	24 (100)	7	154 (57–207)	104 (8–572)	22 (6–33)	47 (21; 8–158)
NC	28 (28)	3	34 (16–77)	18 (5–91)	8 (5–20)	15 (4; 7–48)
NJ	20 (95)	3	82 (55–98)	91 (18–230)	17 (8–31)	49 (9; 10–82)
NY	51 (82)	3	65 (31–91)	76 (7–785)	17 (5–33)	50 (23; 7–75)
PA	45 (67)	6	133 (19–189)	18 (4–200)	11 (5–32)	49 (28; 7–65)
RI	5 (100)	2	45 (43–47)	55 (9–123)	16 (6–17)	10 (1; 10)
VA	47 (41)	6	129 (21–233)	8 (4–622)	7 (5–27)	39 (19; 7–149)
WV	10 (18)	5	186 (160–245)	9 (4–44)	7 (5–12)	37 (6; 10–92)
Total or median	251 (51)	1 (1–7)	82 (16–245)	57 (4–785)	14 (5–33)	48 (124; 7–158)

Values for the duration of the first epizootic, the first epizootic period, and the inter-epizootic interval are shown (see Methods). All values represent the median values (minimum-maximum) for individual counties except where specified differently. 

^*The number of counties is less than total due to censoring of data (i.e., not all had defined onset of second epizootic). 

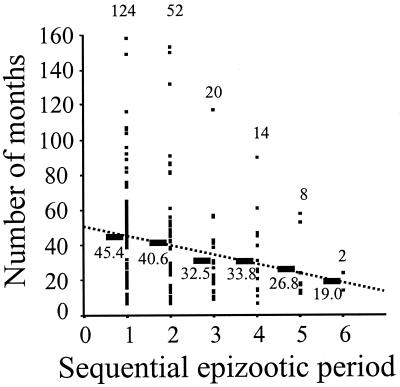
Marked periodicity in the reporting of rabid raccoons was apparent in many of the time series of county surveillance data (Fig. 1b). The median value for the first epizootic period was 48 months (range 7 to 158) (Table 1), and there was a dominant mode between 41 and 60 months [56 (45%) of 124 county values fell within this range]. Using linear regression, we found that the epizootic periods decreased by approximately 5 months between each successive epizootics (Fig. 2).

Figure 2.

Successive epizootic periods, from the start of epizootic (n) to the start of epizootic (n + 1), show a significant decline in length (α = 50.1 months, β = −4.82 months, r² = 0.03, P = 0.006). Mean values are indicated next to the horizontal bars, and sample sizes are indicated above each group.

Application of EA1 to various numerical solutions of the Coyne et al. model (13) produced a range of outcomes that bracketed the median values obtained from our empirical analyses (Table 2). Over the range of time series generated by the EM, the duration of the first epizootic was predicted to be between 7 and 15 months, and the first epizootic period ranged between 26 and 100 months. Our observed median values of 14 for the duration of the first epizootic and 48 months for the first epizootic period derived by applying EA1 to data, fit the predicted time series corresponding to those with low levels of immunity (1–5%). Epizootics subsequent to the first also were predicted to have progressively shorter epizootic periods, reduced to about 65–80% of the first epizootic period by the fourth epizootic (Table 2). Varying β at levels 25% above or below the initial value did not dramatically change the results of our analyses; the best fit to the observed median values still occurred at levels of immunity well below the original 20% estimate (Table 2).

Table 2.

Predictions based on the Coyne et al. (13) model of the time course of epizootic rabies

% immune [(1 − ρ) × 100]*	β		0.75 β		1.25 β
	Duration (mo)†	Period (mo)	Duration (mo)	Period (mo)	Duration (mo)	Period (mo)
1	16	100	15	107	22	97
	(24, 28, 31)	(77, 71, 66)	(21, 24, 28)	(87, 74, 66)	(34, 39, 42)	(87, 83, 80)
2	10	81	11	86	10	74
	(14, 16, 17)	(64, 56, 50)	(14, 16, 18)	(66, 56, 51)	(13, 15, 17)	(60, 52, 47)
5	9	51	10	58	8	45
	(12, 13, 14)	(50, 37, 36)	(13, 14, 16)	(45, 40, 38)	(11, 12, 13)	(36, 33, 32)
10	8	36	8	41	8	31
	(10, 10, 11)	(29, 29, 29)	(11, 13, 14)	(33, 32, 32)	(10, 10, 8)	(27, 27)‡
20	7	26	8	31	6	23
	(7, ‡)	(‡)	(9, ‡)	(‡)	(6, ‡)	(‡)

In the time series shown the proportion of raccoons that developed immunity after exposure to rabies virus was varied from 1% to 20%, and the transmission rate, β, was varied ±25% of the value used in the original report (13). 

^*Percentage of raccoons recovering to become immune after exposure to rabies virus. 

^†Brackets give values for the successive 2nd–4th epizootics. 

^‡No additional or discernible epizootic(s) defined. 

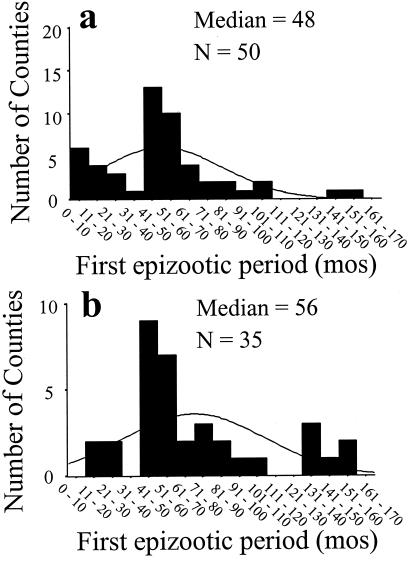
The distinctive first epizootic period of approximately 48 months was apparent after analysis of county data with the modified EA2 (Fig. 3 a and b). The conclusions of our analyses appeared robust to small modifications in the rabies epizootic algorithm. The sensitivity and specificity of EA2 for classifying individual months as epizootic or nonepizootic, according to the EA1 standard, indicated a high degree of concordance in outcomes. The mean sensitivity was 90.3% for 51 counties in New York, 84.7% for 24 counties in Maryland, and 70.0% for seven counties in West Virginia. The mean specificity was 94.1%, 94.0%, and 95.6%, respectively, for the same counties. The mean kappa statistic indicated excellent agreement between algorithm outcomes for counties in New York (0.83) and Maryland (0.79), and good agreement for counties in West Virginia (0.62).

Figure 3.

The distributions of the first epizootic periods, as defined by two different algorithms (see Methods), for counties within Maryland, New York, and West Virginia. (a) The median value of 48 months, with a dominant mode between 41 and 60 months, was identical to the distribution when all 124 counties were considered (Table 1). (b) The distribution of epizootic period values derived from the modified algorithm was statistically indistinguishable from that derived with the original algorithm in a (Kolmogorov-Smirnov two-sample test, z = 1.14, P = 0.15). A significant decrease in epizootic period with successive epizootics was still apparent (α = 97.1 months, β = −23.0 months, r² = 0.21, P = 0.003).

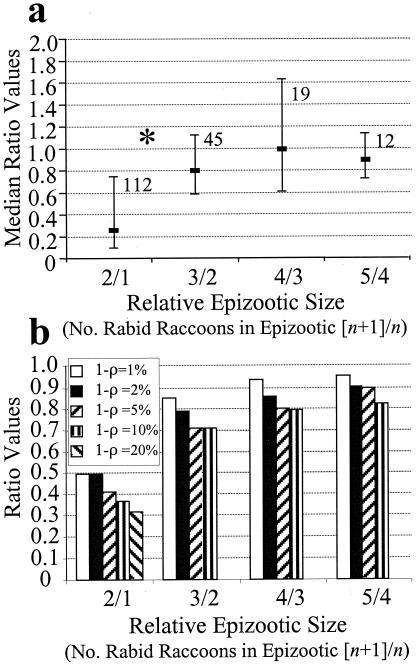
The number of rabid raccoons reported in sequential epizootics within individual counties tended to decline, as demonstrated by the plots of ratios of summed values of reported rabid raccoons in successive epizootics (Fig. 4a). Numbers of rabid raccoons occurring in the first epizootic experienced by a county were substantially greater (mean = 80.5) than the average for all subsequent epizootics (mean = 17.3). As a consequence, the ratio values for epizootic two to epizootic one (2/1 in Fig. 4a) were significantly smaller than values for epizootic three to epizootic two (3/2). No other significant differences were detected between ratio values.

Figure 4.

The numerical relationships of relative sizes of successive epizootics are shown for surveillance data and solutions to the EM with varying (1 − ρ) (note differences in y axis scale). The number of rabid raccoons reported in the first epizootic of rabies among raccoons was quantitatively different from all subsequent epizootics and resulted in significantly lower ratio values. (a) Medians of individual county ratio values (horizontal bar), interquartile range (vertical bar), and numbers of paired-county comparisons are indicated. * indicates a significant difference (Mann–Whitney u test, Z = −4.86, P < 0.001) between the ratios of the number of rabid raccoons occurring in epizootic 2 to the number of rabid raccoons occurring in epizootic 1 (2/1) as compared with 3/2. All median values for ratios were ≤1. (b) Ratio values generated by solving the Coyne et al. (13) model with varying rates of (1 − ρ) were in good agreement with the surveillance data. Only ratios from five epizootics are shown because very few counties experienced more epizootics.

Varying values of (1 − ρ) produced ratios values for the numerically solved EM that were consistently below 1.0, with values from epizootics 2/1 slightly greater (range 0.31 to 0.50) than the median of 0.26 obtained from surveillance data (Fig. 4b). Ratio values from the EM for epizootics 3/2 through 5/4 ranged between 0.71 and 0.94, only slightly lower than medians obtained from the surveillance data (range, 0.80 to 1.00). Ratio values for epizootics 6/5 and 7/6 were not generated as the number of occurrences were so few (six counties with six epizootics and two with seven epizootics) in the surveillance database.

Discussion

Our results show distinctive temporal patterning to epizootics of rabies occurring among raccoons at the level of the county. Although Coyne et al. (13) were unable to detect periodicity in epizootics of rabies among raccoons with the data available in 1989, we found a distinctive period of 48 months between the beginning of first and second epizootics of rabies. Over 45% of the values for first epizootic periods from the 124 counties experiencing at least two epizootics were between 41 and 60 months. In addition, the systematic decrease in length of epizootic period and decline in epizootic size were consistent with predictions based on numerical solutions to the SEIR model in both the original report (13) and in our reanalyses.

Similar epidemic models have been applied to the epizootic of rabies among red foxes in Europe (3–5). The pattern of periodic epizootics, smaller epizootics subsequent to the first, and incident rabies gradually settling to a steady enzootic state fits field observations from France (3). However, fluctuations in rabies incidence among red foxes are influenced by the density of the population in a given locale, which varies because of the heterogeneous nature of the environment (3). These environmental effects are relevant to further attempts to examine local patterns of rabies incidence among raccoons in the United States.

Comparisons of model-derived values to our empirical results offered some independent criteria with which to assess the appropriateness of our epizootic algorithm and permitted some informed speculation on assumptions used to fit parameters in the original model. The median values derived from analyses of the surveillance data fell within the range of values generated from the model using varied estimates of (1 − ρ), and the overall agreement in theory and observation appeared excellent. Although not the main focus of this report, results obtained by varying β indicated that the EM predictions were robust to ±25% variation in the transmission rate. However, the model-generated values that best fit the observed values occurred when the immune compartment of raccoons surviving an epizootic of rabies was substantially smaller than 20%. We hypothesize that future evaluations of raccoon populations assessed after epizootic exposure to rabies virus will find little evidence of an immune class.

The epidemiologic significance of immunity to rabies in natural populations of raccoons has never been established. Antibody reactive to rabies virus can be demonstrated in wild populations of raccoons (15–17), and raccoons can survive a rabies virus challenge and subsequently develop antibody (18). However, some of these data have been derived from situations in which raccoons were naturally infected or challenged with rabies virus variants adapted to other terrestrial reservoir species, such as skunks (17, 18), rather than infected with the rabies virus variant involved in the mid-Atlantic epizootic. The mid-Atlantic rabies virus variant is unique and highly adapted to raccoons (19, 20). In sites where the raccoon-associated virus is enzootic, serum neutralizing antibody prevalences of 2–20% have been reported (6, 15). However, the demonstration of nonspecific virus-neutralizing factors in raccoon sera has raised doubts about the interpretation of many early reports (17).

In natural systems, raccoon populations appear to have high mortality and show little evidence of an immune class after a rabies epizootic. In a systematically monitored, radio-tagged population of raccoons in Appalachian Virginia, no significant titers of rabies antibody were detected in raccoons during a 20-month period after the initial rabies epizootic (21). During this rabies epizootic, the first in this location involving the raccoon-adapted variant of rabies virus, the survival rate for raccoons was 40% of the subsequent rate and the number of raccoons alive during the epizootic was half of that 3 years later (21). Other data also indicate that raccoon populations decline substantially after rabies epizootics, suggesting high mortality (22, 23). Given the uncertainty surrounding the interpretation of antirabies virus antibody prevalences reported in free-ranging raccoons, it is likely that if immunity occurs, it is at levels well below estimates of 20%. Our analyses suggest levels of immunity of 1–5% are more realistic.

Despite limitations inherent in using surveillance data gathered on wildlife diseases (24), our analyses produced patterns and trends in the time structure of epizootics that were consistent across a wide region of the United States and in accord with a priori predictions. Analyses with modified algorithm parameters resulted in reproducible patterns in important outcomes. Moreover, the concordance between empirical data and data generated by a mathematical model was further indication that our analyses captured important elements in the time course of epizootic rabies. The excellent agreement between SEIR model predictions and data are a confirmation of theoretical epidemiologic applications and holds promise for the use of model-guided intervention strategies to help halt the dramatic expansion of rabies into raccoon populations in the western United States and Canada.

Abbreviations

SEIR

susceptible, exposed, infectious, and recovered

EA1

epizootic algorithm 1

EA2

epizootic algorithm 2

EM

epizootic model